Evaluation of a Smectite Adsorption-Based Electrostatic System to Decontaminate F− Rich Thermal Waters
Abstract
:1. Introduction
2. Materials and Methods
2.1. System Configuration
2.2. Mathematical Modeling and Equations
2.3. Simulation Overview
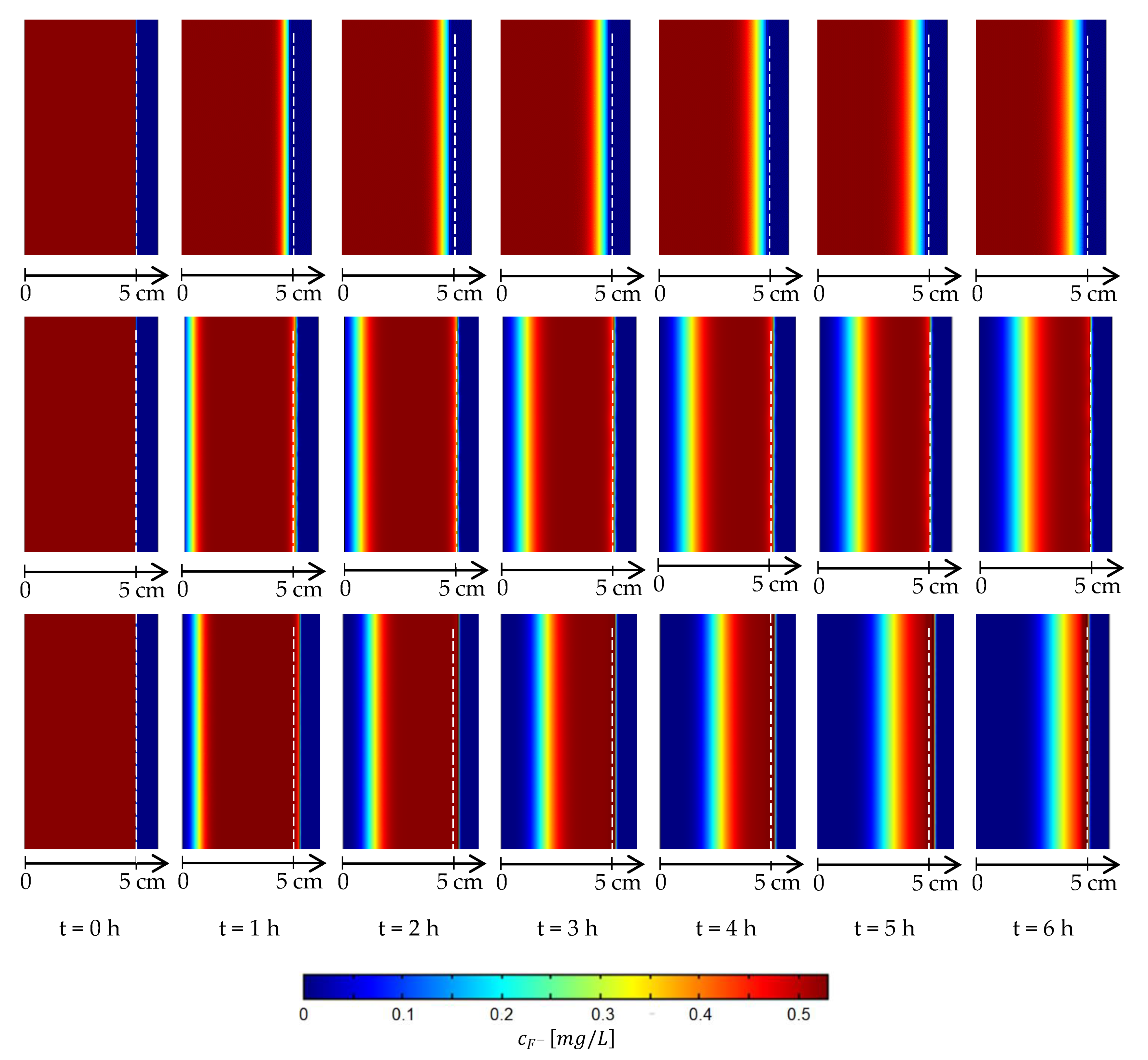
3. Results
4. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization 1 in 3 People Globally Do Not Have Access to Safe Drinking Water—UNICEF, WHO. Available online: https://www.who.int/news/item/18-06-2019-1-in-3-people-globally-do-not-have-access-to-safe-drinking-water-unicef-who (accessed on 2 August 2021).
- UNICEF; WHO. The Measurement and Monitoring of Water Supply, Sanitation and Hygiene (WASH) Affordability: A Missing Element of Monitoring of Sustainable Development Goal (SDG) Targets 6.1 and 6.2; WHO: Geneva, Switzerland, 2021; pp. 1–121. [Google Scholar]
- Jagtap, S.; Yenkie, M.K.; Labhsetwar, N.; Rayalu, S. Fluoride in Drinking Water and Defluoridation of Water. Chem. Rev. 2012, 112, 2454–2466. [Google Scholar] [CrossRef] [PubMed]
- Kloos, H.; Tekle Haimanot, R. Distribution of Fluoride and Fluorosis in Ethiopia and Prospects for Control. Trop. Med. Int. Health 1999, 4, 355–364. [Google Scholar] [CrossRef] [Green Version]
- Abiye, T. Groundwater dynamics in the East African rift system. In Sustainable Groundwater Resources in Africa; CRC Press: Boca Raton, FL, USA, 2009; pp. 93–106. ISBN 0203859456. [Google Scholar]
- Rango, T.; Bianchini, G.; Beccaluva, L.; Tassinari, R. Geochemistry and Water Quality Assessment of Central Main Ethiopian Rift Natural Waters with Emphasis on Source and Occurrence of Fluoride and Arsenic. J. Afr. Earth Sci. 2010, 57, 479–491. [Google Scholar] [CrossRef]
- Ayenew, T. The Distribution and Hydrogeological Controls of Fluoride in the Groundwater of Central Ethiopian Rift and Adjacent Highlands. Environ. Geol. 2008, 54, 1313–1324. [Google Scholar] [CrossRef]
- Tekle-Haimanot, R.; Melaku, Z.; Kloos, H.; Reimann, C.; Fantaye, W.; Zerihun, L.; Bjorvatn, K. The Geographic Distribution of Fluoride in Surface and Groundwater in Ethiopia with an Emphasis on the Rift Valley. Sci. Total Environ. 2006, 367, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Errico, M.; Desogus, F.; Mascia, M.; Tola, G.; Dendena, L. Soil Adsorption Defluoridation of Drinking Water for an Ethiopian Rural Community. Chem. Pap. 2006, 60, 460–465. [Google Scholar] [CrossRef]
- Schulze, D.G. Clay Minerals. In Encyclopedia of Soils in the Environment; Elsevier: Amsterdam, The Netherlands, 2005; pp. 246–254. [Google Scholar]
- van Olphen, H. A Tentative Method for the Determination of the Base Exchange Capacity of Small Samples of Clay Minerals. Clay Miner. 1951, 1, 169–170. [Google Scholar] [CrossRef]
- Van Olphen, H. Rheological Phenomena of Clay Sols in Connection with the Charge Distribution on the Micelles. Discuss. Faraday Soc. 1951, 11, 82–84. [Google Scholar] [CrossRef]
- Theng, B.K.G.; Russell, M.; Churchman, G.J.; Parfitt, R.L. Surface Properties of Allophane, Halloysite, and Imogolite. Clays Clay Miner. 1982, 30, 143–149. [Google Scholar] [CrossRef]
- Dohrmann, R.; Kaufhold, S.; Lundqvist, B. Handbook of Clay Science; Elsevier: Amsterdam, The Netherlands, 2013; Volume 5, ISBN 9780080993645. [Google Scholar]
- Huang, H.; Liu, J.; Zhang, P.; Zhang, D.; Gao, F. Investigation on the Simultaneous Removal of Fluoride, Ammonia Nitrogen and Phosphate from Semiconductor Wastewater Using Chemical Precipitation. Chem. Eng. J. 2017, 307, 696–706. [Google Scholar] [CrossRef]
- Siaurusevičiūtė, I.; Albrektienė, R. Removal of Fluorides from Aqueous Solutions Using Exhausted Coffee Grounds and Iron Sludge. Water (Switz.) 2021, 13, 1512. [Google Scholar] [CrossRef]
- Bouhadjar, S.I.; Kopp, H.; Britsch, P.; Deowan, S.A.; Hoinkis, J.; Bundschuh, J. Solar Powered Nanofiltration for Drinking Water Production from Fluoride-Containing Groundwater—A Pilot Study towards Developing a Sustainable and Low-Cost Treatment Plant. J. Environ. Manag. 2019, 231, 1263–1269. [Google Scholar] [CrossRef]
- Owusu-Agyeman, I.; Reinwald, M.; Jeihanipour, A.; Schäfer, A.I. Removal of Fluoride and Natural Organic Matter Removal from Natural Tropical Brackish Waters by Nanofiltration/Reverse Osmosis with Varying Water Chemistry. Chemosphere 2019, 217, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Zheng, Y.; Ding, J.; Gao, C.; van der Bruggen, B.; Shen, J. Fluoride Removal from Water by Membrane Capacitive Deionization with a Monovalent Anion Selective Membrane. Ind. Eng. Chem. Res. 2018, 57, 7048–7053. [Google Scholar] [CrossRef]
- Aliaskari, M.; Schäfer, A.I. Nitrate, Arsenic and Fluoride Removal by Electrodialysis from Brackish Groundwater. Water Res. 2021, 190, 116683. [Google Scholar] [CrossRef] [PubMed]
- Jiang, K.; Zhou, K.G. Recovery and Removal of Fluoride from Fluorine Industrial Wastewater by Crystallization Process: A Pilot Study. Clean Technol. Environ. Policy 2017, 19, 2335–2340. [Google Scholar] [CrossRef]
- Pillai, P.; Dharaskar, S.; Pandian, S.; Panchal, H. Overview of Fluoride Removal from Water Using Separation Techniques. Environ. Technol. Innov. 2021, 21, 101246. [Google Scholar] [CrossRef]
- Guan, C.; Lv, X.; Han, Z.; Chen, C.; Xu, Z.; Liu, Q. The Adsorption Enhancement of Graphene for Fluorine and Chlorine from Water. Appl. Surf. Sci. 2020, 516, 146157. [Google Scholar] [CrossRef]
- Ruan, Z.; Tian, Y.; Ruan, J.; Cui, G.; Iqbal, K.; Iqbal, A.; Ye, H.; Yang, Z.; Yan, S. Synthesis of Hydroxyapatite/Multi-Walled Carbon Nanotubes for the Removal of Fluoride Ions from Solution. Appl. Surf. Sci. 2017, 412, 578–590. [Google Scholar] [CrossRef]
- He, Y.; Zhang, L.; An, X.; Wan, G.; Zhu, W.; Luo, Y. Enhanced Fluoride Removal from Water by Rare Earth (La and Ce) Modified Alumina: Adsorption Isotherms, Kinetics, Thermodynamics and Mechanism. Sci. Total Environ. 2019, 688, 184–198. [Google Scholar] [CrossRef]
- Liu, J.; Yue, X.; Lu, X.; Guo, Y. Uptake Fluoride from Water by Starch Stabilized Layered Double Hydroxides. Water 2018, 10, 745. [Google Scholar] [CrossRef] [Green Version]
- Borgohain, X.; Boruah, A.; Sarma, G.K.; Rashid, M.H. Rapid and Extremely High Adsorption Performance of Porous MgO Nanostructures for Fluoride Removal from Water. J. Mol. Liq. 2020, 305, 112799. [Google Scholar] [CrossRef]
- Gao, Y.; Li, M.; Ru, Y.; Fu, J. Fluoride Removal from Water by Using Micron Zirconia/Zeolite Molecular Sieve: Characterization and Mechanism. Groundw. Sustain. Dev. 2021, 13, 100567. [Google Scholar] [CrossRef]
- Ghomashi, P.; Charkhi, A.; Kazemeini, M.; Yousefi, T. Removal of Fluoride from Wastewater by Natural and Modified Nano Clinoptilolite Zeolite. J. Water Environ. Nanotechnol. 2020, 5, 270–282. [Google Scholar] [CrossRef]
- Vences-Alvarez, E.; Flores-Arciniega, J.L.; Flores-Zuñiga, H.; Rangel-Mendez, J.R. Fluoride Removal from Water by Ceramic Oxides from Cerium and Manganese Solutions. J. Mol. Liq. 2019, 286, 110880. [Google Scholar] [CrossRef]
- Kim, W.; Singh, R.; Smith, J.A. Modified Crushed Oyster Shells for Fluoride Removal from Water. Sci. Rep. 2020, 10, 5759. [Google Scholar] [CrossRef]
- Mohan, D.; Sharma, R.; Singh, V.K.; Steele, P.; Pittman, C.U. Fluoride Removal from Water Using Bio-Char, a Green Waste, Low-Cost Adsorbent: Equilibrium Uptake and Sorption Dynamics Modeling. Ind. Eng. Chem. Res. 2012, 51, 900–914. [Google Scholar] [CrossRef]
- Bizeray, A.M.; Howey, D.A.; Monroe, C.W. Resolving a Discrepancy in Diffusion Potentials, with a Case Study for Li-Ion Batteries. J. Electrochem. Soc. 2016, 163, E223–E229. [Google Scholar] [CrossRef]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric Effects in the Dynamics of Electrolytes at Large Applied Voltages. I. Double-Layer. Charging. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2007, 75, 021503. [Google Scholar] [CrossRef] [Green Version]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric Effects in the Dynamics of Electrolytes at Large Applied Voltages. II. Modified Poisson-Nernst-Planck Equations. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2007, 75, 061909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ehlinger, V.M.; Crothers, A.R.; Kusoglu, A.; Weber, A.Z. Modeling Proton-Exchange-Membrane Fuel Cell Performance/Degradation Tradeoffs with Chemical Scavengers. JPhys Energy 2020, 2, 044006. [Google Scholar] [CrossRef]
- Crothers, A.R.; Darling, R.M.; Kushner, D.I.; Perry, M.L.; Weber, A.Z. Theory of Multicomponent Phenomena in Cation-Exchange Membranes: Part III. Transport in Vanadium Redox-Flow-Battery Separators. J. Electrochem. Soc. 2020, 167, 013549. [Google Scholar] [CrossRef]
- Chung, M.H. Numerical Method for Analysis of Tertiary Current Distribution in Unsteady Natural Convection Multi-Ion Electrodeposition. Electrochim. Acta 2000, 45, 3959–3972. [Google Scholar] [CrossRef]
- Chu, K.T.; Bazant, M.Z. Nonlinear Electrochemical Relaxation around Conductors. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2006, 74, 011591. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.; Popov, B.N.; Ploehn, H.J. Modeling the Effects of Electrode Composition and Pore Structure on the Performance of Electrochemical Capacitors. J. Electrochem. Soc. 2002, 149, A167. [Google Scholar] [CrossRef] [Green Version]
- Li, B. Continuum Electrostatics for Ionic Solutions with Non-Uniform Ionic Sizes. Nonlinearity 2009, 22, 811–833. [Google Scholar] [CrossRef] [Green Version]
- Lodi, M.B.; Fanari, F.; Fanti, A.; Desogus, F.; Getaneh, W.; Mazzarella, G.; Valera, P. Preliminary Study and Numerical Investigation of an Electrostatic Unit for the Removal of Fluoride from Thermal Water of Ethiopian Rift Valley. IEEE J. Multiscale Multiphysics Comput. Tech. 2020, 5, 72–82. [Google Scholar] [CrossRef]
- Welch, R.S.; Wilkinson, C.J.; Mauro, J.C.; Bragatto, C.B. Charge Carrier Mobility of Alkali Silicate Glasses Calculated by Molecular Dynamics. Front. Mater. 2019, 6, 121. [Google Scholar] [CrossRef]
- Danilov, D.; Notten, P.H.L. Mathematical Modelling of Ionic Transport in the Electrolyte of Li-Ion Batteries. Electrochim. Acta 2008, 53, 5569–5578. [Google Scholar] [CrossRef]
- Millington, R.J.; Quirk, J.P. Permeability of Porous Solids. Trans. Faraday Soc. 1961, 57, 1200–1207. [Google Scholar] [CrossRef]
- Belhachemi, M.; Addoun, F. Comparative Adsorption Isotherms and Modeling of Methylene Blue onto Activated Carbons. Appl. Water Sci. 2011, 1, 111–117. [Google Scholar] [CrossRef] [Green Version]
- Lu, R.; Leaist, D.G. Mutual Diffusion in Solutions of Alkali Metal Halides: Aqueous LiF, NaF and KF at 25 °C. J. Chem. Soc. Faraday Trans. 1998, 94, 111–114. [Google Scholar] [CrossRef]
- WHO. World Health Organization guidelines for drinking-water quality. In WHO Chronicle; WHO: Geneva, Switzerland, 2011; Volume 1, ISBN 978 92 4 154761 1. [Google Scholar]
- Mudzielwana, R.; Gitari, M.W. Removal of Fluoride from Groundwater Using MnO2 Bentonite-Smectite Rich Clay Soils Composite. Groundw. Sustain. Dev. 2021, 14, 100623. [Google Scholar] [CrossRef]
- Zhang, Z.; Tan, Y.; Zhong, M. Defluorination of Wastewater by Calcium Chloride Modified Natural Zeolite. Desalination 2011, 276, 246–252. [Google Scholar] [CrossRef]
- Hamdi, N.; Srasra, E. Removal of Fluoride from Acidic Wastewater by Clay Mineral: Effect of Solid–Liquid Ratios. Desalination 2007, 206, 238–244. [Google Scholar] [CrossRef]
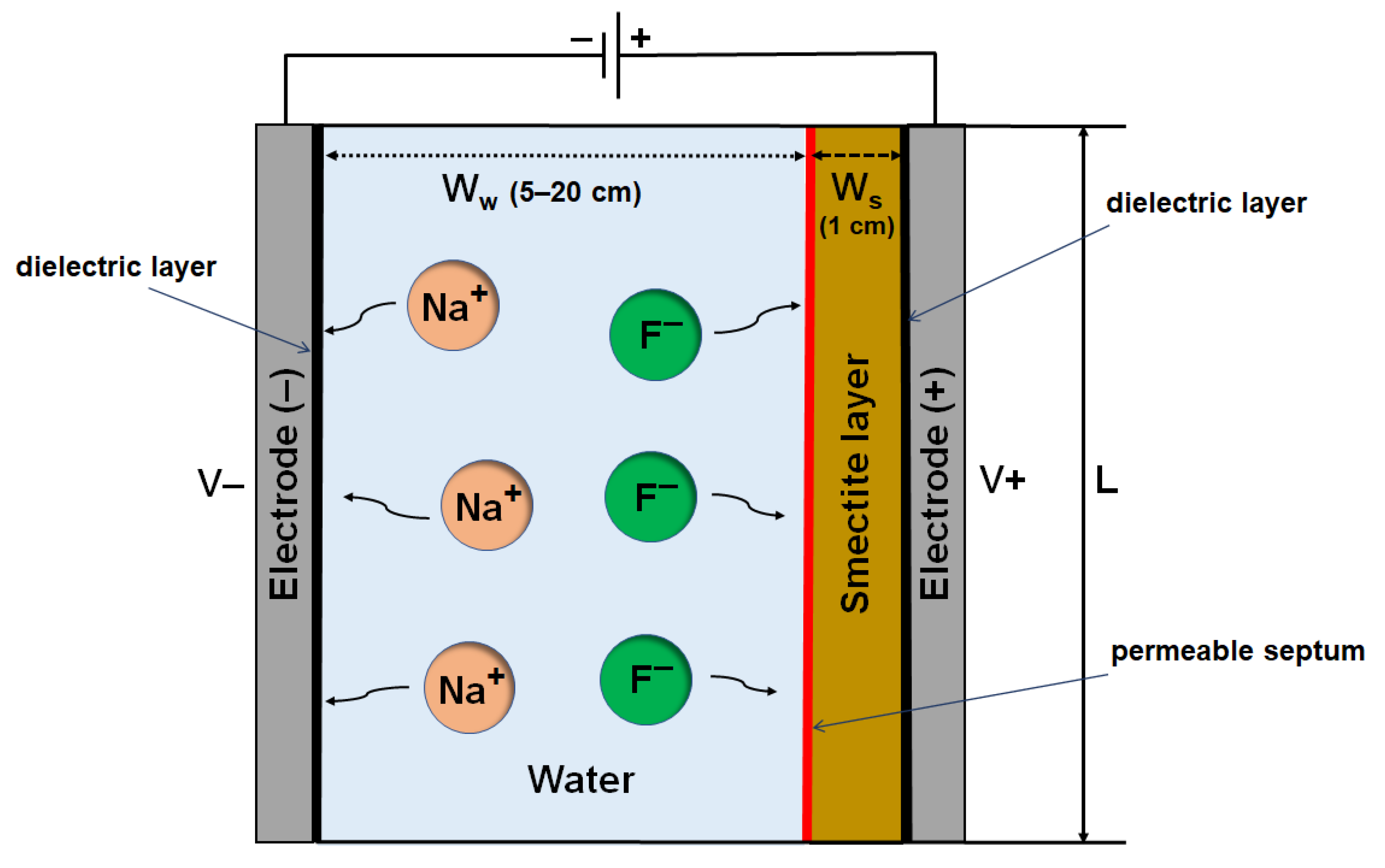
| Parameter | Description | Value | Reference |
|---|---|---|---|
| T | Temperature of the solution | 37 °C | |
| Dielectric constant of the solution | 78 | [42] | |
| Spacing between densely packed ions | 0.35 nm | [34,35] | |
| F− diffusion coefficient in water | 1.35 × 10−9 m2/s | [47] | |
| Smectite clay layer porosity | 0.33 | [9] | |
| Smectite clay layer density | 1590 kg/m3 | [9] | |
| Coefficient of dispersion of F− in the porous material | 7× 10−10 m2/s | [9] | |
| Langmuir free energy adsorption constant | 4.5391 m3/mol | [9] | |
| Langmuir maximum adsorption capacity | 0.01476 mol/kg | [9] | |
| Applied electrostatic potential | 0–9 V | ||
| L | Device length | 1 m | |
| ww | Water filled device width | 5–20 cm | |
| ws | Smectite filled device width | 1 cm | |
| Initial concentration of F− in the water | 5 mg/L; 10 mg/L |
| Defluoridation Time (h) | ||||||
|---|---|---|---|---|---|---|
| V0 | cn0 = 5 mg/L ww = 5 cm | cn0 = 10 mg/L ww = 5 cm | cn0 = 5 mg/L ww = 10 cm | cn0 = 10 mg/L ww = 10 cm | cn0 = 5 mg/L ww = 20 cm | cn0 = 10 mg/L ww = 20 cm |
| 0 V | >48 | >48 | >48 | >48 | >48 | >48 |
| 0.1 V | >48 | >48 | >48 | >48 | >48 | >48 |
| 0.2 V | 27.8 | 39.2 | >48 | >48 | >48 | >48 |
| 0.3 V | 18.7 | 25.3 | >48 | >48 | >48 | >48 |
| 0.5 V | 11.2 | 14.7 | 41.1 | >48 | >48 | >48 |
| 1 V | 5.6 | 7.1 | 20.6 | 26.0 | >48 | >48 |
| 3 V | 1.9 | 2.3 | 6.9 | 8.5 | 26.3 | 32.5 |
| 5 V | 1.1 | 1.4 | 4.1 | 5.1 | 15.8 | 19.5 |
| 9 V | 0.6 | 0.8 | 2.3 | 2.8 | 8.8 | 10.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fanari, F.; Lodi, M.B.; Getaneh, W.; Fanti, A.; Desogus, F.; Valera, P. Evaluation of a Smectite Adsorption-Based Electrostatic System to Decontaminate F− Rich Thermal Waters. Water 2022, 14, 167. https://doi.org/10.3390/w14020167
Fanari F, Lodi MB, Getaneh W, Fanti A, Desogus F, Valera P. Evaluation of a Smectite Adsorption-Based Electrostatic System to Decontaminate F− Rich Thermal Waters. Water. 2022; 14(2):167. https://doi.org/10.3390/w14020167
Chicago/Turabian StyleFanari, Fabio, Matteo Bruno Lodi, Worash Getaneh, Alessandro Fanti, Francesco Desogus, and Paolo Valera. 2022. "Evaluation of a Smectite Adsorption-Based Electrostatic System to Decontaminate F− Rich Thermal Waters" Water 14, no. 2: 167. https://doi.org/10.3390/w14020167








