Water Resources Allocation in the Tingjiang River Basin: Construction of an Interval-Fuzzy Two-Stage Chance-Constraints Model and Its Assessment through Pearson Correlation
Abstract
:1. Introduction
2. Case Study
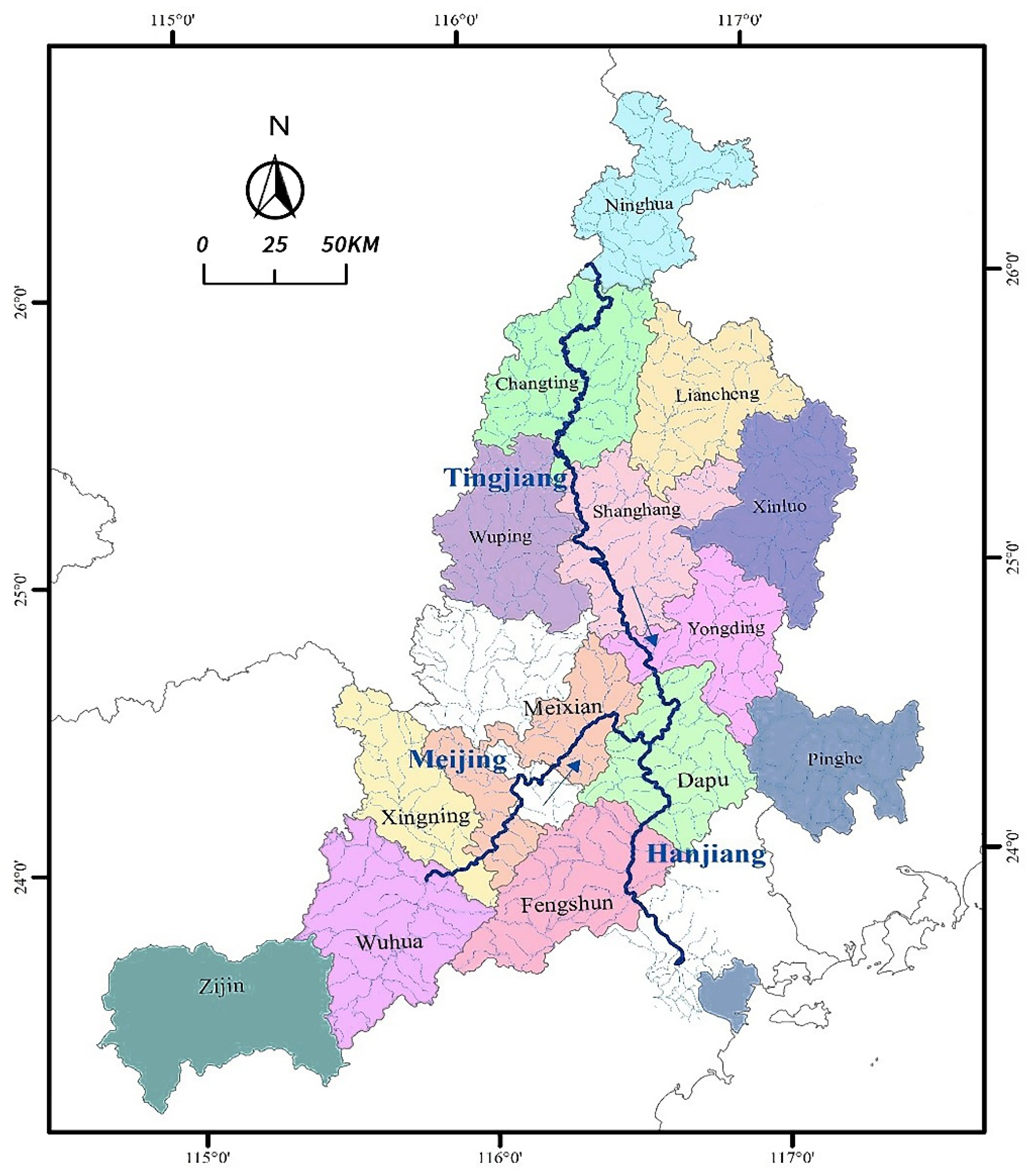
2.1. Natural Characteristics and Optimization Background of the Tingjiang River Basin
2.2. Research Object and Constraint Parameters
3. Model Formulation
3.1. Watershed IFTSC Model Construction
- (1)
- Economic scale constraints [13]:
- (2)
- The water resources utilization online:
- (3)
- Water quality requirements in the basin:
- (4)
- Minimum development requirements for each region in the basin:
3.2. Solution of IFTSC Model for Watershed
3.3. Correlation Analysis Model Based on Pearson’s Correlation Coefficient
4. Results and Discussion
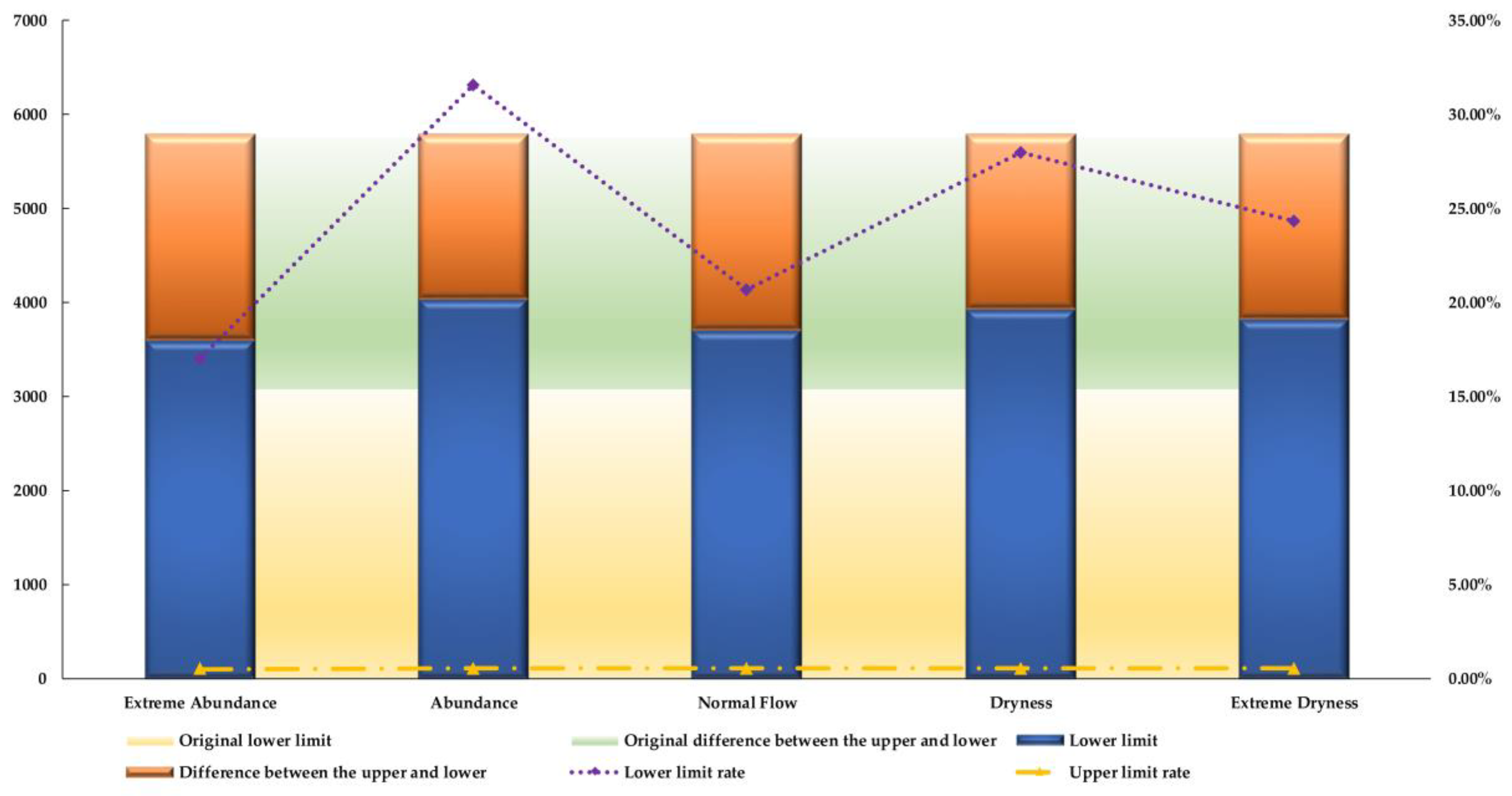
4.1. Analysis of IFTSC Model Simulating Two-Stage Water Resource Allocation in Tingjiang River Basin
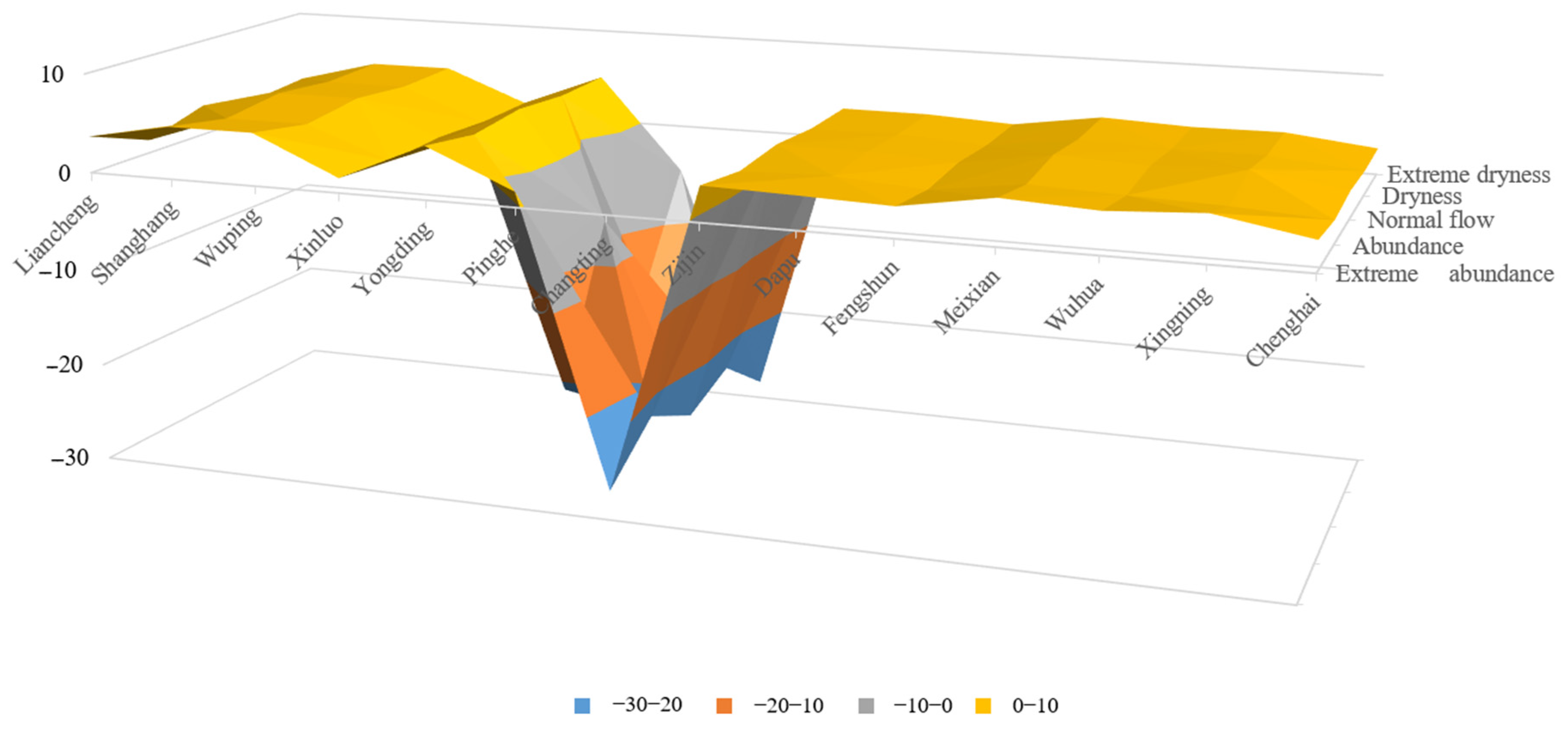
4.2. Economic Benefit Analysis of the Tingjiang River Basin Based on the IFTSC Model
4.3. Comparison of the IFTSC Model Optimized by Chance Constraint with the IFTS Model
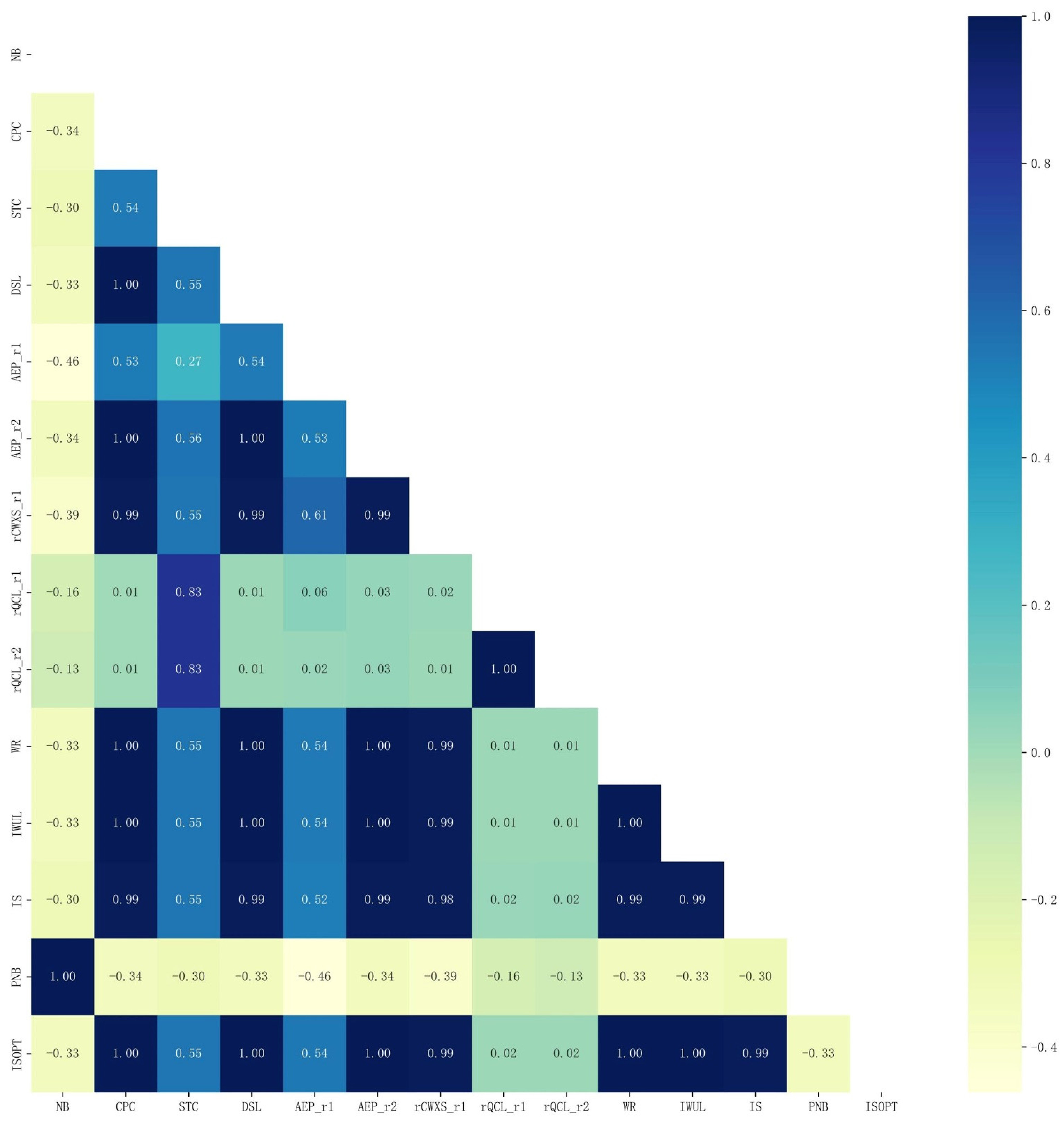
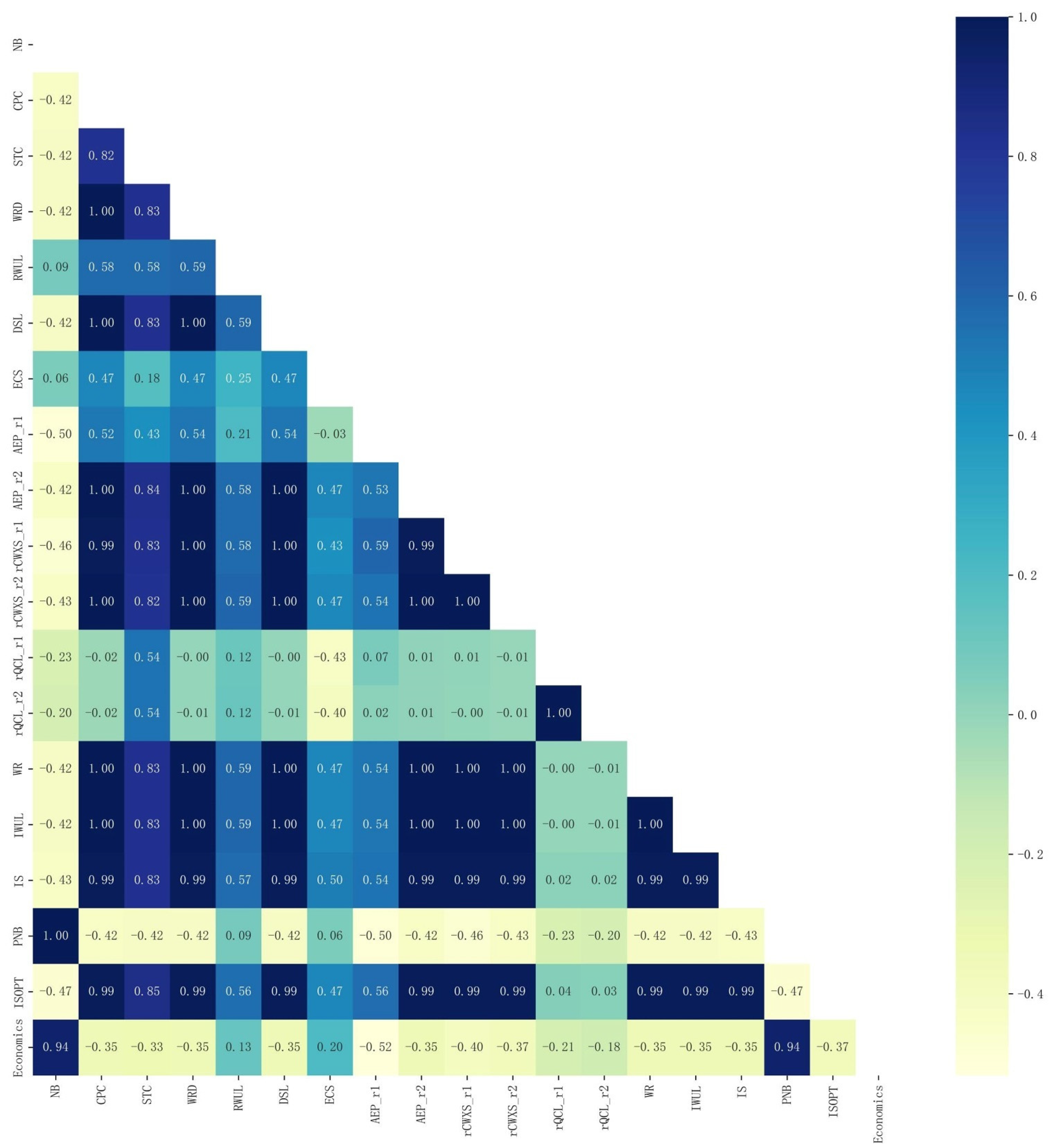
4.4. Analysis of Factors Influencing Water Allocation Based on Pearson Correlation Coefficient
5. Conclusions
- (1)
- The second-stage penalty value of the IFTSC model in the Tingjiang River basin was less than the original IFTS model, as evidenced by the decrease in the second-stage penalty value of the industrial sector by 9.7% under the dry hydrological scenario. The first stage is characterized by a relatively reasonable water allocation with improved water resources utilization rate and greatly relieves the water pressure of various departments and industries while minimizing the water resources waste or economic development restriction caused by unreasonable water resources allocation.
- (2)
- The stochastic optimization method with chance-constraint was introduced based on the original IFTS model to effectively reduce the uncertainty of minimum development requirements in the Tingjiang River basin. At the same time, the IFTSC model was allowed to violate the constraint conditions within a specified confidence interval to make it more realistic with a wider range of applications, which can satisfy the more differential and complex realistic hydrological scenarios to a certain extent.
- (3)
- The total economic benefits of the Tingjiang River basin simulated by the IFTSC model show an increasing trend compared with the original IFTS model (an increase of 49.36 × 108 CNY under the abundant hydrology scenario), which further ensures the overall economic development of the Tingjiang River basin and balances the economic relationship between Fujian and Guangdong provinces upstream and downstream of the Tingjiang River basin while rationalizing water resources allocation.
- (4)
- Pearson correlation coefficient shows that water allocation in the Tingjiang River basin is positively correlated with seven parameters (CPC, DSL, AER_r2, rCWXS_r1, WR, IWUL and IS) and that economic efficiency in the Tingjiang River basin is positively correlated with two parameters (NB and PNB). In the water management process, the focus can be on these parameters and simpler and more efficient measures can be taken to address the environmental management objectives of the basin.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Economic benefit of water, 104 CNY. | |
| Water consumption cost, 104 CNY. | |
| Cost of environmental management of water, 104 CNY. | |
| Eco-compensation quota, 104 CNY. | |
| The second stage to optimize the penalty value. | |
| The lowest economic benefit of the basin, 104 CNY. | |
| The highest economic benefit of the basin, 104 CNY. | |
| Administrative units (14 districts and counties). | |
| Major water consumption sectors (= 1, 2, 3, 4 denote Industry, Municipal, Agriculture, Ecology). | |
| Different industry categories within each sector | |
| Watershed partition ( = 1 denotes the regional scope of upstream Fujian province, and = 2 denotes the regional scope of downstream Guangdong province). | |
| Hydrological situation (= 1, 2, 3, 4, 5 denote extreme abundance, abundance, normal flow, dryness, and extreme dryness, with respective probabilities of 0.1, 0.3, 0.15, 0.25, and 0.2). | |
| Output value per unit scale, 104 CNY/104 t. | |
| The optimal solution for water consumption in the first stage. | |
| The unit price of water 104 CNY/104 t. | |
| Comprehensive pollution production coefficient, 104 g/104 t. | |
| Pollution control cost, 104 CNY/104 t. | |
| Downstream water price, 104 CNY/104 t. | |
| The proportion of downstream use of incoming water from the upstream. | |
| Eco-compensation determination coefficient (the water quality is better than the III standard, = 1; the water quality is inferior to class V, = −1; in other cases, = 0). | |
| Hydrological scenario probability. | |
| The water supply that cannot meet the loss caused by the original water supply, 104 CNY/104 t. | |
| Lack of water, 104 t. | |
| The maximum water resources utilization stipulated by different regions and departments, 104 t. | |
| The maximum utilization of water resources in different regions, 104 t. | |
| The ecological area range of different regions in the watershed, 104 t. | |
| The maximum utilization of water resources in the basin, 104 t. | |
| Different pollutants. | |
| Pollutants producing coefficient, 104 g/104 t. | |
| Pollutant removal rate. | |
| Maximum allowable discharge of pollutants, 104 t. | |
| Minimum regional development requirements, 104 CNY. | |
| The risk of default. | |
| Expected value of (= 1, 2). | |
| Expected value of (= 1, 2). | |
| The variances of the (= 1, 2). | |
| The variances of the (= 1, 2). |
References
- Liu, X.F.; Yu, X.F.; Yu, K. The current situation and sustainable development of water resources in China. Proc. Eng. 2012, 28, 522–526. [Google Scholar] [CrossRef]
- Wang, W.D.; Yang, T.; Guan, W.B.; Peng, W.X.; Wu, P.; Zhong, B.; Zhou, C.D.; Chen, Q.H.; Zhang, R.B.; Xu, K.W.; et al. Ecological wetland paradigm drives water source improvement in the stream network of Yangtze River Delta. J. Environ. Sci. 2021, 110, 55–72. [Google Scholar] [CrossRef] [PubMed]
- Wada, Y.; Flörke, M.; Hanasaki, N.; Eisner, S.; Fischer, G.; Tramberend, S.; Satoh, Y.; van Vliet, M.T.H.; Yillia, P.; Ringler, C.; et al. Modeling Global Water Use for the 21st century: The Water Futures and Solutions (WFaS) Initiative and its Approaches. Geosci. Model. Dev. 2016, 9, 175–222. [Google Scholar] [CrossRef]
- Roshan, A.; Kumar, M. Water End-Use Estimation Can Support the Urban Water Crisis Management: A Critical Review. J. Environ. Manag. 2020, 268, 110663. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.X.; Wang, Y.; Su, X.L.; Qi, L.; Liu, M. Evaluation of the comprehensive carrying capacity of interprovincial water resources in China and the spatial effect. J. Hydrol. 2019, 575, 794–809. [Google Scholar] [CrossRef]
- Da Silva, L.C.C.; Filho, D.O.; Silva, I.R.; Pinto, A.C.V.E.; Vaz, P.N. Water Sustainability Potential in a university Building—Case Study. Sustain. Cities Soc. 2019, 47, 101489. [Google Scholar] [CrossRef]
- Hou, J.; Wang, N.; Luo, J.G.; Zhang, X.; Wang, Z.H.; Xie, J.C. A multi-method integrated simulation system for water resources allocation. Water Supply 2021, 22, 2518–2532. [Google Scholar] [CrossRef]
- Wen, Q.; Zhang, L.D.; Fei, X.X.; Li, J.D. Discussions about Water Resources Allocation. In Proceedings of the 2019 3rd International Workshop on Renewable Energy and Development (IWRED 2019), Guangzhou, China, 8–10 March 2019; Volume 267, p. 022030. [Google Scholar]
- Sun, T.; Zhang, H.W.; Wang, Y. The application of information entropy in basin level water waste permits allocation in China. Resour. Conserv. Recycl. 2013, 70, 50–54. [Google Scholar] [CrossRef]
- Chen, Y.; Dou, S.Q.; Xu, D. The effectiveness of eco-compensation in environmental protection-A hybrid of the government and market. J. Environ. Manag. 2021, 280, 111840. [Google Scholar] [CrossRef]
- Wunder, S.; Engel, S.; Pagiola, S. Taking stock: A comparative analysis of payments for environmental services programs in developed and developing countries. Ecol. Econ. 2008, 65, 834–852. [Google Scholar] [CrossRef]
- Wunder, S. Revisiting the concept of payments for environmental services. Ecol. Econ. 2015, 117, 234–243. [Google Scholar] [CrossRef]
- Hao, N.; Sun, P.X.; Yang, L.Z.; Qiu, Y.; Chen, Y.Z.; Zhao, W.J. Optimal Allocation of Water Resources and Eco-Compensation Mechanism Model Based on the Interval-Fuzzy Two-Stage Stochastic Programming Method for Tingjiang River. Int. J. Environ. Res. Public Health. 2021, 19, 149. [Google Scholar] [CrossRef]
- Abichou, T.; Clark, J.; Tan, S.; Chanton, J.; Hater, G.; Green, R.; Goldsmith, D.; Barlaz, M.A.; SWAN, N. Uncertainties Associated with the Use of Optical Remote Sensing Technique to Estimate Surface Emissions in Landfill Applications. J. Air Waste Manag. Assoc. 2010, 60, 460–470. [Google Scholar] [CrossRef]
- Meng, C.; Wang, X.L.; Li, Y. An Optimization Model for Water Management Based on Water Resources and Environmental Carrying Capacities: A Case Study of the Yinma River Basin, Northeast China. Water 2018, 10, 565. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Y.P.; Huang, G.H. A queuing-theory-based interval-fuzzy robust two-stage programming model for environ-mental management under uncertainty. Eng. Optimiz. 2012, 44, 707–724. [Google Scholar] [CrossRef]
- Feng, X.X.; Zhang, Y.Q.; Wu, J.L. Interval analysis method based on Legendre polynomial approximation for uncertain multibody systems. Adv. Eng. Softw. 2018, 121, 223–234. [Google Scholar] [CrossRef]
- Fu, Q.; Zhao, K.; Liu, D.; Jiang, Q.X.; Li, T.X.; Zhu, C.H. Two-stage interval-parameter stochastic programming model based on adaptive water resource management. Water Resour. Manag. 2016, 30, 2097–2109. [Google Scholar] [CrossRef]
- Zhang, C.; Li, M.; Guo, P. An interval multistage joint-probabilistic chance-constrained programming model with left-hand-side randomness for crop area planning under uncertainty. J. Clean Prod. 2017, 167, 1276–1289. [Google Scholar] [CrossRef]
- Meng, C.; Li, W.; Cheng, R.H.; Zhou, S.Y. An Improved Inexact Two-Stage Stochastic with Downside Risk-Control Programming Model for Water Resource Allocation under the Dual Constraints of Water Pollution and Water Scarcity in Northern China. Water 2021, 13, 1318. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, J.; Xu, Y.; Sun, W.; Chen, D. An inexact log-normal distribution-based stochastic chance-constrained model for agricultural water quality management. Eng. Optimiz. 2018, 50, 840–855. [Google Scholar] [CrossRef]
- Kon, M. A scalarization method for fuzzy set optimization problems. Fuzzy Optim. Decis. Mak. 2020, 19, 135–152. [Google Scholar] [CrossRef]
- Ni, J.N.; Xu, J.P.; Zhang, M.X. Constructed wetland modelling for watershed ecosystem protection under a certain economic load: A case study at the Chaohu Lake watershed, China. Ecol. Model. 2018, 368, 180–190. [Google Scholar] [CrossRef]
- Ranarahu, N.; Dash, J.K. Computation of multi-objective two-stage fuzzy probabilistic programming problem. Soft Comput. 2022, 26, 271–282. [Google Scholar] [CrossRef]
- Steinfeld, C.M.M.; Sharma, A.; Mehrotra, R.; Kingsford, R.T. The human dimension of water availability: Influence of management rules on water supply for irrigated agriculture and the environment. J. Hydrol. 2020, 588, 125009. [Google Scholar] [CrossRef]
- Vorosmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef]
- Shi, H.H.; Weng, W.G.; Zhai, Z.G.; Li, Y.Y. The Relationship and Regression Analysis of Urban Water Supply and Temperature. Appl. Mech. Mater. 2012, 256, 2420–2423. [Google Scholar] [CrossRef]
- Hu, Z.H.; Zhang, Y.R.; Zhao, Y.C.; Xie, M.S.; Zhong, J.Z.; Tu, Z.G.; Liu, J.T. A Water Quality Prediction Method Based on the Deep LSTM Network Considering Correlation in Smart Mariculture. Sensors 2019, 19, 1420. [Google Scholar] [CrossRef]
- Ion, A.; Vladescu, L.; Badea, I.A.; Comanescu, L. Monitoring and evaluation of the water quality of Budeasa Reservoir-Arges River, Romania. Environ. Monit. Assess. 2016, 188, 535. [Google Scholar] [CrossRef]
- Rodriguez, F.M.; Garcia, S.G.; Corro, R.J.; Liesa, M.S.; Barón, F.R.; Martín, F.S.; Feu, O.A.; Rodríguez, R.M.; Mavrich, H.V. Spanish bottled and tap water analysis and their relation with urinary lithiasis. Actas Urol. Esp. 2009, 33, 778–793. [Google Scholar]
- Godeke, S.H.; Malik, O.A.; Lai, D.T.C.; Bretzler, A.; Schirmer, M.; Mansor, N.H. Water quality investigation in Brunei Darussalam: Investigation of the influence of climate change. Environ. Earth Sci. 2020, 79, 419. [Google Scholar] [CrossRef]
- Lin, W.; Yang, F.; Zhou, L.; Xu, J.G.; Zhang, X.Q. Using modified Soil Conservation Service curve number method to simulate the role of forest in flood control in the upper reach of the Tingjiang River in China. J. Mt. Sci. 2017, 14, 1–14. [Google Scholar] [CrossRef]
- Zhang, L.L.; Lv, J.G. Ecological risk assessment of the metallic pollution in the soil and sediment in Tingjiang basin. Environ. Earth Sci. 2015, 73, 1799–1803. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.D.; Wan, L.W.; Yang, C.X.; Ye, C. The Contributions of Climate Change and Human Activities on Runoff of the Tingjiang River. J. South China Norm. Univ. 2017, 49, 84–91. [Google Scholar]
- Qiu, Y. Study on Optimization of Water Resource Allocation and Eco-Compensation in Tingjiang Basin under Uncertainty. Ph.D. Thesis, Jilin University, Jilin, China, 2020. [Google Scholar]
- Li, H.Q.; Lv, C.M.; Ling, M.H.; Gu, C.K.; Li, Y.; Wu, Z.N.; Yan, D.H. Emergy Analysis and Ecological Spillover as Tools to Quantify Ecological Compensation in Xuchang City, Qingyi River Basin, China. Water 2021, 13, 414. [Google Scholar] [CrossRef]
- Chang, L.J. Research on the Eco-Compensation Patterns between the Upstream and Downstream in Tingjiang River Basin. Master’s Thesis, Xiamen University, Xiamen, China, 2017. [Google Scholar]
- Chen, D.X. Practice and Innovation of Eco-compensation Mechanism Pilot in Tingjiang-Hanjiang River Basin. Environ. Prot. 2017, 45, 31–33. [Google Scholar]
- Ji, Y. Research on Improvement of Interval Double-Hand-Side Chance-Constrained Programming and the Application in Water Quality Management. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2016. [Google Scholar]
- Chinchilli, V.M.; Phillips, B.R.; Manger, D.T.; Szefler, S.J. A general class of correlation coefficients for the 2 × 2 crossover design. Biom. J. 2005, 47, 644–653. [Google Scholar] [CrossRef]
- Feng, W.L.; Zhu, Q.Y.; Zhuang, J.; Yu, S.M. An expert recommendation algorithm based on Pearson correlation coefficient and FP-growth. Cluster Comput. 2019, 22, 7401–7412. [Google Scholar] [CrossRef]
- Edelmann, D.; Mori, T.F.; Szekely, G.J. On relationships between the Pearson and the distance correlation coefficients. Stat. Probab. Lett. 2021, 169, 108960. [Google Scholar] [CrossRef]
- Li, Y.; Xie, J.C.; Jiang, R.G.; Yan, D.F. Application of edge computing and GIS in ecological water requirement prediction and optimal allocation of water resources in irrigation area. PLoS ONE 2021, 16, e0254547. [Google Scholar] [CrossRef]
- Shen, X.; Wu, X.; Xie, X.; Wei, C.; Li, L.Q.; Zhang, J.J. Synergetic Theory-Based Water Resource Allocation Model. Water Resour. Manag. 2021, 35, 2053–2078. [Google Scholar] [CrossRef]
- Chen, Y.B.; Yin, G.W.; Liu, K. Regional differences in the industrial water use efficiency of China: The spatial spillover effect and relevant factors. Resour. Conserv. Recycl. 2021, 167, 105239. [Google Scholar] [CrossRef]
- Amoah, A.; Asiama, R.K.; Korle, K.; Kwablah, E. Domestic water improvement behaviour: The probability determinants and policy implications(dagger). Water Policy 2021, 23, 880–896. [Google Scholar] [CrossRef]
- Xu, H.; Yang, R.; Song, J.F. Agricultural Water Use Efficiency and Rebound Effect: A Study for China. Int. J. Environ. Res. Public Health. 2021, 18, 7151. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Feng, J.; Liu, W.; Yan, S. Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 45, 1–22. [Google Scholar] [CrossRef]
- Kosolapova, N.A.; Matveeva, L.G.; Nikitaeva, A.Y.; Molapisi, L. Modeling resource basis for social and economic development strategies: Water resource case. J. Hydrol. 2017, 553, 438–446. [Google Scholar] [CrossRef]
- Dai, X.L.; Zhu, P.Y.; Zhuang, Y.; Wang, Y. Correlation study of tai lake conventional water quality. Oxid. Commun. 2015, 38, 1364–1372. [Google Scholar]
- Liao, N.D.; Song, Y.Q.; Su, S.; Huang, X.S.; Ma, H.L. Detection of probe flow anomalies using information entropy and random forest method. J. Intell. Fuzzy Syst. 2020, 39, 433–447. [Google Scholar]
| Value Range | Relevance |
|---|---|
| 0–0.2 | Very strong correlation |
| 0.2–0.4 | Strong correlation |
| 0.4–0.6 | Moderate correlation |
| 0.6–0.8 | Weak correlation |
| 0.8–1.0 | Very weak correlation or no correlation |
| Province | Section | Business | Liancheng | Shanghang | Wuping | Xinluo | Yongding | Pinghe | Changting |
|---|---|---|---|---|---|---|---|---|---|
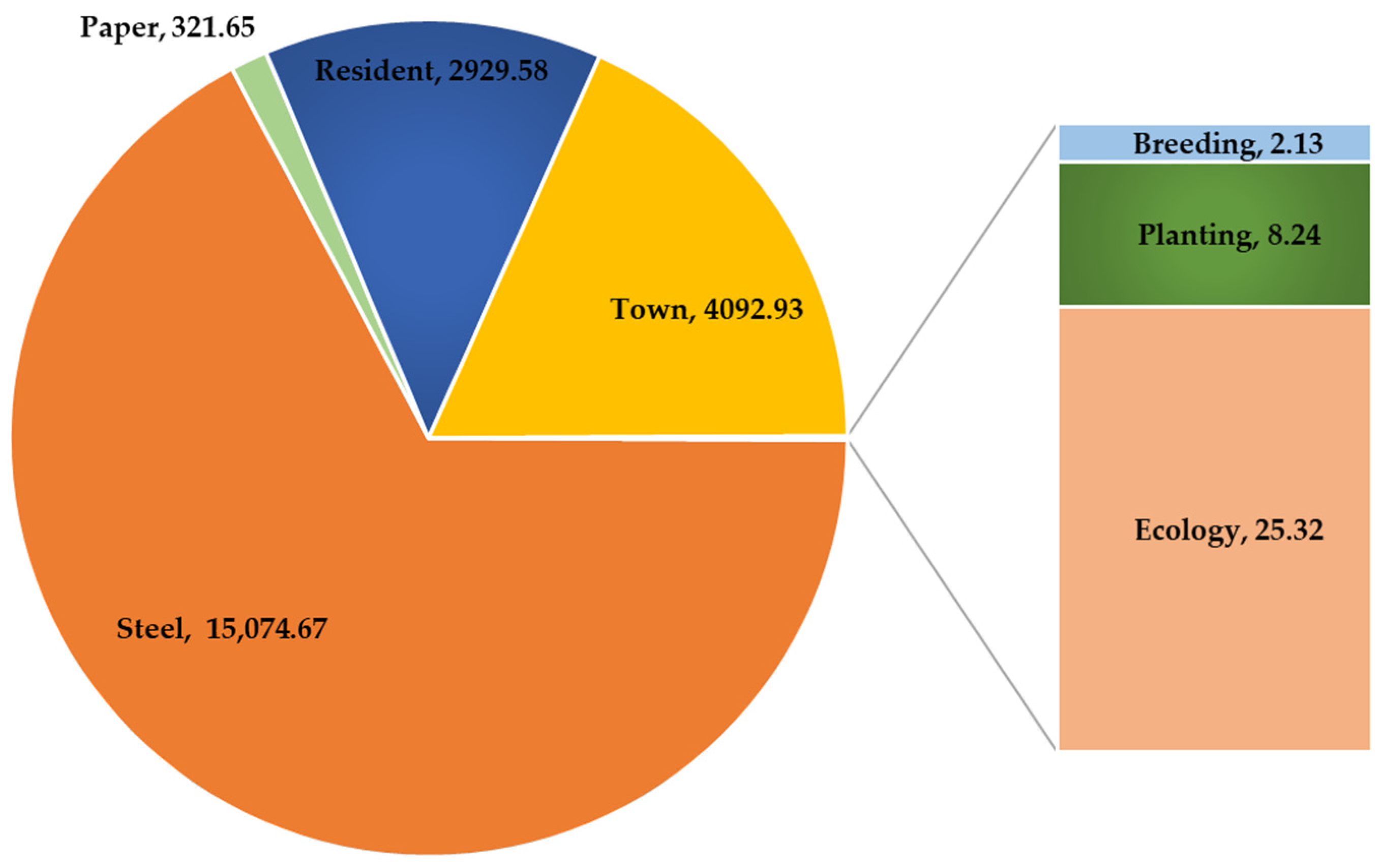
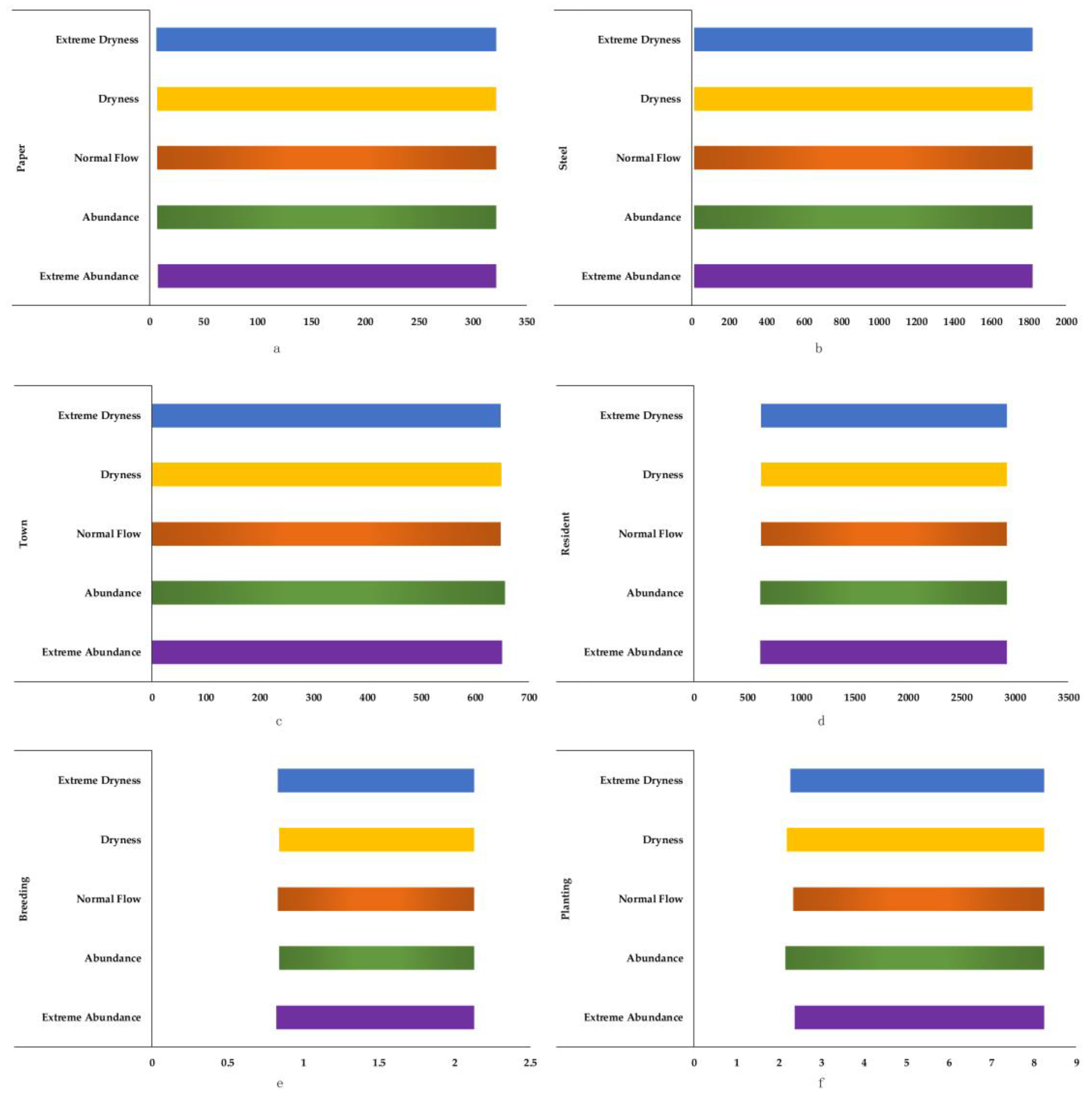
| Fujian | Industry | Paper | 321.65 | 226.17 | 616.05 | 701.21 | 529.15 | 564.41 | 354.76 |
| Steel | 15,074.67 | 14,569.46 | 14,778.34 | 0.00 | 13,062.22 | 0.00 | 0.00 | ||
| Cement | 0.00 | 596.03 | 0.00 | 437.93 | 1802.58 | 13,320.01 | 12,737.94 | ||
| Thermal power | 0.00 | 0.00 | 0.00 | 14,260.86 | 0.00 | 1508.07 | 2263.49 | ||
| Municipal | Town | 4092.93 | 4027.14 | 290.85 | 5112.15 | 2217.80 | 4309.74 | 3131.46 | |
| Resident | 2929.58 | 3108.98 | 6797.56 | 1229.55 | 4809.93 | 2690.86 | 2308.33 | ||
| Agriculture | Breeding | 2.13 | 1.38 | 1.72 | 1.88 | 2.68 | 1.86 | 2.66 | |
| Planting | 8.24 | 9.72 | 9.60 | 27.04 | 22.68 | 25.22 | 5.25 | ||
| Ecology | Ecology | 25.32 | 4.37 | 13.55 | 32.88 | 53.77 | 33.02 | 22.69 | |
| Guangdong | Zijin | Dapu | Fengshun | Meixian | Wuhua | Xingning | Chenghai | ||
| Industry | Paper | 255.24 | 220.66 | 209.29 | 419.66 | 314.71 | 463.06 | 211.66 | |
| Steel | 19,759.37 | 18,894.87 | 19,806.31 | 0.00 | 200.44 | 0.00 | 0.00 | ||
| Cement | 0.00 | 897.31 | 0.00 | 19,323.88 | 19,489.32 | 19,319.52 | 214.85 | ||
| Thermal power | 0.00 | 0.00 | 0.00 | 249.18 | 0.00 | 217.38 | 19,579.52 | ||
| Municipal | Town | 4393.67 | 3979.43 | 3776.06 | 3403.44 | 3164.00 | 4155.35 | 3938.43 | |
| Resident | 3717.65 | 4062.76 | 4337.99 | 4623.53 | 4871.07 | 3901.09 | 4115.70 | ||
| Agriculture | Breeding | 2.88 | 1.86 | 2.33 | 2.65 | 4.01 | 2.52 | 3.63 | |
| Planting | 12.19 | 12.30 | 14.24 | 11.43 | 87.82 | 34.32 | 7.88 | ||
| Ecology | Ecology | 32.83 | 37.01 | 39.52 | 44.00 | 25.12 | 53.82 | 107.52 |
| Number | Region | Lower Limit (×108 CNY) | Economic Benefits of Each District and County under Five Hydrological Scenarios of IFTSC Model (×108 CNY) | Change Interval (%) | ||||
|---|---|---|---|---|---|---|---|---|
| p (1) | p (2) | p (3) | p (4) | p (5) | ||||
| 1 | Liancheng | 165.47 | 201.26 | 215.37 | 204.79 | 211.84 | 208.32 | [21.63, 30.16] |
| 2 | Shanghang | 313.07 | 375.71 | 381.68 | 377.20 | 380.18 | 378.69 | [20.01, 21.92] |
| 3 | Wuping | 111.80 | 186.78 | 222.86 | 195.80 | 213.84 | 204.82 | [67.07, 99.34] |
| 4 | Xinluo | 767.60 | 907.11 | 946.29 | 916.91 | 936.50 | 926.70 | [18.17, 23.28] |
| 5 | Yongding | 184.43 | 244.79 | 274.75 | 252.28 | 267.26 | 259.77 | [32.73, 48.97] |
| 6 | Pinghe | 219.29 | 243.19 | 258.39 | 247.33 | 254.79 | 251.15 | [10.90, 17.83] |
| 7 | Changting | 207.96 | 244.52 | 257.76 | 248.02 | 254.61 | 251.38 | [17.58, 23.95] |
| 8 | Zijin | 89.85 | 92.48 | 128.54 | 101.50 | 119.52 | 110.51 | [2.93, 43.06] |
| 9 | Dapu | 61.37 | 59.69 | 89.01 | 67.03 | 81.63 | 74.35 | [−2.74, 45.04] |
| 10 | Fengshun | 67.29 | 68.45 | 98.33 | 75.92 | 90.86 | 83.39 | [1.72, 46.13] |
| 11 | Meixian | 164.19 | 169.49 | 230.89 | 184.84 | 215.54 | 200.19 | [3.23, 40.62] |
| 12 | Wuhua | 127.47 | 133.45 | 178.54 | 144.73 | 167.27 | 156.00 | [4.69, 40.06] |
| 13 | Xingning | 149.59 | 147.86 | 215.74 | 164.81 | 198.87 | 181.76 | [−1.16, 44.22] |
| 14 | Chenghai | 439.93 | 517.53 | 539.64 | 523.06 | 534.12 | 528.59 | [17.64, 22.66] |
| Total | 3069.32 | 3592.31 | 4037.79 | 3704.22 | 3926.83 | 3815.62 | [17.04, 31.55] | |
| Number | Region | Upper Limit (×108 CNY) | Economic Benefits of Each District and County under Five Hydrological Scenarios of IFTSC Model (×108 CNY) | Change Interval (%) | ||||
|---|---|---|---|---|---|---|---|---|
| p (1) | p (2) | p (3) | p (4) | p (5) | ||||
| 1 | Liancheng | 315.99 | 314.42 | 313.61 | 314.21 | 313.81 | 313.99 | [−0.75, −0.50] |
| 2 | Shanghang | 504.58 | 503.16 | 501.92 | 502.85 | 502.23 | 502.55 | [−0.53, −0.28] |
| 3 | Wuping | 337.78 | 336.69 | 335.48 | 336.38 | 335.77 | 336.10 | [−0.68, −0.32] |
| 4 | Xinluo | 1160.54 | 1159.93 | 1159.43 | 1159.81 | 1159.55 | 1159.67 | [−0.10, −0.05] |
| 5 | Yongding | 390.41 | 389.22 | 388.26 | 388.98 | 388.52 | 388.91 | [−0.55, −0.30] |
| 6 | Pinghe | 376.92 | 375.54 | 374.87 | 375.30 | 375.01 | 375.15 | [−0.54, −0.37] |
| 7 | Changting | 333.62 | 344.81 | 349.26 | 345.94 | 348.14 | 347.04 | [3.35, 4.69] |
| 8 | Zijin | 278.99 | 282.85 | 283.44 | 283.00 | 283.34 | 283.18 | [1.38, 1.60] |
| 9 | Dapu | 198.00 | 201.40 | 201.95 | 201.52 | 201.85 | 201.68 | [1.72, 1.99] |
| 10 | Fengshun | 236.99 | 240.47 | 240.97 | 240.58 | 240.88 | 240.73 | [1.47, 1.68] |
| 11 | Meixian | 341.22 | 345.53 | 345.92 | 345.68 | 345.91 | 345.83 | [1.26, 1.38] |
| 12 | Wuhua | 268.50 | 272.58 | 273.32 | 272.79 | 273.18 | 272.99 | [1.52, 1.79] |
| 13 | Xingning | 329.36 | 333.89 | 334.38 | 334.05 | 334.34 | 334.24 | [1.37, 1.53] |
| 14 | Chenghai | 683.90 | 686.66 | 686.21 | 686.54 | 686.34 | 686.39 | [0.34, 0.40] |
| Total | 5756.79 | 5787.15 | 5789.02 | 5787.64 | 5788.88 | 5788.45 | [0.53, 0.56] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, N.; Sun, P.; He, W.; Yang, L.; Qiu, Y.; Chen, Y.; Zhao, W. Water Resources Allocation in the Tingjiang River Basin: Construction of an Interval-Fuzzy Two-Stage Chance-Constraints Model and Its Assessment through Pearson Correlation. Water 2022, 14, 2928. https://doi.org/10.3390/w14182928
Hao N, Sun P, He W, Yang L, Qiu Y, Chen Y, Zhao W. Water Resources Allocation in the Tingjiang River Basin: Construction of an Interval-Fuzzy Two-Stage Chance-Constraints Model and Its Assessment through Pearson Correlation. Water. 2022; 14(18):2928. https://doi.org/10.3390/w14182928
Chicago/Turabian StyleHao, Ning, Peixuan Sun, Wei He, Luze Yang, Yu Qiu, Yingzi Chen, and Wenjin Zhao. 2022. "Water Resources Allocation in the Tingjiang River Basin: Construction of an Interval-Fuzzy Two-Stage Chance-Constraints Model and Its Assessment through Pearson Correlation" Water 14, no. 18: 2928. https://doi.org/10.3390/w14182928