Learning Enhancement Method of Long Short-Term Memory Network and Its Applicability in Hydrological Time Series Prediction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model
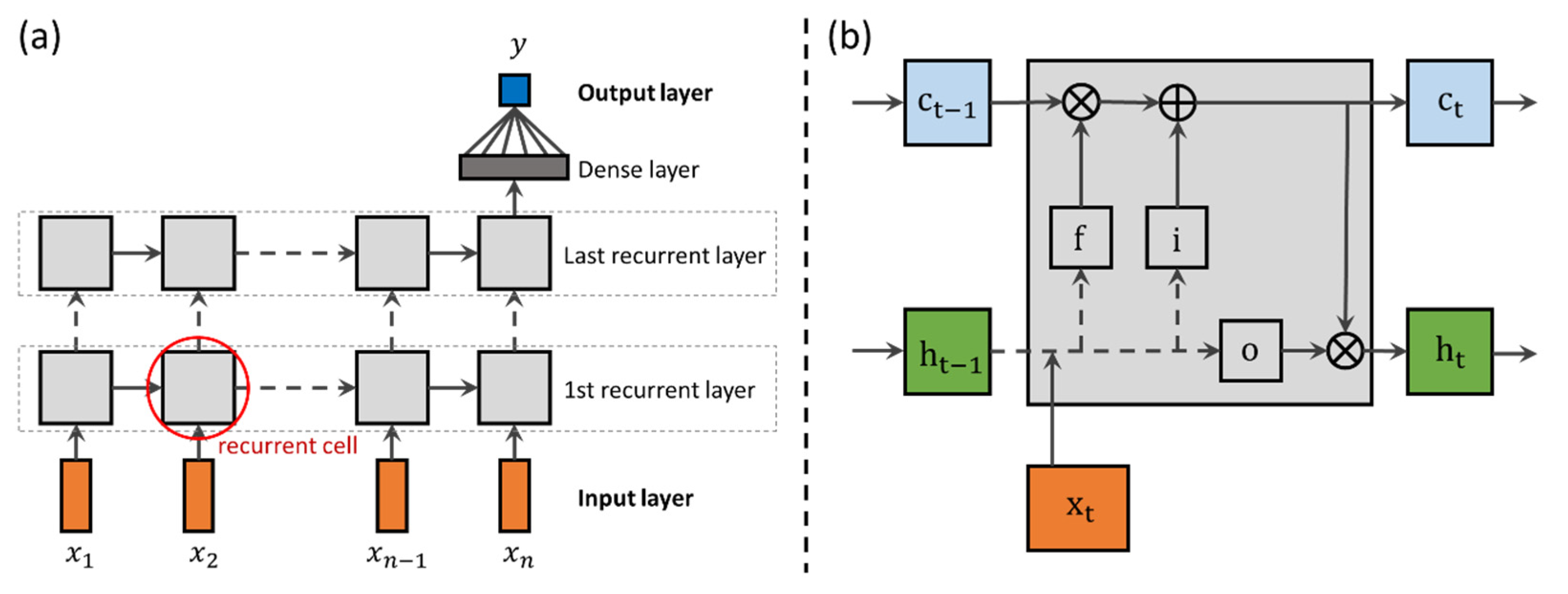
2.1.1. Long Short-Term Memory Network
2.1.2. Benchmark Model
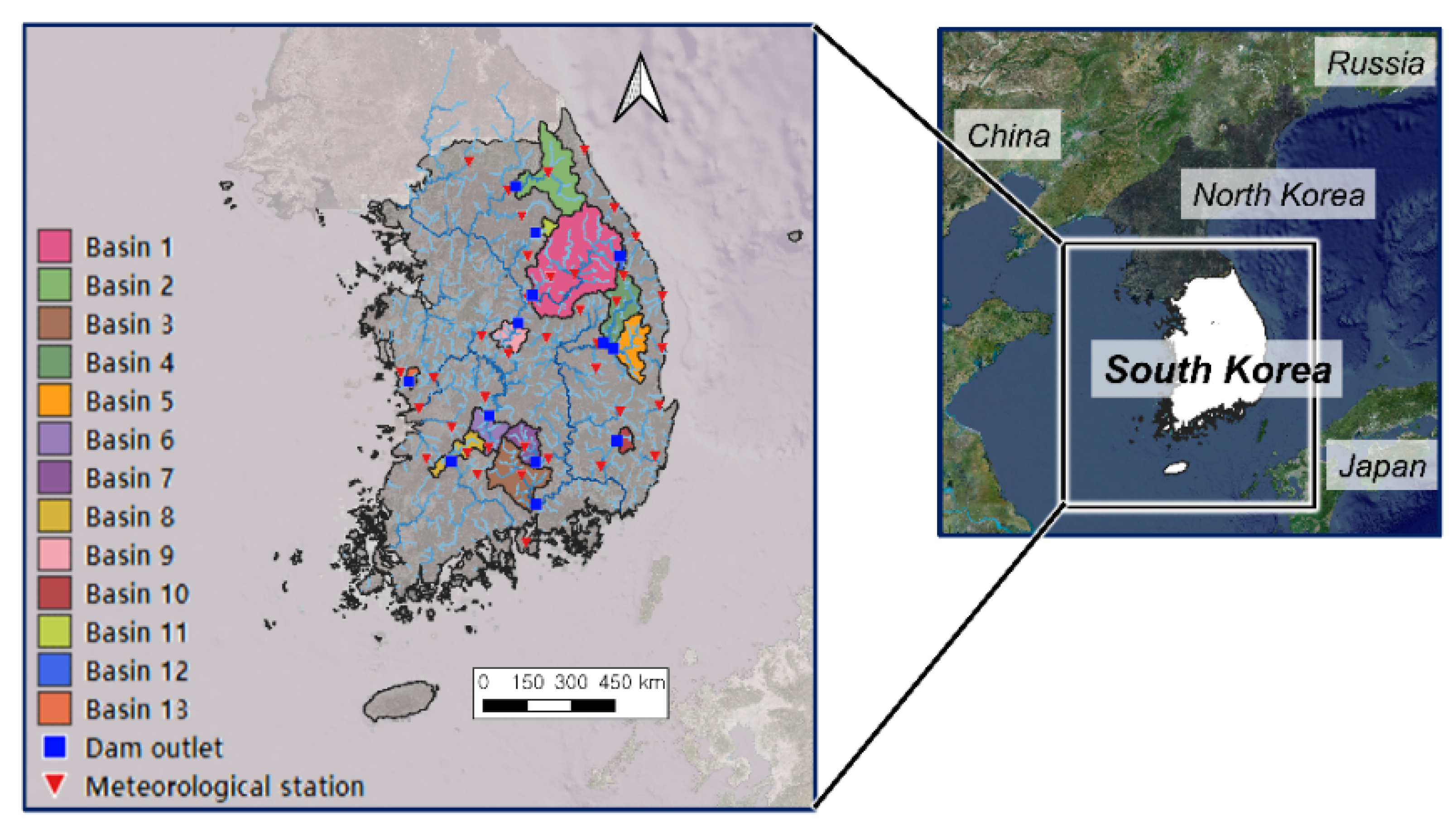
2.2. Study Area and Data
2.3. Experimental Setup
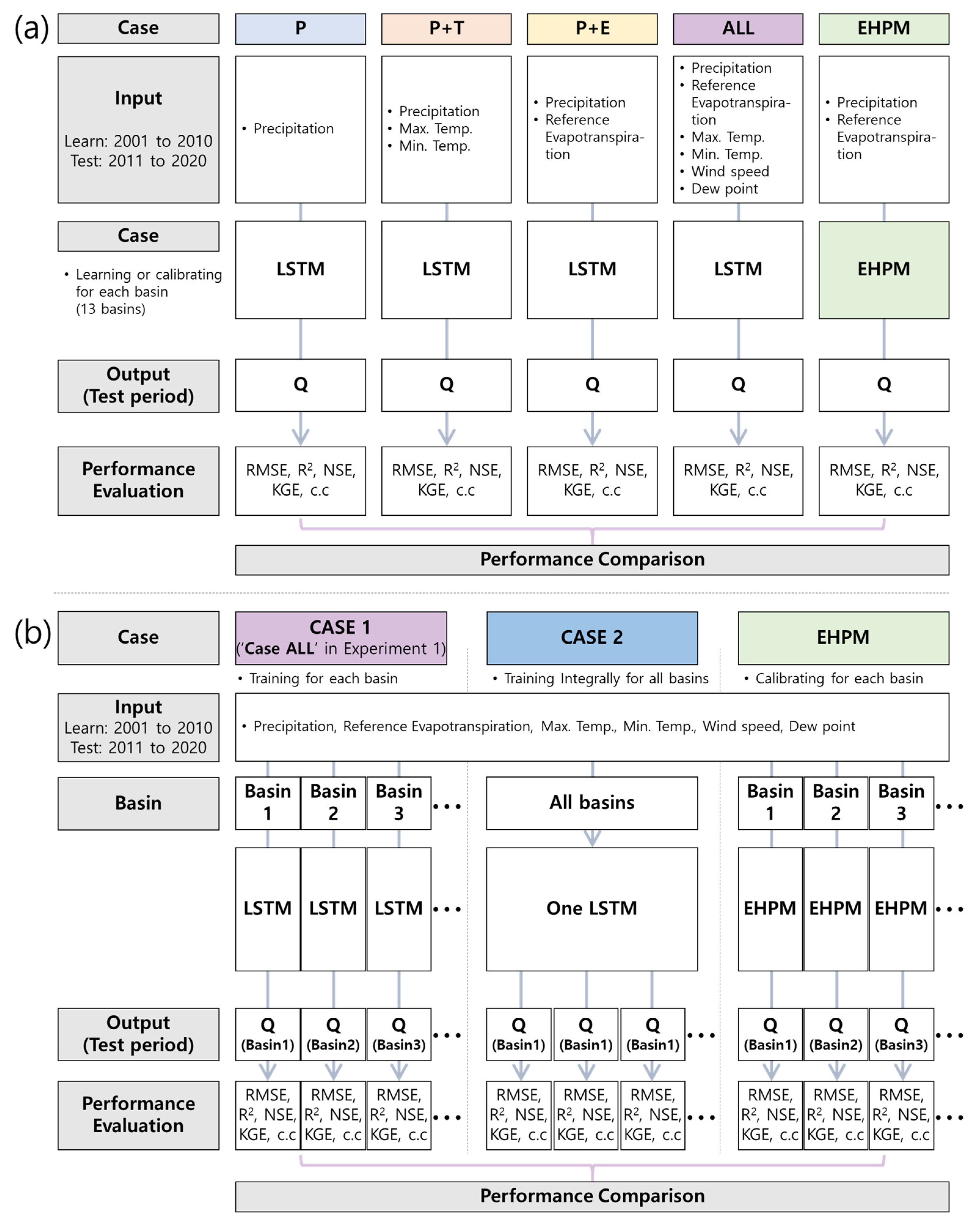
2.3.1. Experiment 1: Combination of Input Data for Learning
2.3.2. Experiment 2: Multi-Basins Integrated Learning
2.4. Model Evaluation
3. Results and Discussion
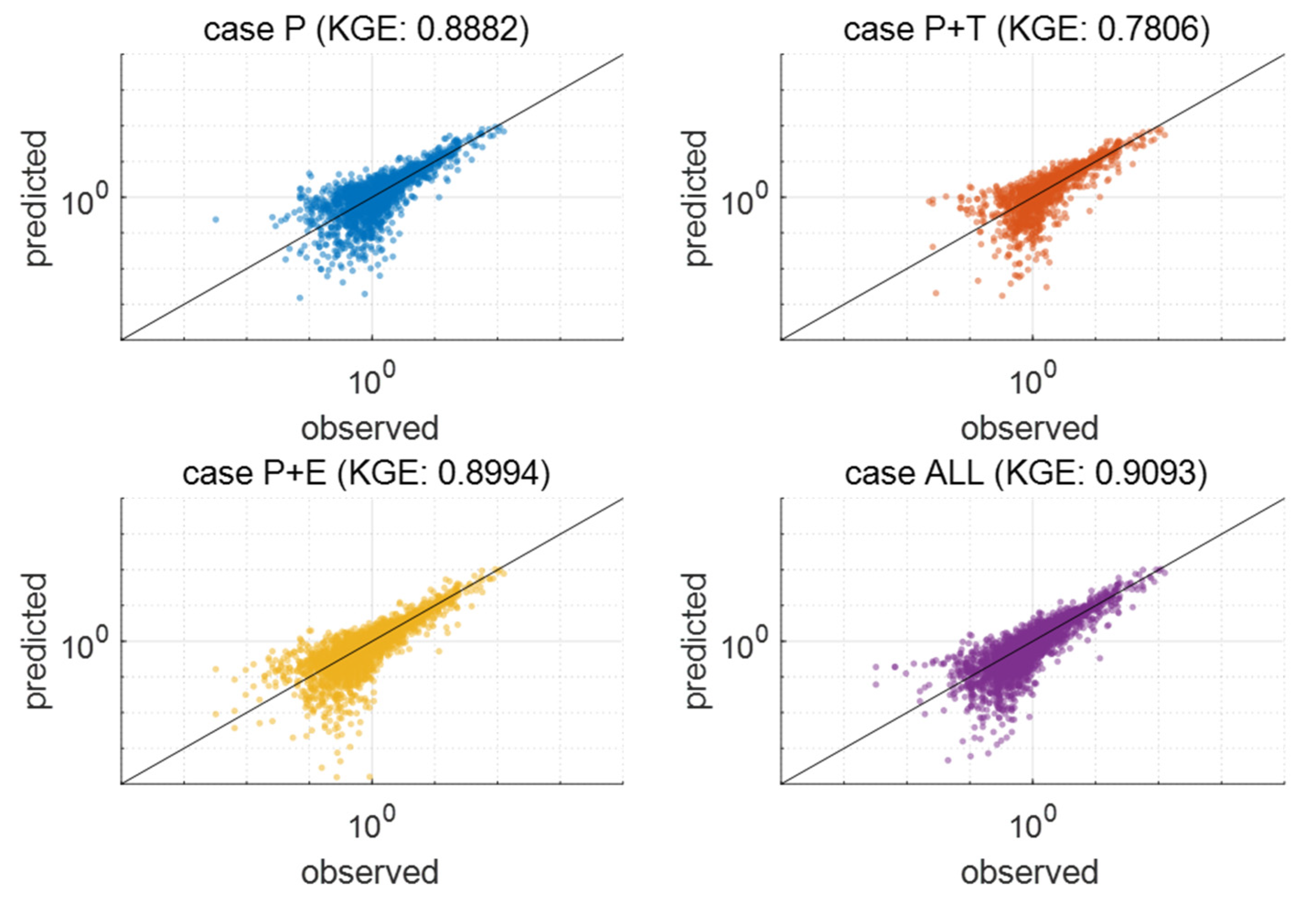
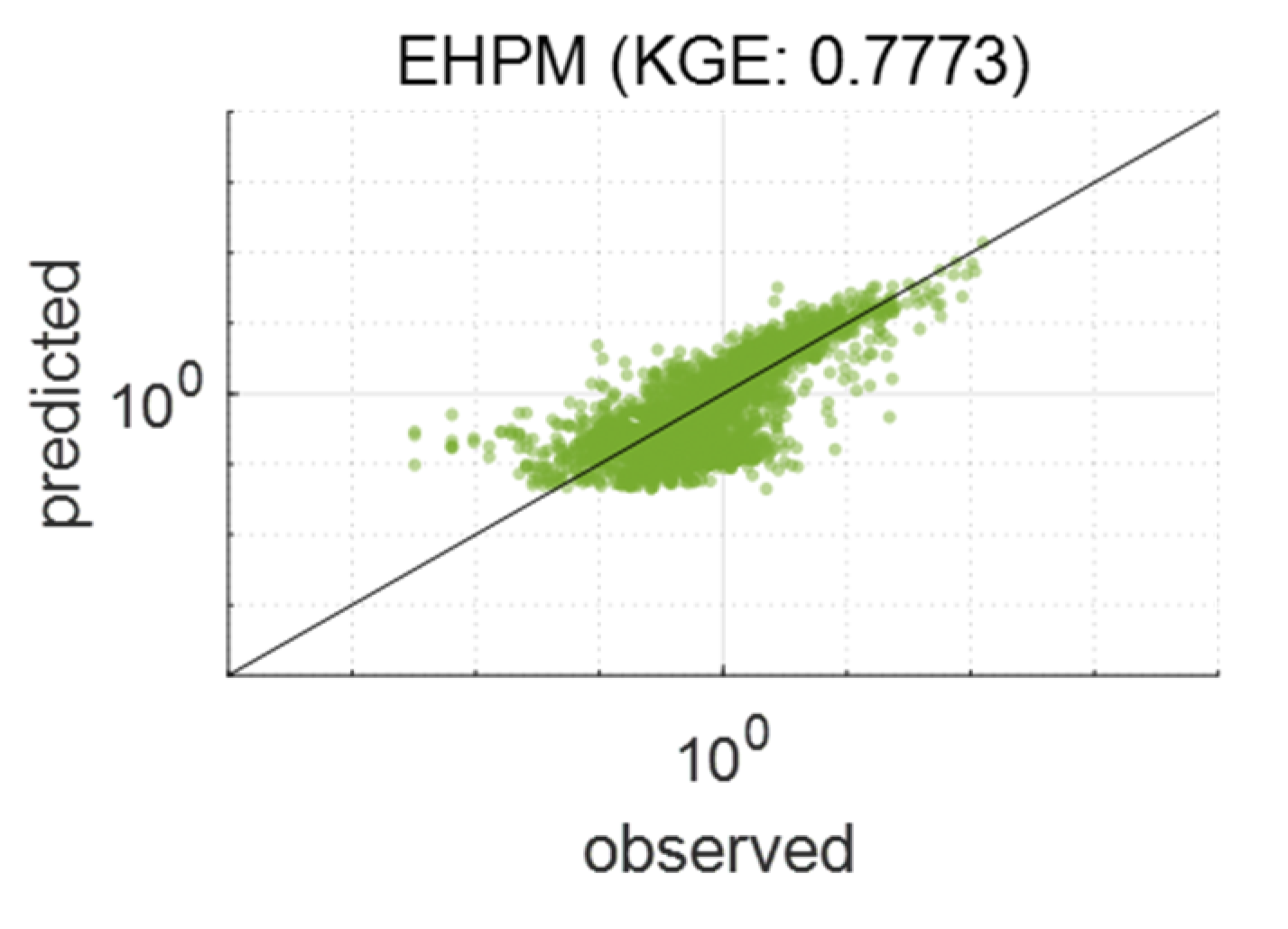
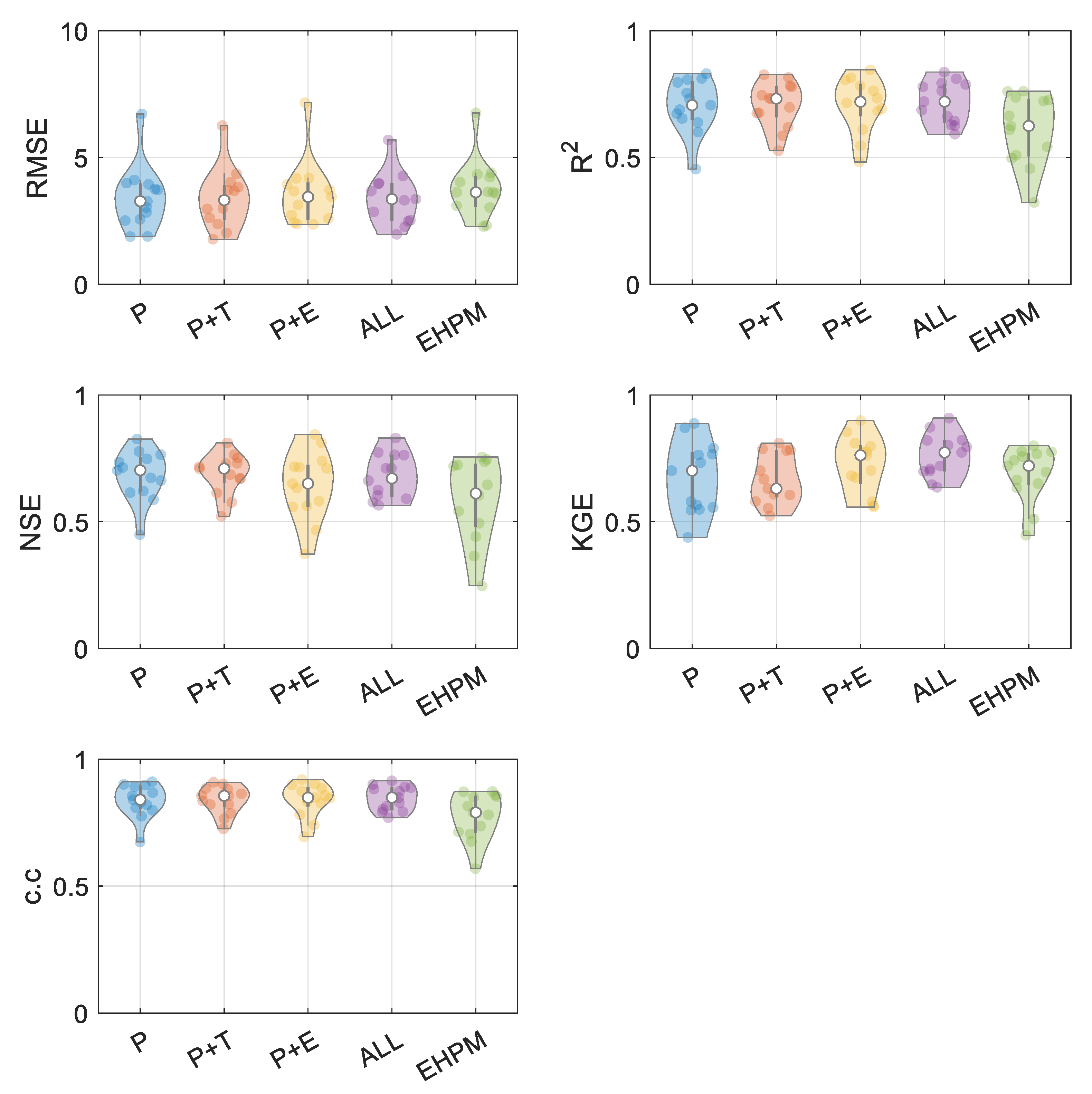
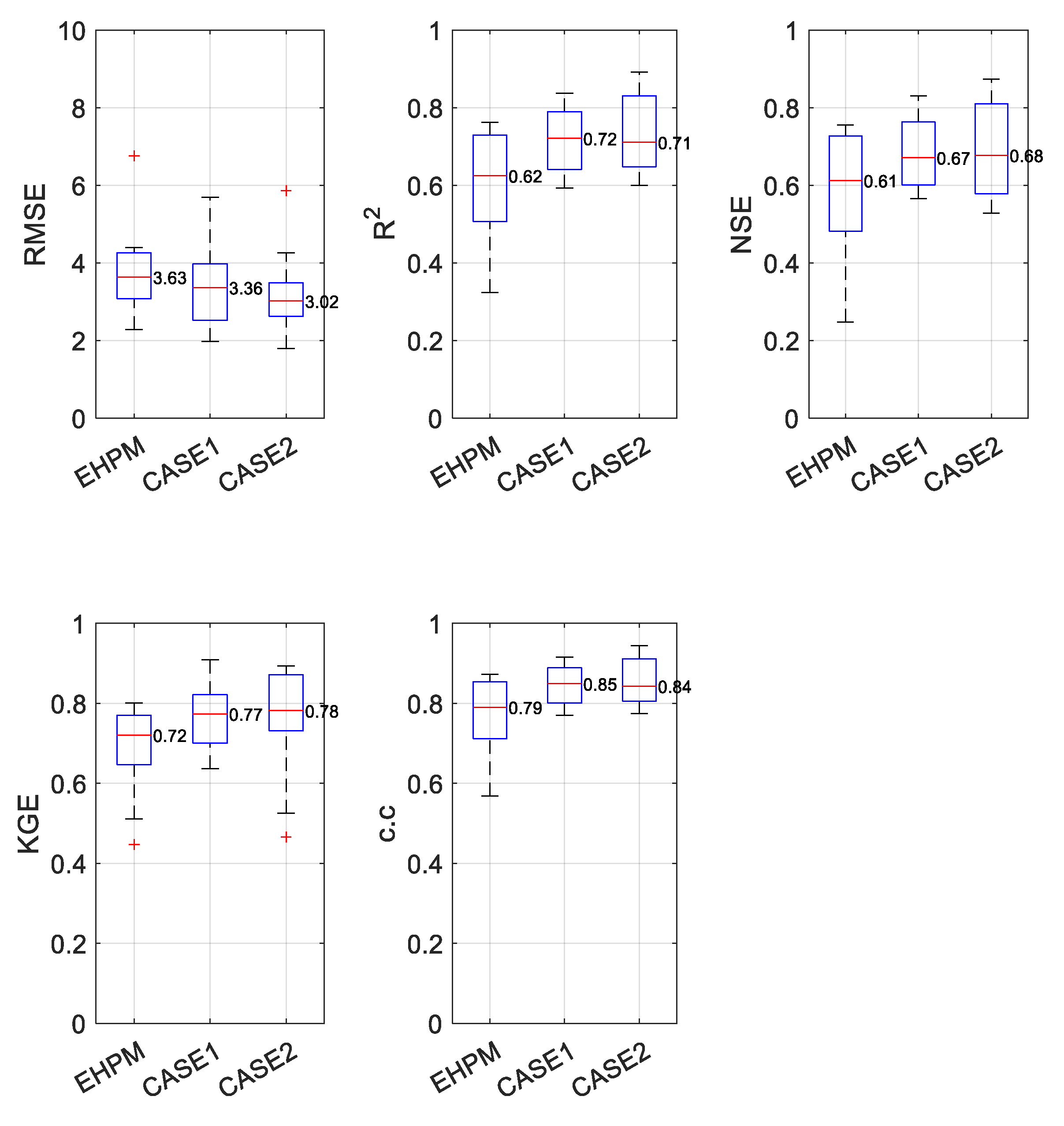
3.1. Best Combination of Input Variables for LSTM Learning
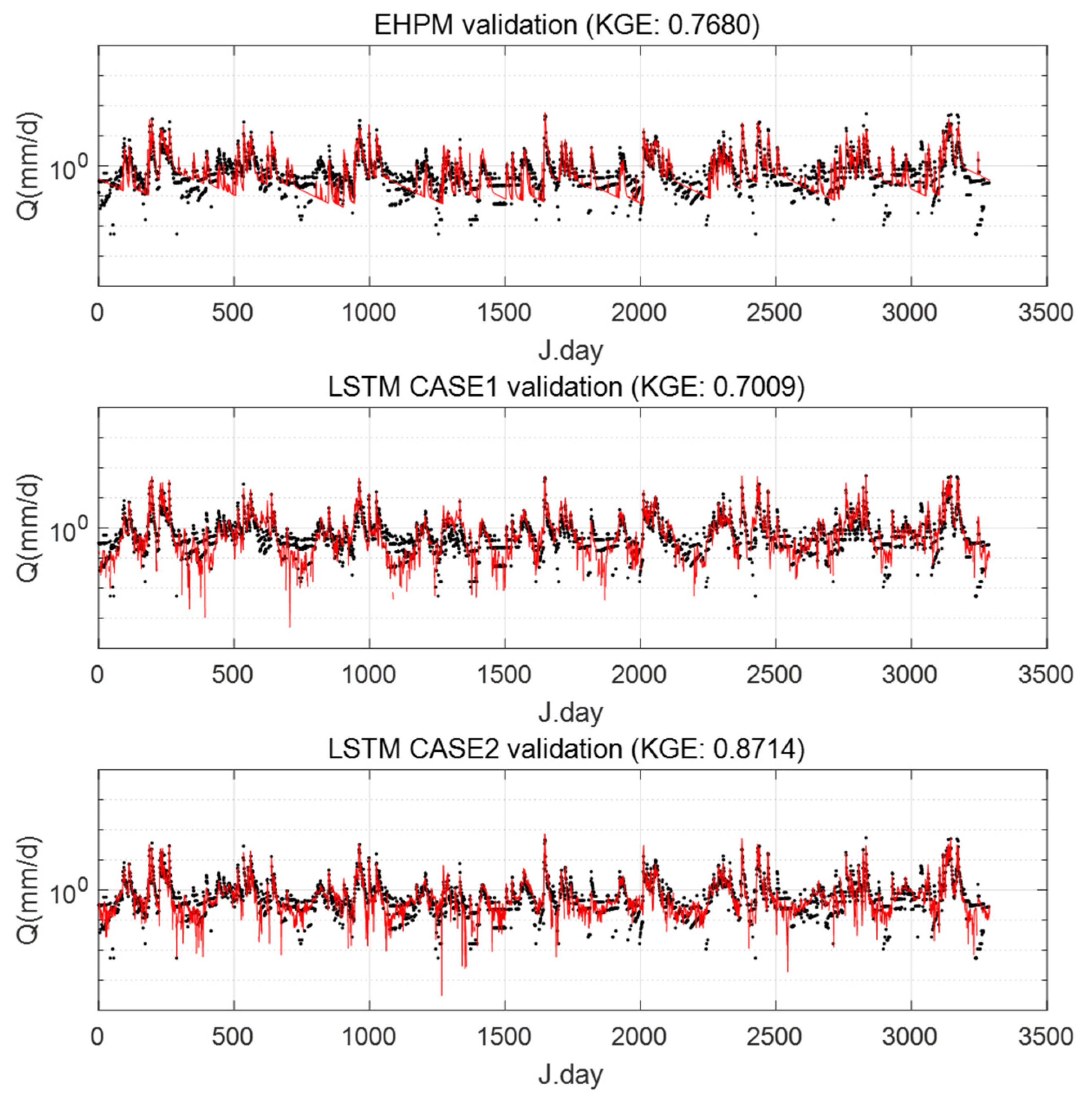
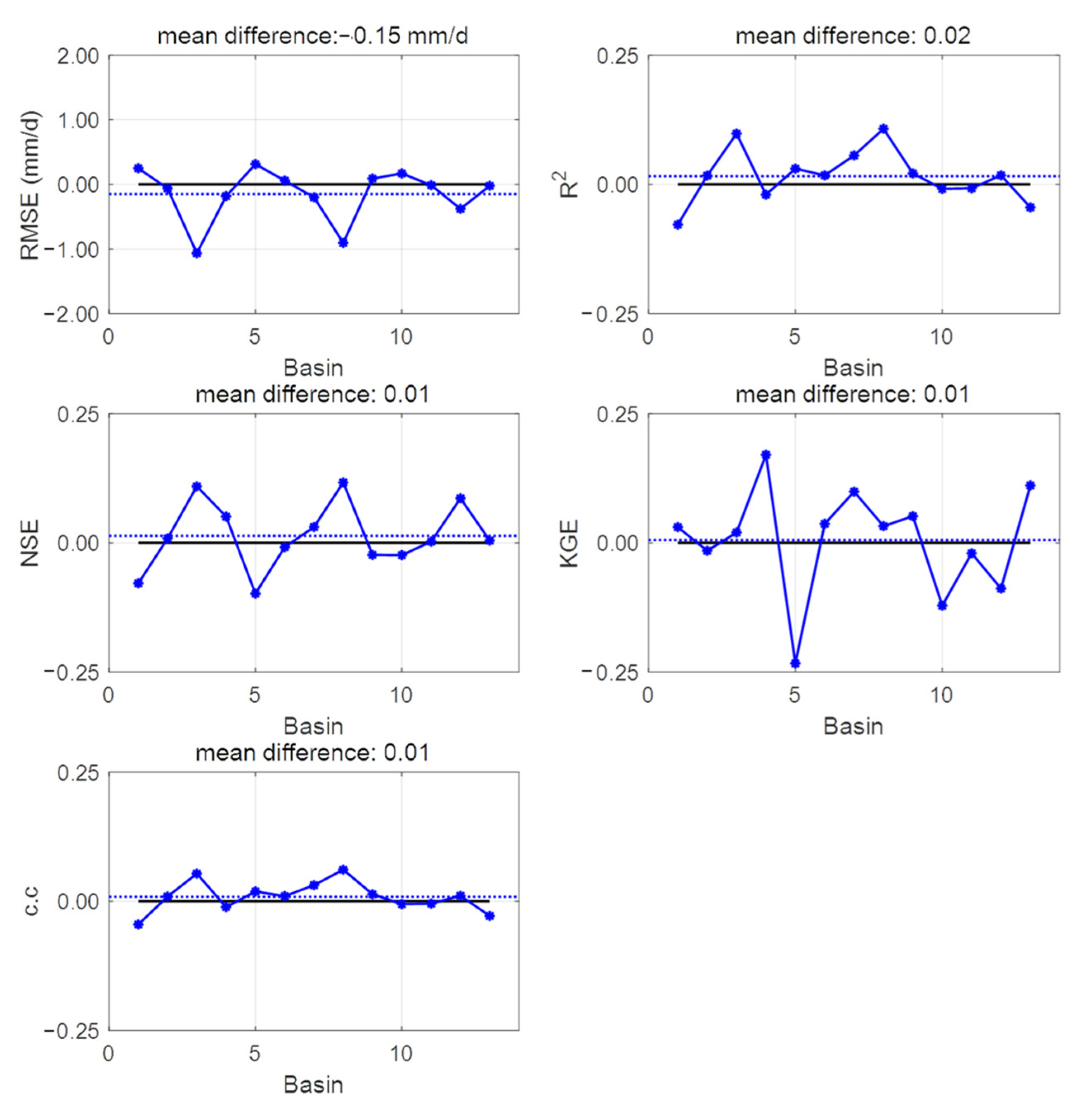
3.2. One LSTM for Predicting Streamflow in Each Basin
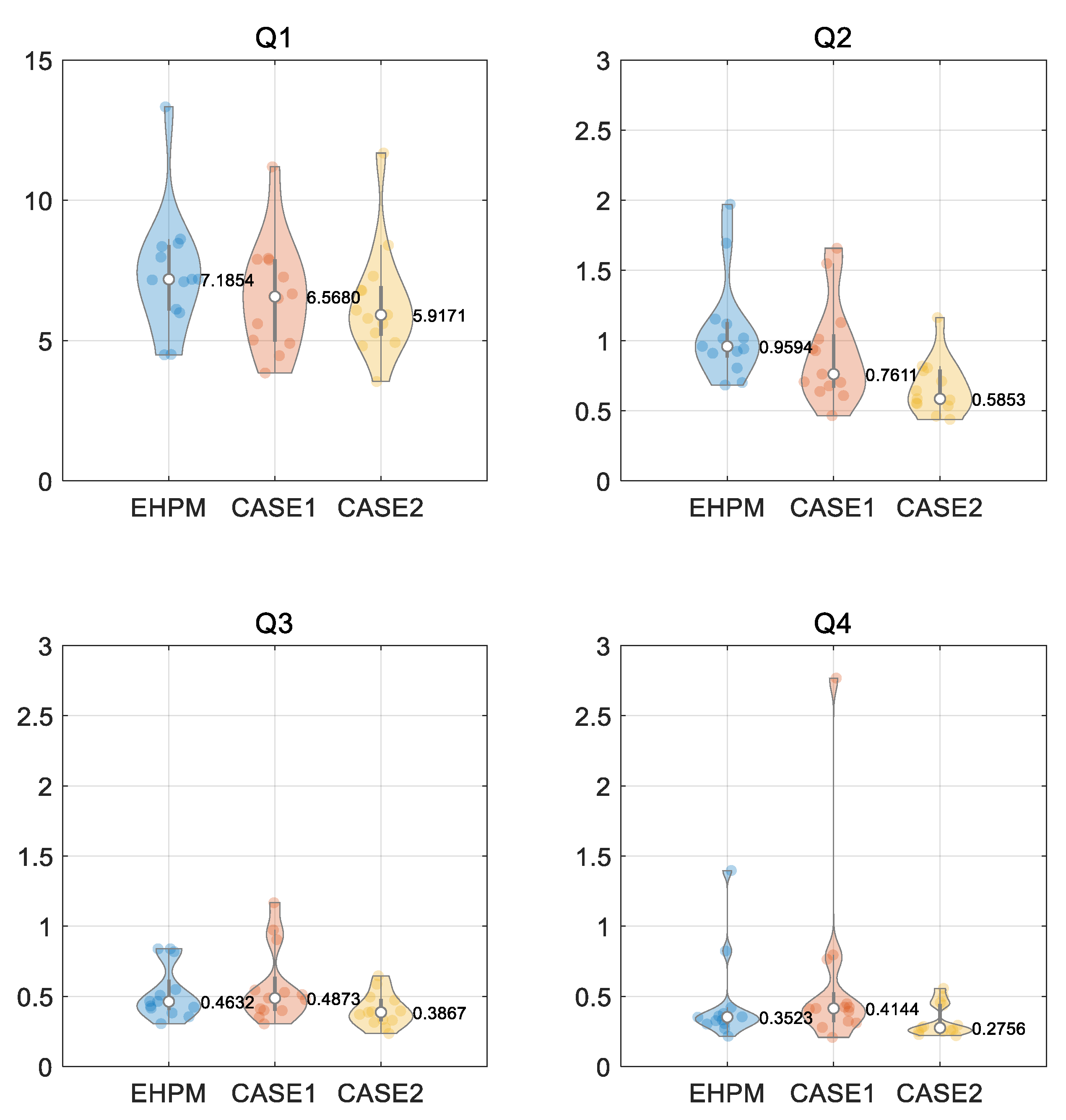
3.3. Performance Evaluation for Flow Segments
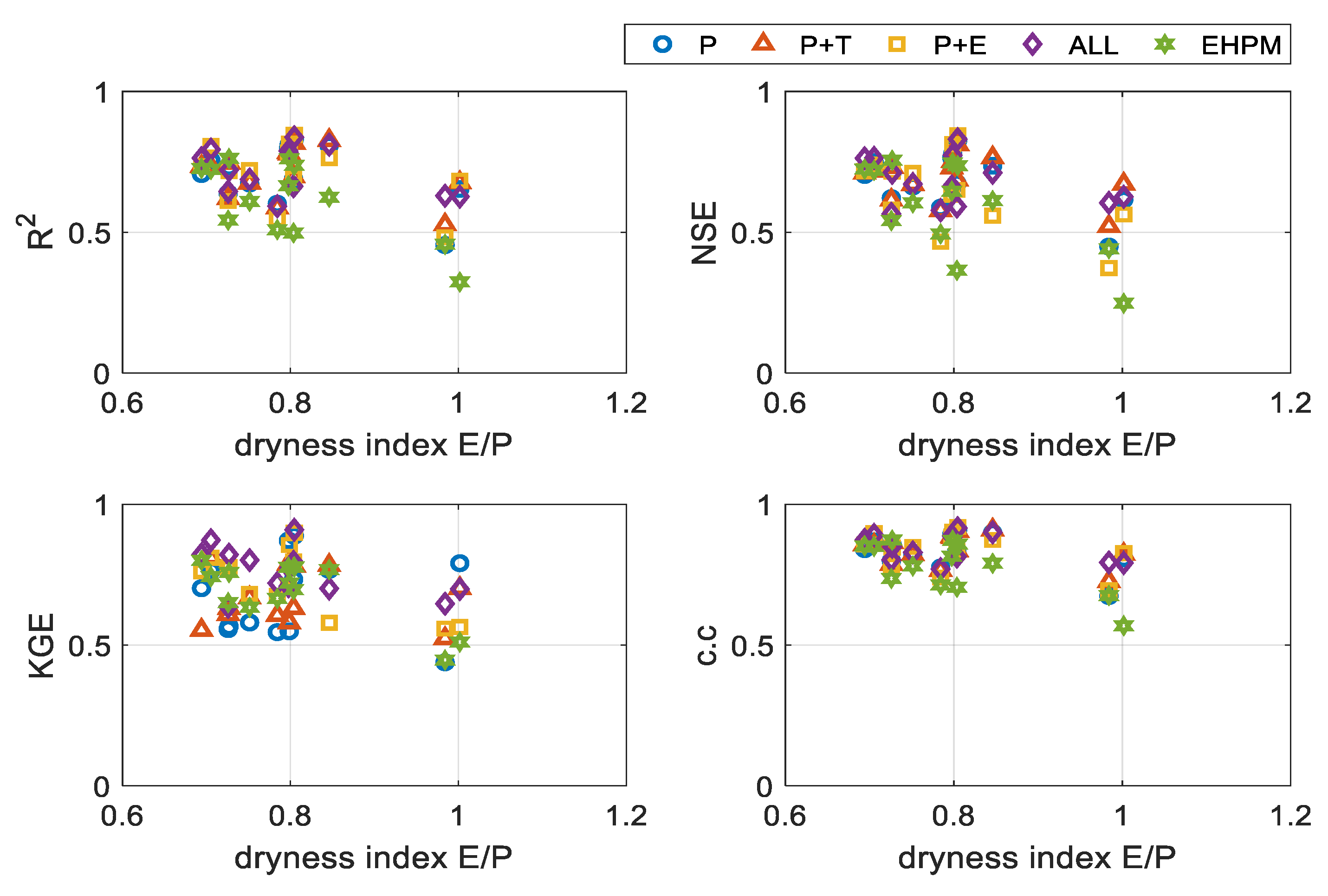
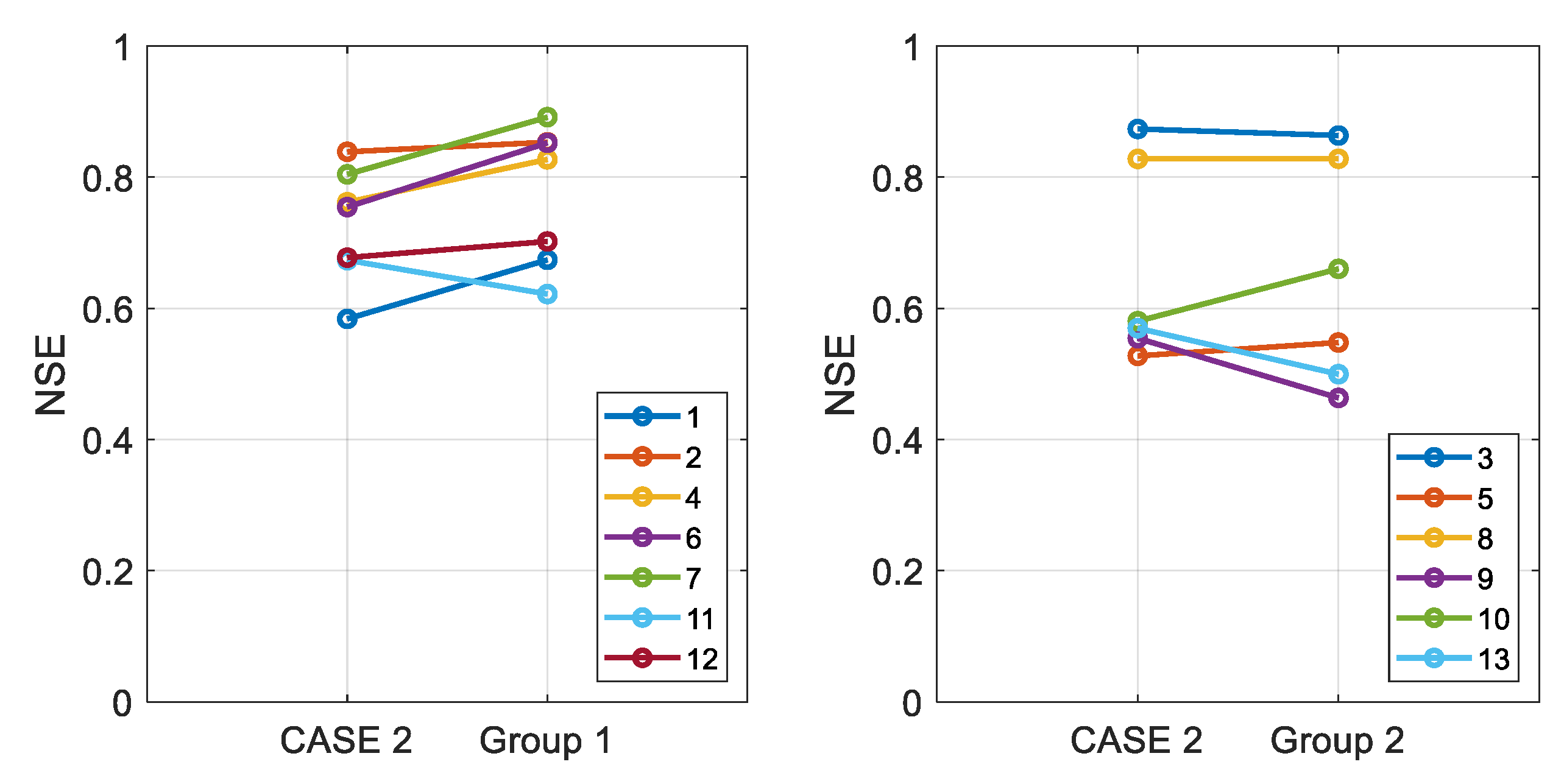
3.4. Integrated Learning Considering a Basin Characteristic
4. Conclusions
- The performance and robustness of the outputs from LSTM can be enhanced by using various meteorological information as an input variable of LSTM;
- The LSTM could reasonably predict streamflow in the basins through the integrated learning method. This result means that the integrated learning method is a possible approach for reducing the data demand, and the concept of regionalization can be applied to LSTM. This regionalization approach may also help the streamflow in ungauged basins through further research;
- In particular, at least in the basins selected in this study, low-flow predictions are improved through the integrated learning;
- The selection of target basins for the integrated learning affects the performance of LSTM. Therefore, further research is needed on this topic.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pagano, T.C.; Wood, A.W.; Ramos, M.H.; Cloke, H.L.; Pappenberger, F.; Clark, M.P.; Cranston, M.; Kavetski, D.; Mathevet, T.; Sorooshian, S.; et al. Challenges of operational river forecasting. J. Hydrometeorol. 2014, 15, 1692–1707. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Salamon, P.; Alfieri, L.; Pozo, J.T.D.; Zsoter, E.; Pappenberger, F. The effect of reference climatology on global flood forecasting. J. Hydrometeorol. 2016, 17, 1131–1145. [Google Scholar] [CrossRef]
- Nourani, V. An emotional ANN (EANN) approach to modeling rainfall-runoff process. J. Hydrol. 2017, 544, 267–277. [Google Scholar] [CrossRef]
- Feng, D.; Fang, K.; Shen, C. Enhancing streamflow forecast and extracting insights using long-short term memory networks with data integration at continental scales. Water Resour. Res. 2020, 56, e2019WR026793. [Google Scholar] [CrossRef]
- Beven, K. Rainfall-Runoff Modelling: The Primer, 2nd ed.; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Beven, K. Linking parameters across scales: Subgrid parameterizations and scale dependent hydrological models. Hydrol. Processes 1995, 9, 507–525. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G.; Parajka, J.D. Regionalization methods in rainfall-runoff modelling using large catchment samples. IAHS Publ. 2006, 307, 117–125. [Google Scholar]
- Gupta, H.V.; Nearing, G.S. Debates--The future of hydrological sciences: A (common) path forward? Using models and data to learn: A systems theoretic perspective on the future of hydrological science. Water Resour. Res. 2014, 50, 5351–5359. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Y.; Zhang, X.; Li, Y.; Zhang, R.; Fu, G. Using long short-term memory networks for river flow prediction. Hydrol. Res. 2020, 51, 1358–1376. [Google Scholar] [CrossRef]
- Tanty, R.; Desmukh, T.S. Application of artificial neural network in hydrology-A review. Int. J. Eng. Technol. Res. 2015, 4, 184–188. [Google Scholar]
- Fang, K.; Shen, C.; Kifer, D.; Yang, X. Prolongation of SMAP to spatiotemporally seamless coverage of continental US using a deep learning neural network. Geophys. Res. Lett. 2017, 44, 11030–11039. [Google Scholar] [CrossRef]
- Shen, C. A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Shen, C.; Laloy, E.; Elshorbagy, A.; Albert, A.; Bales, J.; Chang, F.-J.; Ganguly, S.; Hsu, K.-L.; Kifer, D.; Fang, Z.; et al. HESS Opinions: Incubating deep-learning-powered hydrologic science advances as a community. Hydrol. Earth Syst. Sci. 2018, 22, 5639–5656. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, X.; Yuan, X.; Xu, Z. An improved long short-term memory network for streamflow forecasting in the upper Yangtze River. Stoch. Environ. Res. Risk Assess. 2020, 34, 1313–1329. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C. Near-real-time forecast of satellite-based soil moisture using long short-term memory with an adaptive data integration kernel. J. Hydrometeorol. 2020, 21, 399–413. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Benchmarking a catchment-aware long short-term memory network (LSTM) for large-scale hydrological modeling. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–32. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of long short-term memory (LSTM) neural network for flood forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Sudriani, Y.; Ridwansyah, I.; Rustini, H.A. Long short term memory (LSTM) recurrent neural network (RNN) for discharge level prediction and forecast in Cimandiri river, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2019, 229, 012037. [Google Scholar] [CrossRef]
- Sahoo, B.B.; Jha, R.; Singh, A.; Kumar, D. Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting. Acta Geophys. 2019, 67, 1471–1481. [Google Scholar] [CrossRef]
- Lu, D.; Konapala, G.; Painter, S.L.; Kao, S.C.; Gangrade, S. Streamflow simulation in data-scarce basins using Bayesian and physics-informed machine learning models. Journal of Hydrometeorology 2021, 22, 1421–1438. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Xu, Y.P.; Yang, Z.; Wang, G.; Zhu, Q. Integration of a parsimonious hydrological model with recurrent neural networks for improved streamflow forecasting. Water 2018, 10, 1655. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ayzel, G.; Kurochkina, L.; Abramov, D.; Zhuravlev, S. Development of a Regional Gridded Runoff Dataset Using Long Short-Term Memory (LSTM) Networks. Hydrology 2021, 8, 6. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Choi, J.; Kim, S. Conceptual eco-hydrological model reflecting the interaction of climate-soil-vegetation-groundwater table in humid regions. J. Korea Water Resour. Assoc. 2021, 54, 681–692. (In Korean) [Google Scholar]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39, 1201. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italiy, 1998; Volume 300, p. D05109. [Google Scholar]
- Won, J.; Choi, J.; Lee, O.; Kim, S. Copula-based Joint Drought Index using SPI and EDDI and its application to climate change. Sci. Total Environ. 2020, 744, 140701. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ritter, A.; Munoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Patil, S.D.; Stieglitz, M. Comparing spatial and temporal transferability of hydrological model parameters. J. Hydrol. 2015, 525, 409–417. [Google Scholar] [CrossRef] [Green Version]
- Safrit, M.J.; Wood, T.M. Introduction to Measurement in Physical Education and Exercise Science, 3rd ed.; Times Mirror/Mosby: St. Louis, MO, USA, 1995; p. 71. [Google Scholar]
- Ratner, B. The correlation coefficient: Its values range between+ 1/? 1, or do they? J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef]
- Sivapalan, M. Prediction in ungauged basins: A grand challenge for theoretical hydrology. Hydrol. Processes 2003, 17, 3163–3170. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Savenije, H.; Viglione, A. Runoff Prediction in Ungauged Basins: Synthesis across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013; p. 465. [Google Scholar]
- Alipour, M.H.; Kibler, K.M. A framework for streamflow prediction in the world’s most severely data-limited regions: Test of applicability and performance in a poorly-gauged region of China. J. Hydrol. 2018, 557, 41–54. [Google Scholar] [CrossRef]
- Choi, J.; Lee, J.; Kim, S. Utilization of the Long Short-Term Memory network for predicting streamflow in ungauged basins in Korea. Ecol. Eng. 2022, 182, 106699. [Google Scholar] [CrossRef]
- Aryal, S.K.; Zhang, Y.; Chiew, F. Enhanced low flow prediction for water and environmental management. J. Hydrol. 2020, 584, 124658. [Google Scholar] [CrossRef]
- Nicolle, P.; Pushpalatha, R.; Perrin, C.; François, D.; Thiéry, D.; Mathevet, T.; Le Lay, M.; Besson, F.; Soubeyroux, J.-M.; Viel, C.; et al. Benchmarking hydrological models for low-flow simulation and forecasting on French catchments. Hydrol. Earth Syst. Sci. 2014, 18, 2829–2857. [Google Scholar] [CrossRef]
- Beven, K. Surface water hydrology-runoff generation and basin structure. Rev. Geophys. 1983, 21, 721–730. [Google Scholar] [CrossRef]
- Chatterjee, C.; Jha, R.; Lohani, A.K.; Kumar, R.; Singh, R. Estimation of SCS Curve Numbers for a Basin using rainfall-runoff Data. ISH J. Hydraul. Eng. 2002, 8, 40–49. [Google Scholar] [CrossRef]
- Bhuyan, M.J.; Borah, D.; Nath, B.K.; Deka, N.; Bora, A.K. Runoff Estimation of the Kolong River Basin in Assam, India Using NRCS-Curve Number Method and Geospatial Techniques. In Drainage Basin Dynamics; Springer: Cham, Switzerland, 2022; pp. 441–453. [Google Scholar]
| Basin Number | Basin Name | Area (km2) | Annual Mean Precipitation, P (mm/year) | Annual Mean Streamflow, Q (mm/year) | Runoff Ratio | Curve Number |
|---|---|---|---|---|---|---|
| 1 | Chungju | 6661.5 | 1305.7 | 742.0 | 0.57 | 64.2 |
| 2 | Soyanggang | 2694.3 | 1276.1 | 803.5 | 0.63 | 53.8 |
| 3 | Namgang | 2281.7 | 1519.8 | 1027.1 | 0.68 | 65.2 |
| 4 | Andong | 1590.7 | 1178.0 | 606.0 | 0.51 | 61.4 |
| 5 | Imha | 1367.7 | 1115.5 | 466.9 | 0.42 | 67.8 |
| 6 | Yongdam | 930.4 | 1446.6 | 815.9 | 0.56 | 64.3 |
| 7 | Hapcheon | 928.9 | 1329.0 | 712.5 | 0.54 | 59.5 |
| 8 | Seomjingang | 763.5 | 1388.2 | 785.6 | 0.57 | 69.6 |
| 9 | Goesan | 676.7 | 1294.4 | 651.1 | 0.50 | 68.7 |
| 10 | Woonmoon | 301.9 | 1149.1 | 705.5 | 0.61 | 68.6 |
| 11 | Hoengseong | 207.9 | 1335.0 | 777.7 | 0.58 | 54.1 |
| 12 | Boryeong | 162.3 | 1160.5 | 770.3 | 0.66 | 59.1 |
| 13 | Gwangdong | 120.7 | 1311.2 | 721.4 | 0.55 | 70.1 |
| Segment | Magnitude of Flow | Range of Percentile |
|---|---|---|
| Q1 | Highest flows | 0 to 0.25 |
| Q2 | Higher flows | 0.25 to 0.5 |
| Q3 | Lower flows | 0.5 to 0.75 |
| Q4 | Lowest flows | 0.75 to 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.; Won, J.; Jang, S.; Kim, S. Learning Enhancement Method of Long Short-Term Memory Network and Its Applicability in Hydrological Time Series Prediction. Water 2022, 14, 2910. https://doi.org/10.3390/w14182910
Choi J, Won J, Jang S, Kim S. Learning Enhancement Method of Long Short-Term Memory Network and Its Applicability in Hydrological Time Series Prediction. Water. 2022; 14(18):2910. https://doi.org/10.3390/w14182910
Chicago/Turabian StyleChoi, Jeonghyeon, Jeongeun Won, Suhyung Jang, and Sangdan Kim. 2022. "Learning Enhancement Method of Long Short-Term Memory Network and Its Applicability in Hydrological Time Series Prediction" Water 14, no. 18: 2910. https://doi.org/10.3390/w14182910





