Enhancing a Multi-Step Discharge Prediction with Deep Learning and a Response Time Parameter
Abstract
:1. Introduction
2. Materials and Methods
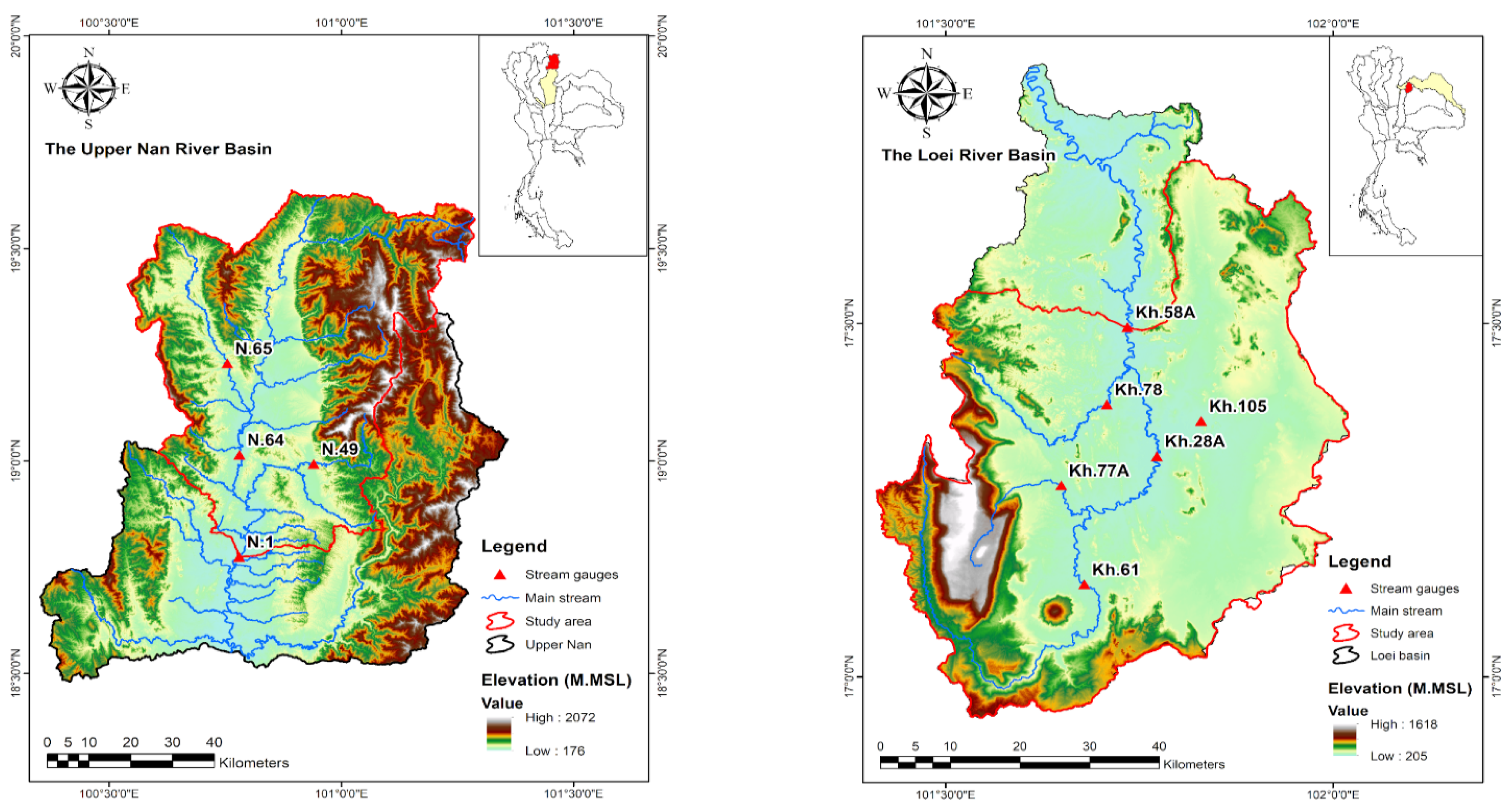
2.1. Study Area
2.2. Methodology
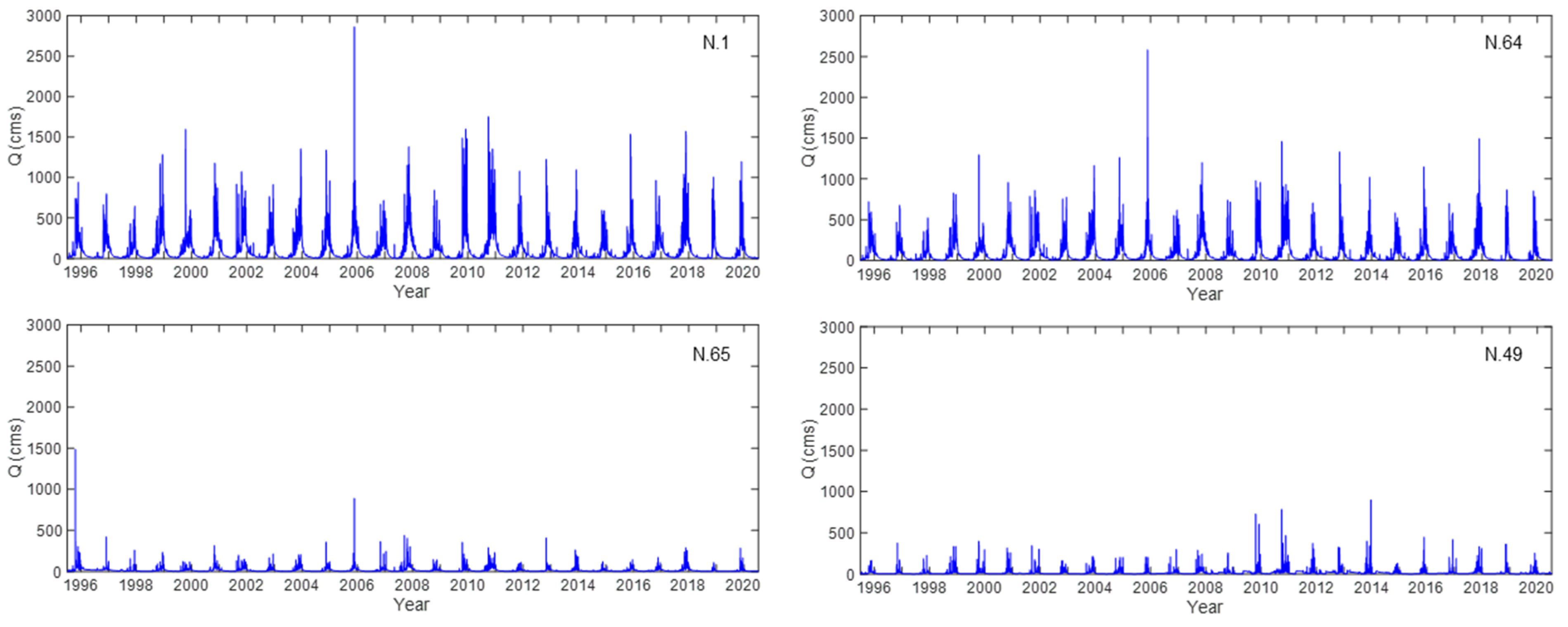
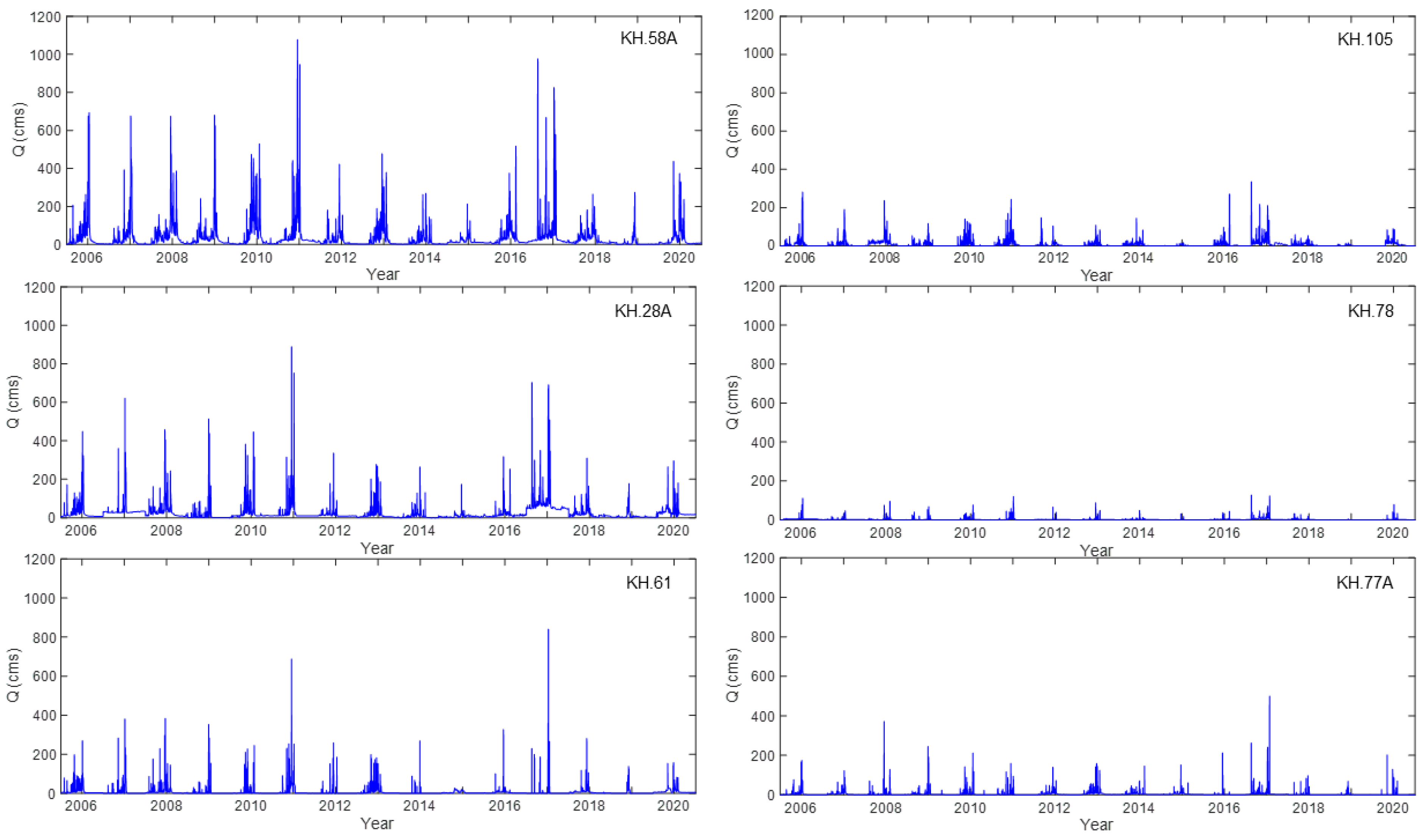
2.2.1. Data Collection and Data Preparation
2.2.2. Model Development
2.2.3. Evaluation Metrics
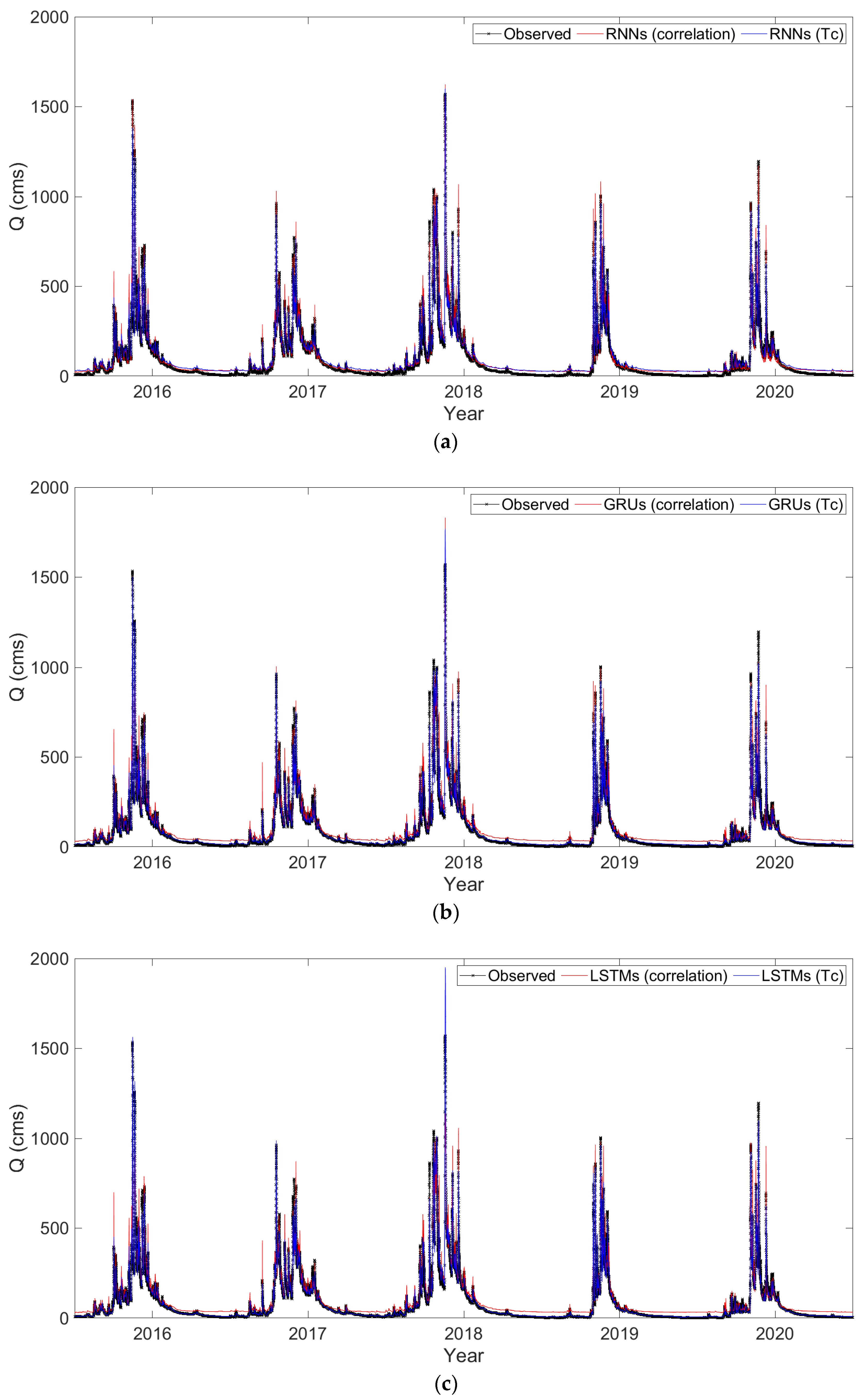
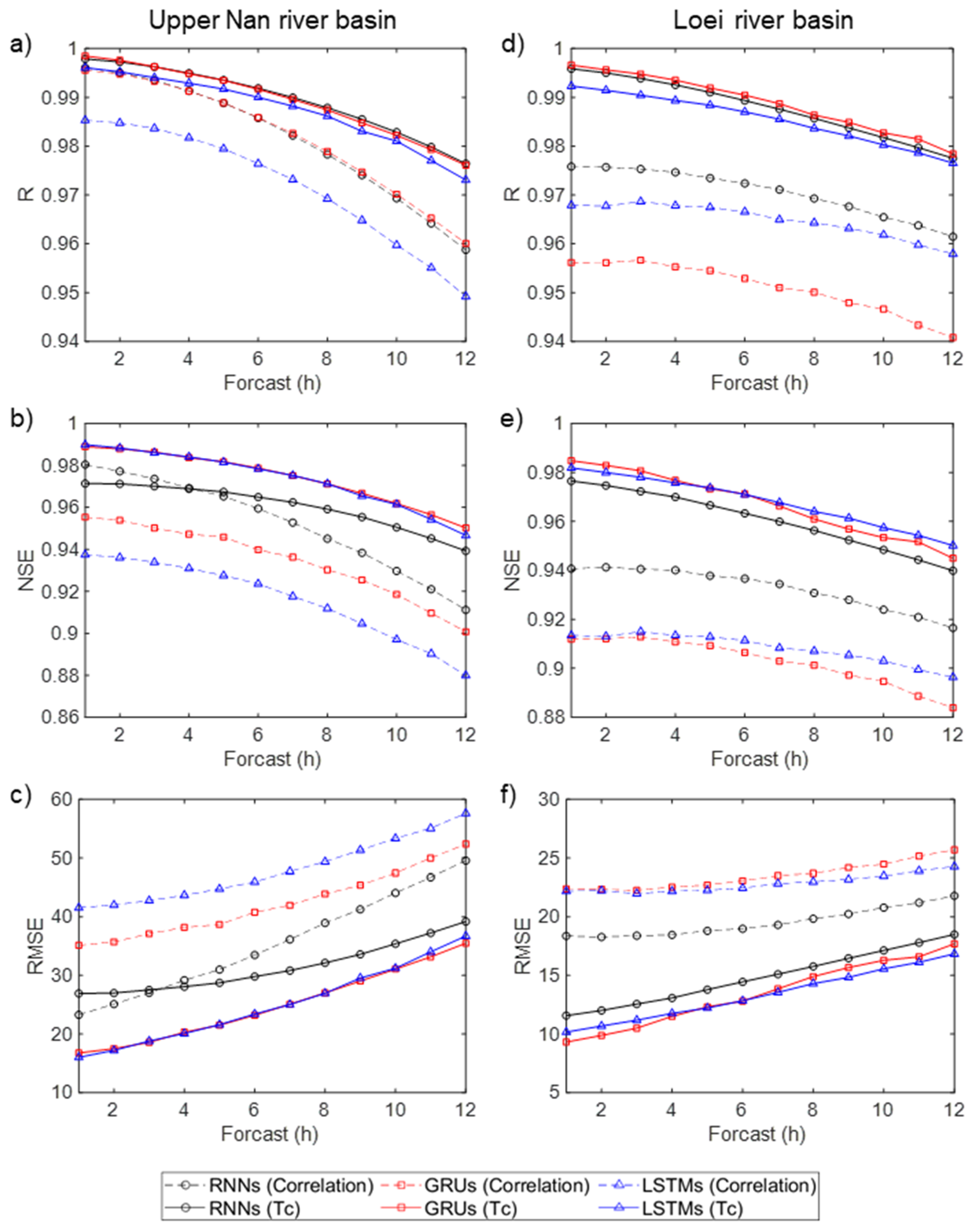
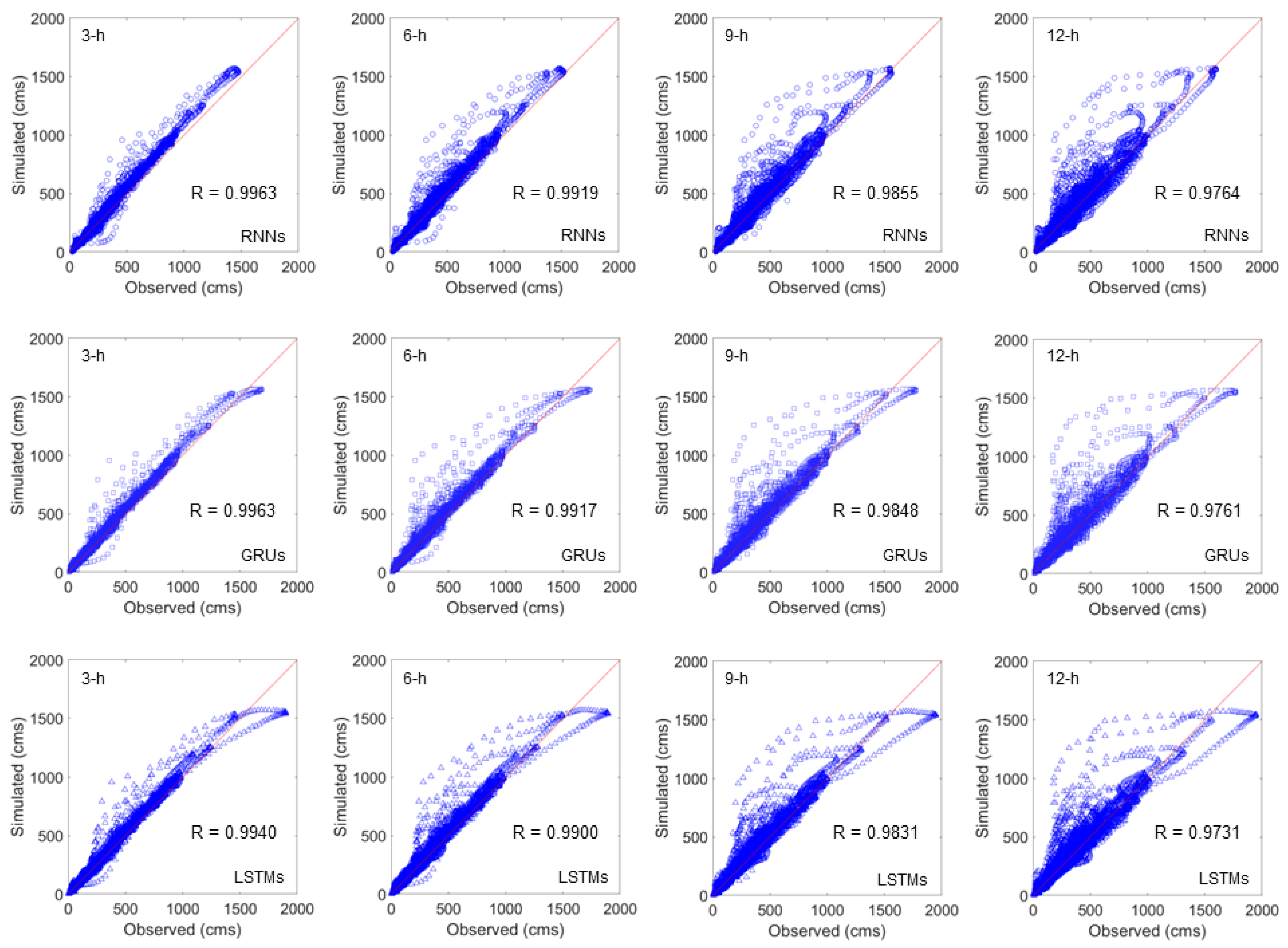
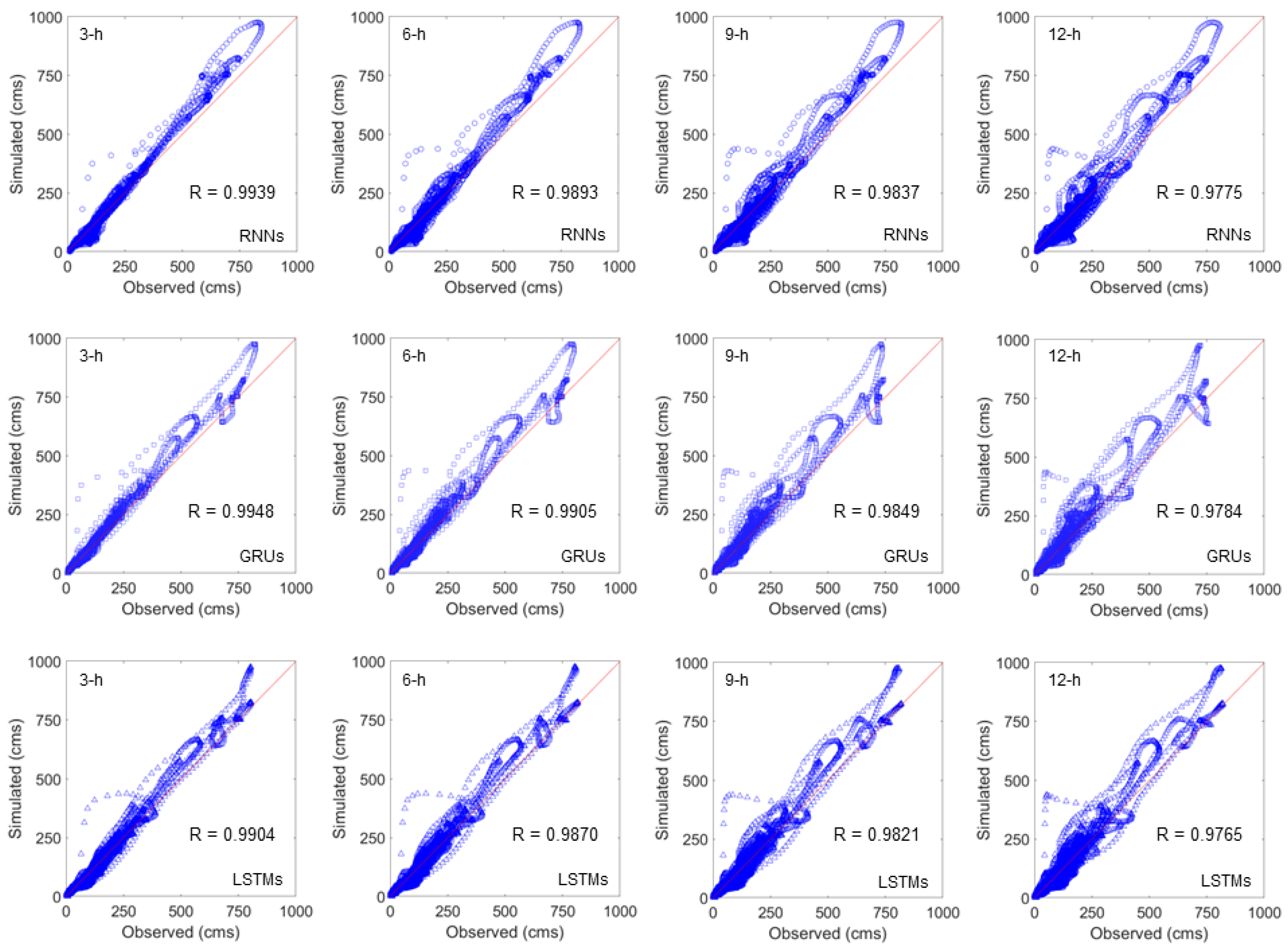
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Noymanee, J.; Theeramunkong, T. Flood Forecasting with Machine Learning Technique on Hydrological Modeling. Procedia Comput. Sci. 2019, 156, 377–386. [Google Scholar] [CrossRef]
- Cloke, H.L.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar] [CrossRef]
- Damle, C.; Yalcin, A. Flood prediction using time series data mining. J. Hydrol. 2007, 333, 305–316. [Google Scholar] [CrossRef]
- Chang, F.J.; Hsu, K.; Chang, L.C. Flood Forecasting Using Machine Learning Methods; MDPI: Basel, Switzerland, 2019; p. 364. [Google Scholar]
- Yaseen, Z.M.; El-Shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-w. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Puttinaovarat, S.; Horkaew, P. Flood Forecasting System Based on Integrated Big and Crowdsource Data by Using Machine Learning Techniques. IEEE Access 2020, 8, 5885–5905. [Google Scholar] [CrossRef]
- Wu, W.; Emerton, R.; Duan, Q.; Wood, A.W.; Wetterhall, F.; Robertson, D.E. Ensemble flood forecasting: Current status and future opportunities. WIREs Water 2020, 7, e1432. [Google Scholar] [CrossRef]
- Ghorpade, P.; Gadge, A.; Lende, A.; Chordiya, H.; Gosavi, G.; Mishra, A.; Hooli, B.; Ingle, Y.S.; Shaikh, N. Flood Forecasting Using Machine Learning: A Review. In Proceedings of the 2021 8th International Conference on Smart Computing and Communications, Kochi, Kerala, India, 1–3 July 2021. [Google Scholar]
- Nguyen, D.T.; Chen, S.-T. Real-Time Probabilistic Flood Forecasting Using Multiple Machine Learning Methods. Water 2020, 12, 787. [Google Scholar] [CrossRef]
- Meshram, S.G.; Meshram, C.; Santos, C.A.G.; Benzougagh, B.; Khedher, K.M. Streamflow Prediction Based on Artificial Intelligence Techniques. Iran. J. Sci. Technol.-Trans. Civ. Eng. 2021, 46, 2393–2403. [Google Scholar] [CrossRef]
- Tongal, H.; Booij, M.J. Simulation and forecasting of streamflows using machine learning models coupled with base flow separation. J. Hydrol. 2018, 564, 266–282. [Google Scholar] [CrossRef]
- Parisouj, P.; Mohebzadeh, H.; Lee, T. Employing Machine Learning Algorithms for Streamflow Prediction: A Case Study of Four River Basins with Different Climatic Zones in the United States. Water Resour. Manag. 2020, 34, 4113–4131. [Google Scholar] [CrossRef]
- Rezaie-Balf, M.; Fani Nowbandegani, S.; Samadi, S.Z.; Fallah, H.; Alaghmand, S. An Ensemble Decomposition-Based Artificial Intelligence Approach for Daily Streamflow Prediction. Water 2019, 11, 709. [Google Scholar] [CrossRef]
- Chen, P.A.; Chang, L.C.; Chang, F.J. Reinforced recurrent neural networks for multi-step-ahead flood forecasts. J. Hydrol. 2013, 497, 71–79. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, P.A.; Lu, Y.R.; Huang, E.; Chang, K.Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Song, T.; Ding, W.; Wu, J.; Liu, H.; Zhou, H.; Chu, J. Flash Flood Forecasting Based on Long Short-Term Memory Networks. Water 2019, 12, 109. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Liu, M.; Huang, Y.; Li, Z.; Tong, B.; Liu, Z.; Sun, M.; Jiang, F.; Zhang, H. The Applicability of LSTM-KNN Model for Real-Time Flood Forecasting in Different Climate Zones in China. Water 2020, 12, 440. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Gude, V.; Corns, S.; Long, S. Flood Prediction and Uncertainty Estimation Using Deep Learning. Water 2020, 12, 884. [Google Scholar] [CrossRef]
- Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K.W. Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting. Water 2020, 12, 1500. [Google Scholar] [CrossRef]
- U.S. Department of Agriculture Natural Resources Conservation Service (USDA-NRCS). Time of concentration. In National Engineering Handbook (NEH); U.S. Department of Agriculture Natural Resources Conservation Service (USDA-NRCS): Washington, DC, USA, 2010; p. 29. [Google Scholar]
- Gericke, O.J.; Smithers, J.C. Review of methods used to estimate catchment response time for the purpose of peak discharge estimation. Hydrol. Sci. J. 2014, 59, 1935–1971. [Google Scholar] [CrossRef]
- Kirpich, Z.P. Time of Concentration of Small Agricultural Watersheds. Civ. Eng. 1940, 10, 362. [Google Scholar]
- Kerby, W.S. Time of Concentration for Overland Flow. Civ. Eng. 1959, 29, 174. [Google Scholar]
- Morgali, J.R.; Linsley, R.K. Computer simulation of overland flow. J. Hydraul. Div. ASCE 1965, 90, 81–100. [Google Scholar] [CrossRef]
- Federal Aviation Administration (FAA). Circular on Airport Drainage; U.S. Department of Transportation: Washington, DC, USA, 1970; p. 80.
- US Bureau of Reclamation (USBR). Design of Small Dams; US Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1973; p. 860.
- Watt, W.E.; Chow, K.C.A. A general expression for basin lag time. Can. J. Civ. Eng. 1985, 12, 294–300. [Google Scholar] [CrossRef]
- Seybert, T.A. Stormwater Management for Land Development; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; p. 372. [Google Scholar]
- Aziz, K.; Haque, M.M.; Rahman, A.; Shamseldin, A.Y.; Shoaib, M. Flood estimation in ungauged catchments: Application of artificial intelligence based methods for Eastern Australia. Stoch. Environ. Res. Risk Assess. 2017, 31, 1499–1514. [Google Scholar] [CrossRef]
- Hazzab, A.; Seddini, A.; Ghenaim, A.; Korichi, K. Hydraulic flood routing in an ephemeral channel: Wadi Mekerra, Algeria. Model. Earth Syst. Environ. 2016, 2, 1–12. [Google Scholar]
- Fang, X.; Thompson, D.B.; Cleveland, T.G.; Pradhan, P. Variations of Time of ConcentrationEstimates Using NRCS Velocity Method. J. Irrig. Drain. Eng. 2007, 133, 314–322. [Google Scholar] [CrossRef]
- Perdikaris, J.; Gharabaghi, B.; Rudra, R. Reference Time of Concentration Estimation for UngaugedCatchments. Earth Sci. Res. J. 2018, 7, 58–73. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A Critical Review of Recurrent Neural Networks for Sequence Learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Rahimzad, M.; Moghaddam Nia, A.; Zolfonoon, H.; Soltani, J.; Danandeh Mehr, A.; Kwon, H.-H. Performance Comparison of an LSTM-based Deep Learning Model versus Conventional Machine Learning Algorithms for Streamflow Forecasting. Water Resour. Manag. 2021, 35, 4167–4187. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Kan, G.; Liang, K.; Yu, H.; Sun, B.; Ding, L.; Li, J.; He, X.; Shen, C. Hybrid machine learning hydrological model for flood forecast purpose. Open Geosci. 2020, 12, 813–820. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thaisiam, W.; Saelo, W.; Wongchaisuwat, P. Enhancing a Multi-Step Discharge Prediction with Deep Learning and a Response Time Parameter. Water 2022, 14, 2898. https://doi.org/10.3390/w14182898
Thaisiam W, Saelo W, Wongchaisuwat P. Enhancing a Multi-Step Discharge Prediction with Deep Learning and a Response Time Parameter. Water. 2022; 14(18):2898. https://doi.org/10.3390/w14182898
Chicago/Turabian StyleThaisiam, Wandee, Warintra Saelo, and Papis Wongchaisuwat. 2022. "Enhancing a Multi-Step Discharge Prediction with Deep Learning and a Response Time Parameter" Water 14, no. 18: 2898. https://doi.org/10.3390/w14182898




