Evaluation of Machine Learning Models for Daily Reference Evapotranspiration Modeling Using Limited Meteorological Data in Eastern Inner Mongolia, North China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Models for Modeling Reference Evapotranspiration
2.1.1. FAO-56 Penman–Monteith Equation
2.1.2. Empirical Models for Predicting Daily ET0
2.1.3. Machine Learning Models for Predicting Daily ET0
2.2. Data Management and the Development of Machine Learning Models
2.3. Model Performance and Assessment
3. Results
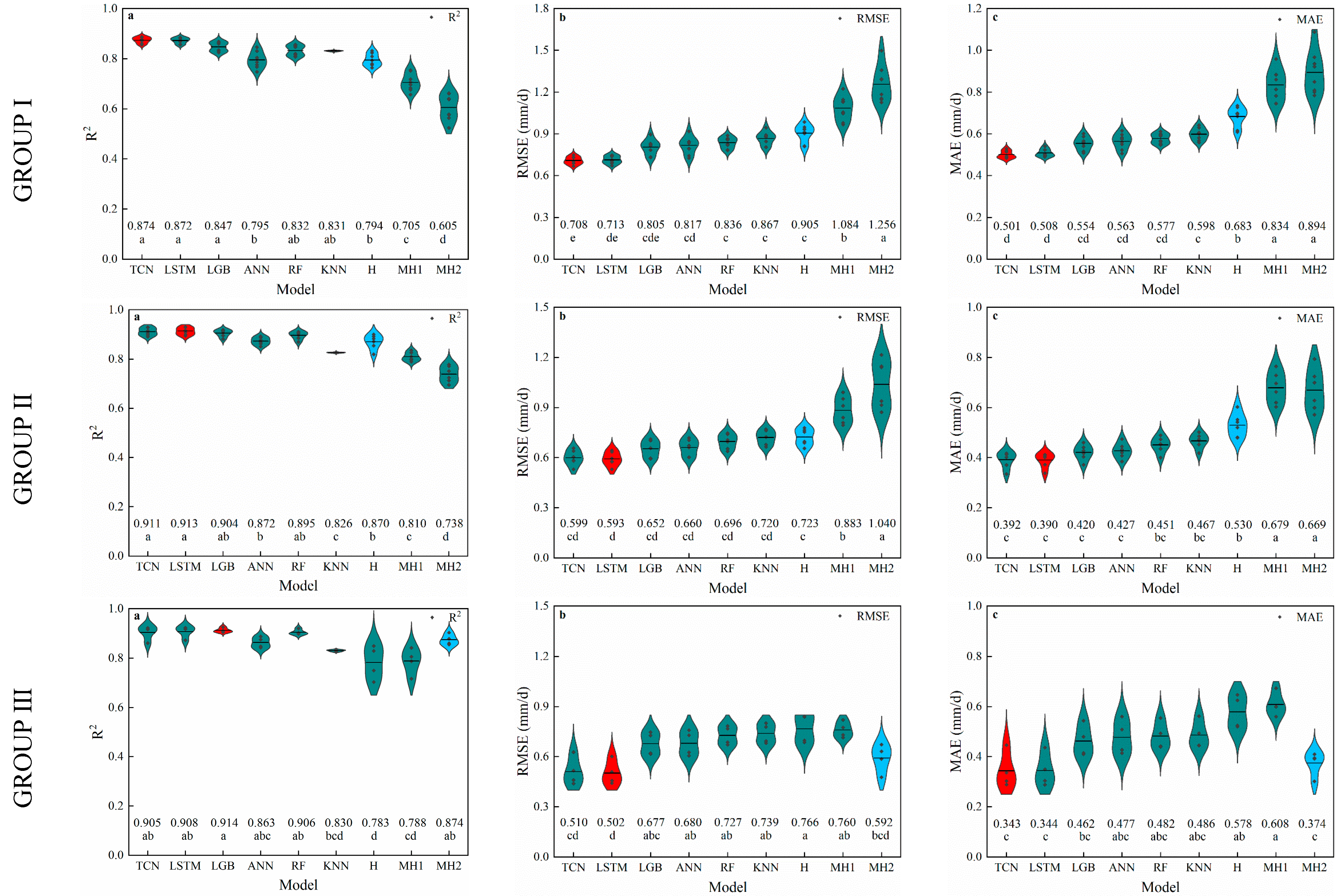
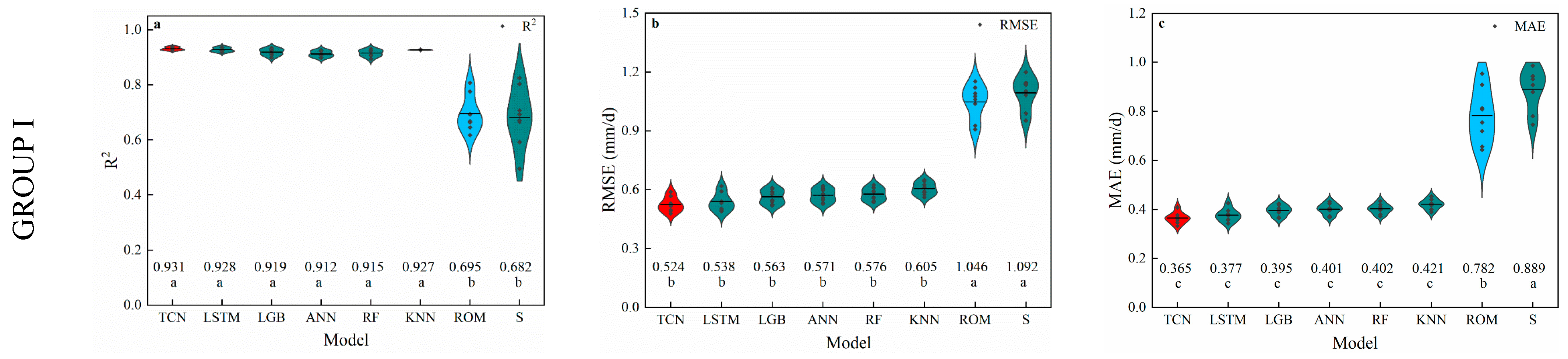
3.1. Temperature-Based Models
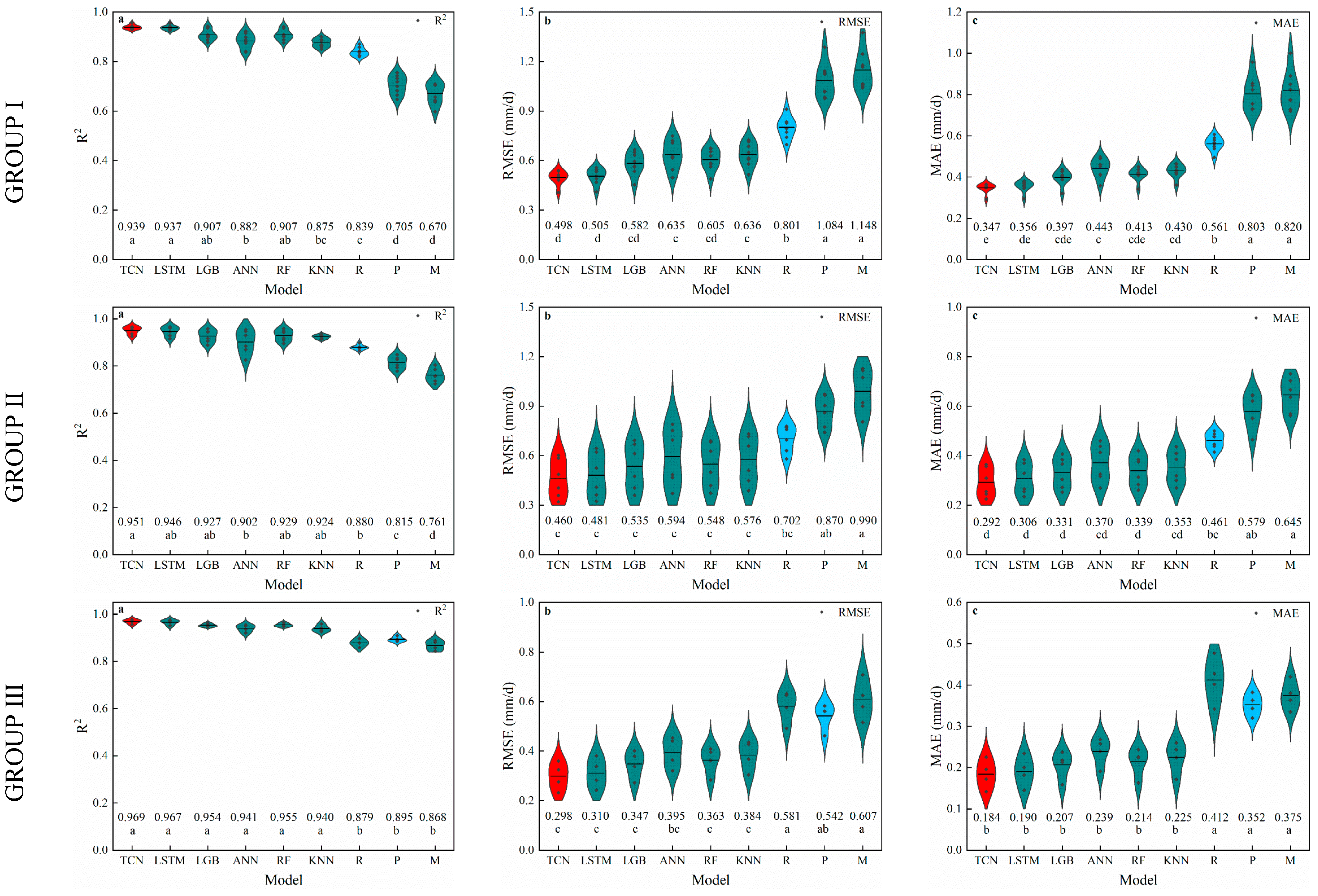
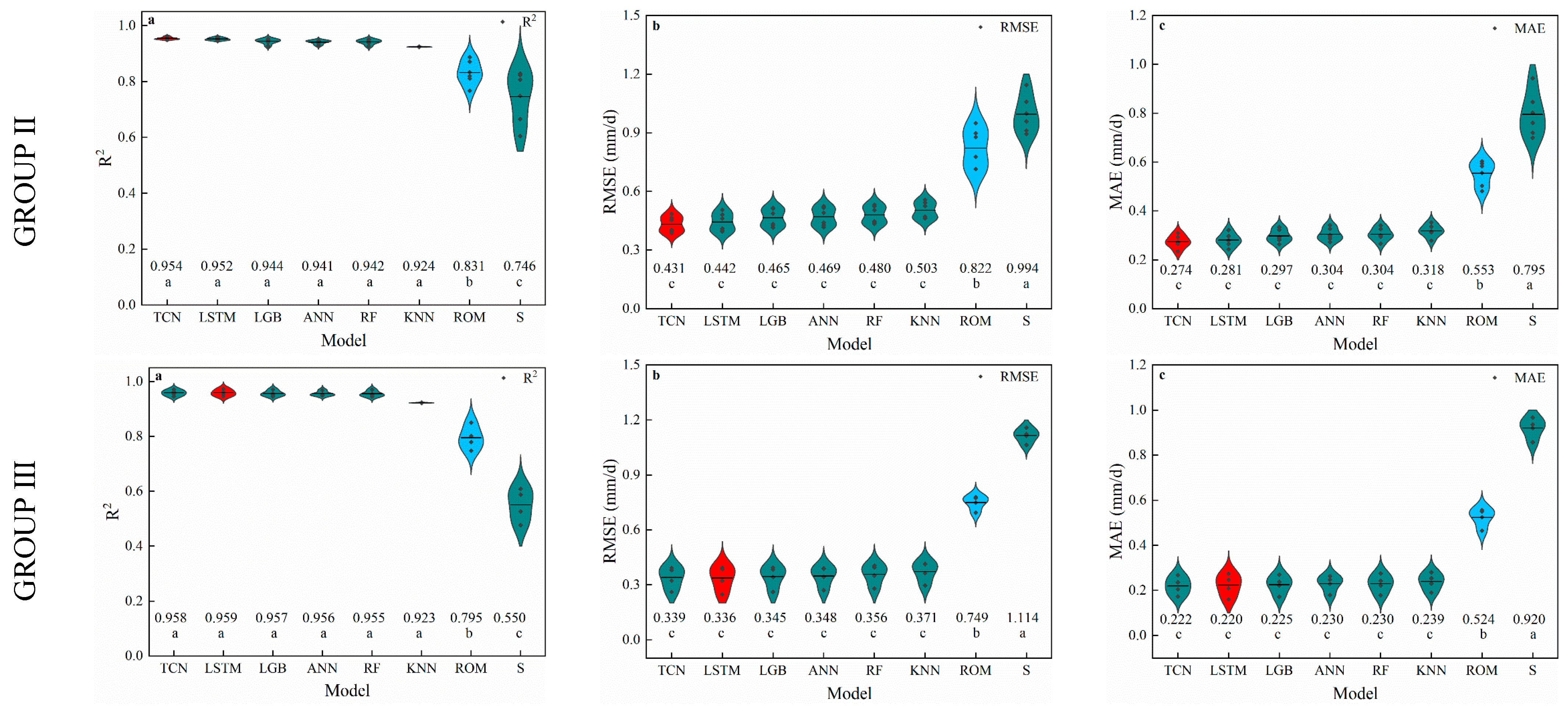
3.2. Radiation-Based Models
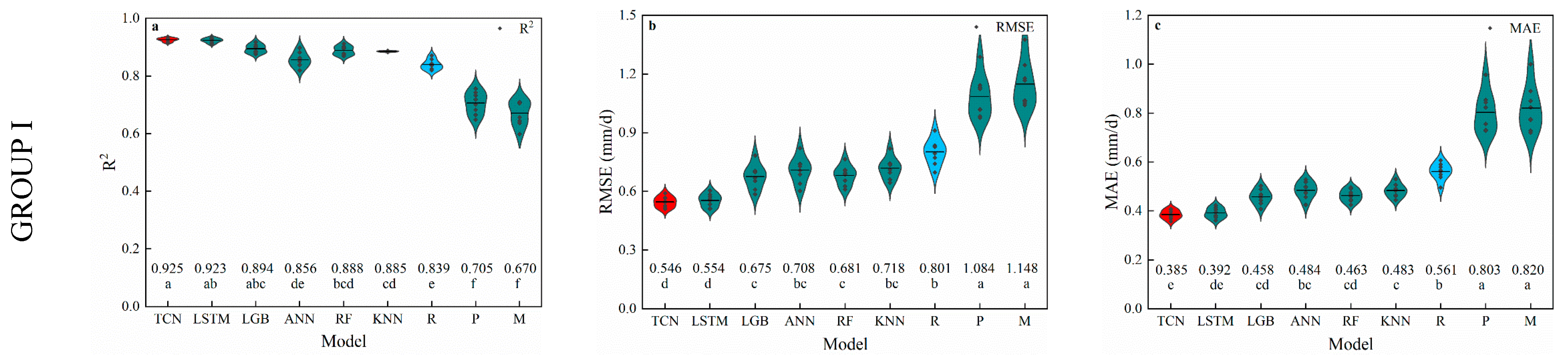
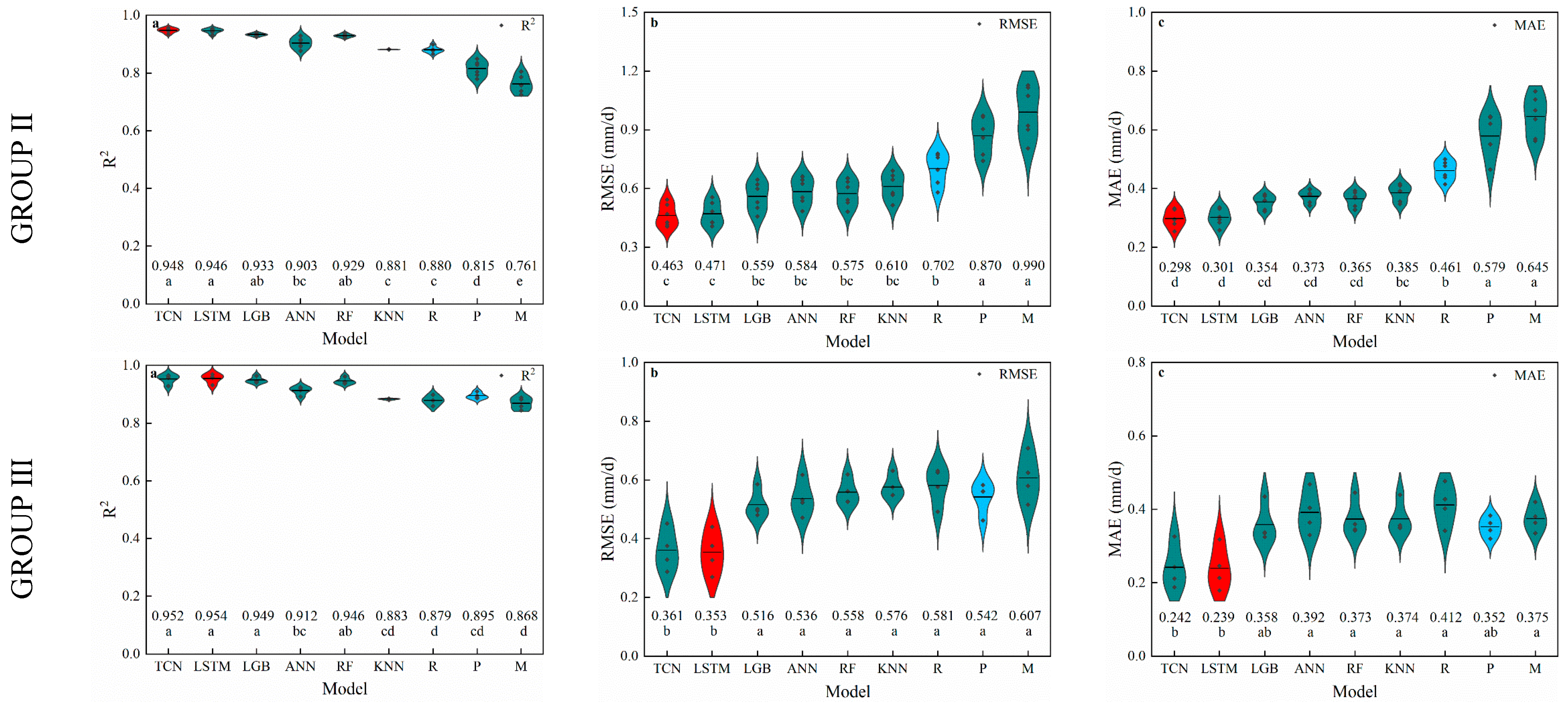
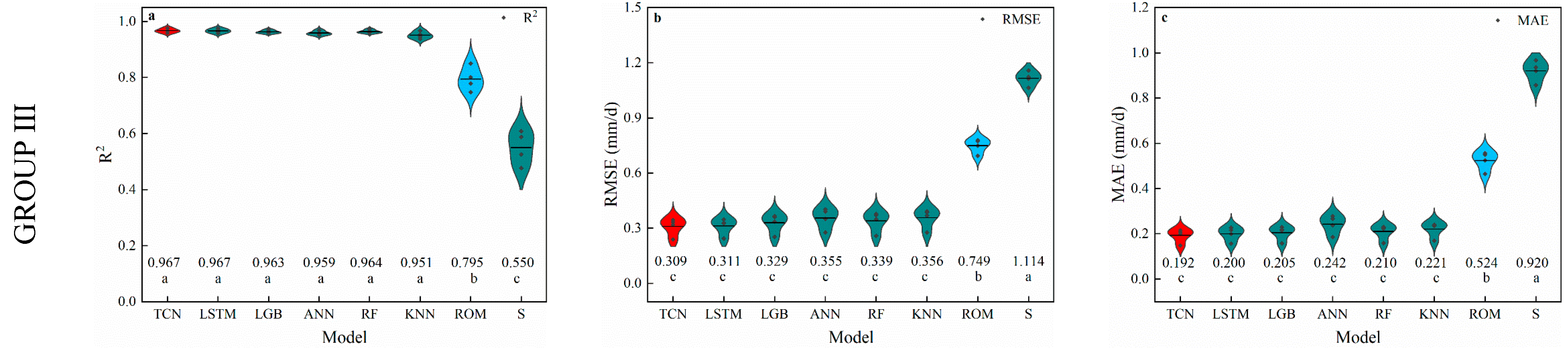
3.3. Humidity-Based Models
4. Discussion
4.1. Performance of Temperature-Based Models
4.2. Performance of Radiation-Based Models
4.3. Performance of Humidity-Based Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kisi, O. Modeling reference evapotranspiration using three different heuristic regression approaches. Agric. Water Manage. 2016, 169, 162–172. [Google Scholar] [CrossRef]
- Shiri, J. Evaluation of FAO56-PM, empirical, semi-empirical and gene expression programming approaches for estimating daily reference evapotranspiration in hyper-arid regions of Iran. Agric. Water Manage. 2017, 188, 101–114. [Google Scholar] [CrossRef]
- Tabari, H.; Kisi, O.; Ezani, A.; Hosseinzadeh Talaee, P. SVM, ANFIS, regression and climate based models for reference evapotranspiration modeling using limited climatic data in a semi-arid highland environment. J. Hydrol. 2012, 444, 78–89. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z.; Antonopoulos, A.V. Daily reference evapotranspiration estimates by artificial neural networks technique and empirical equations using limited input climate variables. Comput. Electron. Agric. 2017, 132, 86–96. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Gong, D.; Zhang, Q.; Zhao, L. Evaluation of random forests and generalized regression neural networks for daily reference evapotranspiration modelling. Agric. Water Manage. 2017, 193, 163–173. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F. New approach to estimate daily reference evapotranspiration based on hourly temperature and relative humidity using machine learning and deep learning. Agric. Water Manage. 2020, 234, 106113. [Google Scholar] [CrossRef]
- Abdullah, S.S.; Malek, M.A.; Abdullah, N.S.; Kisi, O.; Yap, K.S. Extreme Learning Machines: A new approach for prediction of reference evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Ahooghalandari, M.; Khiadani, M.; Jahromi, M.E. Developing equations for estimating reference evapotranspiration in Australia. Water Resour. Manage. 2016, 30, 3815–3828. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Jones, J.; Ritchie, J. Crop growth models. In Management of Farm Irrigation Systems; Hoffman, G.J., Howell, T.A., Solomon, K.H., Eds.; ASAE: St. Joseph, MO, USA, 1990; pp. 63–89. [Google Scholar]
- Valiantzas, J.D. Simplified forms for the standardized FAO-56 Penman–Monteith reference evapotranspiration using limited weather data. J. Hydrol. 2013, 505, 13–23. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F.; de Oliveira, R.A.; Fernandes Filho, E.I. Estimation of reference evapotranspiration in Brazil with limited meteorological data using ANN and SVM—A new approach. J. Hydrol. 2019, 572, 556–570. [Google Scholar] [CrossRef]
- Djaman, K.; Balde, A.B.; Sow, A.; Muller, B.; Irmak, S.; N’Diaye, M.K.; Manneh, B.; Moukoumbi, Y.D.; Futakuchi, K.; Saito, K. Evaluation of sixteen reference evapotranspiration methods under sahelian conditions in the Senegal River Valley. J. Hydol. Reg. Stud. 2015, 3, 139–159. [Google Scholar] [CrossRef]
- Valipour, M. Application of new mass transfer formulae for computation of evapotranspiration. J. Appl. Water Eng. Res. 2014, 2, 33–46. [Google Scholar] [CrossRef]
- Majhi, B.; Naidu, D.; Mishra, A.P.; Satapathy, S.C. Improved prediction of daily pan evaporation using Deep-LSTM model. Neural Comput. Appl. 2019, 32, 7823–7838. [Google Scholar] [CrossRef]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm. Agric. Water Manage. 2020, 237, 106145. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H. Support vector machine enhanced empirical reference evapotranspiration estimation with limited meteorological parameters. Comput. Electron. Agric. 2020, 175, 105577. [Google Scholar] [CrossRef]
- Wen, X.; Si, J.; He, Z.; Wu, J.; Shao, H.; Yu, H. Support-Vector-Machine-Based Models for Modeling Daily Reference Evapotranspiration With Limited Climatic Data in Extreme Arid Regions. Water Resour. Manage. 2015, 29, 3195–3209. [Google Scholar] [CrossRef]
- Shiri, J. Improving the performance of the mass transfer-based reference evapotranspiration estimation approaches through a coupled wavelet-random forest methodology. J. Hydrol. 2018, 561, 737–750. [Google Scholar] [CrossRef]
- Rahimikhoob, A. Comparison between M5 Model Tree and Neural Networks for Estimating Reference Evapotranspiration in an Arid Environment. Water Resour. Manage. 2014, 28, 657–669. [Google Scholar] [CrossRef]
- Kisi, O.; Kilic, Y. An investigation on generalization ability of artificial neural networks and M5 model tree in modeling reference evapotranspiration. Theor. Appl. Climatol. 2015, 126, 413–425. [Google Scholar] [CrossRef]
- Yan, S.; Wu, L.; Fan, J.; Zhang, F.; Zou, Y.; Wu, Y. A novel hybrid WOA-XGB model for estimating daily reference evapotranspiration using local and external meteorological data: Applications in arid and humid regions of China. Agric. Water Manage. 2021, 244, 106594. [Google Scholar] [CrossRef]
- Maroufpoor, S.; Bozorg-Haddad, O.; Maroufpoor, E. Reference evapotranspiration estimating based on optimal input combination and hybrid artificial intelligent model: Hybridization of artificial neural network with grey wolf optimizer algorithm. J. Hydrol. 2020, 588, 125060. [Google Scholar] [CrossRef]
- Patil, A.P.; Deka, P.C. An extreme learning machine approach for modeling evapotranspiration using extrinsic inputs. Comput. Electron. Agric. 2016, 121, 385–392. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Z.; Jiang, H.; Sun, S. Estimating daily reference evapotranspiration based on limited meteorological data using deep learning and classical machine learning methods. J. Hydrol. 2020, 591, 125286. [Google Scholar] [CrossRef]
- Yin, J.; Deng, Z.; Ines, A.V.M.; Wu, J.; Rasu, E. Forecast of short-term daily reference evapotranspiration under limited meteorological variables using a hybrid bi-directional long short-term memory model (Bi-LSTM). Agric. Water Manage. 2020, 242, 106386. [Google Scholar] [CrossRef]
- Petković, B.; Petković, D.; Kuzman, B.; Milovančević, M.; Wakil, K.; Ho, L.S.; Jermsittiparsert, K. Neuro-fuzzy estimation of reference crop evapotranspiration by neuro fuzzy logic based on weather conditions. Comput. Electron. Agric. 2020, 173, 105358. [Google Scholar] [CrossRef]
- Shan, X.; Cui, N.; Cai, H.; Hu, X.; Zhao, L. Estimation of summer maize evapotranspiration using MARS model in the semi-arid region of northwest China. Comput. Electron. Agric. 2020, 174, 105495. [Google Scholar] [CrossRef]
- Mehdizadeh, S. Estimation of daily reference evapotranspiration (ETo) using artificial intelligence methods: Offering a new approach for lagged ETo data-based modeling. J. Hydrol. 2018, 559, 794–812. [Google Scholar] [CrossRef]
- Dou, X.; Yang, Y. Evapotranspiration estimation using four different machine learning approaches in different terrestrial ecosystems. Comput. Electron. Agric. 2018, 148, 95–106. [Google Scholar] [CrossRef]
- Feng, Y.; Peng, Y.; Cui, N.; Gong, D.; Zhang, K. Modeling reference evapotranspiration using extreme learning machine and generalized regression neural network only with temperature data. Comput. Electron. Agric. 2017, 136, 71–78. [Google Scholar] [CrossRef]
- Karbasi, M. Forecasting of Multi-Step Ahead Reference Evapotranspiration Using Wavelet- Gaussian Process Regression Model. Water Resour. Manage. 2018, 32, 1035–1052. [Google Scholar] [CrossRef]
- Trajkovic, S. Hargreaves versus Penman-Monteith under Humid Conditions. J. Irrig. Drain. Eng. 2007, 133, 38–42. [Google Scholar] [CrossRef]
- Dorji, U.; Olesen, J.E.; Seidenkrantz, M.S. Water balance in the complex mountainous terrain of Bhutan and linkages to land use. J. Hydol. Reg. Stud. 2016, 7, 55–68. [Google Scholar] [CrossRef]
- Makkink, G.F. Testing the Penman Formula by Means of Lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Citakoglu, H.; Cobaner, M.; Haktanir, T.; Kisi, O. Estimation of monthly mean reference evapotranspiration in Turkey. Water Resour. Manage. 2014, 28, 99–113. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M.; Allen, R.G.; Pereira, L.S.; Martin, S. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Earnest, A.; Tan, S.B.; Wilder-Smith, A. Meteorological factors and El Niño Southern Oscillation are independently associated with dengue infections. Epidemiol. Infect. 2012, 140, 1244–1251. [Google Scholar] [CrossRef]
- Kohli, S.; Godwin, G.T.; Urolagin, S. Sales Prediction Using Linear and KNN Regression. In Proceedings of the Advances in Machine Learning and Computational Intelligence, Singapore, 6–7 April 2019; pp. 321–329. [Google Scholar]
- Shah, K.; Patel, H.; Sanghvi, D.; Shah, M. A Comparative Analysis of Logistic Regression, Random Forest and KNN Models for the Text Classification. Augment. Hum. Res. 2020, 5, 12. [Google Scholar] [CrossRef]
- Lee, T.; Ouarda, T.B.M.J.; Yoon, S. KNN-based local linear regression for the analysis and simulation of low flow extremes under climatic influence. Clim. Dyn. 2017, 49, 3493–3511. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Cai, J.; Li, X.; Tan, Z.; Peng, S. An assembly-level neutronic calculation method based on LightGBM algorithm. Ann. Nucl. Energy 2021, 150, 107871. [Google Scholar] [CrossRef]
- Yu, Q.; Guan, X.; Zhai, Y.; Meng, Z. The missing data filling method of the industrial internet platform based on rules and lightGBM. IFAC-PapersOnLine 2020, 53, 152–157. [Google Scholar] [CrossRef]
- Sun, X.; Liu, M.; Sima, Z. A novel cryptocurrency price trend forecasting model based on LightGBM. Financ. Res. Lett. 2020, 32, 101084. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Lea, C.; Flynn, M.D.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal Convolutional Networks for Action Segmentation and Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, Hawaii, USA, 21–26 July 2017; pp. 1003–1012. [Google Scholar]
- Feng, Y.; Cui, N.; Zhao, L.; Hu, X.; Gong, D. Comparison of ELM, GANN, WNN and empirical models for estimating reference evapotranspiration in humid region of Southwest China. J. Hydrol. 2016, 536, 376–383. [Google Scholar] [CrossRef]
- Reis, M.M.; da Silva, A.J.; Zullo Junior, J.; Tuffi Santos, L.D.; Azevedo, A.M.; Lopes, É.M.G. Empirical and learning machine approaches to estimating reference evapotranspiration based on temperature data. Comput. Electron. Agric. 2019, 165, 104937. [Google Scholar] [CrossRef]
- Samani, Z. Estimating solar radiation and evapotranspiration using minimum climatological data. J. Irrig. Drain. Eng. 2000, 126, 265–267. [Google Scholar] [CrossRef]




| Station | U2 (m·s−1) | RH (%) | SH (h) | Tmin (°C) | Tmax (°C) | p (mm) | Cluster |
|---|---|---|---|---|---|---|---|
| Eergunaqi | 2.06 | 66.41 | 7.26 | −8.66 | 4.61 | 1.12 | 3 |
| Tulihe | 2.08 | 70.79 | 6.93 | −12.45 | 4.36 | 1.42 | 3 |
| Manzhouli | 3.99 | 62.03 | 8.08 | −6.97 | 6.35 | 0.90 | 2 |
| Hailaer | 3.22 | 66.12 | 7.39 | −6.67 | 5.55 | 1.09 | 2 |
| Xiaoergou | 1.56 | 66.25 | 7.31 | −7.31 | 8.39 | 1.57 | 3 |
| Xinbaerhuyouqi | 3.76 | 59.39 | 8.35 | −4.43 | 7.82 | 0.73 | 2 |
| Xinbaerhuzuoqi | 3.27 | 62.16 | 7.97 | −5.12 | 6.80 | 0.89 | 2 |
| Zhalantun | 2.68 | 56.64 | 7.58 | −2.18 | 9.66 | 1.55 | 2 |
| Aershan | 2.49 | 68.64 | 7.15 | −9.30 | 4.84 | 1.50 | 3 |
| Suolun | 2.82 | 56.82 | 7.74 | −3.88 | 10.38 | 1.40 | 2 |
| Zhaluteqi | 2.70 | 48.23 | 7.90 | 1.27 | 13.28 | 1.13 | 1 |
| Balinzuoqi | 2.66 | 50.02 | 8.31 | −1.04 | 12.92 | 1.11 | 1 |
| Linxi | 2.83 | 49.58 | 8.09 | −1.25 | 11.60 | 1.10 | 1 |
| Kailu | 3.83 | 51.80 | 8.48 | 0.85 | 13.44 | 0.98 | 1 |
| Tongliao | 3.56 | 54.34 | 8.18 | 1.24 | 13.29 | 1.12 | 1 |
| Wengniuteqi | 2.95 | 47.69 | 8.20 | 0.41 | 13.03 | 1.05 | 1 |
| Chifeng | 2.42 | 48.17 | 8.01 | 1.54 | 14.47 | 1.10 | 1 |
| Baoguotu | 3.23 | 49.94 | 7.99 | 1.59 | 13.71 | 1.23 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Meng, F.; Xu, J.; Liu, Z.; Meng, J. Evaluation of Machine Learning Models for Daily Reference Evapotranspiration Modeling Using Limited Meteorological Data in Eastern Inner Mongolia, North China. Water 2022, 14, 2890. https://doi.org/10.3390/w14182890
Zhang H, Meng F, Xu J, Liu Z, Meng J. Evaluation of Machine Learning Models for Daily Reference Evapotranspiration Modeling Using Limited Meteorological Data in Eastern Inner Mongolia, North China. Water. 2022; 14(18):2890. https://doi.org/10.3390/w14182890
Chicago/Turabian StyleZhang, Hao, Fansheng Meng, Jia Xu, Zhandong Liu, and Jun Meng. 2022. "Evaluation of Machine Learning Models for Daily Reference Evapotranspiration Modeling Using Limited Meteorological Data in Eastern Inner Mongolia, North China" Water 14, no. 18: 2890. https://doi.org/10.3390/w14182890
APA StyleZhang, H., Meng, F., Xu, J., Liu, Z., & Meng, J. (2022). Evaluation of Machine Learning Models for Daily Reference Evapotranspiration Modeling Using Limited Meteorological Data in Eastern Inner Mongolia, North China. Water, 14(18), 2890. https://doi.org/10.3390/w14182890








