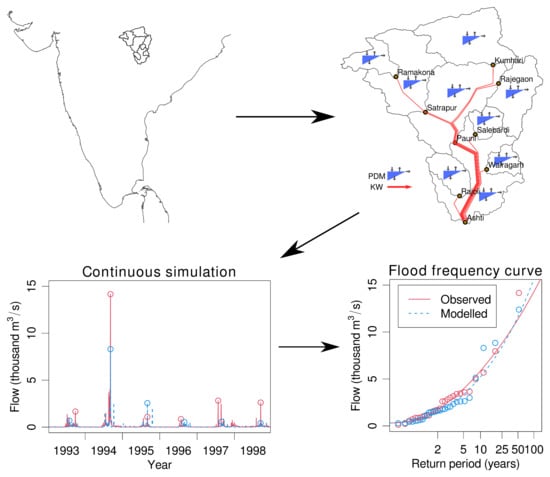
Flood Frequency Estimation in Data-Sparse Wainganga Basin, India, Using Continuous Simulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. River Discharge Data
2.3. Elevation and Flow Direction Data
2.4. Meteorological Data
2.5. Land Cover Data
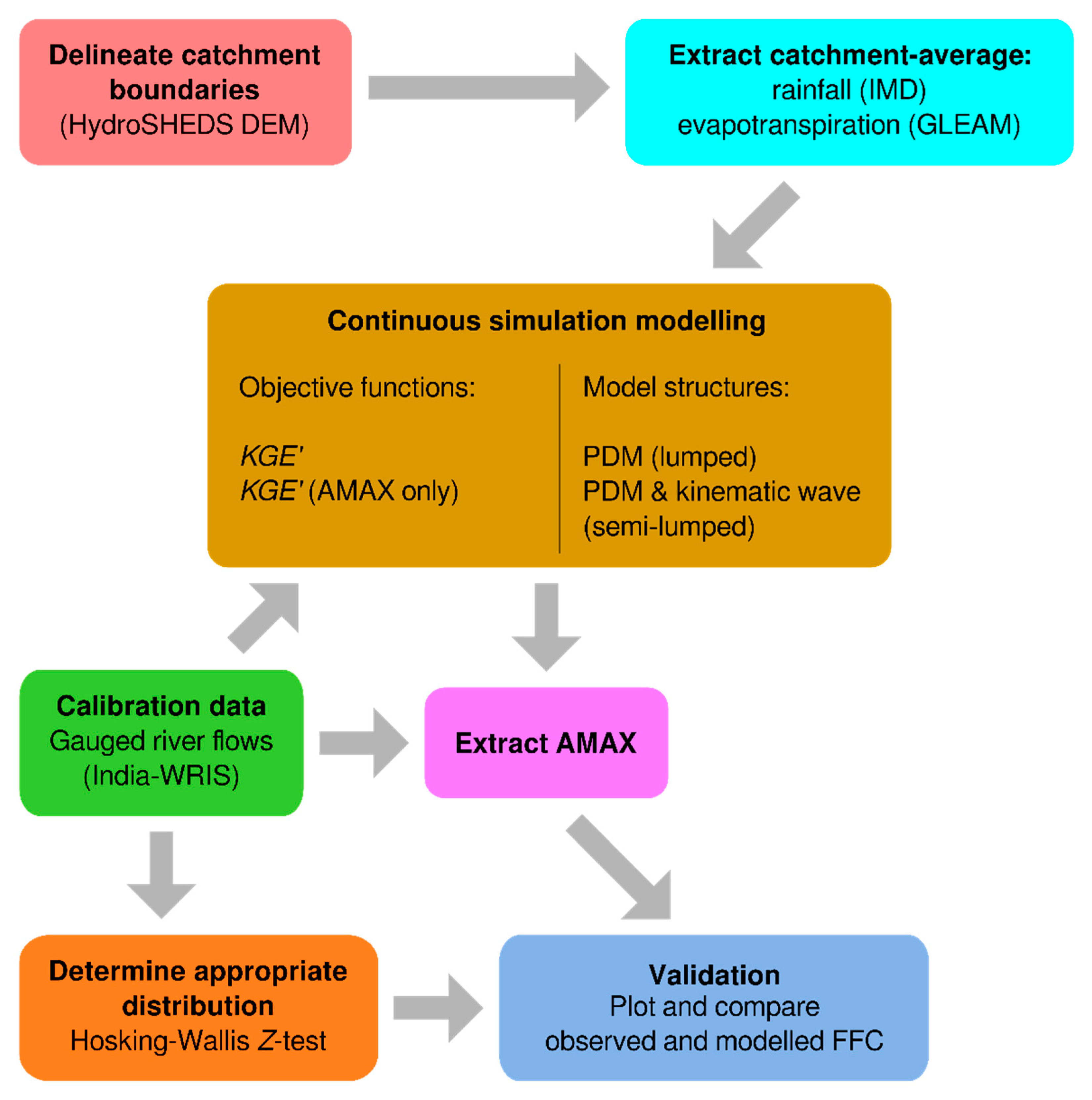
2.6. Statistical Flood Frequency Estimation
2.7. Hydrological Model
2.8. Model Calibration and Validation
3. Results and Discussion
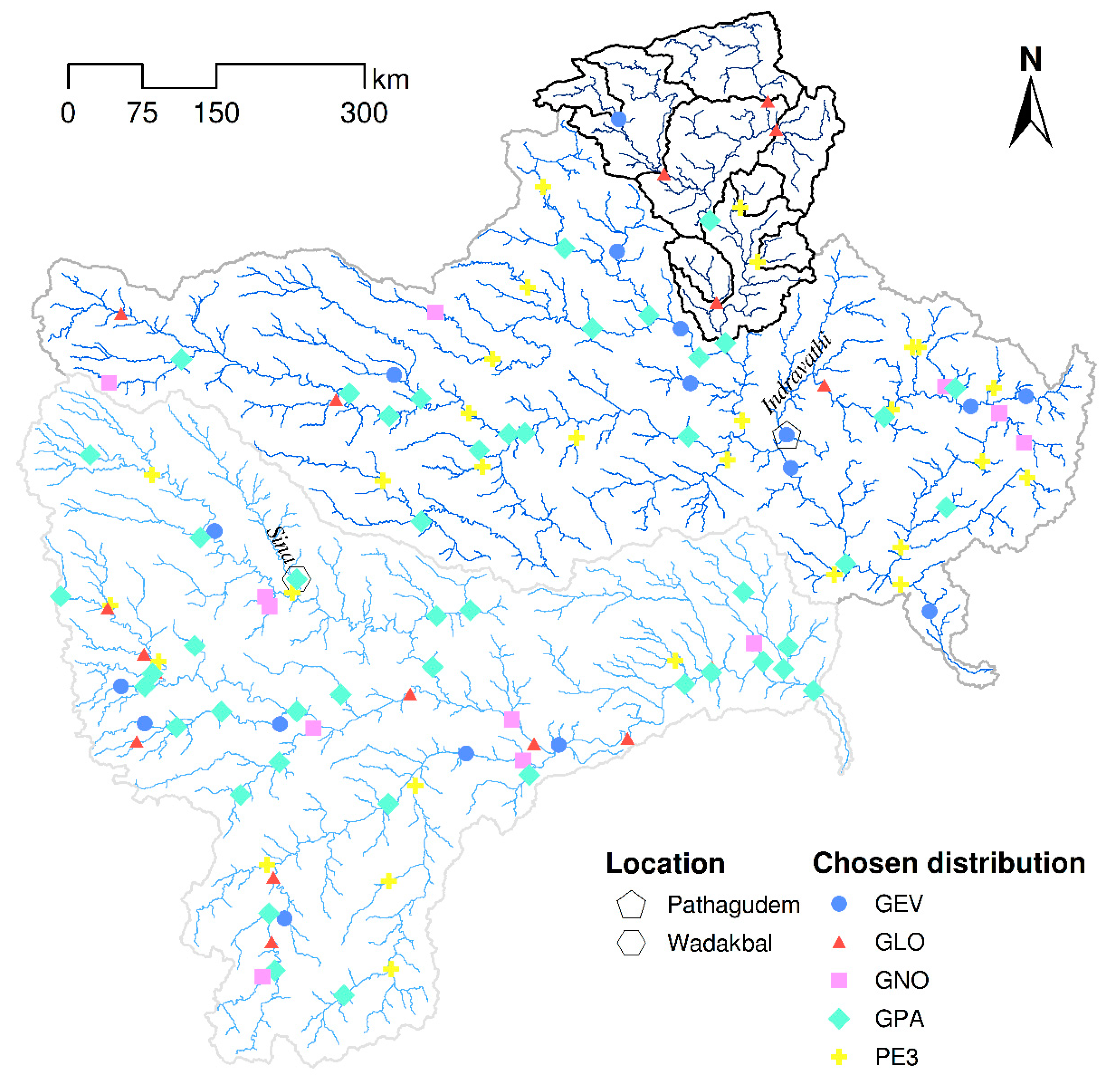
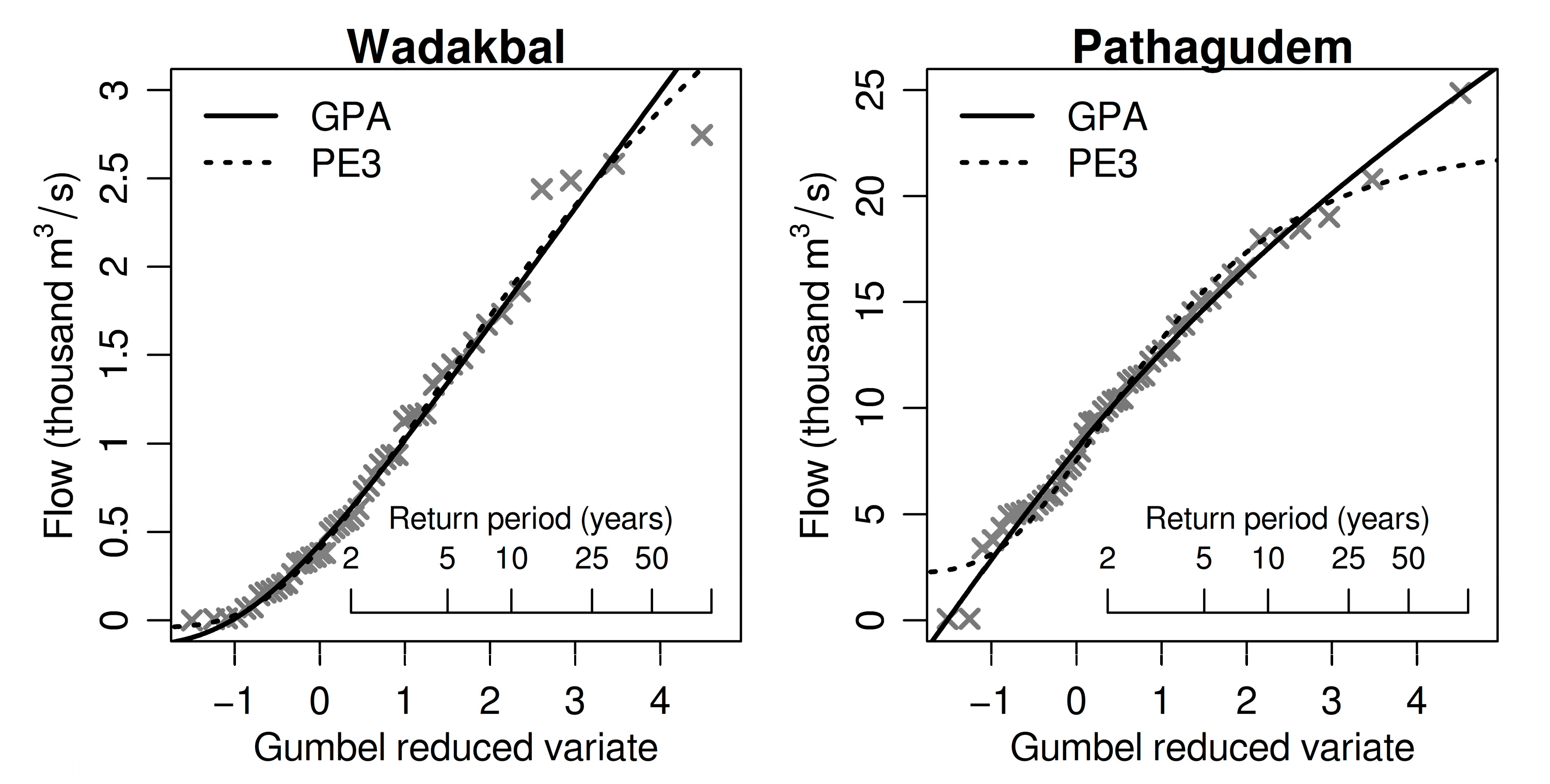
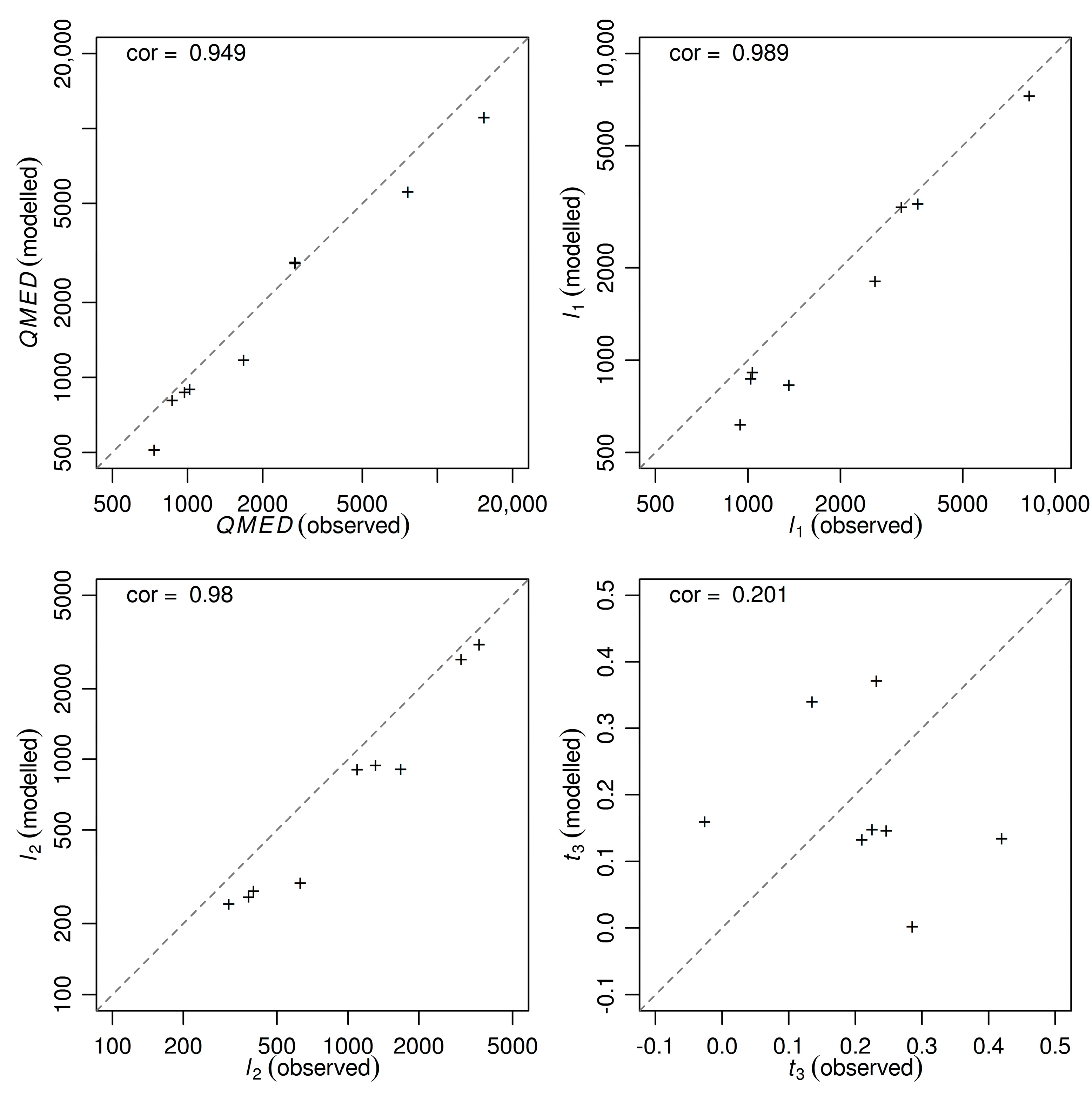
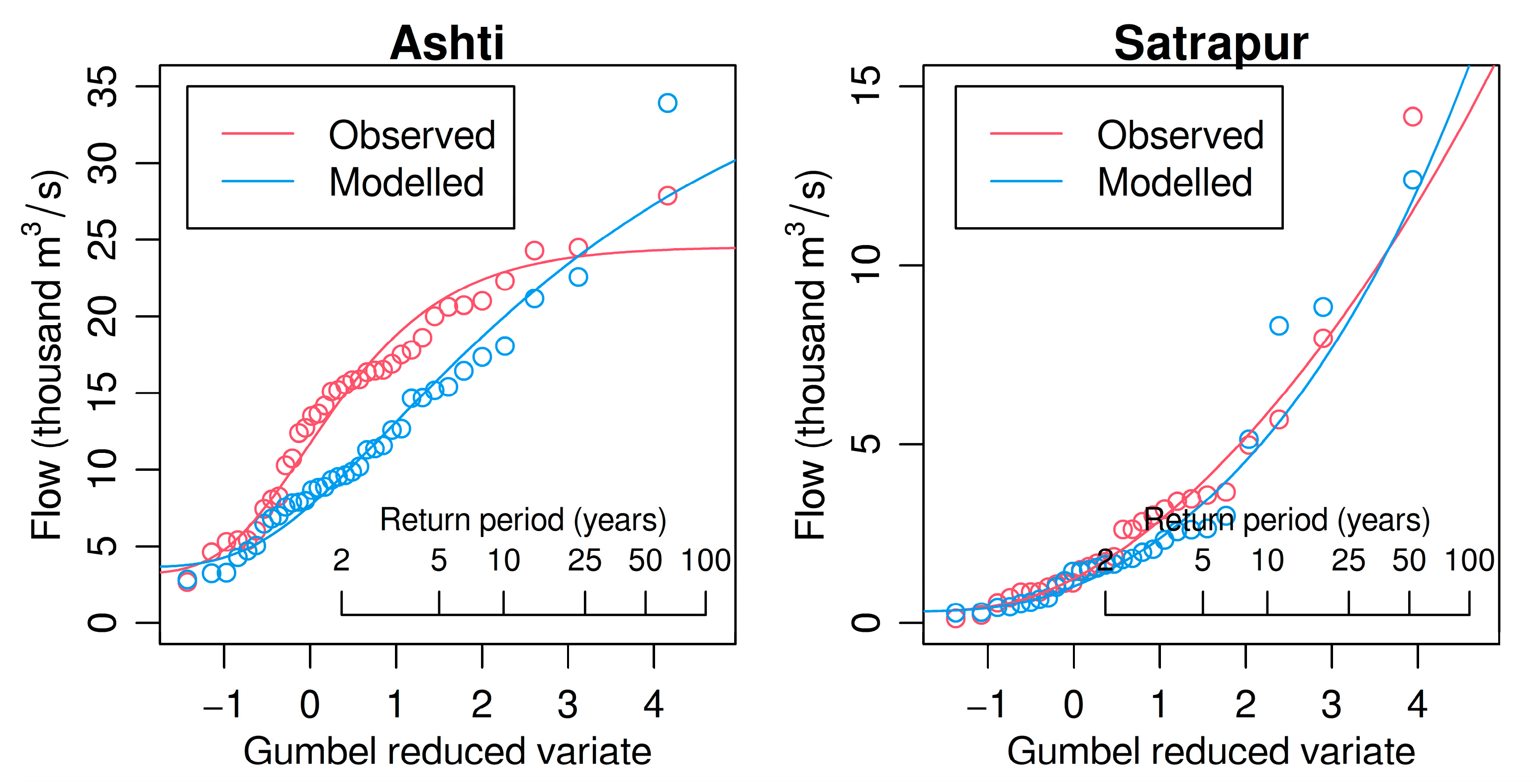
3.1. Distribution Choice
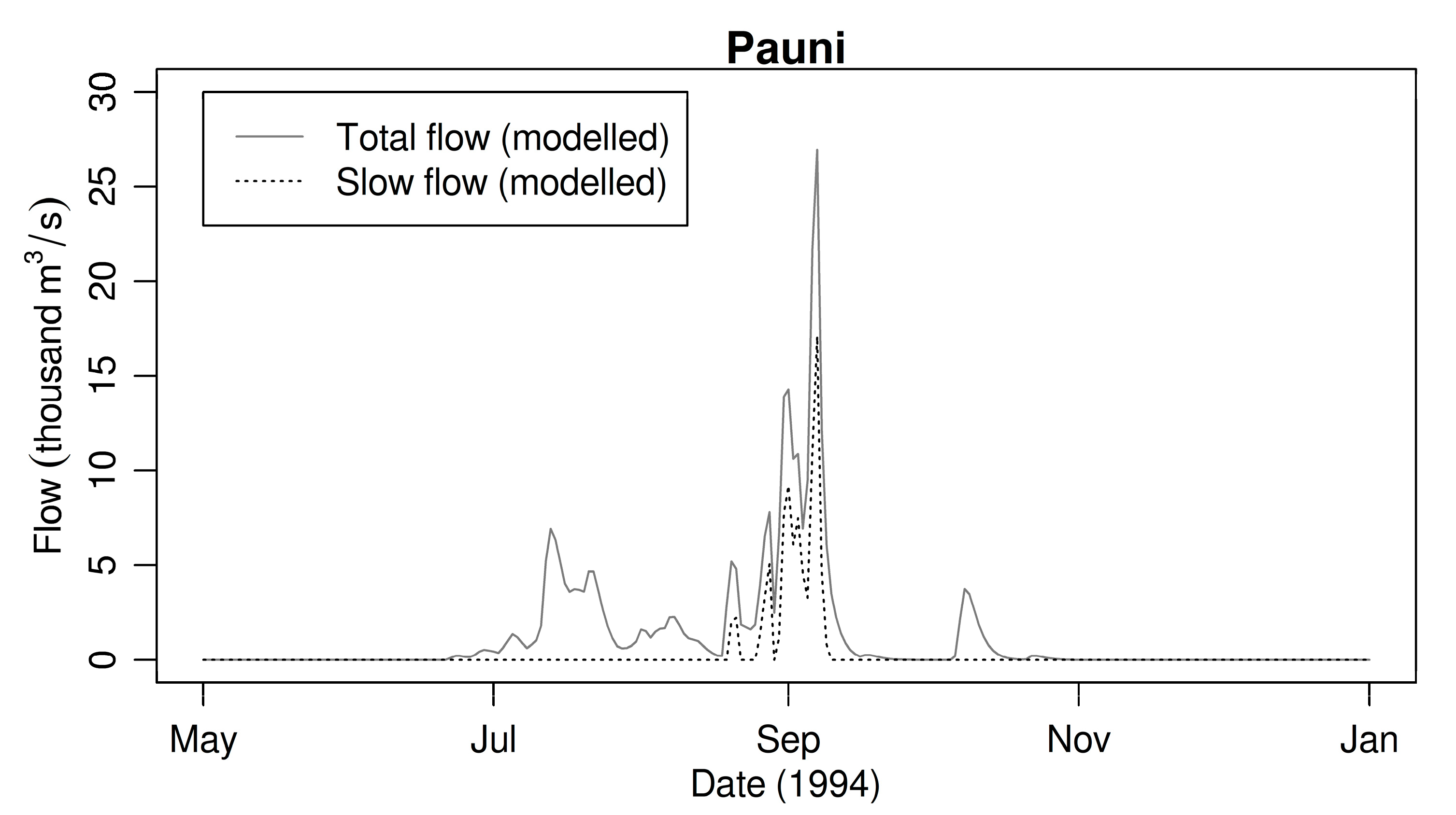
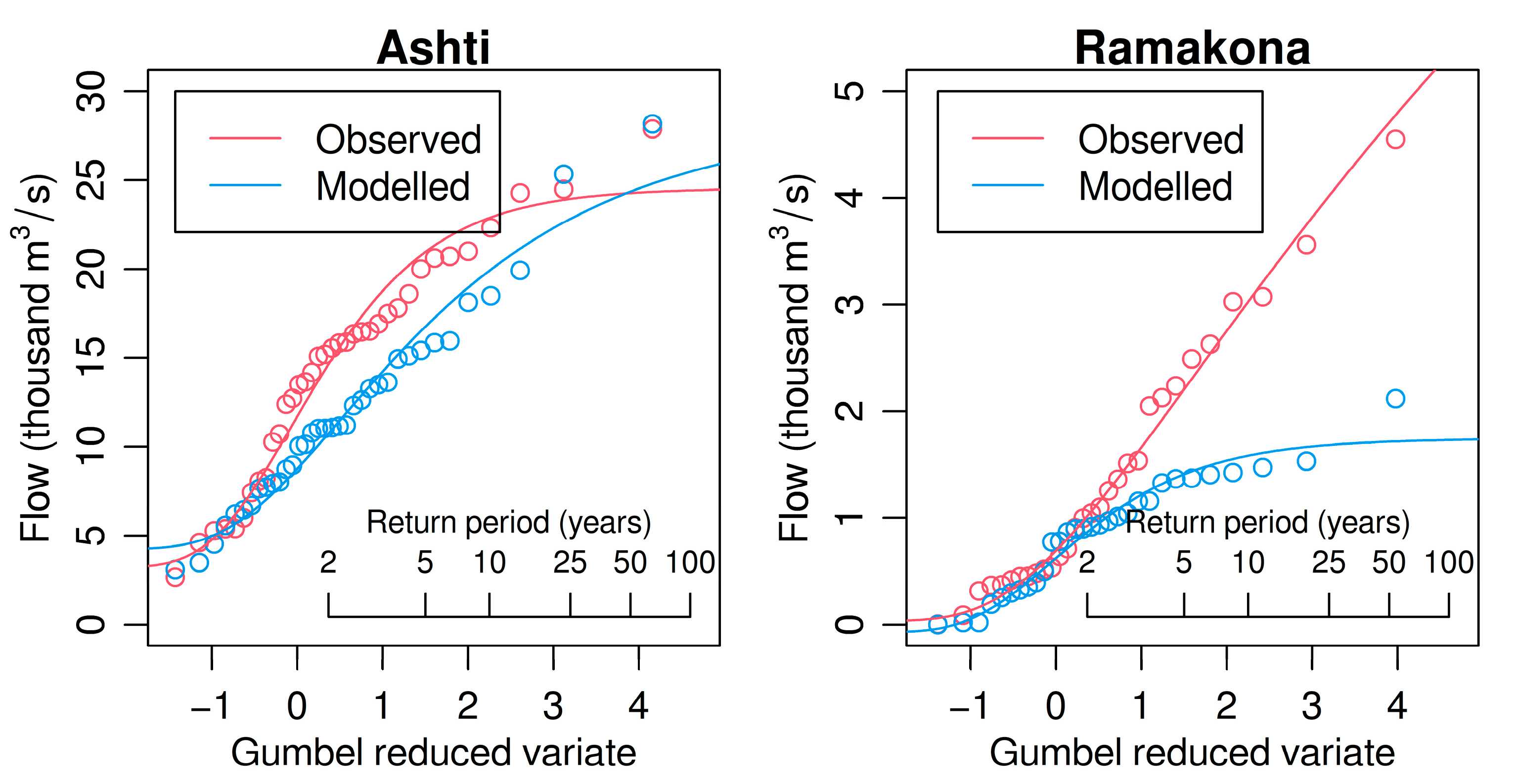
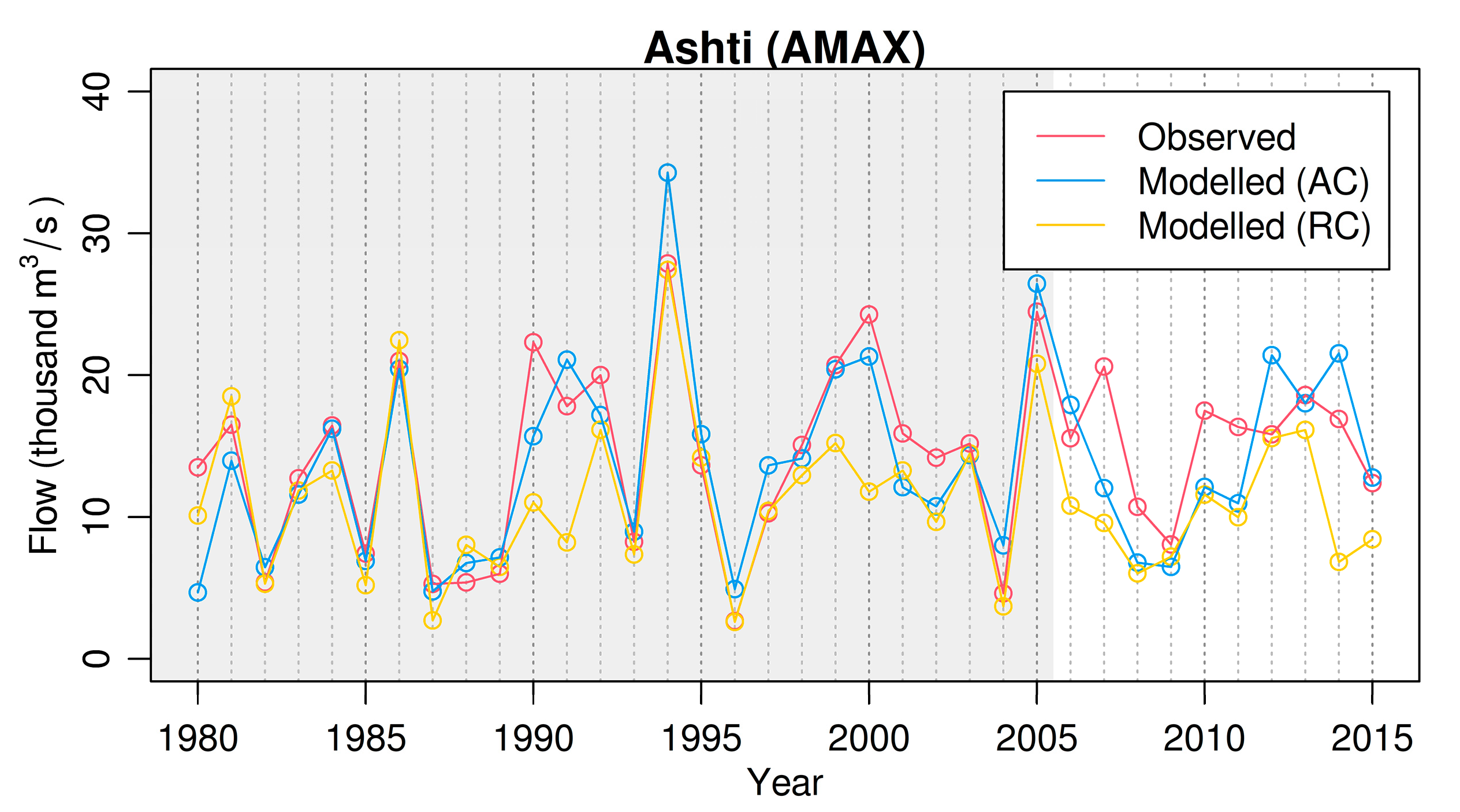
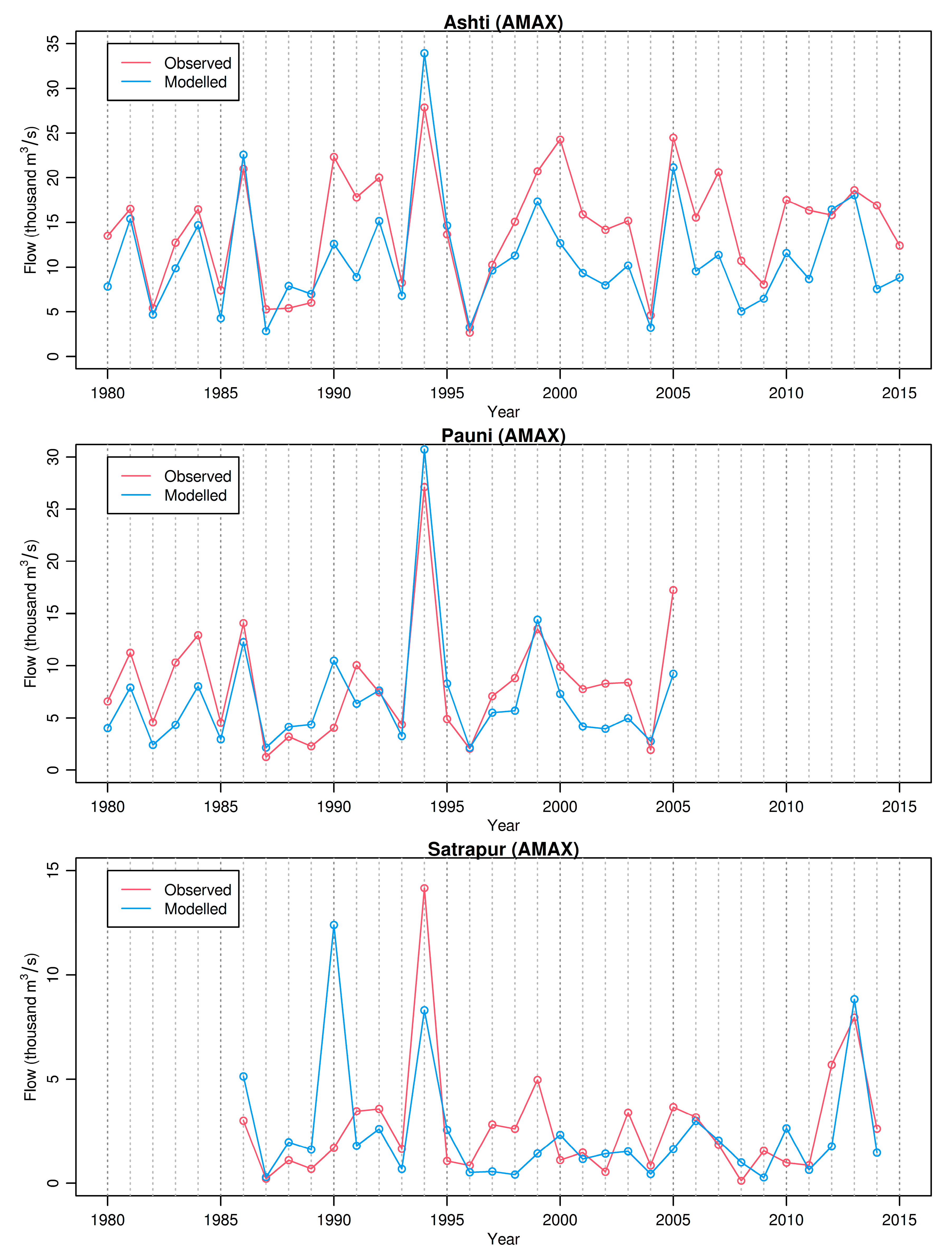
3.2. Lumped Sub-Catchment Modeling
3.3. Lumped Sub-Catchment Modeling (Optimizing AMAX Performance Only)
3.4. Lumped Sub-Catchment Modeling with a Calibration/Validation Period
3.5. Lumped Sub-Catchment Modeling (Single Parameter Set)
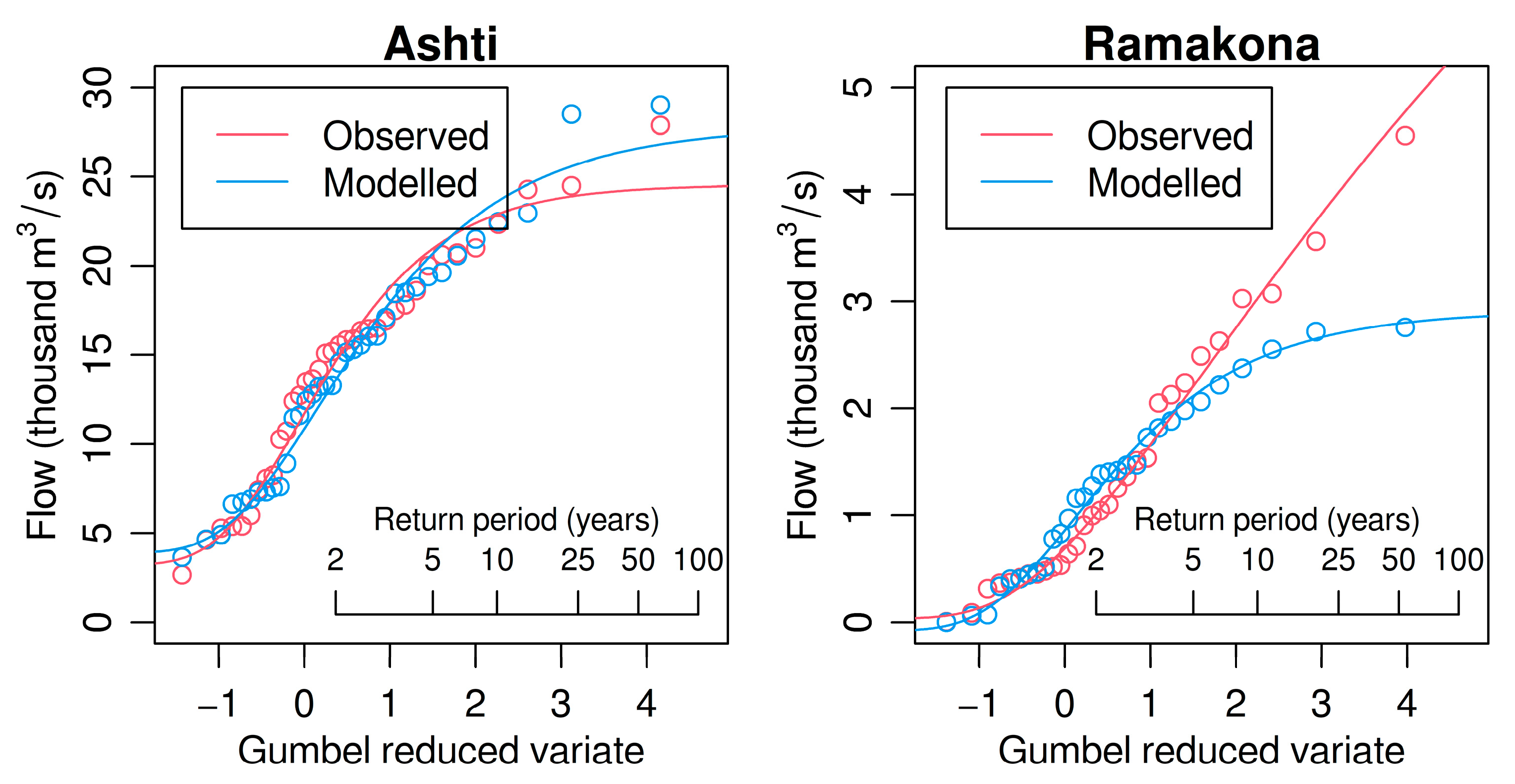
3.6. Semi-Lumped Modeling
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Times of India. Mumbai Rains: Misery All Around, BMC Says the Situation Is ‘Exceptional’. Available online: https://timesofindia.indiatimes.com/city/mumbai/mumbai-rains-misery-all-around-bmc-says-the-situation-is-exceptional/articleshow/60284534.cms (accessed on 16 July 2021).
- Times of India. Sabarmati Sinks Parts of Ahmedabad. Available online: https://timesofindia.indiatimes.com/india/sabarmati-sinks-parts-of-ahmedabad/articleshow/48289938.cms (accessed on 7 June 2022).
- World Meteorological Organization. South Asia Flash Flood Guidance System Launched. Available online: https://public.wmo.int/en/media/news/south-asia-flash-flood-guidance-system-launched (accessed on 21 June 2022).
- Yadav, A.B.P.; Raja, B.S.K.A.; Saxena, C.R.; Bharwani, D.H.; Das, E.A.K.; Giri, F.R.K.; Manik, G.S.K.; Yadav, H.D. Recent Advances in Pluvial Flash Flood Forecasting of India. In Innovative Trends in Hydrological and Environmental Systems; Dikshit, A.K., Narasimhan, B., Kumar, B., Patel, A.K., Eds.; Springer: Singapore, 2022; pp. 605–643. [Google Scholar]
- Central Water Commission. Flood Estimation Report for Lower Godavari Subzone 3(f); Central Water Commission: New Delhi, India, 1980. [Google Scholar]
- Central Water Commission. Flood Estimation Report for Upper Godavari Subzone 3(e); Central Water Commission: New Delhi, India, 1986. [Google Scholar]
- Central Water Commission. Flood Estimation Report for Krishna and Pennar Subzone 3(h); Central Water Commission: New Delhi, India, 2000. [Google Scholar]
- Bhunya, P.K.; Panigrahy, N.; Kumar, R.; Berndtsson, R. Development of a Regional Non-Dimensional Return Period Flood Model. Water Resour. Res. 2010, 24, 1425–1439. [Google Scholar] [CrossRef]
- Garde, R.J.; Kothyari, U.C. Flood Estimation in Indian Catchments. J. Hydrol. 1990, 113, 135–146. [Google Scholar] [CrossRef]
- Swamee, P.K.; Ojha, C.S.P.; Abbas, A. Mean Annual Flood Estimation. J. Water Resour. Plan. Manag. 1995, 121, 403–407. [Google Scholar] [CrossRef]
- Singh, K.K.; Pal, M.; Singh, V.P. Estimation of Mean Annual Flood in Indian Catchments Using Backpropagation Neural Network and M5 Model Tree. Water Resour. Manag. 2010, 24, 2007–2019. [Google Scholar] [CrossRef]
- Formetta, G.; Prosdocimi, I.; Stewart, E.; Bell, V. Estimating the index flood with continuous hydrological models: An application in Great Britain. Hydrol. Res. 2017, 49, 123–133. [Google Scholar] [CrossRef]
- Ministry of Water Resources. Krishna Basin Report Ver. 2; Government of India: New Delhi, India, 2014. [Google Scholar]
- South Asia Network on Dams Rivers and People (SANDRP). Wainganga River: Threatened Lifeline of Vidarbha’s Forests. Available online: https://sandrp.in/2017/04/14/wainganga-river-threatened-lifeline-of-vidarbhas-forests (accessed on 30 July 2021).
- Central Water Commission (CWC). National Register of Large Dams; Central Water Commission: New Delhi, India, 2019. [Google Scholar]
- WAPCOS. PFR Studies of Wainganga H.E. Project; WAPCOS: New Delhi, India, undated.
- National Water Informatics Centre. India-WRIS (India Water Resources Information System). Available online: https://indiawris.gov.in (accessed on 7 June 2022).
- Lehner, B.; Grill, G. Global river hydrography and network routing: Baseline data and new approaches to study the world’s large river systems. Hydrol. Process. 2013, 27, 2171–2186. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. EOS Trans. Am. Geophys. Union 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Lehner, B. HydroSHEDS Technical Documentation (version 1.4); World Wildlife Fund US: Washington, DC, USA, 2022. [Google Scholar]
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the Volume and Age of Water Stored in Global Lakes Using a Geo-Statistical Approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
- Slater, J.A.; Garvey, G.; Johnston, C.; Haase, J.; Heady, B.; Kroenung, G.; Little, J. The SRTM data “finishing” process and products. Photogramm. Eng. Remote Sens. 2006, 72, 237–247. [Google Scholar] [CrossRef]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. Global Reservoir and Dam Database, Version 1 (GRanDv1): Dams, Revision 01; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2011. [Google Scholar]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-Resolution Mapping of the World’s Reservoirs and Dams for Sustainable River-Flow Management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef] [Green Version]
- Pai, D.S.; Sridhar, L.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadyay, B. Development of a new high spatial resolution (0.25° × 0.25°) Long Period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 2014, 65, 1–18. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Miralles, D.G.; Holmes, T.R.H.; de Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Fischer, G.; Nachtergaele, F.O.; Prieler, S.; Teixeira, E.; Toth, G.; van Velthuizen, H.; Verelst, L.; Wiberg, D. Global Agro-Ecological Zones Assessment for Agriculture (GAEZ 2008); IIASA: Laxenburg, Austria; FAO: Rome, Italy, 2012. [Google Scholar]
- Bayliss, A. Catchment Descriptors (Flood Estimation Handbook Volume 5); Institute of Hydrology: Wallingford, UK, 1999. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kjeldsen, T.R.; Jones, D.A.; Bayliss, A.C. Improving the FEH Statistical Procedures for Flood Frequency Estimation; Environment Agency: Bristol, UK, 2008. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Hosking, J.R.M. Regional Frequency Analysis Using L-Moments (R package). Available online: https://cran.r-project.org/package=lmomRFA (accessed on 15 July 2022).
- Moore, R.J. The PDM rainfall-runoff model. Hydrol. Earth Syst. Sci. 2007, 11, 483–499. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424-425, 264–277. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Drissia, T.K.; Jothiprakash, V.; Anitha, A.B. Flood frequency analysis using L-moments: A comparison between at-site and regional approach. Water Resour. Manag. 2019, 33, 1013–1037. [Google Scholar] [CrossRef]
- Guru, N.; Jha, R. Flood frequency analysis of Tel basin of Mahanadi river system, India using annual maximum and POT flood data. Aquat. Procedia 2015, 4, 427–434. [Google Scholar] [CrossRef]
- Swetapadma, S.; Ojha, C.S.P. Selection of a basin-scale model for flood frequency analysis in Mahanadi river basin, India. Nat. Hazards 2020, 102, 519–552. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, N.K.; Chatterjee, C.; Nayak, P.C. Regional flood frequency analysis using soft computing techniques. Water Resour. Manag. 2015, 29, 1965–1978. [Google Scholar] [CrossRef]
- Kumar, R.; Chatterjee, C.; Kumar, S.; Lohani, A.K.; Singh, R.D. Development of regional flood frequency relationships using L-moments for Middle Ganga Plains subzone 1(f) of India. Water Resour. Manag. 2003, 17, 243–257. [Google Scholar] [CrossRef]
- Grimaldi, S.; Nardi, F.; Piscopia, R.; Petroselli, A.; Apollonio, C. Continuous hydrologic modelling for design simulation in small and ungauged basins: A step forward and some tests for its practical use. J. Hydrol. 2021, 595, 125664. [Google Scholar] [CrossRef]
- Ball, J.E. Modelling Accuracy for Reliable Urban Design Flood Estimation. In Proceedings of the HWRS 2021: Digital Water: Hydrology and Water Resources Symposium, Virtual Symposium, 31 August–1 September 2021; Engineers Australia: Barton, Australia, 2021; pp. 35–47. [Google Scholar]
- Hossain, S.; Hewa, G.A.; Wella-Hewage, S. A Comparison of Continuous and Event-Based Rainfall-Runoff (RR) Modelling Using EPA-SWMM. Water 2019, 11, 611. [Google Scholar] [CrossRef]
- Nair, S.C.; Mirajkar, A.B. Integrated watershed development plan for a sub-basin, central India. Water Supply 2022, 22, 3342–3351. [Google Scholar] [CrossRef]
- Criss, R.E.; Winston, W.E. Do Nash values have value? Discussion and alternate proposals. Hydrol. Process. 2008, 22, 2723–2725. [Google Scholar] [CrossRef]
- de Lavenne, A.; Thirel, G.; Andréassian, V.; Perrin, C.; Ramos, M.-H. Spatial variability of the parameters of a semi-distributed hydrological model. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 87–94. [Google Scholar] [CrossRef]
- de Lavenne, A.; Andréassian, V.; Thirel, G.; Ramos, M.-H.; Perrin, C. A regularization approach to improve the sequential calibration of a semi-distributed hydrological model. Water Resour. Res. 2019, 55, 8821–8839. [Google Scholar] [CrossRef]
- Pradhan, C.; Chembolu, V.; Bharti, R.; Dutta, S. Regulated rivers in India: Research progress and future directions. ISH J. Hydraul. Eng. 2021, in press. [Google Scholar] [CrossRef]
- Mubialiwo, A.; Abebe, A.; Onyutha, C. Performance of rainfall-runoff models in reproducing hydrological extremes: A case of the River Malaba sub-catchment. SN Appl. Sci. 2021, 3, 515. [Google Scholar] [CrossRef]
- Soriano, E.; Mediero, L.; Garijo, C. Quantification of Expected Changes in Peak Flow Quantiles in Climate Change by Combining Continuous Hydrological Modelling with the Modified Curve Number Method. Water Resour. Manag. 2020, 34, 4381–4397. [Google Scholar] [CrossRef]
- Le Moine, N. Le Bassin Versant de Surface vu Par le Souterrain: Une Voie D’amélioration des Performances et du Réalisme des Modèles Pluie-Débit? Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2008. [Google Scholar]
- Lobligeois, F. Mieux Connaître la Distribution Spatiale des Pluies Améliore-t-il la Modélisation des Crues? Diagnostic Sur 181 Bassins Versants Français. Ph.D. Thesis, AgroParisTech, Paris, France, 2014. [Google Scholar]
- Pechlivanidis, I.G.; McIntyre, N.R.; Wheater, H.S. Calibration of the semi-distributed PDM rainfall-runoff model in the Upper Lee catchment, UK. J. Hydrol. 2010, 386, 198–209. [Google Scholar] [CrossRef]
- Kjeldsen, T.R. Flood Estimation Handbook Supplementary Report No. 1: The Revitalised FSR/FEH Rainfall-Runoff Method; Centre for Ecology & Hydrology: Wallingford, UK, 2007. [Google Scholar]

| Name | Start Year | End Year | Area (km2) | DPLBAR (km) | DPSBAR (m/km) | CULT (-) | URB (-) | FOR (-) |
|---|---|---|---|---|---|---|---|---|
| Ashti | 1965 | 2016 | 51579 | 339.0 | 33.4 | 0.470 | 0.051 | 0.394 |
| Kumhari | 1986 | 2017 | 8417 | 118.0 | 38.9 | 0.461 | 0.040 | 0.380 |
| Pauni | 1964 | 2016 | 36023 | 217.0 | 36.9 | 0.499 | 0.057 | 0.349 |
| Rajegaon | 1985 | 2017 | 5393 | 69.7 | 48.7 | 0.366 | 0.043 | 0.527 |
| Rajoli | 1986 | 2015 | 2675 | 54.5 | 19.2 | 0.489 | 0.033 | 0.405 |
| Ramakona | 1986 | 2017 | 2488 | 82.3 | 54.9 | 0.538 | 0.041 | 0.295 |
| Salebardi | 1985 | 2014 | 1768 | 44.0 | 30.4 | 0.439 | 0.037 | 0.469 |
| Satrapur | 1984 | 2015 | 11161 | 142.0 | 44.5 | 0.519 | 0.059 | 0.305 |
| Wairagarh | 1992 | 2015 | 1755 | 42.5 | 41.1 | 0.233 | 0.030 | 0.704 |
| Distribution | GLO | GEV | GNO | PE3 | GPA |
|---|---|---|---|---|---|
| Accepted | 67 | 91 | 95 | 101 | 92 |
| Chosen | 17 | 17 | 12 | 29 | 47 |
| Catchment | KGE’ | r | γ | β | NSE |
|---|---|---|---|---|---|
| Ashti | 0.880 | 0.881 | 0.998 | 1.007 | 0.760 |
| Kumhari | 0.512 | 0.513 | 0.965 | 1.001 | 0.057 |
| Pauni | 0.858 | 0.858 | 1.007 | 1.008 | 0.712 |
| Rajegaon | 0.669 | 0.670 | 0.975 | 1.006 | 0.352 |
| Rajoli | 0.548 | 0.558 | 0.905 | 1.010 | 0.183 |
| Ramakona | 0.333 | 0.335 | 0.952 | 0.993 | −0.262 |
| Salebardi | 0.648 | 0.654 | 0.937 | 1.003 | 0.346 |
| Satrapur | 0.573 | 0.575 | 0.964 | 0.981 | 0.194 |
| Wairagarh | 0.486 | 0.488 | 0.971 | 1.032 | −0.026 |
| Catchment | KGE’ | r | γ | β | NSE |
|---|---|---|---|---|---|
| Ashti | 0.647 | 0.860 | 0.922 | 1.315 | 0.602 |
| Kumhari | 0.356 | 0.399 | 1.030 | 0.769 | 0.001 |
| Pauni | 0.667 | 0.744 | 1.132 | 0.833 | 0.510 |
| Rajegaon | 0.353 | 0.561 | 0.855 | 1.452 | −0.163 |
| Rajoli | −0.516 | 0.561 | 0.612 | 2.398 | −0.659 |
| Ramakona | 0.160 | 0.299 | 0.993 | 1.462 | −1.250 |
| Salebardi | 0.397 | 0.637 | 0.753 | 1.413 | 0.209 |
| Satrapur | 0.350 | 0.517 | 1.373 | 0.775 | −0.033 |
| Wairagarh | 0.437 | 0.441 | 0.949 | 0.963 | −0.030 |
| Catchment | KGE’ | r | γ | β | NSE |
|---|---|---|---|---|---|
| Ashti | 0.658 | 0.763 | 1.049 | 0.758 | 0.574 |
| Kumhari | 0.324 | 0.493 | 0.903 | 0.563 | 0.230 |
| Pauni | 0.738 | 0.790 | 1.060 | 0.854 | 0.608 |
| Rajegaon | 0.514 | 0.665 | 0.824 | 0.694 | 0.427 |
| Rajoli | 0.001 | 0.612 | 0.703 | 1.871 | −0.179 |
| Ramakona | 0.293 | 0.349 | 0.742 | 0.900 | 0.020 |
| Salebardi | 0.503 | 0.668 | 0.664 | 0.845 | 0.433 |
| Satrapur | 0.291 | 0.505 | 0.803 | 1.468 | −0.211 |
| Wairagarh | 0.416 | 0.472 | 0.872 | 0.784 | 0.172 |
| Catchment | KGE’ | r | γ | β | NSE | KGE’’ |
|---|---|---|---|---|---|---|
| Ashti | 0.867 | 0.868 | 0.980 | 1.003 | 0.741 | 0.860 |
| Pauni | 0.874 | 0.874 | 0.999 | 1.000 | 0.749 | 0.844 |
| Satrapur | 0.575 | 0.579 | 0.955 | 0.970 | 0.214 | 0.518 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vesuviano, G.; Griffin, A.; Stewart, E. Flood Frequency Estimation in Data-Sparse Wainganga Basin, India, Using Continuous Simulation. Water 2022, 14, 2887. https://doi.org/10.3390/w14182887
Vesuviano G, Griffin A, Stewart E. Flood Frequency Estimation in Data-Sparse Wainganga Basin, India, Using Continuous Simulation. Water. 2022; 14(18):2887. https://doi.org/10.3390/w14182887
Chicago/Turabian StyleVesuviano, Gianni, Adam Griffin, and Elizabeth Stewart. 2022. "Flood Frequency Estimation in Data-Sparse Wainganga Basin, India, Using Continuous Simulation" Water 14, no. 18: 2887. https://doi.org/10.3390/w14182887