The Use of GAMLSS Framework for a Non-Stationary Frequency Analysis of Annual Runoff Data over a Mediterranean Area
Abstract
:1. Introduction
2. Materials and Methods
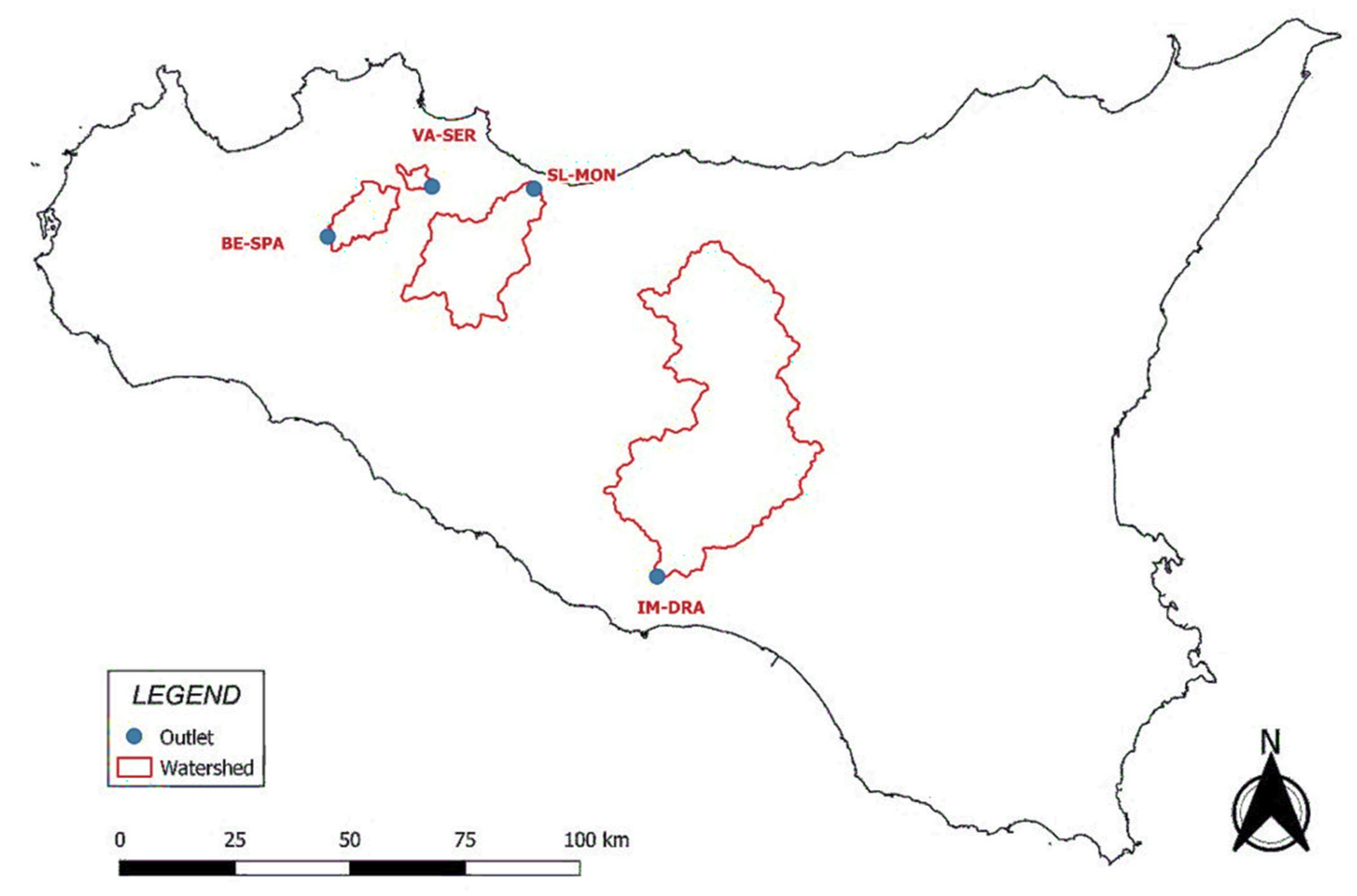
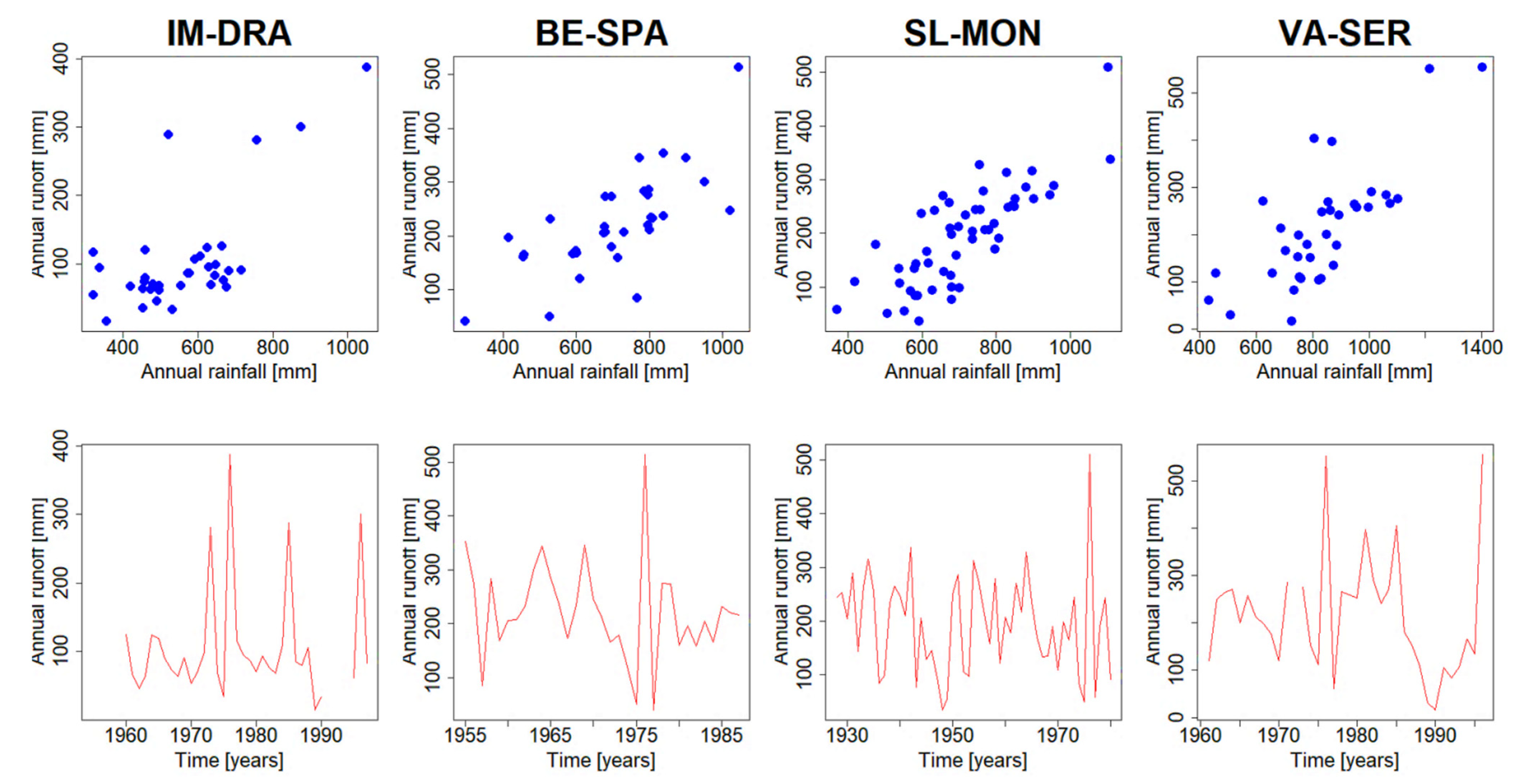
2.1. Data
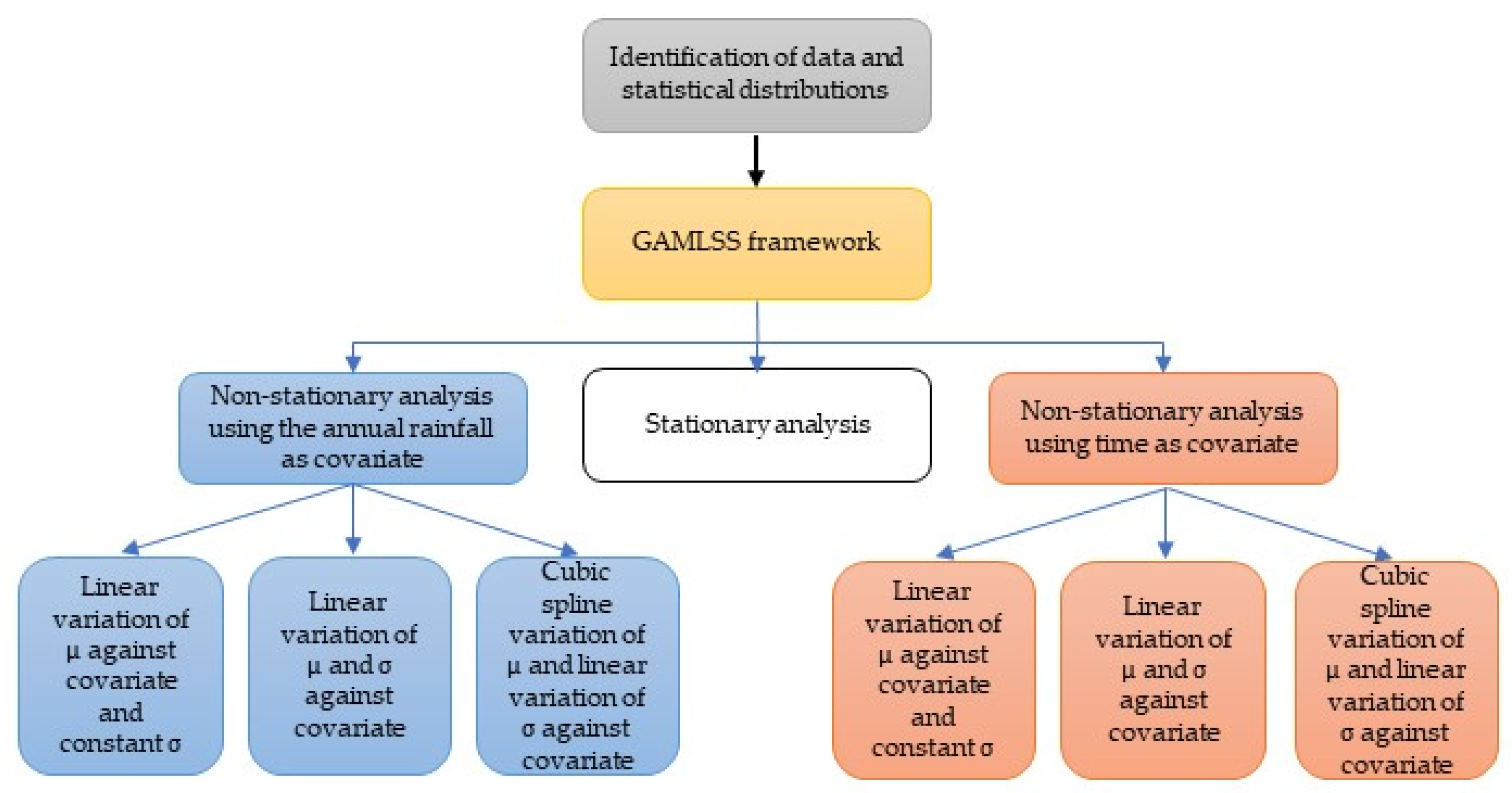
2.2. The Generalized Additive Models in Location, Scale and Shape (GAMLSS) Framework
2.3. Statistical Distributions in GAMLSS
2.4. The AIC Criterion
- 1.
- The number of independent variables used to build the model;
- 2.
- The maximum likelihood estimates of the model.
3. Results and Discussion
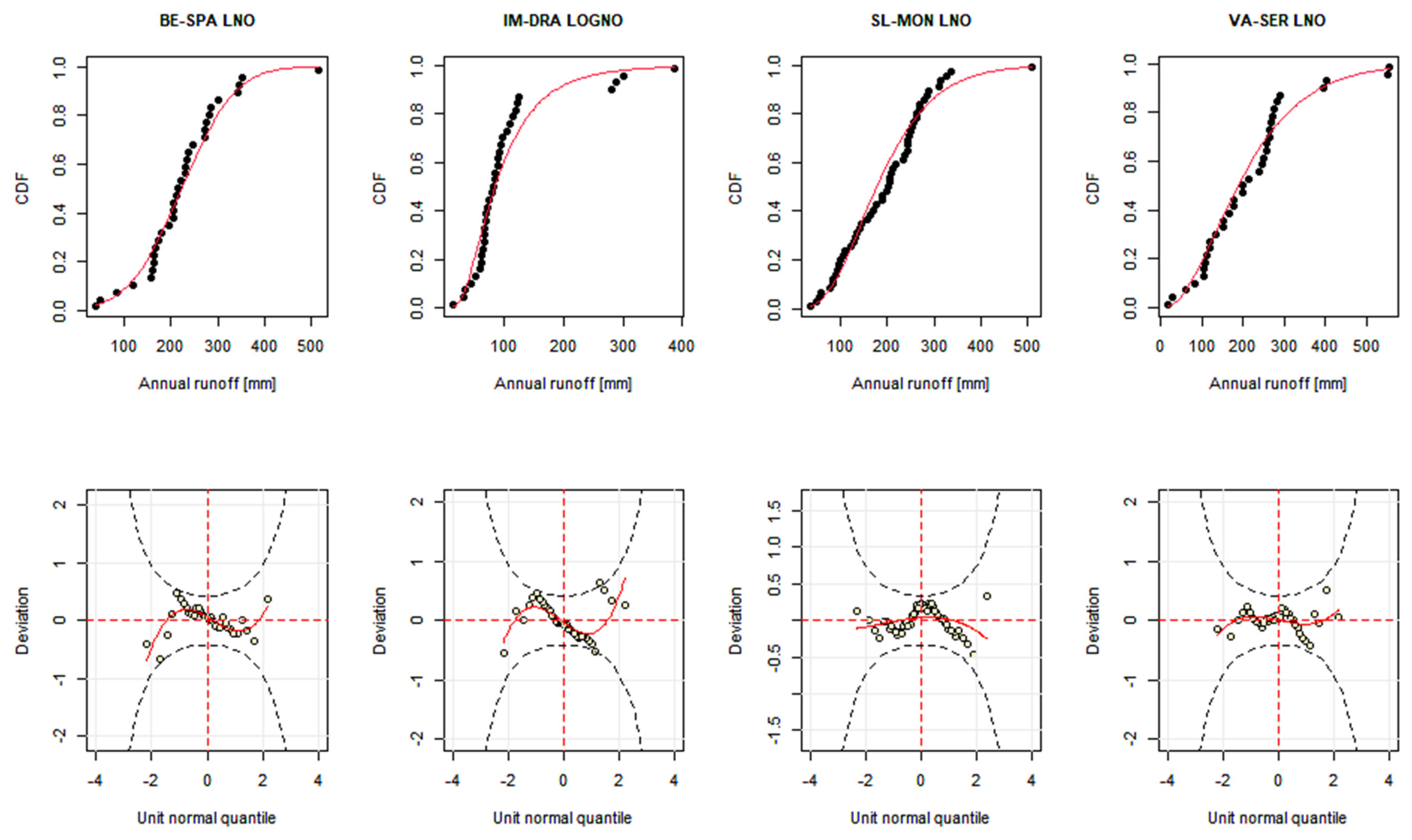
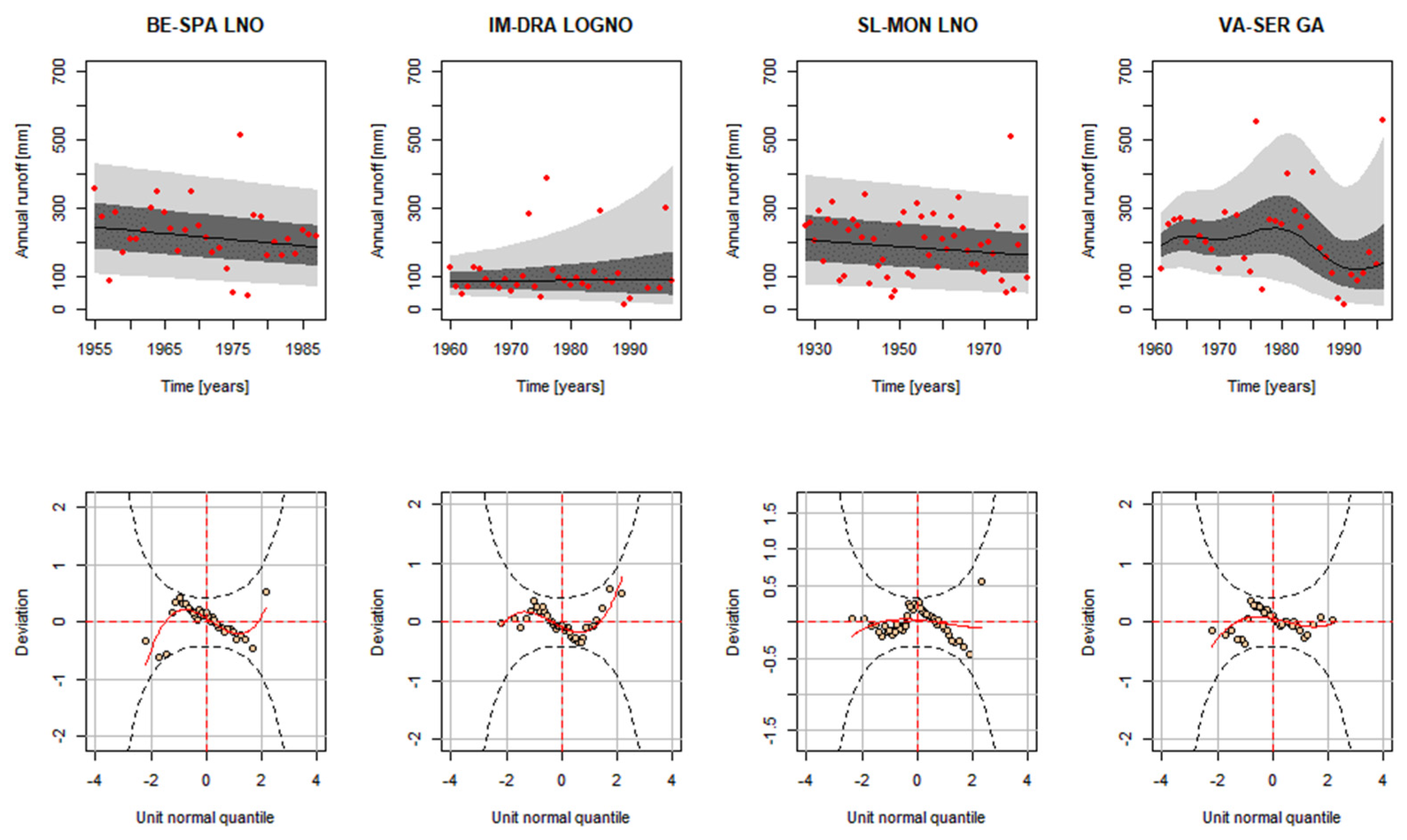
3.1. Stationary Analysis
3.2. Non-Stationary Analysis with Rainfall as a Covariate
3.3. Non-Stationary Analysis with Time as a Covariate
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cannarozzo, M.; Noto, L.; Viola, F.; la Loggia, G. Annual Runoff Regional Frequency Analysis in Sicily. Phys. Chem. Earth Parts A/B/C 2009, 34, 679–687. [Google Scholar] [CrossRef]
- Markovic, R.D. Probability Functions of the Best Fit to Distributions of Annual Precipitation and Runoff Hydrology. Doctoral Dissertation, Colorado State University, Fort Collins, CO, USA, 1965. Paper No. 8. [Google Scholar]
- Vogel, R.M.; Wilson, I. Probability distribution of annual maximum, mean, and minimum streamflows in the united states. J. Hydrol. Eng. 1996, 1, 69–76. [Google Scholar] [CrossRef]
- Salas, J.D. Analysis and Modeling of Hydrological Time Series. Handb. Hydrol. 1993, 19, 11–72. [Google Scholar]
- Liu, L.; Xu, H.; Wang, Y.; Jiang, T. Impacts of 1.5 and 2 °C global warming on water availability and extreme hydrological events in Yiluo and Beijiang River catchments in China. Clim. Change 2017, 145, 145–158. [Google Scholar] [CrossRef]
- Donnelly, C.; Andersson, J.C.M.; Arheimer, B. Using flow signatures and catchment similarities to evaluate the E-HYPE multi-basin model across Europe. Hydrol. Sci. J. 2016, 61, 255–273. [Google Scholar] [CrossRef]
- Li, S.; Qin, Y. Frequency Analysis of the Nonstationary Annual Runoff Series Using the Mechanism-Based Reconstruction Method. Water 2022, 14, 76. [Google Scholar] [CrossRef]
- Sadri, S.; Kam, J.; Sheffield, J. Nonstationarity of low flows and their timing in the eastern United States. Hydrol. Earth Syst. Sci. 2016, 20, 633–649. [Google Scholar] [CrossRef]
- Debele, S.E.; Bogdanowicz, E.; Strupczewski, W.G. Around and about an application of the GAMLSS package to non-stationary flood frequency analysis. Acta Geophys. 2017, 65, 885–892. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Xu, C.Y.; Guo, S. Bivariate frequency analysis of nonstationary low-flow series based on the time-varying copula. Hydrol. Processes 2015, 29, 1521–1534. [Google Scholar] [CrossRef]
- Kang, L.; Jiang, S.; Hu, X.; Li, C. Evaluation of return period and risk in bivariate non-stationary flood frequency analysis. Water 2019, 11, 79. [Google Scholar] [CrossRef]
- Nasri, B.R.; Bouezmarni, T.; St-Hilaire, A.; Ouarda, T. Non-Stationary Hydrologic Frequency Analysis using B-Spline Quantile Regression. J. Hydrol. 2017, 554, 532–544. [Google Scholar] [CrossRef] [Green Version]
- Nogaj, M.; Parey, S.; Dacunha-Castelle, D. Non-stationary extreme models and a climatic application. Nonlinear Processes Geophys. 2007, 14, 305–316. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Napolitano, F. Nonstationary modeling of a long record of rainfall and temperature over Rome. Adv. Water Resour. 2010, 33, 1256–1267. [Google Scholar] [CrossRef]
- Xiong, L.; Jiang, C.; Du, T. Statistical attribution analysis of the nonstationarity of the annual runoff series of the Weihe River. Water Sci. Technol. 2014, 70, 939–946. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Smith, J.A.; Wright, D.B.; Baeck, M.L.; Villarini, G.; Tian, F.; Hu, H. Urbanization and climate change: An examination of nonstationarities in urban flooding. J. Hydrometeorol. 2013, 14, 1791–1809. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Risks from dismissing stationarity. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2014; p. H54F-01. [Google Scholar]
- Matalas, N.C. Comment on the announced death of stationarity. J. Water Resour. Plan. Manag. 2012, 138, 311–312. [Google Scholar] [CrossRef]
- Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Caracciolo, D.; Noto, L.V.; Istanbulluoglu, E.; Fatichi, S.; Zhou, X. Climate change and Ecotone boundaries: Insights from a cellular automata ecohydrology model in a Mediterranean catchment with topography controlled vegetation patterns. Adv. Water Resour. 2014, 73, 159–175. [Google Scholar] [CrossRef]
- Francipane, A.; Fatichi, S.; Ivanov, V.Y.; Noto, L.V. Stochastic assessment of climate impacts on hydrology and geomorphology of semiarid headwater basins using a physically based model. J. Geophys.Res. Earth Surf. 2015, 120, 507–533. [Google Scholar] [CrossRef]
- Giuntoli, I.; Renard, B.; Vidal, J.-P.; Bard, A. Low flows in France and their relationship to large-scale climate indices. J. Hydrol. 2013, 482, 105–118. [Google Scholar] [CrossRef]
- Giuntoli, I.; Villarini, G.; Prudhomme, C.; Hannah, D.M. Uncertainties in projected runoff over the conterminous United States. Clim. Change 2018, 150, 149–162. [Google Scholar] [CrossRef] [Green Version]
- Kormos, P.R.; Luce, C.H.; Wenger, S.J.; Berghuijs, W.R. Trends and sensitivities of low streamflow extremes to discharge timing and magnitude in Pacific Northwest mountain streams. Water Resour. Res. 2016, 52, 4990–5007. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Yan, L.; Dong, J.; Xu, C.-Y. Multivariate hydrologic design methods under nonstationary conditions and application to engineering practice. Hydrol. Earth Syst. Sci. 2019, 23, 1683–1704. [Google Scholar] [CrossRef]
- Li, Y.; Chang, J.; Luo, L.; Wang, Y.; Guo, A.; Ma, F.; Fan, J. Spatiotemporal impacts of land use land cover changes on hydrology from the mechanism perspective using SWAT model with time-varying parameters. Hydrol. Res. 2019, 50, 244–261. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Bales, J.; Bates, P.D.; Krajewski, W.F. Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Adv. Water Resour. 2009, 32, 1255–1266. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat.Soc. Ser. C (Appl.Stat.) 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Wang, D.; Liu, P.; Guo, S.; Xu, C.-Y. Separating the impacts of climate change and human activities on runoff using the Budyko-type equations with time-varying parameters. J. Hydrol. 2015, 522, 326–338. [Google Scholar] [CrossRef]
- Li, J.; Tan, S. Nonstationary flood frequency analysis for annual flood peak series, adopting climate indices and check dam index as covariates. Water Resour. Manag. 2015, 29, 5533–5550. [Google Scholar] [CrossRef]
- López, J.; Francés, F. Non-stationary flood frequency analysis in continental Spanish rivers, using climate and reservoir indices as external covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef]
- Villarini, G.; Strong, A. Roles of climate and agricultural practices in discharge changes in an agricultural watershed in Iowa. Agric. Ecosyst. Environ. 2014, 188, 204–211. [Google Scholar] [CrossRef]
- Li, J.; Gao, Z.; Guo, Y.; Zhang, T.; Ren, P.; Feng, P. Water supply risk analysis of Panjiakou reservoir in Luanhe River basin of China and drought impacts under environmental change. Theor. Appl. Climatol. 2019, 137, 2393–2408. [Google Scholar] [CrossRef]
- Stasinopoulos, M.; Rigby, B.; Akantziliotou, C. Instructions on how to use the gamlss package in R Second Edition. 2008. Available online: http://gamlss.com/wp-content/uploads/2013/01/gamlss-manual.pdf (accessed on 1 August 2022).
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Akaike, H. On the likelihood of a time series model. J. R. Stat.Soc. Ser. D (Stat.) 1978, 27, 217–235. [Google Scholar] [CrossRef]
- Nelson, D.B. Stationarity and persistence in the GARCH (1, 1) model. Econom. Theory 1990, 6, 318–334. [Google Scholar] [CrossRef]
- Shumway, R.; Stoffer, D. Time Series Analysis and Its Applications with R Examples; Springer: New York, NY, USA, 2011; Volume 9. [Google Scholar]
- Chen, H.-L.; Rao, A.R. Testing hydrologic time series for stationarity. J. Hydrol. Eng. 2002, 7, 129–136. [Google Scholar] [CrossRef]
- Buuren, S.v.; Fredriks, M. Worm plot: A simple diagnostic device for modelling growth reference curves. Stat. Med. 2001, 20, 1259–1277. [Google Scholar] [CrossRef]
- Stasinopoulos, M.D.; Rigby, R.A.; Bastiani, F.D. GAMLSS: A distributional regression approach. Stat. Model. 2018, 18, 248–273. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. A semi-parametric additive model for variance heterogeneity. Stat. Comput. 1996, 6, 57–65. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, M.D. Mean and Dispersion Additive Models. In Statistical Theory and Computational Aspects of Smoothing; Physica-Verlag HD: Heidelberg, Germany, 1996; pp. 215–230. [Google Scholar]
- Zhang, T.; Wang, Y.; Wang, B.; Tan, S.; Feng, P. Nonstationary Flood Frequency Analysis Using Univariate and Bivariate Time-Varying Models Based on GAMLSS. Water 2018, 10, 819. [Google Scholar] [CrossRef] [Green Version]
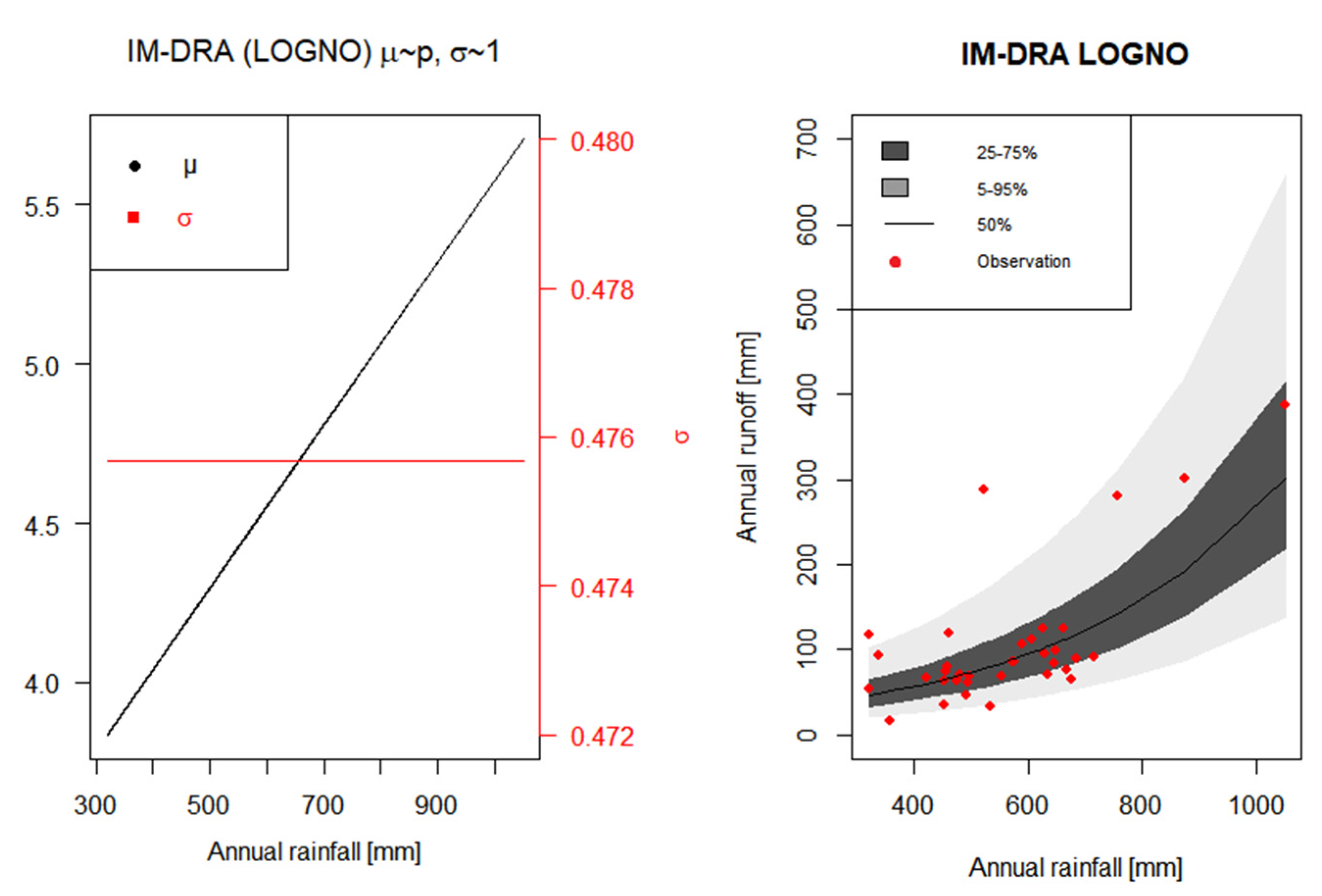
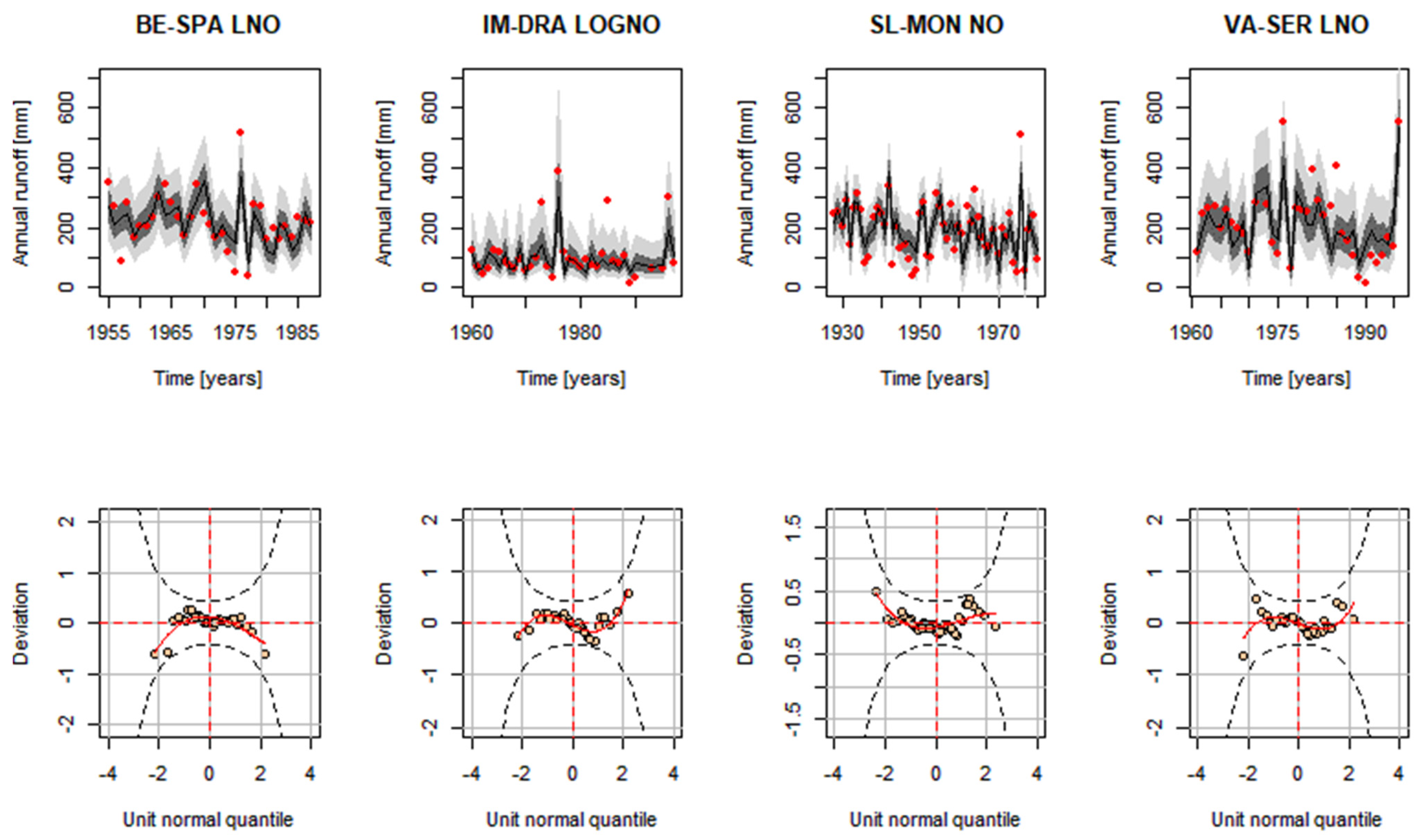
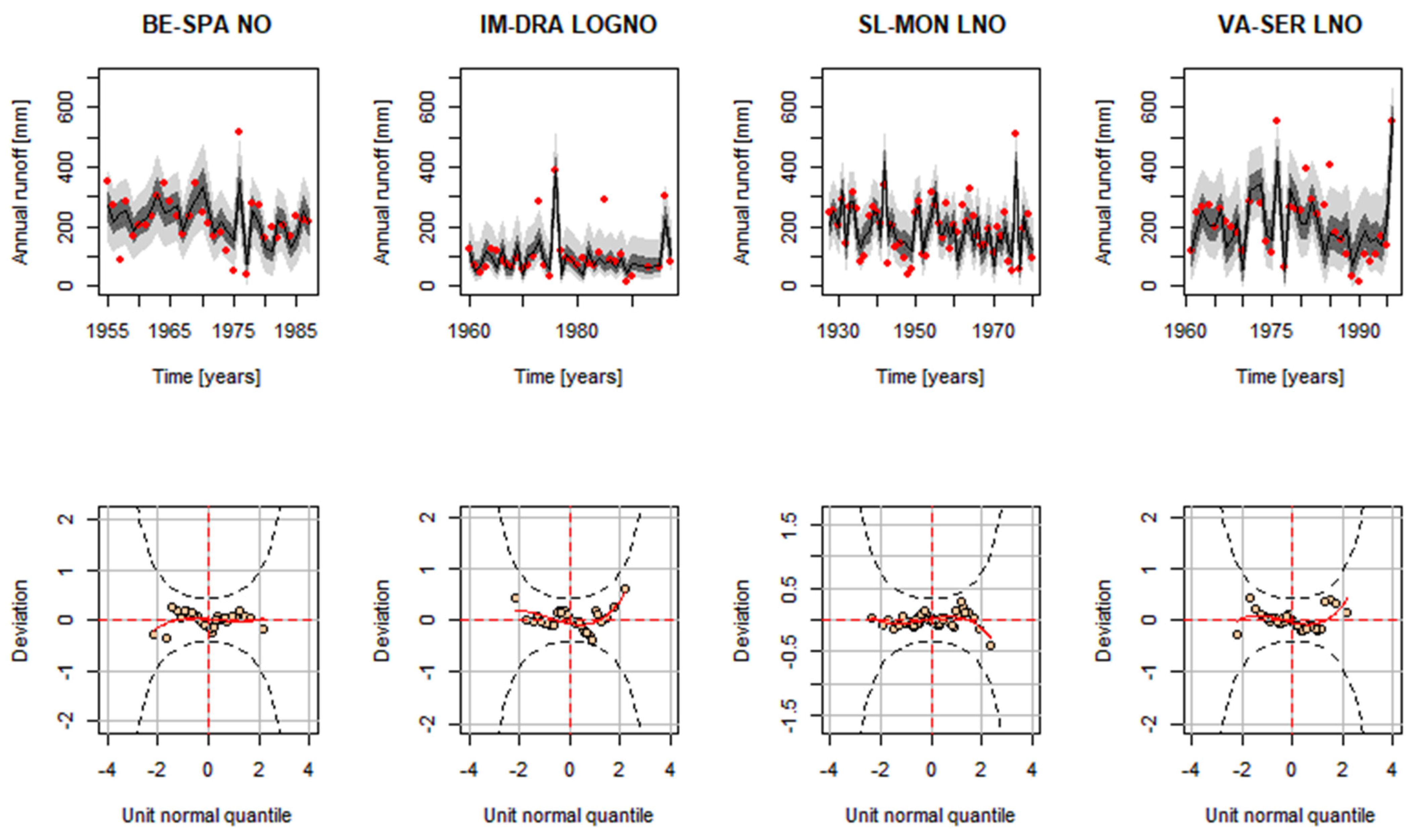
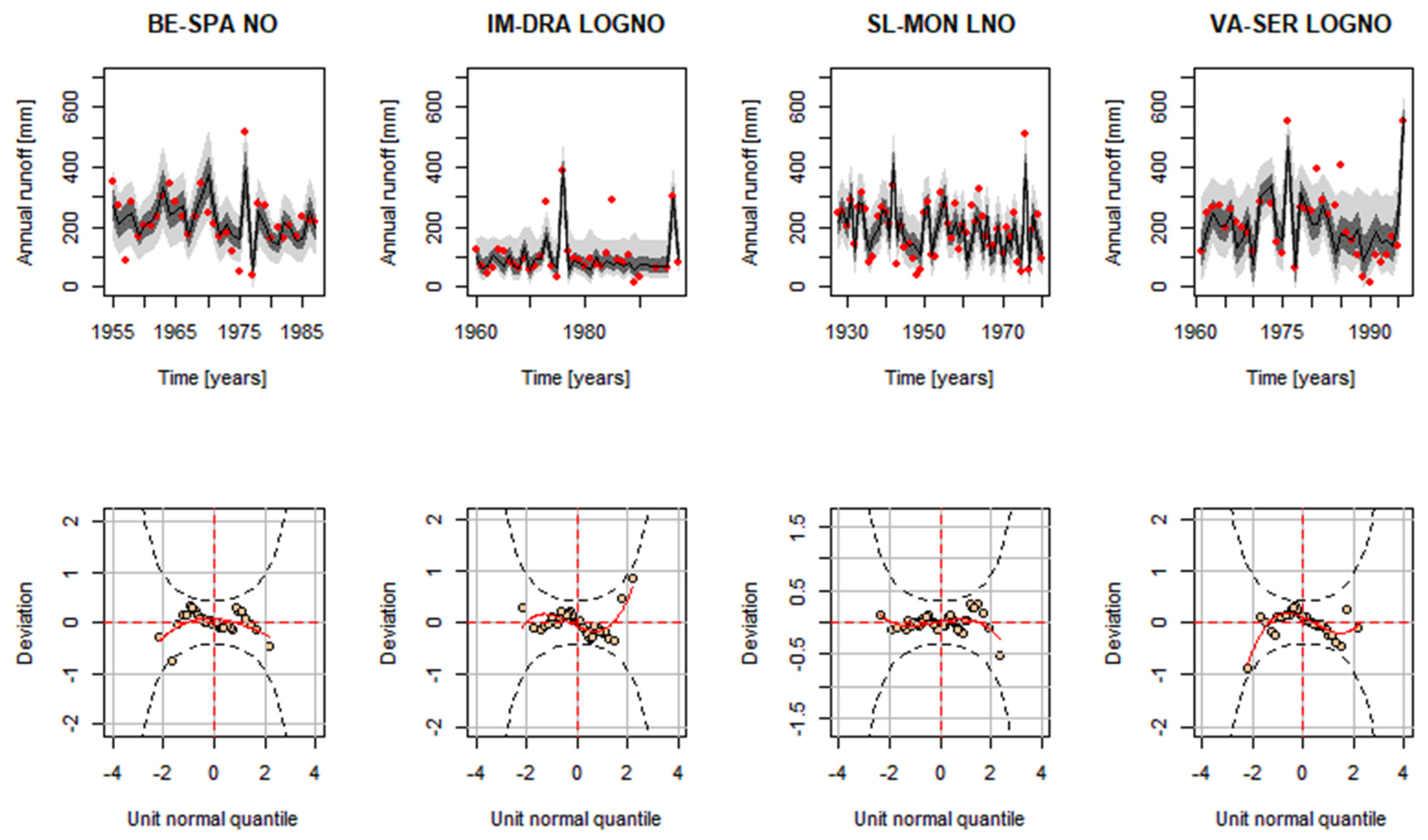
| Distributions | Probability Density Function | Distribution Moments |
|---|---|---|
| Normal (NO) | ; ; | |
| Gamma (GA) | ; | |
| Log-normal 2 parameters (LOGNO) | ; ; where | |
| Log-normal 3 parameters (LNO) | ; ; ; |
| AIC Values | ||||
|---|---|---|---|---|
| Distributions | BE-SPA | IM-DRA | SL-MON | VA-SER |
| Normal (NO) | 394.90 | 410.29 | 632.50 | 440.18 |
| Gamma (GA) | 396.54 | 386.01 | 630.31 | 435.31 |
| Log-normal 2 parameters (LOGNO) | 402.17 | 380.99 | 635.66 | 441.47 |
| Log-normal 3 parameters (LNO) | 394.64 | 390.44 | 629.31 | 434.29 |
| AIC Values | ||||
|---|---|---|---|---|
| Models | BE-SPA | IM-DRA | SL-MON | VA-SER |
| S—Stationary | LNO 394.64 | LOGNO 380.79 | LNO 629.31 | LNO 434.29 |
| P1—µ~p, σ~c | LNO 373.41 | LOGNO 365.33 | NO 581.02 | LNO 409.10 |
| P2—µ~p, σ~p | NO 373.36 | LOGNO 361.12 | LNO 580.46 | LNO 407.57 |
| P3—µ~cs(p), σ~p | NO 374.66 | LOGNO 362.94 | LNO 584.36 | LOGNO 405.71 |
| AIC Values | ||||
|---|---|---|---|---|
| Models | BE-SPA | IM-DRA | SL-MON | VA-SER |
| S—Stationary | LNO 394.64 | LOGNO 380.79 | LNO 629.31 | LNO 434.29 |
| T1—µ~t, σ~c | LNO 395.48 | LOGNO 382.98 | LNO 630.21 | LNO 434.96 |
| T2—µ~t, σ~t | LNO 397.42 | LOGNO 380.87 | LNO 630.99 | GA 429.06 |
| T3—µ~cs(t), σ~t | LNO 400.30 | LOGNO 383.96 | LNO 631.10 | GA 428.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scala, P.; Cipolla, G.; Treppiedi, D.; Noto, L.V. The Use of GAMLSS Framework for a Non-Stationary Frequency Analysis of Annual Runoff Data over a Mediterranean Area. Water 2022, 14, 2848. https://doi.org/10.3390/w14182848
Scala P, Cipolla G, Treppiedi D, Noto LV. The Use of GAMLSS Framework for a Non-Stationary Frequency Analysis of Annual Runoff Data over a Mediterranean Area. Water. 2022; 14(18):2848. https://doi.org/10.3390/w14182848
Chicago/Turabian StyleScala, Pietro, Giuseppe Cipolla, Dario Treppiedi, and Leonardo Valerio Noto. 2022. "The Use of GAMLSS Framework for a Non-Stationary Frequency Analysis of Annual Runoff Data over a Mediterranean Area" Water 14, no. 18: 2848. https://doi.org/10.3390/w14182848
APA StyleScala, P., Cipolla, G., Treppiedi, D., & Noto, L. V. (2022). The Use of GAMLSS Framework for a Non-Stationary Frequency Analysis of Annual Runoff Data over a Mediterranean Area. Water, 14(18), 2848. https://doi.org/10.3390/w14182848






