1. Introduction
In order to design hydraulic structures to manage runoff from rainfall, it is essential to determine the morphometric parameters and the time of concentration of the water basins [
1]. In hydrology studies, the time of concentration [
2,
3,
4] is used to estimate the maximum flow rate by means of rainfall-runoff models, from which the maximum flow rate of design for sizing of the hydraulic structures is determined [
5].
The time of concentration is defined as the time it takes a drop of water to travel from the most distant point to a determined drainage outlet [
6,
7], which is equivalent to the minimum time required for the entire basin to feed water to the drainage outlet [
8].
Determination of the time of concentration requires the interpretation both of rainfall records [
9] of hydrological stations located within a basin, and of outflow records from a station located at the basin’s drainage outlet. This information is generally obtained from basins that are equipped with adequate instrumentation.
When the above information is not available, designers use equations based on the morphometric parameters of the water basins, such as the slope and length of the watercourse and the type of cover on the basin’s ground. Such equations focus on determining the flow rate [
10], and have been developed from basins equipped with instrumentation in Europe and the United States [
3,
11]. Adequate selection of these equations is crucial in order to avoid over and under-estimating time of concentration values, which would lead to over or under-estimating the maximum flow rates of design for the hydraulic works. Some of the equations used to determine the time of concentration include those by: Témez, William, Kirpich, California Culvert Practice, Giandotti, S.C.S., Ventura-Heron, Brausby-William, Passini, Izzard, Federal Aviation Administration, Morgali and Linsley, Aron and Erborge [
12]. Use of these equations depends on the morphometric features of the basins [
13].
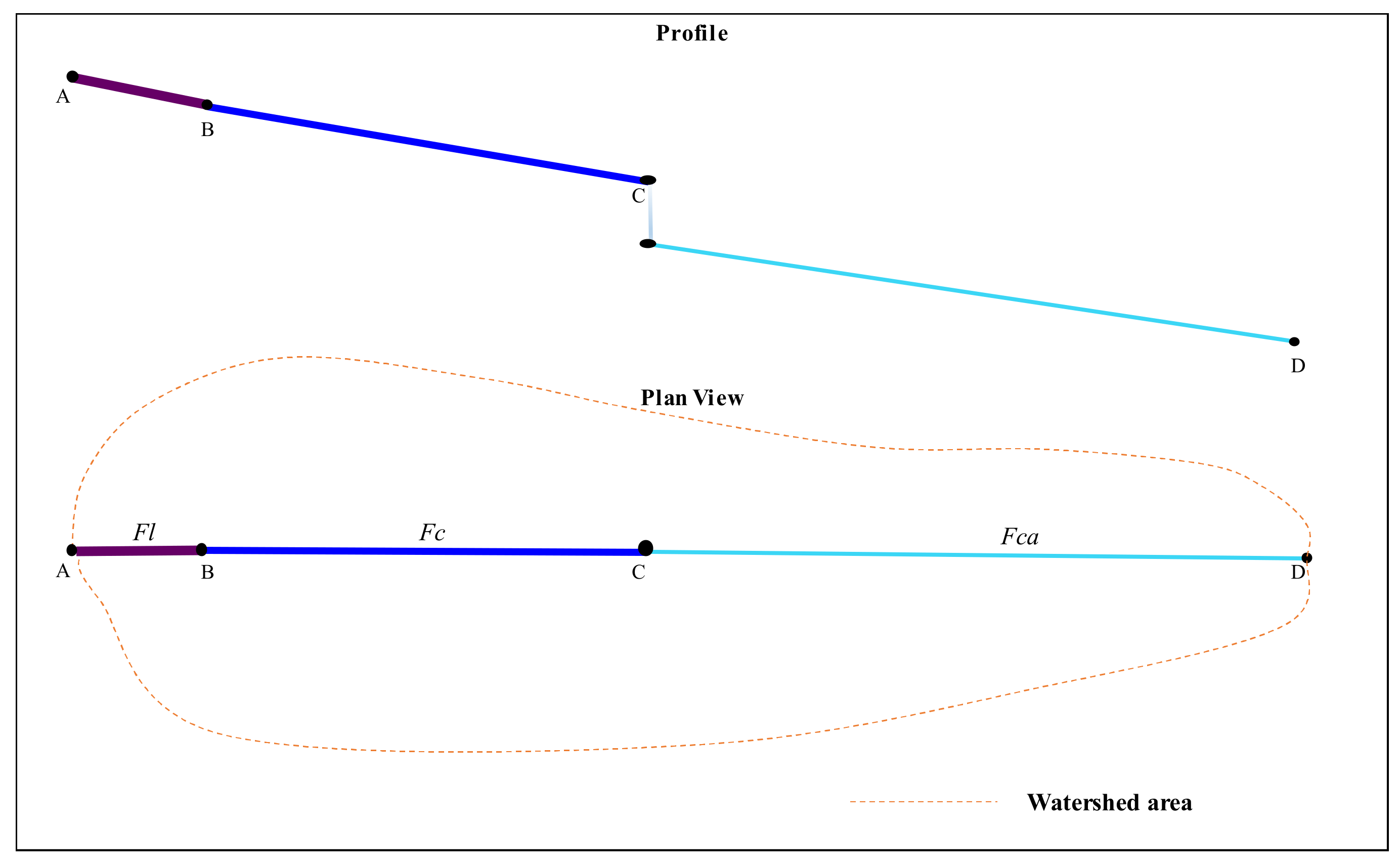
The Natural Resources Conservation Service (NRCS) proposed a formula that is almost fully based on physics to estimate the time of concentration; the formula requires detailed input information for the calculation. The equation proposed by the NRCS is based on determining the travel time for sheet, concentrated and channel flow conditions [
14].
Figure 1 presents the plan and side views of the locations where these three types of flows occur. Sheet flow (
Fl) occurs at the headwaters of a basin, concentrated flows (
Fc) arise immediately after the sheet flow, and channel flow (
Fca) takes place in the drainage channel.
Figure 2 displays the differences between the concentrated flow and the channel-type flow, using as reference the behavior of one of the small watersheds of the study following a rainfall event.
In order to improve the characterization of the small urban watersheds and their watercourses, local drawings were used containing elevation data with precision of up to one centimeter, produced from topographic measurements performed by the company responsible for local basic sanitation. Topographic measurements were also made in the field to enable the instrumentation of the main watercourses, providing reliable values for the calculation of the time of concentration, primarily with the baseline equation.
This study aims to determine the sensitivity of the parameters of the empirical equations for the calculation of the time of concentration, using the small watersheds located in the city of Montería, Colombia. The values of time of concentration obtained from the empirical equations are compared to the equation almost fully based on physics developed by the NRCS (called here the baseline equation). This research presents the expression to compute the sheet flow using the NRCS equation in the metric system to avoid confusion in future developments. In addition, it can be used for engineers and designers in the city of Montería, Colombia, to select a priori the best empirical equation to calculate time of concentration of urbanized watersheds.
2. Case Study
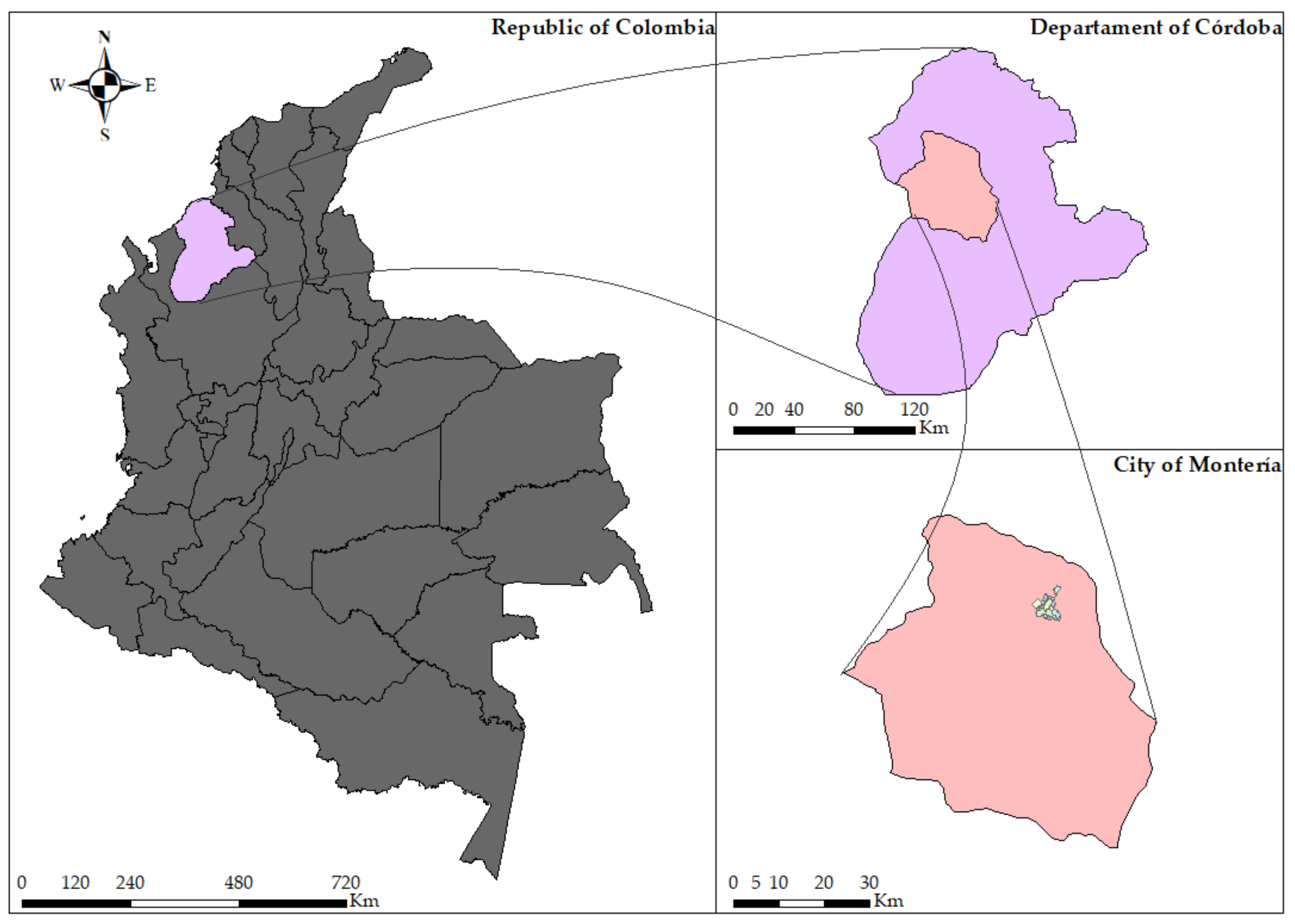
The small urban watersheds of the study are located in the city of Montería, department of Córdoba, Colombia (see
Figure 3). It covers an area of approximately 3142 km
2 and its topography is basically flat with a few elevations. The city is surrounded by numerous creeks and streams, and the city’s main water source is the Sinú River. The region has a rainy season between April and September and a dry season between December and April. The city of Montería has an average slope of 0.2%, and a rainfall drainage system that starts out on the streets as a concentrated flow, and whose superficial runoff is subsequently fed into a drainage channel.
The small watersheds of the study and their respective main watercourses were identified beforehand by means of a geographic information system, performing altimetric tracking in Google Earth, which enabled identifying the perimeters and areas of the urban watersheds, and planimetric tracking, which enabled establishing the layout of the main watercourses.
Afterwards, given that the average topographic slope of the city is flat, adjustments were made to the polygons of small watersheds that had been previously delimited in Google Earth, because the measurement precision of this geographic information is only up to one meter, which creates uncertainty as to the actual perimeter of the small watersheds of the case study. These parameters were adjusted based on the city drawings of the sewage network of the city of Montería, which were provided by the municipal basic sanitation service operator and which contain the elevations above sea level at the city’s main street intersections.
First, the paths followed by the sheet flow and concentrated flow were identified, and afterwards a topographic survey was performed in order to obtain precise information on the magnitudes of the geometric and hydraulic parameters of the drainage channels (channel flow). Field work was also performed to identify the channel sections with homogeneous cover materials, finding that the geometry of the cross-section is typical, and that the longitudinal slope is constant. Information on the channels was obtained using equipment such as: electronic total station, a Topcon high-precision level, and RTK Trimble GPS technology equipment.
Following the selection of the small watersheds of the study and their respective main watercourses, calculations were performed of the morphometric parameters to be used in the study.
3. Materials and Methods
The research process began by determining the small urban watersheds in the area of the study, which were delimited and adjusted for the effects of calculating the morphometric, rainfall and ground cover parameters. Lastly, the main channels were selected, calculating their respective hydraulic and geometric parameters.
Figure 4 displays the small watersheds of the study and their corresponding watercourses.
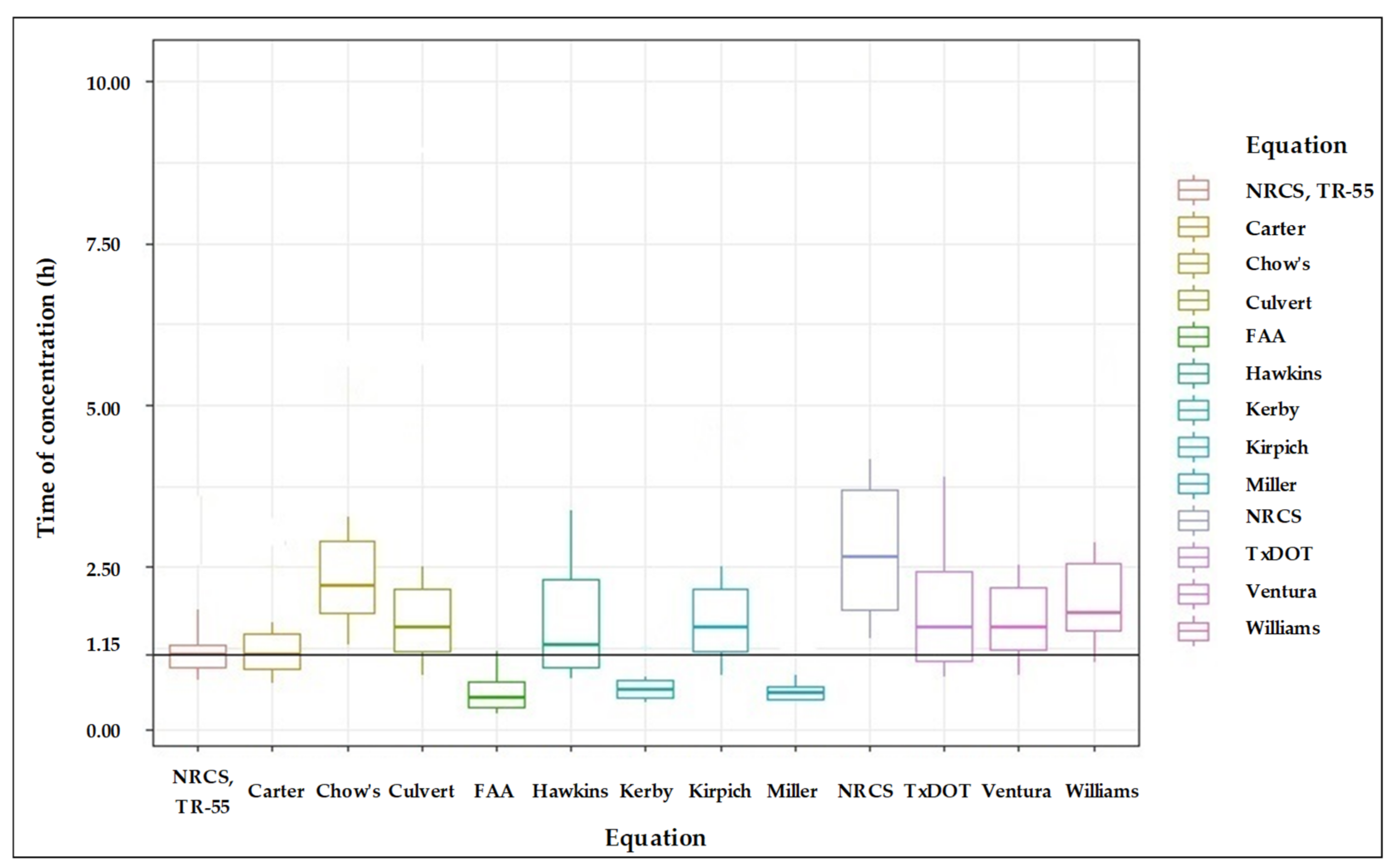
Table 1 presents the morphometric features of the small watersheds of the study. Their areas (
Ac) are between 0.53 and 5.52 km
2, with a minimum watershed slope (
S) of 0.00060 m/m and a maximum slope of 0.00225 m/m, which are consistent with the local topographic conditions. The review of ground cover results indicates that urbanized cover is predominant in terms of the runoff coefficient (
C) and the weighted curve number (
CN). Δ
H is a different elevation in a main watercourse.
P2 is the maximum daily precipitation associated to a return period (
Tr) of 2 yr. Lastly, Manning’s roughness coefficient (
n) highlights that most watercourses are covered in concrete, which increases the runoff flow rate.
Once the information required for calculation of time of concentration was acquired, the results obtained using the twelve empirical equations were compared to those of the equation developed by the NRCS. The equation that is almost fully based on physics developed by the NRCS is expressed as follows:
where
Tc = Time of concentration (h), and
m = Number of branches.
The equations were adjusted and presented under the conditions of the International System, which is not published.
The travel time for the sheet flow (
Fl) was calculated based on Manning’s roughness coefficient (
n), the length and slope of the watercourse and the maximum precipitation of design associated to a two-year return period. The following is the expression used for the calculation:
where
Tfl = Sheet flow travel time (h),
Lfl = Sheet flow length (m),
n = Manning’s roughness coefficient, P
2 = Maximum precipitation in 24 h for a 2-year return period (mm), and
Sc = Average watercourse slope (m/m).
The formula for the travel time of the concentrated flow (Fc) assumes that the sheet flow becomes a superficial concentrated flow. The average velocity of this flow is determined based on the following expressions:
Once the estimated average velocity is calculated, the travel time of the concentrated flow is calculated using the following expression:
where
Tfc = Concentrated flow travel time (h),
Lfc = Concentrated flow length (m), and
V = Average velocity (m/s).
Lastly, the travel time for the channel-type flow (
Fca) is calculated for open channels with defined hydraulic characteristics in the cross-section. Manning’s equation or the information of the profile of the water surface is used to estimate the average flow velocity.
where
V = Average velocity (m/s), r = Hydraulic radius (m),
Sc = average watercourse slope (in this case corresponds to the hydraulic slope of the channel) (m/m), and
n = Manning’s roughness coefficient.
Based on the concentrated flow travel time equation, the channel flow travel time is calculated.
where
Tfca = Channel flow travel time (h) and
Lfca = Channel flow length (m).
For analysis, the NRCS formulation is considered as the baseline equation.
In this study, 12 empirical equations were used, which are listed in
Table 2.
Statistical analysis was performed based on the Tc values produced by the baseline equation and by the empirical equations, using analysis of variance (ANOVA). Then Dunnet’s test of multiple comparisons of means was used to select the equations whose Tc is similar to the times of concentration calculated using the baseline equation with a 5% significance level. However, the method used to select the equation that is best suited for the conditions of the basins of the city of Montería, Córdoba was multiple linear regression analysis, using as decision criteria the coefficient of determination (R2) and the mean square error (MSE).
In order to observe the behavior of the Tc calculated values, sensitivity analysis was conducted in four stages.
The first sensitivity analysis focused on finding the variability of the Tc value calculated by means of the baseline equation by calculating the maximum precipitation in 24 h associated with the 2-year return period, as proposed by the different authors cited in [
14,
30], who recommend the use of distribution methods, from among which GEV, Log Pearson Type III and Pearson Type III were selected. The result was compared to the value used as reference (Gumbel) [
31]. This value is necessary in order to calculate the sheet flow travel time.
The second sensitivity analysis focused on the variability of the roughness coefficient used in the baseline equation to calculate sheet flow and concentrated flow travel time. To this effect, analysis was performed using the values defined as the minimum, normal and maximum values depending on the type of channel and its description. After recalculating the travel times and the time of concentration, statistical analysis was performed to assess the sensitivity of this variable compared to the empirical equations.
The third sensitivity analysis was performed by calculating the time of concentration value using the baseline equation, initially without considering the sheet flow travel time, and afterwards without considering the concentrated flow travel time. The obtained values were compared to the values calculated by the different equations to estimate Tc, using MSE and R2 as the criteria for comparison. The empirical equations used for the comparison were those that did not display significant differences in the statistical analysis.
The fourth and last sensitivity analysis focused on verifying the behavior of the empirical equations as a function of variations in the length of the main watercourse and the ground cover of the different urban watersheds. The equations selected for this analysis were those that did not display significant differences compared to the baseline equation according to Dunnet’s test. It should be noted that sensitivity to the two variables mentioned above was not assessed for all the selected equations, either because such variables were not included or were not relevant in the equations. Lastly, time of concentration was calculated using the selected equations, and the results obtained were compared to the values of the baseline equation. The variation found in the results obtained in this analysis was assessed by means of MSE.
5. Discussion
The small watersheds that drain towards the city of Montería were selected and determined using as reference cartographic and topographic information in order to determine their morphometric characteristics. The results obtained are displayed in
Table 1 which consists of 11 densely urbanized small watersheds with areas between 0.53 and 5.52 km
2 and lengths of main watercourses between 1.19 and 6.81 km, approximately. Consequently, in order to delimit the small watersheds and define their morphometric parameters, as a minimum, it is necessary to have geographic information available in the form of cartographic charts or satellite images. This methodology is supported by Kobiyama, M., Grison, F., Lino, J.F., & Silva, R.V. (2006) [
32], who used for their study a map with scale of 1:10,000 to establish the morphometric parameters of the basin studied in the campus of Universidad Federal de Santa Catarina (UFSC) (BC). Based on the above and an analysis of the methods used to characterize water basins, it is observed that the definition and delimitation of the basin’s area and other morphometric parameters can be performed by means of geographic information; however, for the assessment of small basins with primarily flat topography, aerial photographs, cartographic maps or a DEM will not suffice, because their precision is up to one meter, and therefore miss elevated points on the surface that are not within that range, in this case one meter, which can produce inconsistencies in the delimitation of the basins. Consequently, more precise information is required such as cartographic drawings that contain field measurements using high-precision equipment, in order to improve reliability at the time of defining the area and other morphometric parameters of the basin.
The time of concentration was calculated using the method proposed by the NRCS as the baseline equation for the effects of comparing it to the empirical methods. This method has been used as a baseline equation by numerous authors, who sometimes refer to it as the real equation. This methodology has been endorsed by Sharifi, S., & Hosseini, S.M. (2011) [
13], who used the equation of the Natural Resource Conservation Service (NRCS) as a baseline equation to identify the best method to calculate the Tc of basins in the region of Khorasan Razavi, Iran. In addition, McCuen, R.H., Wong, S.L., & Rawls, W.J. (1984) [
6] used as a baseline equation for the calculation of urban concentration the velocity method of the NRCS. For this reason, in the analysis of the composition of this equation, and on the basis of reliable information on the variables required for the calculation of the three types of flows, it should be highlighted that it is of utmost importance to know with precision the average slope of the sheet flow and concentrated flow for the effects of calculating travel time. This lends greater weight to the fact that for this study, topographic information was available with sub-metric precision, which enabled calculating the slopes with a high level of reliability. Regarding the geometric measurements of the main channels, having measured them with topographic equipment enabled instrumenting the main watercourses, thereby obtaining the highly accurate geometric and hydraulic values that are required to calculate the channel flow.
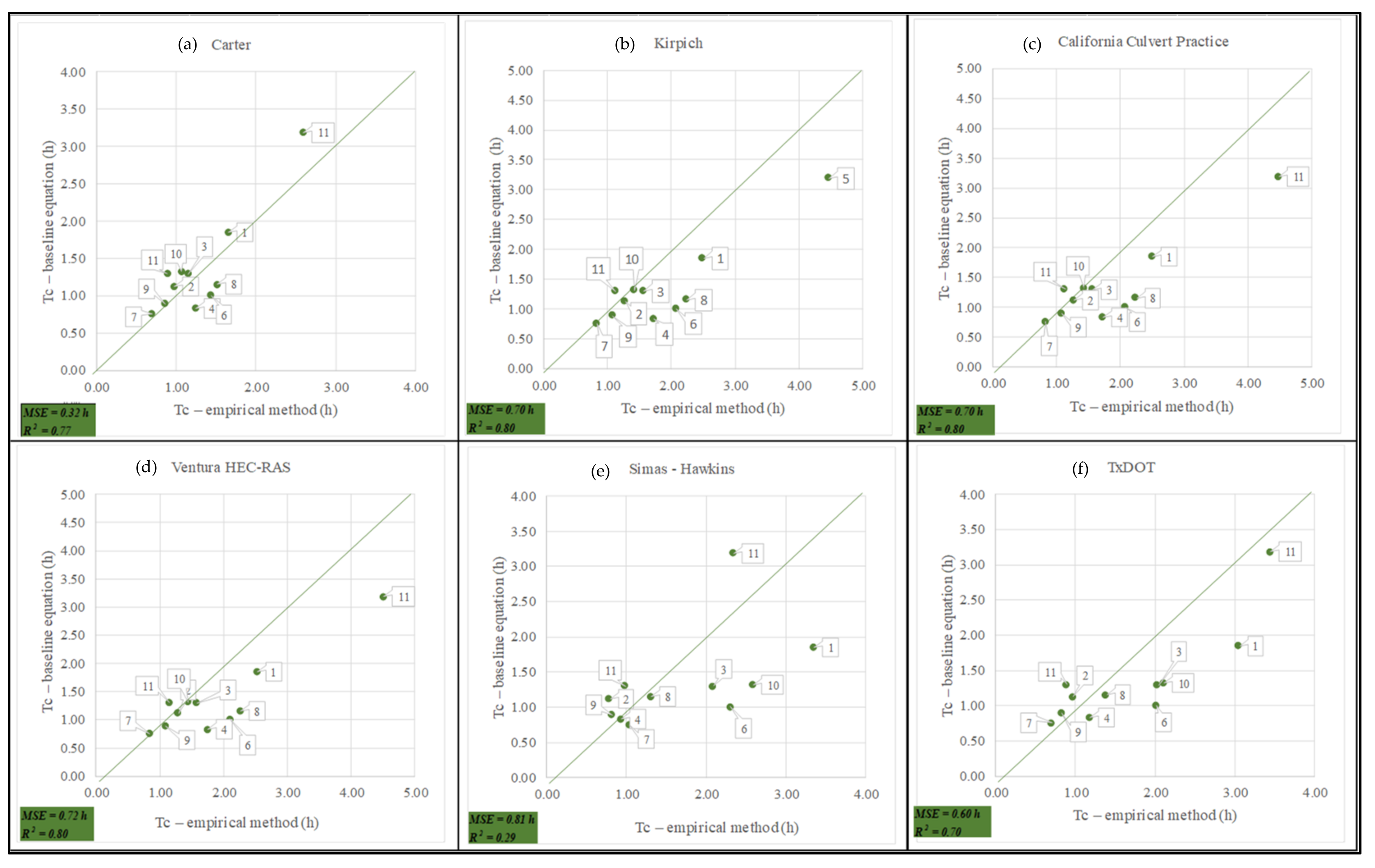
To estimate the time of concentration of the different selected water basins, in this study 12 empirical equations were used, the resulting values of which are displayed in
Table 4. In effect, it was found that there were significant differences in the calculated Tc values when the results of each equation are compared for each studied basin. In this regard, Vélez and Gutiérrez (2011) [
3] consider that it is appropriate to use a large number of equations to calculate the time of concentration in order to reduce the level of uncertainty of the calculated data, and to discard the equations that are outside the range. Due to the above, it is of great value to have a significant number of empirical equations to calculate the time of concentration in a specific region, because it creates a range of alternatives that can be assessed by the researchers in terms of the results obtained, and enables the use of statistical comparison methods to filter and reduce the number of initial equations to a small number that according to the comparison test provides similar values for the calculation of Tc.
When the method for estimating Tc is categorized by means of statistical analysis (ANOVA), Dunn’s means comparison test, and the calculation of R
2 and MSE, the results of the formal hypothesis test of the Tc (treatments), Fo = 17.15, yielded a
p value < 0.0001, and additional hypothesis testing was performed for the micro-basins (blocks), Fo = 23.26, with a
p value < 0.0001. The results obtained in the comparison test are displayed in
Table 6, and
Table 7 displays the goodness of fit results. These results lead to the belief that of the 12 empirical equations selected, 6 did not display significant differences when the mean values are compared to those of the baseline equation, among which the Carter equation was the equation with the best goodness of fit according to the selection criteria that were adopted. However, the results of the other equations cannot be ruled out because the decision criteria are not rejected for these cases either. The results of the means comparison test can be compared to those obtained by Vahabzadeh, G., Saleh, I., Safari, A., & Khosravi, K. (2013) [
2], who used the Tukey means comparison test to categorize the best equations. Additionally, the comparison criteria used in this study are supported by Ravazzani, G., Boscarello, L., Cislaghi, A., & Mancini, M. (2019) [
19], who based their goodness of fit of the methods on MSE and R
2. On the above, it is important to mention that the use of a means comparison test plays an important role in the categorization of the equations of the study, as it enables the researcher the rule out many of the equations that were initially selected that do meet the expected objectives. Afterwards, assessing which of the resulting methods is most accurate compared to the baseline equation brings the researcher closer to the desired objective, providing backing for the methodological approach and validation that an empirical equation may be highly correlated with an equation almost fully based on physics. Lastly, it can be said that these statistical methods leave a window open to study the remaining equations from a different perspective (sensitivity analysis). The curve number was estimated for each urbanized watershed and extreme scenarios of antecedent moisture conditions were considered [
33].
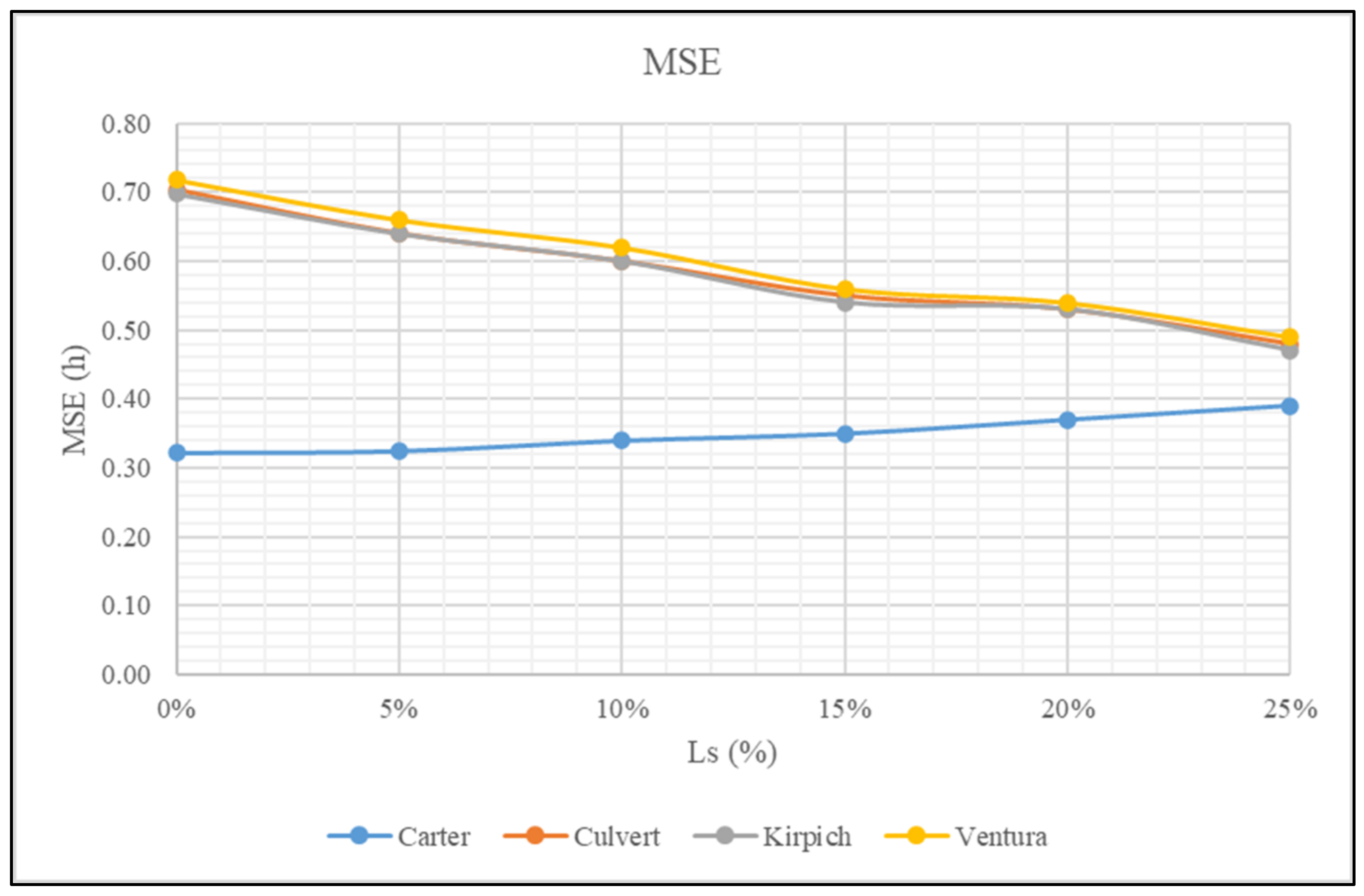
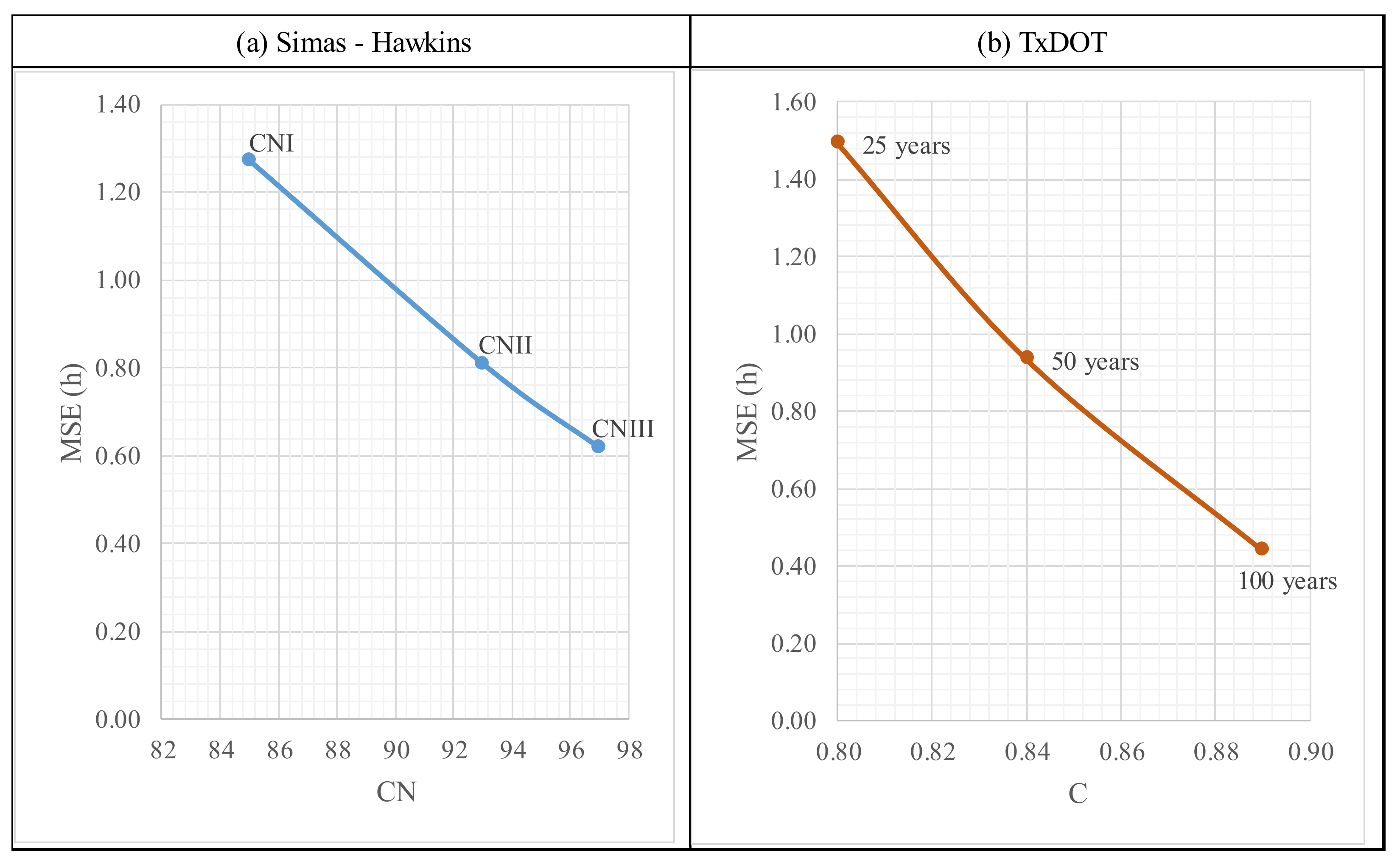
For the effects of sensitivity analysis, changes were made to the magnitudes of some parameters for the calculation of the time of concentration of the selected equations. Four sensitivity analyses were conducted with the results displayed in
Table 8,
Table 9 and
Table 10 and
Figure 7 and
Figure 8. These results show that by changing the magnitude of the sensitized parameters, in some cases no sensitivity was observed, as in the case of changing the sheet flow travel time. In other cases, the precision of the statistical analysis (MSE) was negatively affected, as when the travel times of the baseline equation were discriminated. Lastly, in some empirical equations (Kirpich and TxDOT), the difference compared to the NRCS equation decreased when lengths and ground cover were changed. These results can be compared with those of the study by Michailidi, E.M., Antoniadi, S., Koukouvinos, A., & Bacchi, B. &. (2018) [
34], who performed sensitivity analysis with changes in the discretization of the accumulation of the flow and changed the roughness coefficient. In analyzing these results, it can be inferred that in some equations, when the magnitude of parameters is adequately changed, efficient results are obtained, which may represent an alternative for the effects of calculating Tc. In this way, the researcher is not limited to solely approaching the calculation of the runoff flow rate using the Carter equation in this case. Instead, there are other alternatives available as demonstrated in this study. They could be useful for verifying the Tc value by means of alternative and reliable equations, thus increasing the reliability of the process of calculating the flow rate using rainfall-runoff models. The sensitivity analysis was only conducted for urban catchments considering similar empirical equations used by other authors [
35].
6. Conclusions
The rigorous approach of this research study is evident in the methodology presented for its performance. The delimitation of the urban watersheds is the starting point for a series of processes that must be conducted in order to estimate the time of concentration, such as the identification of the morphometric and geometric parameters of the main watercourses of the basins of the study. The information required for this research study on the aforementioned parameters was obtained from drawings with topographic information and field measurements made with high-precision topographic equipment. This equipment was used to perform plan and altitude surveys using conventional methodologies of direct measurement with electronic total station and indirect measurements using RTK GPS technology.
The equation proposed by the NRCS was used as reference (or baseline formulation) to determine the time of concentration of basins under general conditions, and for this reason, whenever possible, this method should be the first choice for calculating Tc. However, when there is not sufficient information available to calculate Tc using the baseline equation, or depending on the stage of phase of the project to be implemented (pre-feasibility or feasibility), empirical equations that do not display significant differences may be used.
The most effective method for estimating the time of concentration of the urban watersheds of the city of Montería is the Carter equation based on Mean Square Error (MSE) and Coefficient of Determination (R
2). These values were found taking into consideration the total length of the main watercourse using the Carter equation, which is equivalent to the sum of the different travel times of the baseline equation using laminar, concentrate, and channel flow. Complementarily, it can be concluded that the Carter equation was found to have highly significant similarity with the baseline equation for the effects of calculating the Tc, which is validated by the value found in the means in the statistical analysis, in which values were reported of 1.34 h for the baseline equation and 1.28 h for the Carter equation (see
Figure 5).
The comparison of the baseline equation to the empirical methods that estimate Tc enabled showing the correlations between them. However, statistical analysis is the best way to select the adjustment method that demonstrates the relevance of the model for a particular basin. In this study, statistical analysis enabled the disaggregation of the components used in engineering to calculate the Tc of a basin. Thanks to the analysis of variance, the significant differences between the times of concentration of the proposed equations steered the study towards application of Dunnet’s comparison of means test, which helped select the set of equations that, in this case, best fit the requirements of the urban watersheds of the city of Montería, Córdoba.
By means of sensitivity analysis it was shown that the results of the equations with best goodness of fit according to the statistical analysis were those by Kirpich, California Culvert Practice and Ventura, which were the equations that displayed sensitivity to the length of the main watercourse (Ls). As Ls decreased, MSE decreased, and a 25% reduction was the largest reduction of Ls at which the MSE stabilized. The ground cover and texture were found to be highly sensitive variables when the Simas-Hawkins equation is used, which is a function of the curve number, and the TxDOT, as a function of the runoff coefficient. It can be concluded that for the first equation mentioned here, MSE decreased considerably when background conditions of moisture were considered (AMC III), with MSE of 0.62 h. In the second equation mentioned in this point, it is concluded that as the value of the runoff coefficient (C) increases as a function of the return period, MSE decreases, with a result of 0.44 h for a 100-year Tr.
For future works, the use of data in monitored basins should be utilized to measure the time concentration (time between rain end and superficial flow end) for comparing these values with the NRCS equation (baseline formulation) and the twelve empirical equations.