Predicting Aquaculture Water Quality Using Machine Learning Approaches
Abstract
:1. Introduction
2. Material and Methods
2.1. Selection of Water Quality Prediction Model
2.1.1. Back Propagation Neuron Network (BPNN)
2.1.2. Radial Basis Function Neuron Network (RBFNN)
2.1.3. Support Vector Regression Machine (SVM)
2.1.4. Least Squares Support Vector Machine (LSSVM)
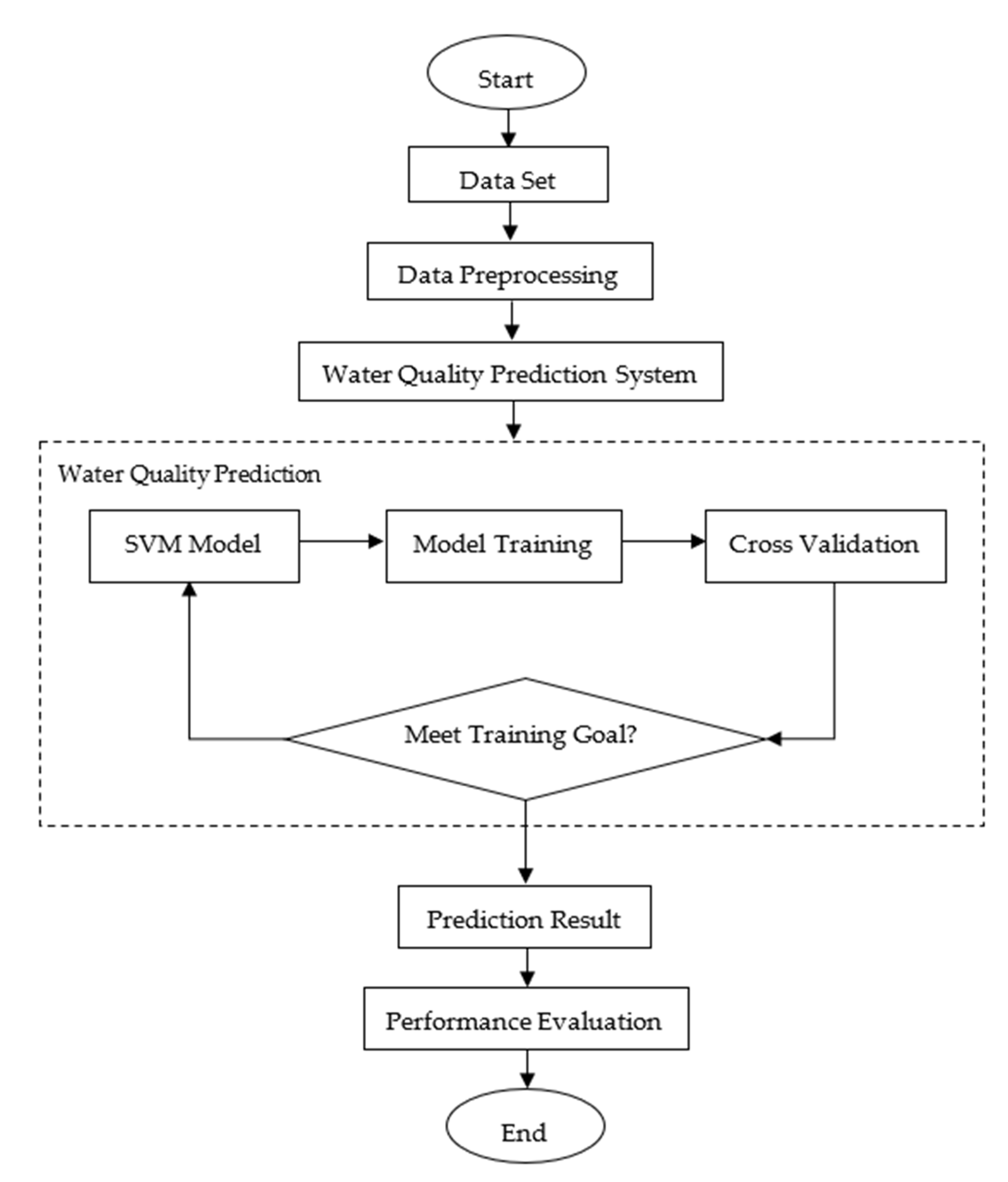
2.2. Simulation and Prediction by Using the Empirical Data
2.2.1. Data Sources
2.2.2. Algorithm Implementation
2.2.3. Metric Evaluation Models
2.2.4. Sensitivity Analysis
3. Results and Discussion
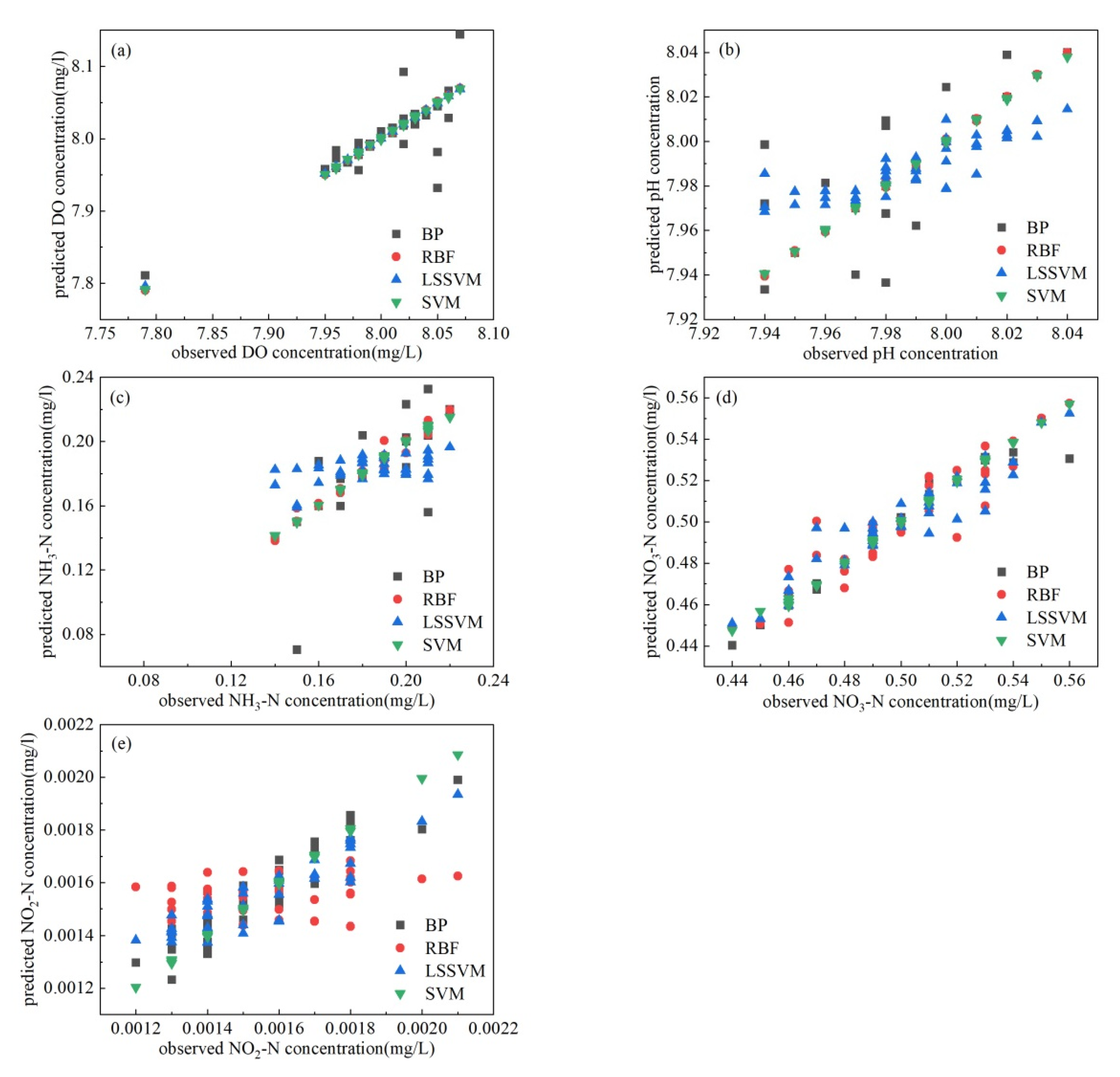
3.1. Model Screening for Predicting Water Quality
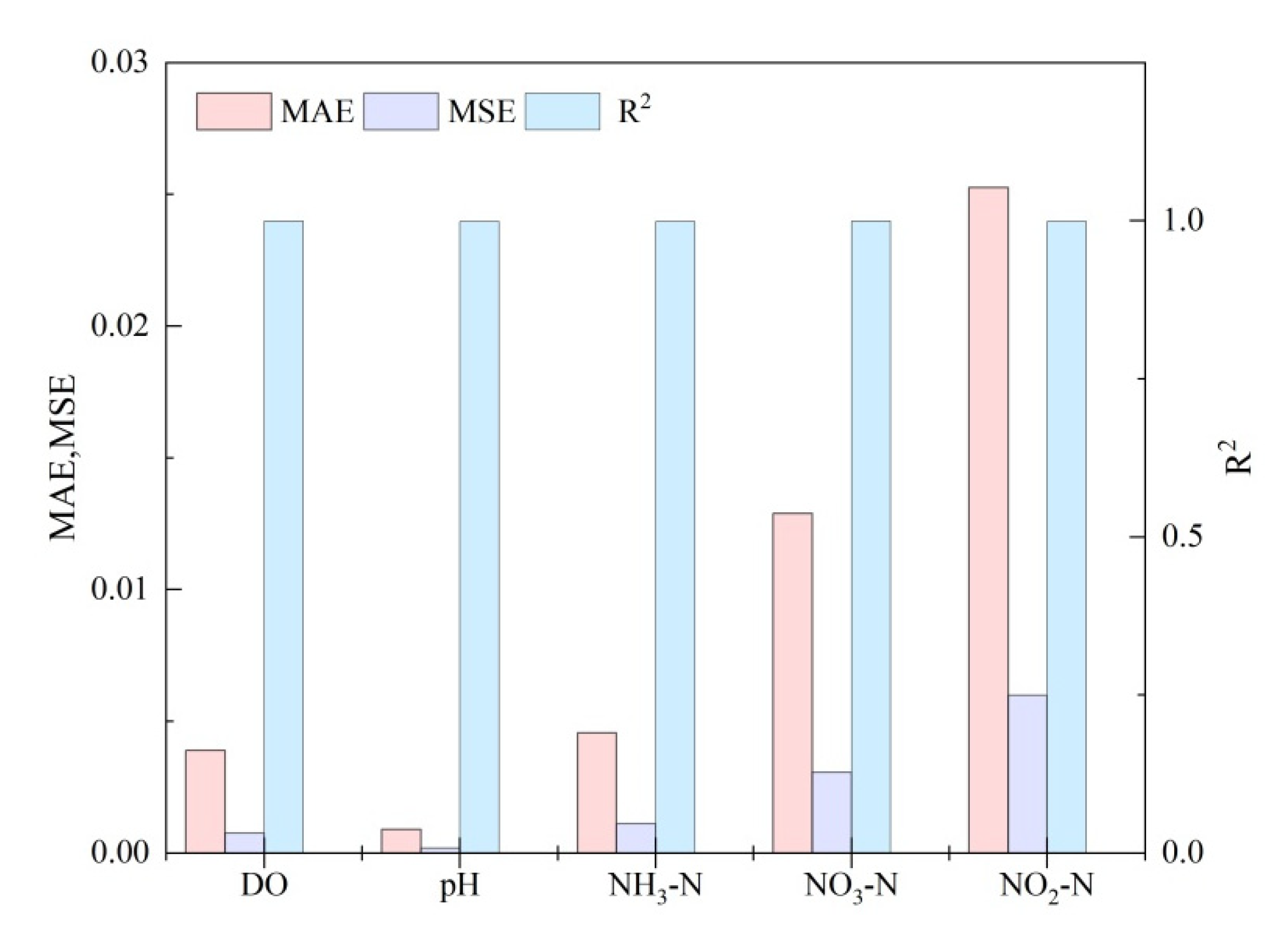
3.2. Simulation and Prediction by Using Support Vector Machine
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, J.; Lin, Y.C.; Wu, J.; Zhang, C. Continental-scale spatial distribution, sources, and health risks of heavy metals in seafood: Challenge for the water-food-energy nexus sustainability in coastal regions? Environ. Sci. Pollut. Res. 2021, 28, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Wu, J.; Wang, J.H. Metagenomic analysis on resistance genes in water and microplastics from a mariculture system. Front Environ. Sci. Eng. 2022, 16, 4. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Y.X.; Wu, J.; Wang, J.H. Intervention of antimicrobial peptide usage on antimicrobial resistance in aquaculture. J. Hazard. Mater. 2022, 427, 128154. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, A.H.; Saad, F.S.; Sudin, S.; Ahmad, Z.A.; Ahmad, I.; Abu, B.N.; Omar, S.; Sulaiman, S.F.; Che, M.H.; Umoruddin, N.A.; et al. Development of aquaculture water quality real-time monitoring using multi-sensory system and internet of things. J. Phys. Conf. Ser. 2021, 1, 2107. [Google Scholar] [CrossRef]
- Nguyen, X.C.; Nguyen, T.; La, D.D.; Kumar, G.; Nguyen, V.K. Development of machine learning—based models to forecast solid waste generation in residential areas: A case study from Vietnam. Resour. Conserv. Recycl. 2021, 167, 105381. [Google Scholar] [CrossRef]
- Rajaee, T.; Mirbagheri, S.A.; Zounemat-Kermani, M.; Nourani, V. Daily suspended sediment concentration simulation using ANN and neuro-fuzzy models. Sci. Total Environ. 2009, 407, 17. [Google Scholar] [CrossRef]
- Shouliang, H.; Zhuoshi, H.; Jing, S.; Beidou, X.; Chaowei, Z. Using Artificial Neural Network Models for Eutrophication Prediction. Procedia Environ. Sci. 2013, 18, 310–316. [Google Scholar]
- Chang, F.J.; Chen, P.A.; Chang, L.C.; Tsai, Y.H. Estimating spatio-temporal dynamics of stream total phosphate concentration by soft computing techniques. Sci. Total Environ. 2016, 562, 228–236. [Google Scholar] [CrossRef]
- Markus, M.; Tsai, C.W.S.; Demissie, M. Uncertainty of weekly nitrate-nitrogen forecasts using artificial neural networks. J. Environ. Eng. 2003, 129, 267–274. [Google Scholar] [CrossRef]
- Suen, J.P.; Eheart, J.W. Evaluation of neural networks for modeling nitrate concentrations in rivers. J. Water Resour. Plan. Manag. 2003, 129, 505–510. [Google Scholar] [CrossRef]
- Xu, X.; Sun, Z.J.; Wang, L.; Fu, J.; Wang, C. A Comparative Study of Customer Complaint Prediction Model of Time Series, Multiple Linear Regression and BP Neural Network. J. Phys. Conf. Ser. 2019, 1187, 052036. [Google Scholar] [CrossRef]
- Fan, Y.; Lu, W.X.; Miao, T.S.; An, Y.; Li, J.; Luo, J. Optimal design of groundwater pollution monitoring network based on the SVR surrogate model under uncertainty. Environ. Sci. Pollut. Res. Int. 2020, 27, 24090–24102. [Google Scholar] [CrossRef] [PubMed]
- Chia, S.L.; Chia, M.Y.; Koo, C.H.; Huang, Y.F. Integration of advanced optimization algorithms into least-square support vector machine (LSSVM) for water quality index prediction. Water Sci. Technol. Water Supply. 2022, 22, 1951–1963. [Google Scholar] [CrossRef]
- Kisi, O. Modeling discharge-suspended sediment relationship using least square support vector machine. J. Hydrol. 2012, 456, 110–120. [Google Scholar] [CrossRef]
- Deng, T.; Chau, K.W.; Duan, H.F. Machine learning based marine water quality prediction for coastal hydro-environment management. J. Environ. Manage. 2021, 284, 112051. [Google Scholar] [CrossRef]
- Mirarabi, A.; Nassery, H.R.; Nakhaei, M.; Adamowski, J.; Akbarzadeh, A.H.; Alijani, F. Evaluation of data-driven models (SVR and ANN) for groundwater-level prediction in confined and unconfined systems. Environ. Earth Sci. 2019, 78, 1–15. [Google Scholar] [CrossRef]
- Mirza, A.S.; Leal, J. Emulation of 2D Hydrodynamic Flood Simulations at Catchment Scale Using ANN and SVR. Water. 2021, 13, 2858. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Lnaa, B.; Jtb, B.; Taa, B. Ensemble method based on Artificial Neural Networks to estimate air pollution health risks—ScienceDirect. Environ. Model. Softw. 2020, 123, 104567. [Google Scholar]
- Li, J. Construction of legal incentive evaluation model based on BP neural network with multiple hidden layers. J. Phys. Conf. Ser. 2021, 1941, 012087. [Google Scholar] [CrossRef]
- Lourakis, M.I.A. A Brief Description of the Levenberg-Marquardt Algorithm Implemened by levmar. Found. Res. Technol. 2005, 4, 1–6. [Google Scholar]
- Kc, A.; Hc, B.; Cz, B. Comparative analysis of surface water quality prediction performance and identification of key water parameters using different machine learning models based on big data—ScienceDirect. Water Res. 2019, 171, 115454. [Google Scholar]
- Dandy, M. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef]
- Liu, X.P.; Lu, M.Z.; Chai, Y.Z.; Tang, J.; Gao, J.Y. A comprehensive framework for HSPF hydrological parameter sensitivity, optimization and uncertainty evaluation based on SVM surrogate model—A case study in Qinglong River watershed, China. Environ. Model Softw. 2021, 143, 150126. [Google Scholar]
- Leong, W.C.; Bahadori, A.; Zhang, J. Prediction of water quality index (WQI) using support vector machine (SVM) and least square-support vector machine (LS-SVM). Int. J. River Basin Manag. 2019, 19, 149–156. [Google Scholar] [CrossRef]
- Xu, W.; Wang, G.; Zhang, X. Prediction of Chlorophyll-a content using hybrid model of least squares support vector regression and radial basis function neural networks. In Proceedings of the 2016 Sixth International Conference on Information Science & Technology, Dalian, China, 6–8 May 2016. [Google Scholar]
- Del, G.D.; Muenich, R.L.; Kalcic, M.M. On the practical usefulness of least squares for assessing uncertainty in hydrologic and water quality predictions. Environ. Model Softw. 2018, 105, 286–295. [Google Scholar]
- Lei, T. Based on the Neural Network Model to Predict Water Quality; Haikou, D., Ed.; Hainan University: Haikou, China, 2015. [Google Scholar]
- Wang, S.; Yu, L.; Tang, L. A novel seasonal decomposition based least squares support vector regression ensemble learning approach for hydropower consumption forecasting in China. Energy 2011, 36, 6542–6554. [Google Scholar] [CrossRef]
- Sakaa, B.; Elbeltagi, A.; Boudibi, S.; Chaffaï, H.; Islam, A.R.M.T.; Kulimushi, L.C.; Choudhari, P.; Hani, A.; Brouziyne, Y.; Wong, Y.J. Water quality index modeling using random forest and improved SMO algorithm for support vector machine in Saf-Saf river basin. Environ. Sci. Pollut Res. Int. 2022, 29, 32. [Google Scholar]
- Cai, O.; Xiong, Y.; Yang, H. Phosphorus transformation under the influence of aluminum, organic carbon, and dissolved oxygen at the water-sediment interface: A simulative study. Front. Environ. Sci. Eng. 2020, 3, 165–176. [Google Scholar] [CrossRef]
- Iraní, S.M.; Vanessa, R.R.; Fernanda, L.A. The influence of the water pH on the sex ratio of tambaqui colossoma macropomum (CUVIER, 1818). Aquac. Rep. 2020, 17, 100334. [Google Scholar]
- Li, Y.; Ling, J.; Chen, P. Pseudomonas mendocina LYX: A novel aerobic bacterium with advantage of removing nitrate high effectively by assimilation and dissimilation simultaneously. Front. Environ. Sci. Eng. 2021, 15, 57. [Google Scholar] [CrossRef]



| Data | Measurement Methods |
|---|---|
| DO | DO sensor |
| pH | pH meter |
| NH3-N | Nessler’s reagent spectrophotometry |
| NO3-N | Ultraviolet spectrophotometric method |
| NO2-N | 1,2-diaminoethane dihydrochioride spectrophotometry |
| Published Data | Aquaculture Water Quality Data in Industrial Aquaculture Systems | ||||||
|---|---|---|---|---|---|---|---|
| Water Quality Parameter | Model | Result | Water Quality Parameter | Model | Result | ||
| MSE | R2 | MSE | R2 | ||||
| DO | BPNN | 0.092 | 0.60 | DO | SVM | 0.001 | 0.99 |
| RBFNN | 0.002 | 0.99 | |||||
| SVM | 0.003 | 0.99 | |||||
| LSSVM | 0.004 | 0.99 | |||||
| pH | BPNN | 0.053 | 0.56 | pH | SVM | 0.0002 | 0.99 |
| RBFNN | 0.002 | 0.84 | |||||
| SVM | 0.002 | 0.99 | |||||
| LSSVM | 0.052 | 0.57 | |||||
| NH3-N | BPNN | 0.055 | 0.28 | NH3-N | SVM | 0.001 | 0.99 |
| RBFNN | 0.001 | 0.88 | |||||
| SVM | 0.004 | 0.99 | |||||
| LSSVM | 0.056 | 0.25 | |||||
| NO3-N | BPNN | 0.017 | 0.96 | NO3-N | SVM | 0.003 | 0.99 |
| RBFNN | 0.002 | 0.87 | |||||
| SVM | 0.006 | 0.99 | |||||
| LSSVM | 0.031 | 0.87 | |||||
| NO2-N | BPNN | 0.002 | 0.87 | NO2-N | SVM | 0.006 | 0.99 |
| RBFNN | 0.351 | 0.08 | |||||
| SVM | 0.001 | 0.99 | |||||
| LSSVM | 0.064 | 0.75 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Lu, J.; Wu, J.; Zhang, Z.; Chen, L. Predicting Aquaculture Water Quality Using Machine Learning Approaches. Water 2022, 14, 2836. https://doi.org/10.3390/w14182836
Li T, Lu J, Wu J, Zhang Z, Chen L. Predicting Aquaculture Water Quality Using Machine Learning Approaches. Water. 2022; 14(18):2836. https://doi.org/10.3390/w14182836
Chicago/Turabian StyleLi, Tingting, Jian Lu, Jun Wu, Zhenhua Zhang, and Liwei Chen. 2022. "Predicting Aquaculture Water Quality Using Machine Learning Approaches" Water 14, no. 18: 2836. https://doi.org/10.3390/w14182836
APA StyleLi, T., Lu, J., Wu, J., Zhang, Z., & Chen, L. (2022). Predicting Aquaculture Water Quality Using Machine Learning Approaches. Water, 14(18), 2836. https://doi.org/10.3390/w14182836






