On the Shift of Glacier Equilibrium Line Altitude (ELA) under the Changing Climate
Abstract
:1. Introduction
2. Overview of the ELA Variations
2.1. The Longest Observation of the ELA
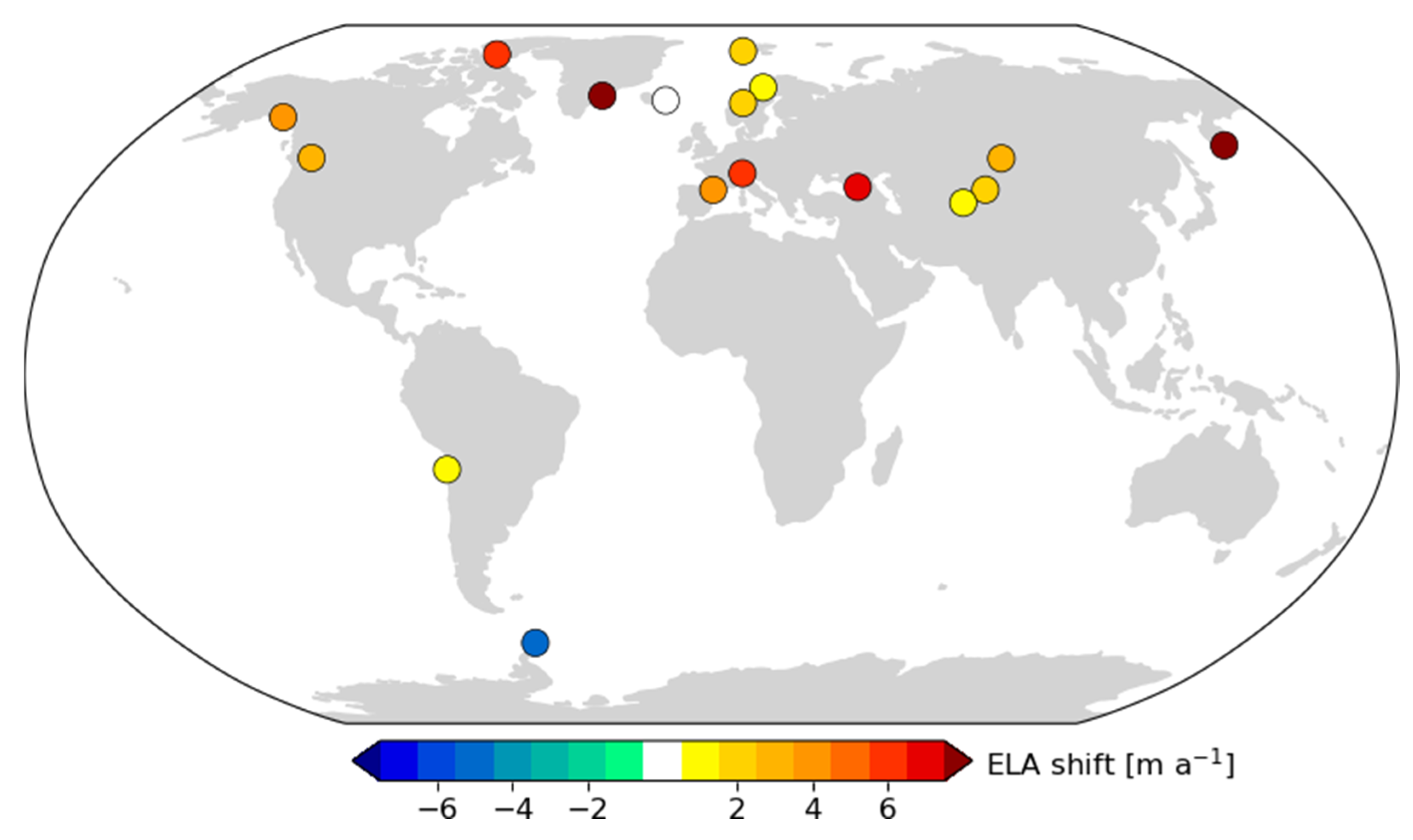
2.2. ELA Changes on Observed Glaciers World Over
3. The Data Sources and Their Treatment
3.1. Publications and On-Line Accessible Data Files
3.2. Examination and Construction of the ELA Timeseries
4. The Climatology of the Equilibrium Line Shift
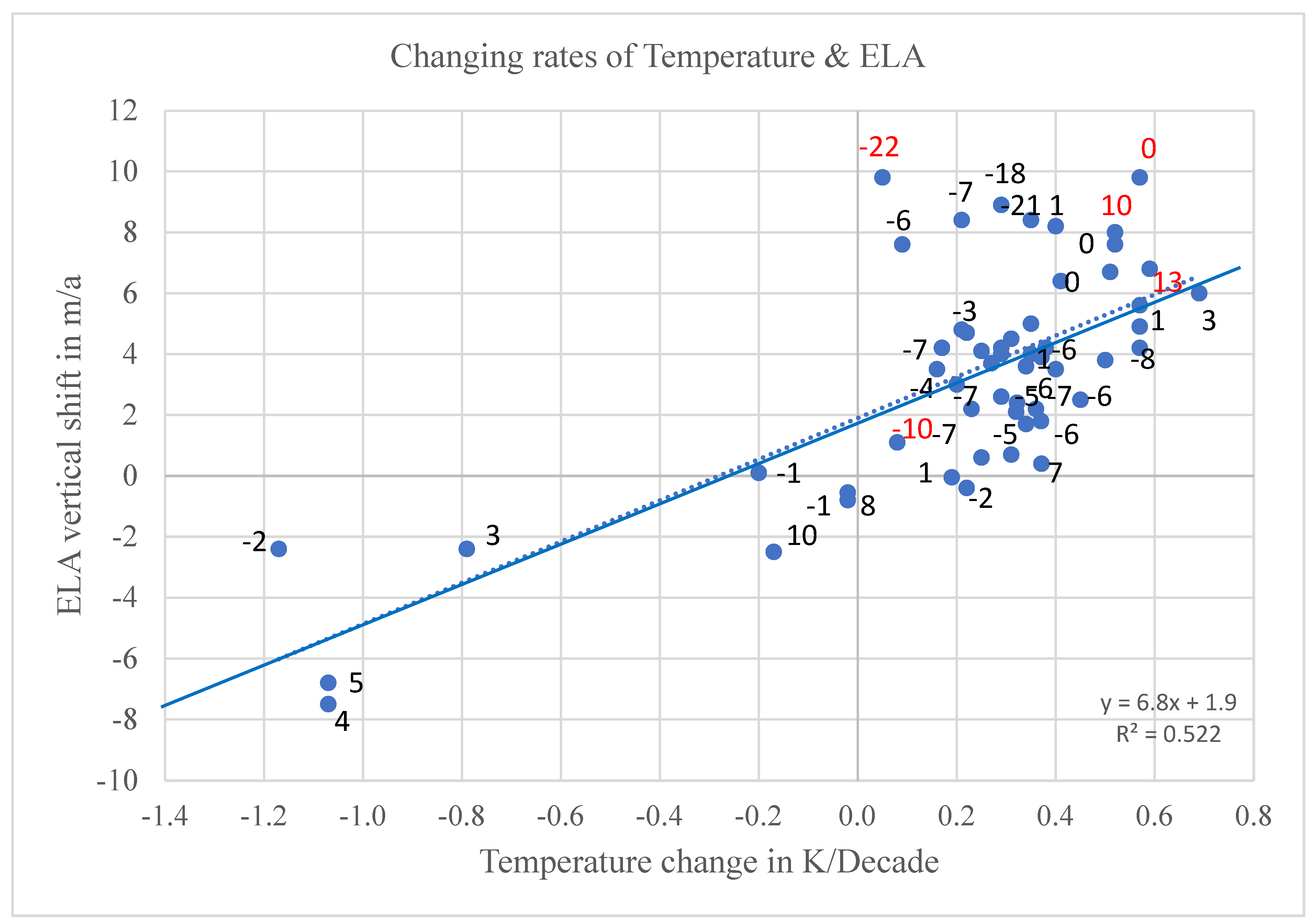
4.1. Search for the Universal Relationship between the ELA Shift and Climate Change
4.2. Significance of Equation (1), Physical Content of c, and the Situation of Outliers
5. Results and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- WGMS-FoG-2021-05-E-MASS-BALANCE_OVERVIEW, and WGMS-FoG-2021-05-EE-MASS-BALANCE, World Glacier Monitoring Service (WGMS), Zurich
- Glaciological Investigations in Norway (1963-2020), Norwegian Water Resources and Energy Directorate
- Gletscherberichte (later under Die Gletscher der Schweizer Alpen, and further, Schnee, Gletscher und Permafrost) (1880-2020), Glacier Commission, Swiss Academy of Natural Sciences
- Baker, E. H., McNeil, C. J., Sass, L. C., Peitzsch, E. H., Whorton, E. N., Florentine, C. E., Clark, A. M., Miller, Z. S., Fagre, D. B., and O’Neel, S., 2018, USGS Benchmark Glacier Mass Balance and Project Data: U.S. Geological Survey data release, https://doi.org/10.5066/F7BG2N8R.
- McNeil, C. J., Sass, L. C., Florentine, C. E., Baker, E. H., Peitzsch, E. H., Whorton, E. N., Miller, Z. S., Fagre, D. B., Clark, A. M., and O’Neel, S., 2016, Glacier-Wide Mass Balance and Compiled Data Inputs: USGS Benchmark Glaciers: U.S. Geological Survey data release, https://doi.org/10.5066/F7HD7SRF.
- ERA5 reanalysis
- CRUTEM (Climate Research Unit, University of East Anglia)
- GHCN (Global Historical Climatology Network). For the Alpine region
- HISTALP (Historial Instrumental Climatological Surface Time Series of the Greater Alpine Region)
- National Meteorological and Geophysical Service of Austria (Zentral Anstalt für Meteorologie und Geodynamik)
- Swiss Federal Office for Meteorology and Climatology (MeteoSwiss)
- German Weather Service
- Canadian Meteorological Service
- Swedish Meteorological and Hydrological Institute
- Norwegian Meteorological Institute
- Bergen radiation reports, Geophysical Institute, University of Bergen
- WRDC (World Radiation Data Centre, Sankt Petersburg)
- GEBA (Global Energy Balance Archive, ETH, Zurich)
- BSRN (Baseline Surface Radiation Network, AWI, Bremerhaven)
References
- Braithwaite, R.J. From Doctor Kurowski’s Schneegrenze to our modern glacier equilibrium line altitude (ELA). Cryosphere 2015, 9, 2135–2148. [Google Scholar] [CrossRef]
- Rutgers, F. Bericht der Gletscher-Kommission der Physikalischen Gesellschaft Zürich. Polarforschung 1914, 36, 75–76. [Google Scholar]
- Hock, R. Temperature index melt modelling in mountain area. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Huss, M.; Bauder, A.; Linsbauer, A.; Gabbi, J.; Kappenberger, G.; Steinegger, U.; Farinotti, D. More than a century of direct glacier mass-balance observations on Claridenfirn, Switzerland. J. Glaciol. 2021, 67, 697–713. [Google Scholar] [CrossRef]
- Cogley, J.G.; Adams, W.P.; Ecclestone, M.A.; Jung-Rothenhäusler, F.; Ommanney, C.S.L. Mass balance of Axel Heiberg Island Glaciers 1960–1991. NHRI Sci. Rep. 1995, 6, 168. [Google Scholar]
- Johansson, M. Mass Balance Data from Arctic Glaciers; IASC working Group for Arctic Glaciers, IASC: Geneva, Switzerland, 2002; 20p. [Google Scholar]
- Kuhn, M.; Kaser, G.; Markl, G.; Wagner, H.P.; Schneider, H. 25 Jahre Massenhaushaltsuntersuchungen am Hintereisferner; Institute of Meteorology and Geophysics, University of Innsbruck: Innsbruck, Austria, 1979; 80p. [Google Scholar]
- Kuhn, M.; Abermann, J.; Bacher, M.; Olefs, M. Transfer of mass-balance profiles to unmeasured glaciers. Ann. Glaciol. 2009, 50, 185–190. [Google Scholar] [CrossRef]
- Lambrecht, A.; Kuhn, M. Glacier changes in the Austrian Alps during the last three decades, derived from the new Austrian glacier inventory. Ann. Glaciol. 2007, 46, 177–184. [Google Scholar] [CrossRef]
- Holmlund, P.; Jansson, P.; Pettersson, R. A re-analysis of the 58 year mass-balance record of Storglaciären, Sweden. Ann. Glaciol. 2005, 42, 489–495. [Google Scholar] [CrossRef]
- Dyurgerov, M. Mass Balance Monitoring of Mountain Glaciers; Nauka: Moscow, Russia, 1993; 125p. (In Russian) [Google Scholar]
- Andreassen, L.M.; Elvehøy, H.; Kjøllmoen, B.; Belart, J.M.C. Glacier change in Norway since 1960s—an overview of mass balance, area, length and surface elvation changes. J. Glaciol. 2020, 66, 313–328. [Google Scholar] [CrossRef]
- Auer, I.; Reinhard, B.; Anita, J.; Wolfgang, L.; Alexander, O.; Roland, P.; Wolfgang, S.; Markus, U.; Christoph, M.; Keith, B. HISTALP-historical instrumental climatological surface time series of the Greater Alpine Regions. Int. J. Climatol. A J. R. Meteorol. Soc. 2007, 27, 17–46. [Google Scholar] [CrossRef]
- Hans, H.; Bill, B.; Paul, B.; Shoji, H.; András, H.; Joaquín, M.-S.; Julien, N.; Carole, P.; Raluca, R.; Dinand, S. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Wild, M.; Ohmura, A.; Schär, C.; Müller, G.; Folini, D.; Schwarz, M.; Hakuba, M.Z.; Sanches-Lorenzo, A. The Global Energy Balance Archive (GEBA) version 2017: A database for worldwide measured surface energy fluxes. Earth Syst. Sci. Data 2017, 9, 601–613. [Google Scholar] [CrossRef] [Green Version]
- Amelie, D.; John, A.; Klaus, B.; Sergio, C.; Christopher, C.; Emilio, C.-A.; Fred, M.D.; Thierry, D.; Masato, F.; Hannes, G. Baseline Surface Radiation Network (BSRN): Structure and data description (1992-2017). Earth Syst. Sci. Data 2018, 10, 1491–1501. [Google Scholar]
- Bidlake, W.R.; Josberger, E.G.; Savoca, M.E. Water, Ice, and Meteorological Measurements at South Cascade Glacier, Washington, Balance Year 2003; Scientific Investigations Report 2005-5210; U.S. Geological Survey: Reston, VA, USA, 2005; p. 48. [Google Scholar]
- Ohmura, A.; Kasser, P.; Funk, M. Climate at the equilibrium line of glaciers. J. Glaciol. 1992, 38, 397–411. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; García-Herrera, R.; Peña-Angulo, D.; Tomas-Burguera, M.; Domínguez-Castro, F.; Noguera, I.; Calvo, N.; Murphy, C.; Nieto, R.; Gimeno, L.; et al. Do CMIP models capture long-term observed annual precipitation trends? Clim. Dyn. 2022, 58, 2825–2842. [Google Scholar] [CrossRef]
- Ahlmann, H.W.S. Le niveau de glaciation comme function de l’accumulation d’humidité sous forme solide. Méthode pour le calcul de l’humidité condensée dans la haute montagne et pour l’étude de la fréquence des glaciers. Geografiska Annaler 1924, 6, 223–272. [Google Scholar]
- Ohmura, A.; Boettcher, M. Climate on the equilibrium line altitudes of glaciers: Theoretical background behind Ahlmann’s P/T diagram. J. Glaciol. 2018, 64, 489–505. [Google Scholar] [CrossRef]
- Braithwaite, R.J.; Hughes, P.D. Positive degree-day sums in the Alps: A direct link between glacier melt and international climate policy. J. Glaciol. 2022, 2022, 1–11. [Google Scholar] [CrossRef]
- Ohmura, A.; Bauder, A.; Müller, H.; Kappenberger, G. Longterm change of mass balance and the role of radiation. Ann. Glaciol. 2007, 46, 1–8. [Google Scholar] [CrossRef]
- Wild, M. Decadal changes in radiative fluxes at land and ocean surfaces and their relevance for global warming. Wiley Interdiscip. Rev. Clim. Chang. 2016, 7, 91–107. [Google Scholar] [CrossRef]
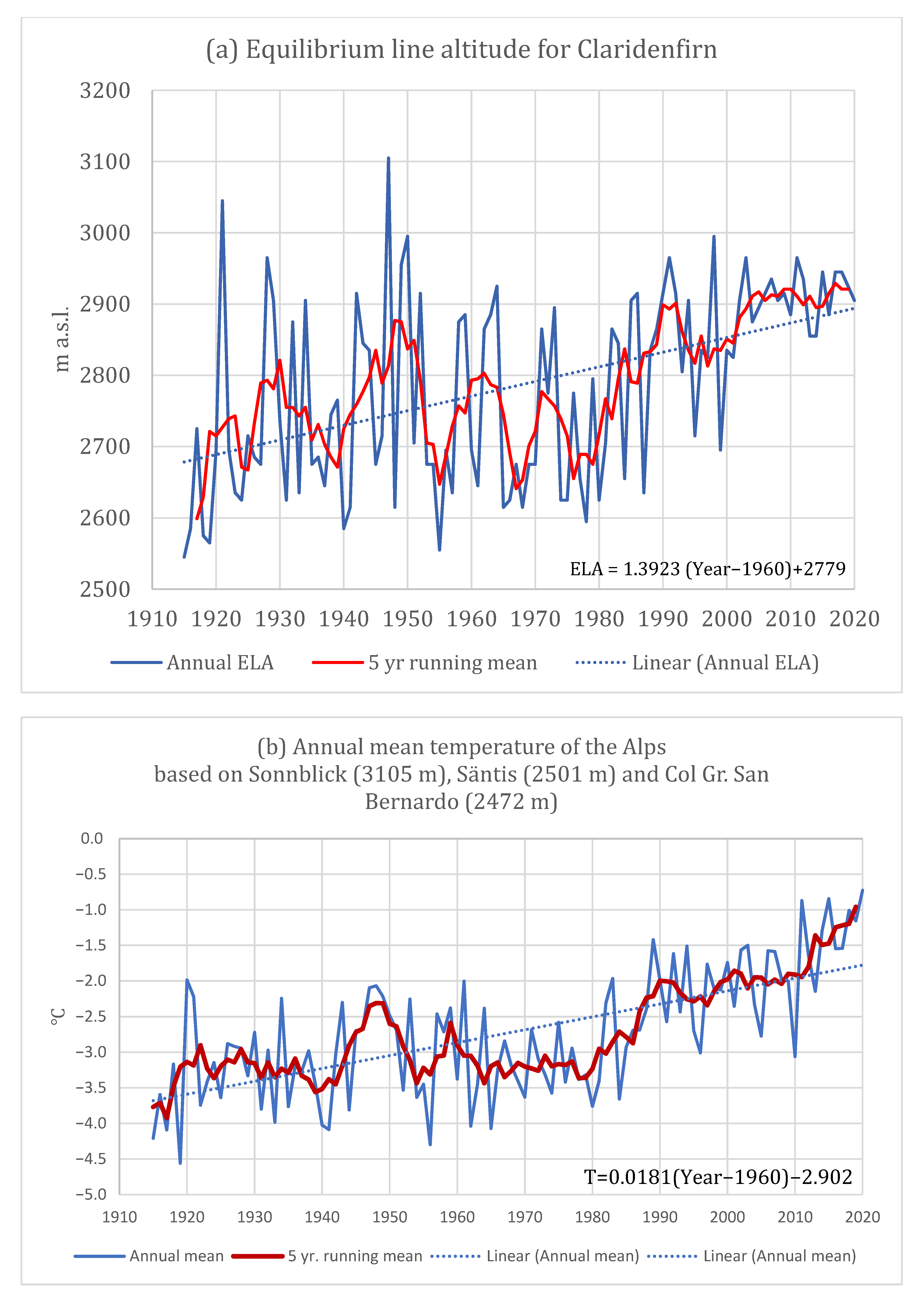
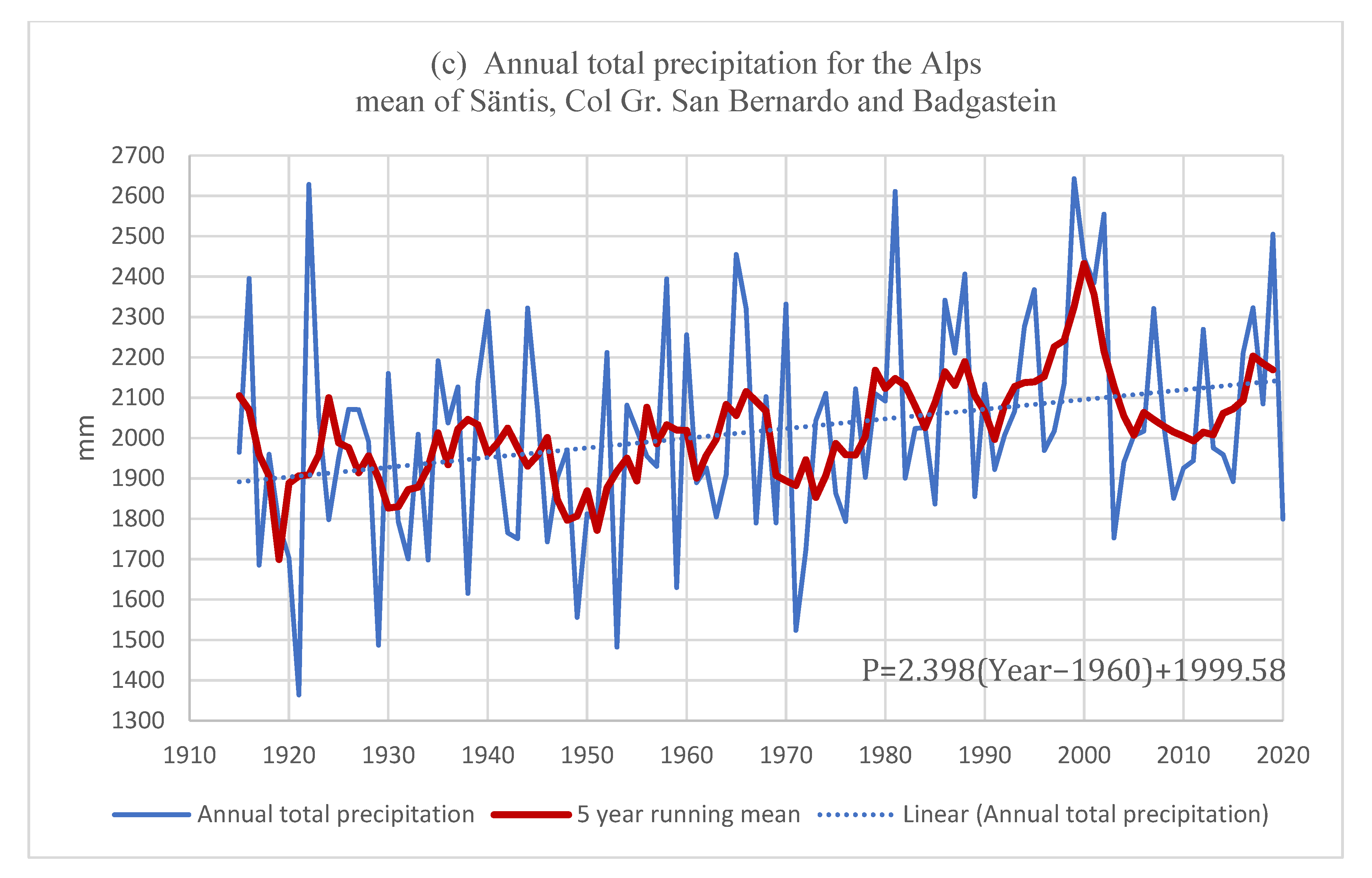
| Year | Bw (mm) | Bs (mm) | Bn (mm) | Off Glacier | Reported | With All Data | Excluding Above | Only Negative |
|---|---|---|---|---|---|---|---|---|
| ELA m a.s.l. | glacier ELA | Bn years | ||||||
| 1953 | −600 | |||||||
| 1955 | 300 | |||||||
| 1956 | 200 | |||||||
| 1957 | −200 | |||||||
| 1958 | −3300 | |||||||
| 1959 | 3290 | −2560 | 730 | |||||
| 1960 | 2220 | −2690 | −470 | 1880 | ||||
| 1961 | 2410 | −3480 | −1070 | 1950 | ||||
| 1962 | 2510 | −2280 | 230 | 1860 | ||||
| 1963 | 2240 | −3510 | −1270 | 2040 | ||||
| 1964 | 3260 | −2030 | 1230 | 1795 | ||||
| 1965 | 3490 | −3630 | −140 | 1880 | ||||
| 1966 | 2480 | −3480 | −1000 | 2380 | 2009 | 2043 | 2034 | |
| 1967 | 3300 | −3900 | −600 | 1870 | ||||
| 1968 | 3010 | −2970 | 40 | 2080 | ||||
| 1969 | 3180 | −3880 | −700 | 1910 | ||||
| 1970 | 2420 | −3590 | −1170 | 2050 | ||||
| 1971 | 3520 | −2890 | 630 | 1820 | ||||
| 1972 | 4280 | −2820 | 1460 | 1770 | ||||
| 1973 | 2220 | −3230 | −1010 | 2070 | ||||
| 1974 | 3660 | −2610 | 1050 | 1850 | ||||
| 1975 | 3070 | −3090 | −20 | 1800 | ||||
| 1976 | 3540 | −2560 | 980 | 1825 | ||||
| 1977 | 1580 | −2850 | −1270 | > | 2250 | 2036 | 2076 | 2076 |
| 1978 | 2500 | −2850 | −350 | 1925 | ||||
| 1979 | 2190 | −3720 | −1530 | 2225 | ||||
| 1980 | 1840 | −2830 | −990 | > | 2150 | 2008 | 2041 | 2033 |
| 1981 | 2290 | −3100 | −810 | 1990 | 2019 | 2005 | ||
| 1982 | 3120 | −3010 | 110 | 1896 | 1905 | 1862 | ||
| 1983 | 1920 | −2660 | −740 | 1982 | 2010 | 1994 | ||
| 1984 | 2390 | −2240 | 150 | 1892 | 1900 | 1856 | ||
| 1985 | 2190 | −3360 | −1170 | 2026 | 2064 | 2061 | ||
| 1986 | 2480 | −3340 | −860 | 1995 | ||||
| 1987 | 1960 | −4050 | −2090 | 2189 | ||||
| 1988 | 2210 | −3400 | −1190 | 2028 | 2066 | 2064 | ||
| 1989 | 2400 | −3590 | −1190 | 2024 | ||||
| 1990 | 2530 | −2880 | −350 | 1889 | ||||
| 1991 | 3650 | −4020 | −370 | 1883 | ||||
| 1992 | 1850 | −4050 | −2200 | 2080 | ||||
| 1993 | 1880 | −2920 | −1040 | 1991 | ||||
| 1994 | 2350 | −4120 | −1770 | > | 2244 | 2087 | 2138 | 2153 |
| 1995 | 2980 | −4000 | −1020 | 1997 | ||||
| 1996 | 2860 | −2970 | −110 | 1868 | ||||
| 1997 | 3470 | −3140 | 330 | 1835 | ||||
| 1998 | 3070 | −4950 | −1880 | > | 2137 | 2098 | 2152 | 2170 |
| 1999 | 4040 | −2480 | 1560 | 1847 | ||||
| 2000 | 3110 | −2580 | 530 | 1840 | ||||
| 2001 | 1760 | −2550 | −790 | 1966 | ||||
| 2002 | 3990 | −3400 | 590 | 1856 | ||||
| 2003 | 2460 | −4690 | −2230 | > | 2125 | 2133 | 2195 | 2225 |
| 2004 | 2060 | −3660 | −1600 | 2108 | ||||
| 2005 | 2090 | −4470 | −2380 | > | 2317 | 2149 | 2214 | 2248 |
| 2006 | 2600 | −3830 | −1230 | > | 2754 | 2032 | 2071 | 2070 |
| 2007 | 3490 | −3470 | 20 | 1869 | ||||
| 2008 | 3280 | −3120 | 160 | 1850 | ||||
| 2009 | 2730 | −4380 | −1650 | > | 2331 | 2075 | 2123 | 2135 |
| 2010 | 2700 | −2930 | −230 | 1907 | ||||
| 2011 | 3550 | −2150 | 1400 | 1794 | ||||
| 2012 | 3530 | −3430 | 100 | 1854 | ||||
| 2013 | 3280 | −3940 | −660 | 1915 | ||||
| 2014 | 3710 | −3840 | −130 | 1926 | ||||
| 2015 | 2730 | −5950 | −3220 | 2174 | ||||
| 2016 | 3410 | −4170 | −760 | 1963 | ||||
| 2017 | 3960 | −4570 | −610 | 1941 | ||||
| 2018 | 3800 | −4480 | −680 | 2040 | ||||
| 2019 | 2440 | −4490 | −2050 | > | 3264 | 2115 | 2173 | 2197 |
| 2020 | 3210 | −3270 | −60 | 1885 |
| Glacier | Latitude | Longitude | Mean ELA m a.s.l. | Observed Period | Used Period | ELA Change m/a | Temp Change K/Decade | Bw Change mm w.e./a | Comments | Meteorol. Stations Used |
|---|---|---|---|---|---|---|---|---|---|---|
| Canadian Arctic | ||||||||||
| White Glacier | 79.50 | −90.97 | 1066 | 1960–2020 | 1979–2018 | 6.7 | 0.51 | 0.42 | Bw precipitation Eureka | Eureka |
| Devon Ice Cap NW | 75.25 | −82.00 | 1154 | 1961–2018 | 1979–2018 | 8.2 | 0.40 | 0.51 | Resolute | |
| Greenland | ||||||||||
| Mittivakkat | 65.70 | −37.80 | 750 | 1996–2019 | 1996–2018 | 7.6 | 0.52 | −0.4 | Angmagssalik | |
| Iceland | ||||||||||
| Hofsjokull E | 64.48 | −15.57 | 1228 | 1989–2020 | 1989–2018 | 1.1 | 0.08 | −10.0 | Bergstsdir, Lambavatn | |
| Svalbard | ||||||||||
| Austre Breggerbreen | 78.88 | 11.83 | 432 | 1967–2017 | 1979–2017 | 2.1 | 0.32 | −5.4 | Ny-Alesund | |
| Midtre Lovenbreen | 78.88 | 12.07 | 407 | 1968–2017 | 1979–2017 | 1.7 | 0.34 | −5.0 | Ny-Alesund | |
| Kongsvegen | 78.80 | 12.98 | 547 | 1996–2020 | 1987–2018 | 2.2 | 0.36 | −8.9 | Ny-Alesund | |
| Hansbreen | 77.08 | 15.67 | 355 | 1987–2019 | 1989–2018 | −0.05 | 0.19 | 1.3 | Too short ELA | Barentsburg |
| Alaska | ||||||||||
| Gulkana Glacier | 63.30 | −145.42 | 1774 | 1966–2020 | 1979–2018 | 4.2 | 0.17 | −7.1 | ||
| Wolverine Glacier | 60.40 | −148.90 | 1172 | 1966–2020 | 1979–2018 | 3.5 | 0.16 | −3.8 | ||
| Taku | 58.55 | −134.13 | 1006 | 1946–2016 | 1979–2018 | 7.6 | 0.09 | −6.2 | ||
| Lemon Creek Glacier | 58.38 | −134.23 | 1066 | 1953–2020 | 1979–2018 | 9.8 | 0.05 | −21.8 | Bw only after 98 | |
| N. American Cordillera | ||||||||||
| Peyto Glacier | 51.67 | −116.55 | 2724 | 1966–2018 | 1979–2018 | 4.8 | 0.21 | −3.2 | Tatlayoko Lake | |
| Place Glacier | 50.27 | −122.60 | 2257 | 1965–2019 | 1979–2018 | 0.1 | −0.20 | −1.0 | Bannf | |
| Helm Glacier | 49.97 | −123.00 | 2082 | 1976–2019 | 1979–2018 | 0.8 | −0.02 | −1.0 | Banff | |
| South Cascade | 48.75 | −121.05 | 1954 | 1960–2020 | 1979–2018 | −2.5 | −0.17 | 10.3 | Winthrop, Vancouver | |
| Scandinavia | ||||||||||
| Langfjordjøkelen | 70.128 | 21.735 | 1062 | 1989–2019 | 1989–2018 | 8.4 | 0.35 | −21.3 | Nordstraum I, Kvaenangen | |
| Ruikojietna | 68.08 | 18.05 | 1408 | 1986–2019 | 1986–2018 | 3.6 | 0.34 | −14.5 | Tromso-Langnes | |
| Marmaglaciären | 68.08 | 18.68 | 1616 | 1990–2019 | 1990–2018 | 2.2 | 0.23 | −7.3 | Too short | Tromso-Langnes, Andoya |
| Rabots Glacier | 67.91 | 18.5 | 1451 | 1982–2019 | 1982–2018 | 3.5 | 0.40 | −11.0 | Kiruna Fly | |
| Storglaciären | 67.90 | 18.57 | 1489 | 1946–2020 | 1979–2018 | 1.8 | 0.37 | −6.1 | Kiruna Fly | |
| Engabreen | 66.65 | 13.85 | 1114 | 1970–2019 | 1979–2018 | 2.4 | 0.322 | 0.4 | Glomfjord | |
| Austdalsbreen | 61.82 | 7.35 | 1506 | 1988–2019 | 1988–2018 | 8.9 | 0.29 | −17.9 | Abjorsbraten | |
| Alfotbreen | 61.75 | 5.65 | 1168 | 1963–2019 | 1979–2018 | 4.5 | 0.31 | −8.7 | Sognefjellhytta | |
| Hansebreen | 61.75 | 5.68 | 1194 | 1986–2019 | 1986–2018 | 3.9 | 0.37 | −3.7 | Sognefjellhytta | |
| Nigårdsbreen | 61.72 | 7.13 | 1510 | 1958–2019 | 1979–2018 | 0.4 | 0.37 | 6.6 | Sognefjellhytta | |
| Gråsubreen | 61.65 | 8.60 | 2163 | 1958–2019 | 1979–2018 | 4 | 0.29 | −6.1 | Drevsjo | |
| Hellstungubreen | 61.57 | 8.43 | 1932 | 1963–2019 | 1979–2018 | 4.2 | 0.29 | −5.7 | Drevsjo | |
| Storbreen | 61.57 | 8.13 | 1785 | 1949–2019 | 1979–2018 | 3.7 | 0.27 | −7.4 | Drevsjo | |
| Hardangerjökulen | 60.55 | 7.37 | 1671 | 1963–2019 | 1979–2018 | 2.6 | 0.29 | −5.3 | Mosstrand II | |
| Alps | ||||||||||
| Vernagtferner | 46.87 | 10.82 | 3144 | 1965–2020 | 1979–2018 | 2.5 | 0.45 | −6.2 | Sonnblick, Säntis | |
| Claridenfirn | 46.85 | 8.90 | 2771 | 1915–2018 | 1979–2018 | 4.2 | 0.38 | −2.2 | Säntis, Weissfluejoch | |
| Silvretta | 46.85 | 10.08 | 2794 | 1920–2018 | 1979–2018 | 5.6 | 0.57 | 0.8 | Weisfluejoch | |
| Hintereisferner | 46.80 | 10.77 | 3157 | 1953–2020 | 1979–2018 | 8.0 | 0.52 | 10.3 | Bw change for 1993–2018 | |
| Fontana Bianca | 46.48 | 10.77 | 3399 | 1982–2017 | 1982–2017 | 4.2 | 0.57 | 2.0 | Sonnblick, Säntis | |
| Griesgletscher | 46.43 | 8.33 | 3004 | 1962–2018 | 1979–2018 | 6.8 | 0.59 | 13.4 | Jungfraujoch, St. Bernardo | |
| Basodino | 46.42 | 8.48 | 2985 | 1992–2016 | 1992–2018 | 9.8 | 0.57 | −0.2 | Jungfraujoch | |
| Allalingletscher | 46.05 | 7.93 | 3306 | 1956–2018 | 1979–2018 | 4.9 | 0.57 | −8.1 | Jungfraujoch, Locarno-Monti | |
| Gietro | 46.00 | 7.38 | 3227 | 1967–2018 | 1979–2018 | 4.1 | 0.25 | −4.2 | Jungfraujoch, Locarno-Monti | |
| Caucasus | ||||||||||
| Garabashi | 43.3 | 42.47 | 3853 | 1984–2019 | 1984–2018 | 6 | 0.69 | 3.3 | Shadzhatmaz | |
| Tienshan, Altai | ||||||||||
| Leviy Aktru | 50.08 | 87.69 | 3195 | 1977–2012 | 1979–2012 | 5.0 | 0.35 | −13.2 | Ust-Koksa | |
| Maliy Aktru | 50.05 | 87.75 | 3178 | 1962–2012 | 1979–2012 | 4.0 | 0.35 | −10.8 | Ust-Koksa | |
| No. 1 Glacier Urumqi | 43.12 | 86.82 | 4068 | 1959–2020 | 1979–2018 | 3.8 | 0.50 | 3.1 | Daxigou, CN | |
| Tsentr.Tuyuksuyskiy | 43.05 | 77.08 | 3826 | 1957–2020 | 1979–2018 | −0.4 | 0.22 | −2.0 | Bayanbulak, CN | |
| Golubin | 42.46 | 74.50 | 3868 | 1972–2020 | 1979–2018 | 0.7 | 0.31 | 7.7 | Much missing | Bayanbulak, CN |
| Karabatkak | 42.15 | 78.30 | 3856 | 1976–2020 | 1979–2018 | 6.4 | 0.41 | 0.1 | Almaty | |
| Pamir | ||||||||||
| Abramov | 39.63 | 71.6 | 4230 | 1968–2020 | 1979–2018 | −0.8 | −0.02 | 8.1 | Dzhalalabad | |
| Kamchatka | ||||||||||
| Kozelskiy | 53.23 | 158.82 | 1351 | 1973–1997 | 1979–1997 | 8.4 | 0.21 | −6.9 | Kliuchi, Ozernaja | |
| South America | ||||||||||
| Antizana | −0.47 | −78.15 | 5122 | 1995–2019 | 1995–2018 | 0.6 | 0.25 | Pichilingue | ||
| Zongo | −16.28 | −68.14 | 5318 | 1992–2018 | 1992–2018 | 3.0 | 0.2 | 3.0 | Julianca | |
| Chacaltaya | −16.35 | −68.12 | 5441 | 1992–2008 | 1992–2008 | 4.7 | 0.22 | Bw too short record | Julianca | |
| Martial Este | −54.78 | −68.4 | 1082 | 2001–2019 | 2001–2018 | −2.4 | −0.79 | 3.0 | Rio Grande, Ushuaia | |
| The Antarctic | ||||||||||
| Johnsons | −62.67 | −60.35 | 179 | 2002–2019 | 2002–2018 | −6.8 | −1.07 | 4.7 | Arturo Prat, Esperanza | |
| Hurd | −62.68 | −60.4 | 203 | 2002–2019 | 2002–2018 | −7.5 | −1.07 | 4.1 | Arturo Prat, Esperanza | |
| Bahia del Diablo | −63.82 | −57.43 | 377 | 2000–2019 | 2000–2018 | −2.4 | −1.17 | −2.4 | Too short, much missing | Marambio |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohmura, A.; Boettcher, M. On the Shift of Glacier Equilibrium Line Altitude (ELA) under the Changing Climate. Water 2022, 14, 2821. https://doi.org/10.3390/w14182821
Ohmura A, Boettcher M. On the Shift of Glacier Equilibrium Line Altitude (ELA) under the Changing Climate. Water. 2022; 14(18):2821. https://doi.org/10.3390/w14182821
Chicago/Turabian StyleOhmura, Atsumu, and Maxi Boettcher. 2022. "On the Shift of Glacier Equilibrium Line Altitude (ELA) under the Changing Climate" Water 14, no. 18: 2821. https://doi.org/10.3390/w14182821





