Model Experiment Exploration of the Kinetic Dissipation Effect on the Slit Dam with Baffles Tilted in the Downstream Direction
Abstract
:1. Introduction
2. Materials and Methods
2.1. DEM Method
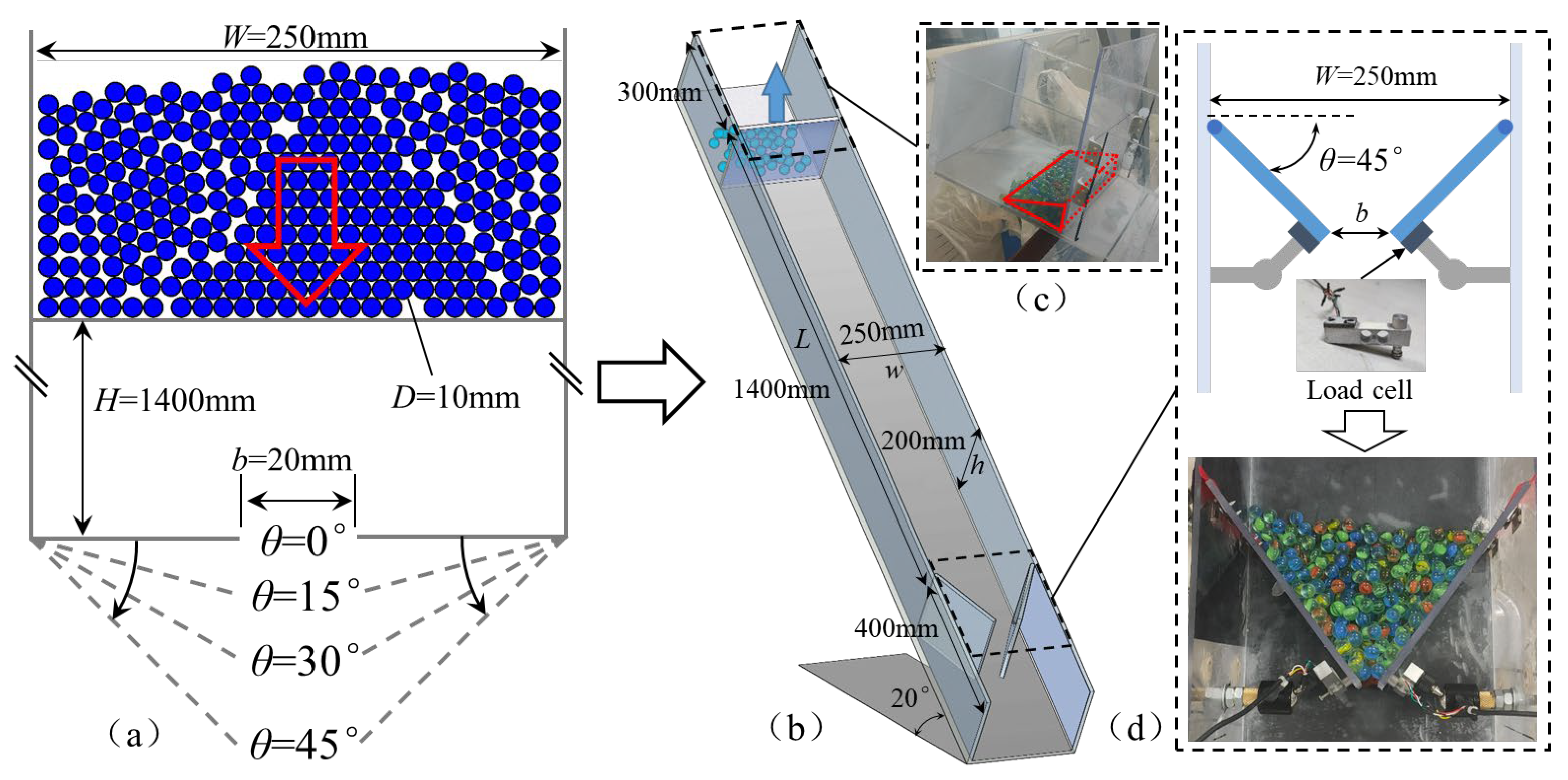
2.1.1. Numerical Simulation Model
2.1.2. Parameters and Process of DEM
2.2. Flume Experiment
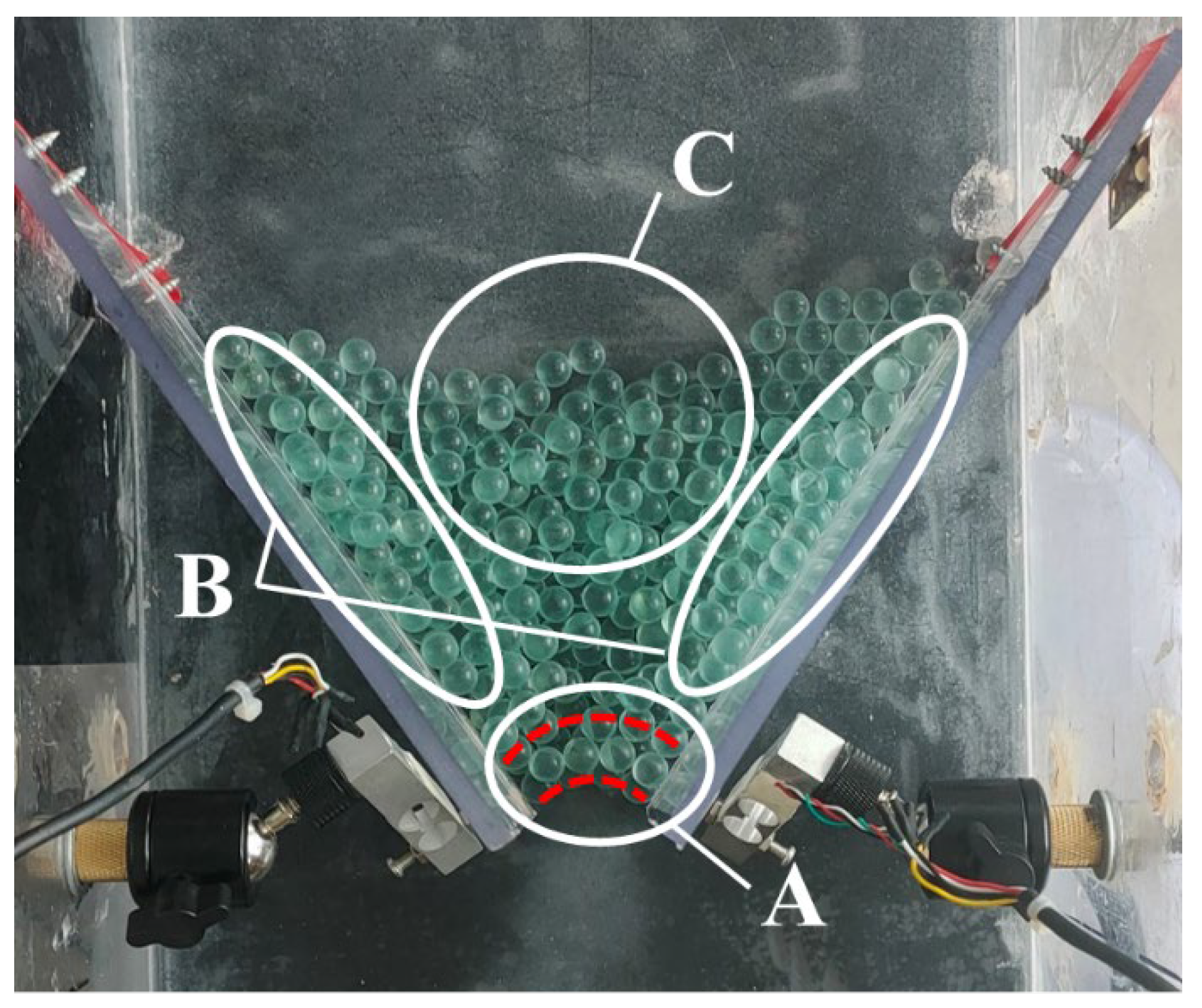
2.2.1. Experimental Device
2.2.2. Experiment Particles
2.2.3. Experimental Steps
3. Results
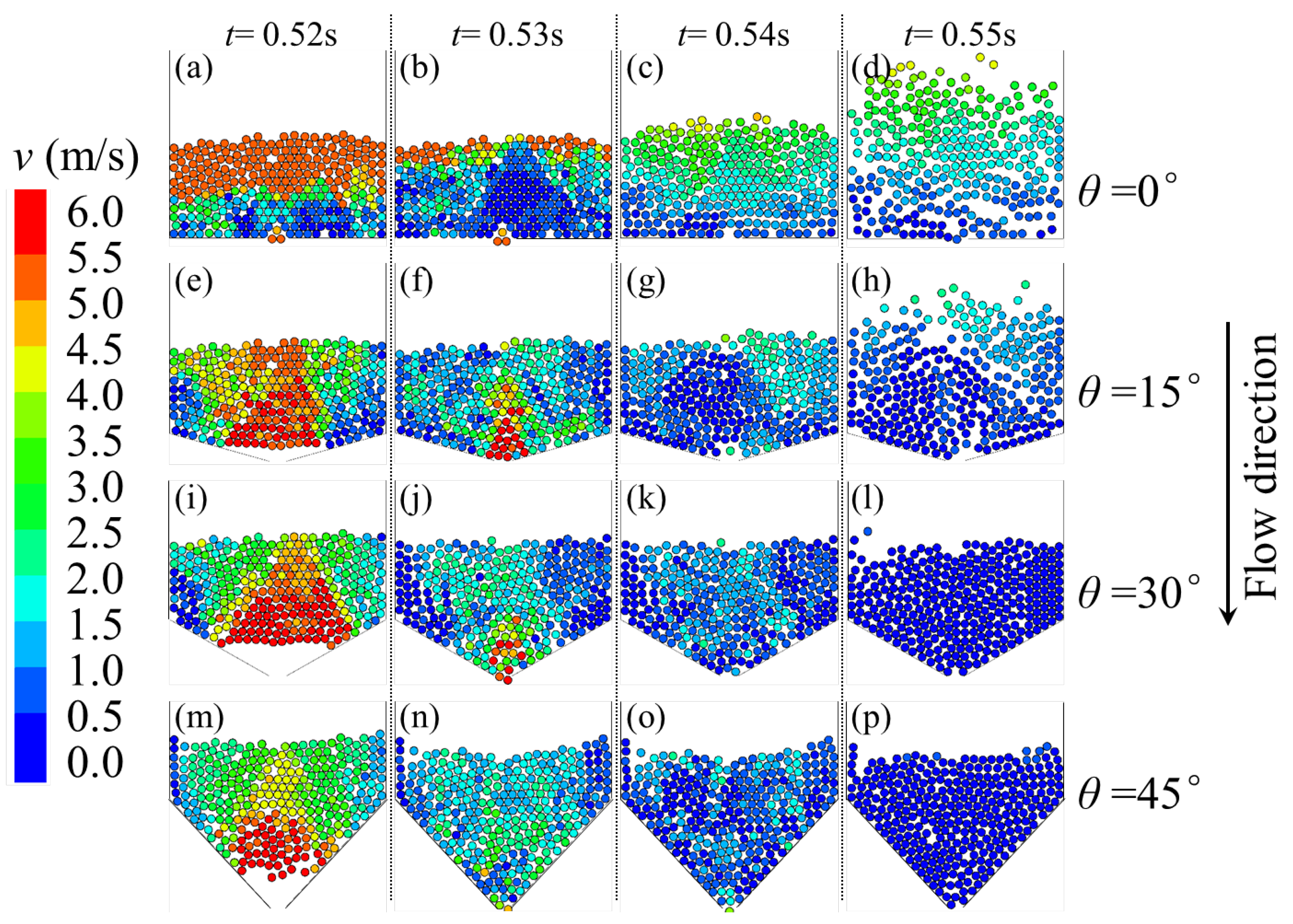
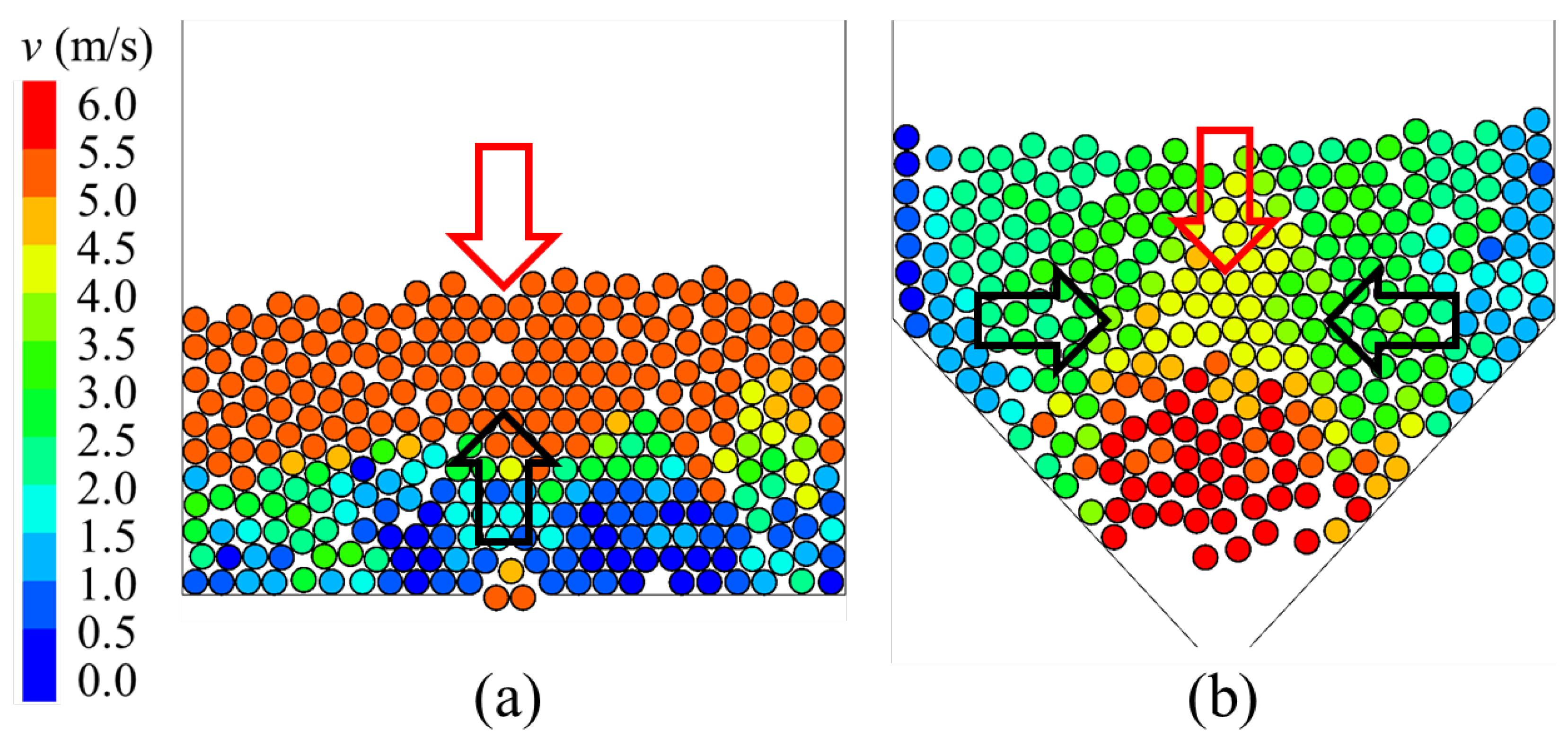
3.1. DEM Simulation Results
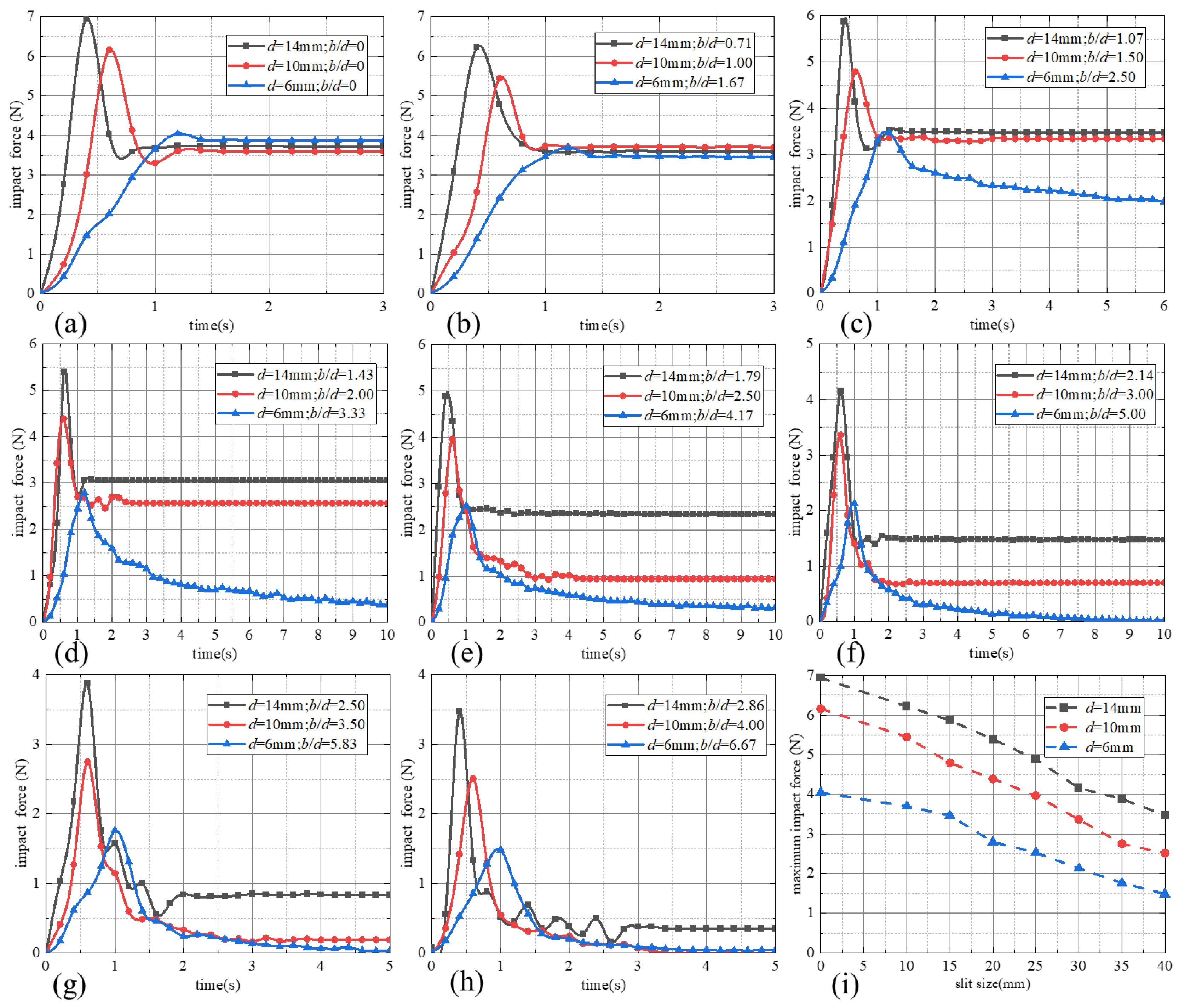
3.2. Experimental Results of the Particle Impact Force
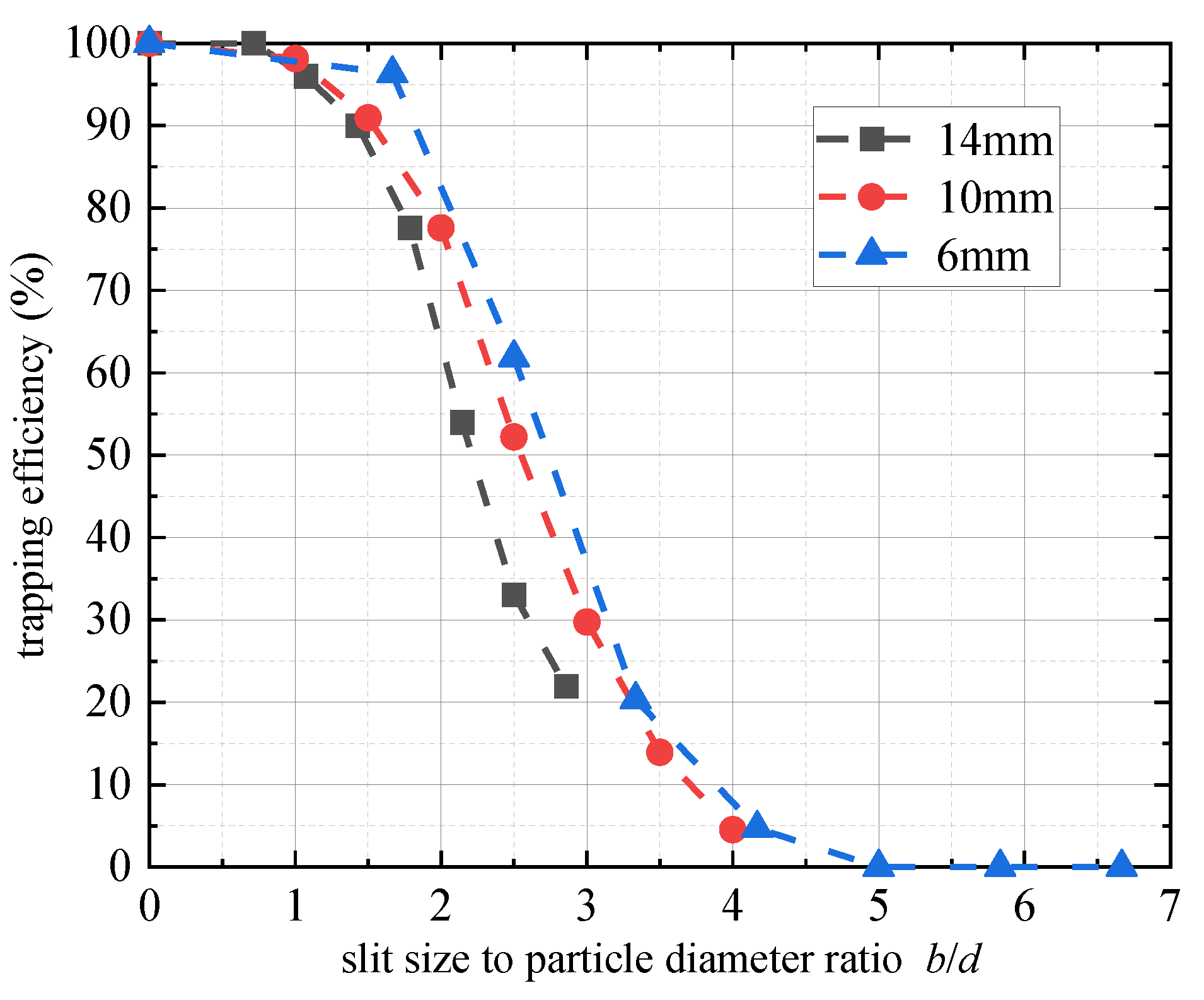
3.3. Experimental Results of the Trapping Efficiency
4. Discussion
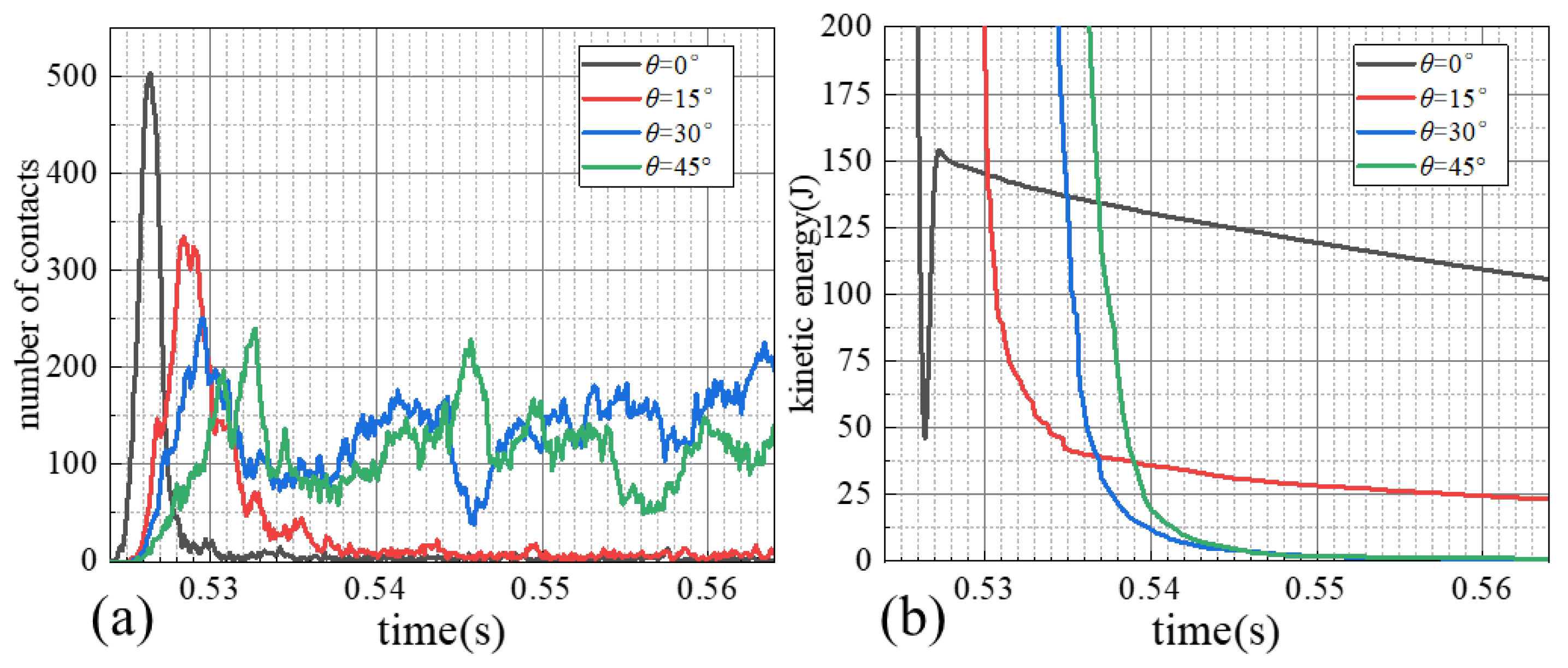
4.1. Influence of Baffle Inclination Angle θ on Particle Kinetic Energy Dissipation (DEM Simulation)
4.2. Influence of the Particle Arch Effect on Trapping Efficiency (Experimental Analysis)
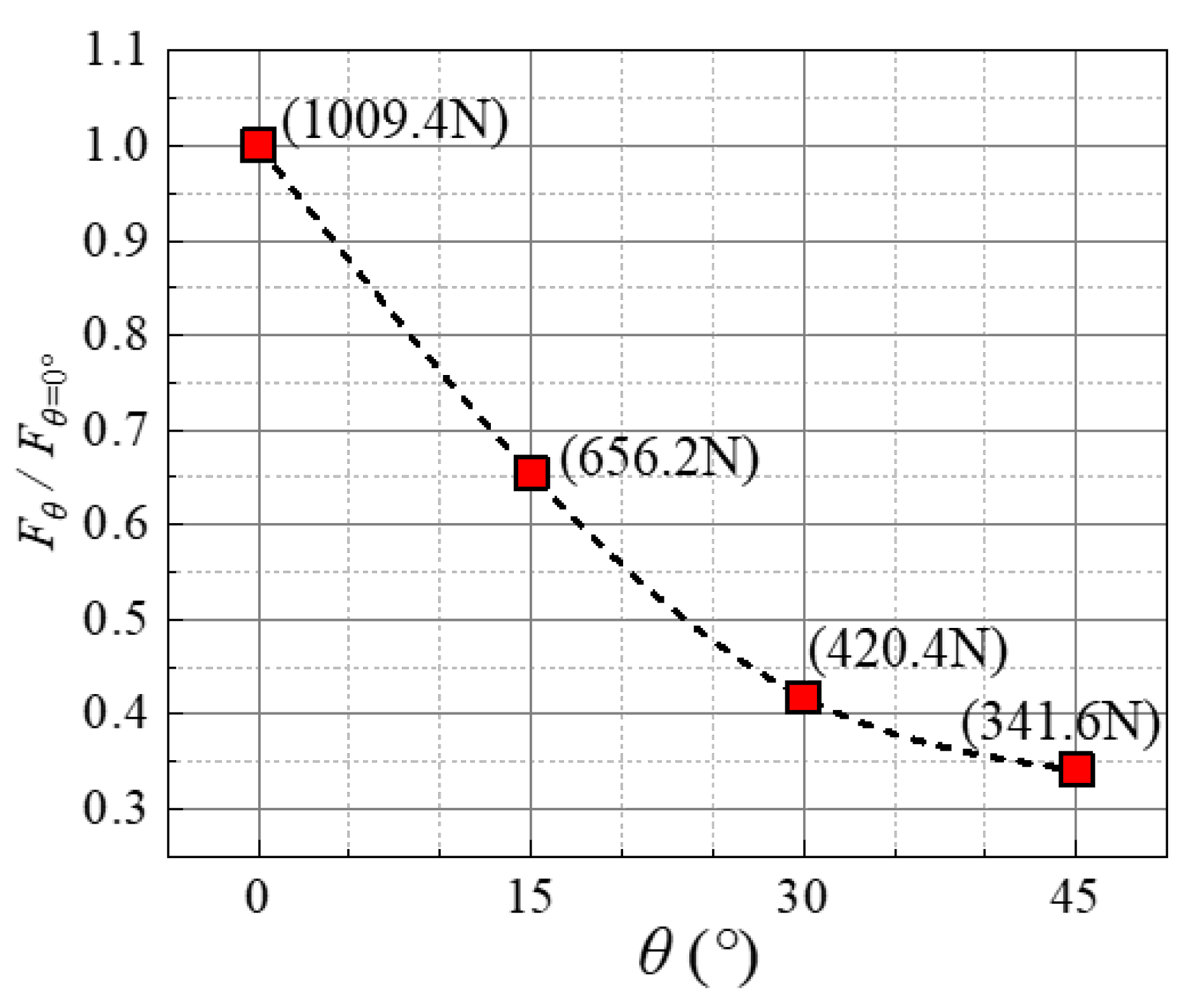
4.3. Trapping Impact Force under Different Relative Opening Widths (Experimental Analysis)
5. Conclusions
- The DEM simulation results indicate that the change of the inclination angle θ of the tilted baffles affects the number of particle collisions, thereby affecting the ability of the baffle structure to dissipate the kinetic energy of particles; when the inclination angle is 30° ≤ θ ≤ 45°, the baffle structure bears less impact force and has better particle kinetic energy dissipation performance.
- The flume experiment results indicate that the particle size d and the baffle opening width b have an influence on the impact force and trapping efficiency of the inclined baffle structure; with the increase of the width diameter ratio b/d, the peak impact force of the inclined baffle structure decreases nearly linearly, while the trapping efficiency decreases nonlinearly; and the tilted baffles can successfully intercept the flowing down particles when the width diameter ratio range is 0 ≤ b/d ≤ 4.
- In this paper, the ratio of the maximum impact force to the trapping efficiency (trapping impact force) is proposed to evaluate the interception effect of the tilted baffles. By analyzing this index, it has been found that when the particle size is in the range of 6~14 mm, a suitable width diameter ratio lies in 1 ≤ b/d ≤ 2, which can ensure an ideal interception state for the tilted baffles with relatively weaker impact force and higher trapping efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Chen, X.; Cui, P.; You, Y.; Chen, J.; Li, D. Engineering measures for debris flow hazard mitigation in the Wenchuan earthquake area. Eng. Geol. 2015, 194, 73–85. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Hutter, K.; Hsiau, S.S.; Tai, S.C.; Wang, Y.; Katzenbach, R. Rapid flow of dry granular materials down inclined chutes impinging on rigid walls. Phys. Fluids 2007, 19, 053302. [Google Scholar] [CrossRef]
- Chen, H.X.; Li, J.; Feng, S.J.; Gao, H.Y.; Zhang, D.M. Simulation of interactions between debris flow and check dams on three-dimensional terrain. Eng. Geol. 2019, 251, 48–62. [Google Scholar] [CrossRef]
- Dai, Z.L.; Huang, Y.; Cheng, H.L.; Xu, Q. SPH model for fluid–structure interaction and its application to debris flow impact estimation. Landslides 2017, 14, 917–928. [Google Scholar] [CrossRef]
- Shen, W.; Zhao, T.; Zhao, J.; Dai, F.; Zhou, G.G.D. Quantifying the impact of dry debris flow against a rigid barrier by DEM analyses. Eng. Geol. 2018, 241, 86–96. [Google Scholar] [CrossRef]
- Canelli, L.; Ferrero, A.M.; Migliazza, M.; Segalini, A. Debris flow risk mitigation by the means of rigid and flexible barriers—Experimental tests and impact analysis. Nat. Hazards Earth Syst. Sci. 2012, 12, 1693–1699. [Google Scholar] [CrossRef]
- Leonardi, A.; Goodwin, G.R.; Pirulli, M. The force exerted by granular flows on slit dams. Acta Geotech. 2019, 14, 1949–1963. [Google Scholar] [CrossRef]
- Tan, D.Y.; Feng, W.Q.; Yin, J.H.; Zhu, Z.H.; Qin, J.Q. Numerical study of retention efficiency of a flexible barrier in mitigating granular flow comparing with large-scale physical modeling test data. Acta Geotech. 2021, 16, 433–448. [Google Scholar] [CrossRef]
- Castanon-Jano, L.; Blanco-Fernandez, E.; Castro-Fresno, D.; Ballester-Munoz, F. Energy dissipating devices in falling rock protection barriers. Rock Mech. Rock Eng. 2017, 50, 603–619. [Google Scholar] [CrossRef] [Green Version]
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren LK, A.; Gerber, W.; Jaboyedoff, M. Rockfall characterisation and structural protection—A review. Nat. Hazards Earth Syst. Sci. 2011, 11, 2617–2651. [Google Scholar] [CrossRef]
- Suwa, H.; Okano, K.; Kanno, T. Behavior of debris flows monitored on test slopes of Kamikamihorizawa Creek, Mount Yakedake, Japan. Int. J. Eros. Control. Eng. 2009, 2, 33–45. [Google Scholar] [CrossRef]
- Brighenti, R.; Segalini, A.; Ferrero, A.M. Debris flow hazard mitigation: A simplified analytical model for the design of flexible barriers. Comput. Geotech. 2013, 54, 1–15. [Google Scholar] [CrossRef]
- Wang, D.P.; Li, Q.Z.; Bi, Y.Z.; He, S.M. Effects of new baffles system under the impact of rock avalanches. Eng. Geol. 2020, 264, 105261. [Google Scholar] [CrossRef]
- Bi, Y.Z.; Du, Y.J.; He, S.M.; Sun, X.P.; Wang, D.P.; Li, X.P.; Liang, H.; Wu, Y. Numerical analysis of effect of baffle configuration on impact force exerted from rock avalanches. Landslides 2018, 15, 1029–1043. [Google Scholar] [CrossRef]
- Lei, M.; Yang, P.; Wang, Y.K. Numerical analyses of the influence of baffles on the dynamics of debris flow in a gully. Arab. J. Geosci. 2020, 13, 1052. [Google Scholar] [CrossRef]
- Ng, C.W.; Liu, H.; Choi, C.E.; Kwan, J.S.; Pun, W.K. Impact dynamics of boulder-enriched debris flow on a rigid barrier. J. Geotech. Geoenviron. Eng. 2021, 147, 04021004. [Google Scholar] [CrossRef]
- Ng CW, W.; Choi, C.E.; Liu LH, D.; Wang, Y.; Song, D.; Yang, N. Influence of particle size on the mechanism of dry granular run-up on a rigid barrier. Géotech. Lett. 2017, 7, 79–89. [Google Scholar]
- Zhang, B.; Huang, Y.; Lu, P.; Li, C. Numerical Investigation of Multiple-Impact Behavior of Granular Flow on a Rigid Barrier. Water 2020, 12, 3228. [Google Scholar] [CrossRef]
- Redaelli, I.; di Prisco CCalvetti, F. Dry granular masses impacting on rigid obstacles: Numerical analysis and theoretical modelling. Acta Geotech. 2021, 16, 3923–3946. [Google Scholar] [CrossRef]
- Ahmadipur, A.; Qiu, T. Impact force to a rigid obstruction from a granular mass sliding down a smooth incline. Acta Geotech. 2018, 13, 1433–1450. [Google Scholar] [CrossRef]
- Bernard, M.; Boreggio, M.; Degetto, M.; Gregoretti, C. Model-based approach for design and performance evaluation of works controlling stony debris flow with an application to a case study at Rovina di Cancia (Venetian Dolomites, Northeast Italy). Sci. Total Environ. 2019, 688, 1373–1388. [Google Scholar] [CrossRef] [PubMed]
- Rossi, G.; Armanini, A. Impact force of a surge of water and sediments mixtures against slit check dams. Sci. Total Environ. 2019, 683, 351–359. [Google Scholar] [CrossRef] [PubMed]
- Sanvitale, N.; Bowman, E.; Cabrera, M.A. Experimental investigation on the impact dynamics of saturated granular flows on rigid barriers. Environ. Eng. Geosci. 2021, 27, 127–138. [Google Scholar] [CrossRef]
- Song, E.; Sangjum, I. Influence of debris flow impact on structural stability of check dams. Front. Earth Sci. 2022, 10, 887102. [Google Scholar] [CrossRef]
- Piton, G.; Godwin, S.R.; Mark, E.; Strout, A. Debris flows, boulders and constrictions: A simple framework modeling jamming and its consequences on outflow. J. Geophys. Res. Earth Surf. 2022, 127, e2021JF006447. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Towhata, I. Experimental Study of Dry Granular Flow and Impact Behavior against a Rigid Retaining Wall. Rock Mech. Rock Eng. 2013, 46, 713–729. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Zhao, Y.; Towhata, I.; Liu, D.X. Influence of particle characteristics on impact event of dry granular flow. Powder Technol. 2015, 270, 53–67. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Zhao, Y. Experimental investigation of dry granular flow impact via both normal and tangential force measurements. Géotech. Lett. 2015, 5, 33–38. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Fan, X.Y.; Li, T.H.; Xiao, S.Y. Influence of particle-size segregation on the impact of dry granular flow. Powder Technol. 2018, 340, 39–51. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Fan, X.Y.; Su, L.J.; Xiao, S.-Y.; Sui, J.; Zhang, R.-X.; Song, Y.; Shen, Z.-W. Experimental validation of a new semi-empirical impact force model of the dry granular flow impact against a rigid barrier. Landslides 2021, 18, 1387–1402. [Google Scholar] [CrossRef]
- Sun, H.; You, Y.; Liu, J.; Zhang, G.; Feng, T.; Wang, D. Experimental study on discharge process regulation to debris flow with open-type check dams. Landslides 2021, 18, 967–978. [Google Scholar] [CrossRef]
- Choi, C.E.; Goodwin, G.R.; Ng CW, W.; Cheung DK, H.; Kwan, J.S.; Pun, W.K. Coarse granular flow interaction with slit structures. Géotech. Lett. 2016, 6, 267–274. [Google Scholar] [CrossRef]
- Goodwin, G.R.; Choi, C.E. Slit structures: Fundamental mechanisms of mechanical trapping of granular flows. Comput. Geotech. 2020, 119, 103376. [Google Scholar] [CrossRef]
- Marchelli, M.; Leonardi, A.; Pirulli, M.; Scavia, C. On the efficiency of slit-check dams in retaining granular flows. Géotechnique 2020, 70, 226–237. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, Y.; Liu, J. Micro-mechanism and efficiency of baffle structure in deceleration of granular flows. Acta Geotech. 2021, 16, 3667–3688. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, B.; Zhu, C. Computational assessment of baffle performance against rapid granular flows. Landslides 2021, 18, 485–501. [Google Scholar] [CrossRef]
- Sun, H.; You, Y.; Liu, J.F. Experimental study on characteristics of trapping and regulating sediment with an open-type check dam in debris flow hazard mitigation. J. Mt. Sci. 2018, 15, 2001–2012. [Google Scholar] [CrossRef]
- Ishikawa, N.; Shima, J.; Matsubara, T.; Tatesawa, H.; Horiguchi, T.; Mizuyama, T. Trapping mechanism of debris flow by steel open dams. In Proceedings of the INTERPRAEVENT, 2014 International Symposium, Nara, Japan, 25–28 November 2014. [Google Scholar]
- Law, R.P.H.; Choi, C.E.; Ng, C.W.W. Discrete-element investigation of influence of granular debris flow baffles on rigid barrier impact. Can. Geotech. J. 2016, 53, 179–185. [Google Scholar] [CrossRef]
- Gong, S.; Zhao, T.; Zhao, J.; Dai, F.; Zhou, G.G.D. Discrete element analysis of dry granular flow impact on slit dams. Landslides 2021, 18, 1143–1152. [Google Scholar] [CrossRef]
- Cui, Y.; Choi, C.E.; Liu, L.H.D.; Ng, C.W.W. Effects of particle size of mono-disperse granular flows impacting a rigid barrier. Nat. Hazards 2018, 91, 1179–1201. [Google Scholar] [CrossRef]
- Fang, Y.; Guo, L.; Hou, M. Arching effect analysis of granular media based on force chain visualization. Powder Technol. 2020, 363, 621–628. [Google Scholar] [CrossRef]
- Fang, Y.; Li, X.; Guo, L.; Gu, R.; Luo, W. The experiment and analysis of the repose angle and the stress arch-caused stress dip of the sandpile. Granul. Matter 2022, 24, 7. [Google Scholar] [CrossRef]


| Parameters | Values |
|---|---|
| Wall normal stiffness (N/m) | 1 × 108 [42] |
| Wall normal-to-shear stiffness ratio (dimensionless) | 1 [42] |
| Particle normal stiffness (N/m) | 1 × 108 [42] |
| Particle normal-to-shear stiffness ratio (dimensionless) | 1 [42] |
| Ball radius (mm) | 5 |
| Ball density (kg/m3) | 2550 |
| Inter-ball friction coefficient (dimensionless) | 0.36 [42] |
| Interface-ball friction coefficient (dimensionless) | 0.4 [42] |
| Gravitational acceleration (m/s2) | 9.81 [42] |
| Coefficient of restitution (dimensionless) | 0.78 [42] |
| Parameters | Values | ||
|---|---|---|---|
| Diameter(mm) | 6 | 10 | 14 |
| Density (kg/m3) | 2550 | 2550 | 2550 |
| Initial bulk density (kg/m3) | 1549 | 1487 | 1380 |
| Young’s modulus (GPa) | 60 | 60 | 60 |
| Poisson ratio | 0.25 | 0.25 | 0.25 |
| Dynamic friction angle (°) | 17.2 | 16.6 | 14.7 |
| Static friction angle (°) | 28 | 30 | 34 |
| Experiment ID | Slit Size, b (mm) | Particle Diameter, d (mm) | Slit Size to Particle Size Ratio, b/d |
|---|---|---|---|
| B0-D6 | 0 | 6 | 0.00 |
| B0-D10 | 0 | 10 | 0.00 |
| B0-D14 | 0 | 14 | 0.00 |
| B10-D6 | 10 | 6 | 1.67 |
| B10-D10 | 10 | 10 | 1.00 |
| B10-D14 | 10 | 14 | 0.71 |
| B15-D6 | 15 | 6 | 2.50 |
| B15-D10 | 15 | 10 | 1.50 |
| B15-D14 | 15 | 14 | 1.07 |
| B20-D6 | 20 | 6 | 3.33 |
| B20-D10 | 20 | 10 | 2.00 |
| B20-D14 | 20 | 14 | 1.43 |
| B25-D6 | 25 | 6 | 4.17 |
| B25-D10 | 25 | 10 | 2.50 |
| B25-D14 | 25 | 14 | 1.79 |
| B30-D6 | 30 | 6 | 5.00 |
| B30-D10 | 30 | 10 | 3.00 |
| B30-D14 | 30 | 14 | 2.14 |
| B35-D6 | 35 | 6 | 5.83 |
| B35-D10 | 35 | 10 | 3.50 |
| B35-D14 | 35 | 14 | 2.50 |
| B40-D6 | 40 | 6 | 6.67 |
| B40-D10 | 40 | 10 | 4.00 |
| B40-D14 | 40 | 14 | 2.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Liu, H.; Guo, L.; Li, X. Model Experiment Exploration of the Kinetic Dissipation Effect on the Slit Dam with Baffles Tilted in the Downstream Direction. Water 2022, 14, 2772. https://doi.org/10.3390/w14182772
Fang Y, Liu H, Guo L, Li X. Model Experiment Exploration of the Kinetic Dissipation Effect on the Slit Dam with Baffles Tilted in the Downstream Direction. Water. 2022; 14(18):2772. https://doi.org/10.3390/w14182772
Chicago/Turabian StyleFang, Yingguang, Hao Liu, Lingfeng Guo, and Xiaolong Li. 2022. "Model Experiment Exploration of the Kinetic Dissipation Effect on the Slit Dam with Baffles Tilted in the Downstream Direction" Water 14, no. 18: 2772. https://doi.org/10.3390/w14182772
APA StyleFang, Y., Liu, H., Guo, L., & Li, X. (2022). Model Experiment Exploration of the Kinetic Dissipation Effect on the Slit Dam with Baffles Tilted in the Downstream Direction. Water, 14(18), 2772. https://doi.org/10.3390/w14182772







