Attribution Analysis of Runoff in the Upper Reaches of Jinsha River, China
Abstract
:1. Introduction
2. Data and Methods
2.1. Reanalysis Data
2.2. Rainfall and Runoff Data
2.3. Relative Importance Analysis
3. Results
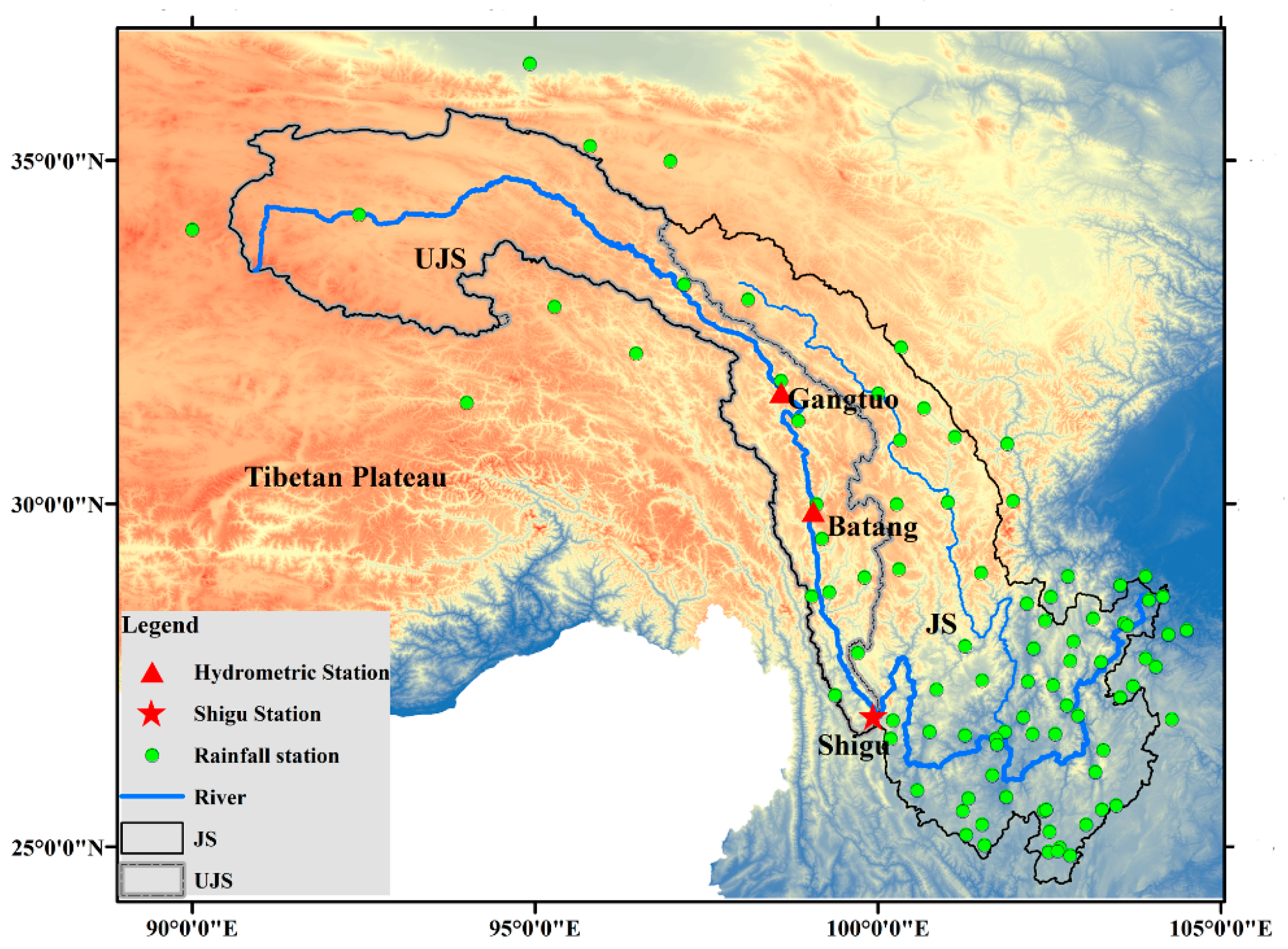
3.1. Analysis of Water Resources Characteristics of the Upper Jinsha River
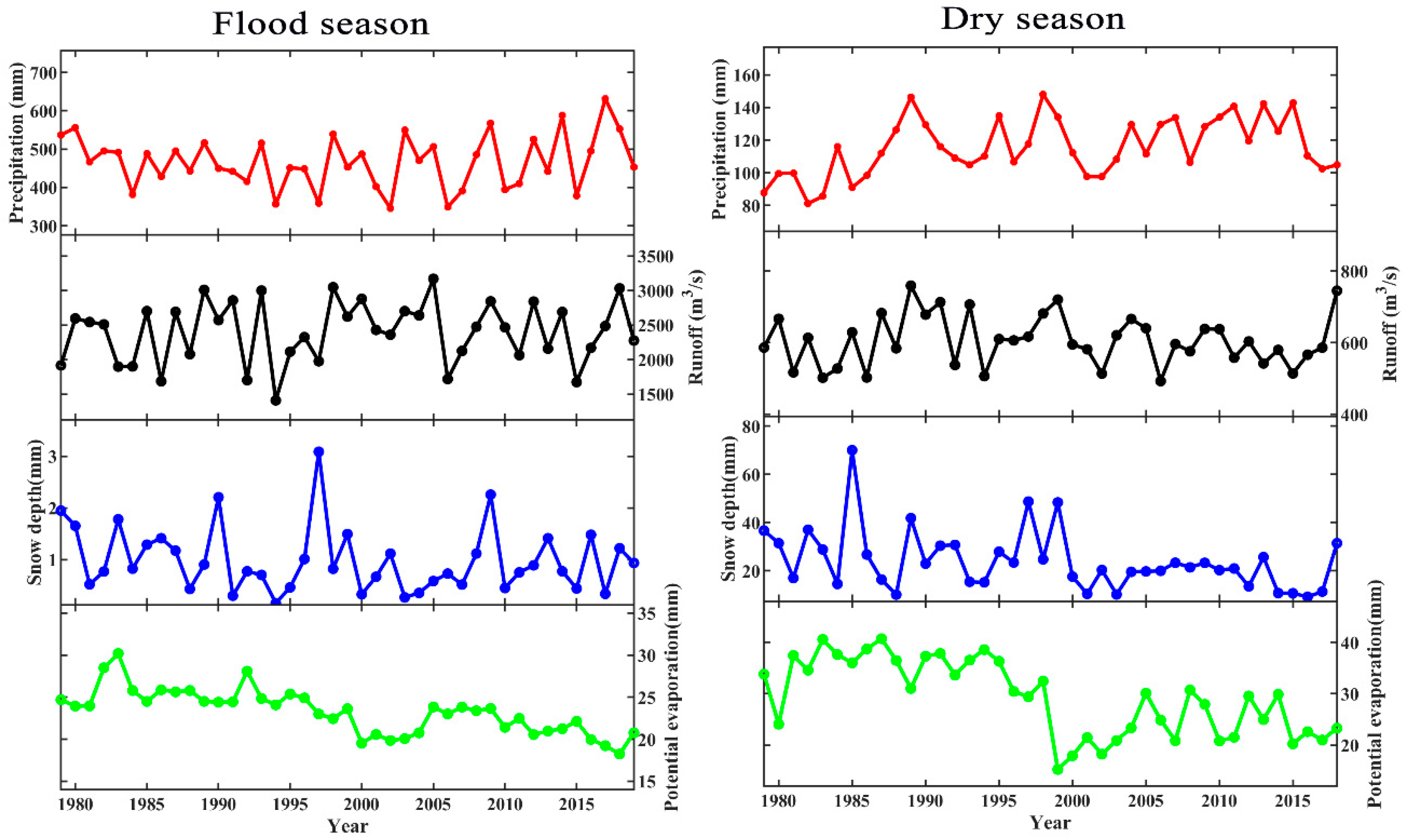
3.2. Runoff Correlation Analysis
3.3. Analysis of the Causes of Runoff
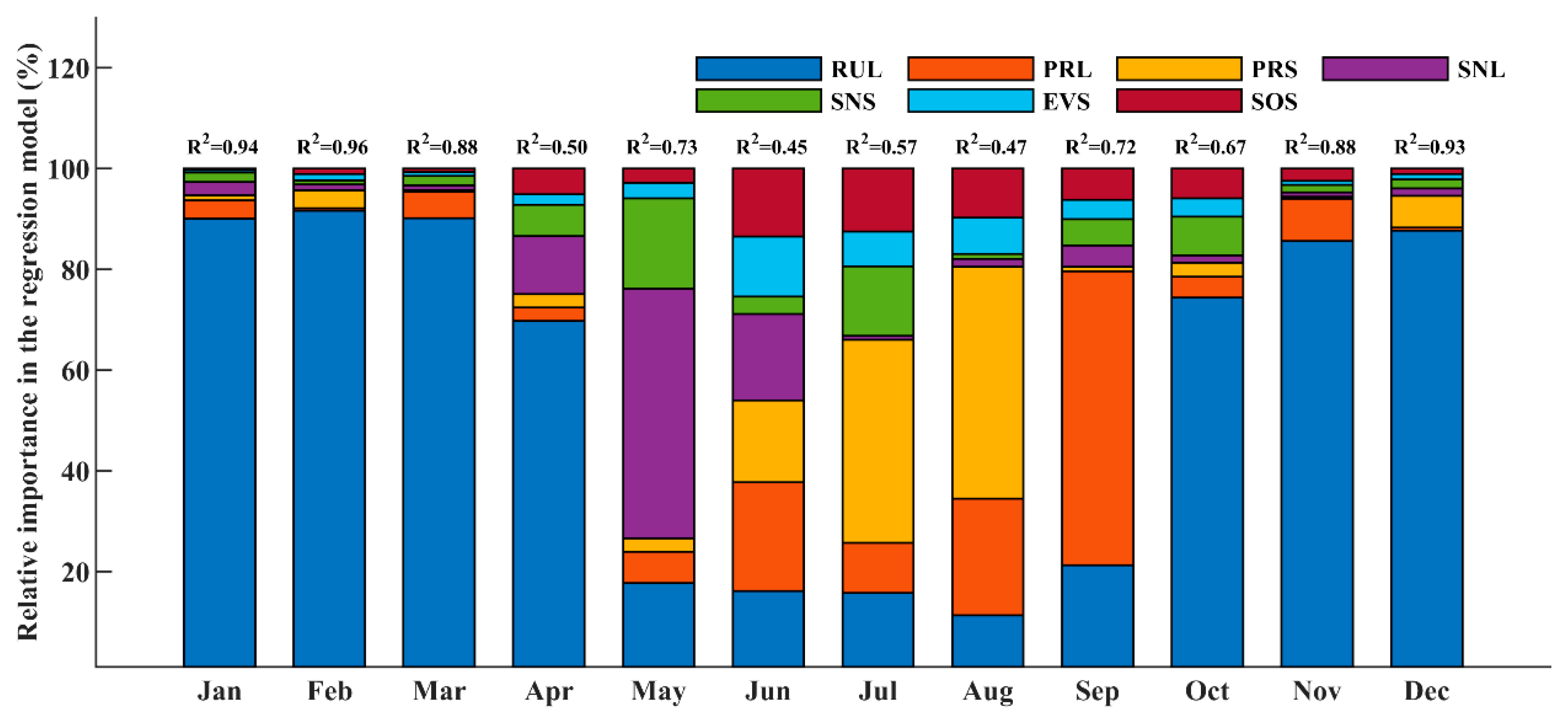
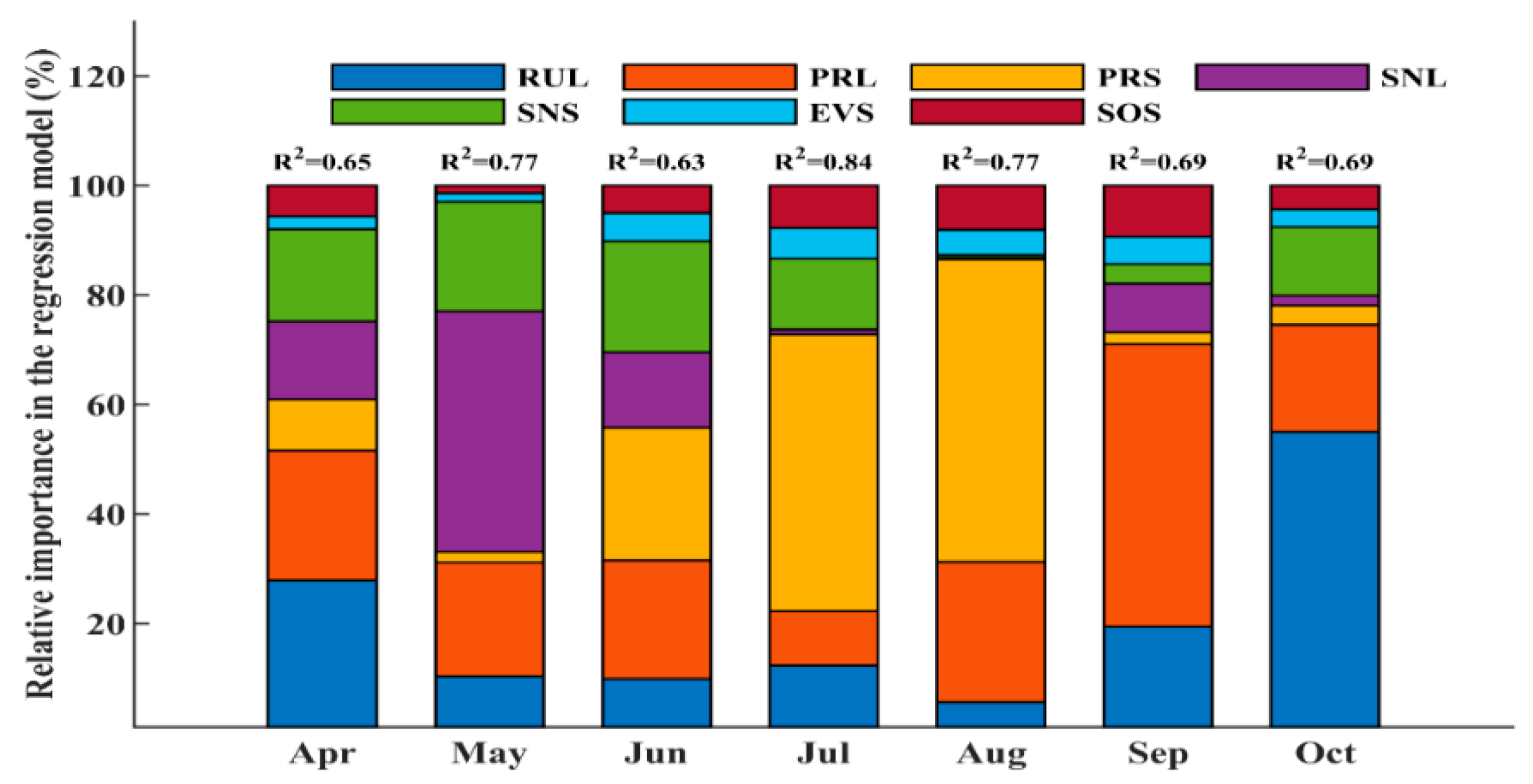
3.3.1. Monthly Contribution Analysis
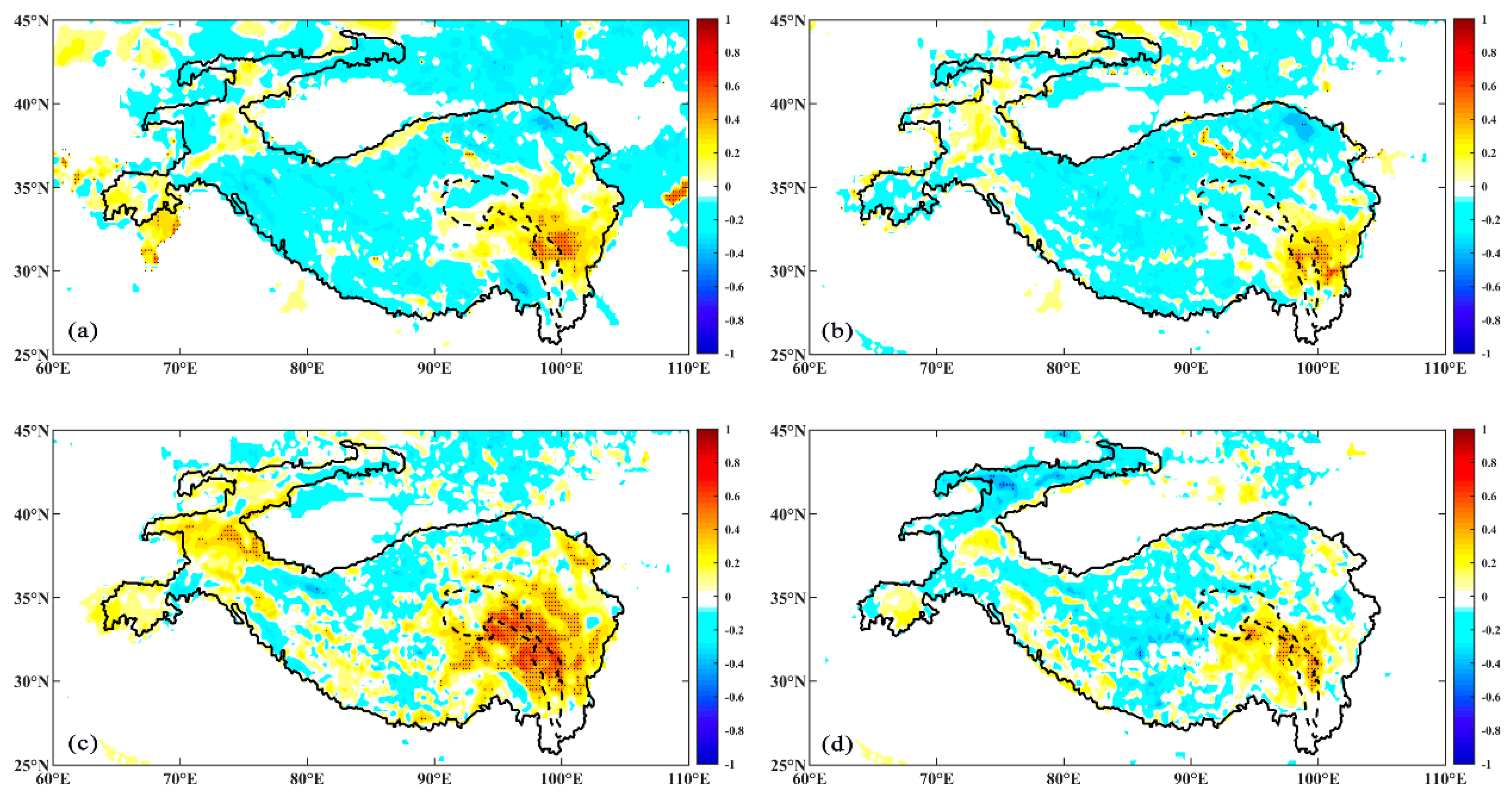
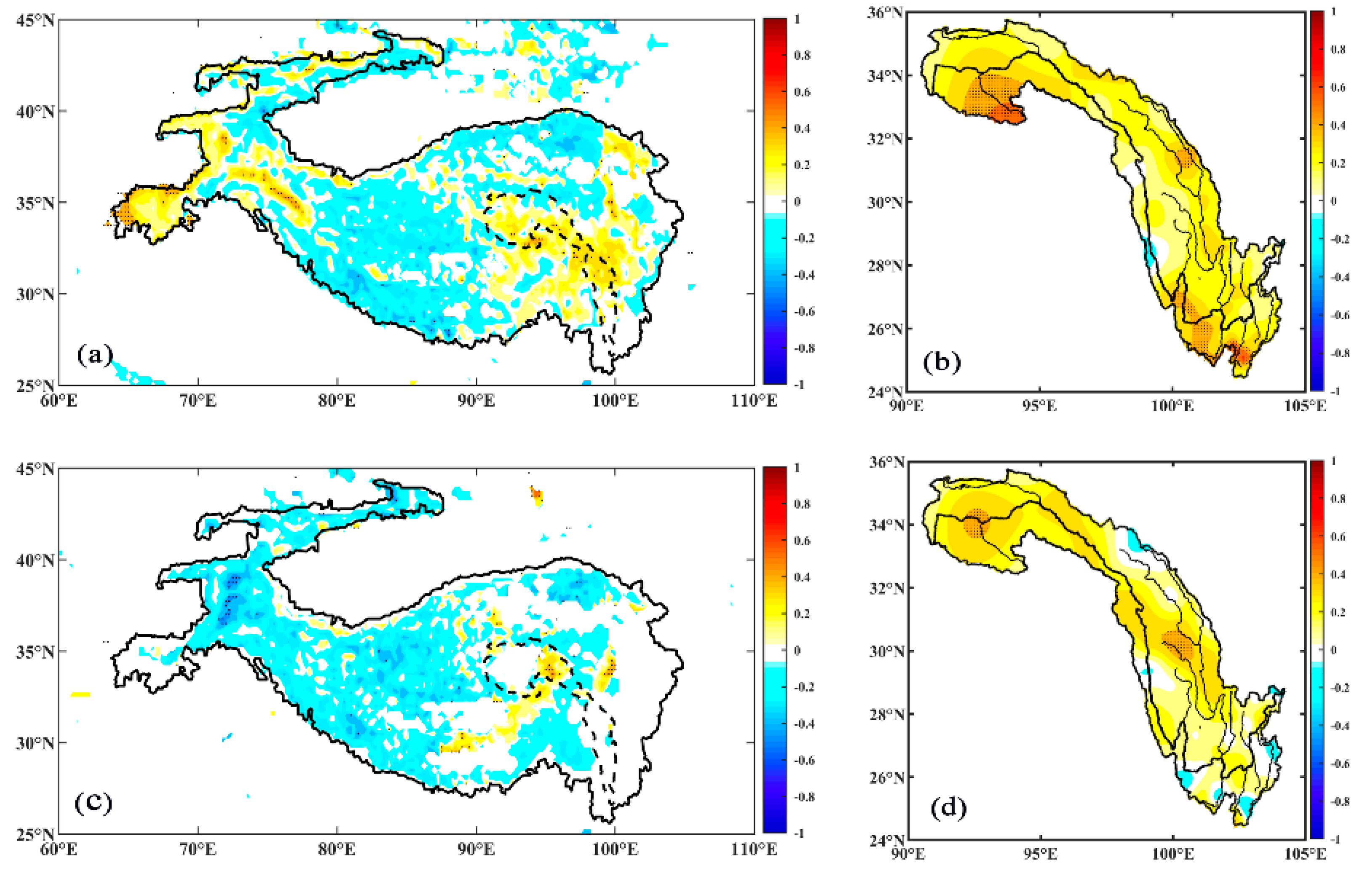
3.3.2. Analysis of Key Areas
- RUL influence period
- 2.
- Snowmelt influence period
- 3.
- Pre-flood period in June
- 4.
- Main flood season
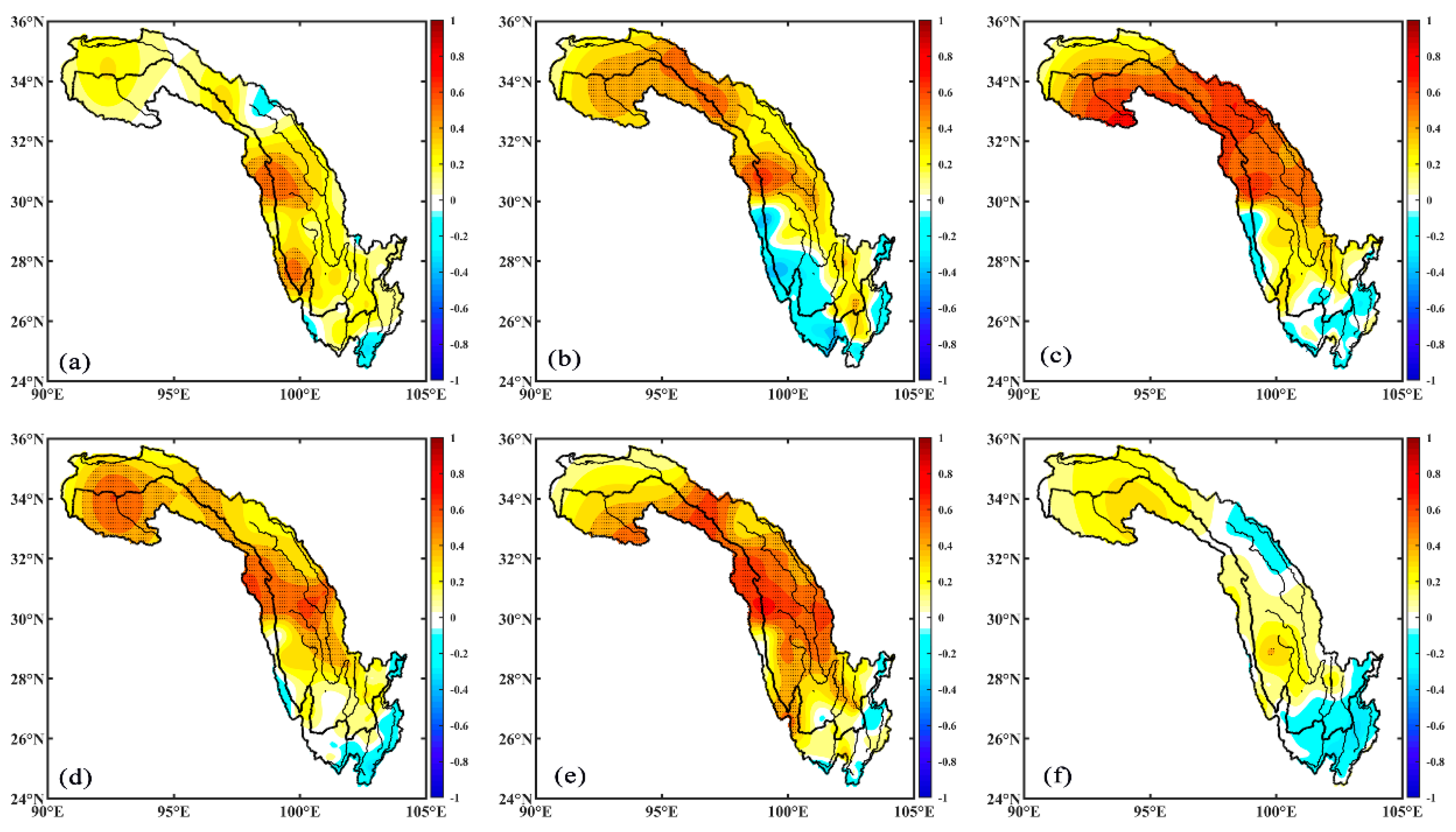
3.3.3. Contribution of Key Areas
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, S.Q. Prospect of Jinsha River—A huge hydropower base in China. China Power Enterp. Manag. 2003, 9, 32–34. (In Chinese) [Google Scholar]
- Cui, L.; Gu, H.B.; Gao, F. Analysis and suggestions on hydropower development utilizing the natural river sections of Jinsha River. Water Power 2022, 48, 1–4. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, Y.C.; Liu, J.; Shang, Y. Research on the influence of climate change on the different runoff components in the permafrost area: A case study of the source area of the Yangtze River. China Rural. Water Hydropower 2021, 3, 63–68. (In Chinese) [Google Scholar]
- Mao, T.X.; Wang, G.X.; Zhang, T. Impacts of climatic change on hydrological regime in the Three-River Headwaters Region, China, 1960–2009. Water Resour. Manag. 2016, 30, 115–131. (In Chinese) [Google Scholar] [CrossRef]
- Liu, G.S.; Wang, G.X.; Zhang, W. Research on climate and runoff variation characteristics in the Three-river headwater region. Resour. Environ. Yangtze Basin 2012, 21, 302–309. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, S.F.; Hua, D.; Meng, X.J.; Zhang, Y.Y. Climate change and its driving effect on the runoff in the “Three-River Headwaters” region. J. Geogr. Sci. 2011, 21, 963–978. [Google Scholar] [CrossRef]
- Li, Y.; Li, Q.J.; Liu, X.S.; Duan, S.; Cai, Y. Analysis of runoff variation in source region of Yangtze River. J. China Hydrol. 2017, 37, 92–95. (In Chinese) [Google Scholar]
- Du, J.N.; Cai, Y.Q.; Li, Y.; Li, Q.; Liu, X. Attribution analysis of runoff in the source region of the Yangtze River. J. China Hydrol. 2021, 41, 73–78. (In Chinese) [Google Scholar] [CrossRef]
- Li, Q.J. Investigation of runoff evolution at the headwaters of Yangtze River and its driving forces. J. Yangtze River Sci. Res. Inst. 2018, 35, 1–5. (In Chinese) [Google Scholar]
- Wang, L.J.; Yan, H.Y. Analysis of impacting factor on change of annual runoff distribution in head-water area of the Yangtze River. J. Water Resour. Water Eng. 2011, 22, 174–176. [Google Scholar]
- Evans, S.G.; Ge, S.; Liang, S. Analysis of groundwater flow in mountainous, headwater catchments with permafrost. Water Resour. Res. 2015, 51, 9564–9576. [Google Scholar] [CrossRef]
- Li, L.; Shen, H.; Dai, S.; Li, H.; Xiao, J. Response of water resources to climate change and its future trend in the source region of the Yangtze River. J. Geogr. Sci. 2013, 23, 208–218. [Google Scholar] [CrossRef]
- Qi, D.M.; Li, Y.Q.; Chen, Y.R.; Zhao, X.; Zhou, C. Changing characteristics and cause analysis of the runoff in the source regions of the Yangtze River under the background of climate change. J. Glaciol. Geocryol. 2015, 37, 1075–1086. [Google Scholar]
- Jiang, C.; Li, D.; Gao, Y.; Liu, X.; Liu, W.; Zhang, L. Spatiotemporal variability of streamflow and attribution in the Three-Rivers Headwater Region, northwest China. J. Water Clim. Chang. 2016, 7, 637–649. [Google Scholar] [CrossRef]
- Ji, G.X.; Song, H.Y.; Wei, H.; Wu, L. Attribution analysis of climate and anthropic factors on runoff and vegetation changes in the source area of the Yangtze River from 1982 to 2016. Land 2021, 10, 612. [Google Scholar] [CrossRef]
- Deng, H.; Chen, Y. Influences of recent climate change and human activities on water storage variations in Central Asia. J. Hydrol. 2017, 544, 46–57. [Google Scholar] [CrossRef]
- Ahmed, N.; Wang, G.; Lü, H.; Booij, M.J.; Marhaento, H.; Prodhan, F.A.; Ali, S.; Imran, M.A. Attribution of changes in streamflow to climate change and land cover change in Yangtze River source region, China. Water 2022, 14, 259. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, J.; He, R.; Liu, C.; Ma, T.; Bao, Z.; Liu, Y. Runoff sensitivity to climate change for hydro-climatically different catchments in China. Stoch. Environ. Res. Risk Assess. 2017, 31, 1011–1021. [Google Scholar] [CrossRef]
- Crossman, J.; Futter, M.; Oni, S.; Whitehead, P.; Jin, L.; Butterfield, D.; Baulch, H.; Dillon, P. Impacts of climate change on hydrology and water quality: Future proofing management strategies in the Lake Simcoe watershed, Canada. J. Great Lakes Res. 2013, 39, 19–32. [Google Scholar] [CrossRef]
- Ning, T.; Li, Z.; Liu, W. Separating the impacts of climate change and land surface alteration on runoff reduction in the Jing River catchment of China. Catena 2016, 147, 80–86. [Google Scholar] [CrossRef]
- Zhou, Y.; Lai, C.; Wang, Z.; Chen, X.; Zeng, Z.; Chen, J.; Bai, X. Quantitative evaluation of the impact of climate change and human activity on runoff change in the Dongjiang River Basin, China. Water 2018, 10, 571. [Google Scholar] [CrossRef]
- Pocock, S.J.; Stone, G.W. The Nature of the p Value. New Engl. J. Med. 2016, 375, 2205. [Google Scholar] [CrossRef] [PubMed]
- Fields, G.S. Accounting for Income in Equality and Its Change: A New Method, with Application to the Distribution of Earnings in the United States. In Worker Well-Being and Public Policy; Emerald Group Publishing Limited: Bingley, UK, 2003. [Google Scholar] [CrossRef]
- Israeli, O. A Shapley-based decomposition of the R-square of a linear regression. J. Econ. Inequal. 2007, 5, 199–212. [Google Scholar] [CrossRef]
- Shorrocks, A.F. Decomposition procedures for distributional analysis: A unified framework based on the Shapley value. J. Econ. Inequal. 2013, 11, 99–126. [Google Scholar] [CrossRef]
- Ye, D.; Ng, Y.K.; Lian, Y. Culture and Happiness. Soc. Indic. Res. 2015, 123, 519–547. [Google Scholar] [CrossRef] [Green Version]
- Budescu, D.V. Dominance analysis: A new approach to the problem of relative importance of predictors in multiple regression. Psychol. Bull. 1993, 114, 542. [Google Scholar] [CrossRef]
- Azen, R.; Budescu, D.V. The dominance analysis approach for comparing predictors in multiple regression. Psychol. Methods 2003, 8, 129. [Google Scholar] [CrossRef]
- Tonidandel, S.; LeBreton, J.M. Relative importance analysis: A useful supplement to regression analysis. J. Bus. Psychol. 2011, 26, 1–9. [Google Scholar] [CrossRef]
- Sirami, C.; Gross, N.; Baillod, A.B.; Bertrand, C.; Carrié, R.; Hass, A.; Henckel, L.; Miguet, P.; Vuillot, C.; Alignier, A.; et al. Increasing crop heterogeneity enhances multitrophic diversity across agricultural regions. Proc. Natl. Acad. Sci. USA 2019, 116, 16442–16447. [Google Scholar] [CrossRef]
- Dai, L.Y.; Che, T.; Ding, Y.J.; Hao, X.H. Evaluation of snow cover and snow depth on the Qinghai–Tibetan Plateau derived from passive microwave remote sensing. Cryosphere 2017, 11, 1933–1948. [Google Scholar] [CrossRef] [Green Version]



| RUL | PRL | PRS | SNL | SNS | EVS | SOS | |
|---|---|---|---|---|---|---|---|
| Jan | 0.97 ** | 0.15 | 0.10 | 0.20 | 0.18 | 0.10 | −0.07 |
| Feb | 0.97 ** | 0.05 | 0.22 | 0.17 | 0.14 | 0.22 | −0.18 |
| Mar | 0.93 ** | 0.28 | 0.0003 | 0.13 | 0.20 | 0.09 | −0.10 |
| Apr | 0.62 ** | 0.08 | −0.04 | 0.27 | 0.24 | 0.02 | 0.003 |
| May | 0.36 * | 0.32 * | −0.07 | 0.74 ** | 0.56 ** | 0.14 | −0.08 |
| Jun | 0.24 | 0.25 | 0.31 * | 0.32 * | 0.08 | −0.34 * | 0.37 * |
| Jul | 0.26 | 0.29 | 0.54 ** | 0.03 | 0 | −0.24 | 0.36 * |
| Aug | 0.31 * | 0.46 ** | 0.57 ** | 0 | −0.06 | −0.35 * | 0.40 ** |
| Sep | 0.57 ** | 0.80 ** | 0.08 | −0.31 * | −0.28 | −0.28 | 0.36 * |
| Oct | 0.72 ** | 0.20 | 0.22 | −0.07 | 0.16 | −0.23 | 0.29 |
| Nov | 0.92 ** | 0.38 * | 0.01 | 0.08 | 0.17 | −0.07 | 0.17 |
| Dec | 0.94 ** | −0.07 | 0.30 | 0.19 | 0.21 | −0.14 | 0.07 |
| RUL | PRL | PRS | SNL | SNS | EVS | SOS | |
|---|---|---|---|---|---|---|---|
| Jan | 90 | 3.7 | 1.1 | 2.6 | 1.8 | 0.5 | 0.3 |
| Feb | 91.6 | 0.4 | 3.6 | 1.1 | 0.8 | 1.3 | 1.1 |
| Mar | 90.1 | 5.2 | 0.3 | 1 | 1.9 | 0.7 | 0.7 |
| Apr | 69.8 | 2.6 | 2.7 | 11.5 | 6.2 | 2.1 | 5.1 |
| May | 17.7 | 6.2 | 2.7 | 49.6 | 17.9 | 3.1 | 2.8 |
| Jun | 16.1 | 21.7 | 16.2 | 17.1 | 3.5 | 11.9 | 13.5 |
| Jul | 15.7 | 9.9 | 40.3 | 0.8 | 13.8 | 6.9 | 12.5 |
| Aug | 11.3 | 23.1 | 46 | 1.6 | 1 | 7.2 | 9.7 |
| Sep | 21.3 | 58.3 | 1 | 4.2 | 5.2 | 3.8 | 6.3 |
| Oct | 74.4 | 4.1 | 2.8 | 1.4 | 7.7 | 3.7 | 5.9 |
| Nov | 85.6 | 8.3 | 0.4 | 0.9 | 1.5 | 0.7 | 2.5 |
| Dec | 87.7 | 0.6 | 6.3 | 1.5 | 1.8 | 1 | 1.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Cao, H.; Li, Y.; Feng, B.; Qiu, H.; Zhang, H. Attribution Analysis of Runoff in the Upper Reaches of Jinsha River, China. Water 2022, 14, 2768. https://doi.org/10.3390/w14172768
Wang L, Cao H, Li Y, Feng B, Qiu H, Zhang H. Attribution Analysis of Runoff in the Upper Reaches of Jinsha River, China. Water. 2022; 14(17):2768. https://doi.org/10.3390/w14172768
Chicago/Turabian StyleWang, Le, Hui Cao, Yurong Li, Baofei Feng, Hui Qiu, and Hairong Zhang. 2022. "Attribution Analysis of Runoff in the Upper Reaches of Jinsha River, China" Water 14, no. 17: 2768. https://doi.org/10.3390/w14172768




