Inspection of Cracks in the Piston Rod of a Hydraulic Cylinder Using Injected Alternating Current-Field Measurement
Abstract
:1. Introduction
2. Theories of IAC-FM
2.1. Theoretical Model
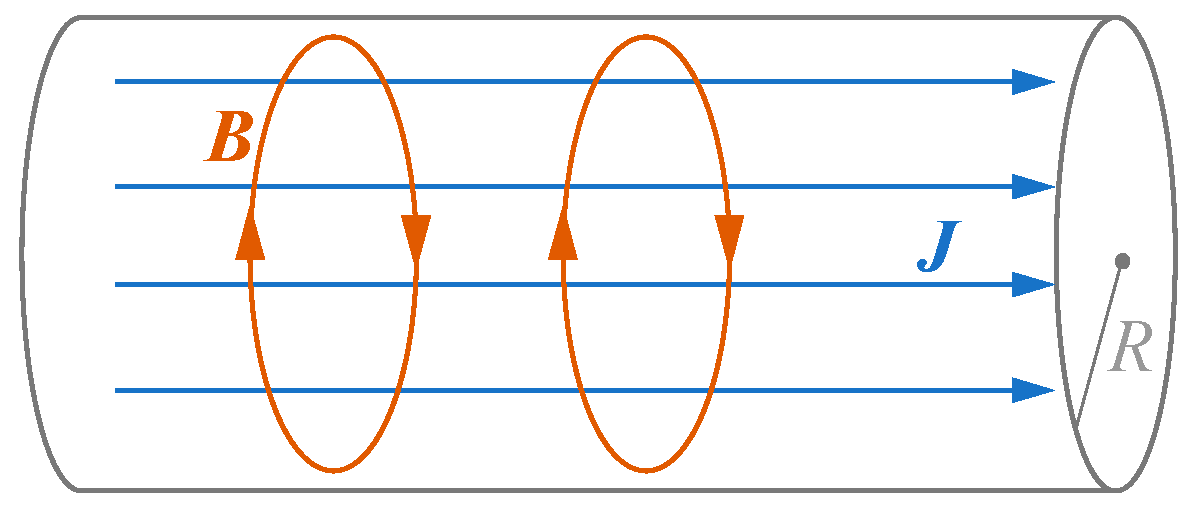
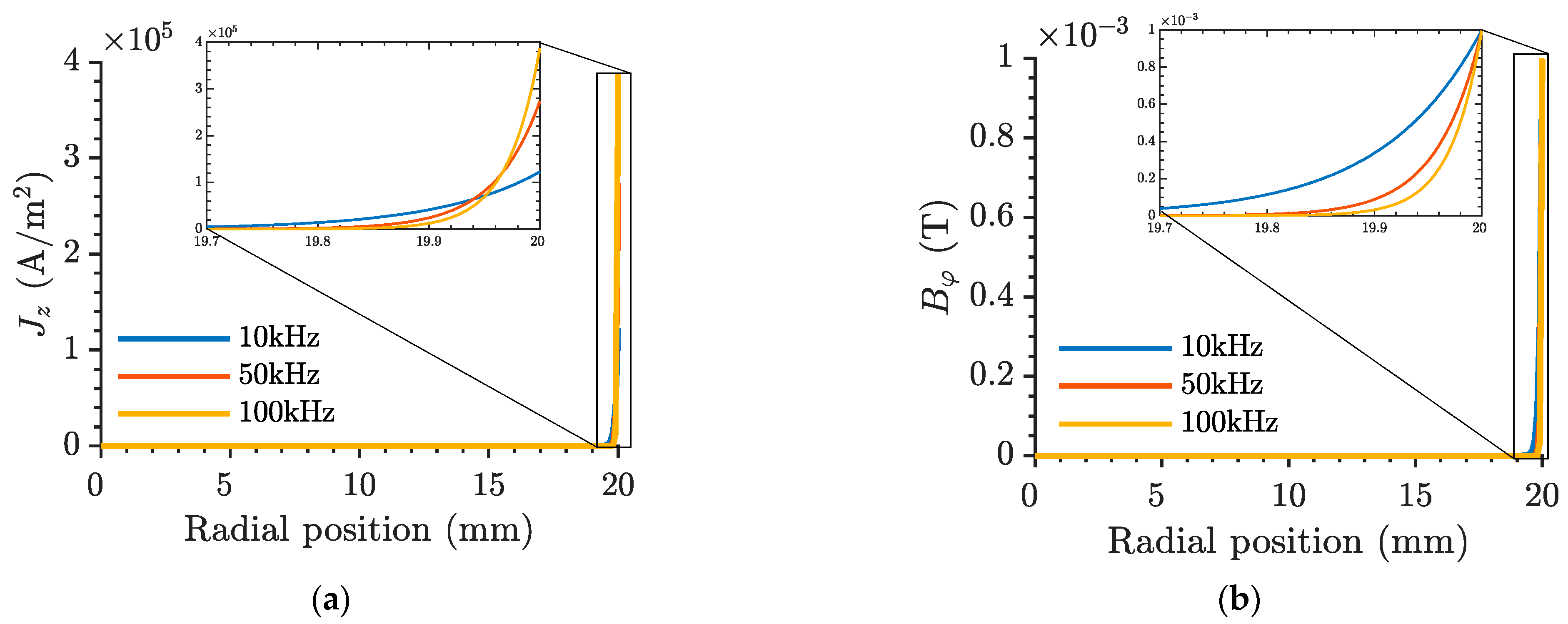
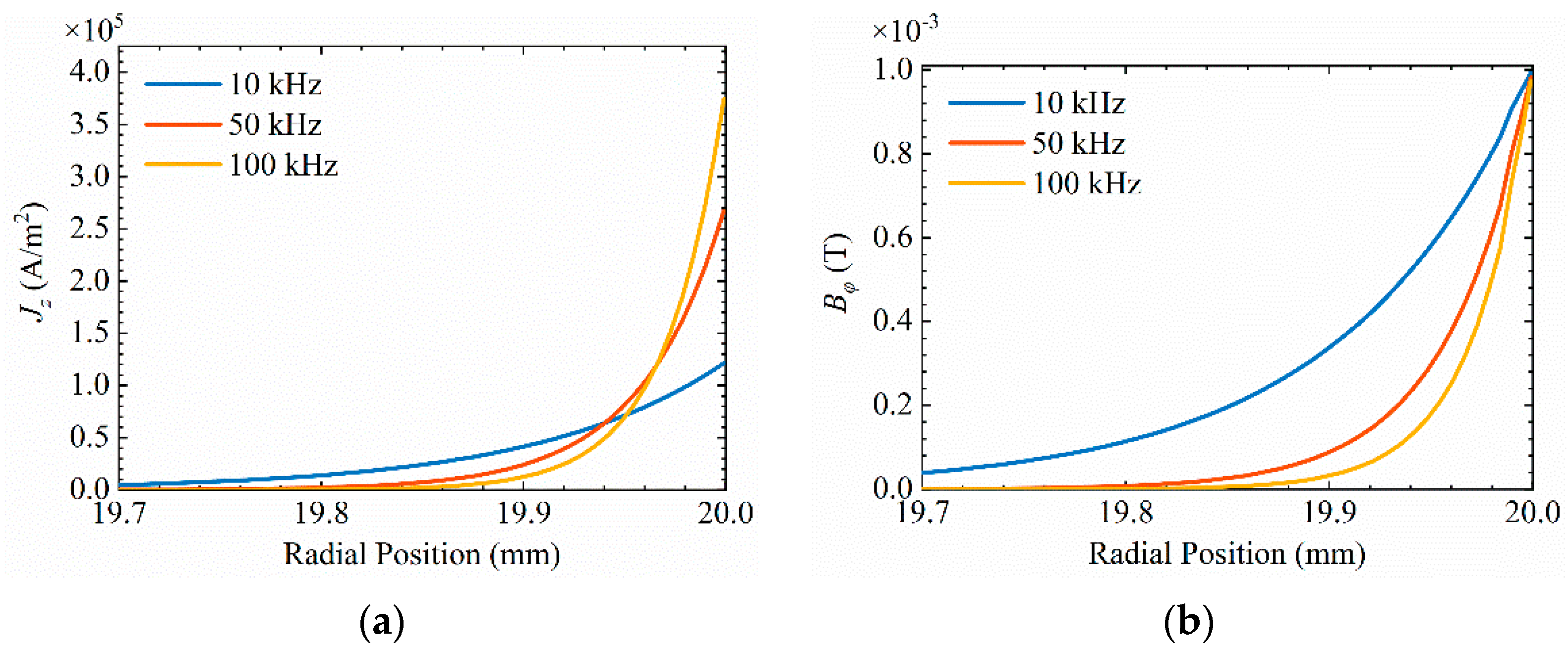
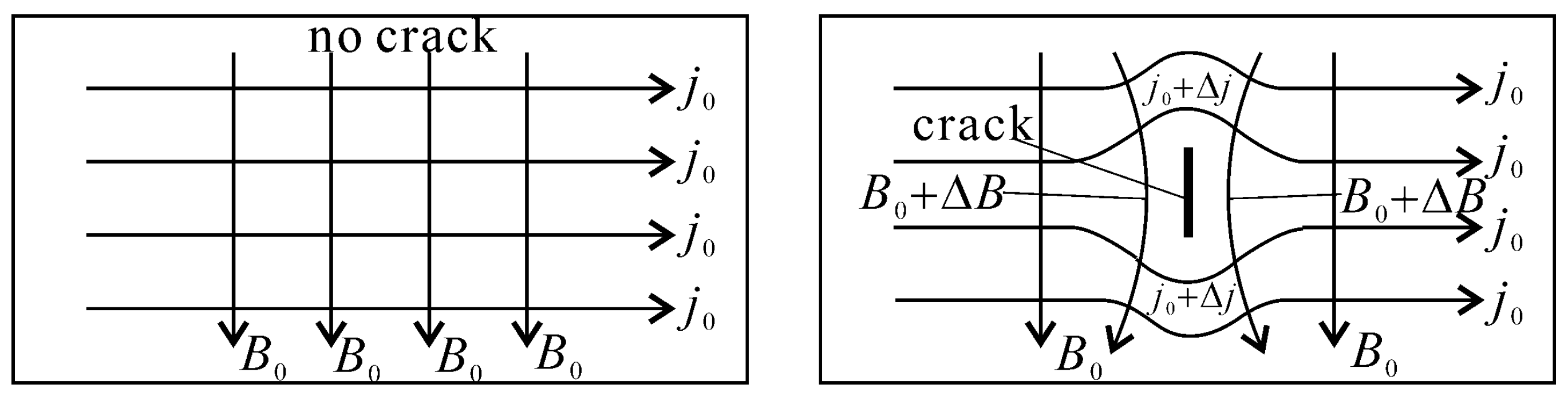
2.2. Distribution of Eddy Current and Magnetic Field
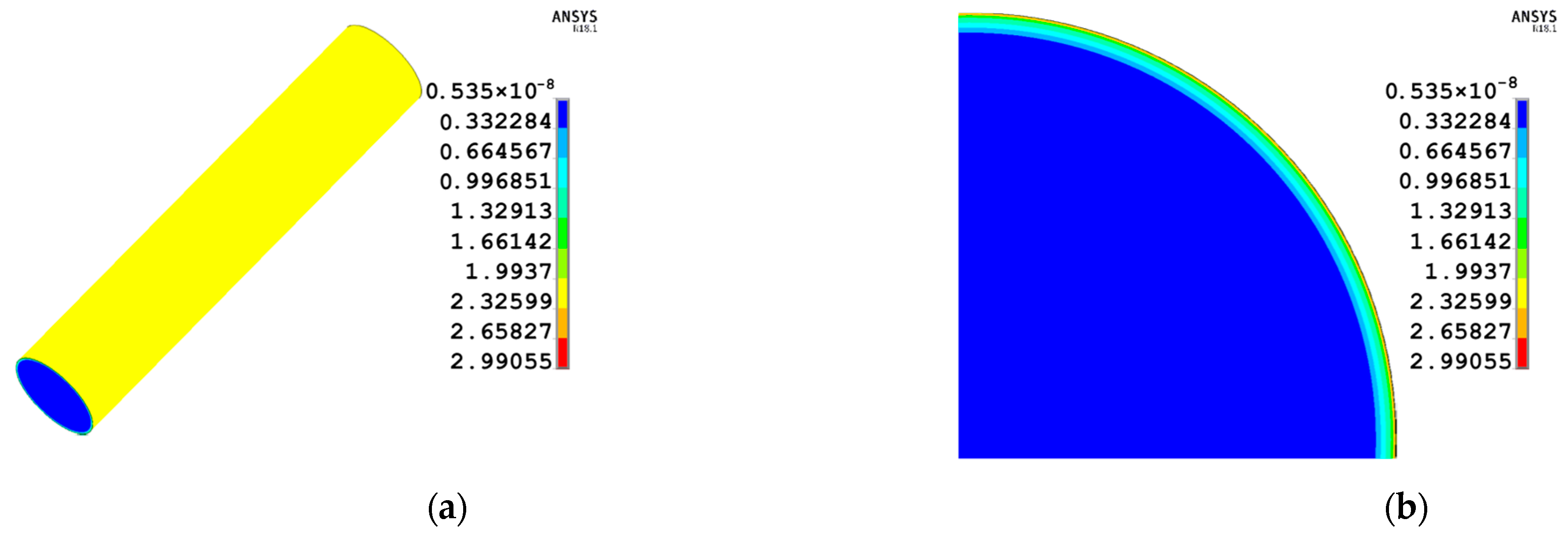
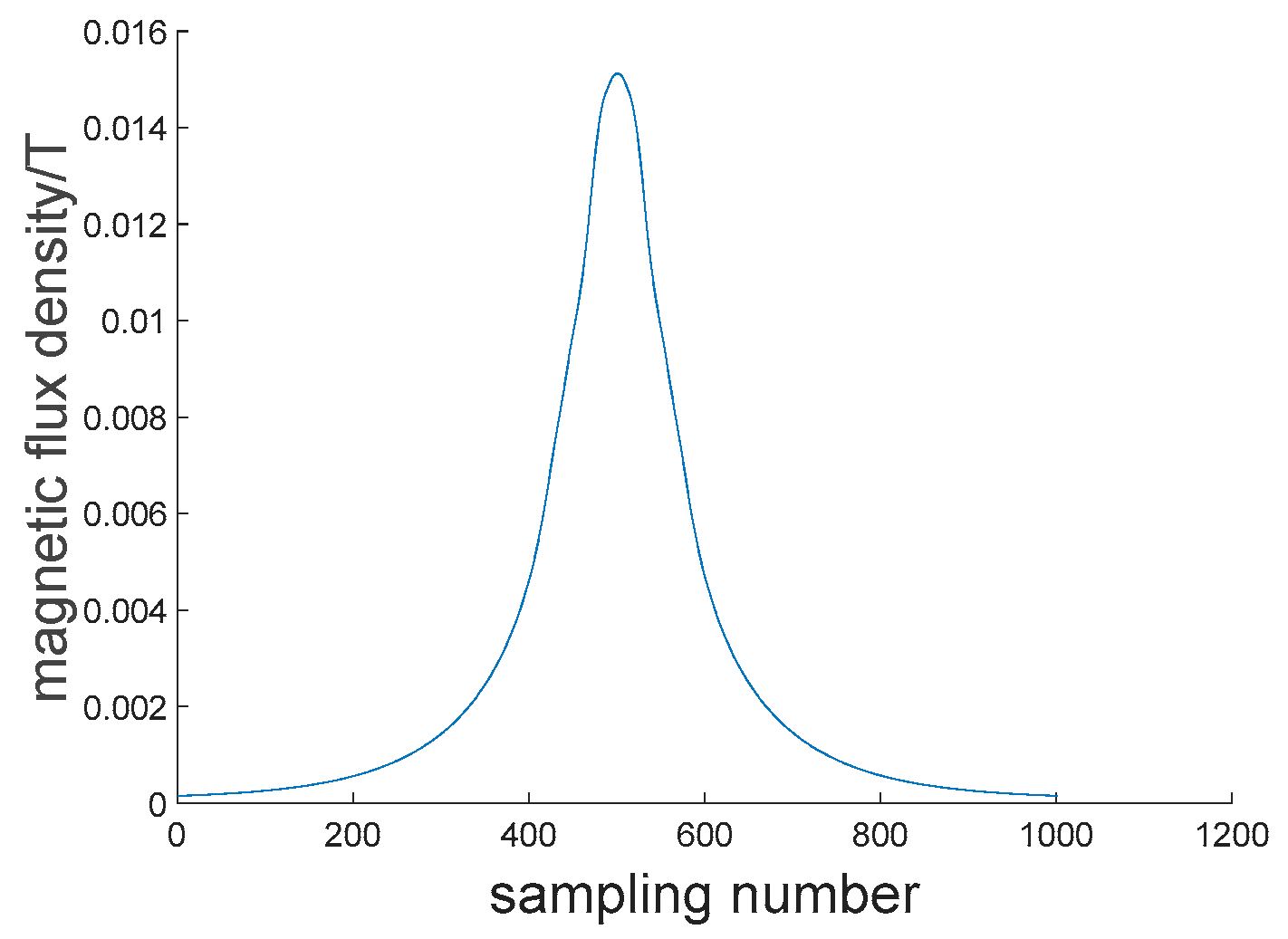
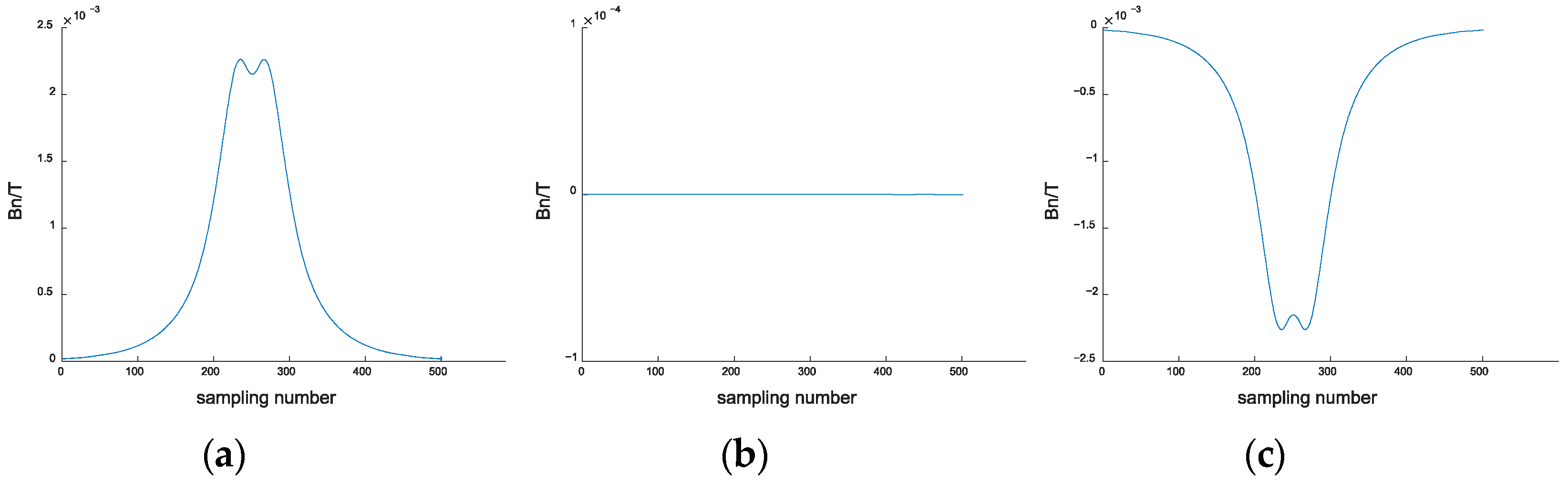
3. Finite Element Simulation
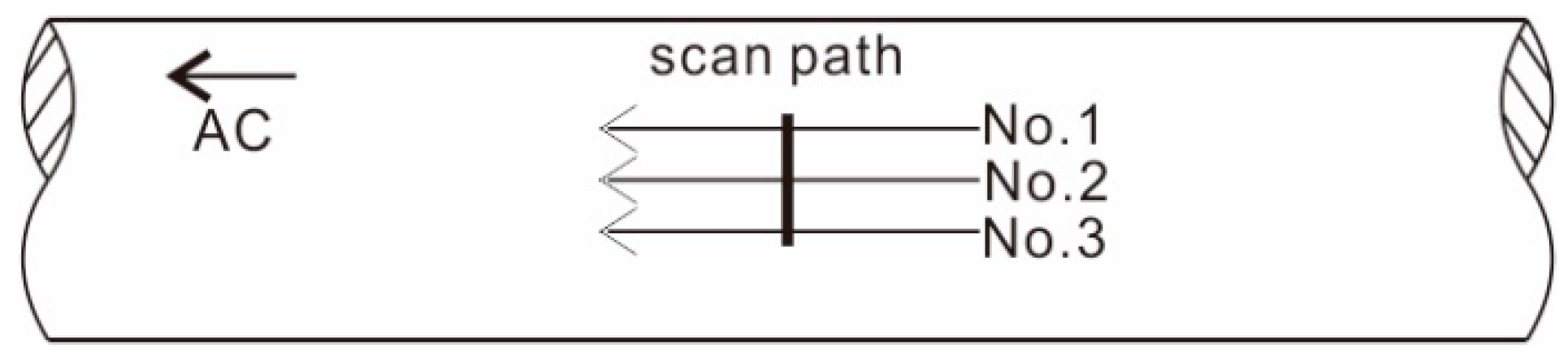
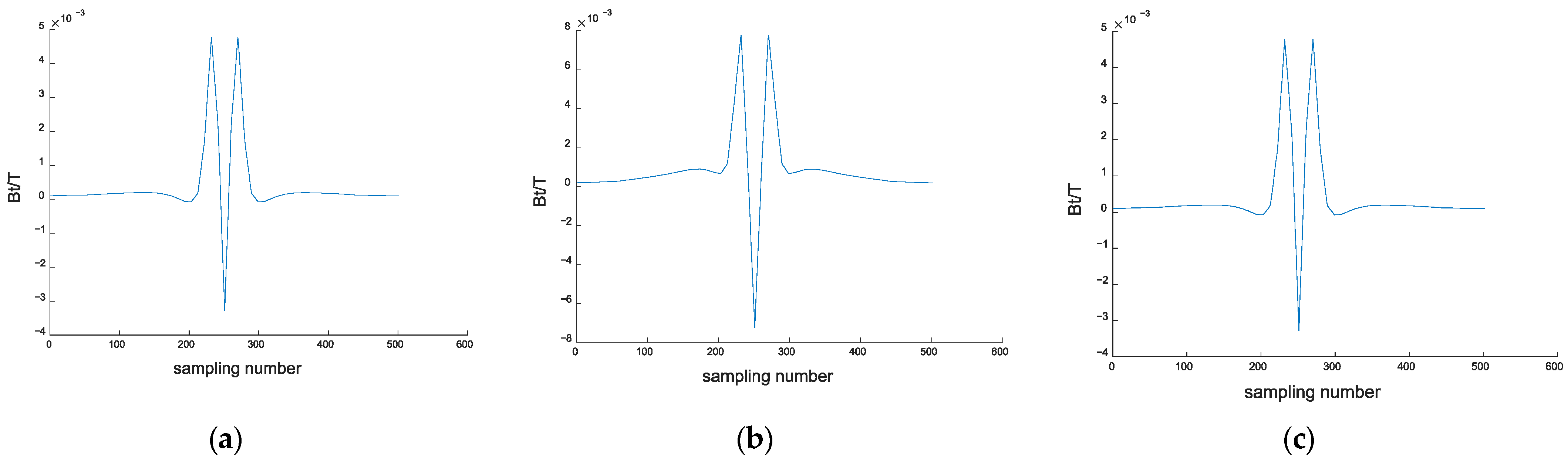
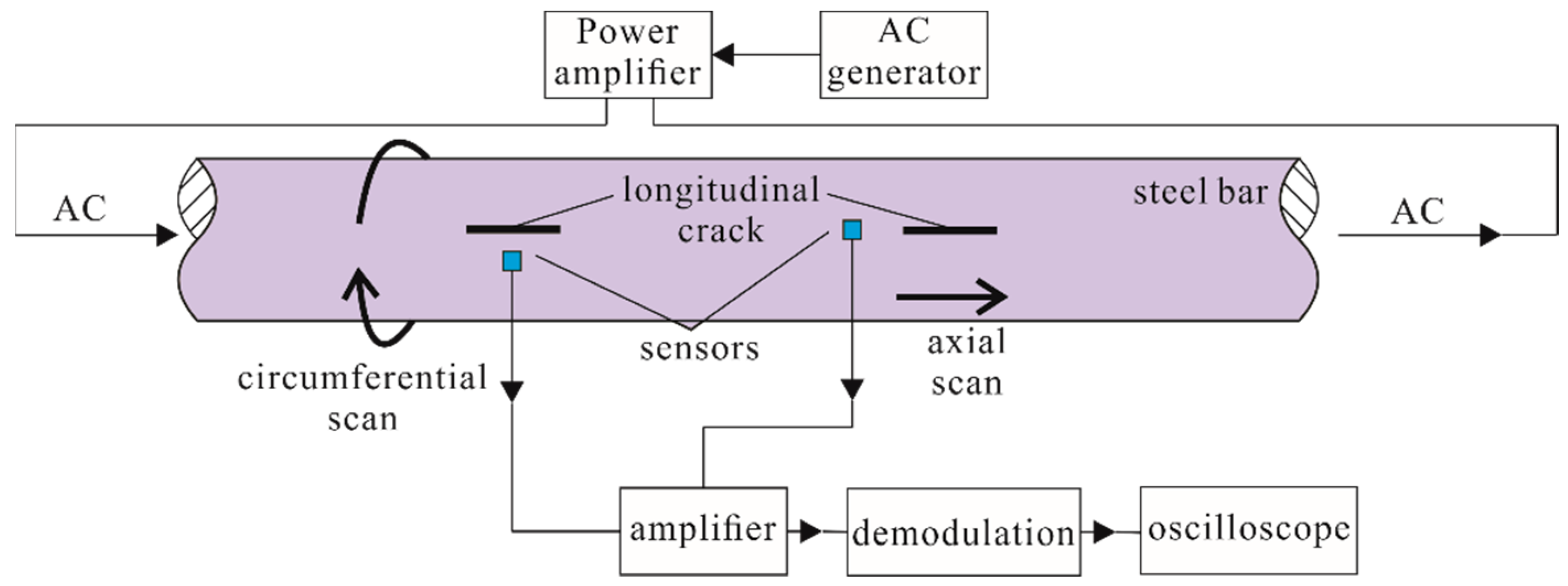
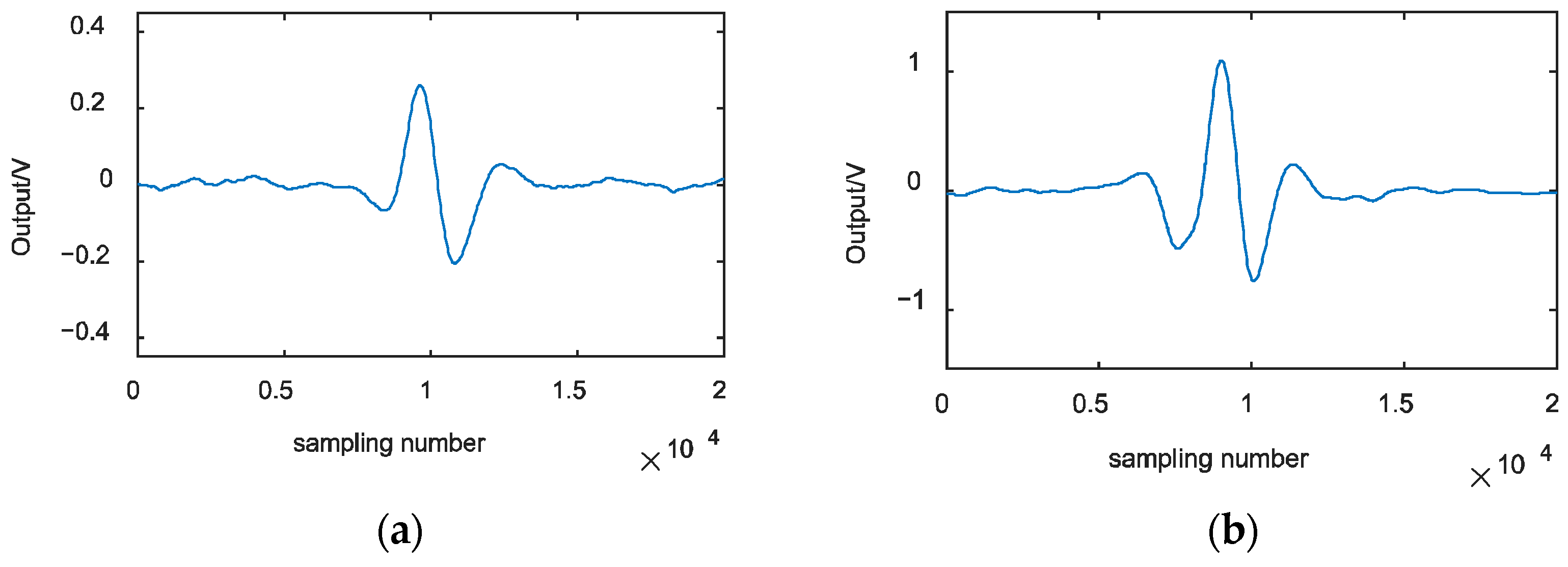
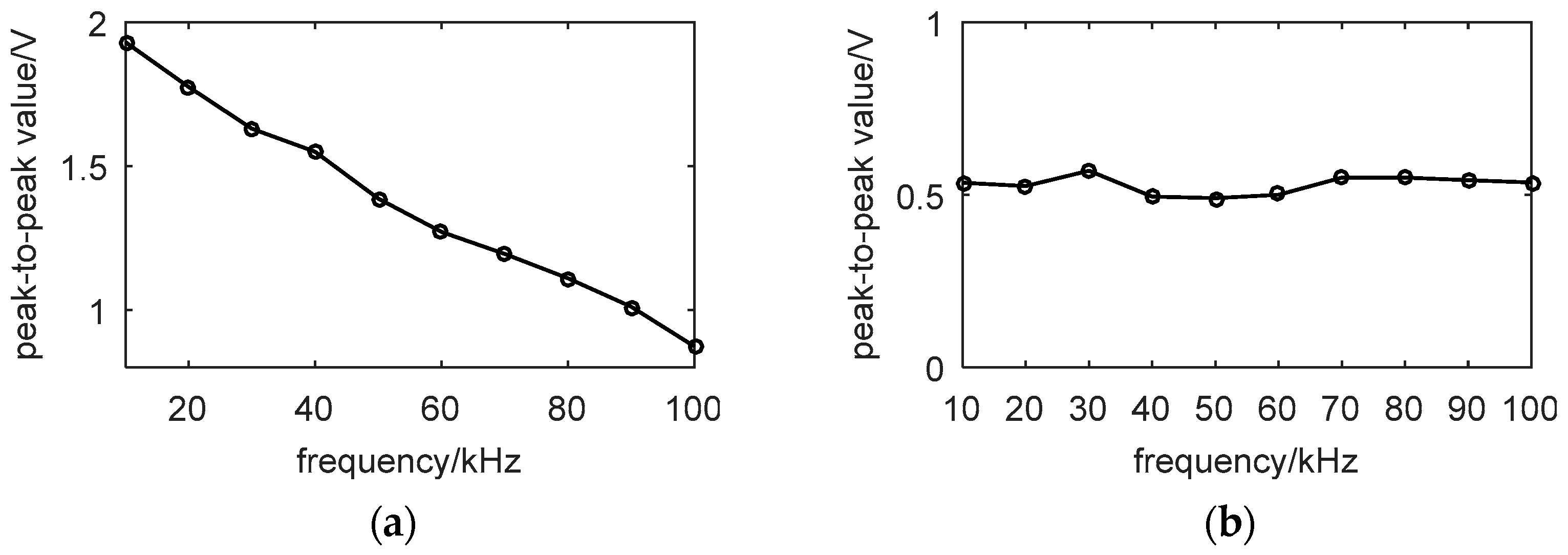
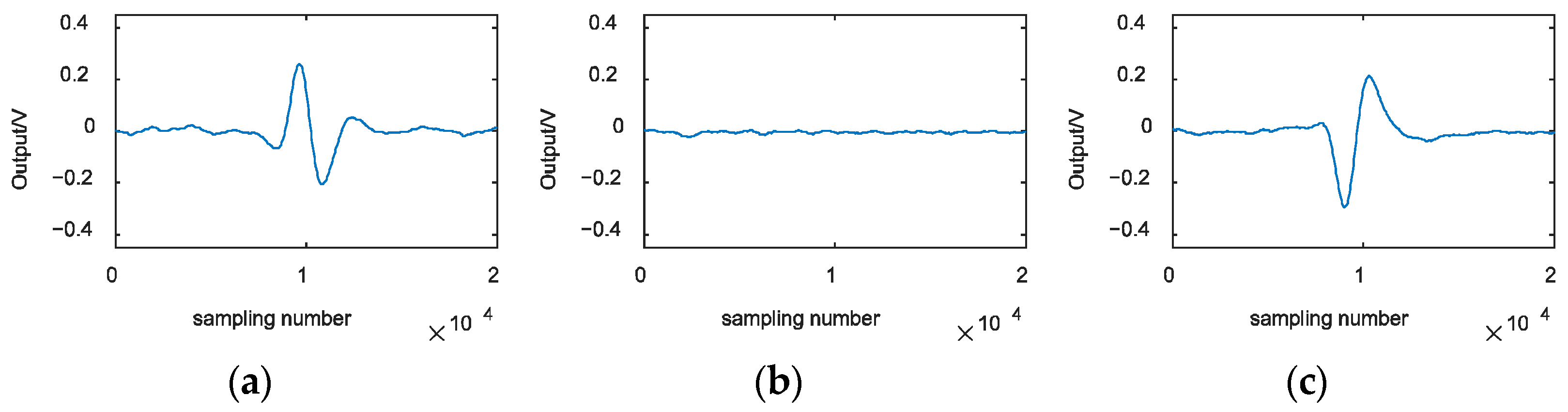
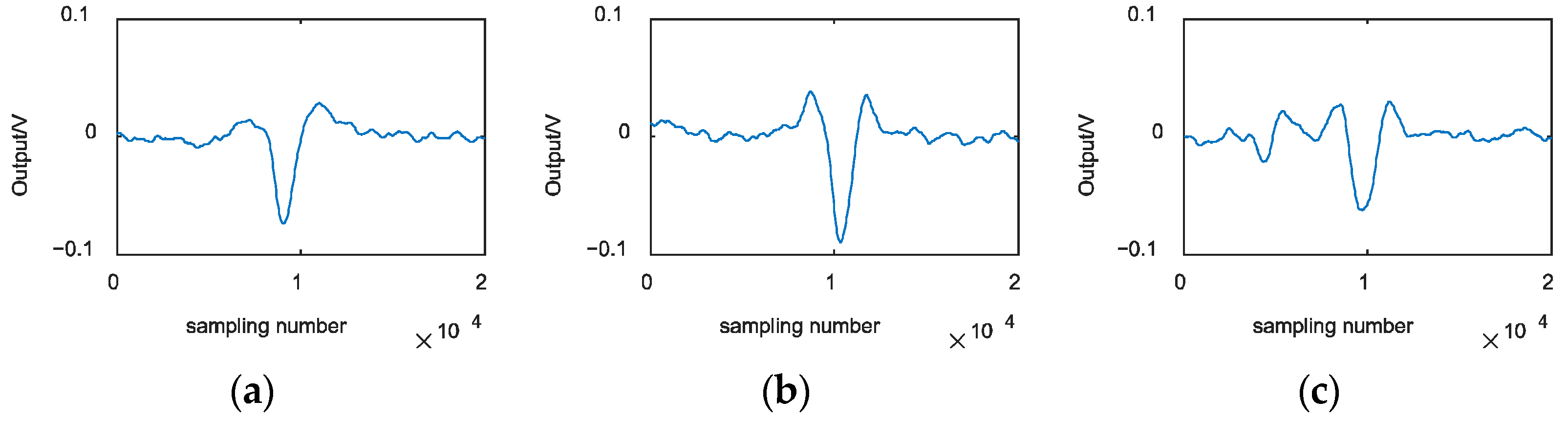
4. Experiments and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Park, J.; Won, C.; Lee, H.-J.; Yoon, J. Integrated Machine Vision System for Evaluating Hole Expansion Ratio of Advanced High-Strength Steels. Materials 2022, 15, 553. [Google Scholar] [CrossRef] [PubMed]
- Choi, D.-C.; Jeon, Y.-J.; Lee, S.J.; Yun, J.P.; Kim, S.W. Algorithm for detecting seam cracks in steel plates using a Gabor filter combination method. Appl. Opt. 2014, 53, 4865–4872. [Google Scholar] [CrossRef] [PubMed]
- Feng, B.; Kang, Y.; Sun, Y.; Deng, Z. Magnetization time lag caused by eddy currents and its influence on high-speed MFL testing. Res. Nondestruct. Eval. 2019, 30, 189–204. [Google Scholar] [CrossRef]
- Feng, B.; Kang, Y.; Sun, Y.; Yang, Y.; Yan, X. Influence of motion induced eddy current on the magnetization of steel pipe and MFL signal. Int. J. Appl. Electromagn. Mech. 2016, 52, 357–362. [Google Scholar] [CrossRef]
- Jiang, X.; Sun, Y.; Feng, B.; Liu, M.; Jiang, X.; Li, R.; He, L.; Kang, Y. New On-Line MFL Testing Method and Apparatus for Winding Mine Hoist Wire Rope. Appl. Sci. 2022, 12, 6970. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, J.; Feng, B.; Kang, Y. An Opening Electric-MFL Detector for the NDT of In-Service Mine Hoist Wire. IEEE Sens. J. 2014, 14, 2042–2047. [Google Scholar] [CrossRef]
- Ditchburn, R.J.; Burke, S.K.; Posada, M. Eddy-Current Nondestructive Inspection with Thin Spiral Coils: Long Cracks in Steel. J. Nondestruct. Eval. 2003, 22, 63–77. [Google Scholar] [CrossRef]
- Helifa, B.; Oulhadj, A.; Benbelghit, A.; Lefkaier, I.; Boubenider, F.; Boutassouna, D. Detection and measurement of surface cracks in ferromagnetic materials using eddy current testing. NDT E Int. 2006, 39, 384–390. [Google Scholar] [CrossRef]
- Xie, L.; Gao, B.; Tian, G.; Tan, J.; Feng, B.; Yin, Y. Coupling pulse eddy current sensor for deeper defects NDT. Sens. Actuators A Phys. 2019, 293, 189–199. [Google Scholar] [CrossRef]
- Bowler, N. Theory of Four-Point Direct-Current Potential Drop Measurements on a Metal Plate. Res. Nondestruct. Eval. 2006, 17, 29–48. [Google Scholar] [CrossRef]
- Bowler, N.; Huang, Y. Electrical conductivity measurement of metal plates using broadband eddy-current and four-point methods. Meas. Sci. Technol. 2005, 16, 2193–2200. [Google Scholar] [CrossRef]
- Bowler, N.; Huang, Y. Model-based characterization of homogeneous metal plates using four-point alternating current po-tential drop measurements. IEEE Trans. Magn. 2005, 41, 2102–2110. [Google Scholar] [CrossRef]
- Bowler, J.R.; Huang, Y.; Sun, H.; Brown, J.; Bowler, N. Alternating current potential-drop measurement of the depth of case-hardening in steel rods. Meas. Sci. Technol. 2008, 19, 075204. [Google Scholar] [CrossRef]
- Li, D.; Sun, Y.; Ye, Z.; Kang, Y. Electric field leakage nondestructive testing principle and its simulations. Mater. Eval. 2015, 11, 1438–1445. [Google Scholar]
- Li, D.; Kang, Y.; Sun, Y.; Ye, Z.; Ding, Y. Nondestructive Evaluation of Conducting Materials Using a Direct Current Perturbation Method. In Proceedings of the 19th International Workshop on Electromagnetic Non-Destructive Evaluation (ENDE), Xian, China, 25–28 June 2014. [Google Scholar] [CrossRef]
- Ye, Z.; Kang, Y.; Sun, Y.; Yang, G.; Feng, B.; Zhou, Q. Theoretical analyses of an alternating current electric flux leakage inspection method and ex-perimental verification. Insight 2015, 57, 78–84. [Google Scholar] [CrossRef]
- Desjardins, D.R.; Krause, T.W.; Clapham, L. Transient response of a driver coil in transient eddy current testing. NDT E Int. 2015, 73, 22–27. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Huang, Y.; Tang, J.; Zhou, F.; Kang, Y.; Feng, B. Inspection of Cracks in the Piston Rod of a Hydraulic Cylinder Using Injected Alternating Current-Field Measurement. Water 2022, 14, 2736. https://doi.org/10.3390/w14172736
Zhang J, Huang Y, Tang J, Zhou F, Kang Y, Feng B. Inspection of Cracks in the Piston Rod of a Hydraulic Cylinder Using Injected Alternating Current-Field Measurement. Water. 2022; 14(17):2736. https://doi.org/10.3390/w14172736
Chicago/Turabian StyleZhang, Jikai, Yuewen Huang, Jian Tang, Fangfang Zhou, Yihua Kang, and Bo Feng. 2022. "Inspection of Cracks in the Piston Rod of a Hydraulic Cylinder Using Injected Alternating Current-Field Measurement" Water 14, no. 17: 2736. https://doi.org/10.3390/w14172736
APA StyleZhang, J., Huang, Y., Tang, J., Zhou, F., Kang, Y., & Feng, B. (2022). Inspection of Cracks in the Piston Rod of a Hydraulic Cylinder Using Injected Alternating Current-Field Measurement. Water, 14(17), 2736. https://doi.org/10.3390/w14172736








