A Predictive Analysis Method of Shafting Vibration for the Hydraulic-Turbine Generator Unit
Abstract
:1. Introduction
2. Methodology
2.1. Principle of Finite Element Modal Analysis
2.2. Model Simplification and Assumptions
- (1)
- It is assumed that the rotating shaft system is a constant system and also a linear elastomer;
- (2)
- The model material is considered to be isotropic and the density distribution is uniform;
- (3)
- It is assumed that the displacement and deformation are small, i.e., small deformation;
- (4)
- The connection between the components of the shafting shall be treated as an integrated connection, and the shafting shall be regarded as a whole after connection.
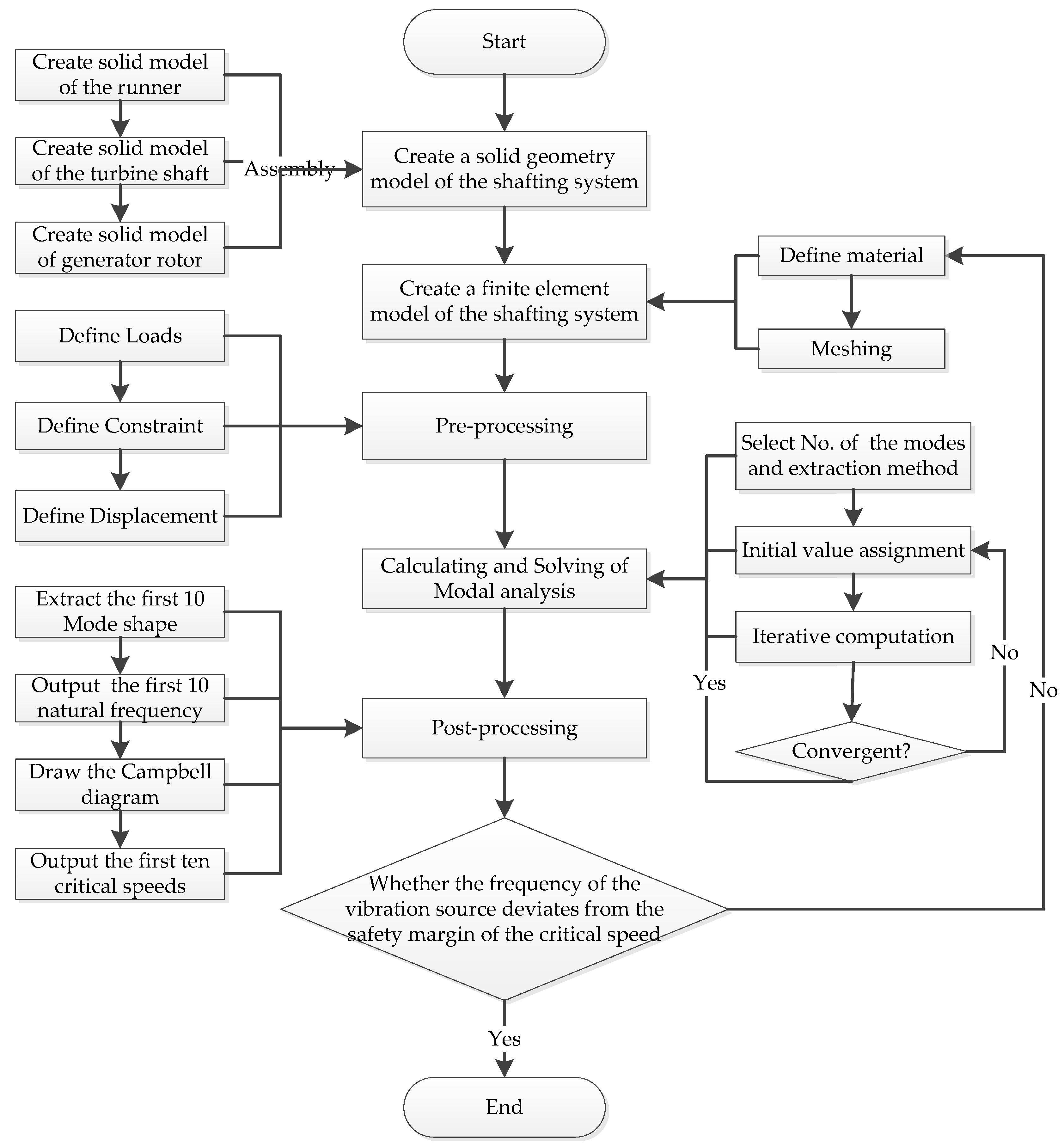
2.3. Predictive Analysis Steps and Processes
2.3.1. Establishing the Solid Geometric Model of the Shaft System
2.3.2. Establishing a Finite Element Calculation Model
2.3.3. Pre-Processing
2.3.4. Calculating and Solving
2.3.5. Post-Processing
3. Case Study
3.1. Basic Parameters of Hydraulic-Turbine Generator Unit
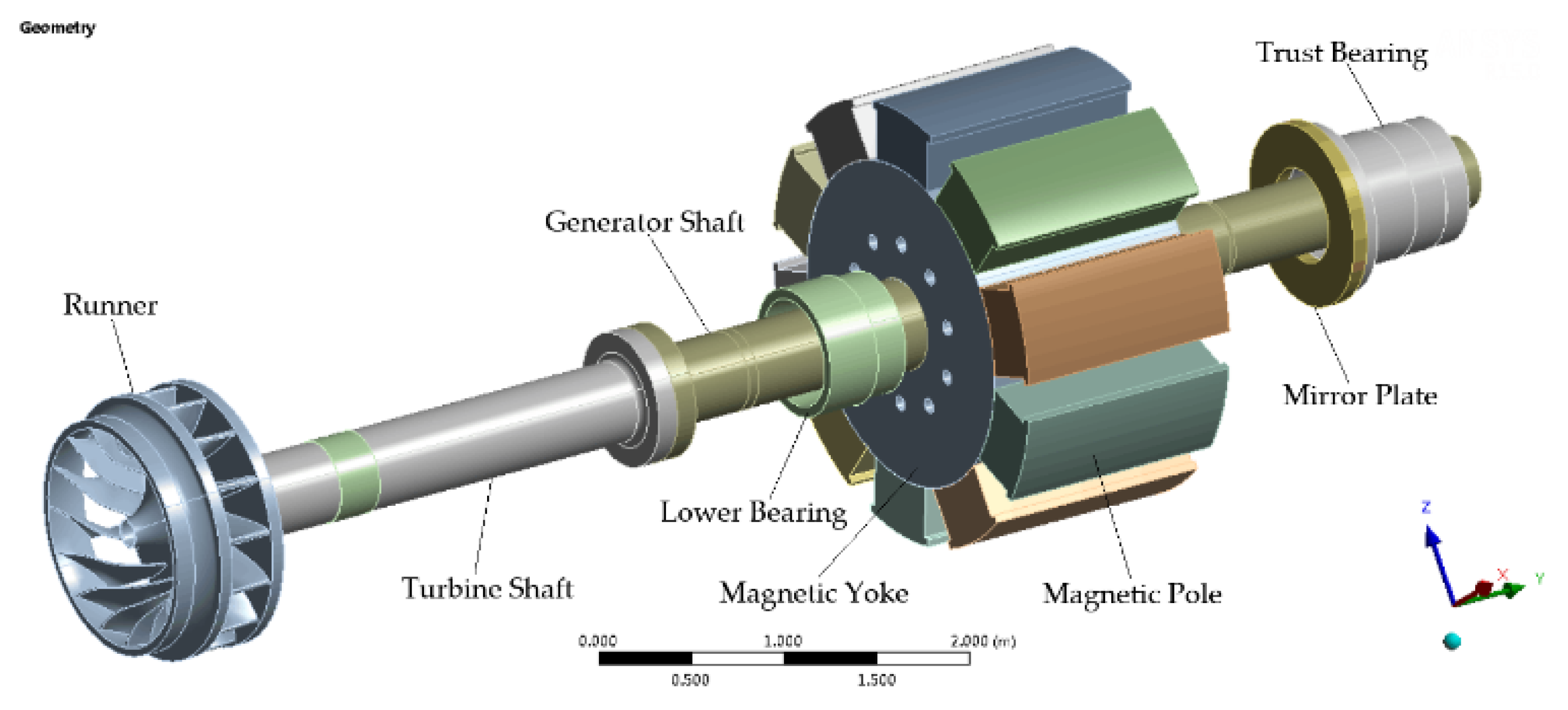
3.2. Shafting Composition and Geometric Dimensions
3.3. Material Properties of Shaft Components
3.4. Shafting’s Solid Geometry Modeling
4. Result and Analysis
4.1. Material Defining and Meshing
4.2. Boundary Conditions and Calculation Settings
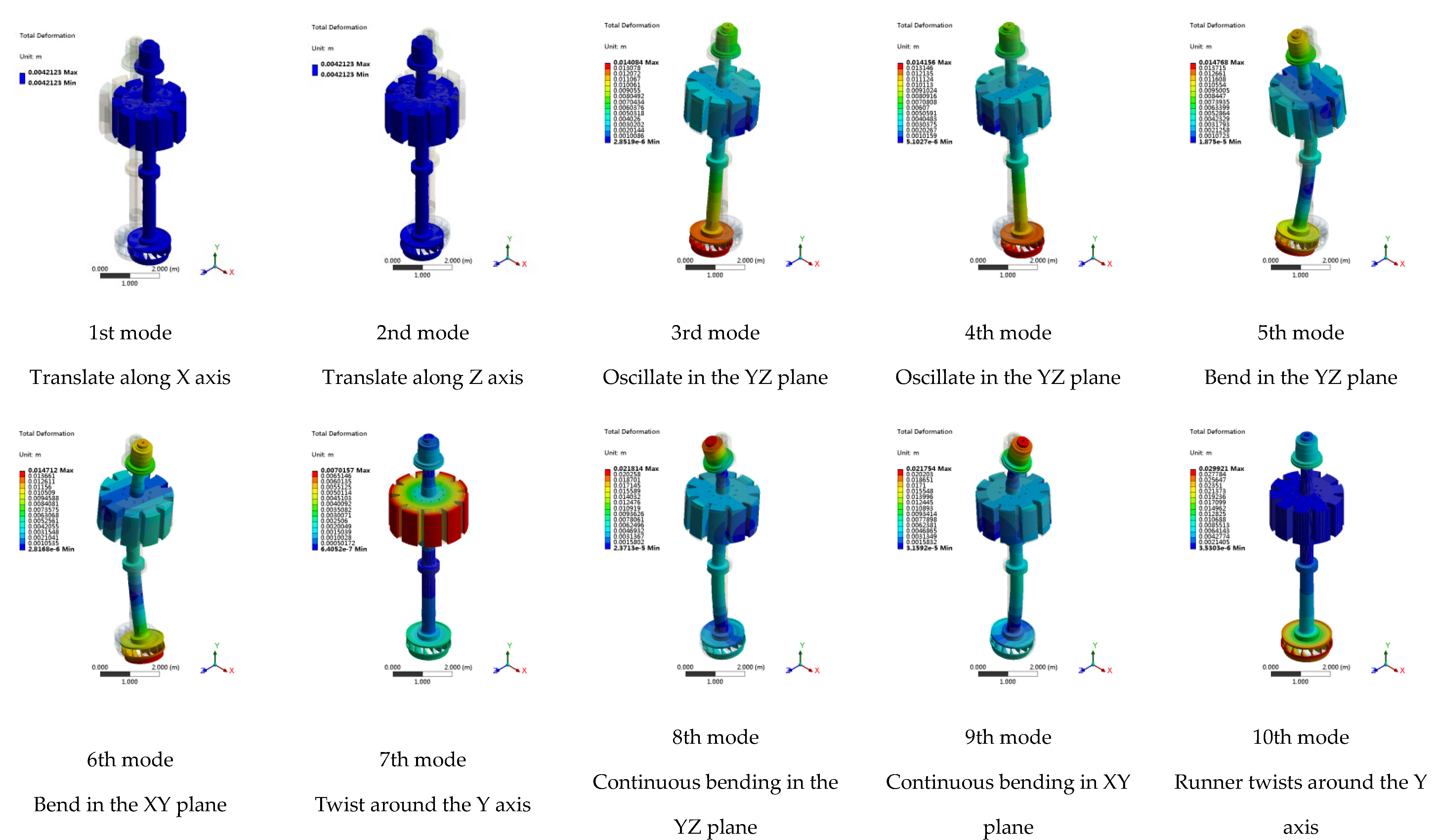
4.3. The First Ten-Order Mode Shapes
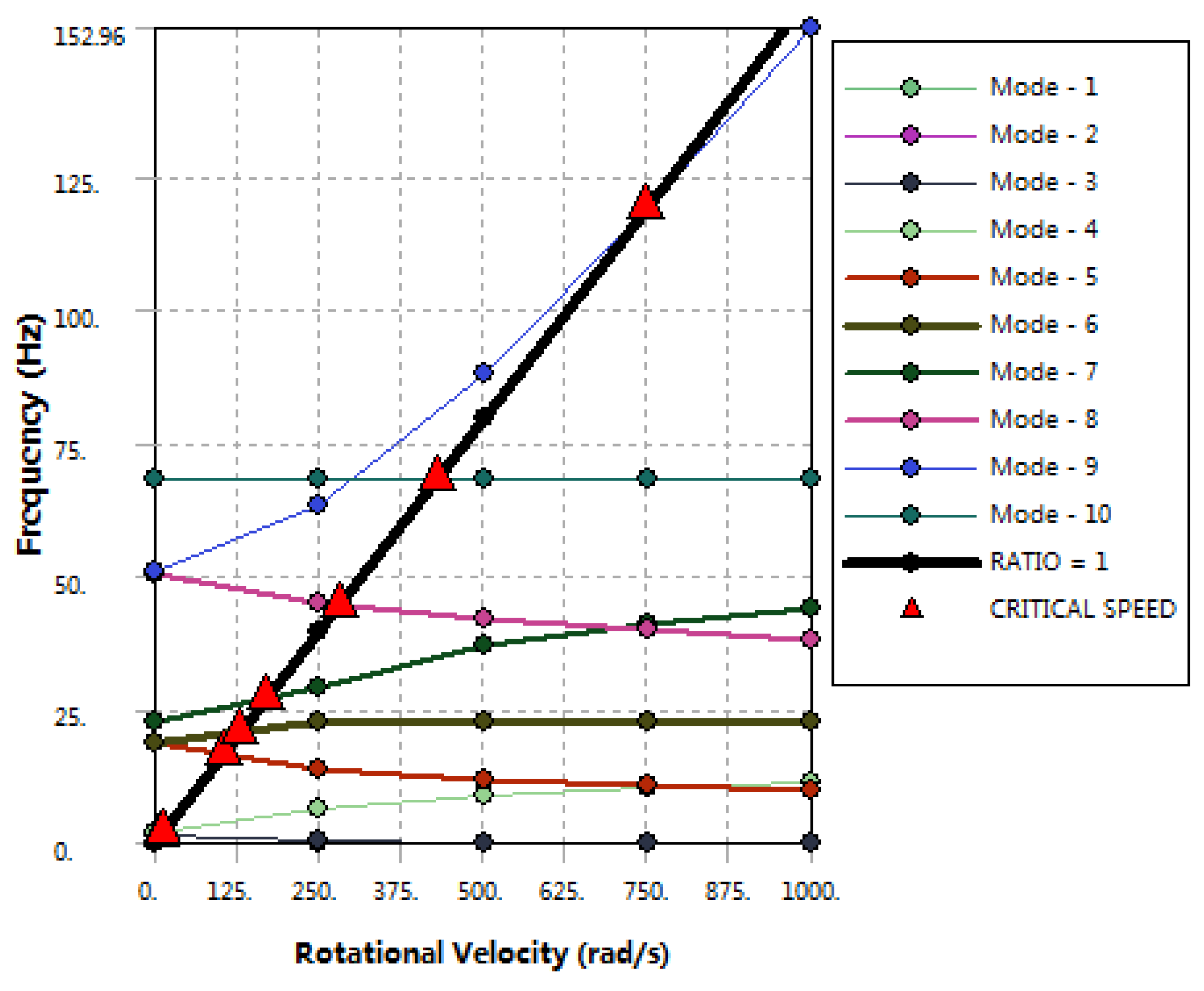
4.4. The First Ten Order Natural Frequency and Critical Speed
5. Conclusions
- (1)
- The mode shapes of the shaft system from low order to high order is a process of change from simple to complex, and generally represent a certain change law starting from translation, swing, bending, and torsion, to complex continuous bending and torsion. The higher the mode order, the more complex the bending and torsional deformation of the shafting.
- (2)
- In practical engineering testing, only the elastic mode of the shaft structure is usually considered, while the rigid body mode is ignored. In this paper, the rigid body mode of the shaft system is restored through numerical calculation, which can completely describe the modal characteristics of the shaft system in theory.
- (3)
- Through the analysis of the critical speed, it can be discovered that the shaft system of the studied case could not cause resonance due to the rotational frequency when it operates at the rated speed, but when the Unit has a runaway accident, there would be a possibility of resonance caused by the rotational frequency.
- (4)
- In view of the structural design of the shaft system, some measures for structural optimization design are proposed by means of this predictive analysis method: one is increasing the stiffness of the shaft system, thereby increasing the critical speed, and making the runaway speed lower than the first-order critical speed and maintaining a certain safety margin. The other is improving the mass distribution of the shafting structure to make it more balanced.
6. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Y. Dynamic Modeling and Simulation Analysis of Shafting System of Large-Scale Hydro-Generator Set. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2012. [Google Scholar]
- Peng, X.L. Research on Vibration Characteristics of Hydroelectric Units Based on Hydroelectric Multifield Coupling Finite Element Method. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2018. [Google Scholar]
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.Q.; Ma, Z.Y. Coupling Vibration Test and Finite Element Numerical Feedback Calculation of Unit and Powerhouse of Hydropower Station. J. Hydroelectr. Eng. 2012, 31, 170–174. [Google Scholar]
- Xu, W.; Ma, Z.Y. Study of the Vibration Transmission and Path Recognition of an Underground Powerhouse Using Energy Finite Element Method. Shock. Vib. 2016, 2016, 5039578. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Solovyeva, E.P. Mathematical modeling of vibrations in turbogenerator sets of Sayano-Shushenskaya Hydroelectric Power Station. Dokl. Phys. 2016, 61, 55–60. [Google Scholar] [CrossRef]
- Qu, L.T.; Zhou, Y. Research on Typical Rotor Dynamics Problems of Hydrogenerator Sets. Large Electr. Mach. Hydraul. Turbine 2020, 2020, 24–28. [Google Scholar]
- Liang, X.D. Research on Operation Stability of Large-scale Hydro-generator Units. Mech. Electr. Inf. 2016, 2016, 27–28. [Google Scholar]
- Zheng, Z.L.; Xie, Y.G.; Zhang, D.; Ye, X.L. Effects of Stator Stiffness, Gap Size, Unbalance, and Shaft’s Asymmetry on the Steady-State Response and Stability Range of an Asymmetric Rotor with Rub-Impact. Shock. Vib. 2019, 8, 1–11. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Peng, X.L.; Peng, X.L.; Li, R.H.; Xu, Y.H.; Liu, H.; Chen, D.Y. Experimental and Finite Element Analysis to Investigate the Vibration of Oblique-Stud Stator Frame in a Large Hydropower Generator Unit. Energies 2017, 10, 2175. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Zhang, H.; Li, C.H.; Zhou, J.Z. Shaft mis-alignment induced vibration of a hydraulic turbine generating system considering parametric uncertainties. J. Sound Vib. 2018, 435, 74–90. [Google Scholar] [CrossRef]
- Dal, A.; Karaçay, T. Effects of angular misalignment on the performance of rotor-bearing systems supported by externally pressurized air bearing. Tribol. Int. 2017, 111, 276–288. [Google Scholar] [CrossRef]
- Bai, B.; Zhang, L.X.; Zhao, L. Influence of guide bearing stiffness on natural vibration characteristics of turbine shafting. Chinese Journal of Drainage and Irrigation Machinery. J. Drain. Irrig. Mach. Eng. 2013, 31, 318–324. [Google Scholar]
- Xu, B.B.; Luo, X.Q.; Egusquiza, M.; Ye, W.; Liu, J.; Egusquiza, E. Nonlinear modal interaction analysis and vibration characteristics of a francis hydro-turbine generator unit. Renew. Energy 2021, 168, 854–864. [Google Scholar] [CrossRef]
- Paturu, P.; Vinoth Kanna, I.; Mallela, G. A detailed analysis of free vibration on 70 MW hydro power turbine rotor. Int. J. Ambient. Energy 2019, 42, 880–887. [Google Scholar] [CrossRef]
- Sun, W.Q.; Guo, Z.Q. Mathematical modeling and nonlinear vibration analysis of a coupled hydro-generator shaft-foundation system. Commun. Nonlinear Sci. Numer. Simul. 2021, 98, 105776. [Google Scholar] [CrossRef]
- Li, M.M.; Li, Z.; Ma, L.L.; Zhu, R.P.; Ma, X.Z. Effect of the Supports’ Positions on the Vibration Characteristics of a Flexible Rotor Shafting. Shock. Vib. 2020, 2020, 1592794. [Google Scholar] [CrossRef]
- Zhuang, K.Y.; Gao, C.D.; Li, Z.; Yan, D.L.; Fu, X.Q. Dynamic Analyses of the Hydro-Turbine Generator Shafting System Considering the Hydraulic Instability. Energies 2018, 11, 2862. [Google Scholar] [CrossRef]
- Wang, J.; Song, Z.Q.; Liu, Y.J. Analysis of Shaft System Vibration of Hydroelectric Unit Based on Reasonable Application of Hydraulic Vibration Source. J. Water Resour. Water Eng. 2018, 29, 188–195. [Google Scholar]
- Song, Z.Q.; Liu, Y.H.; Guo, P.C.; Feng, J.J. Torsional Vibration Analysis of Hydro-Generator Set Considered Electromagnetic and Hydraulic Vibration Resources Coupling. Int. J. Precis. Eng. Manuf. 2018, 19, 939–945. [Google Scholar] [CrossRef]
- Ma, H.; Wang, X.L.; Niu, H.Q.; Wen, B.C. Oil-film instability simulation in an overhung rotor system with flexible coupling misalignment. Arch. Appl. Mech. 2015, 85, 893–907. [Google Scholar] [CrossRef]
- Kim, J.W.; Kwak, W.I.; Choe, B.S.; Kim, H.H.; Suh, S.H.; Lee, Y.B. The rotor dynamic analysis of the vibration considering the hydro-electric force supported by rolling elements in 500 kW Francis turbine. J. Mech. Sci. Technol. 2017, 31, 5153–5159. [Google Scholar] [CrossRef]
- Keller, S.; Xuan, M.T.; Simond, J.J.; Schwery, A. Large low-speed hydro-generators–unbalanced magnetic pulls and additional damper losses in eccentricity conditions. IET Electr. Power Appl. 2007, 1, 657–664. [Google Scholar] [CrossRef]
- Zarko, D.; Ban, D.; Vazdar, I.; Jarica, V. Calculation of Unbalanced Magnetic Pull in a Salient-Pole Synchronous Generator Using Finite-Element Method and Measured Shaft Orbit. IEEE Trans. Ind. Electron. 2012, 59, 2536–2549. [Google Scholar] [CrossRef]
- Xu, X.P.; Han, Q.K.; Chu, F.L. Nonlinear vibration of a generator rotor with unbalanced magnetic pull considering both dynamic and static eccentricities. Arch. Appl. Mech. 2016, 86, 1521–1536. [Google Scholar] [CrossRef]
- He, Y.L.; Sun, Y.X.; Xu, M.X.; Wang, X.L.; Wu, Y.C.; Vakil, G.; Gerada, D.; Gerada, C. Rotor UMP characteristics and vibration properties in synchronous generator due to 3D static air-gap eccentricity faults. IET Electr. Power Appl. 2020, 14, 961–971. [Google Scholar] [CrossRef]
- Mahdi, K.; Korosh, K.; Rossana, D.; Francesco, T. Size-dependent hydroelastic vibration of FG microplates partially in contact with a fluid. Compos. Struct. 2020, 244, 112320. [Google Scholar]
- Lai, X.D.; Zhu, Y.; Liao, G.L.; Zhang, X.; Wang, T.; Zhang, W.B. Lateral Vibration Response Analysis on Shaft System of Hydro Turbine Generator Unit. Adv. Vib. Eng. 2013, 12, 511–524. [Google Scholar]
- Li, R.H.; Li, C.S.; Peng, X.L.; Wei, W. Electromagnetic Vibration Simulation of a 250-MW Large Hydropower Generator with Rotor Eccentricity and Rotor Deformation. Energies 2017, 10, 2155. [Google Scholar] [CrossRef] [Green Version]
- Song, Z.Q.; Ma, Z.Y. Torsional vibration analysis of shaft system of hydroelectric unit considering hydraulic and electromagnetic excitation. J. Hydroelectr. Eng. 2012, 31, 240–245. [Google Scholar]
- Bai, B.; Zhang, L.X.; Guo, T.; Liu, C.Q. Analysis of dynamic characteristics of the main shaft system in a hydro-turbine based on ANSYS. Procedia Eng. 2012, 31, 654–658. [Google Scholar] [CrossRef]
- Zhu, C.X.; Wang, D.Y.; Zhu, C.Q.; Wang, X.W. Comparative analysis of transfer matrix method and finite element method to calculate the critical speed of motor rotor. Electr. Mach. Control. Appl. 2015, 2015, 57–60. [Google Scholar]
- Zhou, W.J.; Wei, X.S.; Wu, G.K.; Liu, W.J.; Wang, L.Q. Numerical research on dynamic lateral vibration of a pump-turbine’s shaft system. J. Eng. Res. 2015, 3, 127–148. [Google Scholar] [CrossRef]
- Niu, L.T.; Su, Q.; Ma, C.Y.; Liao, J.L.; Pu, J.G. Research on Modal Analysis of Rotor Shaft System of Hydro-generator. J. Phys. Conf. Ser. 2020, 1549, 042084. [Google Scholar] [CrossRef]
- Yang, G.B.; Zeng, Y.; Zhang, J.K.; Wang, F.F.; Zhang, Z.K.; Qian, J. Approximate calculation method for shafting stiffness of hydro-generator set. J. Drain. Irrig. Mach. Eng. 2020, 38, 787–793. [Google Scholar]
- Yang, G.B.; Zeng, Y.; Zhang, J.K. Modal analysis of eccentric shaft system of hydro-generator rotor based on finite element method. Water Resour. Power 2019, 37, 119, 136–138. [Google Scholar]
- Huang, Z.H.; Xie, Y.; Deng, Y.; Gao, H.W. Shafting Modal Analysis of Hybrid Excavator Power System. Constr. Mach. Equip. 2012, 43, 25–28. [Google Scholar]
- Knight, J.D.; Plaut, R.H.; Virgin, L.N. A New Method for Predicting Critical Speeds in Rotor dynamics. J. Eng. Gas Turbines Power 2016, 138, 022504. [Google Scholar]
- Murav’ev, O.A. Torsional Vibrations of the Rotating Parts of a Hydroelectric Generating Set in Transient Processes of Hydroelectric Power Plants. Power Technol. Eng. 2019, 52, 548–551. [Google Scholar] [CrossRef]

| Hydro-Turbine | Generator | ||
|---|---|---|---|
| Type | Francis | Rated power | 20,265 kw |
| Rated water head | 181.26 m | Rated voltage | 10,600 V |
| Rated flow rate | 12.5 m3/s | Rated current | 1298.6 A |
| Rated power | 20,892 kW | Rated frequency | 50 Hz |
| Runner diameter | 1430 mm | Rated rotational speed | 600 r/min |
| Moment of inertia | ≥110 ton∙m2 | Runaway speed | 1064 r/min |
| Shafting System | Parts | Dimension | Unit |
|---|---|---|---|
| Generator rotor | Rotor height | 5342 | mm |
| Rotor diameter | 2510 | mm | |
| Trust bearing height | 770 | mm | |
| No. of Magnetic pole | 10 | Pcs. | |
| Turbine shaft | Height | 2805 | mm |
| Runner | Runner diameter | 1430 | mm |
| Runner height | 625 | mm | |
| No. of Blade | 15 | Pcs. |
| Main Parts | Material | Elastic Modulus (MPa) | Poisson’s Ratio | Density (kg/m3) |
|---|---|---|---|---|
| Runner | Stainless Steel (06Cr13Ni4Mo) | 210,000 | 0.3 | 7.90 × 103 |
| Shaft | Forged steel (45A) | 209,000 | 0.269 | 7.89 × 103 |
| Magnetic yoke | Forged steel (45A) | 209,000 | 0.269 | 7.89 × 103 |
| Magnetic pole | Various materials (use Copper instead) | 110,000 | 0.32 | 8.85 × 103 |
| Thrust bearing | Casting steel (ZG270-500) | 202,000 | 0.3 | 7.80 × 103 |
| Mirror plate | Forged steel (45A) | 209,000 | 0.269 | 7.89 × 103 |
| Computational Domain | Physical Characteristics | Mesh | |||
|---|---|---|---|---|---|
| X-axis | 2.4830 m | Volume | 7.1741 m³ | Components | 19 |
| Y-axis | 8.7600 m | Weight | 56,362 kg | Nodes | 59,022 |
| Z-axis | 2.4926 m | Scale | 1:1 | Elements | 28,879 |
| Rotational Velocity | X (rad/s) | Y(rad/s) | Z (rad/s) |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 250 | 0 |
| 3 | 0 | 500 | 0 |
| 4 | 0 | 750 | 0 |
| 5 | 0 | 1000 | 0 |
| Mode | Critical Speed | 0 rad/s | 250 rad/s | 500 rad/s | 750 rad/s | 1000 rad/s |
|---|---|---|---|---|---|---|
| 1 | NONE | 0 Hz | 0 Hz | 0 Hz | 0 Hz | 0 Hz |
| 2 | NONE | 2.2 × 10−4 Hz | 2.2 × 10−4 Hz | 2.223 × 10−4 Hz | 2.2 × 10−4 Hz | 2.2 × 10−4 Hz |
| 3 | 9.359 rad/s | 1.5345 Hz | 0.33331 Hz | 0.17165 Hz | 0.1151 Hz | 8.6498 × 10−2 Hz |
| 4 | 13.257 rad/s | 1.8555 Hz | 6.6546 Hz | 9.1421 Hz | 10.485 Hz | 11.458 Hz |
| 5 | 104.45 rad/s | 18.669 Hz | 13.774 Hz | 11.866 Hz | 10.795 Hz | 10.033 Hz |
| 6 | 130.21 rad/s | 18.754 Hz | 22.536 Hz | 22.536 Hz | 22.536 Hz | 22.536 Hz |
| 7 | 169.81 rad/s | 22.536 Hz | 29.146 Hz | 36.915 Hz | 41.121 Hz | 43.9 Hz |
| 8 | 281.48 rad/s | 50.433 Hz | 45.178 Hz | 42.163 Hz | 39.947 Hz | 38.233 Hz |
| 9 | 748.44 rad/s | 50.796 Hz | 63.473 Hz | 88.105 Hz | 119.31 Hz | 152.96 Hz |
| 10 | 428.76 rad/s | 68.237 Hz | 68.24 Hz | 68.238 Hz | 68.244 Hz | 68.251 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Shang, Y.; Yao, Z. A Predictive Analysis Method of Shafting Vibration for the Hydraulic-Turbine Generator Unit. Water 2022, 14, 2714. https://doi.org/10.3390/w14172714
Wang W, Shang Y, Yao Z. A Predictive Analysis Method of Shafting Vibration for the Hydraulic-Turbine Generator Unit. Water. 2022; 14(17):2714. https://doi.org/10.3390/w14172714
Chicago/Turabian StyleWang, Wuchang, Yizi Shang, and Zhifeng Yao. 2022. "A Predictive Analysis Method of Shafting Vibration for the Hydraulic-Turbine Generator Unit" Water 14, no. 17: 2714. https://doi.org/10.3390/w14172714
APA StyleWang, W., Shang, Y., & Yao, Z. (2022). A Predictive Analysis Method of Shafting Vibration for the Hydraulic-Turbine Generator Unit. Water, 14(17), 2714. https://doi.org/10.3390/w14172714







