Dynamic Change Characteristics of Soil Moisture and Its Relationship with Precipitation in Hani Rice Terraces Water Source Area
Abstract
:1. Introduction
2. Methodology
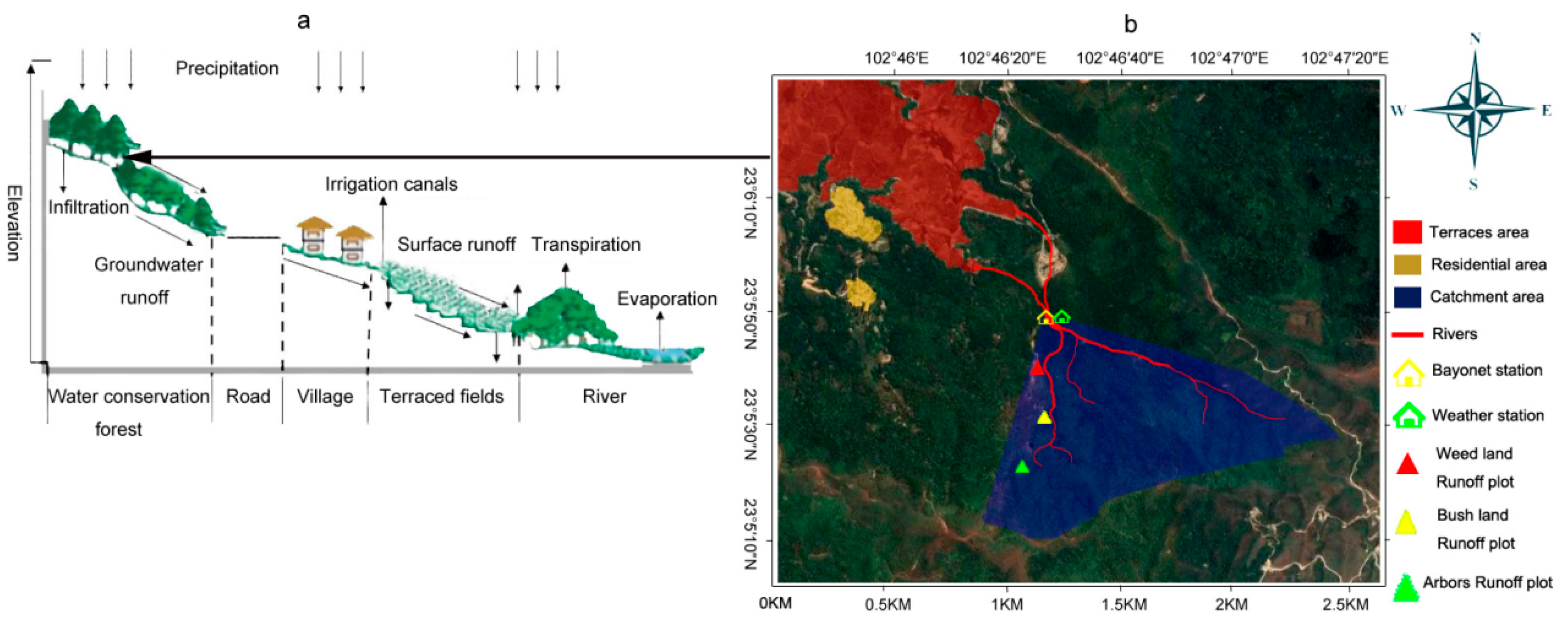
2.1. Study Area
2.2. Data Collection
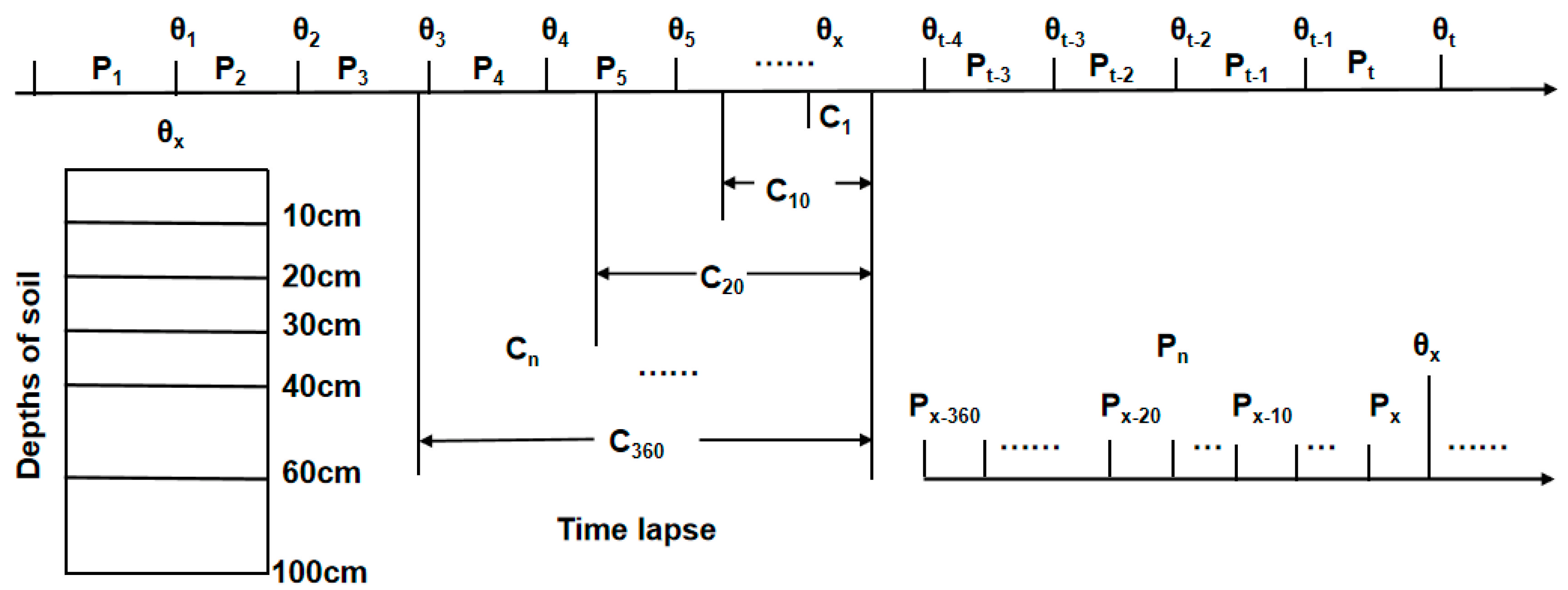
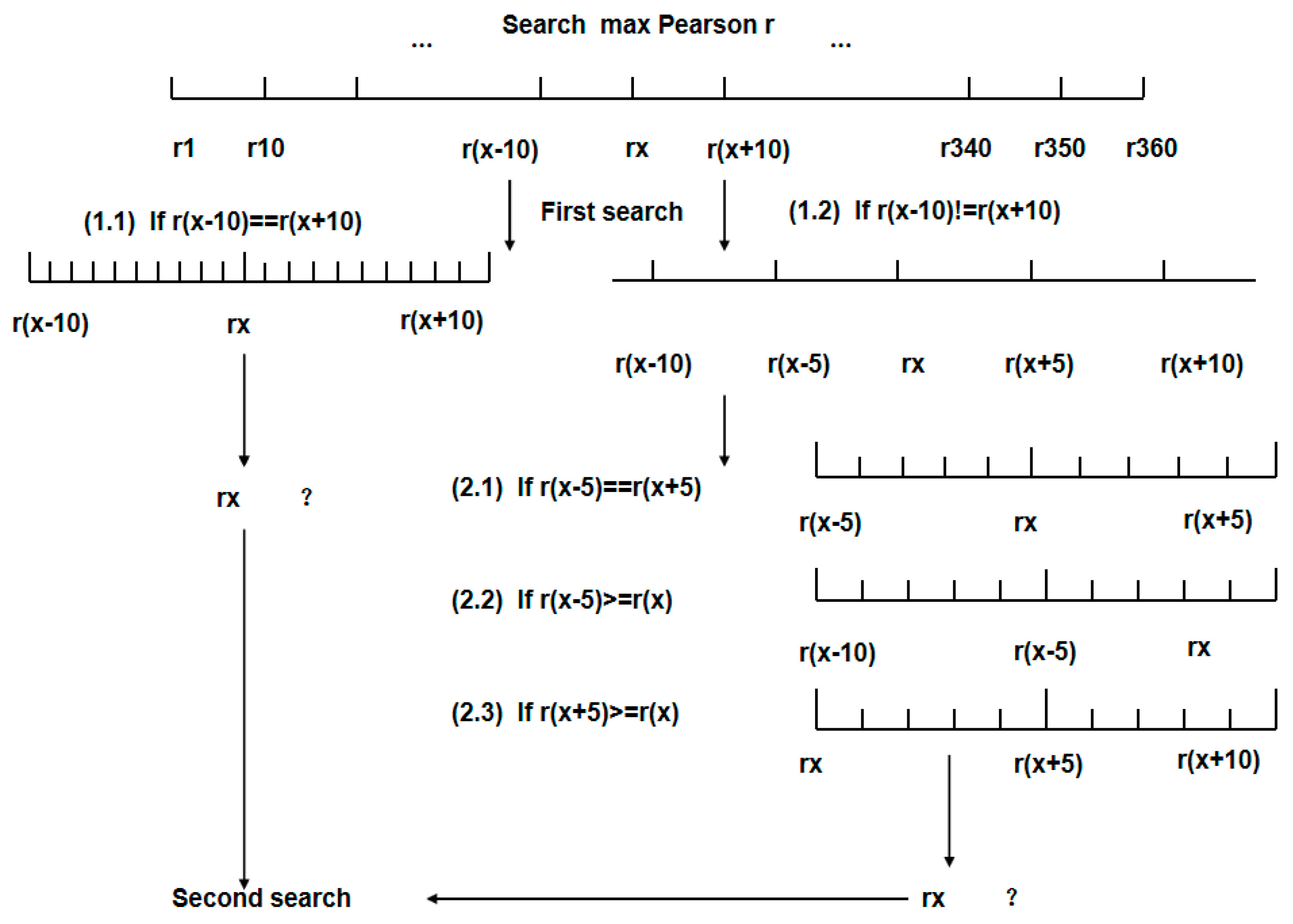
2.3. Methods
3. Results
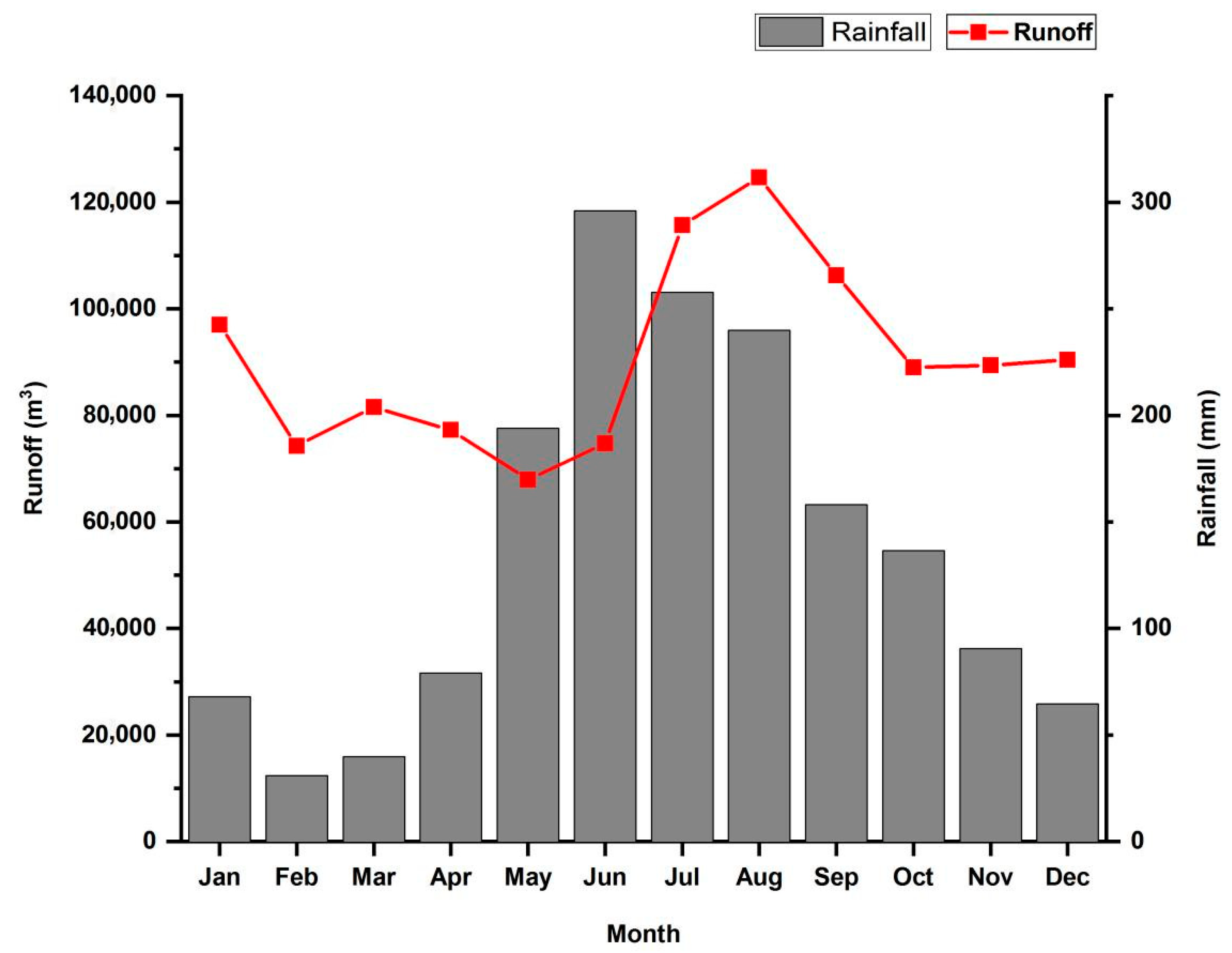
3.1. Monthly Variations of Precipitation and Runoff
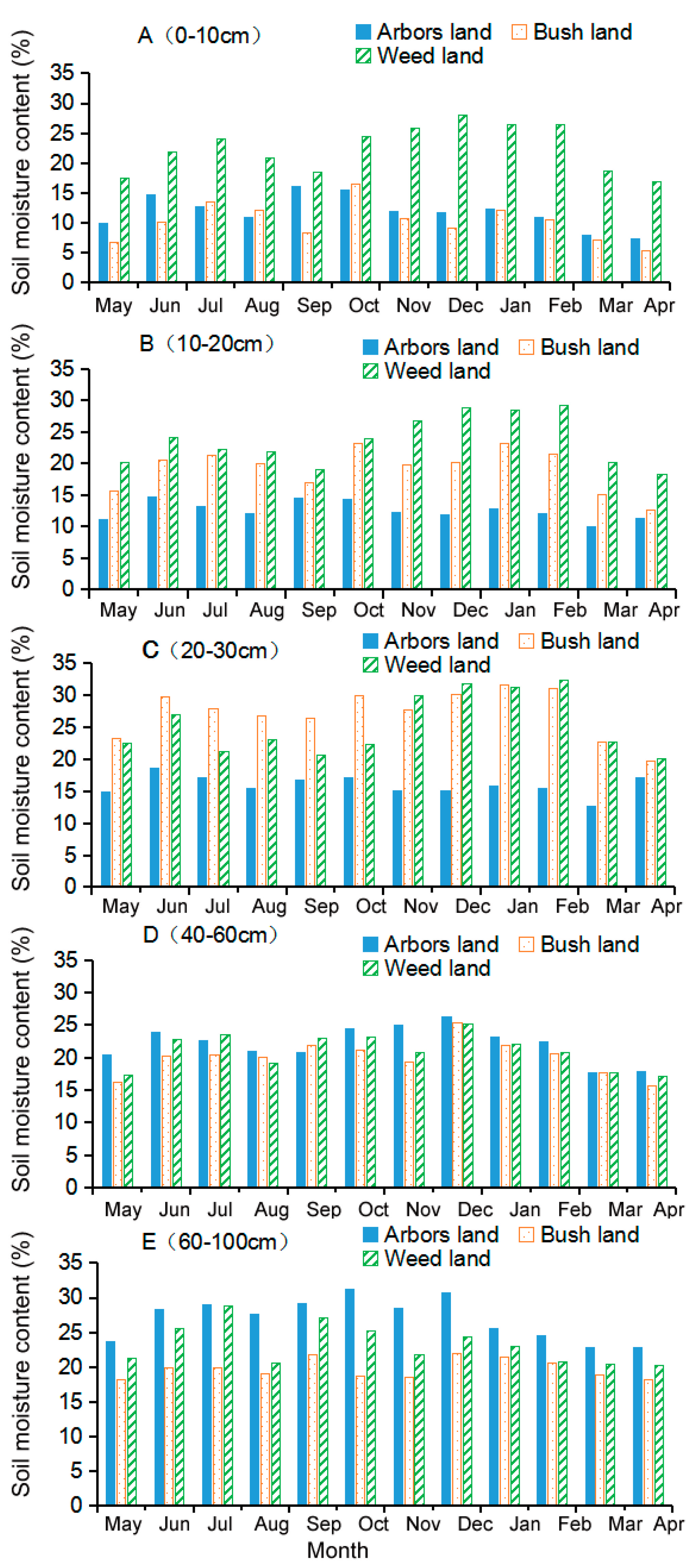
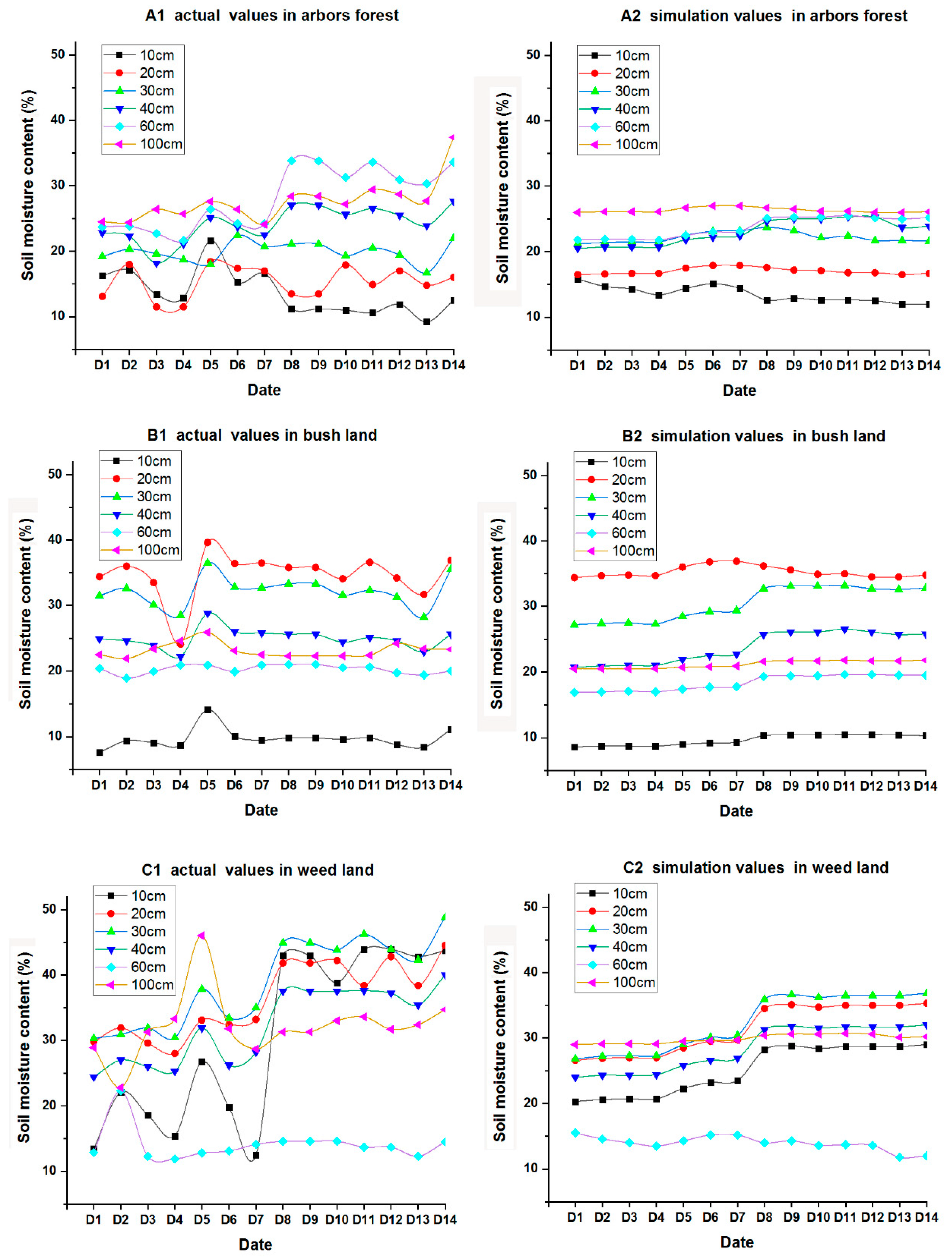
3.2. The Dynamic Characteristics of soil Moisture
- (1)
- On the daily scale: SMC of each layer was different in the 0–100 cm depth of layers in three site types: The highest SMC in arbors forest land occurred at 100 cm, but the highest SMC for both bush and weed land occurred at 20 cm; the lowest SMC occurred at 10 cm in arbors forest land, at 100 cm in bush land, and at 40 cm in weed land.
- (2)
- On the monthly scale (Figure 6): The SMC of the forest land increased with depth within the 0–100 cm depth range, and reached the maximum value between 60–100 cm, which indicated that the root system of the forest land was deeper than that of bush land. Compared with that of weed and bush land, forest land had stronger water and soil retention in the 60–100 cm soil depth layer. The SMC was almost the same in three different site types in the range of 40–60 cm. The greatest value of soil water retention occurred in bush land and weed land in the range of 20–30 cm and 0–20 cm, respectively.
- (3)
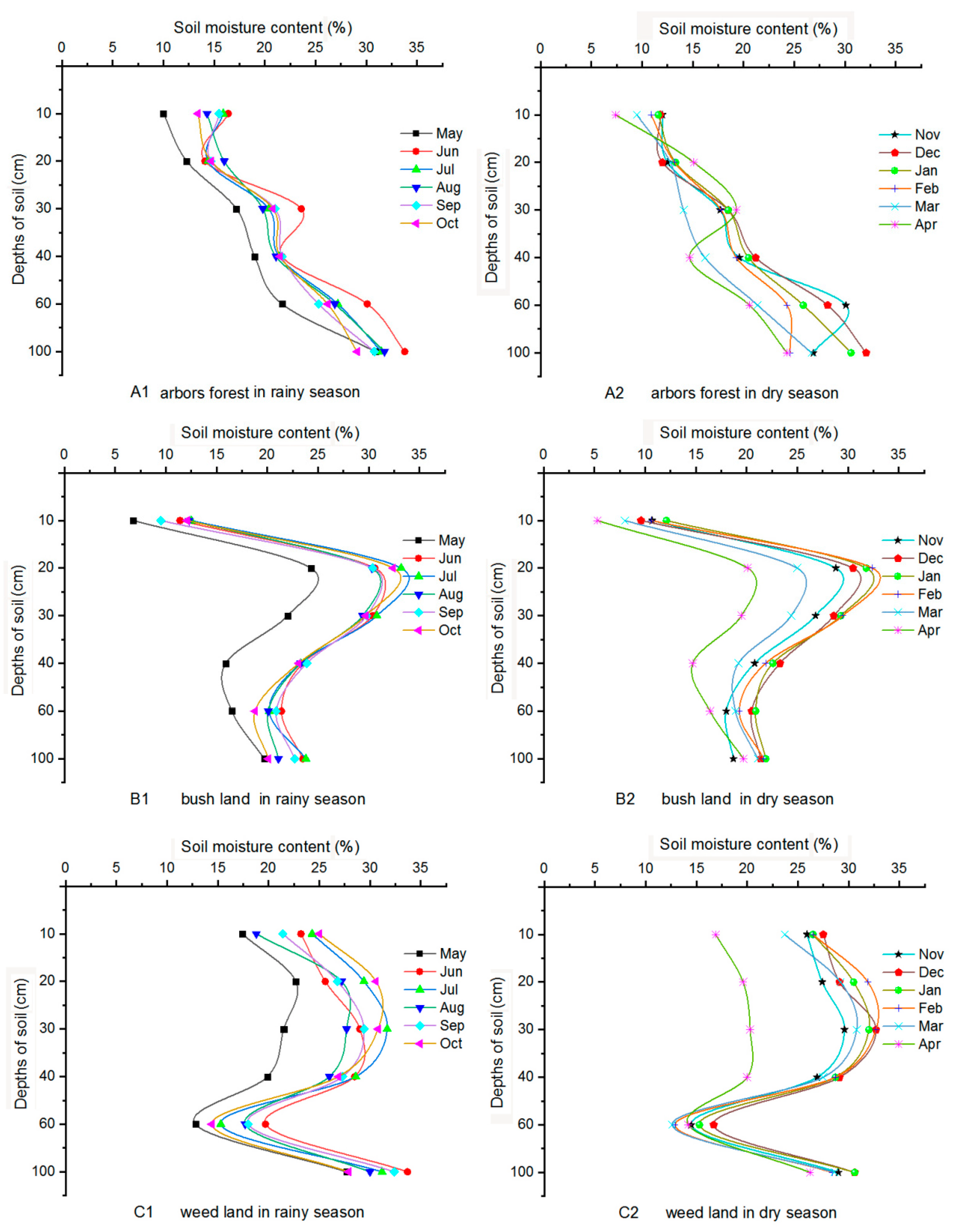
- On the seasonal scale (Figure 7): There were significant differences in SMC among the three different site types. The SMC in arbors forest land appeared as a linear curve in the rainy and dry seasons. The SMC also increases as the depth increases. The SMC curves of bush land in the rainy and dry seasons were waveform in shallow soil layers and linear in deep soil layers. The SMC increased with soil depth and reached the maximum value at 20 cm, then gradually decreased to the minimum value at 40 cm. SMC tended to be stable at 40 cm to 100 cm. The SMC curves of weed land showed a circular shape from 10 cm to 60 cm and linearly increased after reaching the minimum value at 60 cm.
- (4)
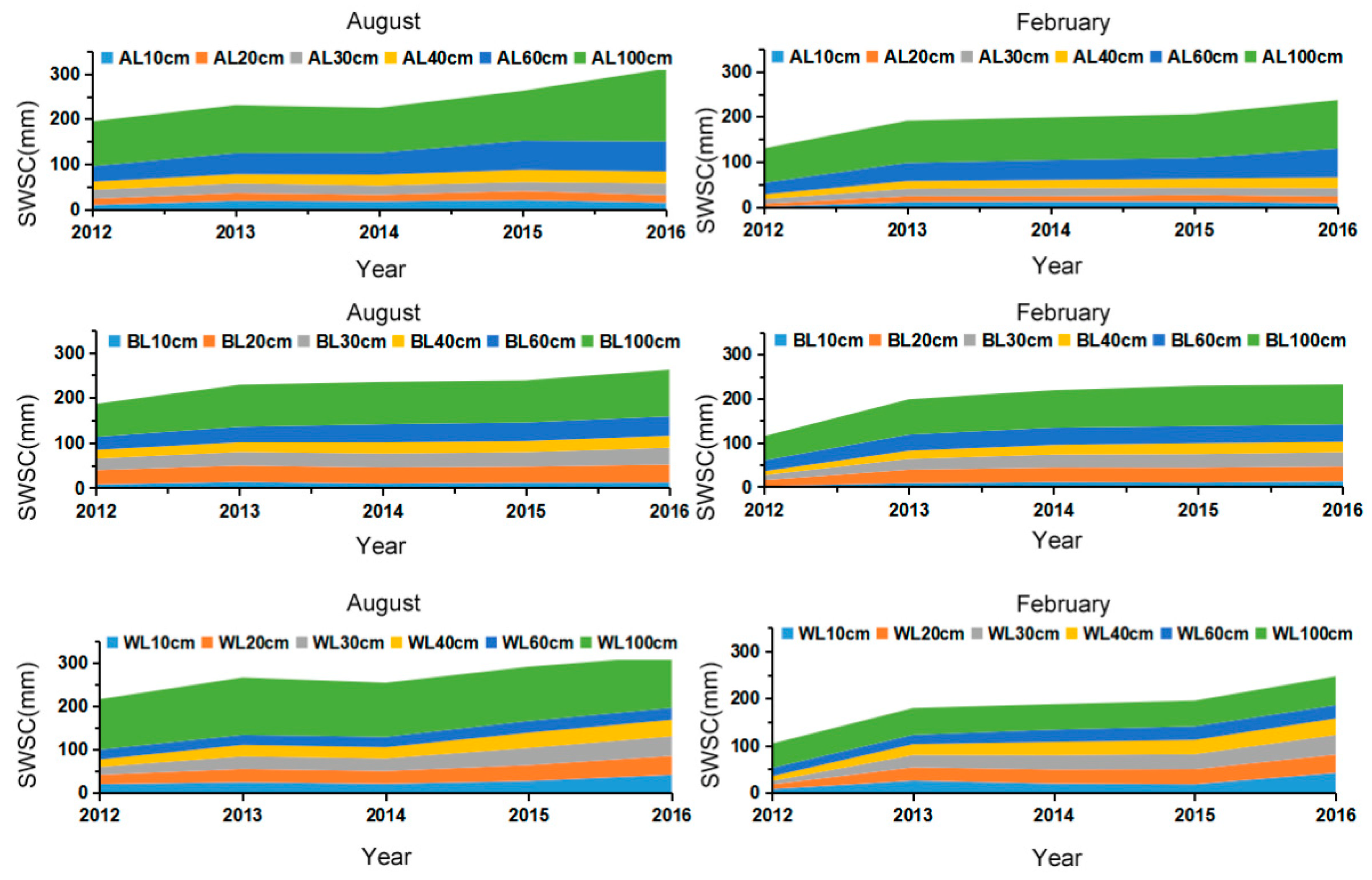
- On the annual scales (Figure 8): Soil water storage for all three stand types showed a steady increase over the five-year study period. The soil water storage in each layer of bush land was most stable. The boundary of them were clear and showed the mildest variation. The soil water storage was showed the greatest change in each layer of weed land. The weed land stored the most water in August, but the least in February. With increasing soil depth, the water storage capacity of arbors forest land becomes stronger.
3.3. The Relationship between Daily Precipitation and Soil Moisture Content
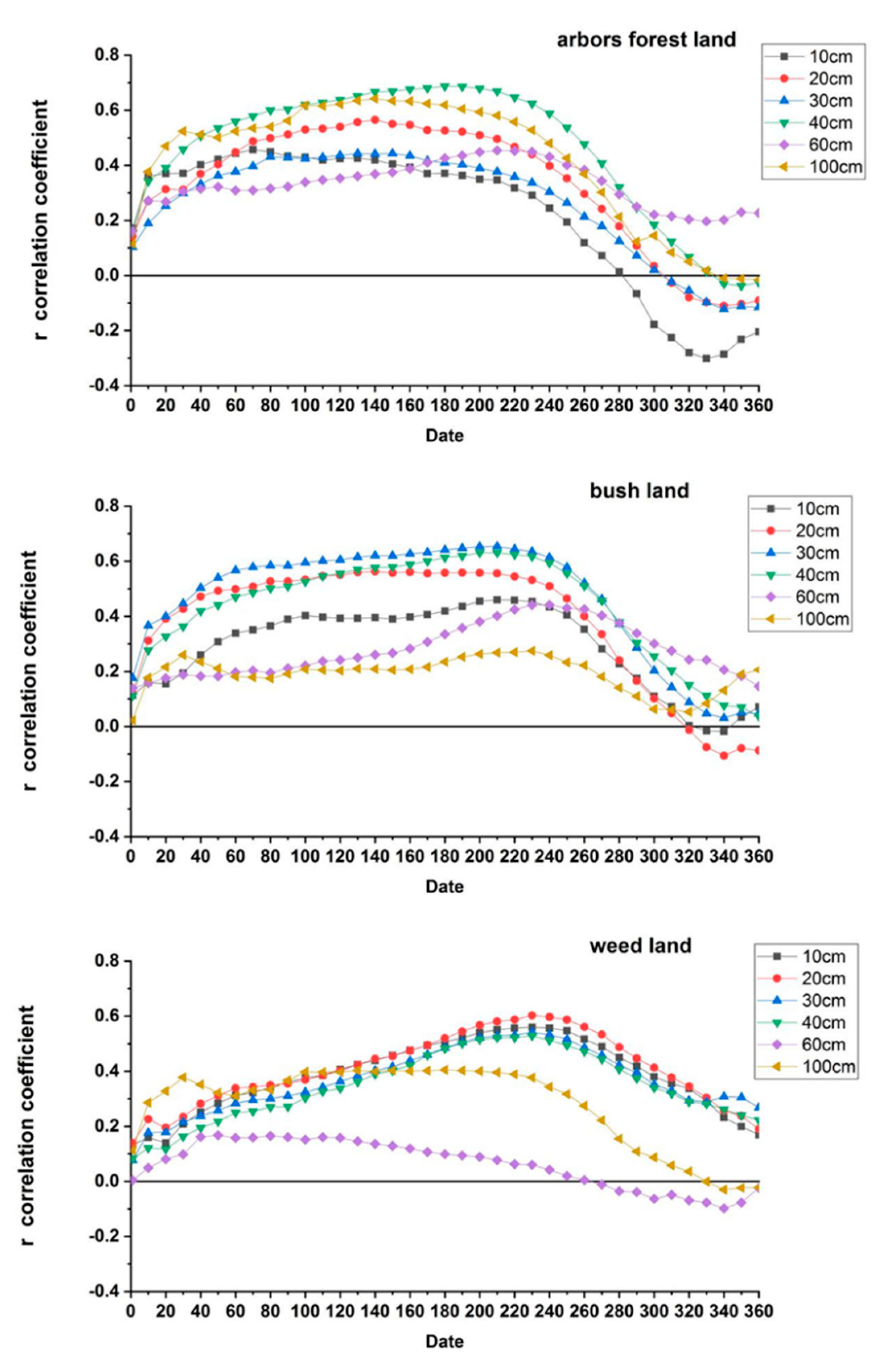
3.4. The Relationship between Accumulated Precipitation and Soil Moisture
3.5. Model Evaluation
4. Discussion
4.1. The Dynamic Characteristics of Soil Moisture
4.2. The Relationship between Daily Precipitation or Accumulated Precipitation and Soil Moisture
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, C.; Fu, B.; Zhang, L.; Xu, Z. Soil moisture–plant interactions: An ecohydrological review. J. Soils Sediments 2019, 19, 1–9. [Google Scholar] [CrossRef]
- Wang, C.; Wang, S.; Fu, B.; Zhang, L.; Lu, N.; Jiao, L. Stochastic soil moisture dynamic modelling: A case study in the Loess Plateau, China. Earth Environ. Sci. Trans. R. Soc. Edinb. 2018, 109, 437–444. [Google Scholar] [CrossRef]
- Zhang, P.; Xiao, P.; Yao, W.; Liu, G.; Sun, W. Profile distribution of soil moisture response to precipitation on the Pisha sandstone hillslopes of China. Sci. Rep. 2020, 10, 9136. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.F.; Zhu, X.; He, Z.B.; Du, J.; Chen, L.F. Research progress on soil moisture temporal stability. Acta Ecol. Sin. 2018, 38, 3403–3413. [Google Scholar]
- Robock, A.; Vinnikov, Y.K.; Srinivasan, G.; Entin, J.K.; Liu, S.; Namkhai, A. The Global Soil Moisture Data Bank. Bull. Am. Meteorol. Soc. 2000, 81, 1281–1299. [Google Scholar] [CrossRef]
- Shin, Y.; Mohanty, B.P.; Ines, A.V.M. Development of non-parametric evolutionary algorithm for predicting soil moisture dynamics. J. Hydrol. 2018, 564, 208–221. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, J.; Cheng, F.; Chen, Y. Soil Moisture by Remote Sensing Retrieval in the Tropic of Cancer of Yunnan Province. Pol. J. Environ. Stud. 2020, 29, 1981–1993. [Google Scholar] [CrossRef]
- Jia, Y.-H.; Shao, M.-A. Dynamics of deep soil moisture in response to vegetational restoration on the Loess Plateau of China. J. Hydrol. 2014, 519, 523–531. [Google Scholar] [CrossRef]
- Mulebeke, R.; Kironchi, G.; Tenywa, M.M. Soil moisture dynamics under different tillage practices in cassava–sorghum based cropping systems in eastern Uganda. Ecohydrol. Hydrobiol. 2013, 13, 22–30. [Google Scholar] [CrossRef]
- Ghajarnia, N.; Kalantari, Z.; Orth, R.; Destouni, G. Close co-variation between soil moisture and runoff emerging from multi-catchment data across Europe. Sci. Rep. 2020, 10, 4817. [Google Scholar] [CrossRef]
- Philip, J.R. Hillslope infiltration: Planar slopes. Water Resour. Res. 1991, 1, 109–117. [Google Scholar] [CrossRef]
- Yu, Z.; Carlson, T.N.; Barron, E.J.; Schwartz, F.W. On evaluating the spatial-temporal variation of soil moisture in the Susquehanna River Basin. Water Resour. Res. 2001, 37, 1313–1326. [Google Scholar] [CrossRef]
- Sun, L.; Yang, L.; Chen, L.; Li, S.; Zhao, F.; Sun, S. Tracing the soil water response to autumn precipitation in different land uses at multi-day timescale in a subtropical zone. Catena 2019, 180, 355–364. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Q.; Chao, L.; Ye, J.; Li, Z.; Yu, Z.; Yang, T.; Ju, Q. Ground observation-based analysis of soil moisture spatiotemporal variability across a humid to semi-humid transitional zone in China. J. Hydrol. 2019, 574, 903–914. [Google Scholar] [CrossRef]
- Hagen, K.; Berger, A.; Gartner, K.; Geitner, C.; Kofler, T.; Kogelbauer, I.; Kohl, B.; Markart, G.; Meißl, G.; Niedertscheider, K. Event-based dynamics of the soil water content at Alpine sites (Tyrol, Austria). Catena 2020, 194, 104682. [Google Scholar] [CrossRef]
- Zuo, Z.; Zhang, R. The spring soil moisture and the summer precipitation in eastern China. Chin. Sci. Bull. 2007, 52, 3310–3312. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.X.; Wang, H.Y.; Wang, J.; Sun, C.J. Dynamic response characteristics of soil moisture on slope cultivated land and abandoned land to different precipitation intensities in Loess hilly region. Acta Ecol. Sin. 2022, 42, 332–339. [Google Scholar] [CrossRef]
- Entekhabi, D.; Rodriguez-Iturbe, I. Analytical framework for the characterization of the space-time variability of soil moisture. Adv. Water Resour. Res. 1994, 17, 35–45. [Google Scholar] [CrossRef]
- Kirshner, S. Modeling of Multivariate Time Series Using Hidden Markov Models. Ph.D. Thesis, University of California, Irvine, CA, USA, 2005. [Google Scholar]
- Penna, D.; Borga, M.; Norbiato, D.; Dalla Fontana, G. Hillslope scale soil moisture variability in a steep alpine terrain. J. Hydrol. 2009, 364, 311–327. [Google Scholar] [CrossRef]
- Pan, F.; Nieswiadomy, M.; Qian, S. Application of a soil moisture diagnostic equation for estimating root-zone soil moisture in arid and semi-arid regions. J. Hydrol. 2015, 524, 296–310. [Google Scholar] [CrossRef]
- Kim, S. Time series modeling of soil moisture dynamics on a steep mountainous hillside. J. Hydrol. 2016, 536, 37–49. [Google Scholar] [CrossRef]
- Zhao, W.; Fang, X.; Daryanto, S.; Zhang, X.; Wang, Y. Factors influencing soil moisture in the Loess Plateau, China: A review. Earth Environ. Sci. Trans. R. Soc. Edinb. 2018, 109, 501–509. [Google Scholar] [CrossRef]
- Ma, J.; Song, W.; Wu, J.; Liu, Z.; Wei, Z. Identifying the mean residence time of soil water for different vegetation types in a water source area of the Yuanyang Terrace, southwestern China. Isot. Environ. Health Stud. 2019, 55, 272–289. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.-J.; Song, W.-F.; Wu, J.-K.; Wang, Z.-J. Charcteristics of Hydrogen and Oxygen Isotopes of Soil Water in the Water Source Area of Yuanyang Terrace. Environ. Sci. 2015, 36, 2102–2108. [Google Scholar]
- Jiao, Y.; Liu, C.; Gao, X.; Xu, Q.; Ding, Y.; Liu, Z. Impacts of moisture sources on the isotopic inverse altitude effect and amount of precipitation in the Hani Rice Terraces region of the Ailao Mountains. Sci. Total Environ. 2019, 687, 470–478. [Google Scholar] [CrossRef]
- Yao, M.; Cui, B.-S.; Cui, B.-S. The vertical characteristics of ecosystem of Hani terrace paddyfield in Yunnan, China. Ecol. Soc. China 2006, 26, 2115–2124. [Google Scholar]
- Jiao, Y.; Zhao, D.; Xu, Q.; Liu, Z.; Ding, Z.; Ding, Y.; Liu, C.; Zha, Z. Mapping lateral and longitudinal hydrological connectivity to identify conservation priority areas in the water-holding forest in Honghe Hani Rice Terraces World Heritage Site. Landsc. Ecol. 2020, 35, 709–725. [Google Scholar] [CrossRef]
- Yu, B.; Liu, G.; Liu, Q. Effects of land use changes for ecological restoration on soil moisture on the Chinese Loess Plateau: A meta-analytical approach. J. For. Res. 2018, 31, 443–452. [Google Scholar] [CrossRef]
- Huang, X.; Shi, Z.H.; Zhu, H.D.; Zhang, H.Y.; Ai, L.; Yin, W. Soil moisture dynamics within soil profiles and associated environmental controls. Catena 2016, 136, 189–196. [Google Scholar] [CrossRef]
- Yang, L.; Wei, W.; Chen, L.; Mo, B. Response of deep soil moisture to land use and afforestation in the semi-arid Loess Plateau, China. J. Hydrol. 2012, 475, 111–122. [Google Scholar] [CrossRef]
- Yang, L.; Wei, W.; Chen, L.; Chen, W.; Wang, J. Response of temporal variation of soil moisture to vegetation restoration in semi-arid Loess Plateau, China. Catena 2014, 115, 123–133. [Google Scholar] [CrossRef]
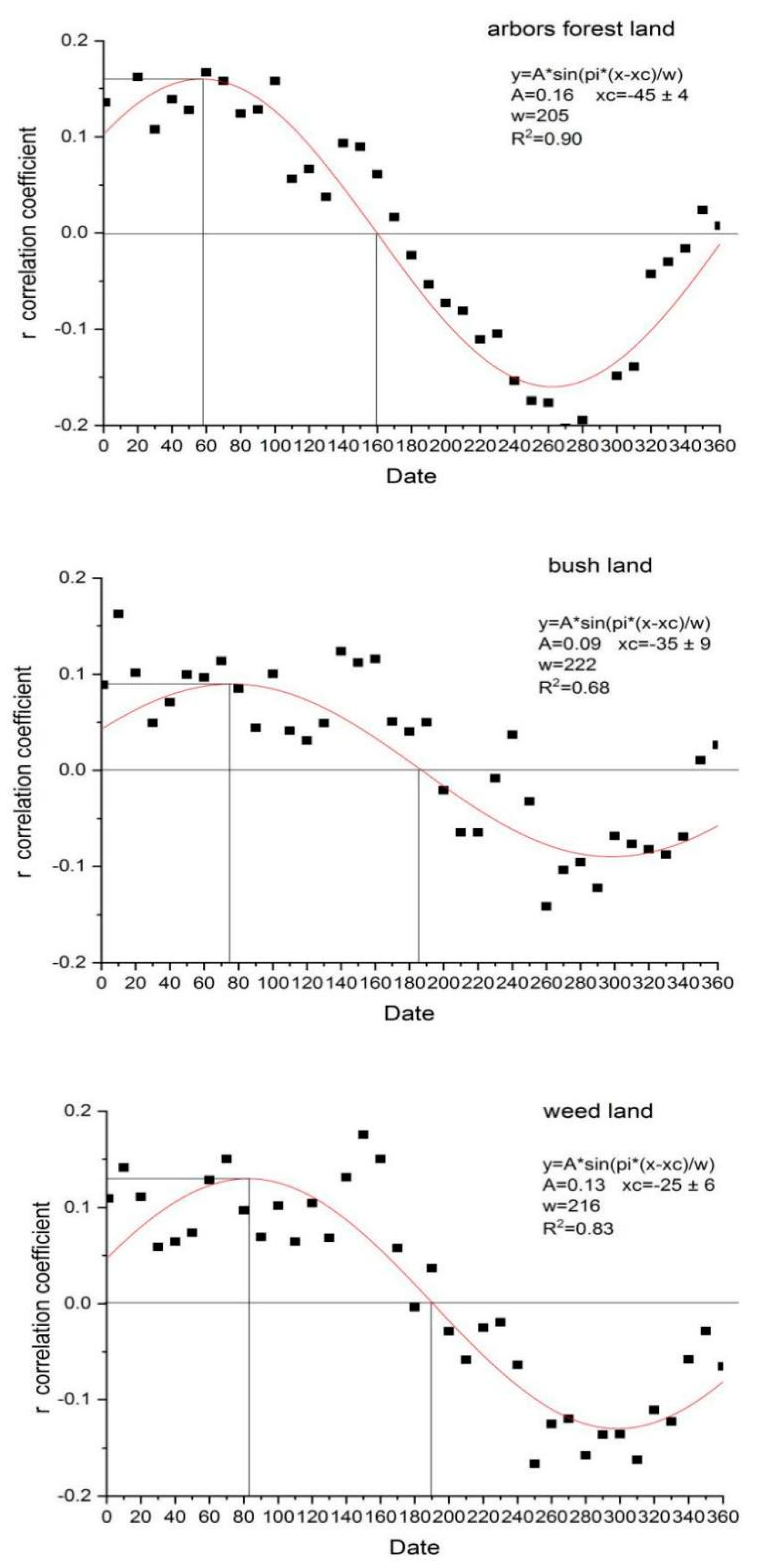
| SD | Pearson’s Correlation Coefficient r | ||||||||||||||||||
| rP1 | rP10 | rP20 | rP30 | rP40 | rP50 | rP60 | rP70 | rP80 | rP90 | rP100 | rP110 | rP120 | rP130 | rP140 | rP150 | rP160 | rP170 | rP180 | |
| 10 cm | 0.17 | 0.28 | 0.04 | 0.09 | 0.14 | 0.17 | 0.18 | 0.14 | 0.07 | 0.11 | 0.21 | 0.04 | 0.07 | −0.03 | 0.03 | −0.01 | 0.01 | −0.05 | 0.00 |
| 20 cm | 0.14 | 0.24 | 0.06 | 0.09 | 0.21 | 0.20 | 0.26 | 0.17 | 0.09 | 0.19 | 0.28 | 0.13 | 0.07 | 0.04 | 0.05 | 0.03 | 0.01 | −0.01 | −0.06 |
| 30 cm | 0.10 | 0.14 | 0.08 | 0.06 | 0.14 | 0.14 | 0.17 | 0.14 | 0.22 | 0.06 | 0.05 | 0.03 | 0.09 | 0.01 | 0.20 | 0.11 | −0.01 | −0.05 | 0.03 |
| 40 cm | 0.16 | 0.26 | 0.20 | 0.12 | 0.18 | 0.20 | 0.21 | 0.23 | 0.16 | 0.15 | 0.18 | 0.08 | 0.10 | 0.10 | 0.14 | 0.12 | 0.10 | 0.00 | −0.03 |
| 60 cm | 0.16 | 0.17 | 0.17 | 0.03 | 0.05 | 0.07 | 0.09 | 0.15 | 0.07 | 0.00 | 0.00 | −0.01 | 0.05 | 0.03 | 0.13 | 0.17 | 0.15 | 0.11 | −0.01 |
| 100 cm | 0.12 | 0.25 | 0.23 | 0.16 | 0.16 | 0.10 | 0.17 | 0.15 | 0.14 | 0.20 | 0.22 | 0.08 | 0.06 | 0.05 | 0.07 | 0.08 | 0.06 | 0.02 | −0.04 |
| 0–100 cm | 0.14 | 0.23 | 0.16 | 0.11 | 0.14 | 0.13 | 0.17 | 0.16 | 0.12 | 0.13 | 0.16 | 0.06 | 0.07 | 0.04 | 0.09 | 0.09 | 0.06 | 0.02 | −0.02 |
| SD | Pearson’s Correlation Coefficient r | ||||||||||||||||||
| rP190 | rP200 | rP210 | rP220 | rP230 | rP240 | rP250 | rP260 | rP270 | rP280 | rP290 | rP300 | rP310 | rP320 | rP330 | rP340 | rP350 | rP360 | ||
| 10 cm | −0.11 | −0.07 | −0.15 | −0.17 | −0.11 | −0.16 | −0.16 | −0.14 | −0.15 | −0.17 | −0.16 | −0.12 | −0.04 | 0.08 | 0.06 | 0.06 | 0.04 | 0.09 | |
| 20 cm | 0.00 | −0.09 | −0.17 | −0.14 | −0.07 | −0.12 | −0.15 | −0.20 | −0.15 | −0.16 | −0.19 | −0.11 | −0.17 | −0.02 | 0.08 | 0.03 | 0.00 | 0.00 | |
| 30 cm | −0.09 | −0.07 | −0.08 | −0.11 | −0.10 | −0.13 | −0.16 | −0.16 | −0.17 | −0.16 | −0.16 | −0.11 | −0.09 | −0.06 | −0.05 | −0.02 | −0.02 | −0.01 | |
| 40 cm | −0.05 | −0.10 | −0.11 | −0.14 | −0.14 | −0.17 | −0.24 | −0.24 | −0.27 | −0.29 | −0.25 | −0.20 | −0.16 | −0.10 | −0.12 | −0.06 | 0.00 | −0.01 | |
| 60 cm | 0.00 | −0.04 | −0.05 | −0.01 | −0.04 | −0.04 | −0.16 | −0.15 | −0.10 | −0.14 | −0.15 | −0.10 | −0.08 | −0.04 | −0.13 | −0.01 | 0.01 | −0.05 | |
| 100 cm | −0.07 | −0.08 | −0.05 | −0.13 | −0.14 | −0.22 | −0.18 | −0.18 | −0.27 | −0.23 | −0.26 | −0.19 | −0.19 | −0.06 | 0.00 | −0.04 | 0.05 | 0.02 | |
| 0–100 cm | −0.05 | −0.07 | −0.08 | −0.11 | −0.10 | −0.15 | −0.17 | −0.18 | −0.20 | −0.19 | −0.21 | −0.15 | −0.14 | −0.04 | −0.03 | −0.02 | 0.02 | 0.01 | |
| SD | Arbors Forest Land | ||||
| First Search | Second Search | Pearson r | Equation | Sign. | |
| 10 cm | r70 | r75 | 0.459 | y = (7.7 + 0.01x)/100 | 0.000 |
| 20 cm | r130 | r138 | 0.568 | y = (9.45 + 0.007x)/100 | |
| 30 cm | r145 | r143 | 0.449 | y = (12.2 + 0.009x)/100 | |
| 40 cm | r180 | r184 | 0.689 | y = (11.15 + 0.009x)/100 | |
| 60 cm | r210 | r207 | 0.455 | y = (15.45+ 0.006x)/100 | |
| 100 cm | r140 | r137 | 0.644 | y = (20.96 + 0.005x)/100 | |
| SD | Bush Land | ||||
| First Search | Second Search | Pearson r | Equation | Sign. | |
| 10 cm | r210 | r216 | 0.462 | y = (5.44 + 0.003x)/100 | 0.000 |
| 20 cm | r140 | r137 | 0.565 | y = (22.35 + 0.012x)/100 | |
| 30 cm | r210 | r205 | 0.655 | y = (16.67 + 0.01x)/100 | |
| 40 cm | r200-r210 | r210-r211 | 0.633 | y = (11.25 + 0.009x)/100 | |
| 60 cm | r240 | r242 | 0.444 | y = (12.62 + 0.004x)/100 | |
| 100 cm | r230 | r235 | 0.314 | y = (18.3 + 0.002x)/100 | |
| SD | Weed Land | ||||
| First Search | Second Search | Pearson r | Equation | Sign. | |
| 10 cm | r230 | r229 | 0.561 | y =(6.64 + 0.013x)/100 | 0.000 |
| 20 cm | r230 | r229 | 0.601 | y = (12.92 + 0.013x)/100 | |
| 30 cm | r230 | r230 | 0.542 | y = (11.01 + 0.015x)/100 | |
| 40 cm | r230 | r230 | 0.529 | y = (11.35 + 0.012x)/100 | |
| 60 cm | r50 | r45 | 0.172 | y = (10.35 + 0.012x)/100 | 0.002 |
| 100 cm | r180 | r184 | 0.406 | y = (25.93 + 0.003x)/100 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Song, W.; Ma, J.; Ma, J.; He, X. Dynamic Change Characteristics of Soil Moisture and Its Relationship with Precipitation in Hani Rice Terraces Water Source Area. Water 2022, 14, 2690. https://doi.org/10.3390/w14172690
Ma Z, Song W, Ma J, Ma J, He X. Dynamic Change Characteristics of Soil Moisture and Its Relationship with Precipitation in Hani Rice Terraces Water Source Area. Water. 2022; 14(17):2690. https://doi.org/10.3390/w14172690
Chicago/Turabian StyleMa, Ze, Weifeng Song, Jiangang Ma, Jing Ma, and Xiaokang He. 2022. "Dynamic Change Characteristics of Soil Moisture and Its Relationship with Precipitation in Hani Rice Terraces Water Source Area" Water 14, no. 17: 2690. https://doi.org/10.3390/w14172690
APA StyleMa, Z., Song, W., Ma, J., Ma, J., & He, X. (2022). Dynamic Change Characteristics of Soil Moisture and Its Relationship with Precipitation in Hani Rice Terraces Water Source Area. Water, 14(17), 2690. https://doi.org/10.3390/w14172690







