Copula-Based Multivariate Simulation Approach for Flood Risk Transfer of Multi-Reservoirs in the Weihe River, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Copula Method
2.2. Common Copula Functions
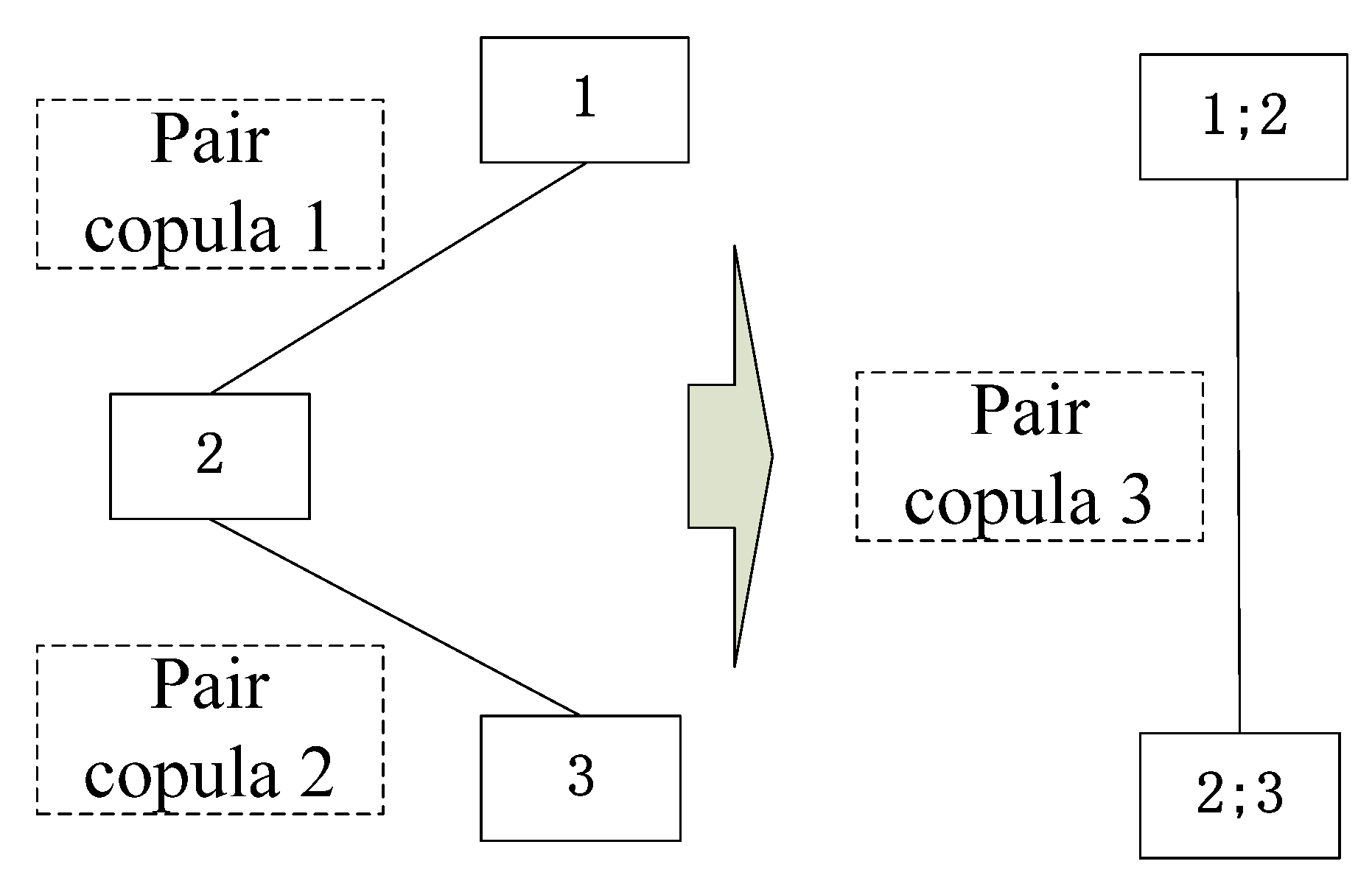
2.3. Pair-Copula Method
- 1.
- Step 1: The first layer pair-copula sequence is constructed using bivariate copula functions of one random variable with other random variables as follows:
- 2.
- Step 2: The second layer pair-copula sequence is constructed from distribution functions of Step 1 as new random variable sequences as follows:
- 3.
- Step 3: Step 2 is repeated until the last bivariate copula is obtained:
- 4.
- Finally, the joint density function of x1, x2, …, xn can be described as:
2.4. Correlation Analysis Method
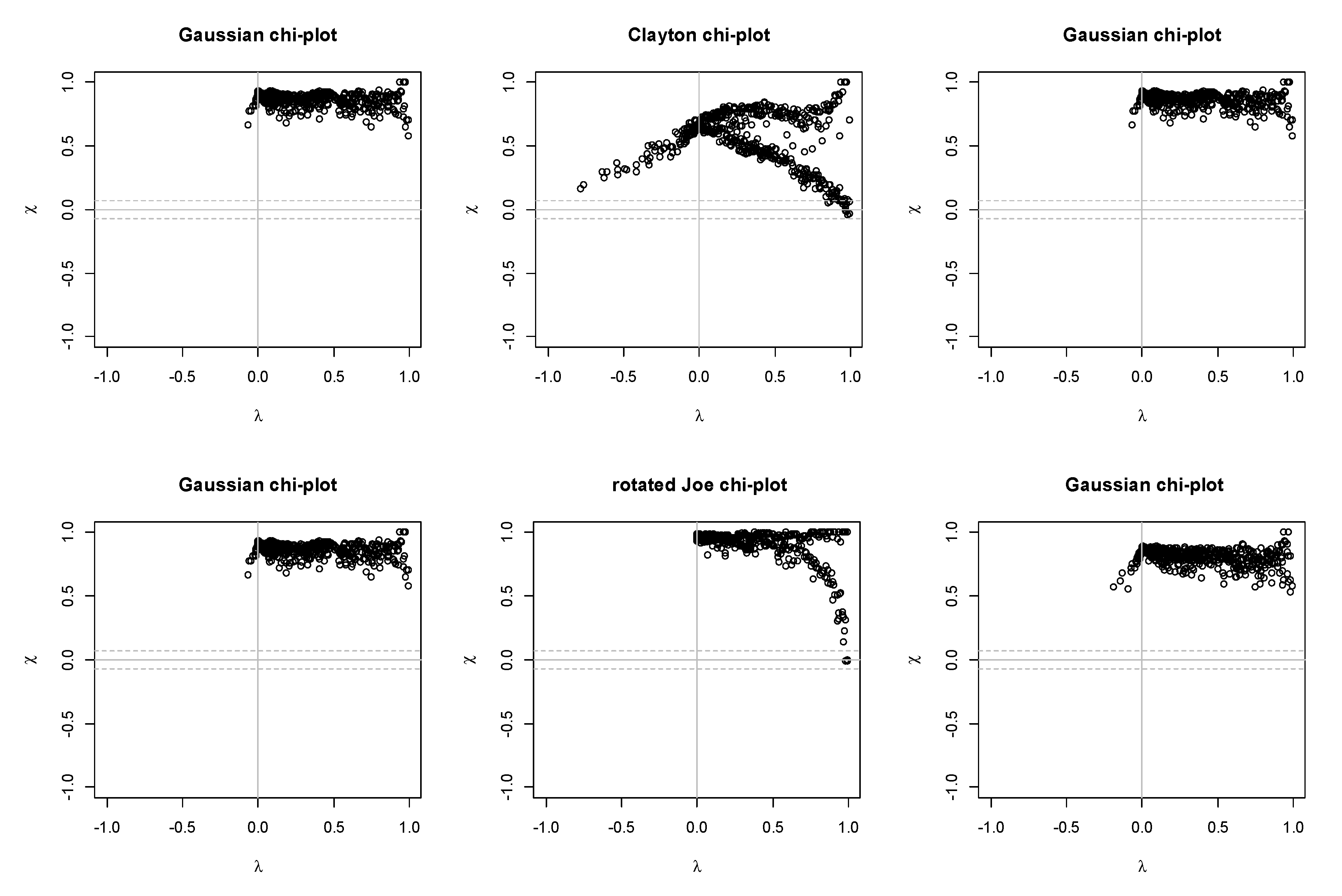
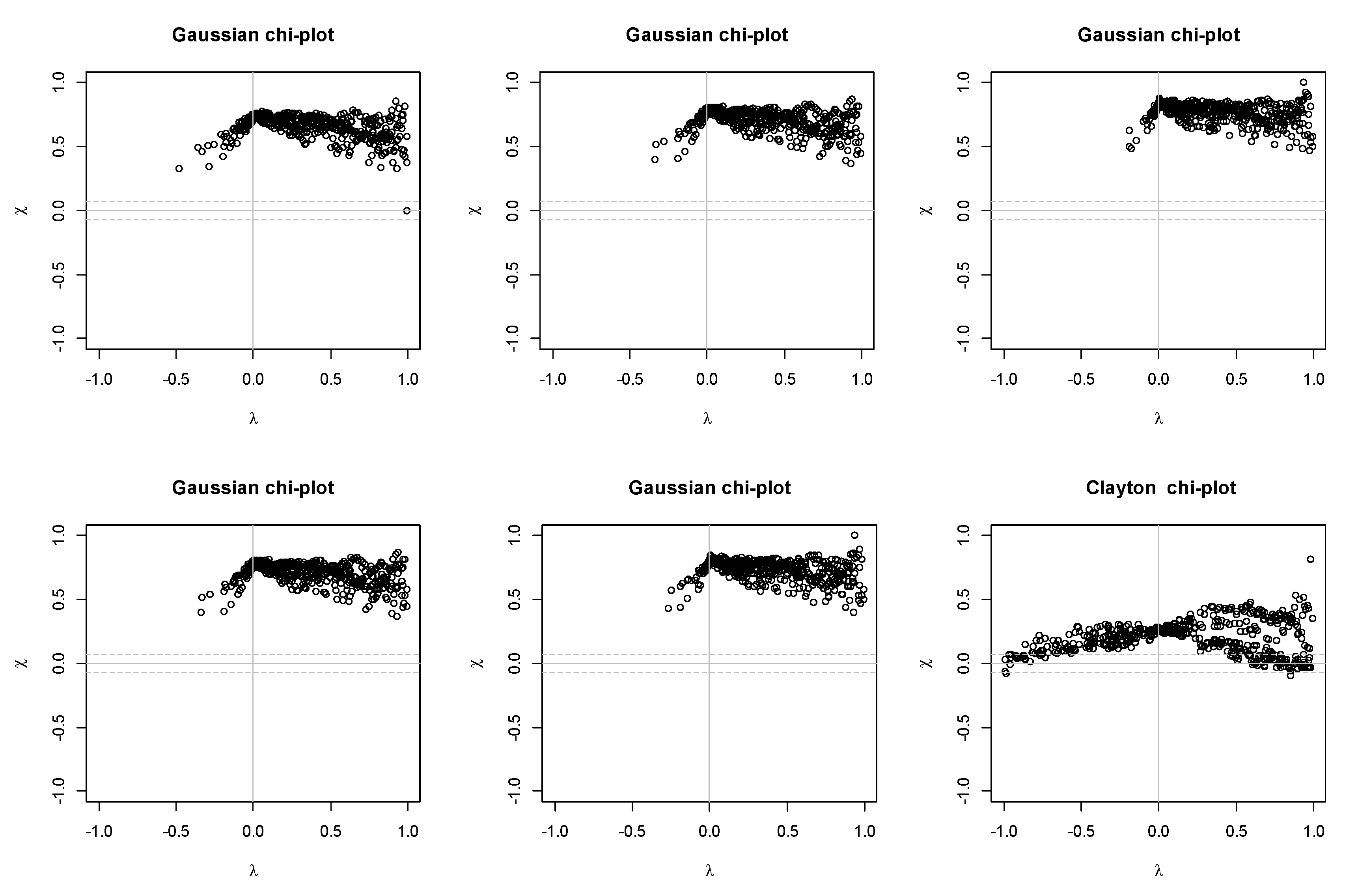
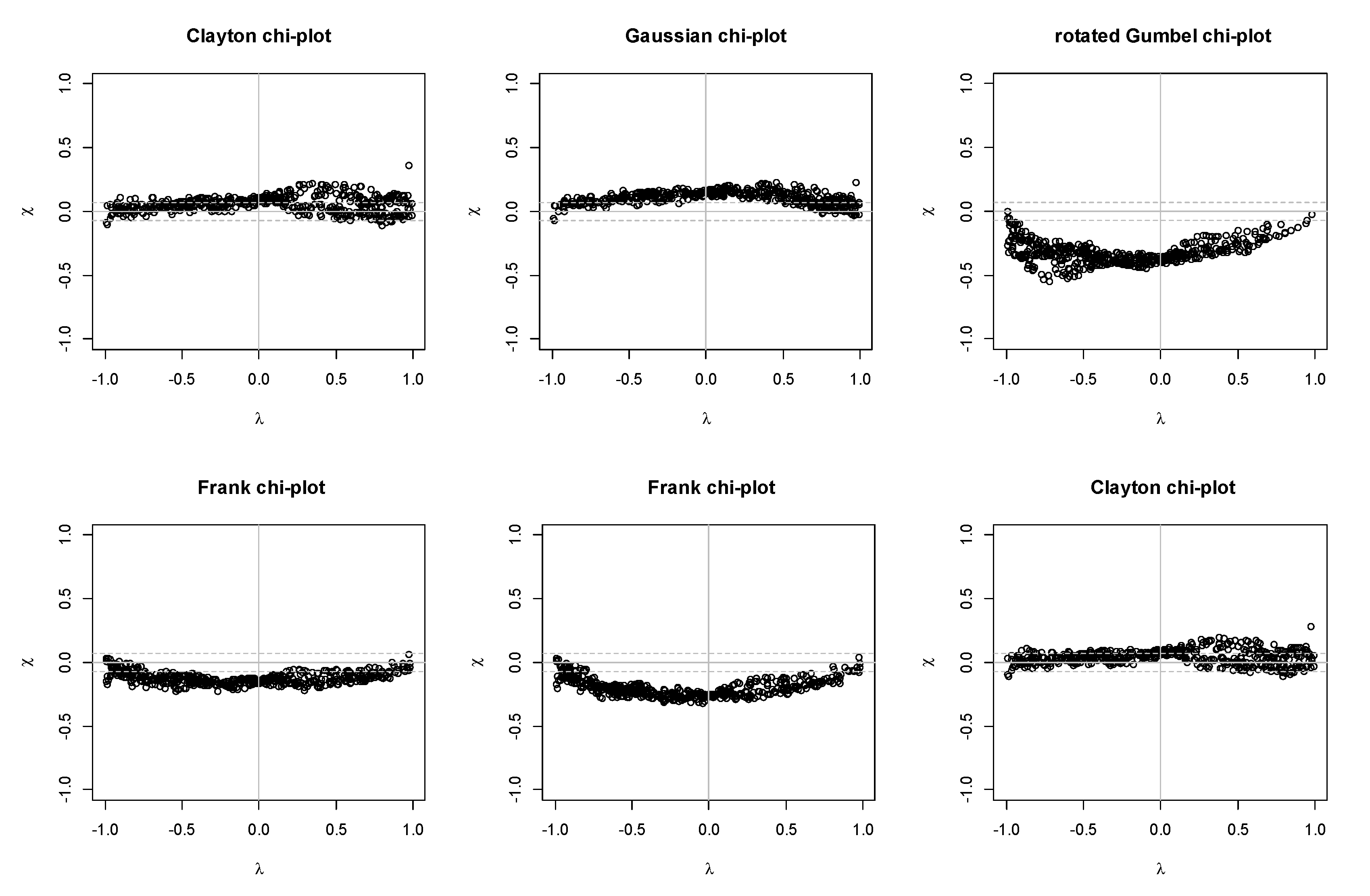
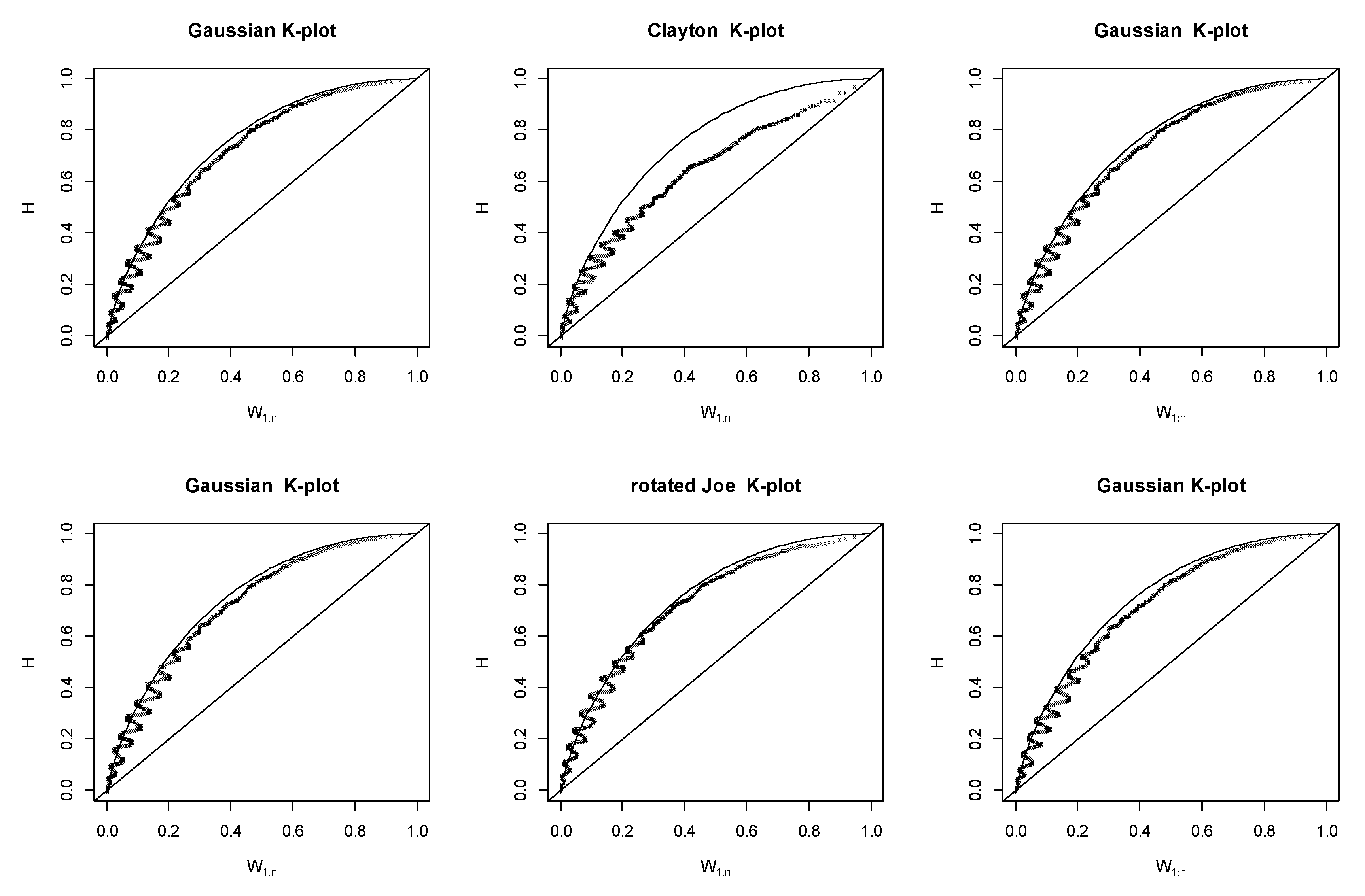
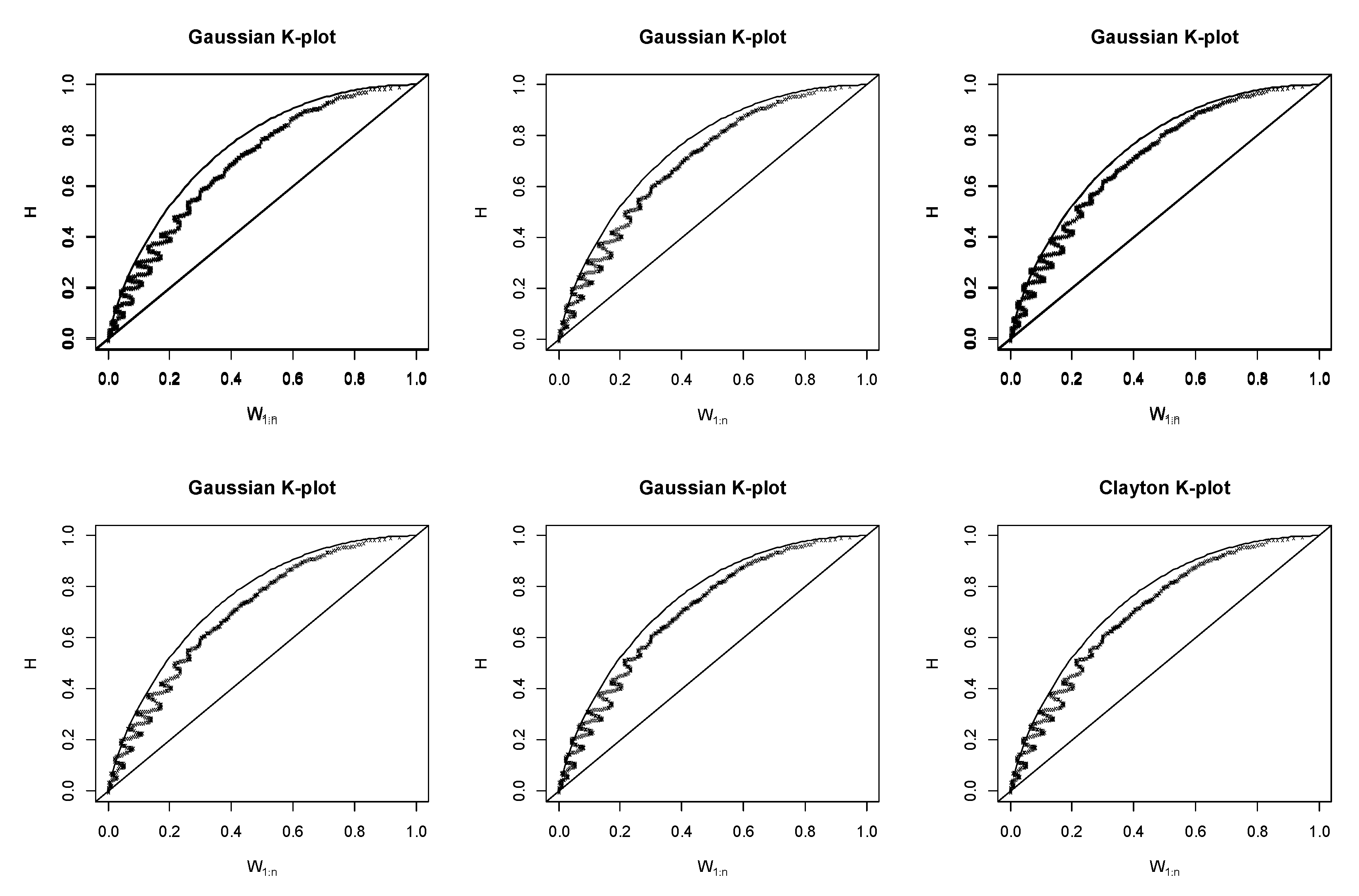
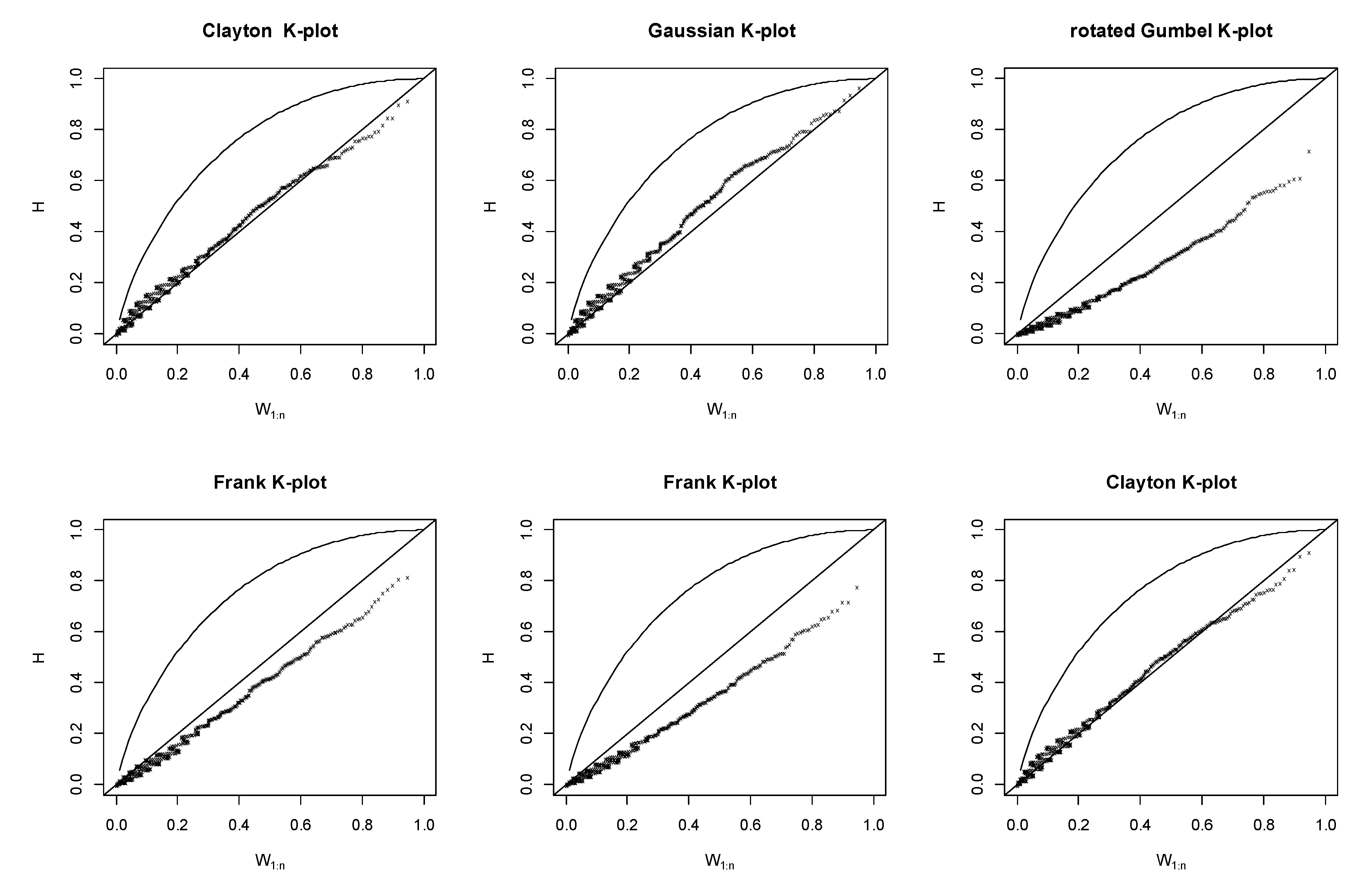
2.4.1. Kendall’s (K-) Plots
2.4.2. Chi-Plot
2.5. Verification Method
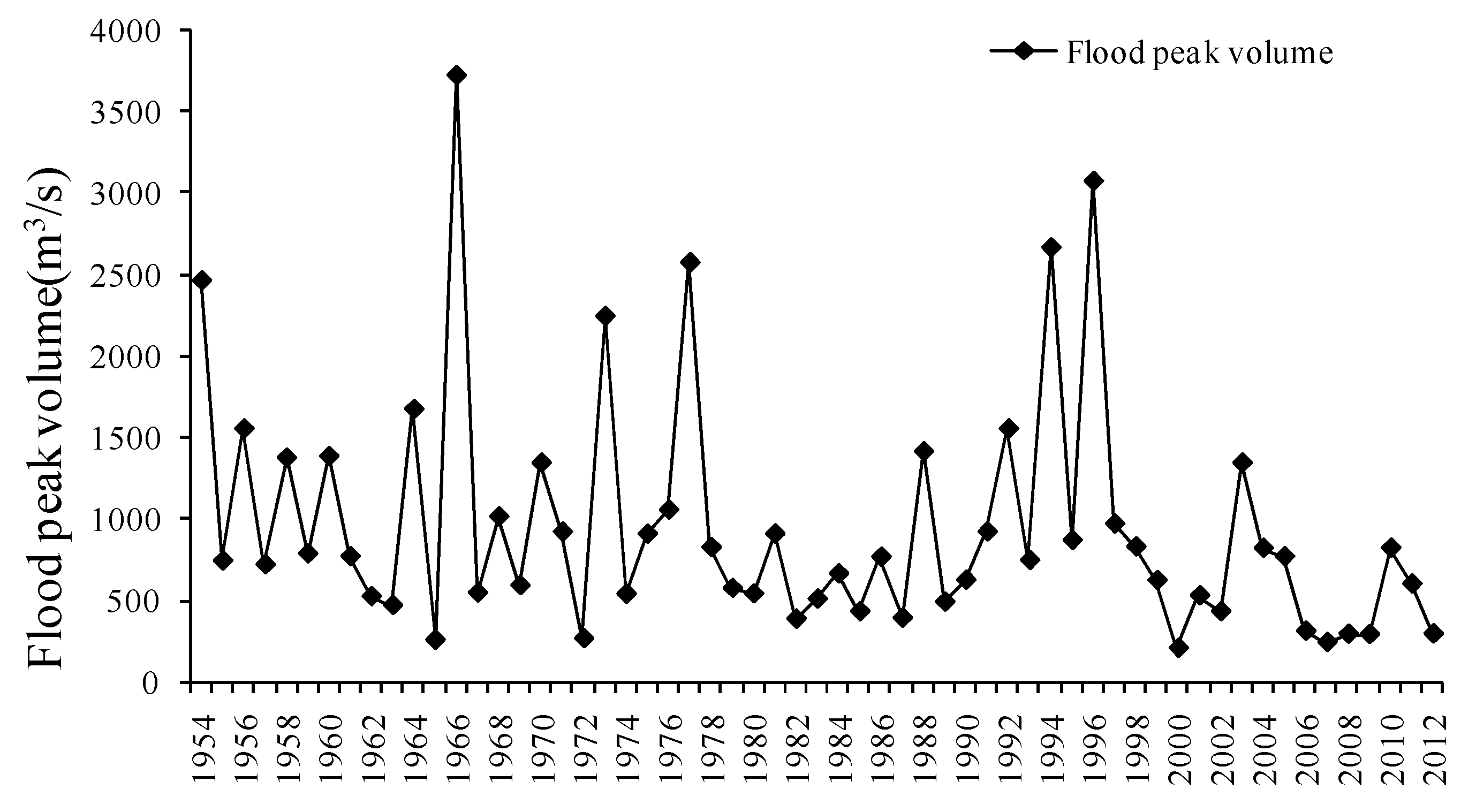
3. Case Study
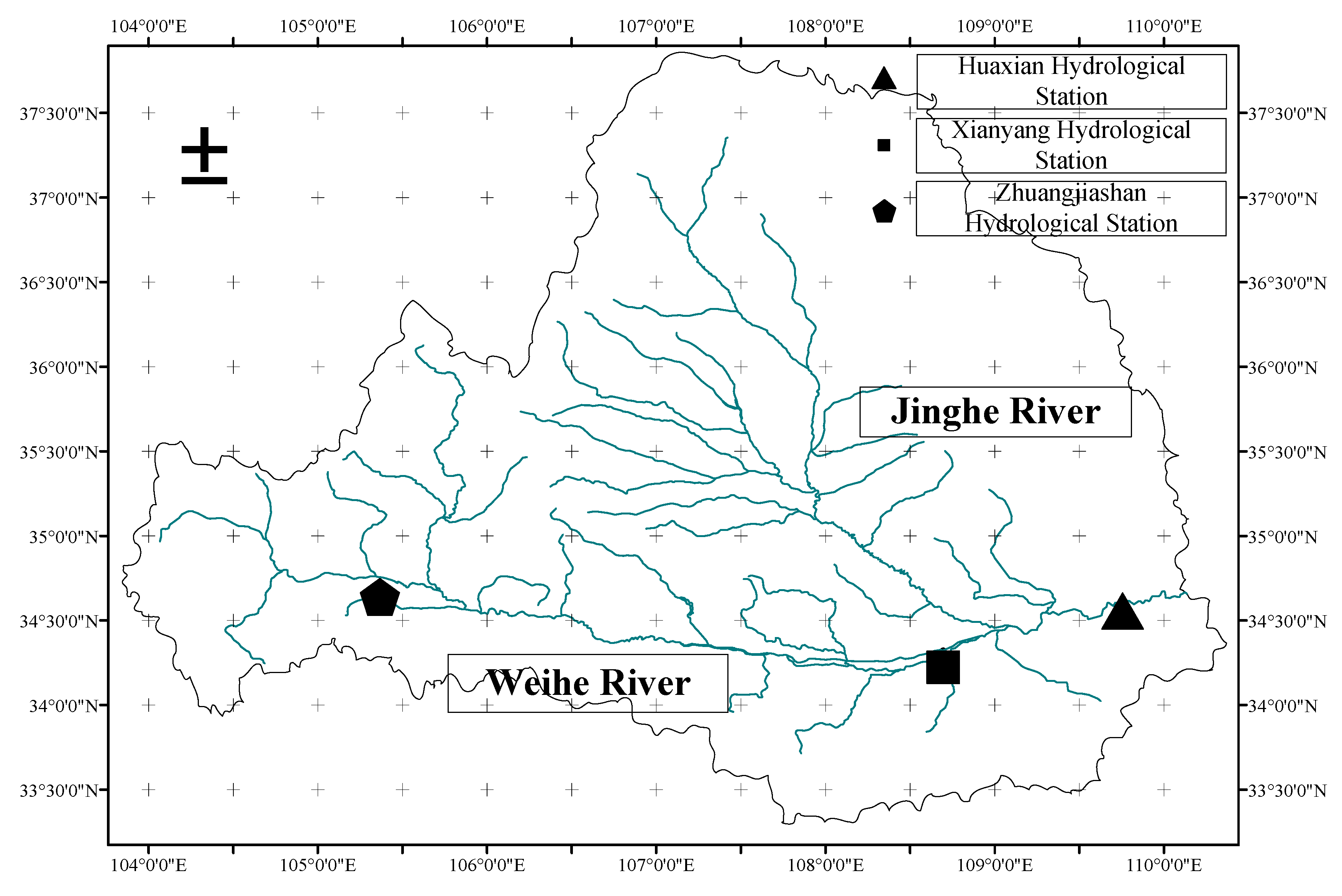
3.1. Overview of the Weihe River
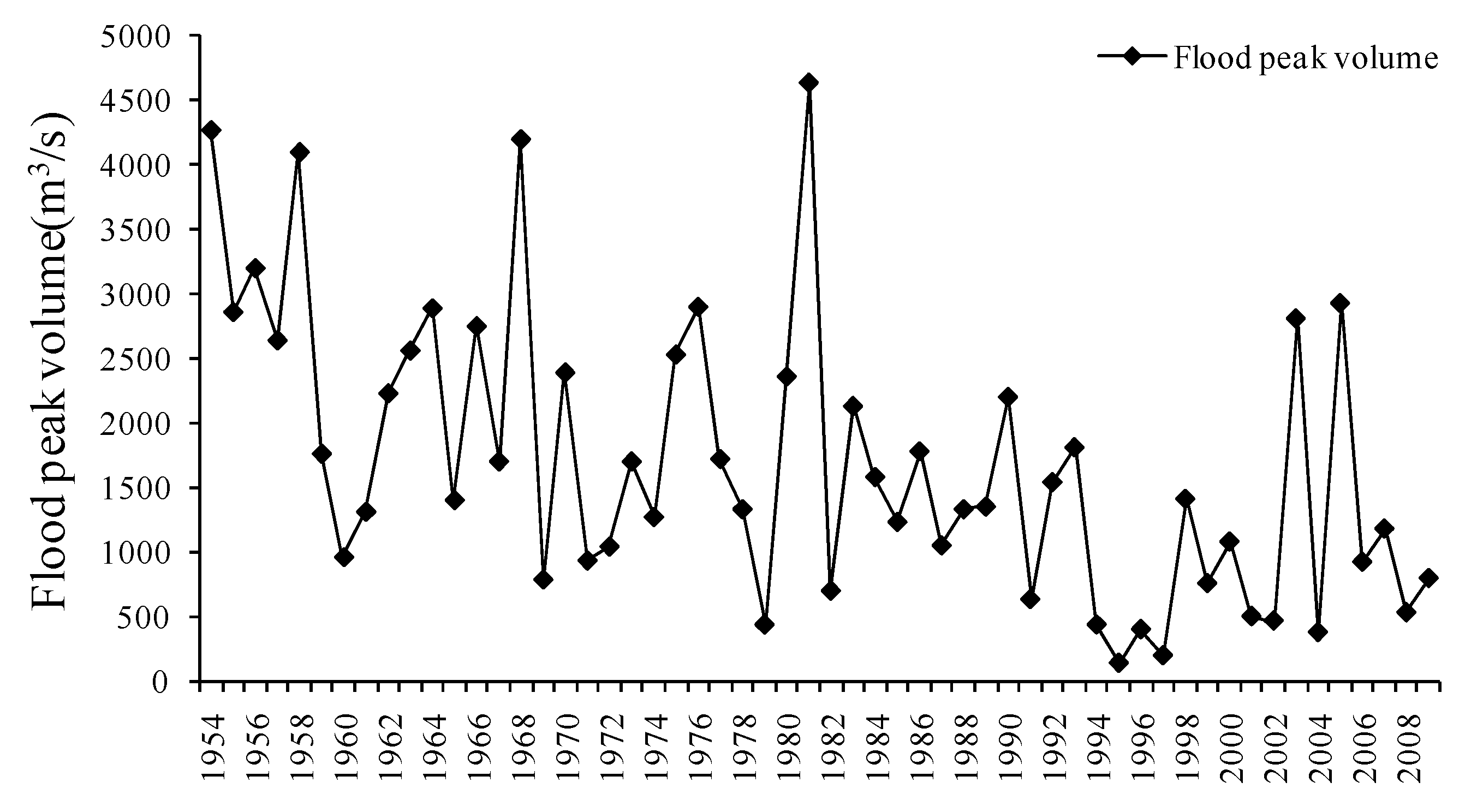
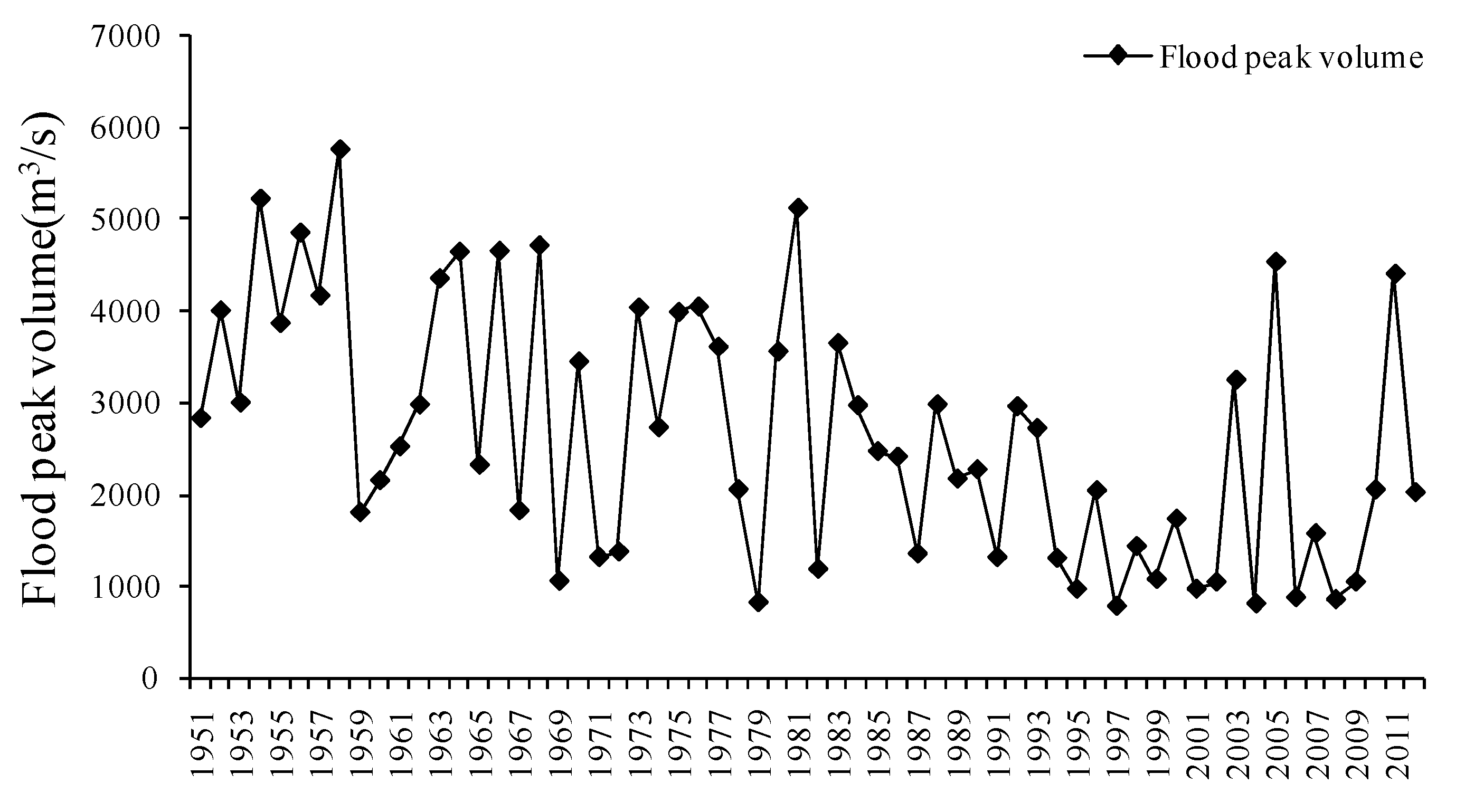
3.2. Multi-Reservoir Joint Distribution and Data Collection
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rauter, M.; Thaler, T.; Attems, M.-S.; Fuchs, S. Obligation or Innovation: Can the EU Floods Directive Be Seen as a Tipping Point Towards More Resilient Flood Risk Management? A Case Study From Vorarlberg, Austria. Sustainability 2019, 11, 5505. [Google Scholar] [CrossRef]
- Obeidat, M.; Awawdeh, M.; Al-Hantouli, F. Morphometric Analysis and Prioritisation of Watersheds for Flood Risk Management in Wadi Easal Basin (WEB), Jordan, Using Geospatial Technologies. J. Flood Risk Manag. 2021, 14, e12711. [Google Scholar] [CrossRef]
- Pangali Sharma, T.P.; Zhang, J.; Khanal, N.R.; Prodhan, F.A.; Nanzad, L.; Zhang, D.; Nepal, P. A Geomorphic Approach for Identifying Flash Flood Potential Areas in the East Rapti River Basin of Nepal. ISPRS Int. J. Geo Inf. 2021, 10, 247. [Google Scholar] [CrossRef]
- Seleem, O.; Heistermann, M.; Bronstert, A. Efficient Hazard Assessment for Pluvial Floods in Urban Environments: A Benchmarking Case Study for the City of Berlin, Germany. Water 2021, 13, 2476. [Google Scholar] [CrossRef]
- Jin, S.Y.; Guo, S.M.; Huo, W.H. Analysis on the Return Period of “7.20” Rainstorm in the Xiaohua Section of the Yellow River in 2021. Water 2022, 14, 2444. [Google Scholar] [CrossRef]
- Chen, F.L.; Zheng, J.T.; Li, S.F.; Long, A.H. Effects of the Land Use and Check Dams on Flood in Upper Catchment of Fuping Hydrological Station by Hydrological Modeling. Water Resour. 2018, 45, 508–522. [Google Scholar] [CrossRef]
- El-Rawy, M.; Elsadek, W.M.; De Smedt, F.D. Flash Flood Susceptibility Mapping in Sinai, Egypt Using Hydromorphic Data, Principal Component Analysis and Logistic Regression. Water 2022, 14, 2434. [Google Scholar] [CrossRef]
- Tanim, A.H.; McRae, C.B.; Tavakol-Davani, H.; Goharian, E. Flood Detection in Urban Areas Using Satellite Imagery and Machine Learning. Water 2022, 14, 1140. [Google Scholar] [CrossRef]
- Zhou, Z.; Smith, J.A.; Wright, D.B.; Baeck, M.L.; Yang, L.; Liu, S. Storm Catalog-Based Analysis of Rainfall Heterogeneity and Frequency in a Complex Terrain. Water Resour. Res. 2019, 55, 1871–1889. [Google Scholar] [CrossRef]
- Prairie, J.; Rajagopalan, B.; Lall, U.; Fulp, T. A Stochastic Nonparametric Technique for Space-Time Disaggregation of Streamflows. Water Resour. Res. 2007, 43, W03432. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Singh, V.P. Modeling Multisite Streamflow Dependence With Maximum Entropy Copula. Water Resour. Res. 2013, 49, 7139–7143. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Zhou, J.; Zhang, J. Copula-Based Method for Multisite Monthly and Daily Streamflow Simulation. J. Hydrol. 2015, 528, 369–384. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. A Multivariate Stochastic Flood Analysis Using Entropy. In Hydrologic Frequency Modeling; Singh, V.P., Ed.; Reidel: Dordrecht, The Netherlands, 1987; pp. 515–539. [Google Scholar]
- Yue, S. The Bivariate Lognormal Distribution to Model a Multi Variate Flood Episode. Hydrol. Process. 2000, 14, 2575–2588. [Google Scholar] [CrossRef]
- Escalante-Sandoval, C. Application of Bivariate Extreme Value Distribution to Flood Frequency Analysis: A Case Study of Northwestern Mexico. Nat. Hazards. 2007, 42, 37–46. [Google Scholar] [CrossRef]
- Sandoval, C.E.; Raynal-Villaseñor, J. Trivariate Generalized Extreme Value Distribution in Flood Frequency Analysis. Hydrol. Sci. J. 2008, 53, 550–567. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Asymmetric Copula in Multivariate Flood Frequency Analysis. Adv. Water Resour. 2006, 29, 1155–1167. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Trivariate Flood Frequency Analysis Using the Gumbel–Hougaard Copula. J. Hydrol. Eng. 2007, 12, 431–439. [Google Scholar] [CrossRef]
- Pinya, M.A.S.; Madsen, H.; Rosbjerg, D. Assessment of the Risk of Inland Flooding in a Tidal Sluice Regulated Catchment Using Multi-variate Statistical Techniques. Phys. Chem. Earth Parts A B C 2009, 34, 662–669. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Frequency Analysis via Copulas: Theoretical Aspects and Applications to Hydrological Events. Water Resour. Res. 2004, 40, 12. [Google Scholar] [CrossRef]
- Karmakar, S.; Simonovic, S.P. Bivariate Flood Frequency Analysis. Part 2: A Copula-Based Approach With Mixed Marginal Distributions. J. Flood Risk Manag. 2009, 2, 32–44. [Google Scholar] [CrossRef]
- Latif, S.; Mustafa, F. Copula-Based Multivariate Flood Probability Construction: A Review. Arab. J. Geosci. 2020, 13, 132. [Google Scholar] [CrossRef]
- Zhong, M.; Zeng, T.; Jiang, T.; Wu, H.; Hong, Y. A Copula-Based Multivariate Probability Analysis for Flash Flood Risk Under the Compound Effect of Soil Moisture and Rainfall. Water Resour. Manag. 2021, 35, 83–98. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G.G.S. Copula Based Multisite Model for Daily Precipitation Simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef]
- Requena, A.I.; Mediero, L.; Garrote, L. A Bivariate Return Period Based on Copulas for Hydrologic Dam Design: Accounting for Reservoir Routing in Risk Estimation. Hydrol. Earth Syst. Sci. 2013, 17, 3023–3038. [Google Scholar] [CrossRef]
- Sancetta, A.; Satchell, S. The Bernstein Copula and Its Applications to Modeling and Approximations of Multivariate Distributions. Econ. Theory. 2004, 20, 535–562. [Google Scholar] [CrossRef]
- Tang, X.S.; Li, D.Q.; Zhou, C.B.; Zhang, L.M. Bivariate Distribution Models Using Copulas for Reliability Analysis. Proc. Inst. Mech. Eng. O. 2013, 227, 499–512. [Google Scholar] [CrossRef]
- Tao, S.; Dong, S.; Wang, N.; Guedes Soares, C.G. Estimating Storm Surge Intensity With Poisson Bivariate Maximum Entropy Distributions Based on Copulas. Nat. Hazards. 2013, 68, 791–807. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-Copula Constructions of Multiple Dependence. Ins. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Chen, Q.P. A Study on Pair-Copula Constructions of Multiple Dependence. Appl. Stat. Manag. 2013, 44, 182–198. [Google Scholar]
- Sklar, A. Random Variables, Distribution Functions, and Copulas: A Personal Look Backward and Forward. Lect. Notes-Monograph. 1996, 28, 1–14. [Google Scholar]
- Akaike, H. Information Theory as an Extension of the Maximum Likelihood Principle. In Second International Symposium on Information Theory; Petrov, B.N., Csaki, F., Eds.; Akadémiai Kiadó: Budapest, Hungary, 1973; pp. 276–281. [Google Scholar]
- Banks, H.T.; Joyner, M.L. AIC Under the Framework of Least Squares Estimation. Appl. Math. Lett. 2017, 74, 33–45. [Google Scholar] [CrossRef]
- Bozdogan, H. Model Selection and Akaike’s Information Criterion (AIC): The General Theory and Its Analytical Extensions. Psychometrika 1987, 52, 345–370. [Google Scholar] [CrossRef]
- Hamed, M.M.; Nashwan, M.S.; Shahid, S.; Ismail, T.B.; Wang, X.J.; Dewan, A.; Asaduzzaman, M. Inconsistency in historical simulations and future projections of temperature and rainfall: A comparison of CMIP5 and CMIP6 models over Southeast Asia. Atmos. Res. 2022, 265, 105927. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S. A novel framework for selecting general circulation models based on the spatial patterns of climate. Int. J. Climatol. 2020, 40, 4422–4443. [Google Scholar] [CrossRef]
| Copula | Generating Function | Parameter | |
|---|---|---|---|
| Gumbel copula | [1, ∞) | ||
| Clayton copula | (0, ∞) | ||
| Frank copula | R |
| Multi-Reservoirs | Chosen Copula | AIC | BIC | |
|---|---|---|---|---|
| 1-day volume | 1,2 | Gaussian | −4372.627 | −4356.78 |
| 2,3 | Gaussian | −13,322.1 | −13,314.2 | |
| 1,3:2 | Clayton | −40,068.585 | −40,060.7 | |
| Full | −10,036.55 | −10,023.8 | ||
| 3-day volume | 1,2 | Gaussian | −5542.449 | −5526.6 |
| 2,3 | Clayton | −13,780.09 | −13,772.2 | |
| 1,3:2 | Gaussian | −43,701.22 | −43,693.3 | |
| Full | −11,746.95 | −11,734.2 | ||
| 5-day volume | 1,2 | Gaussian | −6262.168 | −6246.32 |
| 2,3 | Gaussian | −14,147.22 | −14,139.3 | |
| 1,3:2 | Rotated Gumbel | −45,910.489 | −45,902.6 | |
| Full | −12,766.7 | −12,754 | ||
| 9-day volume | 1,2 | Gaussian | −7023.314 | −7007.46 |
| 2,3 | Gaussian | −14,858.63 | −14,850.7 | |
| 1,3:2 | Frank | −48,641.955 | −48,634 | |
| Full | −12,603.55 | −12,590.8 | ||
| 12-day volume | 1,2 | Gaussian | −7376.352 | −7360.5 |
| 2,3 | Rotated Joe | −15,311.32 | −15,303.4 | |
| 1,3:2 | Frank | −49,965.467 | −49,957.5 | |
| Full | −303,895.2 | −303,883 | ||
| Flood peak volume | 1,2 | Clayton | −4372.627 | −4356.78 |
| 2,3 | Gaussian | −13,322.1 | −13,314.2 | |
| 1,3:2 | Clayton | −40,068.585 | −40,060.7 | |
| Full | −3546.92 | −3534.21 |
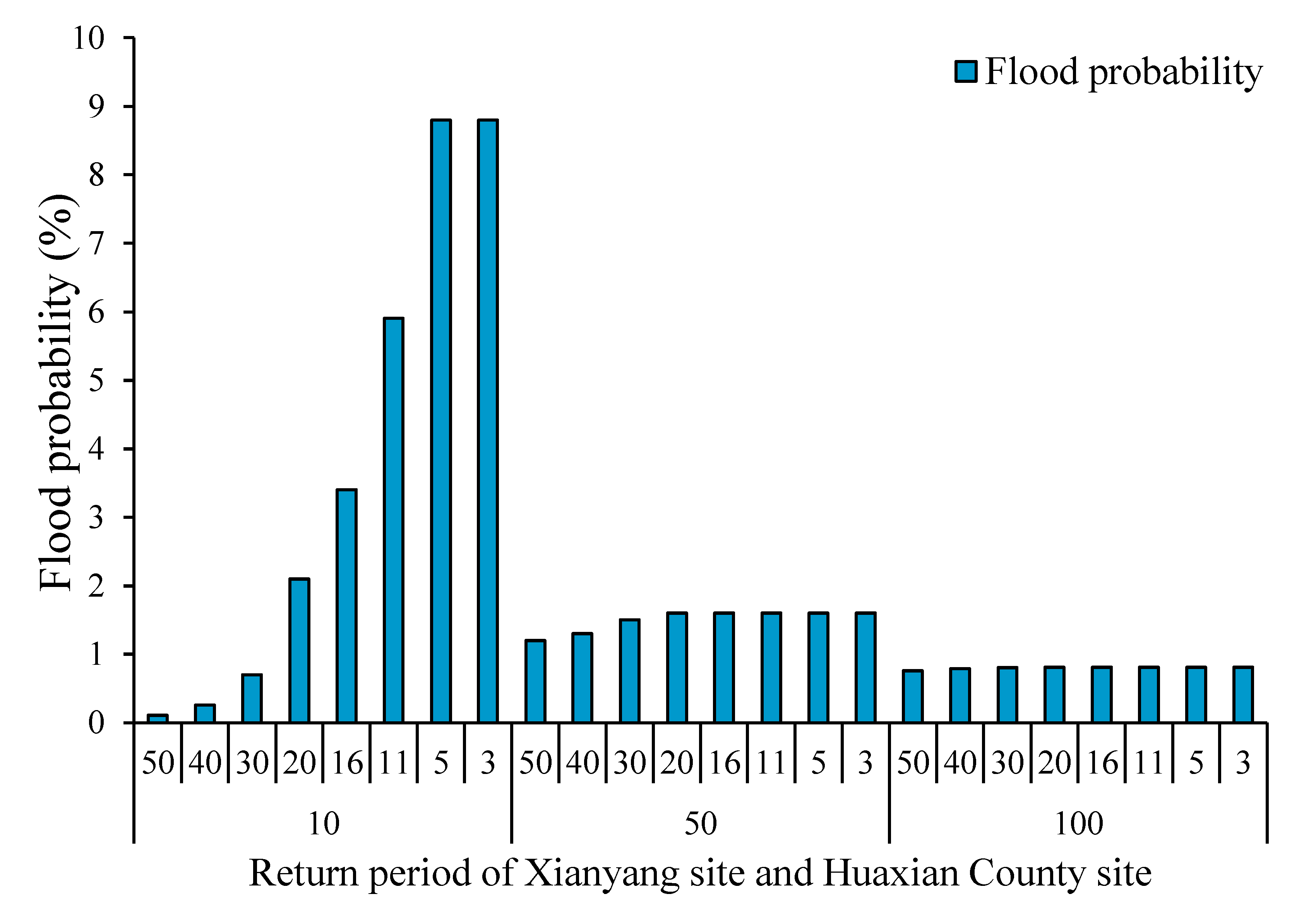
| Return Period of Xianyang Site | ||||||||
|---|---|---|---|---|---|---|---|---|
| 50 | 40 | 30 | 20 | 16 | 11 | 5 | 3 | |
| Flood peak volume | 0.242 | 0.265 | 0.315 | 0.351 | 0.235 | 0.138 | 0.175 | 0.108 |
| 1-day flood volumes | 0.012 | 0.090 | 0.359 | 0.321 | 0.283 | 0.168 | 0.051 | 0.012 |
| 3-day flood volumes | 0.059 | 0.164 | 0.253 | 0.278 | 0.130 | 0.059 | 0.095 | 0.021 |
| 5-day flood volumes | 0.012 | 0.090 | 0.359 | 0.321 | 0.283 | 0.168 | 0.051 | 0.012 |
| 9-day flood volumes | 0.169 | 0.106 | 0.042 | 0.029 | 0.016 | 0.010 | 0.029 | 0.042 |
| 12-day flood volumes | 0.160 | 0.097 | 0.033 | 0.021 | 0.008 | 0.002 | 0.021 | 0.033 |
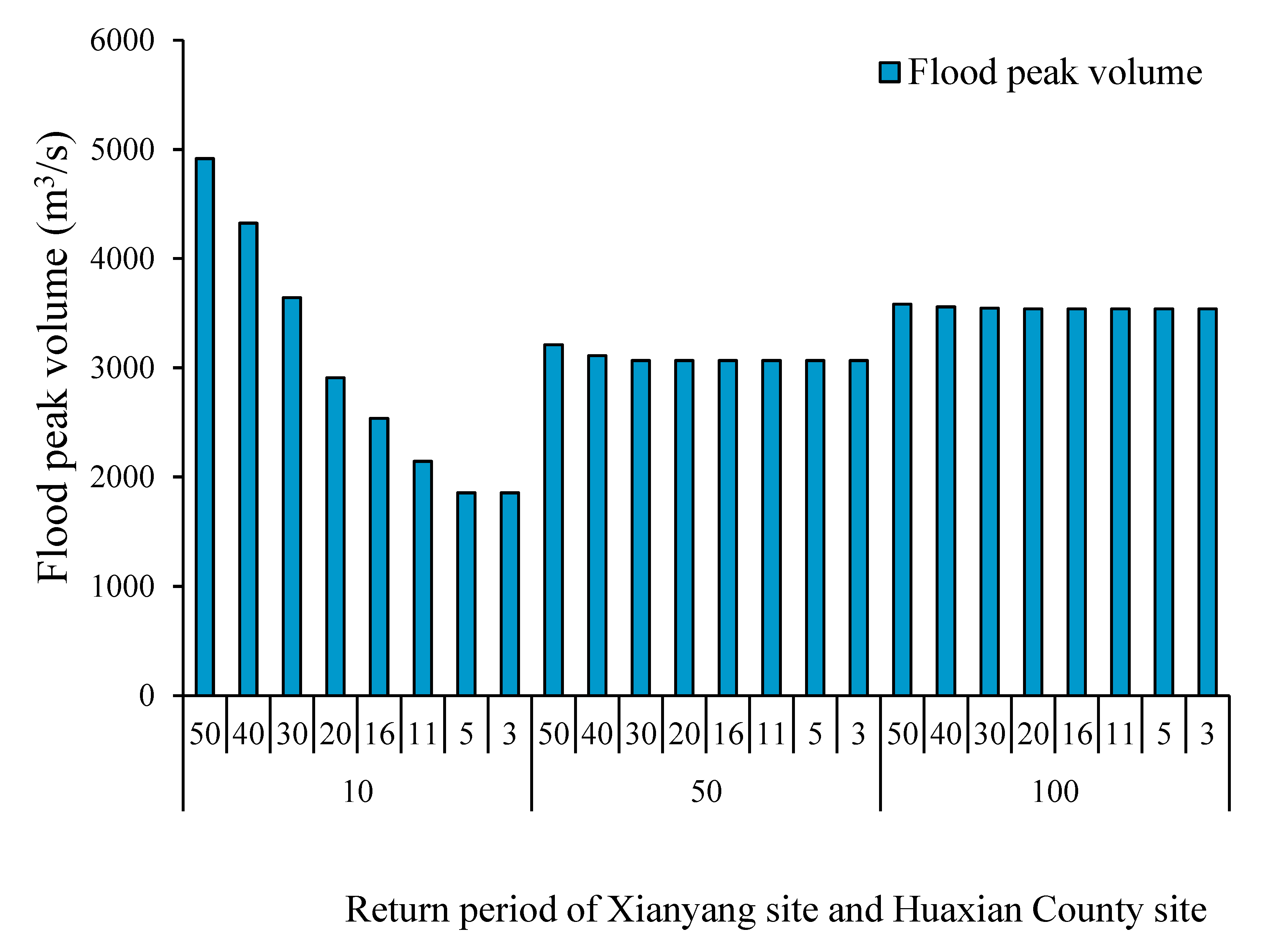
| Return Period | Flood Peak Volume (m3/s) | |
|---|---|---|
| Xianyang | Huaxian County | Zhangjiashan |
| 10 | 50 | 4915 |
| 40 | 4325 | |
| 30 | 3641 | |
| 20 | 2909 | |
| 16 | 2536 | |
| 11 | 2144 | |
| 5 | 1856 | |
| 3 | 1856 | |
| 50 | 50 | 3211 |
| 40 | 3110 | |
| 30 | 3066 | |
| 20 | 3066 | |
| 16 | 3066 | |
| 11 | 3066 | |
| 5 | 3066 | |
| 3 | 3066 | |
| 100 | 50 | 3583 |
| 40 | 3558 | |
| 30 | 3547 | |
| 20 | 3540 | |
| 16 | 3540 | |
| 11 | 3540 | |
| 5 | 3540 | |
| 3 | 3540 | |
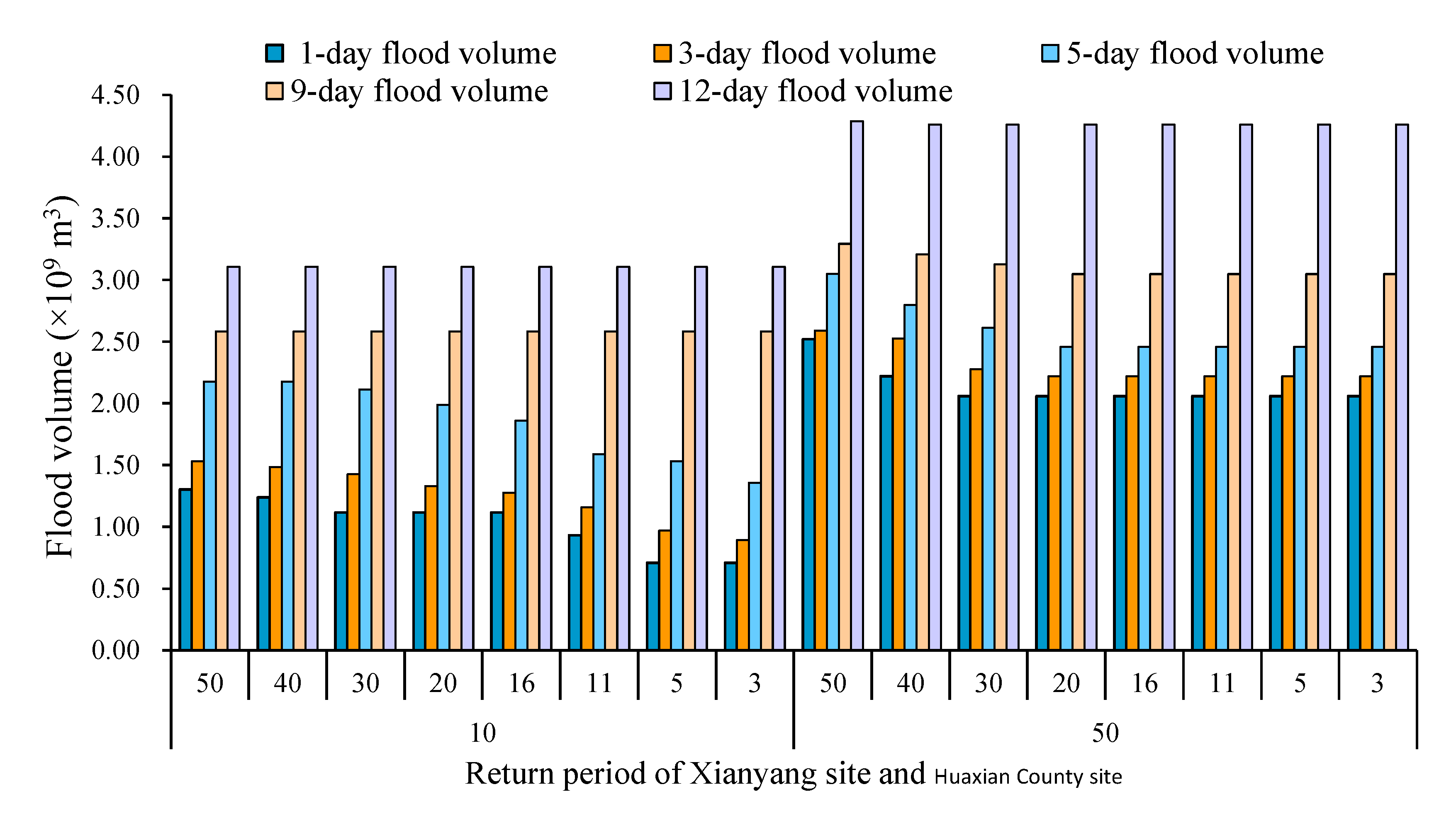
| Return Period | Flood Volume (m3) | |||||
|---|---|---|---|---|---|---|
| Xianyang | Huaxian County | Zhangjiashan Site | ||||
| 10 | 50 | 15,080 | 17,710 | 25,200 | 29,910 | 35,970 |
| 40 | 14,330 | 17,200 | 25,200 | 29,910 | 35,970 | |
| 30 | 12,930 | 16,514 | 24,484 | 29,910 | 35,970 | |
| 20 | 12,930 | 15,410 | 23,027 | 29,910 | 35,970 | |
| 16 | 12,930 | 14,756 | 21,530 | 29,910 | 35,970 | |
| 11 | 10,807 | 13,410 | 18,390 | 29,910 | 35,970 | |
| 5 | 8,200 | 11,230 | 17,746 | 29,910 | 24,176 | |
| 3 | 8,200 | 10,364 | 15,727 | 29,910 | 24,176 | |
| 50 | 50 | 29,190 | 30,000 | 35,300 | 38,124 | 49,598 |
| 40 | 25,710 | 29,250 | 32,388 | 37,124 | 49,307 | |
| 30 | 23,835 | 26,353 | 30,260 | 36,208 | 49,307 | |
| 20 | 23,835 | 25,684 | 28,480 | 35,290 | 49,307 | |
| 16 | 23,835 | 25,684 | 28,480 | 35,290 | 49,307 | |
| 11 | 23,835 | 25,684 | 28,480 | 35,290 | 49,307 | |
| 5 | 23,835 | 25,684 | 28,480 | 35,290 | 49,307 | |
| 3 | 23,835 | 25,684 | 28,480 | 35,290 | 49,307 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wu, J.; Wang, S.; Xie, X.; Fan, Y.; Lv, L.; Huang, G. Copula-Based Multivariate Simulation Approach for Flood Risk Transfer of Multi-Reservoirs in the Weihe River, China. Water 2022, 14, 2676. https://doi.org/10.3390/w14172676
Wang S, Wu J, Wang S, Xie X, Fan Y, Lv L, Huang G. Copula-Based Multivariate Simulation Approach for Flood Risk Transfer of Multi-Reservoirs in the Weihe River, China. Water. 2022; 14(17):2676. https://doi.org/10.3390/w14172676
Chicago/Turabian StyleWang, Shen, Jing Wu, Siyi Wang, Xuesong Xie, Yurui Fan, Lianhong Lv, and Guohe Huang. 2022. "Copula-Based Multivariate Simulation Approach for Flood Risk Transfer of Multi-Reservoirs in the Weihe River, China" Water 14, no. 17: 2676. https://doi.org/10.3390/w14172676
APA StyleWang, S., Wu, J., Wang, S., Xie, X., Fan, Y., Lv, L., & Huang, G. (2022). Copula-Based Multivariate Simulation Approach for Flood Risk Transfer of Multi-Reservoirs in the Weihe River, China. Water, 14(17), 2676. https://doi.org/10.3390/w14172676






