Study on Critical Velocity of Sand Transport in V-Inclined Pipe Based on Numerical Simulation
Abstract
:1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. Turbulence Model
2.3. Computational Domain and Grid-Independent Analysis
2.4. Solution Strategies and Boundary Conditions
3. Results and Discussion
3.1. Comparison between Empirical Formula and Numerical Simulation
3.1.1. Empirical Formula for Critical Velocity
3.1.2. Numerical Simulation for Critical Velocity
3.2. Effect of Simulated Pipeline Length
3.3. Effect of Pipe Inclination
3.4. Effect of Particle Size
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| ASM | algebraic slip mixture |
| DEM | discrete element method |
References
- He, W.Q.; Cai, M.K.; He, X.Y.; Zhang, C.D. Analysis and determination of critical non-silting velocity of muddy water conveyance pipelines in Yellow River irrigation districts. Paiguan Jixie Gongcheng Xuebao/J. Drain. Irrig. Mach. Eng. 2013, 31, 36–40. [Google Scholar]
- Ardiclioglu, M.; Hadi, A.M.W.; Periku, E.; Kuriqi, A. Experimental and Numerical Investigation of Bridge Configuration Effect on Hydraulic Regime. Int. J. Civ. Eng. 2022, 20, 981–991. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Aminvash, E.; Ghaderi, A.; Kuriqi, A.; Abraham, J. Three-Dimensional Investigation of Hydraulic Properties of Vertical Drop in the Presence of Step and Grid Dissipators. Symmetry 2021, 13, 895. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Norouzi, R.; Abbaszadeh, H.; Kuriqi, A.; Di Francesco, S. Influence of Sill on the Hydraulic Regime in Sluice Gates: An Experimental and Numerical Analysis. Fluids 2022, 7, 244. [Google Scholar] [CrossRef]
- Dasineh, M.; Ghaderi, A.; Bagherzadeh, M.; Ahmadi, M.; Kuriqi, A. Prediction of Hydraulic Jumps on a Triangular Bed Roughness Using Numerical Modeling and Soft Computing Methods. Mathematics 2021, 9, 3135. [Google Scholar] [CrossRef]
- Lu, Z.; Xiao, R.; Tao, R.; Li, P.; Liu, W. Influence of guide vane profile on the flow energy dissipation in a reversible pump-turbine at pump mode. J. Energy Storage 2022, 49, 104161. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, F.; Jin, F.; Xiao, R.; Tao, R. Influence of the hydrofoil trailing-edge shape on the temporal-spatial features of vortex shedding. Ocean Eng. 2022, 246, 110645. [Google Scholar] [CrossRef]
- Oudeman, P. Sand Transport and Deposition in Horizontal Multiphase Trunklines of Subsea Satellite Developments. In Offshore Technology Conference; OnePetro: New York, NY, USA, 1992. [Google Scholar]
- Bello, K.; Oyeneyin, B.; Oluyemi, G. Minimum Transport Velocity Models for Suspended Particles in Multiphase Flow Revisited. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011; Volume 4. [Google Scholar]
- Doron, P.; Barnea, D. Pressure Drop and Limit Deposit Velocity for solid–liquid Flow in Pipes. Chem. Eng. Sci. 1995, 50, 1595–1604. [Google Scholar] [CrossRef]
- Doan, Q.; Ali, S.M.; George, A.E.; Oguztoreli, M. Simulation of sand transport in a horizontal well. In Proceedings of the International Conference on Horizontal Well Technology, Calgary, AB, Canada, 18–20 November 1996; pp. 581–593. [Google Scholar]
- Wasp, E.; Kenny, J.; Gandhi, R. Solid liquid flow—Slurry pipeline transportation. Trans. Tech. Publ. Rockport MA 1977, 43, 101–109. [Google Scholar]
- Shook, C. Pipelining Solids: The design of short distance pipelines. Proceedings from the Symposium on Pipeline Transport of Solids; Canadian Society for Chemical Engineering: Toronto, ON, Canada, 1969. [Google Scholar]
- Kokpinar, M.; Gogus, M. Critical Flow Velocity in Slurry Transporting Horizontal Pipelines. J. Hydraul. Eng. 2001, 127, 763–771. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Ahmad, Z. Estimation of Critical Velocity for Slurry Transport through Pipeline Using Adaptive Neuro-Fuzzy Interference System and Gene-Expression Programming. J. Pipeline Syst. Eng. Pract. 2013, 4, 131–137. [Google Scholar] [CrossRef]
- Durand, R. Basic relationships of the transportation of solids in pipes-experimental research. In Proceedings of the International Association of Hydraulic Research, Minneapolis, MN, USA, 1–4 September 1953; pp. 89–103. [Google Scholar]
- Thomas, D. Transport Characteristics of Suspensions: Application of Different Rheological Models to Flocculated Suspension Data. In Progress in International Research on Thermodynamic and Transport Properties; Academic Press: Cambridge, MA, USA, 1962; pp. 704–717. [Google Scholar]
- Graf, W.; Robinson, M.; Yucel, O. Critical velocity for solid–liquid mixtures. In Proceedings of the 1st Conference on Hyd Transport of Solids in Pipes, BHRA Fluid Engineering, Cranfield, UK; 1970. [Google Scholar]
- He, W.; Wang, Y.; Zhang, Y. Experimental on Muddy Water Delivery for Irrigation in Low-pressure Pipeline System. J. Shenyang Agric. Univ. 2007, 38, 98–101. [Google Scholar]
- Jie, A.N.; Zong, Q.; Tang, H. Experimental Study on Non-depositing Critical Velocity of Muddy Water Delivery in Low-pressure Pipeline System. J. Shihezi Univ. (Natl. Sci.) 2012, 30, 83–86. [Google Scholar]
- Sajeev, S.; Mclaury, B.; Shirazi, S. Critical Velocities for Particle Transport from Experiments and CFD Simulations. Int. J. Environ. Ecol. Eng. 2017, 11, 538–542. [Google Scholar]
- Ling, J.; Skudarnov, P.V.; Lin, C.X.; Ebadian, M.A. Numerical investigation of liquid-solid slurry flows in a fully developed turbulent flow region. Int. J. Heat Fluid Flow 2003, 24, 389–398. [Google Scholar] [CrossRef]
- Kaushal, D.R.; Thinglas, T.; Tomita, Y.; Kuchii, S.; Tsukamoto, H. CFD modeling for pipeline flow of fine particles at high concentration. Int. J. Multiph. Flow 2012, 43, 85–100. [Google Scholar] [CrossRef]
- Januário, J.; Maia, C. CFD-DEM Simulation to Predict the Critical Velocity of Slurry Flows. J. Appl. Fluid Mech. 2020, 13, 161–168. [Google Scholar] [CrossRef]
- Dabirian, R.; Arabnejad Khanouki, H.; Mohan, R.S.; Shoham, O. Numerical Simulation and Modeling of Critical Sand-Deposition Velocity for Solid/Liquid Flow. SPE Prod. Oper. 2018, 33, 866–878. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, H.; Wen, C. Sand Transport and Deposition Behaviour in Subsea Pipelines for Flow Assurance. Energies 2019, 12, 4070. [Google Scholar] [CrossRef]
- Al-lababidi, S.; Yan, W.; Yeung, H. Sand Transportations and Deposition Characteristics in Multiphase Flows in Pipelines. J. Energy Resour. Technol. 2012, 134, 034501. [Google Scholar] [CrossRef]
- Danielson, T. Sand Transport Modeling in Multiphase Pipelines. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2007. [Google Scholar]
- Dabirian, R.; Mohan, R.; Shoham, O.; Kouba, G. Sand Transport in Slightly upward-inclined Multiphase Flow. J. Energy Resour. Technol. 2018, 140, 072901. [Google Scholar] [CrossRef]
- Tebowei, R.; Hossain, M.; Islam, S.Z.; Droubi, M.G.; Oluyemi, G. Investigation of sand transport in an undulated pipe using computational fluid dynamics. J. Pet. Sci. Eng. 2018, 162, 747–762. [Google Scholar] [CrossRef]
- Nossair, A.; Rodgers, P.; Goharzadeh, A. Influence of Pipeline Inclination on Hydraulic Conveying of Sand Particles. In Proceedings of the ASME International Mechanical Engineering Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; Volume 7. [Google Scholar]
- Stevenson, P.; Thorpe, R.B. Towards understanding sand transport in subsea flowlines. In Proceedings of the 9th International Conference on Multiphase ’99: Cannes, Paris, France, 16–18 June 1999; pp. 583–594. [Google Scholar]
- Wang, J.; Li, Y.; Pan, L.; Lai, Z.; Jian, S. Study of the Sediment Transport Law in a Reverse-Slope Section of a Pressurized Pipeline. Water 2020, 12, 3042. [Google Scholar] [CrossRef]
- Li, M.Z.; He, Y.P.; Liu, Y.D.; Huang, C. Hydrodynamic simulation of multi-sized high concentration slurry transport in pipelines. Ocean Eng. 2018, 163, 691–705. [Google Scholar] [CrossRef]
- Parkash, O.; Kumar, A.; Sikarwar, B.S. Analytical and comparative investigation of particulate size effect on slurry flow characteristics using computational fluid dynamics. J. Therm. Eng. 2021, 7, 220–239. [Google Scholar] [CrossRef]
- Ekambara, K.; Sanders, R.S.; Nandakumar, K.; Masliyah, J.H. Hydrodynamic Simulation of Horizontal Slurry Pipeline Flow Using ANSYS-CFX. Ind. Eng. Chem. Res. 2009, 48, 8159–8171. [Google Scholar] [CrossRef]
- Alihosseini, M.; Thamsen, P.U. Analysis of sediment transport in sewer pipes using a coupled CFD-DEM model and experimental work. Urban Water J. 2019, 16, 259–268. [Google Scholar] [CrossRef]

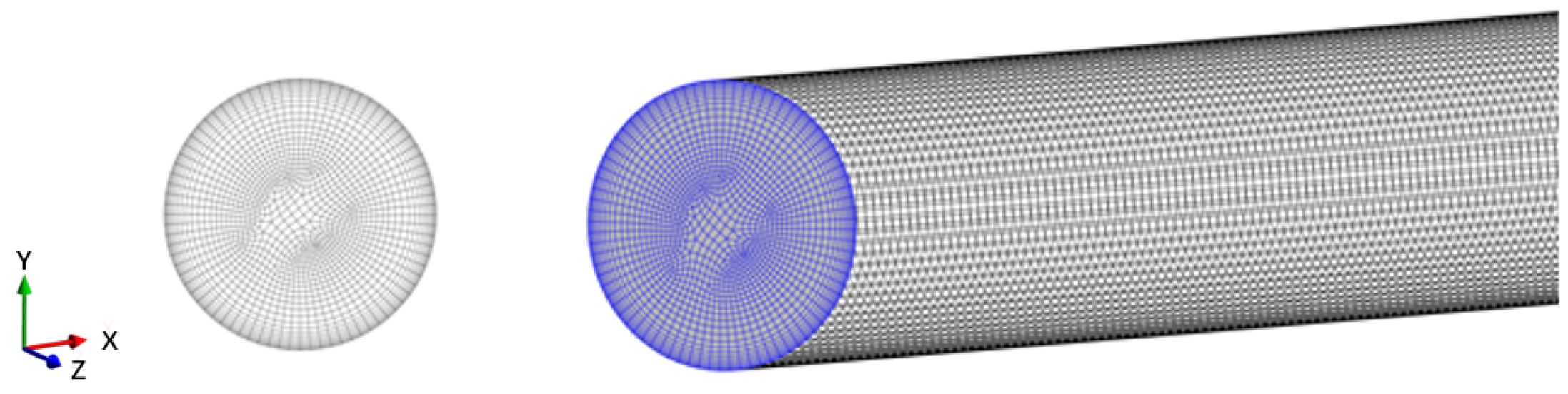
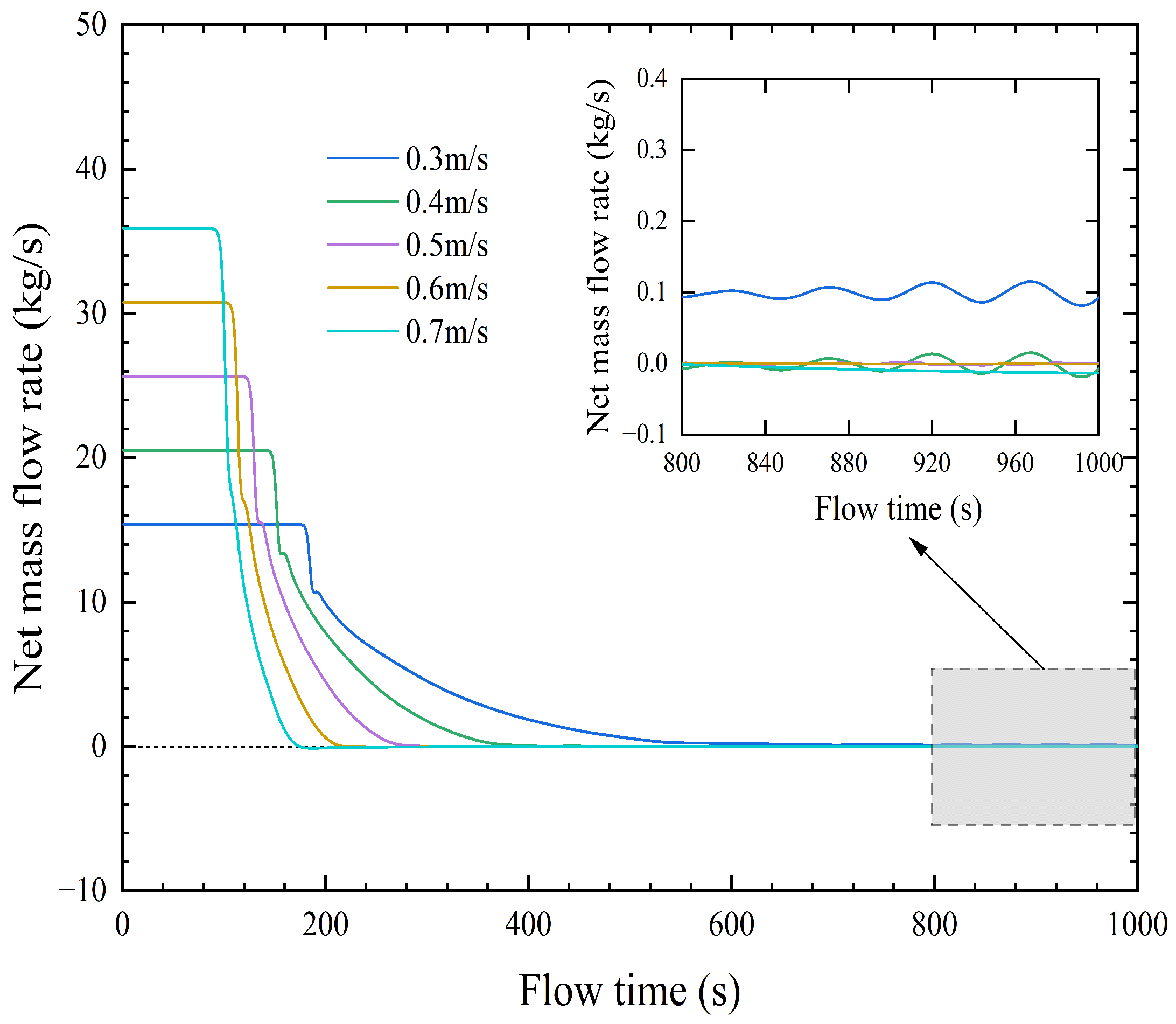
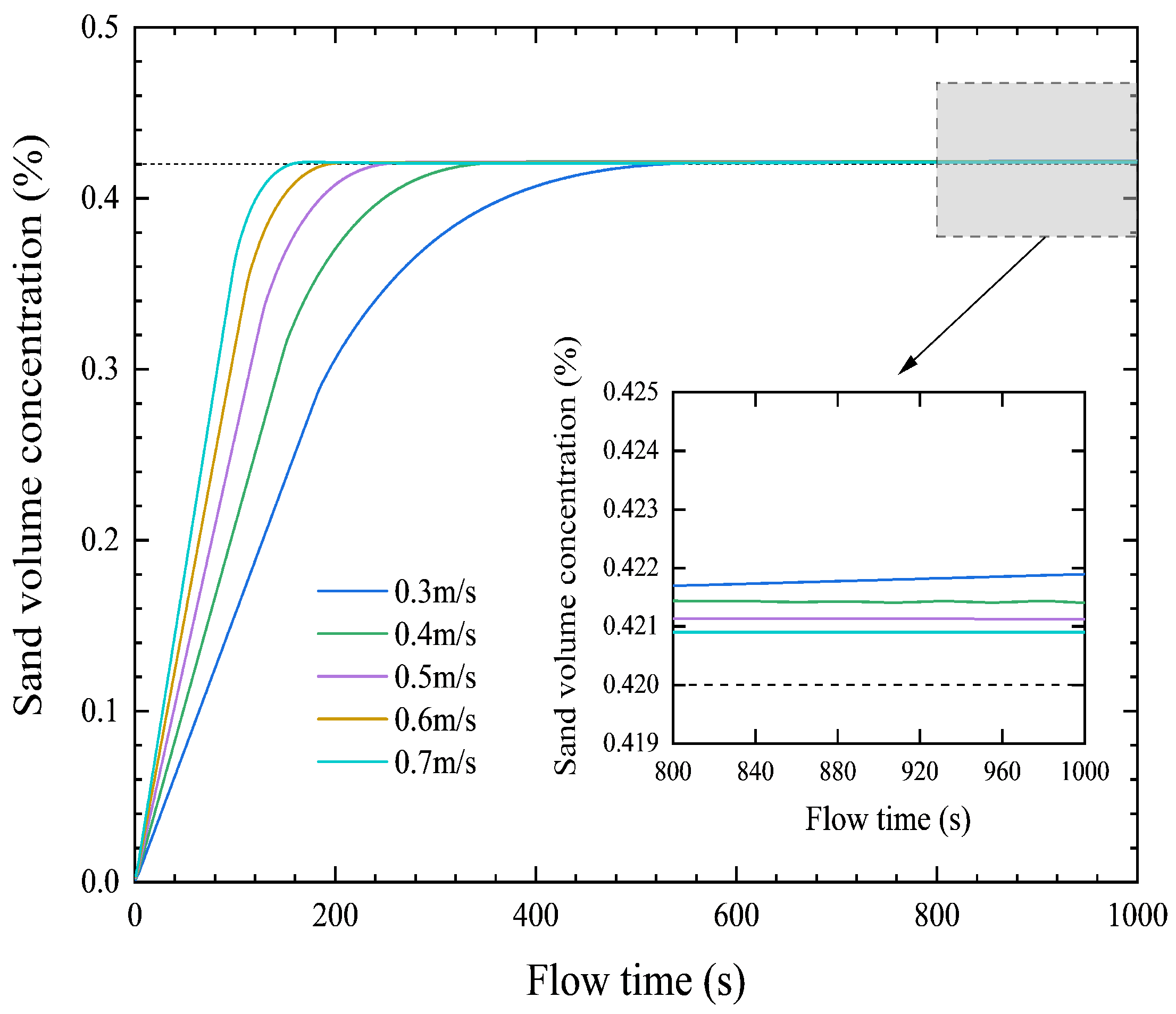

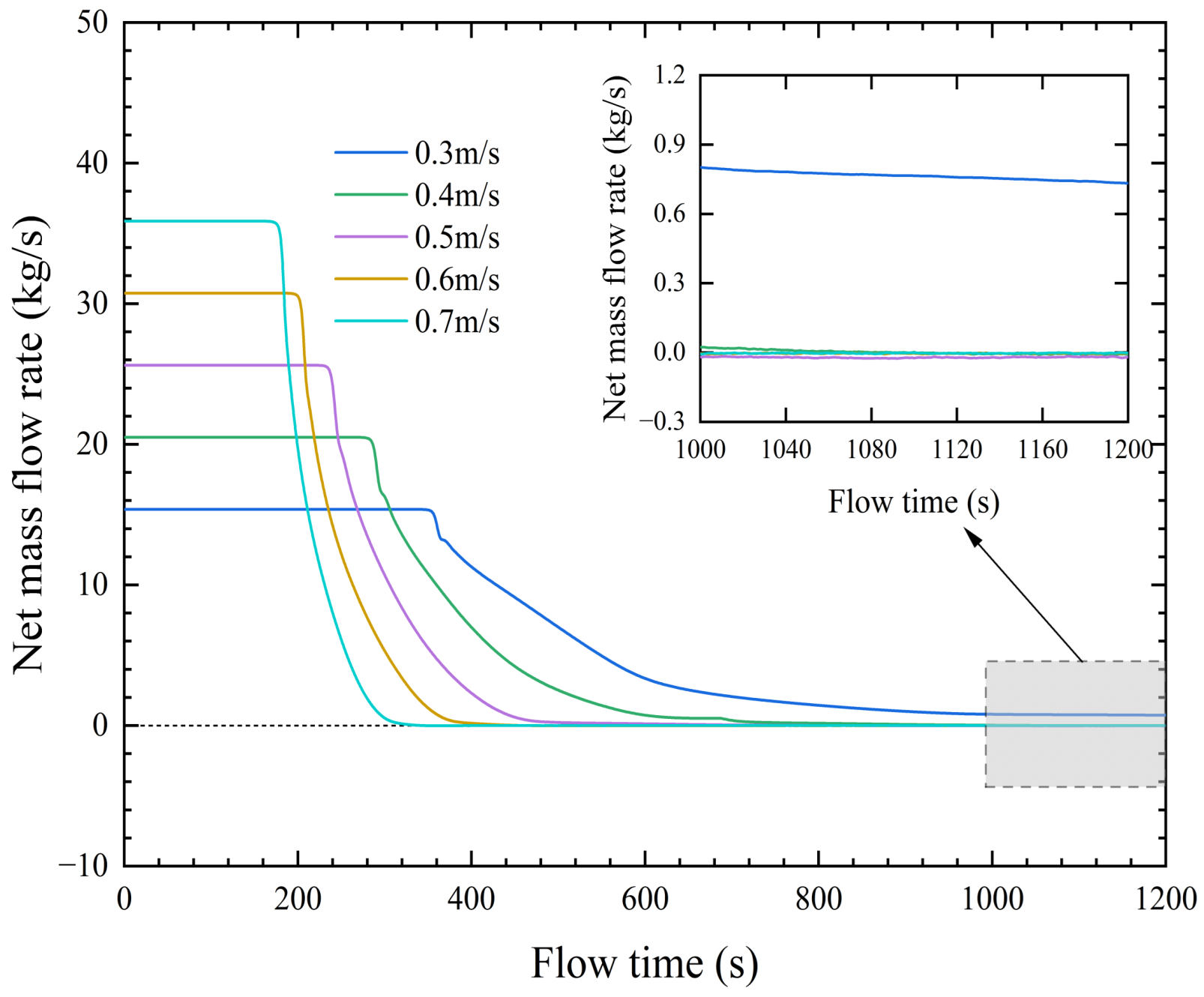

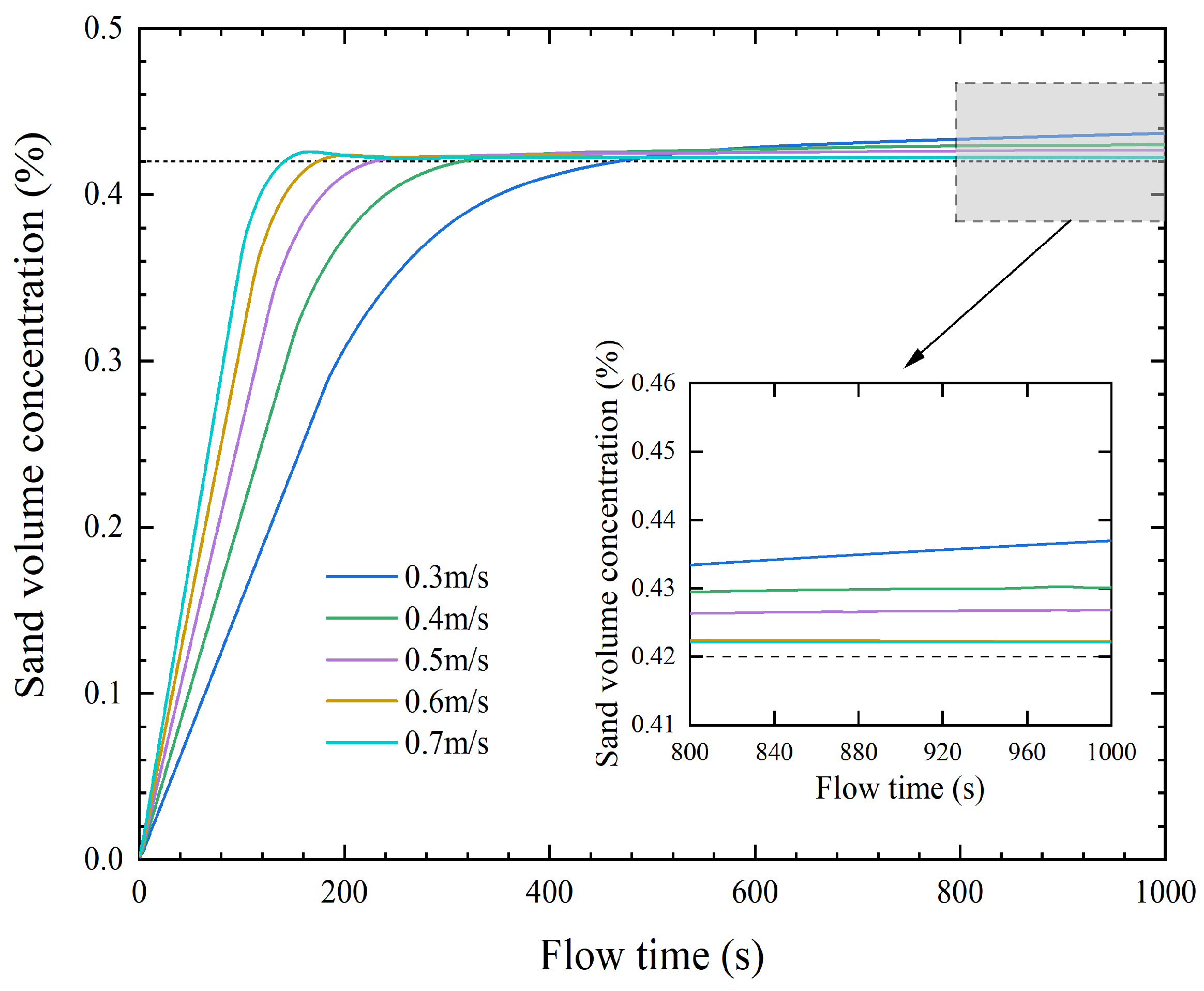
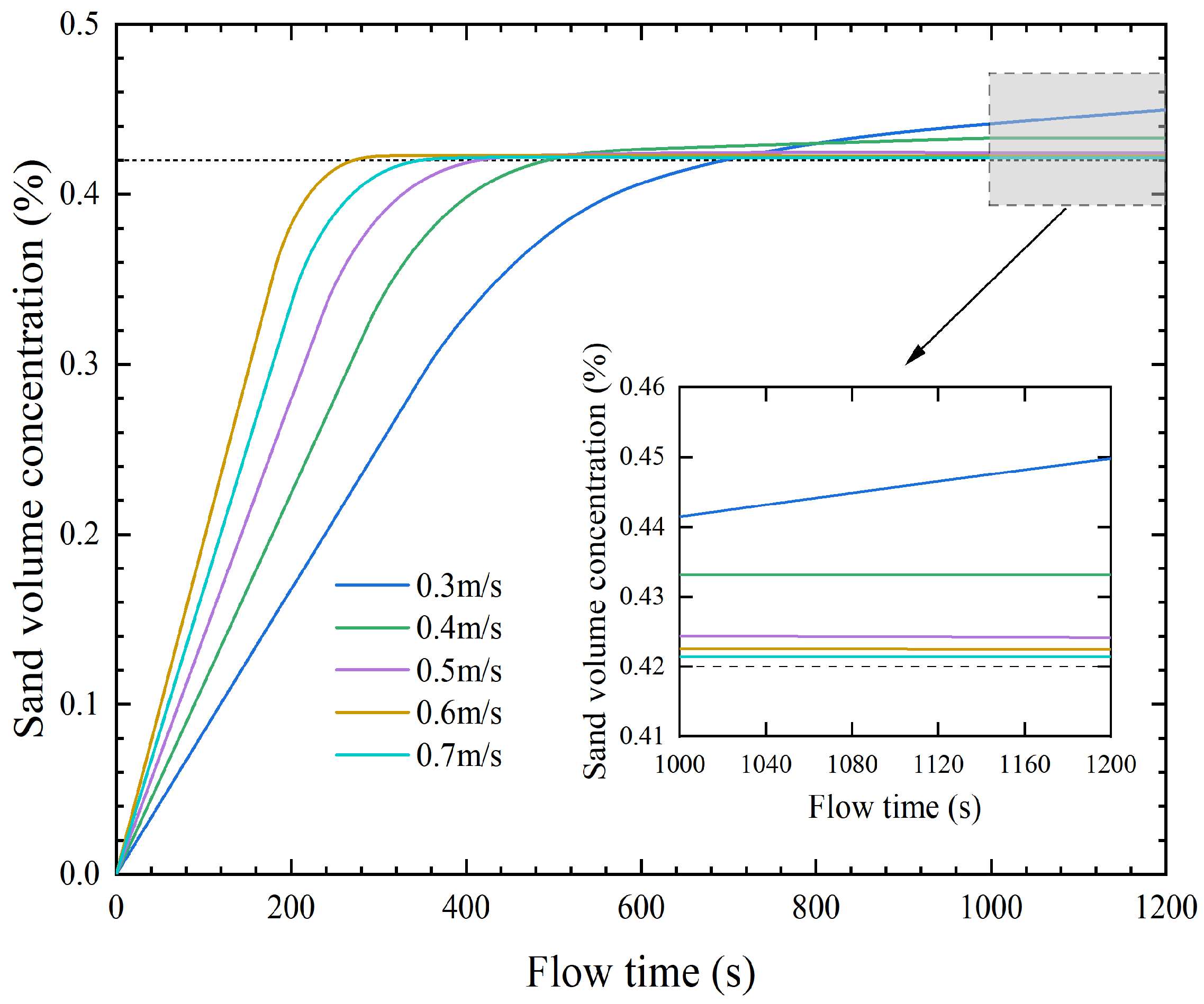
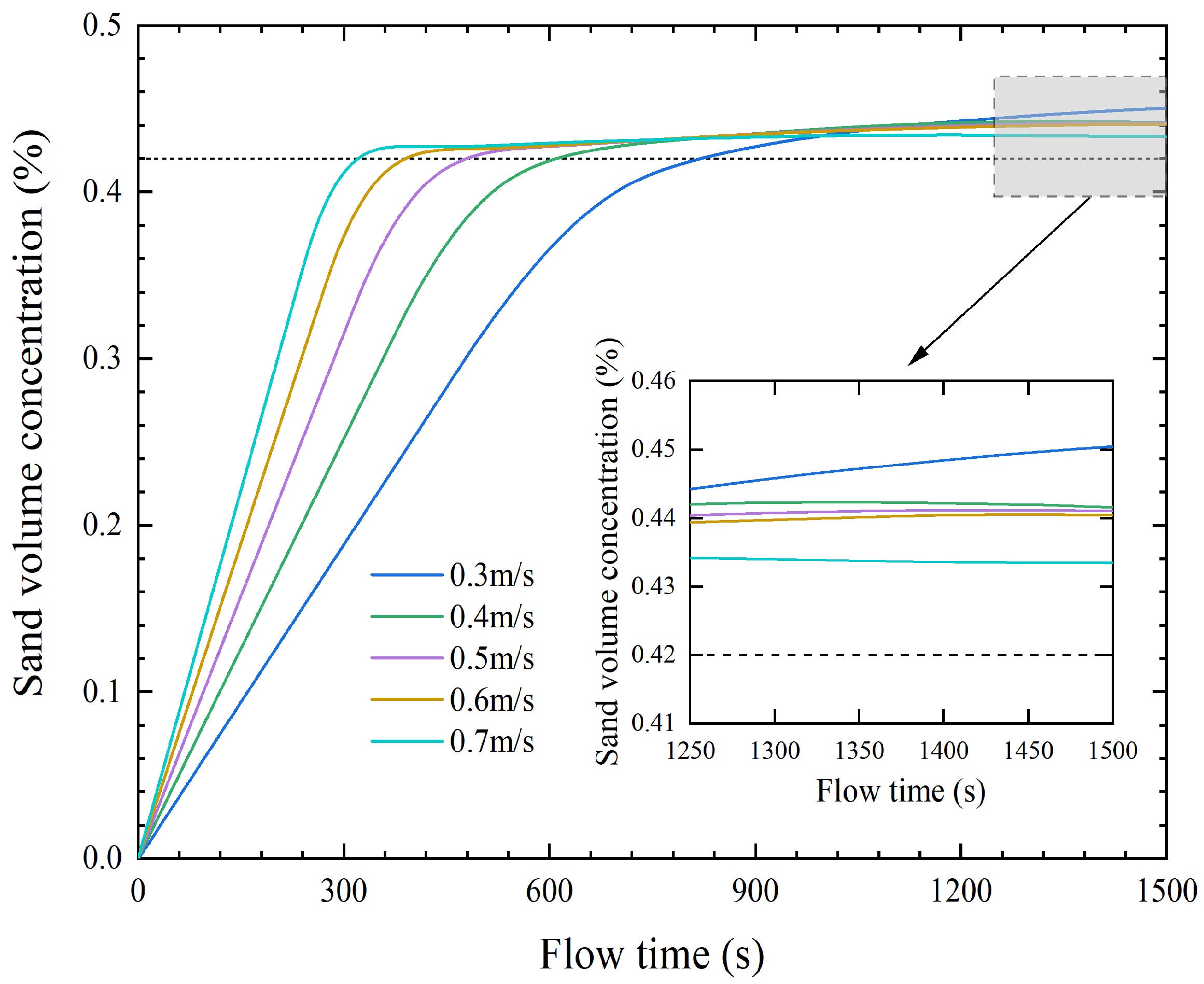
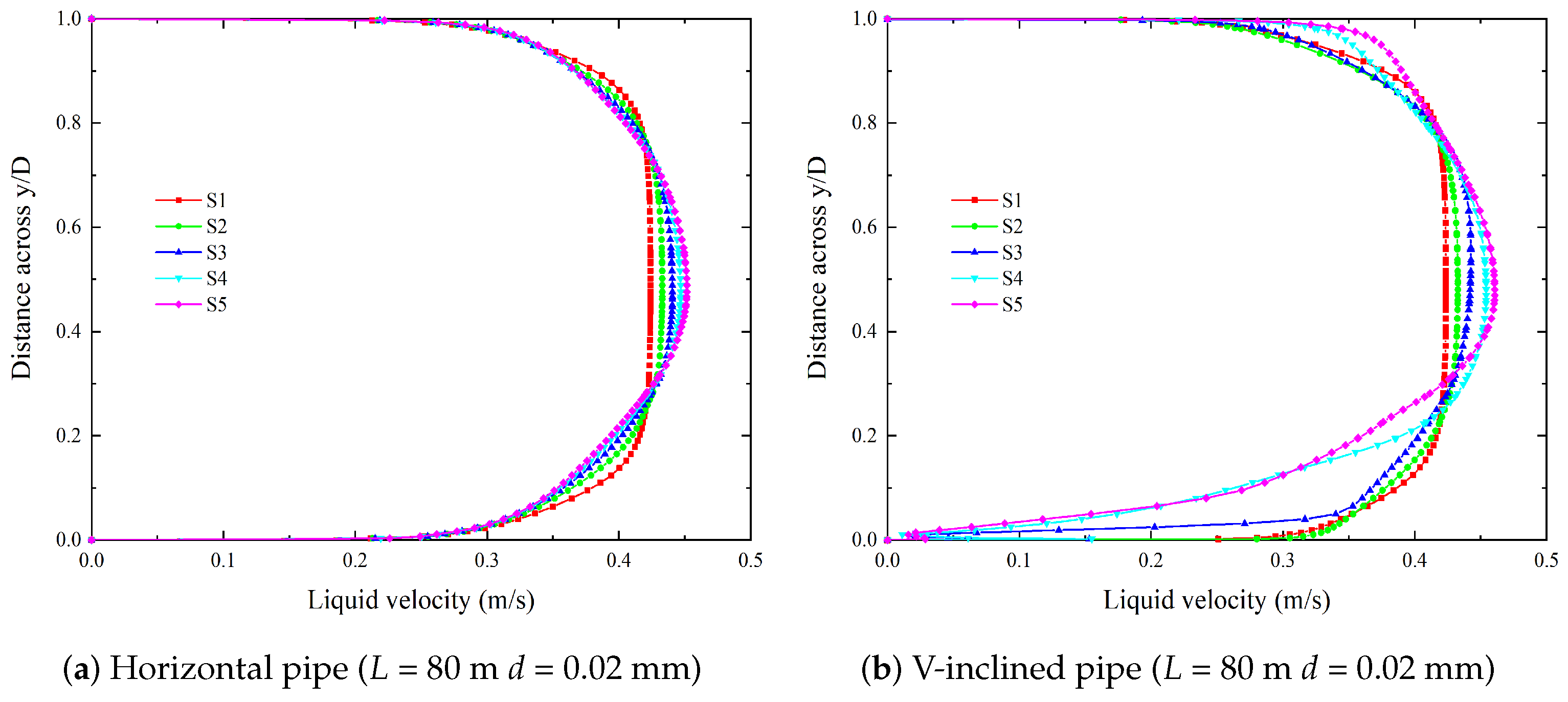


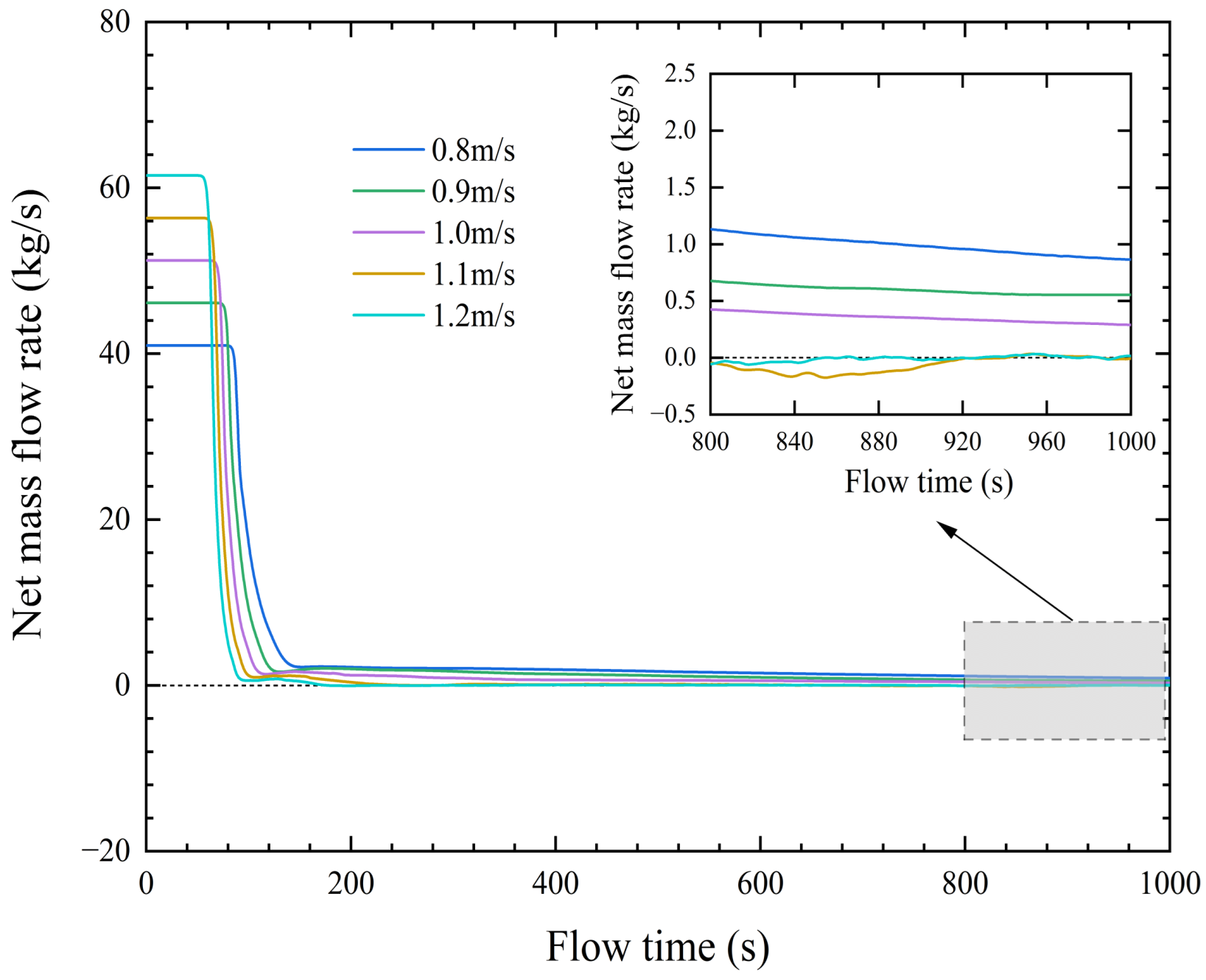
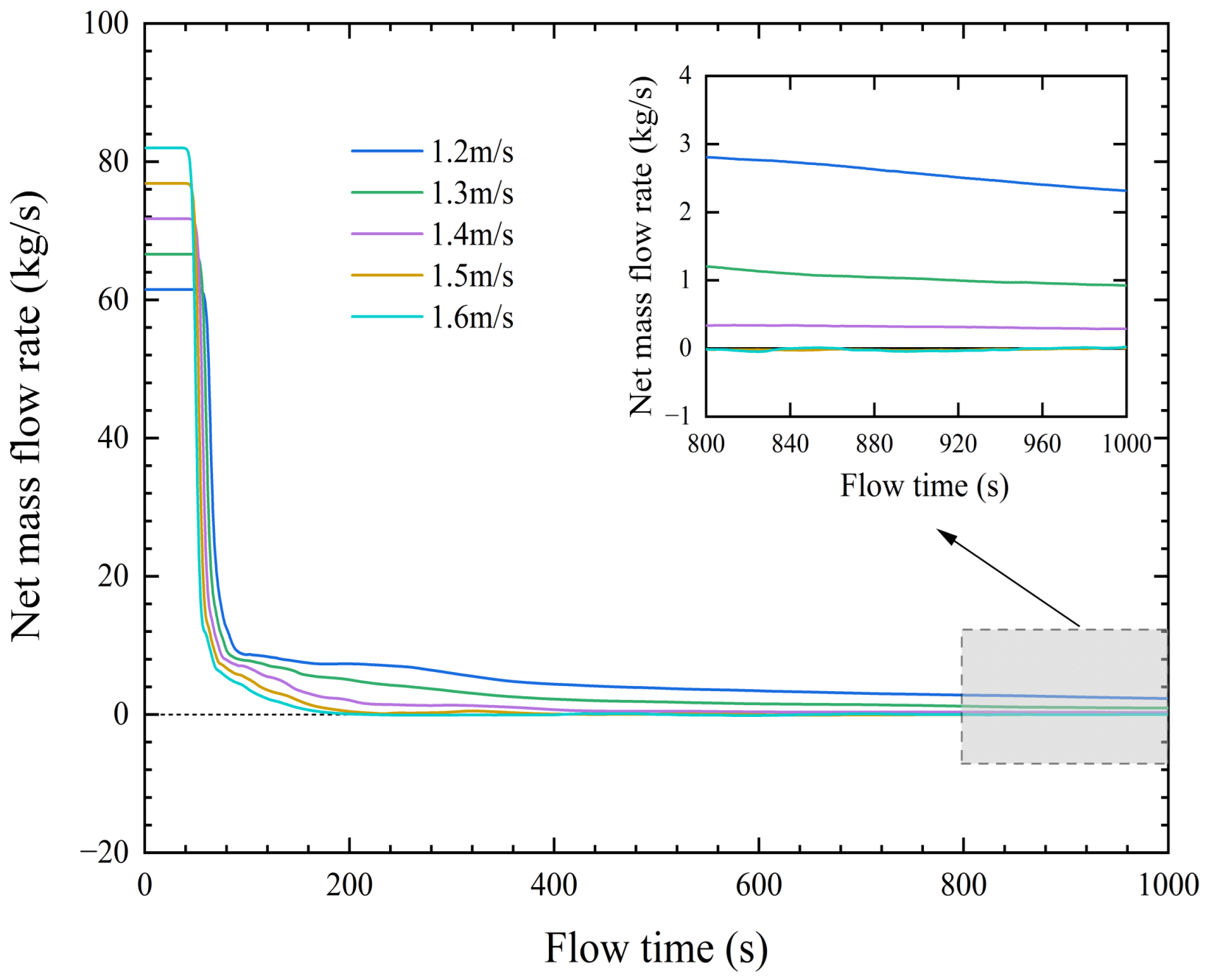
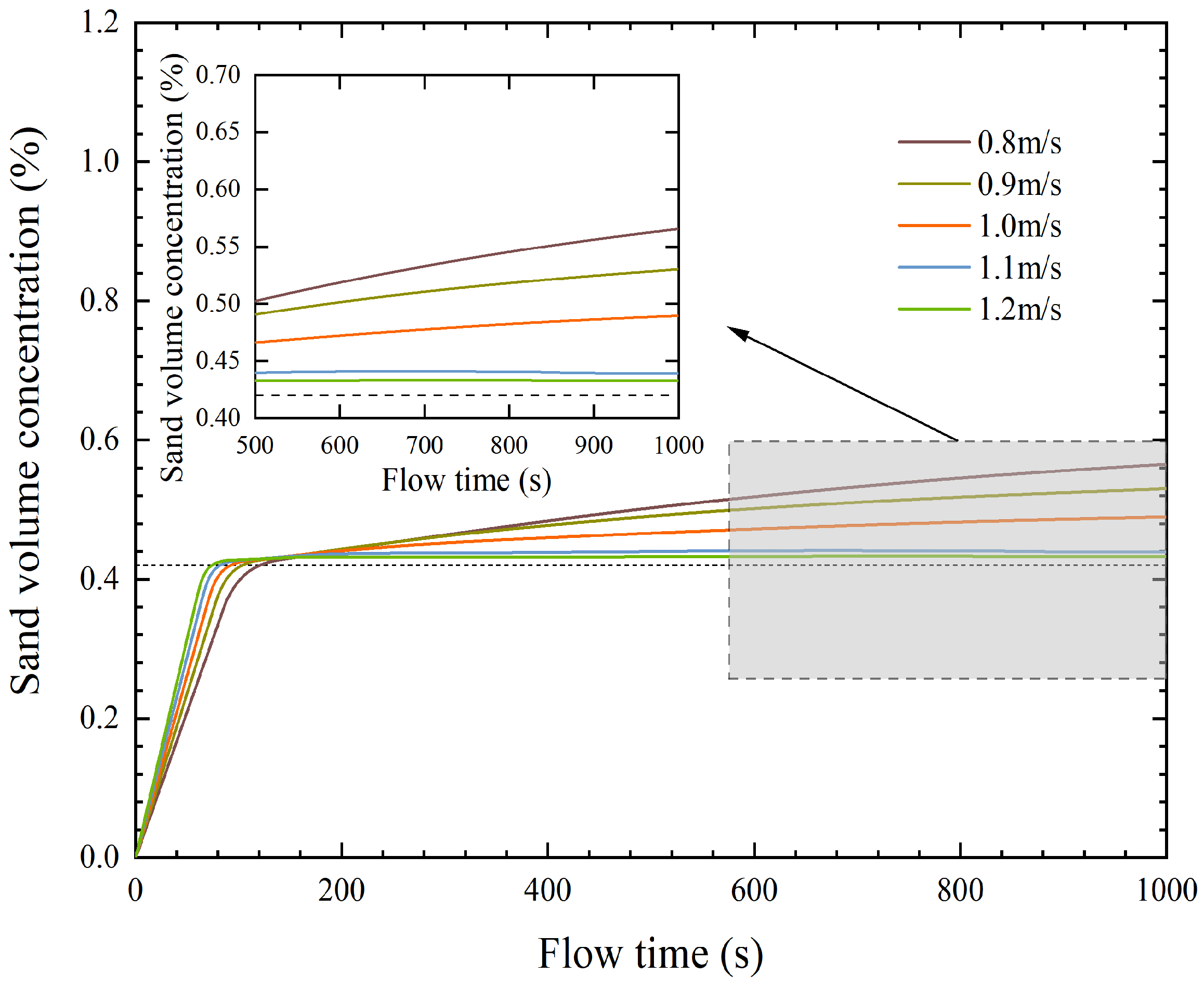

| Scheme Number | Grid Number | Slurry Velocity (m/s) | Relative Error (%) |
|---|---|---|---|
| 1 | 764,000 | 0.3029 | 0.66 |
| 2 | 1,487,600 | 0.3010 | 0.03 |
| 3 | 1,855,600 | 0.3009 | 0 |
| Parameters | Horizontal Pipe | V-Inclined Pipe |
|---|---|---|
| ±2° | ||
| Grid cell size (m) | 0.05 | 0.05 |
| Pipe length L (m) | 80 | 80/150/200 |
| Pipe diameter D (mm) | 2600 | 2600 |
| Liquid density ( ) | 998.2 | 998.2 |
| Sand density () | 2300 | 2300 |
| Particle size d (mm) | 0.02 | 0.02\0.05\0.1 |
| Sand content () | 9.71 | 9.71 |
| Sand volume concentration (%) | 0.42 | 0.42 |
| Inflow velocities (m/s) | 0.3–0.7 | 0.3–1.6 |
| Reference | Empirical Formula |
|---|---|
| Durand [16] | |
| Wasp [12] | |
| Shook [13] | |
| He Wuquan [19] |
| Particle Size | Emprical Formula | Numerical Simulation | |
|---|---|---|---|
| Wasp | He Wuquan | ||
| 0.02 mm | 0.99 m/s | 0.43 m/s | 0.4 m/s |
| 0.05 mm | 1.16 m/s | 1.10 m/s | 1.1 m/s |
| 0.1 mm | 1.30 m/s | 2.05 m/s | 1.5 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, R.; Qi, D.; Zeng, H.; Huang, X.; Li, B.; Wang, Y.; Bai, W.; Wang, Z. Study on Critical Velocity of Sand Transport in V-Inclined Pipe Based on Numerical Simulation. Water 2022, 14, 2627. https://doi.org/10.3390/w14172627
Yao R, Qi D, Zeng H, Huang X, Li B, Wang Y, Bai W, Wang Z. Study on Critical Velocity of Sand Transport in V-Inclined Pipe Based on Numerical Simulation. Water. 2022; 14(17):2627. https://doi.org/10.3390/w14172627
Chicago/Turabian StyleYao, Rao, Dunzhe Qi, Haiyan Zeng, Xingxing Huang, Bo Li, Yi Wang, Wenqiang Bai, and Zhengwei Wang. 2022. "Study on Critical Velocity of Sand Transport in V-Inclined Pipe Based on Numerical Simulation" Water 14, no. 17: 2627. https://doi.org/10.3390/w14172627







