Implementation of TETIS Hydrologic Model into the Hillslope Link Model Framework
Abstract
:1. Introduction
1.1. Deficiencies of Previous Models
1.1.1. Model Performance in Western Iowa
1.1.2. Model Performance in Des Moines Lobe
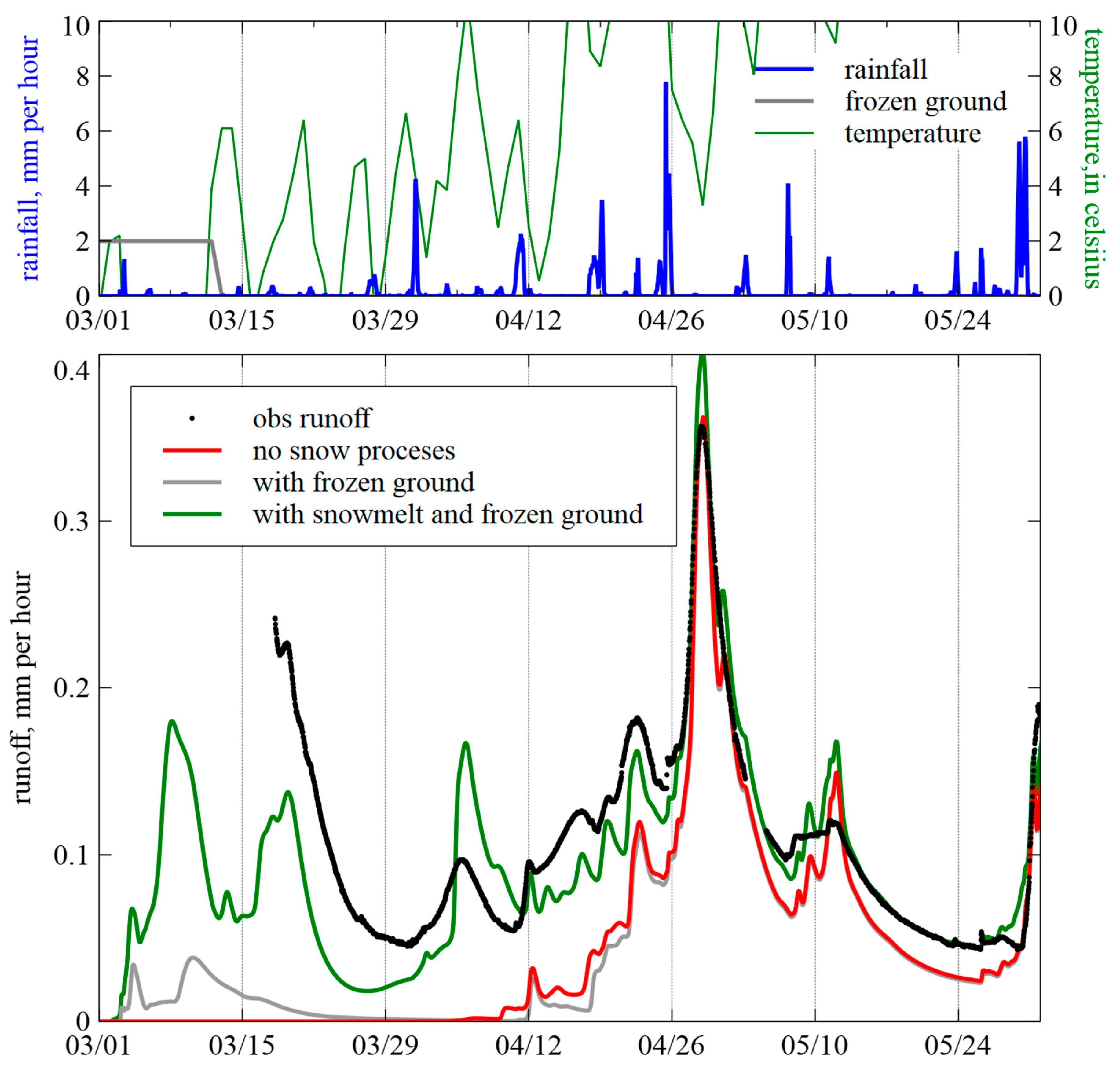
1.1.3. Flow Events Governed by Snowmelt
1.2. Development of a New Model and Novel Contribution
2. Materials and Methods
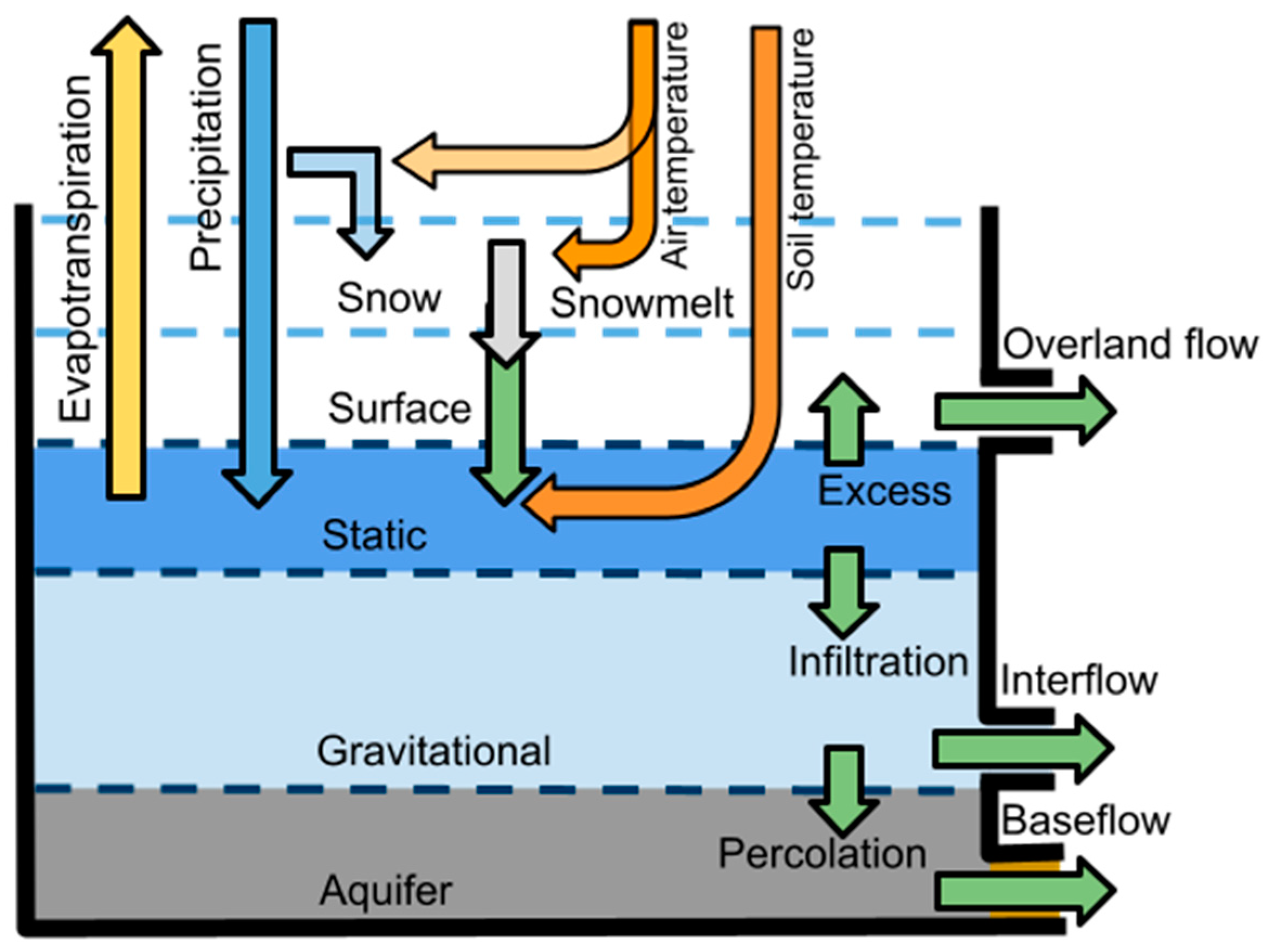
2.1. The Hillslope Link Model Framework
2.2. Model Forcings
2.3. Runoff Generation and Routing
2.3.1. Snow Tank
2.3.2. Static Tank
2.3.3. Surface Tank
2.3.4. Gravitational Tank
2.3.5. Aquifer
2.3.6. Channel
2.4. Study Area
3. Applications
3.1. Simulation of Snow-Related Processes
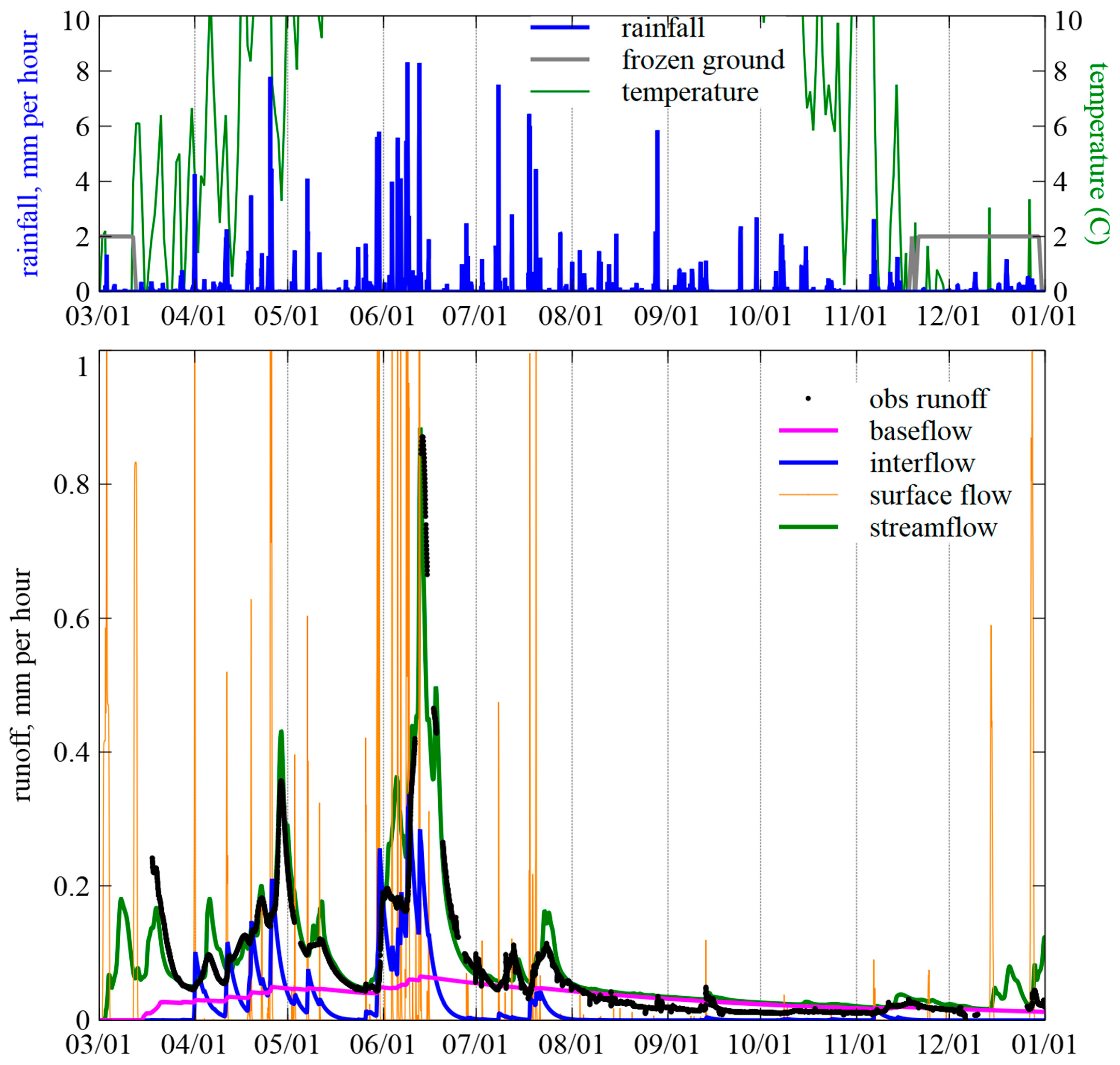
3.2. Simulation of discharge at the Des Moines Lobe and Western Iowa
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Centre for Research on the Epidemiology of Disasters Crunch 66-Disasters Year in Review 2021. Available online: https://cred.be/sites/default/files/CREDCrunch66N.pdf (accessed on 10 May 2022).
- Chatzichristaki, C.; Stefanidis, S.; Stefanidis, P.; Stathis, D. Analysis of the flash flood in rhodes island (south Greece) on 22 November 2013. Silva Balc. 2015, 16, 76–86. [Google Scholar]
- Diakakis, M. Characteristics of Infrastructure and Surrounding Geo-Environmental Circumstances Involved in Fatal Incidents Caused by Flash Flooding: Evidence from Greece. Water 2022, 14, 746. [Google Scholar] [CrossRef]
- Porter, J.R.; Shu, E.; Amodeo, M.; Hsieh, H.; Chu, Z.; Freeman, N. Community flood impacts and infrastructure: Examining national flood impacts using a high precision assessment tool in the united states. Water 2021, 13, 3125. [Google Scholar] [CrossRef]
- Mantilla, R.; Krajewski, W.F.; Velasquez, N.; Small, S.J.; Ayalew, T.B.; Quintero, F.; Jadidoleslam, N.; Fonley, M. The Hydrological Hillslope-Link Model for Space-Time Prediction of Streamflow: Insights and Applications at the Iowa Flood Center. In Extreme Weather Forecasting; Astitha, M., Nikolopoulos, E.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; ISBN 9780128201244. [Google Scholar]
- Quintero, F.; Krajewski, W.F.; Mantilla, R.; Small, S.; Seo, B.-C. A Spatial–Dynamical Framework for Evaluation of Satellite Rainfall Products for Flood Prediction. J. Hydrometeorol. 2016, 17, 2137–2154. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Ceynar, D.; Demir, I.; Goska, R.; Kruger, A.; Langel, C.; Mantilllla, R.; Niemeier, J.; Quintero, F.; Seo, B.C.; et al. Real-time flood forecasting and information system for the state of Iowa. Bull. Am. Meteorol. Soc. 2017, 98, 539–554. [Google Scholar] [CrossRef]
- Fonley, M.R.; Qiu, K.; Velásquez, N.; Haut, N.K.; Mantilla, R. Development and Evaluation of an ODE representation of 3D subsurface tile drainage flow using the HLM flood forecasting system. Water Resour. Res. 2021, 57, e2020WR028177. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R.; Small, S.J. Exploring the effects of hillslope-channel link dynamics and excess rainfall properties on the scaling structure of peak-discharge. Adv. Water Resour. 2014, 64, 9–20. [Google Scholar] [CrossRef]
- Quintero, F.; Krajewski, W.F.; Seo, B.C.; Mantilla, R. Improvement and evaluation of the Iowa Flood Center Hillslope Link Model (HLM) by calibration-free approach. J. Hydrol. 2020, 584, 124686. [Google Scholar] [CrossRef]
- Lin, Y.; Mitchell, K.E. The NCEP Stage II/IV hourly precipitation analyses: Development and applications. In Proceedings of the 19th Conference on Hydrology, American Meteorological Society, San Diego, CA, USA, 9–13 January 2005; Paper 1.2. pp. 2–5. [Google Scholar]
- Seo, B.-C.; Krajewski, W.F. Statewide real-time quantitative precipitation estimation using weather radar and NWP model analysis: Algorithm description and product evaluation. Environ. Model. Softw. 2020, 132, 104791. [Google Scholar] [CrossRef]
- Velásquez, N.; Mantilla, R.; Krajewski, W.; Fonley, M.; Quintero, F. Improving Hillslope Link Model Performance from Non-Linear Representation of Natural and Artificially Drained Subsurface Flows. Hydrology 2021, 8, 187. [Google Scholar] [CrossRef]
- Vélez, J.I. Estrategia de simulación hidrológica distribuida: Integración conceptual de hidrología, hidráulica y geomorfología. Rev. Acad. Colomb. Cienc. Exactas Físicas Nat. 2013, 37, 393–409. [Google Scholar]
- Francés, F.; Vélez, J.I.; Vélez, J.J. Split-parameter structure for the automatic calibration of distributed hydrological models. J. Hydrol. 2007, 332, 226–240. [Google Scholar] [CrossRef]
- Small, S.J.; Jay, L.O.; Mantilla, R.; Curtu, R.; Cunha, L.K.; Fonley, M.; Krajewski, W.F. An asynchronous solver for systems of ODEs linked by a directed tree structure. Adv. Water Resour. 2013, 53, 23–32. [Google Scholar] [CrossRef]
- Singh, V.P. The Snowmelt Runoff Model (SRM). Comput. Model. Watershed Hydrol. 1995, 1, 477–520. [Google Scholar]
- Martinec, J.; Rango, A. Areal distribution of snow water equivalent evaluated by snow cover monitoring. Water Resour. Res. 1981, 17, 1480–1488. [Google Scholar] [CrossRef]
- Budikova, D.; Coleman, J.S.M.; Strope, S.A.; Austin, A. Hydroclimatology of the 2008 Midwest floods. Water Resour. Res. 2010, 46, W12524. [Google Scholar] [CrossRef] [Green Version]
- Krajewski, W.F.; Mantilla, R. Why Were the 2008 Floods So Large? In A Watershed Year: Anatomy of the Iowa Floods of 2008; University of Iowa Press: Iowa City, IA, USA, 2010; p. 9. [Google Scholar]
- Mutel, C.F. A Watershed Year: Anatomy of the Iowa Floods of 2008; University of Iowa Press: Iowa City, IA, USA, 2010. [Google Scholar]
- Todey, D.P.; Herzmann, D.E.; Takle, E.S. The Iowa Environmental Mesonetcombining observing systems into a single network. In Sixth Symposium on Integrated Observing Systems; Iowa State University: Ames, IA, USA, 2002. [Google Scholar]

| Name | Symbol | Units Required |
|---|---|---|
| Air temperature threshold | Tmax | Celsius degree |
| Melting rate | M | mm/day/degree Celsius |
| Maximum storage static tank | Hmax | mm |
| Upper soil infiltration rate | I2 | mm/hour |
| Overland flow velocity | Vsurf | m/s |
| Deep soil infiltration rate | I3 | mm/hour |
| Gravitational storage residence time | C3 | Days |
| Aquifer storage residence time | C4 | Days |
| Flow velocity in channel | Vc | m/s |
| Discharge exponent | ExpQ | Adimensional |
| Drainage Area exponent | ExpA | Adimensional |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintero, F.; Velásquez, N. Implementation of TETIS Hydrologic Model into the Hillslope Link Model Framework. Water 2022, 14, 2610. https://doi.org/10.3390/w14172610
Quintero F, Velásquez N. Implementation of TETIS Hydrologic Model into the Hillslope Link Model Framework. Water. 2022; 14(17):2610. https://doi.org/10.3390/w14172610
Chicago/Turabian StyleQuintero, Felipe, and Nicolás Velásquez. 2022. "Implementation of TETIS Hydrologic Model into the Hillslope Link Model Framework" Water 14, no. 17: 2610. https://doi.org/10.3390/w14172610






