Developing Water-Quality Model for Jingpo Lake Based on EFDC
Abstract
:1. Introduction
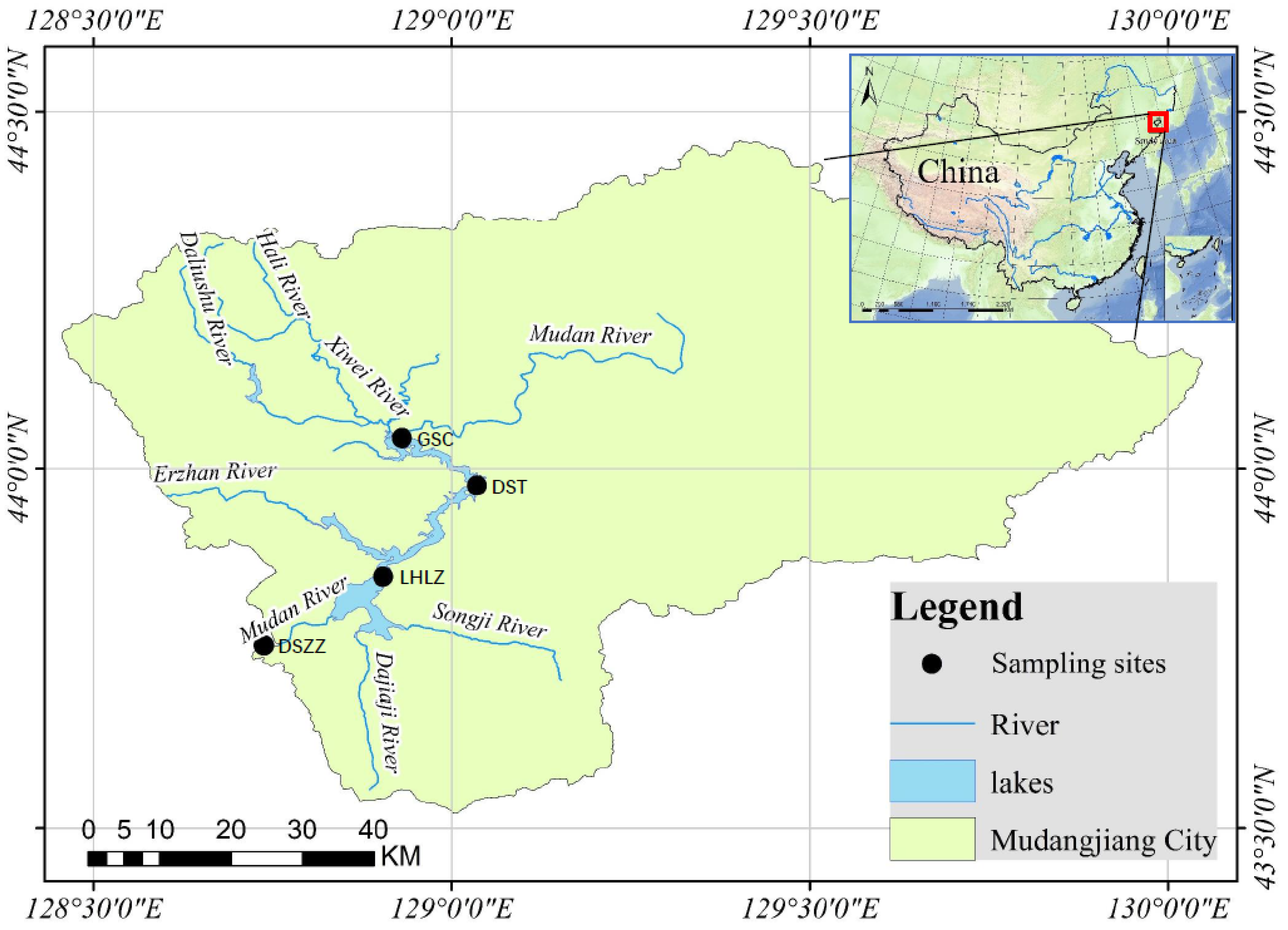
2. Study Area
3. Model Construction
3.1. Principle of the Model
3.2. Grid Division, Initial Conditions and Boundary Conditions Setting
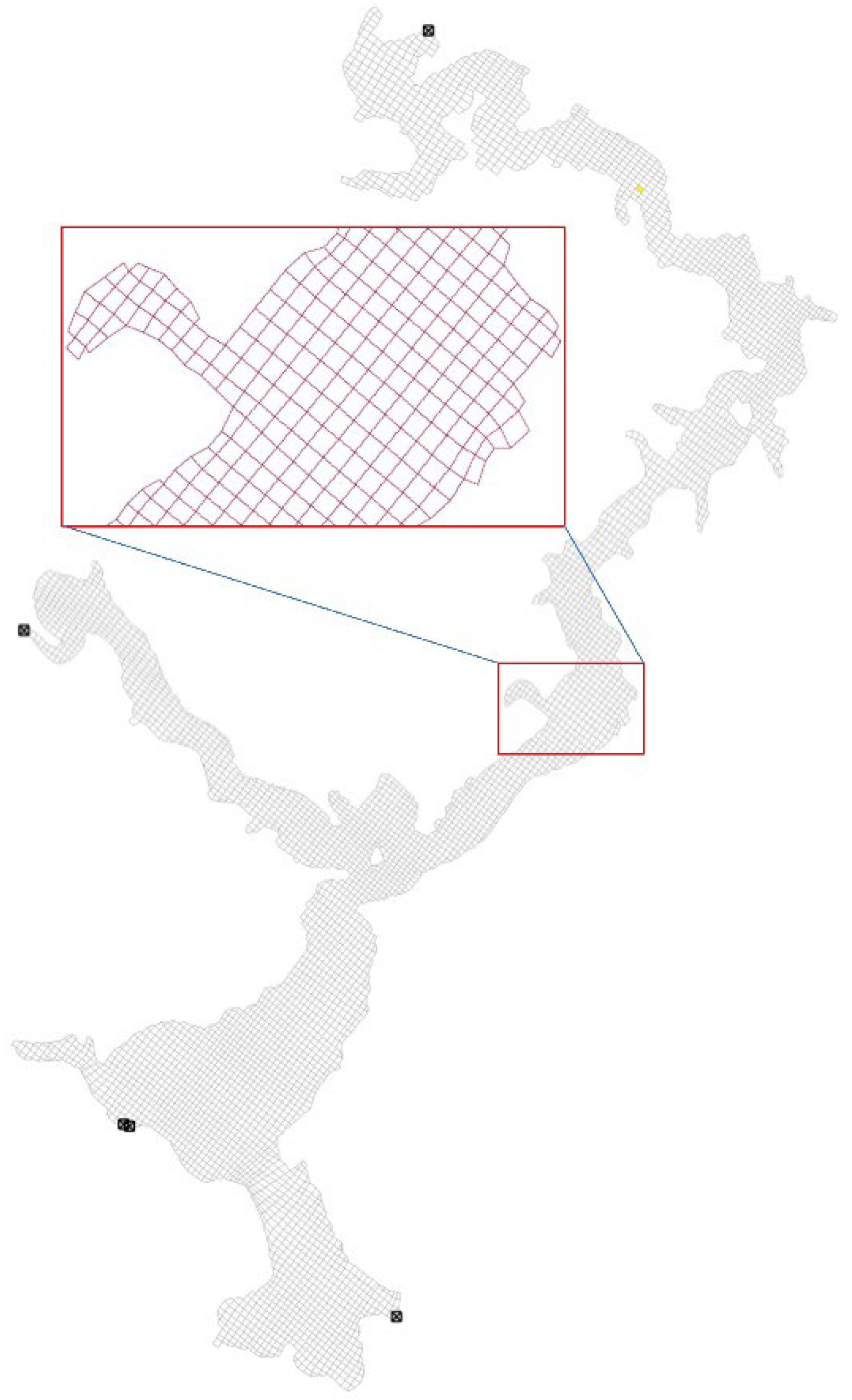
3.2.1. Grid Division
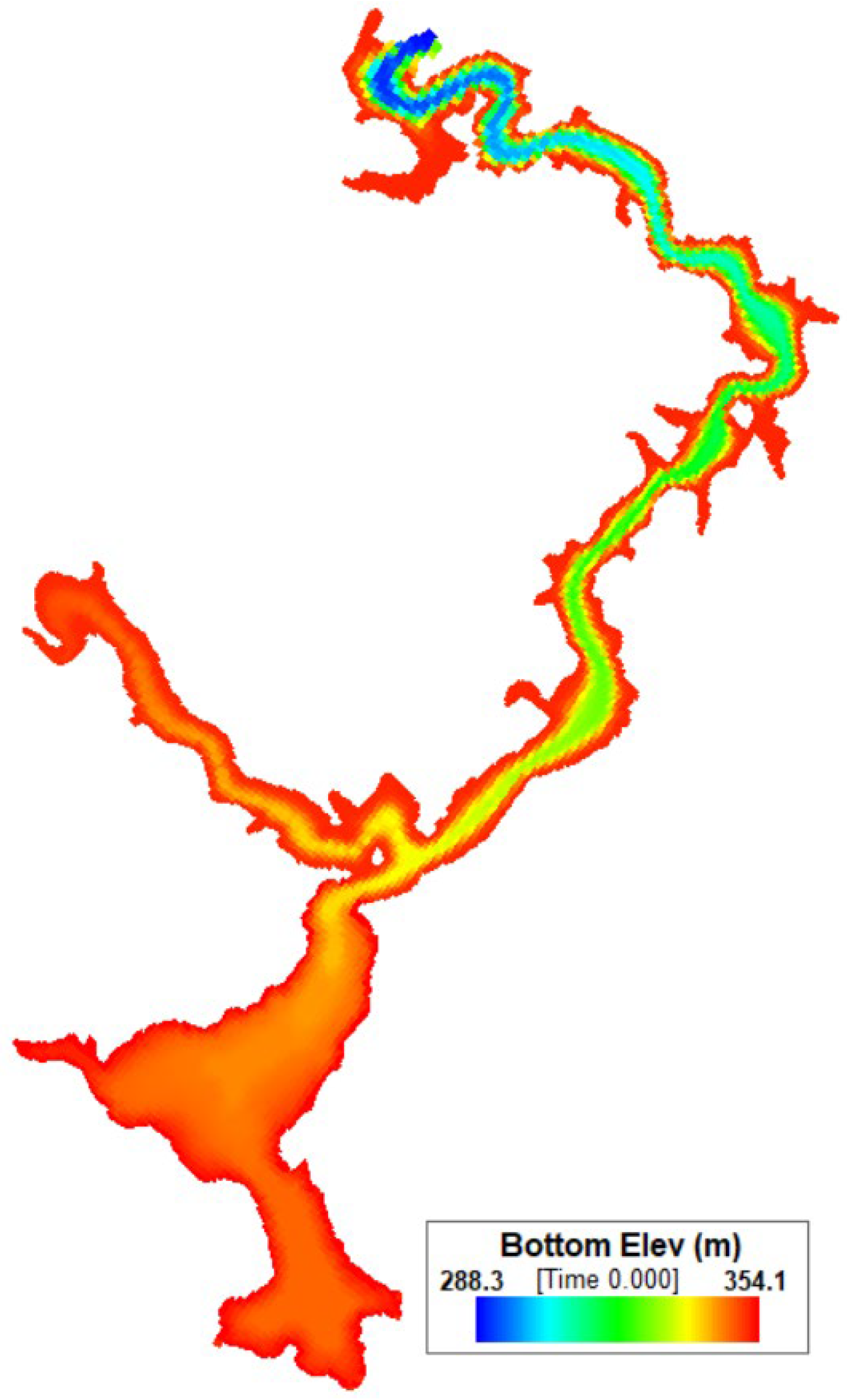
3.2.2. Initial and Boundary Conditions
3.3. Model Parameters and Calibration Method
4. Results and Discussion
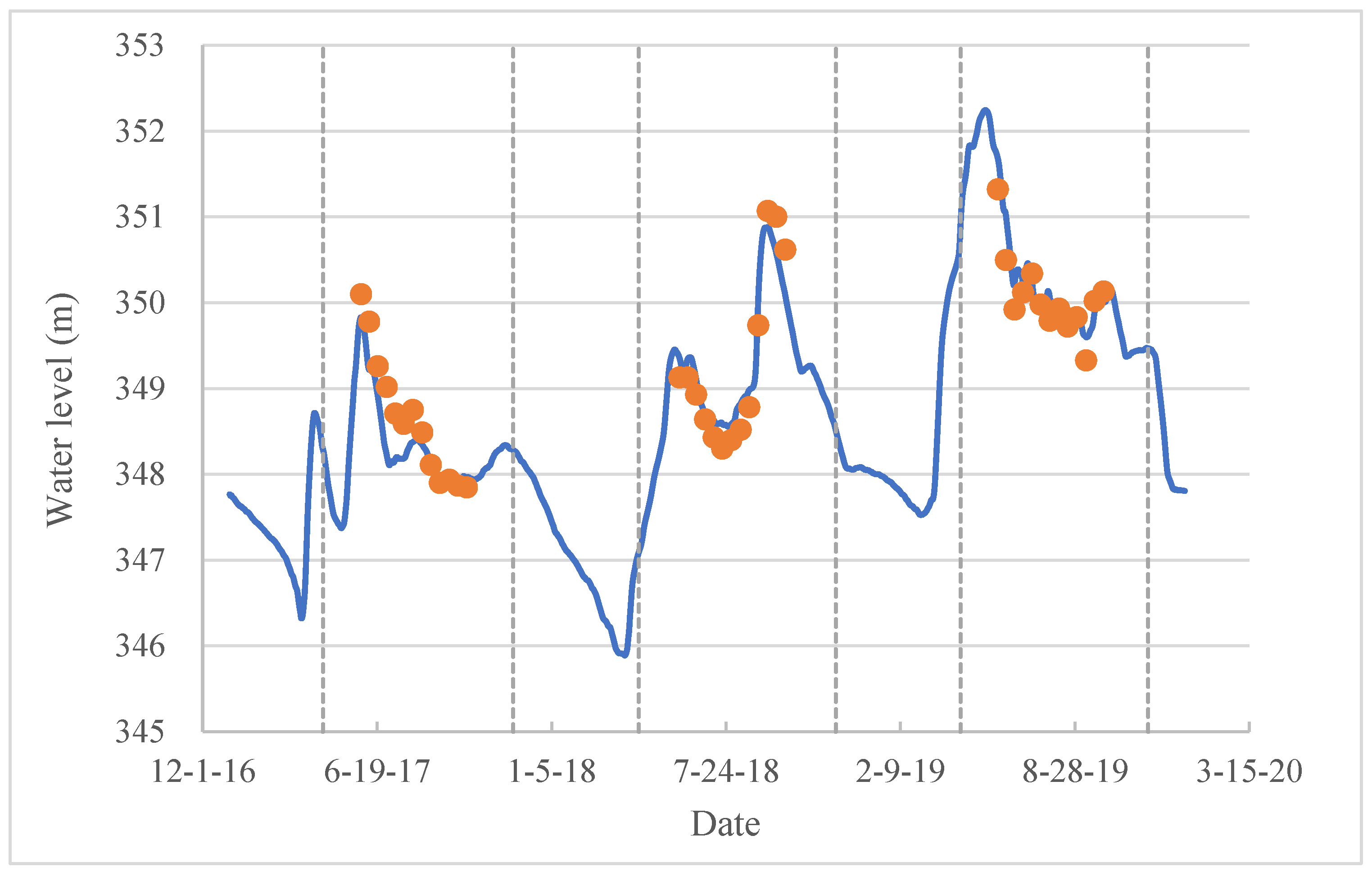
4.1. Hydrodynamics
4.2. Water Quality
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.G. Water Quality Characteristics and Simulation Methods of Northern Rivers during Ice-Covered Periods. Ph.D. Thesis, Tsinghua University, Beijing, China, 2013. [Google Scholar]
- Wang, X.E.; Dong, D.M.; Zhao, W.J.; Li, J.; Zhang, H.L.; Du, Y.G. Reduction Mode of Organic Pollutants in Rivers During the Icebound Season. J. JILIN Univ. Sci. Ed. 2003, 41, 392–395. [Google Scholar]
- Huttulaa, T.; Pulkkanenb, M.; Arkhipovc, B.; Leppäranta, M.; Solbakov, V.; Shirasawa, K.; Salonen, K. Modelling circulation in an ice-covered lake. Est. J. Earth Sci. 2010, 59, 298–309. [Google Scholar] [CrossRef]
- Lotsari, E.; Tarsa, T.; Kämäri, M.; Alho, P.; Kasvi, E. Spatial variation of flow characteristics in a subarctic meandering river in ice-covered and open-channel conditions: A 2D hydrodynamic modelling approach. Earth Surf. Process. Landf. 2019, 44, 1509–1529. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.H. Modelling ocean waves in ice-covered seas. Appl. Ocean Res. 2019, 83, 30–36. [Google Scholar] [CrossRef]
- Yang, B.; Wells, M.G.; McMeans, B.C.; Dugan, H.A.; Rusak, J.A.; Weyhenmeyer, G.A.; Brentrup, J.A.; Hrycik, A.R.; Laas, A.; Pilla, R.M.; et al. A New Thermal Categorization of Ice-Covered Lakes. Geophys. Res. Lett. 2021, 48, e2020GL091374. [Google Scholar] [CrossRef]
- Forrest, A.L.; Laval, B.E.; Pieters, R.; Lim, S.S.D. A cyclonic gyre in an ice-covered lake. Limnol. Oceanogr. 2013, 58, 363–375. [Google Scholar] [CrossRef]
- Kletetschka, G.; Fischer, T.; Mls, J.; Dedecek, P. Temperature fluctuations underneath the ice in Diamond Lake, Hennepin County, Minnesota. Water Resour. Res. 2013, 49, 3306–3313. [Google Scholar] [CrossRef]
- Yang, F.; Feng, W.Y.; Matti, L.; Yang, Y.; Merkouriadi, I.; Cen, R.; Bai, Y.; Li, C.; Liao, H. Simulation and Seasonal Characteristics of the Intra-Annual Heat Exchange Process in a Shallow Ice-Covered Lake. Sustainability 2020, 12, 7832. [Google Scholar] [CrossRef]
- Kubat, I.; Sayed, M.; Savage, S.; Carrieres, T. Numerical simulations of ice thickness redistribution in the Gulf of St. Lawrence. Cold Reg. Sci. Technol. 2010, 60, 15–28. [Google Scholar] [CrossRef]
- Xiao, J.M.; Jin, L.H.; Xie, Y.G.; Huo, Y.D. Study on mechanism of formation and melting of reservoir ice cover in cold area. J. Hydraul. Eng. 2004, 6, 80–85. [Google Scholar]
- Terry, D.P. River-ice ecology. I: Hydrologic, geomorphic, and water-quality aspects. J. Cold Reg. Eng. 2001, 15, 1–16. [Google Scholar]
- Lima Neto, I.E.; Zhu, D.Z.; Rajaratnam, N.; Yu, T.; Spafford, M.; McEachern, P. Dissolved oxygen downstream of an effluent outfall in an ice-covered river: Natural and artificial aeration. J. Environ. Eng. 2007, 133, 1051–1060. [Google Scholar] [CrossRef]
- Obertegger, U.; Obrador, B.; Flaim, G. Dissolved oxygen dynamics under ice: Three winters of high-frequency data from Lake Tovel, Italy. Water Resour. Res. 2017, 53, 7234–7246. [Google Scholar] [CrossRef] [Green Version]
- Arifin, R.R.; James, S.C.; Pitts, D.A.; Hamlet, A.F.; Sharma, A.; Fernandoa, H.J.S. Simulating the thermal behavior in lake Ontario using EFDC. J. Great Lakes Res. 2016, 42, 511–523. [Google Scholar] [CrossRef]
- Lin, S.; Boegman, L.; Valipour, R.; Bouffard, D.; Ackerman, J.D.; Zhao, Y. Three-dimensional modeling of sediment resuspension in a large shallow lake. J. Great Lakes Res. 2021, 47, 970–984. [Google Scholar] [CrossRef]
- Oveisy, A.; Rao, Y.R.; Leon, L.F.; Bocaniov, S.A. Three-dimensional winter modeling and the effects of ice cover on hydrodynamics, thermal structure and water quality in Lake Erie. J. Great Lakes Res. 2021, 40, 19–28. [Google Scholar] [CrossRef]
- Tang, G.L.; Zhu, Y.Q.; Wu, G.Z.; Li, J.; Li, Z.L.; Sun, J.L. Modelling and analysis of hydrodynamics and water quality for rivers in the northern cold region of China. Int. J. Environ. Res. Public Health 2016, 13, 408. [Google Scholar] [CrossRef] [Green Version]
- Su, W.; Wu, G.Z.; Tang, G.L.; Shi, S.H. Modelling and Analysis of Water Quality for Reservoir in the Northern Cold Region of China. Fresen. Environ. Bull. 2021, 30, 8602–8612. [Google Scholar]
- Hosseini, N.; Chun, K.P.; Wheater, H.; Lindenschmidt, K.E. Parameter Sensitivity of a Surface Water Quality Model of the Lower South Saskatchewan River-Comparison Between Ice-On and Ice-Off Periods. Environ. Model. Assess. 2017, 22, 291–307. [Google Scholar] [CrossRef]
- Terry, J.A.; Sadeghian, A.; Lindenschmidt, K.E. Modelling dissolved oxygen/ Sediment oxygen demand under ice in a shallow eutrophic prairie reservoir. Water 2017, 9, 131. [Google Scholar] [CrossRef] [Green Version]
- Terry, J.A.; Sadeghian, A.; Baulch, H.M.; Chapra, S.C.; Lindenschmidt, K.E. Challenges of modelling water quality in a shallow prairie lake with seasonal ice cover. Ecol. Model. 2018, 384, 43–52. [Google Scholar] [CrossRef]
- Wang, Y.H.; Jiang, Y.Z.; Liao, W.H.; Gao, P.; Huang, X.M.; Wang, H. 3-D hydro-environmental simulation of Miyun Reservoir, Beijing. J. Hydro-Environ. Res. 2014, 8, 383–395. [Google Scholar] [CrossRef]
- Cole, T.M.; Wells, S.A. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 4.0. In Department of Civil and Environmental Engineering; Portland State University: Portland, OR, USA, 2016. [Google Scholar]
- Chapra, S.C.; Pelletier, G.J. QUAL2K: A Modeling Framework for Simulating River and Stream Water Quality: Documentation and Users Manual; Tufts University: Medford, MA, USA, 2003. [Google Scholar]
- Mike 21 ECOLab Module, Users Guide and Reference Manual; Danish Hydraulic Institute: Horsholm, Denmark, 2004.
- WL/Delft Hydraulics. Technical Reference Manual Delft3D-WAQ[EB/OL]. Available online: http://www.deltares.nl (accessed on 24 June 2022).
- Wool, T.A.; Ambros, R.B.; Martin, J.L.; Comer, E.A.; US Environmental Protection Agency; Environmental Research Laboratory; USACE; Tetra Tech, Inc. Water Quality Analysis Simulation Program (WASP) Version6.0: Draft User’s Manual; Environmental Protection Agency: Atlanta, GA, USA, 2001. [Google Scholar]
- Park, K.; Kuo, A.Y.; Shen, J.; Hamrick, J.M. A three-dimensional hydrodynamic-eutrophication model ( HEM-3D ): Description of Water Quality and Sediment Process Submodels. In Special Report in Applied Marine Science and Ocean Engineering No. 327; Virginia Institute of Marine Science; College of William & Mary: Gloucester Point, VA, USA, 1995. [Google Scholar]
- Chen, C.C.; Beardsley, R.C.; Cowles, G. An unstructured grid, finite-volume coastal ocean model (FVCOM) system. Oceanography 2006, 19, 78–89. [Google Scholar] [CrossRef] [Green Version]
- Hamrick, J.M.; Wu, T.S. Computational design and optimization of the EFDC/HEM3D surface water hydrodynamic and eutrophication model. In Next Generation Environmental Models and Computational Methods; Delich, G., Wheeler, M.F., Eds.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997; pp. 143–161. [Google Scholar]
- Wu, G.Z.; Xu, Z.X. Prediction of algal blooming using EFDC model: Case study in the Daoxiang Lake. Ecol. Model. 2011, 222, 1245–1252. [Google Scholar] [CrossRef]
- Ji, Z.G.; Mortonb, M.R.; Hamrick, J.M. Wetting and drying simulation of estuarine processes. Estuar. Coast. Shelf Sci. 2001, 53, 683–700. [Google Scholar] [CrossRef]
- Li, Y.P.; Acharya, K.; Chen, D.; Stone, M. Modeling water ages and thermal structure of Lake Mead under changing water levels. Lake Reserv. Manag. 2010, 26, 258–272. [Google Scholar] [CrossRef]
- Gong, W.Q.; Shen, J. A model diagnostic study of age of river-borne sediment transport in the tidal York River Estuary. Environ. Fluid Mech. 2010, 10, 177–196. [Google Scholar] [CrossRef]
- Mansoor, S.Z.; Louie, S.; Lima, A.T.; Cappellen, P.V.; MacVicar, B. The Spatial And Temporal Distribution Of Metals In An Urban Stream: A Case Study Of The Don River In Toronto, Canada. J. Great Lakes Res. 2018, 44, 1314–1326. [Google Scholar] [CrossRef]
- Boussinesq, J. Theorie Aanalyque de la Chaleur; Gathier-Villars: Paris, France, 1903. [Google Scholar]
- Arakawa, A.; Lamb, V.R. Computational design of the basic dynamical processes of the UCLA general circulation model. Methods Comput. Phys. 1977, 17, 174–265. [Google Scholar]
- Madala, R.V.; Piacsek, S.A. A semi-implicit numerical model for Baroclinic Oceans. J. Comput. Phys. 1977, 23, 167–178. [Google Scholar] [CrossRef]
- Sheng, Y.P.; Butler, H.L. Modeling coastal currents and sediment transport. In Proceedings of the 18th International Conference on Coastal Engineering, ASCE, New York, NY, USA, 14–19 November 1982; pp. 1127–1148. [Google Scholar]
- Smolarkiewicz, P.K.; Margolin, L.G. On forward-in-time differencing for fluids: Extension to a curvilinear framework. Mon. Weather Rev. 1993, 121, 1847–1859. [Google Scholar] [CrossRef] [Green Version]
- Sheng, Y.P. Finite-difference models for hydrodynamics of lakes and shallow seas. In Physics-Based Modeling of Lakes, Reservoirs, and Impoundments; Gray, W.G., Ed.; ASCE: New York, NY, USA, 1986; pp. 146–228. [Google Scholar]
- Harmick, J.M. A Three-dimensional Environmental Fluid Dynamics Computer Code: Theoretical and Computational Aspects; The College of William and Mary; Virginia Institute of Marine Science: Gloucester Point, VA, USA, 1992. [Google Scholar]
- The People’s Government of Mudanjiang. Scenarios for Jingpo Lake Water Quality to Regulated Water Quality Standard. Available online: http://www.mdj.gov.cn/ (accessed on 20 June 2022).
- Ji, Z.G. Hydrodynamics and Water Quality: Modeling Rivers, Lakes, and Estuaries; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2007; p. 613. [Google Scholar]
- Ji, Z.G.; Hu, G.D.; Shen, J.; Wan, Y.S. Three-dimensional modeling of hydrodynamic processes in the st. Lucie estuary. Estuar. Coast. Shelf Sci. 2007, 73, 188–200. [Google Scholar] [CrossRef]
- Jin, K.; Hamrick, J.H.; Tisdale, T. Application of three-dimensional hydrodynamic model for lake okeechobee. J. Hydraul. Eng. 2000, 126, 758–771. [Google Scholar] [CrossRef]
- Wei, L.Y. Flow resistance in ice-covered river. Eng. J. Wuhan Univ. 2002, 35, 1–9, 38. [Google Scholar]
- Ji, Z.Y.; Che, Z.H. Analysis of climatic characteristics of Mudanjiang in recent 30 years. Priv. Sci. Technol. 2014, 10, 221. [Google Scholar]
- He, Y.; Li, Y.T. Review of water quality models for sediment-induced pollution. Water Resour. Prot. 2004, 20, 5–9, 15. [Google Scholar]
- Hu, G.H. Simulated research on water quality for such heavy sediment-containing rivers like Yellow River. J. Saf. Environ. 2004, 4, 45–48. [Google Scholar]
- Zheng, D.C.; Cui, G.; Jin, Z.; Li, D.S.; Piao, Z.Z. Hydrological characteristics of the upper reaches of Mudan River. J. Northeast. China Inst. Water Conserv. Hydroelectr. Power 2006, 24, 37–38. [Google Scholar]
- Qu, M.Y.; Li, T. Analysis of River Sediment Supply in Middle and Downstream Section of Mudanjiang River Mainstream. Heilongjiang Sci. Technol. Water Conserv. 2013, 41, 38–40. [Google Scholar]
- Wang, Q.; Qi, J.; Wu, H.; Zeng, Y.; Shui, W.; Zeng, J.; Zhang, X. Freeze-Thaw cycle representation alters response of watershed hydrology to future climate change. Catena 2020, 195, 104767. [Google Scholar] [CrossRef]
- Wang, Q.; Zeng, J.; Qi, J.; Zhang, X.; Zeng, Y.; Shui, W.; Xu, Z.; Zhang, R.; Wu, X.; Cong, J. A multi-scale daily SPEI dataset for drought characterization at observation stations over mainland China from 1961 to 2018. Earth Syst. Sci. Data 2021, 13, 331–341. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, R.; Qu, Y.; Bentod, V.A.; Zhou, T.; Lin, Y.; Wu, X.; Qi, J.; Shui, W.; Wang, Q. Improving the drought monitoring capability of VHI at the global scale via ensemble indices for various vegetation types from 2001 to 2018. Weather Clim. Extrem. 2022, 35, 100412. [Google Scholar] [CrossRef]
- Zhang, R.; Qi, J.; Leng, S.; Wang, Q. Long-Term Vegetation Phenology Changes and Responses to Preseason Temperature and Precipitation in Northern China. Remote Sens. 2022, 14, 1396. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, J.; Li, J.; Cole, J.; Waldhoff, S.; Zhang, X. Nitrate loading projection is sensitive to freeze-thaw cycle representation. Water Res. 2020, 186, 116355. [Google Scholar] [CrossRef]
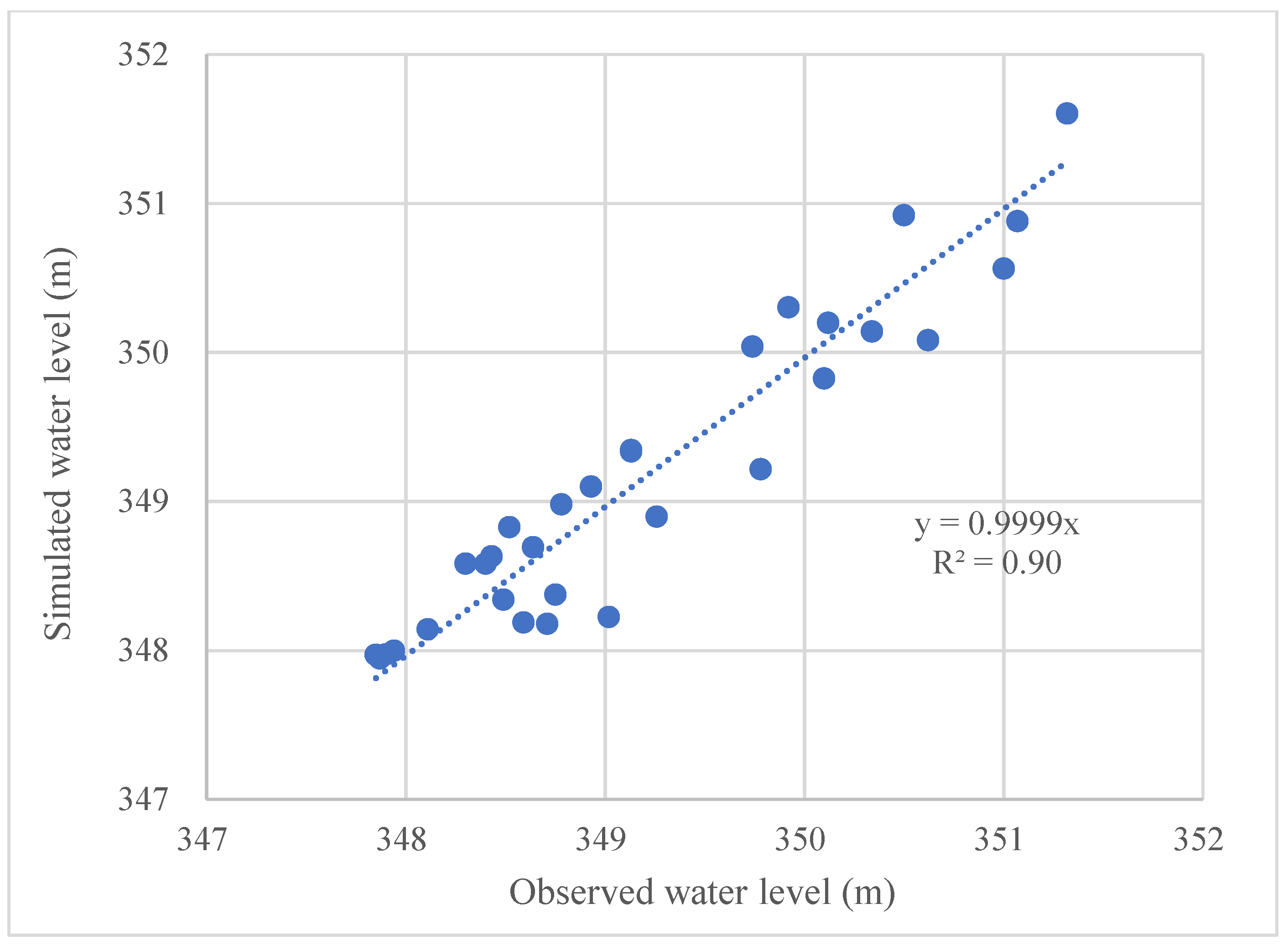
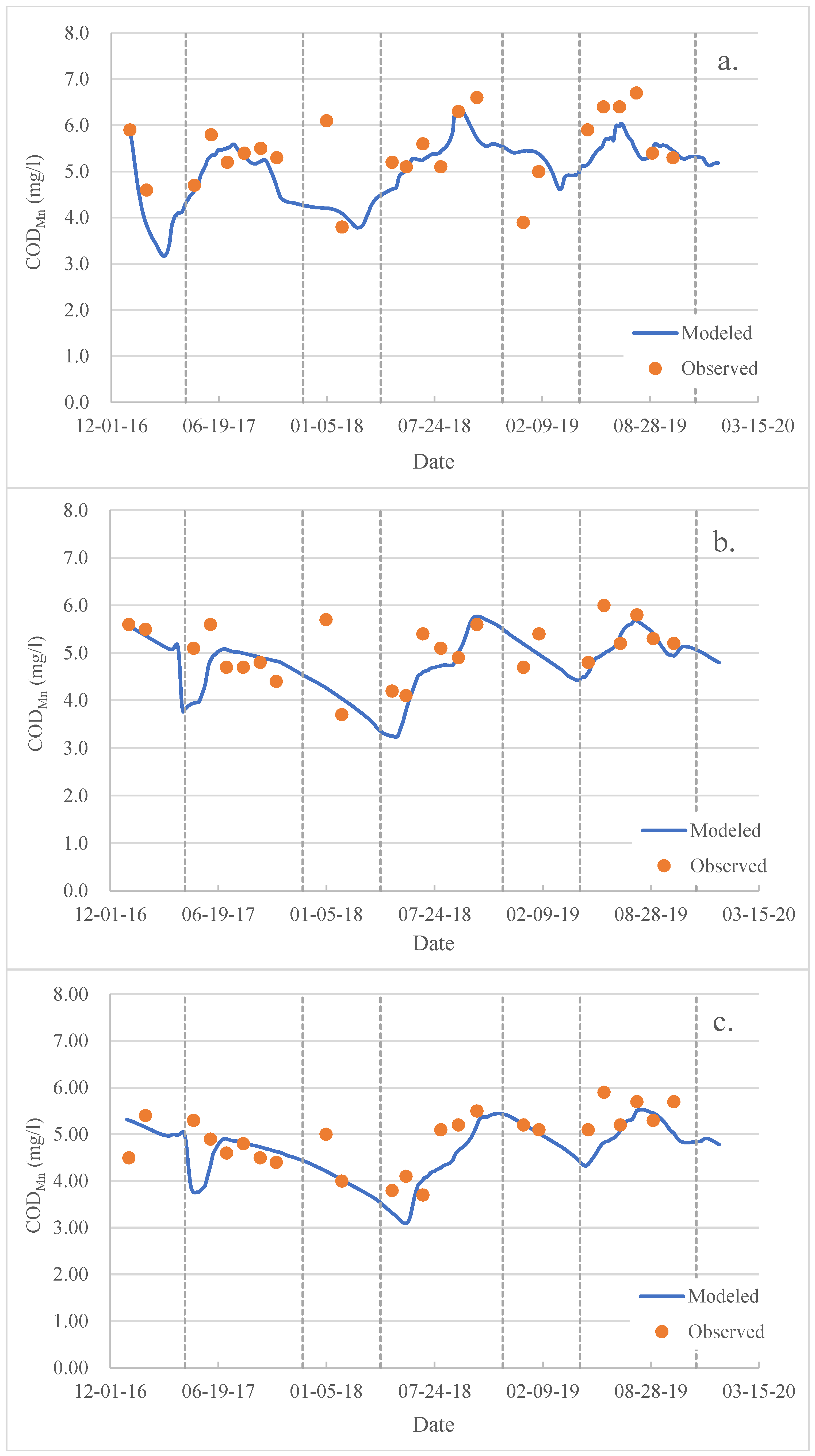
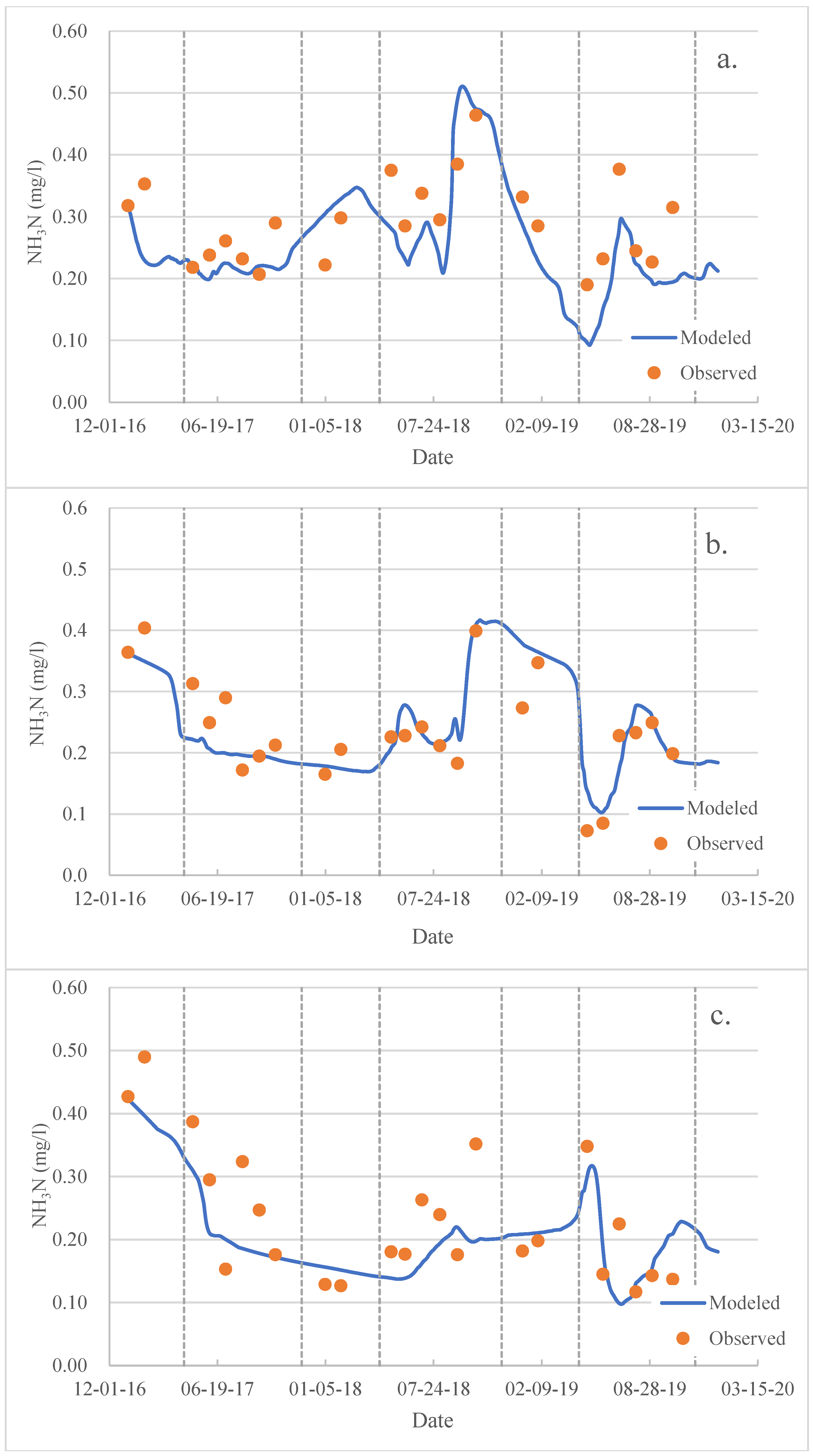
| Parameter | Definition | Value | Unit |
|---|---|---|---|
| ITERM | Maximum number of iterations | 500 | - |
| RP | Over relaxation parameter | 1.8 | - |
| ZROUGH | Bottom roughness | 0.035 | - |
| ICEROUGH | Ice roughness | 0.01 | - |
| ZBRWALL | Side-wall log-law roughness height | 0.002 | - |
| HDRY | Depth at which cell becomes dry | 0.05 | m |
| HWET | Depth at which cell becomes wet | 0.07 | m |
| AHO | Constant horizontal diffusion | 1.0 | m2/s |
| AHD | Dimensionless horizontal momentum diffusivity | 0.05 | - |
| AVO | Background molecular eddy (kinematic) viscosity | 1.0 × 10−7 | m2/s |
| ABO | Background molecular diffusivity | 1.0 × 10−8 | m2/s |
| BSC | Buoyancy influence coefficient | 1.0 | - |
| RKCOD | CODMn concentration decay rate in ice-free period | 0.0020 | 1/day |
| RKCODICE | CODMn concentration decay rate in ice-covered period | 0.0018 | 1/day |
| RKNH3N | NH3N concentration decay rate in ice-free period | 0.0018 | 1/day |
| RKNH3NICE | NH3N concentration decay rate in ice-covered period | 0.0015 | 1/day |
| Simulation Period | LHLZ | DST | GSC | Total | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample Size | MAE (mg/L) | MAPE (%) | Sample Size | MAE (mg/L) | MAPE (%) | Sample Size | MAE (mg/L) | MAPE (%) | Sample Size | MAE (mg/L) | MAPE (%) | |
| Ice-Covered Period | 6 | 0.82 | 17.19 | 6 | 0.48 | 9.30 | 6 | 0.33 | 6.79 | 18 | 0.54 | 11.09 |
| Ice-Free Period | 18 | 0.42 | 7.06 | 18 | 0.43 | 8.52 | 18 | 0.52 | 10.49 | 54 | 0.45 | 8.69 |
| Total | 24 | 0.52 | 9.59 | 24 | 0.44 | 8.71 | 24 | 0.47 | 9.57 | 72 | 0.48 | 9.29 |
| Accuracy | 90.71 | |||||||||||
| Simulation Period | LHLZ | DST | GSC | Total | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample Size | MAE (mg/L) | MAPE (%) | Sample Size | MAE (mg/L) | MAPE (%) | Sample Size | MAE (mg/L) | MAPE (%) | Sample Size | MAE (mg/L) | MAPE (%) | |
| Ice-Covered Period | 6 | 0.06 | 19.39 | 6 | 0.04 | 13.56 | 6 | 0.03 | 13.58 | 0.04 | 15.51 | |
| Ice-Free Period | 18 | 0.06 | 19.78 | 18 | 0.03 | 18.21 | 18 | 0.06 | 27.34 | 0.05 | 21.78 | |
| Total | 24 | 0.06 | 19.68 | 24 | 0.03 | 17.05 | 24 | 0.06 | 23.9 | 0.05 | 20.21 | |
| Accuracy | 79.79 | |||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Z.; He, Z.; Wu, G.; Tang, G.; Wang, Q. Developing Water-Quality Model for Jingpo Lake Based on EFDC. Water 2022, 14, 2596. https://doi.org/10.3390/w14172596
Qin Z, He Z, Wu G, Tang G, Wang Q. Developing Water-Quality Model for Jingpo Lake Based on EFDC. Water. 2022; 14(17):2596. https://doi.org/10.3390/w14172596
Chicago/Turabian StyleQin, Zihan, Zhengwei He, Guozheng Wu, Gula Tang, and Qian Wang. 2022. "Developing Water-Quality Model for Jingpo Lake Based on EFDC" Water 14, no. 17: 2596. https://doi.org/10.3390/w14172596





