Experiments on the Drag and Lift Coefficients of a Spinning Sphere
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Experimental Methods
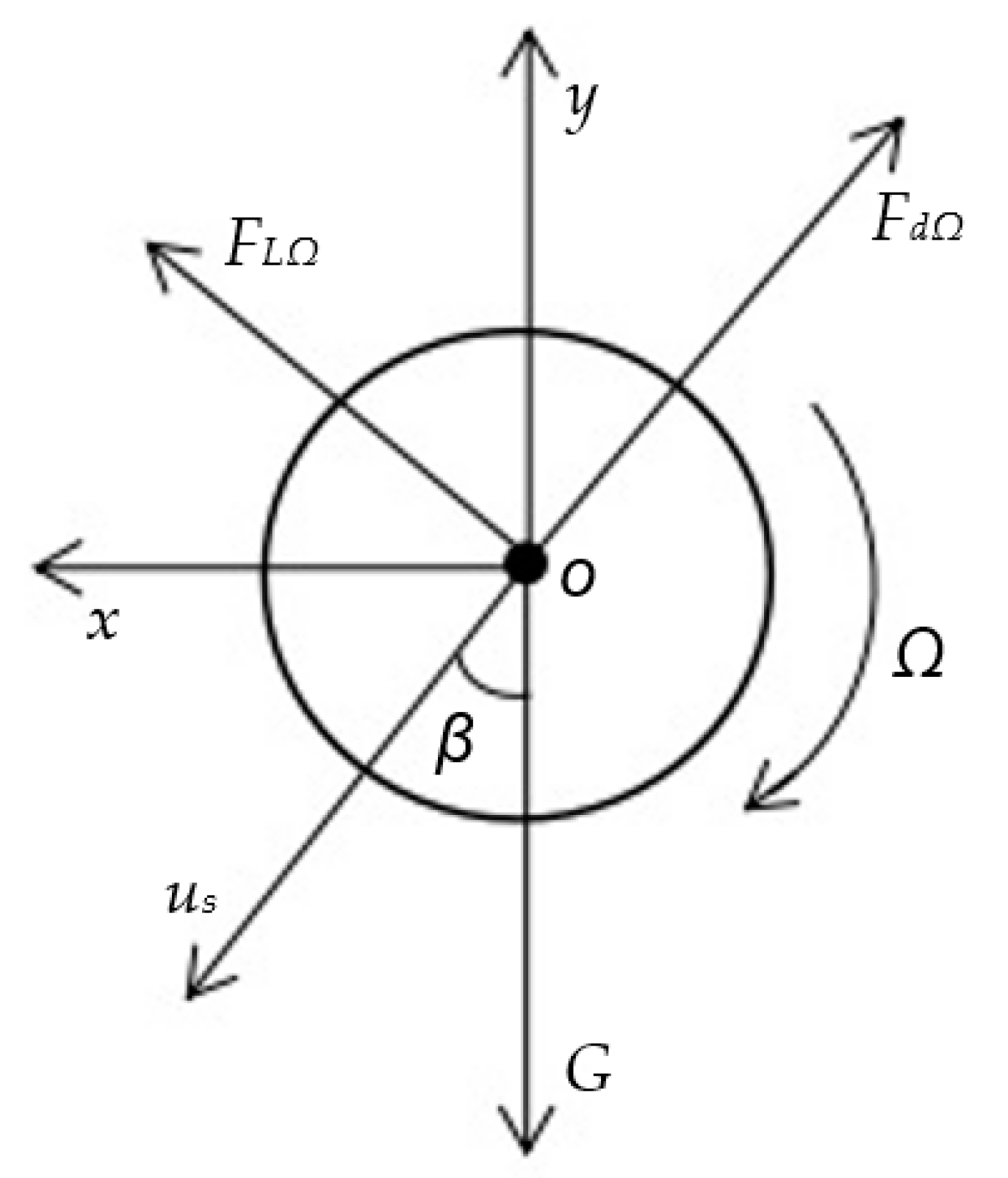
2.2.1. Measuring Procedure
2.2.2. Data Processing Procedure
3. Results and Discussion
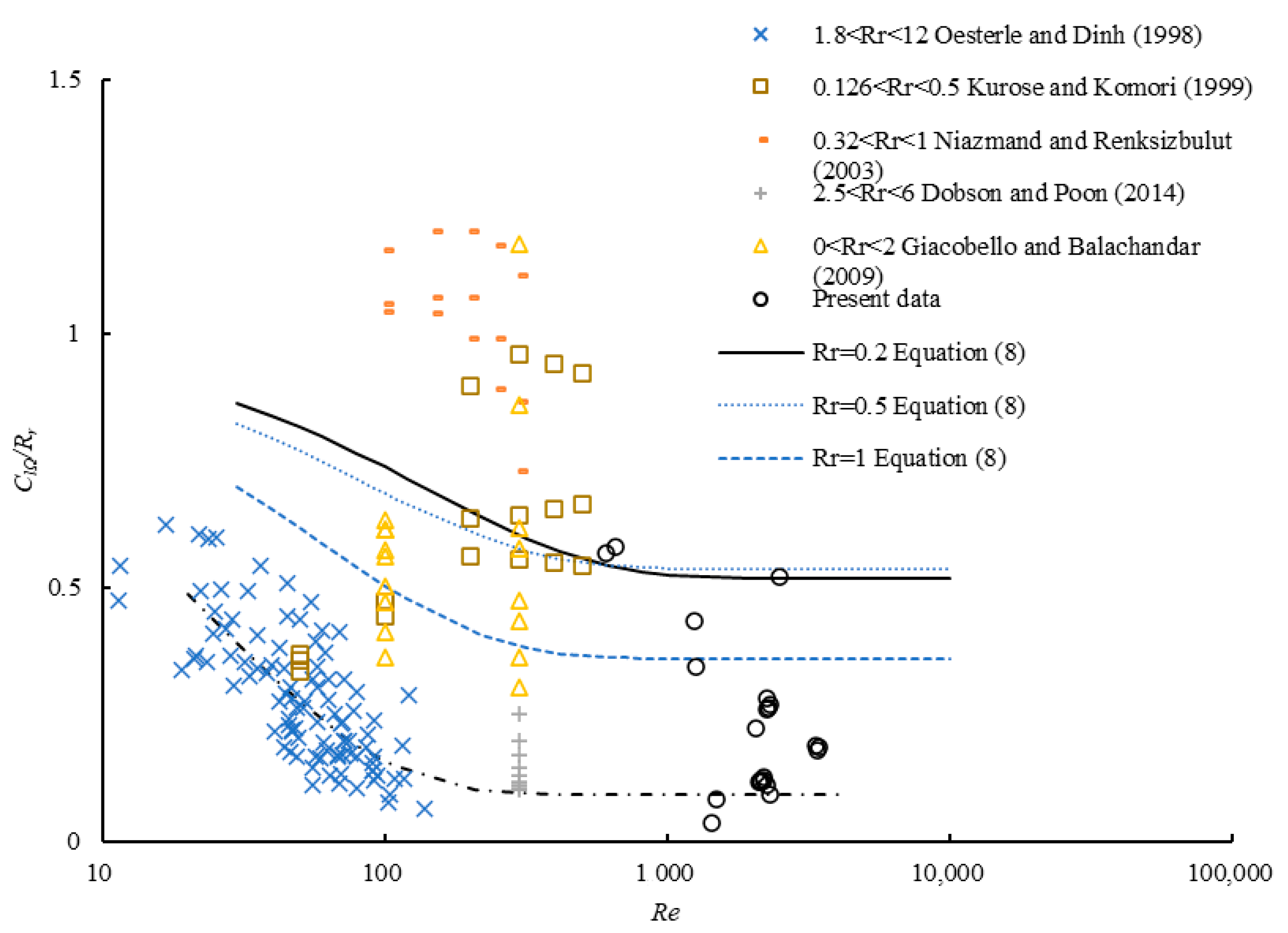
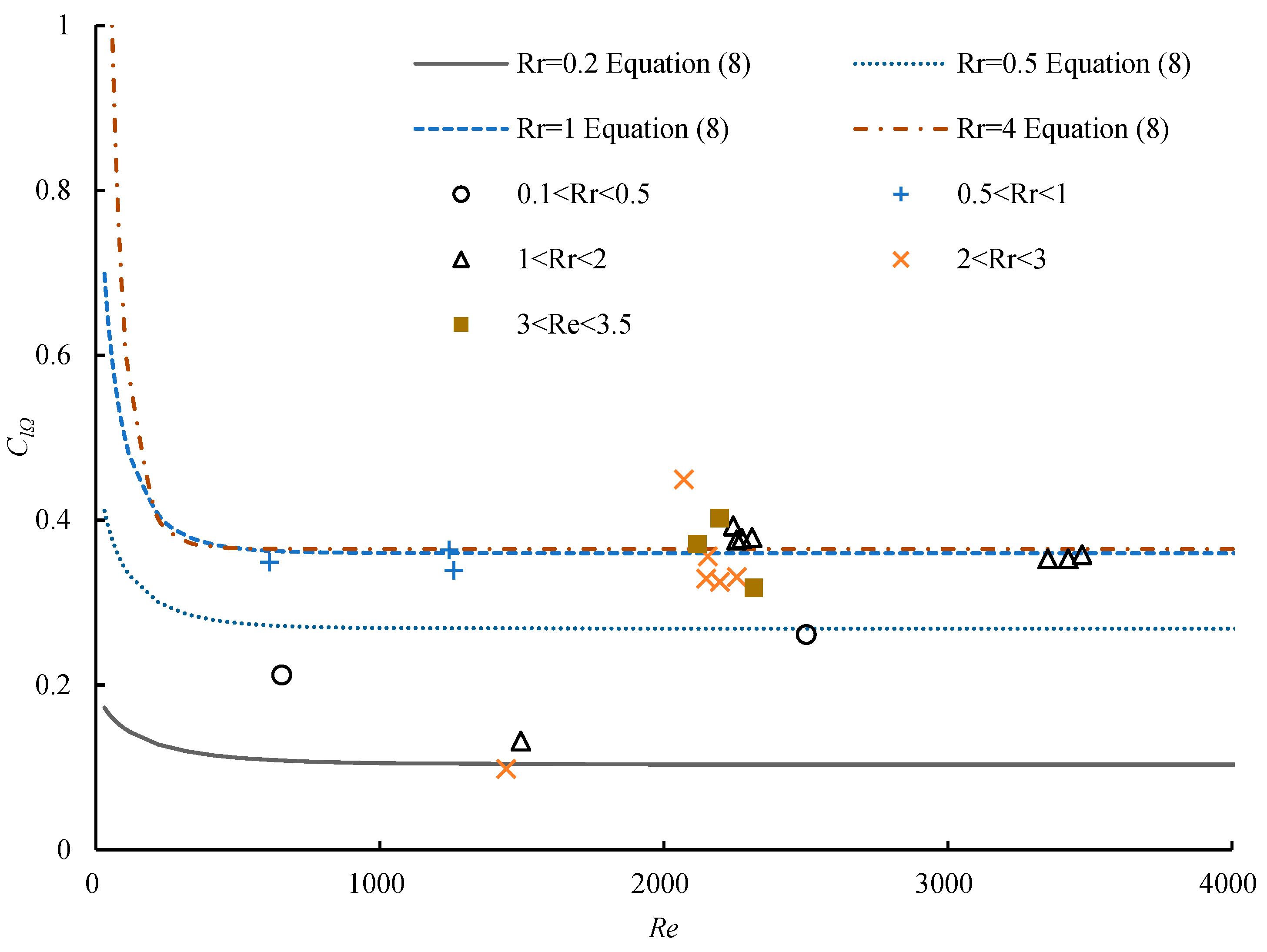
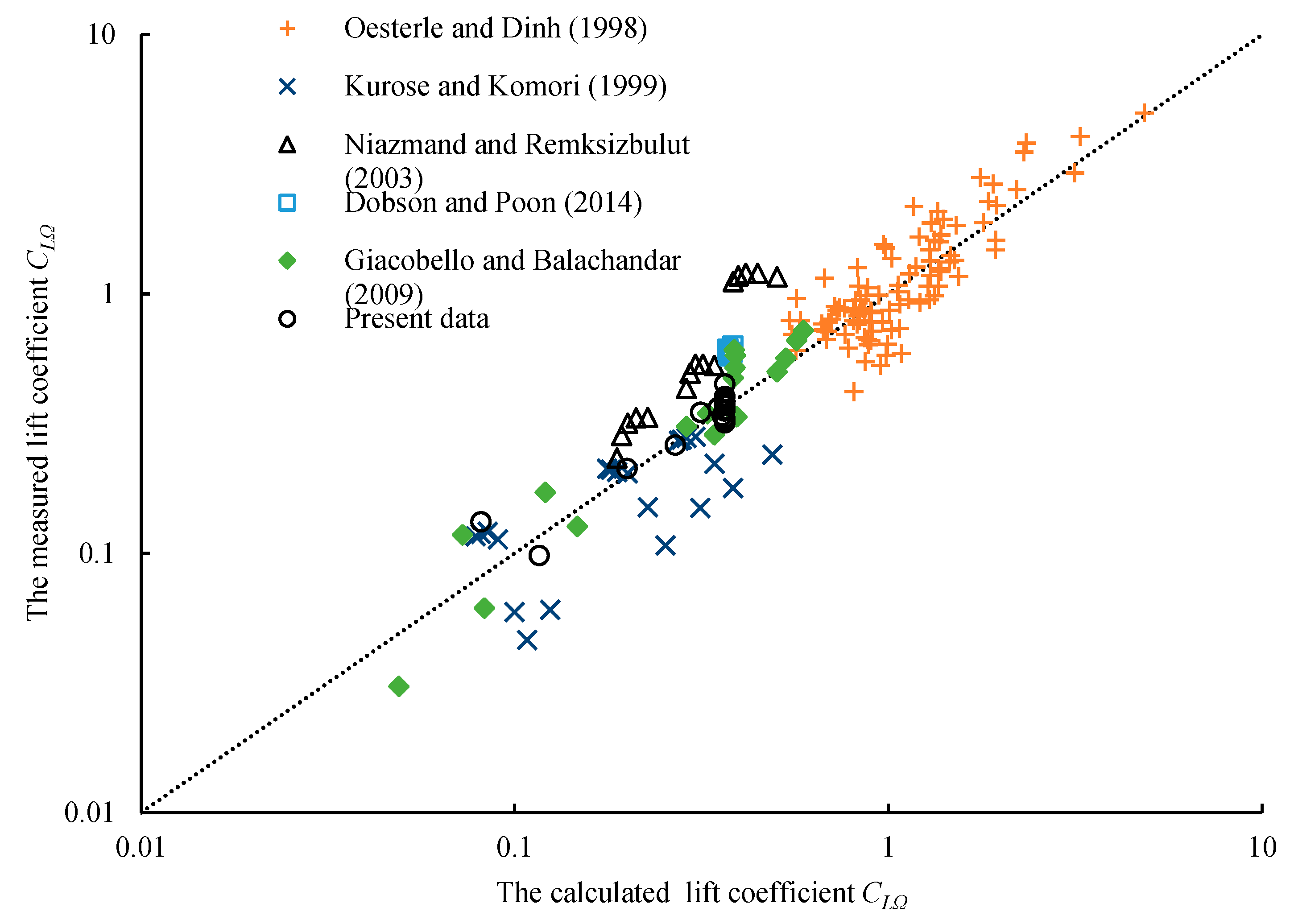
3.1. Lift Coefficient
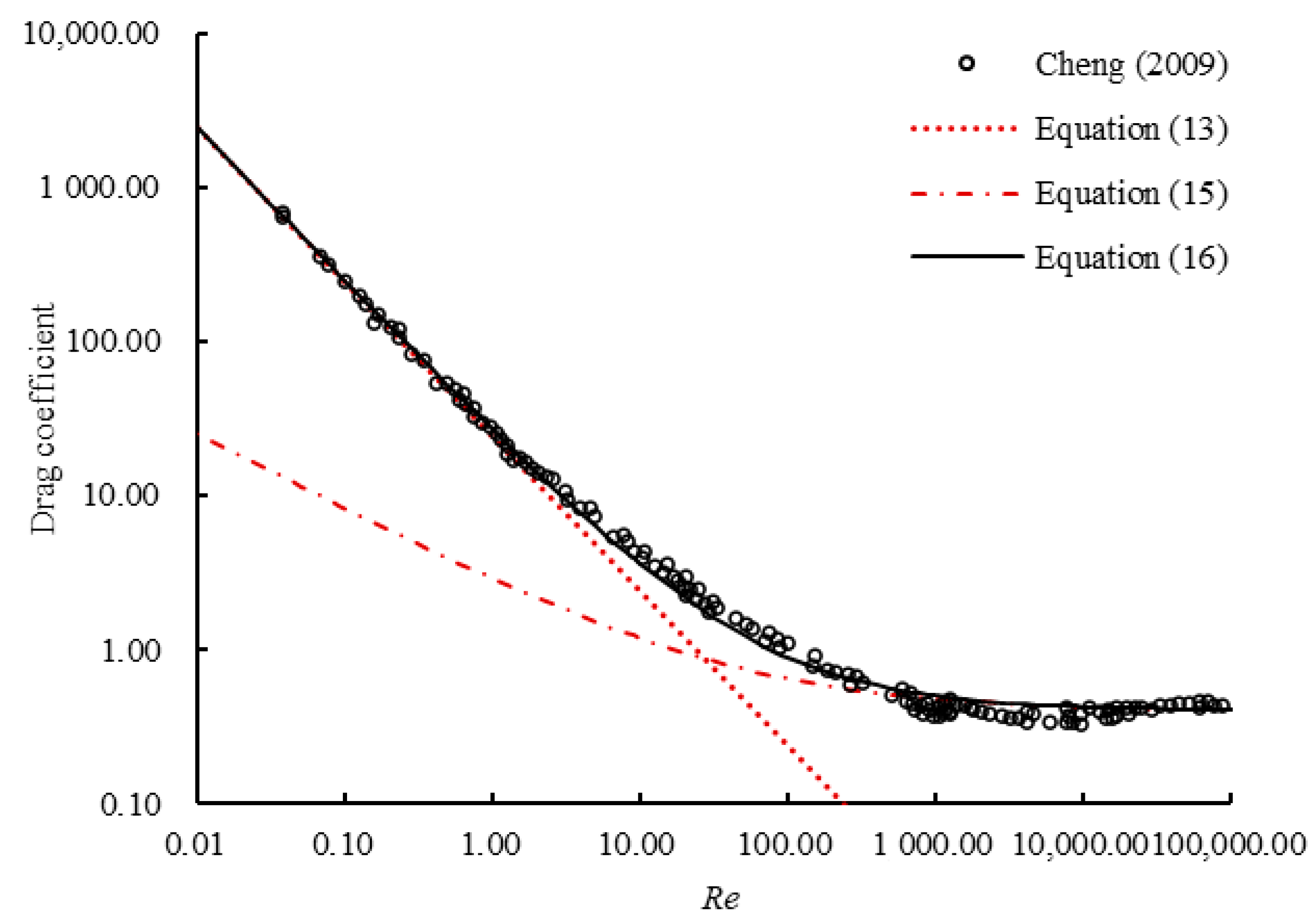
3.2. Drag Coefficient
3.2.1. Drag Coefficient of a Non-Spinning Sphere
3.2.2. Drag Coefficient of A Spinning Sphere
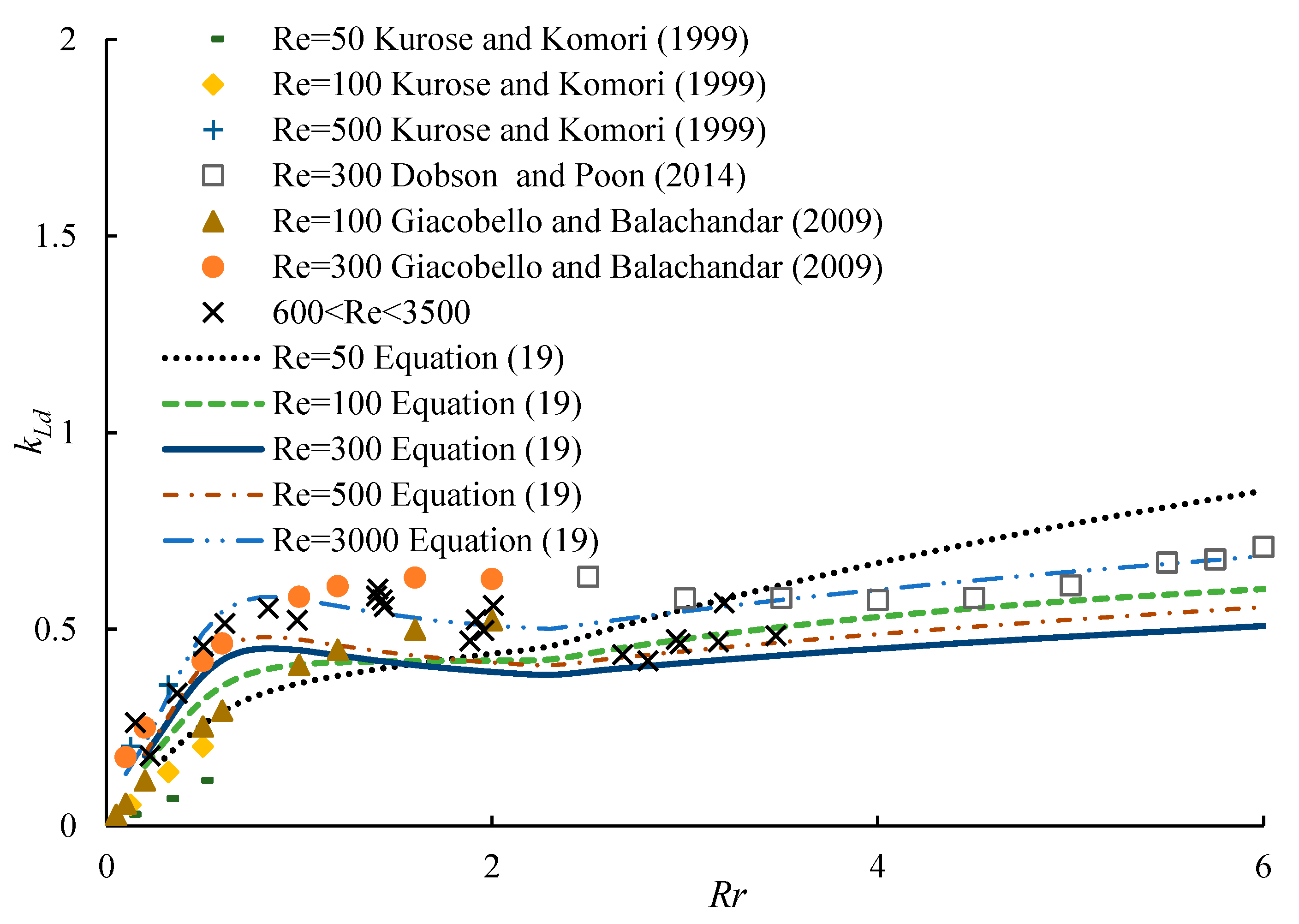
3.3. Lift-to-Drag Ratio
4. Conclusions
- (1)
- The obtained experimental data reveal that the lift coefficient is related to the Reynolds number and dimensional angular speed. There is a critical Reynolds number (Rec) at each dimensionless angular speed. When 0 < Re < Rec, the lift coefficient decreases as the Reynolds number increases, while it is constant when Rec< Re < 3500. The constant lift coefficient corresponding to different spin speeds was defined as the limit value of the lift coefficient. This coefficient is 0.37 when 1 < Rr < 12, while the limit value of the lift coefficient increases with the increase in dimensionless angular speed for 0 < Rr < 1.
- (2)
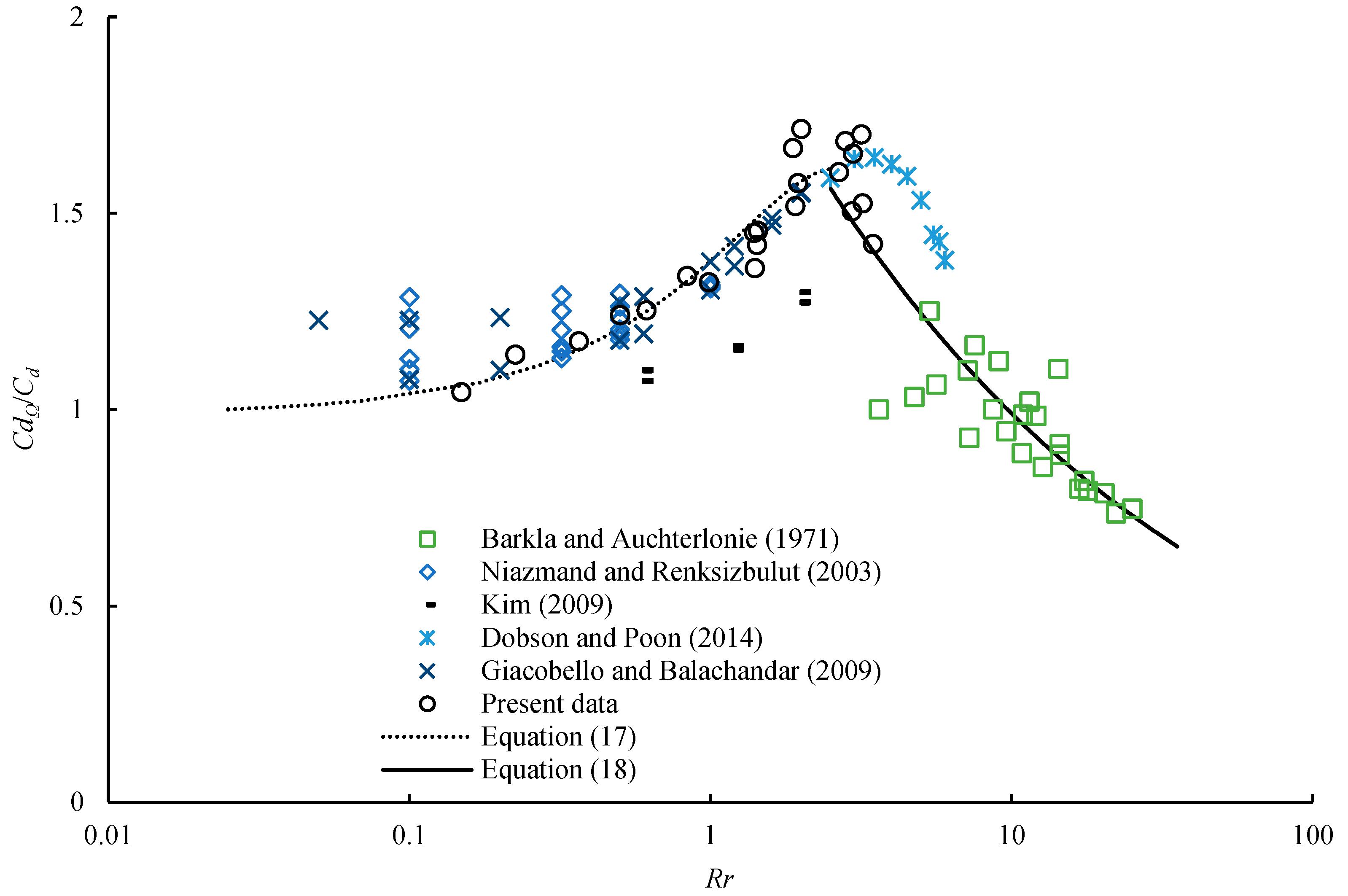
- Compared with the total drag coefficient of a non-spinning sphere at a certain dimensionless angular speed, the drag coefficient of a spinning sphere is higher when 1 < Rr < 10. When 1 < Rr < 10, the ratio of the drag coefficient of a spinning sphere to the total drag coefficient of a non-spinning sphere CdΩ/Cd is between 1 and 1.6. However, the drag coefficient of a spinning sphere is less than the total drag coefficient of a non-spinning sphere when 10 < Rr < 25. The ratio CdΩ/Cd increases with increasing dimensionless angular speed in the range of 0 < Rr < 2.5, while the ratio CdΩ/Cd decreases with an increase in Rr beyond this range. To interpret this phenomenon, two empirical correlations were developed to describe the effect of particle spin on the drag coefficient based on the experimental data and the results from the literature.
- (3)
- When 0 < Re < 100, the lift-to-drag ratio of a spinning sphere kld increases with increasing dimensionless angular speed at a certain Reynolds number. At 100 < Re < 3500 and 0 < Rr < 0.85, kLd increases with increasing dimensionless angular speed at a certain Reynolds number and increases with increasing Reynolds number at a certain angular speed. At 100 < Re < 3500 and 0.85 < Rr < 6, kld increases with increasing Reynolds number at a certain angular speed and can be approximated as a constant value with increasing dimensionless angular speed at a certain Reynolds number.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef] [Green Version]
- Magnus, G. liber die Abweichung der Geschlosse, und eine auffallende Erscheinung bei rotierenden Korpern. Poggendorfs Ann. Phys. Und Chem. 1853, 88, 1. [Google Scholar]
- Young, J.; Leeming, A. A theory of particle deposition in turbulent pipe flow. J. Fluid Mech. 1997, 340, 129–159. [Google Scholar] [CrossRef]
- Barkla, H.M.; Auchterlonie, L.J. The Magnus or Robins effect on rotating spheres. J. Fluid Mech. 1971, 47, 437–447. [Google Scholar] [CrossRef]
- Rubinow, S.I.; Keller, J.B. The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 1961, 11, 447–459. [Google Scholar] [CrossRef]
- Tsuji, Y.; Morikawa, Y.; Mizuno, O. Experimental Measurement of the Magnus Force on a Rotating Sphere at Low Reynolds Numbers. J. Fluids Eng. 1985, 107, 484–488. [Google Scholar] [CrossRef]
- Oesterlé, B.; Dinh, T.B. Experiments on the lift of a spinning sphere in a range of intermediate Reynolds numbers. Exp. Fluids 1998, 25, 16–22. [Google Scholar] [CrossRef]
- Macoll, J.H. Aerodynamics of a Spinning Sphere. J. R. Aeronaut. Soc. 1928, 32, 777–798. [Google Scholar] [CrossRef]
- Davies, J.M. The Aerodynamic of Golf Balls. J. Appl. Phys. 1949, 20, 821–828. [Google Scholar] [CrossRef]
- Tri, B.D.; Oestrele, B.; Deneu, F. Premiers résultats sur la portance d’une sphère en rotation aux nombres de Reynolds intermèdiaires. Comptes Rendus L’académie Des Sciences. Série 2. Mécanique Phys. Chim. Sci. L’univers Sci. Terre 1990, 311, 27–31. [Google Scholar]
- Taneda, S. Negative Magnus Effect. Rep. Res. Inst. Appl. Phys. Kyushu Univ. 1957, 20, 123–128. [Google Scholar]
- Ben Salem, M.; Oesterle, B. A Shear Flow Around a Spinning Sphere: Numerical Study at Moderate Reynolds Numbers. Int. J. Multiph. Flow 1998, 24, 563–585. [Google Scholar] [CrossRef]
- Kurose, R.; Komori, S. Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 1999, 384, 183–206. [Google Scholar] [CrossRef]
- Niazmand, H.; Renksizbulut, M. Surface effects on transient three-dimensional flows around rotating spheres at moderate Reynolds numbers. Comput. Fluids 2003, 32, 1405–1433. [Google Scholar] [CrossRef]
- Kim, D. Laminar flow past a sphere rotating in the transverse direction. J. Mech. Sci. Technol. 2009, 23, 578–589. [Google Scholar] [CrossRef]
- Poon, E.K.W.; Ooi, A.S.H.; Giacobello, M.; Iaccarino, G.; Chung, D. Flow past a transversely rotating sphere at Reynolds numbers above the laminar regime. J. Fluid Mech. 2014, 759, 751–781. [Google Scholar] [CrossRef]
- Citro, V.; Tchoufag, J.; Fabre, D.; Giannetti, F.; Luchini, P. Linear stability and weakly nonlinear analysis of the flow past rotating spheres. J. Fluid Mech. 2016, 807, 62–86. [Google Scholar] [CrossRef]
- Leal, L.G. Particle Motions in a Viscous Fluid. Annu. Rev. Fluid Mech. 1980, 12, 435–476. [Google Scholar] [CrossRef]
- Drew, D.A. Mathematical Modeling of Two-Phase Flow. Annu. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Magnaudet, J.; Eames, I. The Motion of High-Reynolds-Number Bubbles in Inhomogeneous Flows. Annu. Rev. Fluid Mech. 2000, 32, 659–708. [Google Scholar] [CrossRef]
- Tomiyama, A.; Tamai, H.; Zun, I.; Hosokawa, S. Transverse Migration of Single Bubbles in Simple Shear Layers. Chem. Eng. Sci. 2002, 57, 1849–1858. [Google Scholar] [CrossRef]
- Loth, E. Lift of a Spherical Particle Subject to Vorticity and/or Spin. AIAA J. 2008, 46, 801–809. [Google Scholar] [CrossRef]
- Shi, P.; Rzehak, R. Lift forces on solid spherical particles in unbounded flows. Chem. Eng. Sci. 2019, 208, 115145. [Google Scholar] [CrossRef]
- Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Philo. Soc. 1851, 9, 8–106. [Google Scholar]
- Swamee, P.K.; Chandra, S.P. Drag Coefficient and Fall Velocity of nonspherical particles. J. Hydraul. Eng. 1991, 117, 660–667. [Google Scholar] [CrossRef]
- Song, X.; Xu, Z.; Li, G.; Pang, Z.; Zhu, Z. A new model for predicting drag coefficient and settling velocity of spherical and non-spherical particle in Newtonian fluid. Powder Technol. 2017, 321, 242–250. [Google Scholar] [CrossRef]
- Amin, R.; Umut, T. The drag coefficient and settling velocity of natural sediment particles. Comput. Part. Mech. 2019, 6, 427–437. [Google Scholar]
- Flemmer, R.L.C. Banks CL. On the drag coefficient of a sphere. Powder Technol. 1986, 48, 217–221. [Google Scholar] [CrossRef]
- Kelessidis, V.C. An explicit equation for the terminal velocity of solid spheres falling in pseudoplastic liquids. Chem. Eng. Sci. 2004, 59, 4437–4447. [Google Scholar] [CrossRef]
- Cheng, N.S. Comparison of formulas for drag coefficient and settling velocity of spherical particles. Powder Technol. 2009, 189, 395–398. [Google Scholar] [CrossRef]
- Malhotra, S.; Sharma, M.M. Settling of spherical particles in unbounded and confined surfactant-based shear thinning viscoelastic fluids: An experimental study. Chem. Eng. Sci. 2012, 84, 646–655. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, L.; Wu, Y.; Yang, Q. New simple correlation formula for the drag coefficient of calcareous sand particles of highly irregular shape. Powder Technol. 2017, 326, 379–392. [Google Scholar] [CrossRef]
- Dobson, J.; Ooi, A.; Poon, E. The flow structures of a transversely rotating sphere at high rotation rates. Comput. Fluids 2014, 102, 170–181. [Google Scholar] [CrossRef]
- Giacobello, M.; Ooi, A.; Balachandar, S. Wake structure of a transversely rotating sphere at moderate Reynolds numbers. J. Fluid Mech. 2009, 621, 103–130. [Google Scholar] [CrossRef]

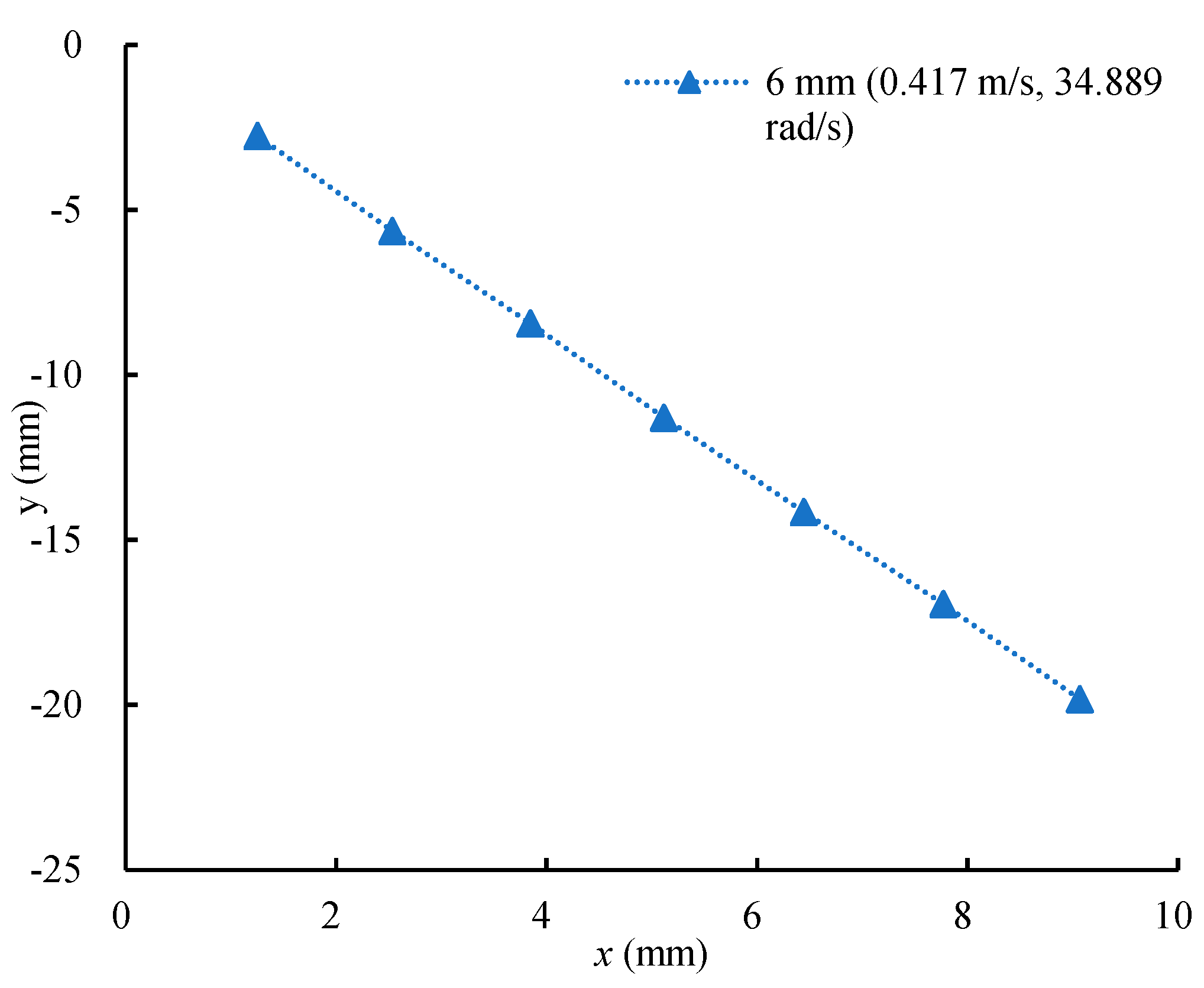
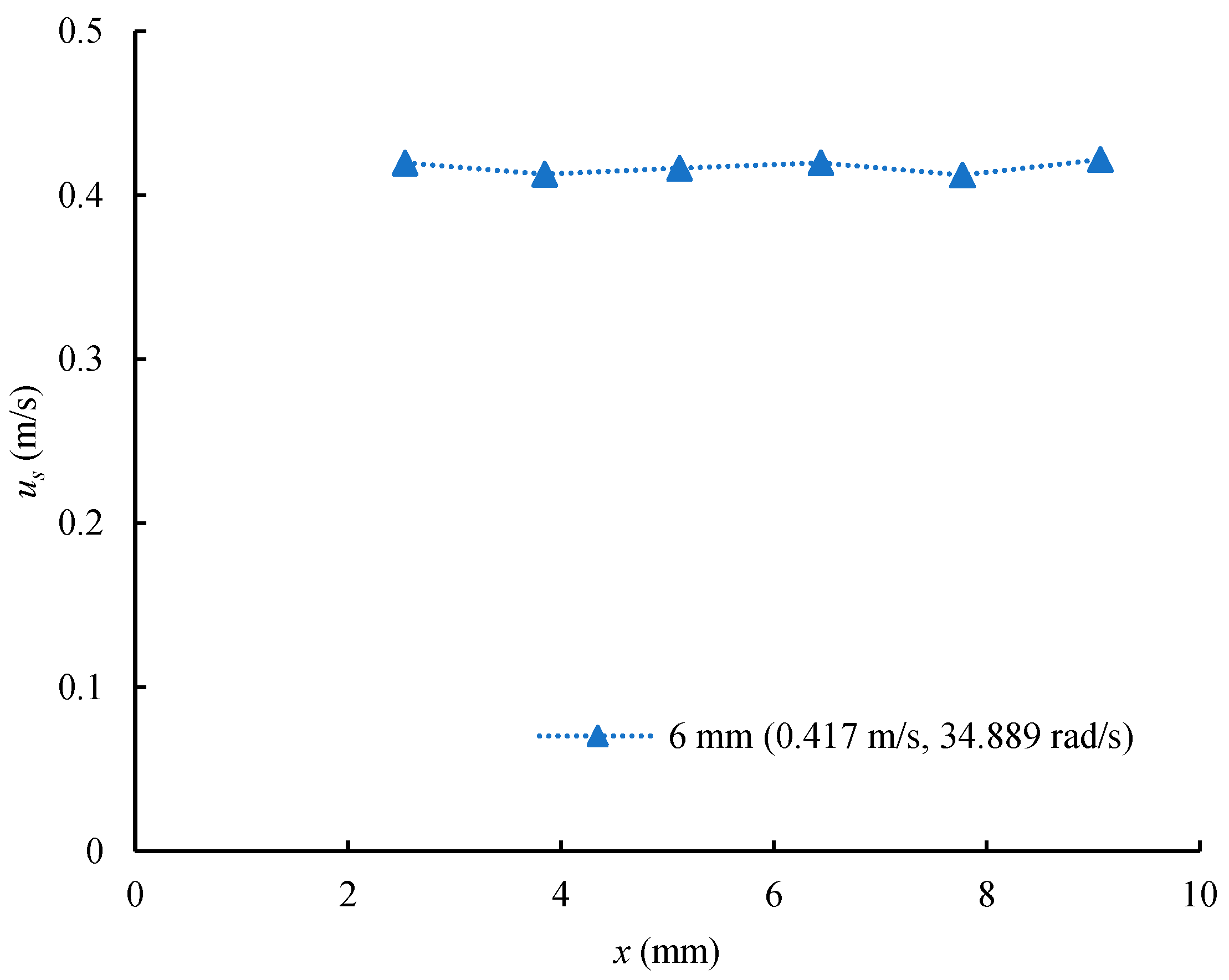
| No. | D (mm) | us (m/s) | Ω (rad/s) | Rr | Re |
|---|---|---|---|---|---|
| 1 | 2.5 | 0.262 | 38.380 | 0.366 | 655.000 |
| 2 | 2.5 | 0.244 | 59.890 | 0.614 | 610.000 |
| 3 | 4 | 0.374 | 13.956 | 0.149 | 1496.000 |
| 4 | 4 | 0.361 | 20.350 | 0.225 | 1444.000 |
| 5 | 4 | 0.311 | 65.130 | 0.838 | 1244.000 |
| 6 | 4 | 0.315 | 77.920 | 0.989 | 1260.000 |
| 7 | 6 | 0.417 | 34.889 | 0.502 | 2502.000 |
| 8 | 6 | 0.386 | 223.290 | 3.471 | 2316.000 |
| 9 | 6 | 0.385 | 90.250 | 1.406 | 2310.000 |
| 10 | 6 | 0.379 | 90.250 | 1.429 | 2274.000 |
| 11 | 6 | 0.376 | 185.140 | 2.954 | 2256.000 |
| 12 | 6 | 0.376 | 90.250 | 1.440 | 2256.000 |
| 13 | 6 | 0.374 | 87.220 | 1.399 | 2244.000 |
| 14 | 6 | 0.366 | 195.380 | 3.203 | 2196.000 |
| 15 | 6 | 0.366 | 163.280 | 2.677 | 2196.000 |
| 16 | 6 | 0.359 | 177.930 | 2.974 | 2154.000 |
| 17 | 6 | 0.358 | 167.470 | 2.807 | 2148.000 |
| 18 | 6 | 0.353 | 186.660 | 3.173 | 2118.000 |
| 19 | 6 | 0.345 | 115.336 | 2.006 | 2070.000 |
| 20 | 8 | 0.434 | 103.980 | 1.917 | 3472.000 |
| 21 | 8 | 0.428 | 104.670 | 1.956 | 3424.000 |
| 22 | 8 | 0.419 | 98.640 | 1.883 | 3352.000 |
| No. | D (mm) | us (m/s) | Ω (rad/s) | Rr | Re | ClΩ | CdΩ |
|---|---|---|---|---|---|---|---|
| 1 | 2.5 | 0.262 | 38.380 | 0.366 | 655.000 | 0.212 | 0.627 |
| 2 | 2.5 | 0.244 | 59.890 | 0.614 | 610.000 | 0.349 | 0.677 |
| 3 | 4 | 0.374 | 13.956 | 0.149 | 1496.000 | 0.132 | 0.502 |
| 4 | 4 | 0.361 | 20.350 | 0.225 | 1444.000 | 0.098 | 0.550 |
| 5 | 4 | 0.311 | 65.130 | 0.838 | 1244.000 | 0.364 | 0.657 |
| 6 | 4 | 0.315 | 77.920 | 0.989 | 1260.000 | 0.339 | 0.648 |
| 7 | 6 | 0.417 | 34.889 | 0.502 | 2502.000 | 0.261 | 0.570 |
| 8 | 6 | 0.386 | 223.290 | 3.471 | 2316.000 | 0.318 | 0.657 |
| 9 | 6 | 0.385 | 90.250 | 1.406 | 2310.000 | 0.379 | 0.629 |
| 10 | 6 | 0.379 | 90.250 | 1.429 | 2274.000 | 0.378 | 0.657 |
| 11 | 6 | 0.376 | 185.140 | 2.954 | 2256.000 | 0.331 | 0.697 |
| 12 | 6 | 0.376 | 90.250 | 1.440 | 2256.000 | 0.376 | 0.674 |
| 13 | 6 | 0.374 | 87.220 | 1.399 | 2244.000 | 0.393 | 0.672 |
| 14 | 6 | 0.366 | 195.380 | 3.203 | 2196.000 | 0.402 | 0.708 |
| 15 | 6 | 0.366 | 163.280 | 2.677 | 2196.000 | 0.325 | 0.745 |
| 16 | 6 | 0.359 | 177.930 | 2.974 | 2154.000 | 0.356 | 0.768 |
| 17 | 6 | 0.358 | 167.470 | 2.807 | 2148.000 | 0.329 | 0.783 |
| 18 | 6 | 0.353 | 186.660 | 3.173 | 2118.000 | 0.371 | 0.792 |
| 19 | 6 | 0.345 | 115.336 | 2.006 | 2070.000 | 0.449 | 0.800 |
| 20 | 8 | 0.434 | 103.980 | 1.917 | 3472.000 | 0.358 | 0.682 |
| 21 | 8 | 0.428 | 104.670 | 1.956 | 3424.000 | 0.353 | 0.709 |
| 22 | 8 | 0.419 | 98.640 | 1.883 | 3352.000 | 0.353 | 0.750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Zhang, G.; Xu, X. Experiments on the Drag and Lift Coefficients of a Spinning Sphere. Water 2022, 14, 2593. https://doi.org/10.3390/w14172593
Zhou S, Zhang G, Xu X. Experiments on the Drag and Lift Coefficients of a Spinning Sphere. Water. 2022; 14(17):2593. https://doi.org/10.3390/w14172593
Chicago/Turabian StyleZhou, Shuang, Genguang Zhang, and Xiaoyang Xu. 2022. "Experiments on the Drag and Lift Coefficients of a Spinning Sphere" Water 14, no. 17: 2593. https://doi.org/10.3390/w14172593
APA StyleZhou, S., Zhang, G., & Xu, X. (2022). Experiments on the Drag and Lift Coefficients of a Spinning Sphere. Water, 14(17), 2593. https://doi.org/10.3390/w14172593