Subtidal Dynamics in a Tidal River with Limited Discharge
Abstract
:1. Introduction
2. Materials and Methods
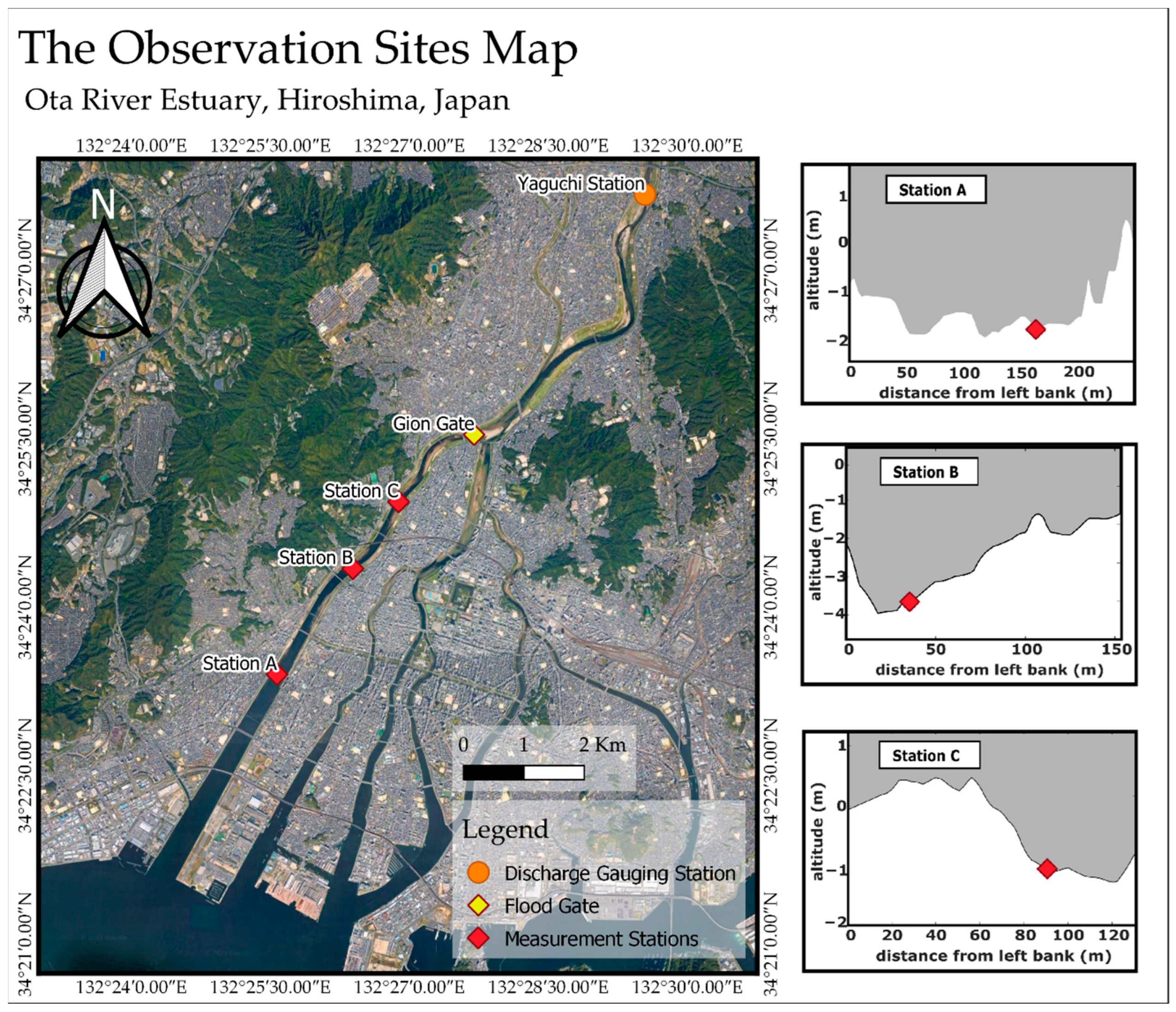
2.1. Field Site
2.2. Data Acquisition
2.3. Data Processing
2.3.1. Tidal Frequency Domain Analysis
- Spectral Analysis
- Harmonic Analysis
2.3.2. Subtidal Friction Decomposition
2.3.3. Stokes Fluxes Analysis
3. Results
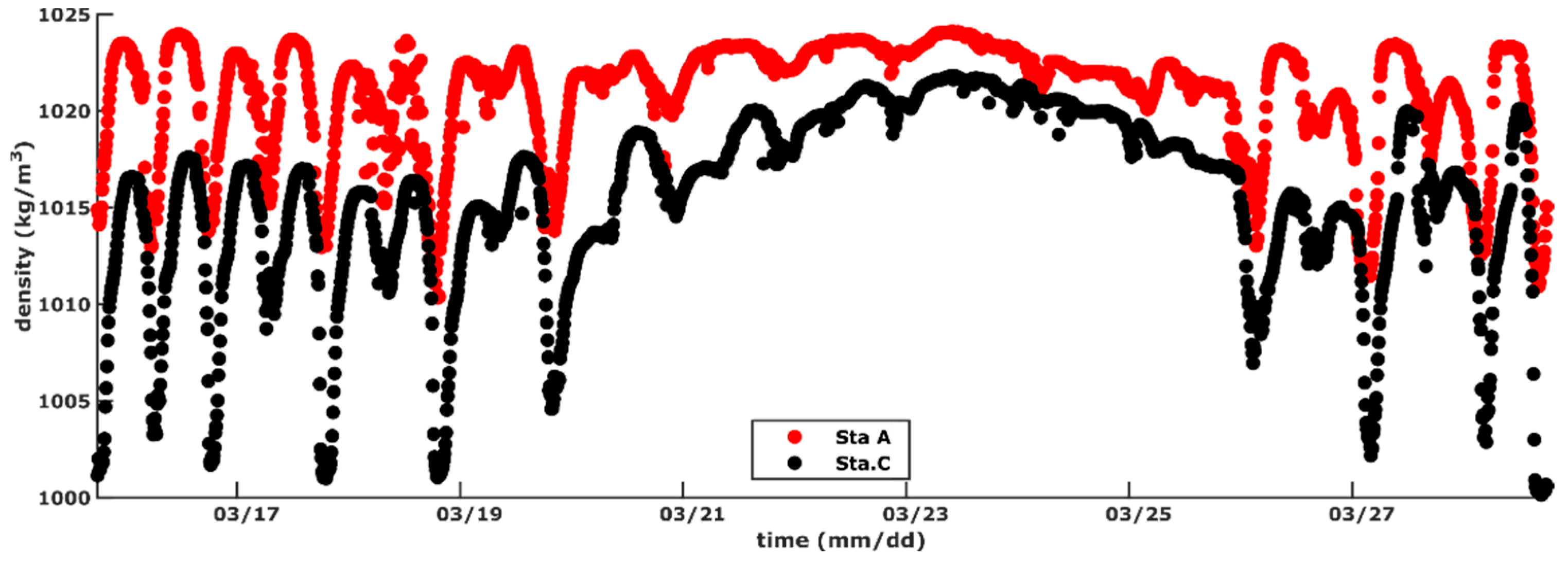
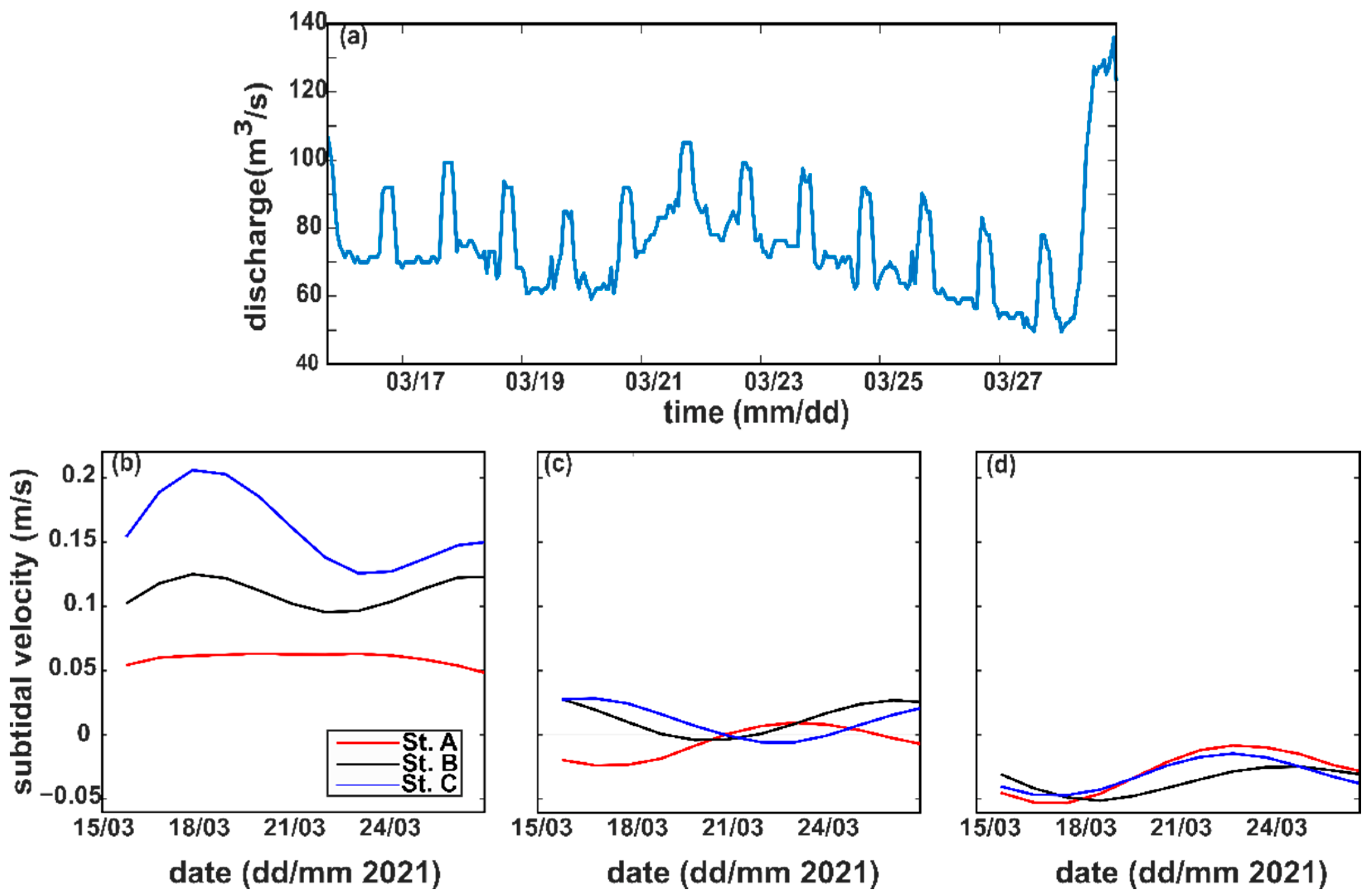
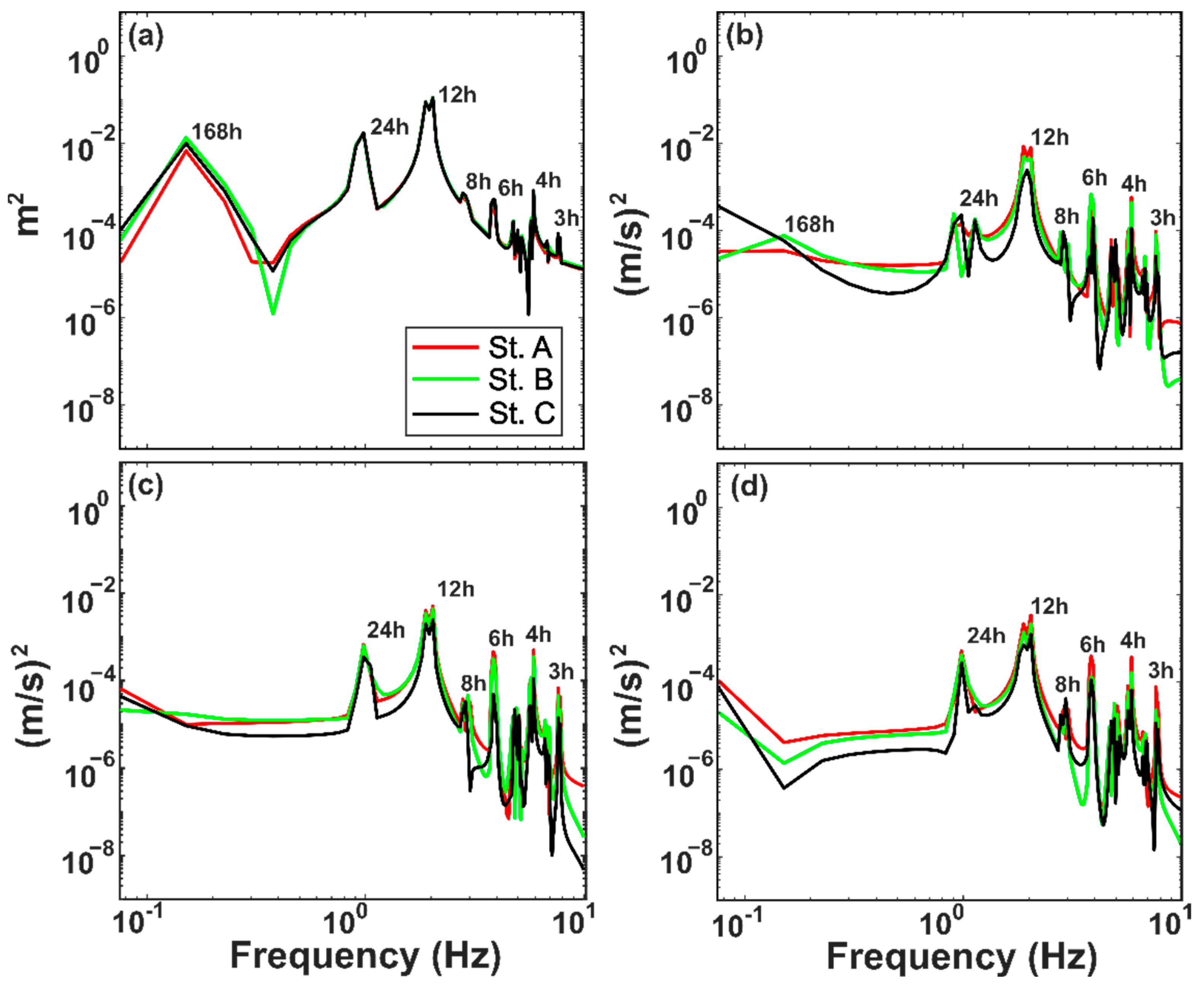
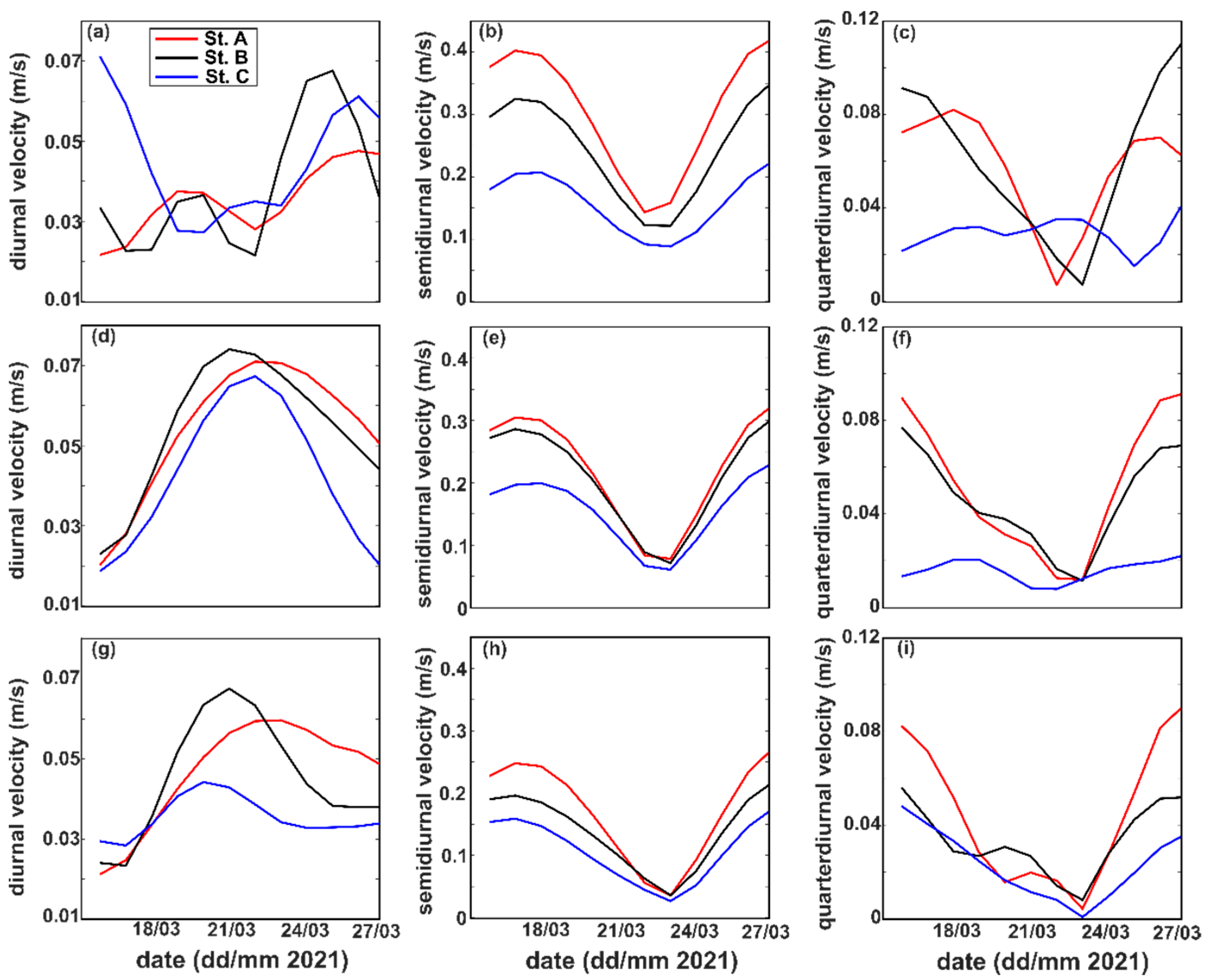
3.1. Time and Frequency Variation of Water Level, Near-Bottom Density, and Current Velocity
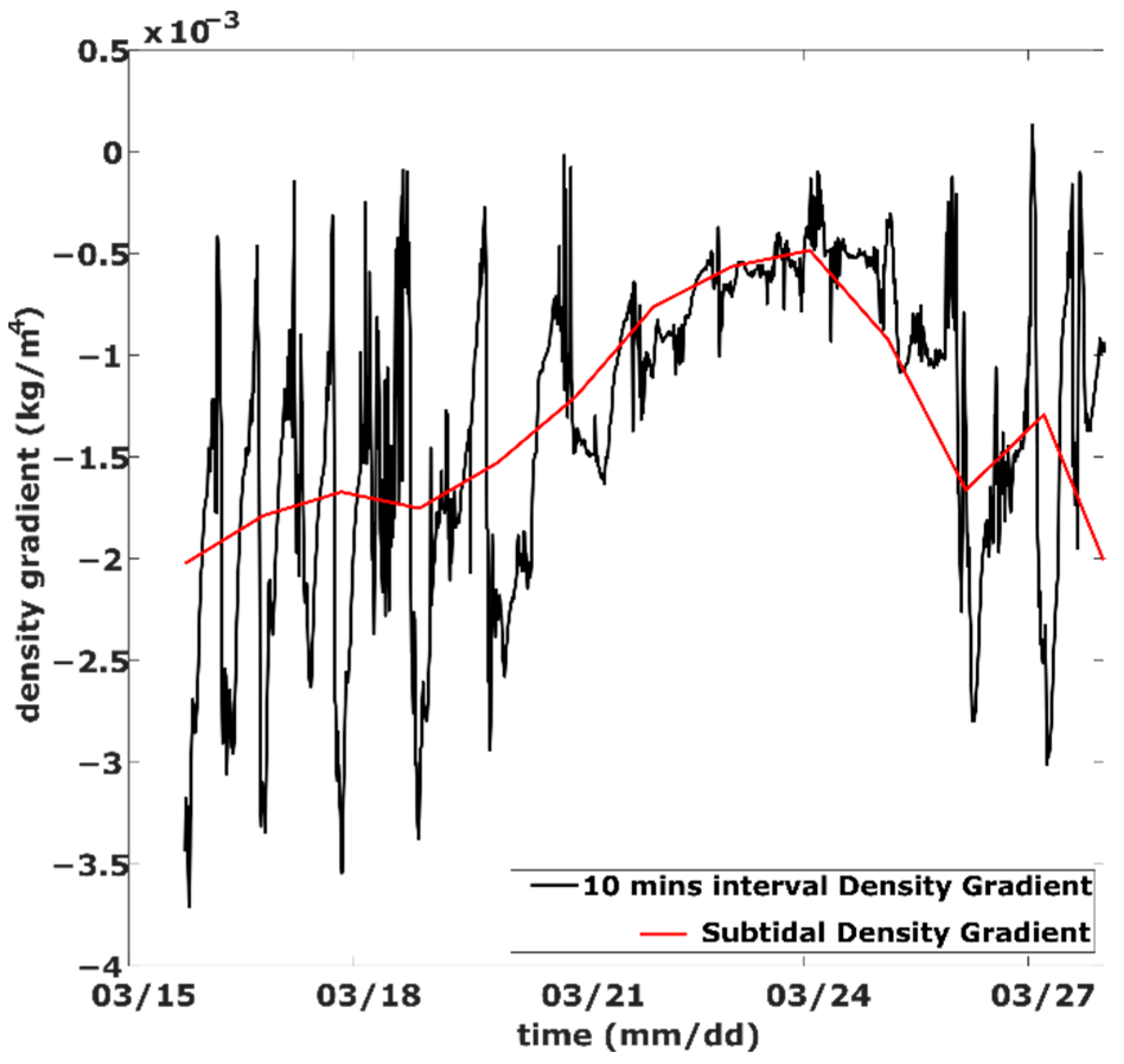
3.2. Subtidal Friction
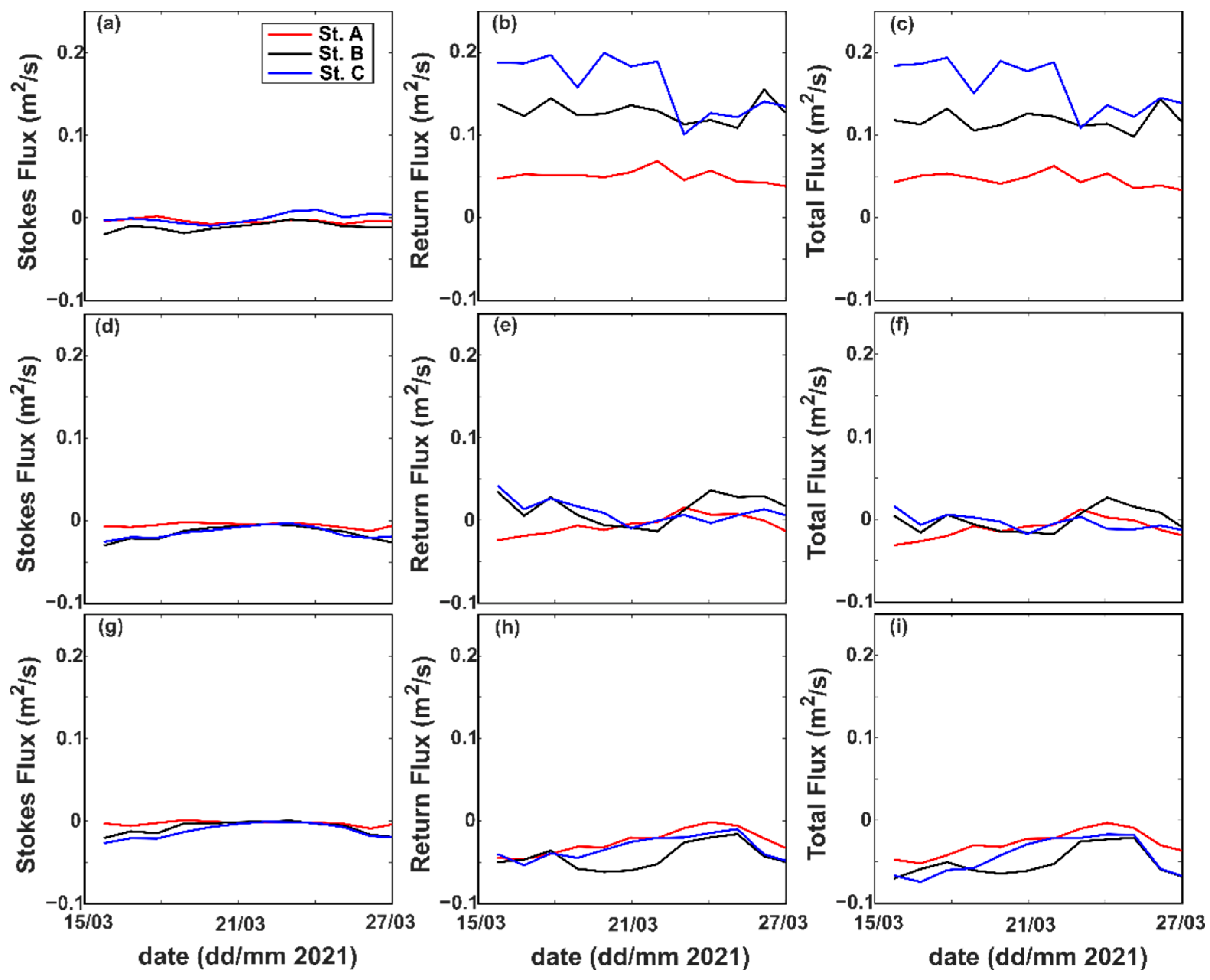
3.3. Stokes Fluxes
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barendregt, A.; Swarth, C.W. Tidal Freshwater Wetlands: Variation and Changes. Estuaries Coasts 2013, 36, 445–456. [Google Scholar] [CrossRef]
- Fricke, A.T.; Nittrouer, C.A.; Ogston, A.S.; Nowacki, D.J.; Asp, N.E.; Souza Filho, P.W.M. Morphology and Dynamics of the Intertidal Floodplain along the Amazon Tidal River. Earth Surf. Process. Landf. 2019, 44, 204–218. [Google Scholar] [CrossRef] [Green Version]
- Camenen, B.; Gratiot, N.; Cohard, J.A.; Gard, F.; Tran, V.Q.; Nguyen, A.T.; Dramais, G.; van Emmerik, T.; Némery, J. Monitoring Discharge in a Tidal River Using Water Level Observations: Application to the Saigon River, Vietnam. Sci. Total Environ. 2021, 761, 143195. [Google Scholar] [CrossRef]
- Wu, Y.; Hannah, C.; Matte, P.; O’Flaherty-Sproul, M.; Mo, R.; Wang, X.; MacAulay, P. Tidal Propagation in the Lower Fraser River, British Columbia, Canada. Estuar. Coast. Shelf Sci. 2022, 264, 107695. [Google Scholar] [CrossRef]
- Haralambidou, K.; Sylaios, G.; Tsihrintzis, V.A. Salt-Wedge Propagation in a Mediterranean Micro-Tidal River Mouth. Estuar. Coast. Shelf Sci. 2010, 90, 174–184. [Google Scholar] [CrossRef]
- Hoitink, A.J.F.; Jay, D.A. Tidal River Dynamics: Implications for Deltas. Rev. Geophys. 2016, 54, 240–272. [Google Scholar] [CrossRef]
- Sarker, S. A Short Review on Computational Hydraulics in the Context of Water Resources Engineering. Open J. Model. Simul. 2022, 10, 1–31. [Google Scholar] [CrossRef]
- Godin, G. The Propagation of Tides up Rivers with Special Considerations on the Upper Saint Lawrence River. Estuar. Coast. Shelf Sci. 1999, 48, 307–324. [Google Scholar] [CrossRef]
- Cai, H.; Savenije, H.H.G.; Jiang, C. Analytical Approach for Predicting Fresh Water Discharge in an Estuary Based on Tidal Water Level Observations. Hydrol. Earth Syst. Sci. 2014, 18, 4153–4168. [Google Scholar] [CrossRef] [Green Version]
- Matte, P.; Jay, D.A.; Zaron, E.D. Adaptation of Classical Tidal Harmonic Analysis to Nonstationary Tides, with Application to River Tides. J. Atmos. Ocean. Technol. 2013, 30, 569–589. [Google Scholar] [CrossRef] [Green Version]
- Reza, A.A.; Sarker, S.; Asha, S.A. An Application of 1-D Momentum Equation To Calculate Discharge in Tidal River: A Case Study on Kaliganga River. Tech. J. River Res. Inst. 2014, 2, 77–86. [Google Scholar]
- Buschman, F.A.; Hoitink, A.J.F.; Van Der Vegt, M.; Hoekstra, P. Subtidal Water Level Variation Controlled by River Flow and Tides. Water Resour. Res. 2009, 45, W10420. [Google Scholar] [CrossRef]
- Sassi, M.G.; Hoitink, A.J.F. River Flow Controls on Tides and Tide-Mean Water Level Profiles in a Tidal Freshwater River. J. Geophys. Res. Ocean. 2013, 118, 4139–4151. [Google Scholar] [CrossRef]
- Guo, L.; Wegen, M.; van der Jay, D.A.; Matte, P.; Wang, Z.B.; Roelvink, D.; He, Q. Journal of Geophysical Research: Oceans Nonlinear Tidal Behavior in the Yangtze River Estuary. J. Geophys. Res. C Ocean. 2015, 120, 3499–3521. [Google Scholar] [CrossRef] [Green Version]
- Buschman, F.A.; Hoitink, A.J.F.; Van Der Vegt, M.; Hoekstra, P. Subtidal Flow Division at a Shallow Tidal Junction. Water Resour. Res. 2010, 46, W12515. [Google Scholar] [CrossRef] [Green Version]
- Sassi, M.G.; Hoitink, A.J.F.; De Brye, B.; Vermeulen, B.; Deleersnijder, E. Tidal Impact on the Division of River Discharge over Distributary Channels in the Mahakam Delta. Ocean Dyn. 2011, 61, 2211–2228. [Google Scholar] [CrossRef]
- Wünchow, A.; Masse, A.K.; Garvine, R.W. Astronomical and Nonlinear Tidal Currents in a Coupled Estuary Shelf System. Cont. Shelf Res. 1992, 12, 471–498. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, H.; Hoitink, A.J.F.; Zhu, Y.; Gong, F.; Zheng, J. Tidal Impacts on the Subtidal Flow Division at the Main Bifurcation in the Yangtze River Delta. Estuar. Coast. Shelf Sci. 2017, 196, 301–314. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, H.; Zhu, Y.; Zheng, J.; Hoitink, A.J.F. Subtidal Flow Reversal Associated With Sediment Accretion in a Delta Channel. Water Resour. Res. 2019, 55, 10781–10795. [Google Scholar] [CrossRef] [Green Version]
- Wahyudin; Yamamoto, T. Modeling Bottom-up and Top-down Controls on the Low Recruitment Success of Oyster Larvae in Hiroshima Bay, Japan. Aquaculture 2020, 529, 735564. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Kawanisi, K.; Sawaf, M.B. Al Acoustic Monitoring of Tidal Flow and Salinity in a Tidal Channel. J. Mar. Sci. Eng. 2021, 9, 1180. [Google Scholar] [CrossRef]
- Kawanisi, K.; Razaz, M.; Kaneko, A.; Watanabe, S. Long-Term Measurement of Stream Flow and Salinity in a Tidal River by the Use of the Fluvial Acoustic Tomography System. J. Hydrol. 2010, 380, 74–81. [Google Scholar] [CrossRef]
- Kawanishi, K. Variability of Tidal Current, Density Stratification and Tidal Flat Sediment in a Tidal River. WIT Trans. Ecol. Environ. 2006, 88, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Kawanisi, K. Evaluation of M-Y Closure Model in Tidal Estuary with Turbulence Data from High-Resolution Current Profiler. WIT Trans. Built Environ. 2003, 70, 101–110. [Google Scholar]
- Khadami, F.; Kawanisi, K.; Al Sawaf, M.B.; Gusti, G.N.N.; Xiao, C. Spatiotemporal Response of Currents and Mixing to the Interaction of Tides and River Runoff in a Mesotidal Estuary. Ocean Sci. J. 2022, 57, 37–51. [Google Scholar] [CrossRef]
- Razaz, M.; Kawanisi, K. Turbulence Characteristics in the Bottom Layer of a Shallow Tidal Channel. J. Turbul. 2012, 13, 1–22. [Google Scholar] [CrossRef]
- Soltaniasl, M.; Kawanisi, K.; Yano, J.; Ishikawa, K. Variability in Salt Flux and Water Circulation in Ota River Estuary, Japan. Water Sci. Eng. 2013, 6, 283–295. [Google Scholar] [CrossRef]
- Gotoh, T.; Fukuoka, S.; Miyagawa, Y. Topographic Changes of Tidal Flats in the Ota River Estuary by Flood Flows. Adv. River Sediment Res. 2013, 1337–1345. Available online: https://sfuku.r.chuo-u.ac.jp/top/sfuku/paper/ISRS2013gotoh.pdf (accessed on 1 August 2022).
- Xiao, C.; Kawanisi, K.; Al Sawaf, M.B. Suspended Particulate Matter Concentration in Response to Tidal Hydrodynamics in a Long Mesotidal Floodway. Estuar. Coast. Shelf Sci. 2020, 233, 106525. [Google Scholar] [CrossRef]
- Jay, D.A.; Leffler, K.; Diefenderfer, H.L.; Borde, A.B. Tidal-Fluvial and Estuarine Processes in the Lower Columbia River: I. Along-Channel Water Level Variations, Pacific Ocean to Bonneville Dam. Estuaries Coasts 2015, 38, 415–433. [Google Scholar] [CrossRef]
- Sarker, S. A Story on the Wave Spectral Properties of Water Hammer. Appl. Mech. 2022, 3, 799–814. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical Tidal Harmonic Analysis Including Error Estimates in MATLAB Using TDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Godin, G. Compact Approximations to the Bottom Friction Term, for the Study of Tides Propagating in Channels. Cont. Shelf Res. 1991, 11, 579–589. [Google Scholar] [CrossRef]
- Schramkowski, G.P.; de Swart, H.E. Morphodynamic Equilibrium in Straight Tidal Channels: Combined Effects of Coriolis Force and External Overtides. J. Geophys. Res. Ocean. 2002, 107, 20-1–20-17. [Google Scholar] [CrossRef]
- Speer, P.E.; Aubrey, D.G. A Study of Non-Linear Tidal Propagation in Shallow Inlet/Estuarine Systems Part II: Theory. Estuar. Coast. Shelf Sci. 1985, 21, 207–224. [Google Scholar] [CrossRef]
- Gong, W.; Shen, J.; Jia, L. Salt Intrusion during the Dry Season in the Huangmaohai Estuary, Pearl River Delta, China. J. Mar. Syst. 2013, 111–112, 235–252. [Google Scholar] [CrossRef]
- Burchard, H.; Hetland, R.D. Quantifying the Contributions of Tidal Straining and Gravitational Circulation to Residual Circulation in Periodically Stratified Tidal Estuaries. J. Phys. Oceanogr. 2010, 40, 1243–1262. [Google Scholar] [CrossRef]
- Geyer, W.R.; MacCready, P. The Estuarine Circulation. Annu. Rev. Fluid Mech. 2014, 46, 175–197. [Google Scholar] [CrossRef]
- Pu, X.; Shi, J.Z.; Hu, G.D.; Xiong, L.B. Circulation and Mixing along the North Passage in the Changjiang River Estuary, China. J. Mar. Syst. 2015, 148, 213–235. [Google Scholar] [CrossRef]
- Burchard, H.; Hetland, R.D.; Schulz, E.; Schuttelaars, H.M. Drivers of Residual Estuarine Circulation in Tidally Energetic Estuaries: Straight and Irrotational Channels with Parabolic Cross Section. J. Phys. Oceanogr. 2011, 41, 548–570. [Google Scholar] [CrossRef]
- Ridd, P.V.; Stieglitz, T. Dry Season Salinity Changes in Arid Estuaries Fringed by Mangroves and Saltflats. Estuar. Coast. Shelf Sci. 2002, 54, 1039–1049. [Google Scholar] [CrossRef]
- Xie, D.; Pan, C.; Gao, S.; Wang, Z.B. Morphodynamics of the Qiantang Estuary, China: Controls of River Flood Events and Tidal Bores. Mar. Geol. 2018, 406, 27–33. [Google Scholar] [CrossRef]
- Xie, D.; Wang, Z.B. Seasonal Tidal Dynamics in the Qiantang Estuary: The Importance of Morphological Evolution. Front. Earth Sci. 2021, 9, 782640. [Google Scholar] [CrossRef]
- Xie, D.; Bing Wang, Z.; Huang, J.; Zeng, J. River, Tide and Morphology Interaction in a Macro-Tidal Estuary with Active Morphological Evolutions. Catena 2022, 212, 106131. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gusti, G.N.N.; Kawanisi, K.; Sawaf, M.B.A.; Khadami, F. Subtidal Dynamics in a Tidal River with Limited Discharge. Water 2022, 14, 2585. https://doi.org/10.3390/w14162585
Gusti GNN, Kawanisi K, Sawaf MBA, Khadami F. Subtidal Dynamics in a Tidal River with Limited Discharge. Water. 2022; 14(16):2585. https://doi.org/10.3390/w14162585
Chicago/Turabian StyleGusti, Gillang Noor Nugrahaning, Kiyosi Kawanisi, Mohamad Basel Al Sawaf, and Faruq Khadami. 2022. "Subtidal Dynamics in a Tidal River with Limited Discharge" Water 14, no. 16: 2585. https://doi.org/10.3390/w14162585





