1. Introduction
Spatiotemporal predictive learning is an essential branch of predictive learning, and it has rich potential application scenarios for many practical problems, such as precipitation nowcasting [
1,
2,
3,
4], traffic flow prediction [
5,
6], behavior recognition prediction [
7], physical scene understanding [
8], and video understanding [
9]. Such a wide range of potential applications have attracted increasing interest in the machine learning and deep learning communities. Meanwhile, many fruitful methods have also been proposed. Among these methods, to fully capture the relationship of spatiotemporal data’s dependencies in both the temporal and spatial dimensions, t a Recurrent Neural Network (RNN) has been adopted, with stacked Convolutional Long Short-Term Memory (ConvLSTM) [
10] units. This recurrent neural network is mainly inspired by the widely used natural language-processing-related technologies, such as machine translation, audio recognition, and natural language understanding. These scenarios have rich and skillful means of mining and using sequence data time-series information.
One of the tricks is that the ConvLSTM unit includes a memory unit, which stores the historical variations. Some of the studies have shown that the information retained by the memory unit is mainly the hidden state’s gradient of the ConvLSTM. On the one hand, the cumulative retention of the information of the hidden state’s gradient makes the historical information more effective for backward transmission; on the other hand, it significantly alleviates the RNN gradient’s disappearance problem. Another trick is that the ConvLSTM unit contains a series of gated structures. These gated structures are mainly based on the current input information, enabling adaptive transfer control and selective access to the historical information.
There are other studies, in addition to storing the historical variations in the time dimension to describe the changes in the time series, and adding the ConvLSTM unit to store the spatial detail variations in the spatial dimension. However, when the ConvLSTM unit models the spatiotemporal prediction model, its internal state transition may not be optimal. Due to the changes in the spatiotemporal dimension of the natural scene being full of randomness, the whole process could be highly nonlinear and non-stationary. Although it can be considered to decompose the non-stationary process into the sum of a deterministic time-varying polynomial and a zero-mean random variable, according to the Cramer decomposition, some high-order variation information will still be lost in the actual model learning.
Firstly, the convolution parameters in the ConvLSTM unit are highly shared in the spatiotemporal dimension, which leads to the penalty of spatiotemporal prediction learning mainly for the overall changes in the spatiotemporal process. They cannot regard the penalties for some of the local and highly nonlinear changes. The main reason for sharing these parameters in the spatiotemporal dimension is the graphics card’s memory limitation. Secondly, the status transition in the ConvLSTM unit only relies on the status information of the previous moment. It is based on the assumption that the spatiotemporal process described approximates a first-order Markov process or a first-order Markov process converted by some transformation. For some of the slow and general nonlinear spatiotemporal processes, this assumption is reasonable. However, for a spatiotemporal process, such as radar echo, due to the sudden appearance and expansion, shrinking, disappearing, and other highly nonlinear changes that are frequently occurring, many of the variations will be lost based on this assumption. Finally, the gate structure is adopted in the ConvLSTM unit. The characteristic of the gated structure is that each transfer of historical status information is a selective transfer after synthesizing the current input information. To some extent, this selective transfer is beneficial to the current moment, there is no guarantee that it is also beneficial to the status information transfer in the next moment.
Therefore, we consider, in the time dimension, the ConvLSTM unit should add more historical state information, that is, not relying on only the state of the previous moment, but also relying on the state of the earlier moments. Combining our knowledge of the ConvLSTM unit, we propose a spatiotemporal predictive recurrent neural network, with the gated attention mechanism (GARNN). The network inherits the commonly used stacked structure, meaning the mode of stacked cell blocks. The design of the cell block refers to the Spatiotemporal Long Short-Term Memory (ST-LSTM) structure in the Predictive Recurrent Neural Network (PredRNN) model [
11], and the memory flow in the spatial dimension, which is added to improve the ability of the cell block to maintain the small shape changes in the spatial dimension. The cell block achieves innovation in the time dimension by relying on the state information of multiple moments in the past. When we obtain the state information of multiple moments in the past, we do not simply accumulate and sum the past state information after transforming it, but refer to the attention mechanism. Because the states of the multiple historical moments have different influences on the future, to effectively utilize the state information with great influence, the attention mechanism is used to selectively extract the information of the past moments. Based on the current input information, the meaningful historical state information is selectively obtained from the state information of the multiple historical moments. Then, the meaningful historical state information at each moment is synthesized to obtain the most valuable information for the current input.
Intuitively, the spatiotemporal prediction recurrent neural network, GARNN, of the gated attention mechanism that we propose, no longer passively accepts the historical state of the previous moment but actively selects the historical status of multiple moments. This network construction provides structural support for the highly nonlinear changes, making it possible for the neural networks to learn them. We trained and validated the GARNN model on the radar echo prediction dataset. Compared with the PredRNN model and the ConvLSTM model, the prediction performance of our proposed recurrent neural network with the gated attention mechanism was greatly improved.
2. Related Work
According to the different neural network structures, the spatiotemporal process’s prediction learning can be roughly divided into three types [
12,
13]: 1. Generative Adversarial Network (GAN)-based methods; 2. RNN-based methods; 3. Convolutional Neural Network (CNN) and RNN-based methods.
Mathieu et al. [
14] proposed a multi-scale GAN architecture model based on the differential loss function of the image gradient, which solves the problem of predicting the video frame blur to a certain extent. Liu et al. [
15] added the spatial and motion constraint losses on top of the loss based on the image intensity and gradient and then used a FlowNet network to compute the optical flow information to predict temporally consistent frames. Similarly, Yi et al. [
16] proposed a GAN network structure with a dual learning mode, using the relationship between the multiple domains for the image-to-image translation. Liang et al. [
17] proposed a Dual Motion GAN (DMGAN) architecture that ensures that the model-predicted future frames are consistent with the pixel flow in the video, through a dual learning mechanism. The dual training method ensures that the predicted optical flow can help the network to reason, making the predicted future frames more realistic, and the future frame prediction task also makes the predicted optical flow information more realistic. Kwon et al. [
18] proposed a unified generative adversarial network (comprising a generator and two discriminators) to predict the video frames accurately, maintain the consistency of the predicted past and future frames with the video sequence through circular retrospective restrictions, and reduce the blurring of predicted frames. Compared with the RNN models, these models transform complex state transitions into the operations between convolutional channels by stacking convolutional layers, so they are often unable to effectively capture the dependencies between video frames that are widely separated in time.
The RNN model was initially proposed to process the one-dimensional time-series information, such as text, which better captures the correlation of sequence elements in a time series. Given this perspective, some scholars tried to use the RNN model to predict future sequences according to the historical video sequences [
19,
20,
21]. Ranzato et al. [
22] proposed a recurrent convolutional neural network inspired by language modeling. Under the assumption of local space and time stationarity, the visual features generated by the clustering image patches were used to predict the future video frames. Srivastava et al. [
23] used an LSTM Encoder to map the input video sequence to a fixed-length representation, and then used a single-layer/multi-layer LSTM Decoder to decode the learned representation, reconstruct the input video sequence and predict the future video sequences. Babaeizadeh et al. [
24] believed that the future of many natural processes is not deterministic, and there may be multiple reasonable futures, so they proposed a Stochastic Variational Video Prediction (SV2P) method that predicts a different probable future for each sample of its potential variables. Denton et al. [
25] introduced an unsupervised video generation model. The model learned a prior model of the uncertainty in the given environment and then drew samples from this prior model and combined them with the deterministic estimation of future frames to generate the final future frames. Some other scholars also believed that the future is not certain and have completed a lot of preliminary research [
26,
27,
28,
29,
30]. These RNN-based methods mainly model the time series relationship and characterize the uncertainty. However, they mainly model the spatiotemporal process’s high-level features dynamically, leading to the inevitable loss of detailed information in the actual natural process.
To address the loss of detailed information in the RNN model when modeling the spatiotemporal processes, Shi et al. [
10] combined the advantages of the convolution operation and LSTM. They proposed the convolutional neural network ConvLSTM that used convolution instead of the original matrix multiplication operation, allowing LSTM to maintain the two-dimensional characteristics of the image. Shi et al. [
31] also combined the convolution operation with the GRU model [
32,
33], and proposed the Trajectory GRU (TrajGRU) model, which can actively learn the position-changing structure of the recurrent connections. Wang et al. [
34] proposed an Eidetic 3D LSTM (E3D-LSTM), which integrated 3D convolution into RNN, and the encapsulated 3D-Conv enabled the local perceptron of RNN to have motion-sensing capability and enabled the memory cells to store better short-term features. Wang et al. [
35,
36] proposed a PredRNN model using zigzag memory flow, the core of which is a new spatiotemporal LSTM (ST-LSTM) unit, which can simultaneously extract and memorize variations on both the temporal and spatial dimensions. Wang et al. [
37] proposed a Memory In Memory (MIM) network and a corresponding recurrent block. The MIM module uses the differential signal between the adjacent cyclic states to simulate the non-stationary and nearly stationary characteristics of the spatiotemporal dynamics of two cascaded, self-updated memory modules. The above method combines convolution with RNN, extracts the information in both time and space dimensions, and significantly improves the prediction tasks for many of the natural spatiotemporal processes. However, when the cell blocks of these networks are in the state of transition, the historical state information they rely on is only from the previous moment. This dependence is based on the assumption that the described spatiotemporal process is an approximate first-order Markov process, or is transformed into a first-order Markov process by some transformation. However, in fact, the natural spatiotemporal process is often non-stationary and highly nonlinear.
4. Methods
As mentioned above, in the previous stacked recurrent neural networks used for spatiotemporal prediction, the passivity of the historical state transition brought about by relying only on the latest moment’s historical state information has not been fully recognized. To overcome this passivity, it is first necessary to ensure that the historical state information is obtained from multiple moments in the past, and the second issue is how to obtain the historical state information at different moments. Considering these issues, we propose a Gated Attention LSTM (GA-LSTM) block to actively obtain the historical state we need from the state information of multiple past moments’ information. In this chapter, we will first introduce the GA-LSTM block in detail, how to realize the initiative to obtain the historical state information, and then use the GA-LSTM block in combination with the commonly used stacked structure to construct a different RNN from the previous one. Intuitively, the new architecture of the network is different from the previous RNN architecture, in that each GA-LSTM unit no longer only obtains the state information from the previous moment but obtains the historical state information from multiple historical moments. The GA-LSTM block we propose is an improvement of the ST-LSTM block based on the PredRNN model, but it is feasible to apply the GA (Gated Attention) part to any unit similar to ConvLSTM.
4.1. GA-LSTM Block
In real natural spatiotemporal process, dynamic changes in the time dimension are usually very nonlinear, and the historical state that best matches the current input is often not the state information of the previous moment. For example, if a mouse shifts one step to the right at time t−2, one step downward at time t−1, and one step to the right at time t, then the motion state at time t is obviously more related to the state at time t−2. The previous stacked spatiotemporal prediction model lacks such a direct state transfer mechanism across time, so it cannot directly transfer the state across time and can only transfer the long-term state indirectly and iteratively. However, this iterative transfer will perform the filter based on the input information at that time in each iteration, and this filtering will largely filter out the information related to the current input.
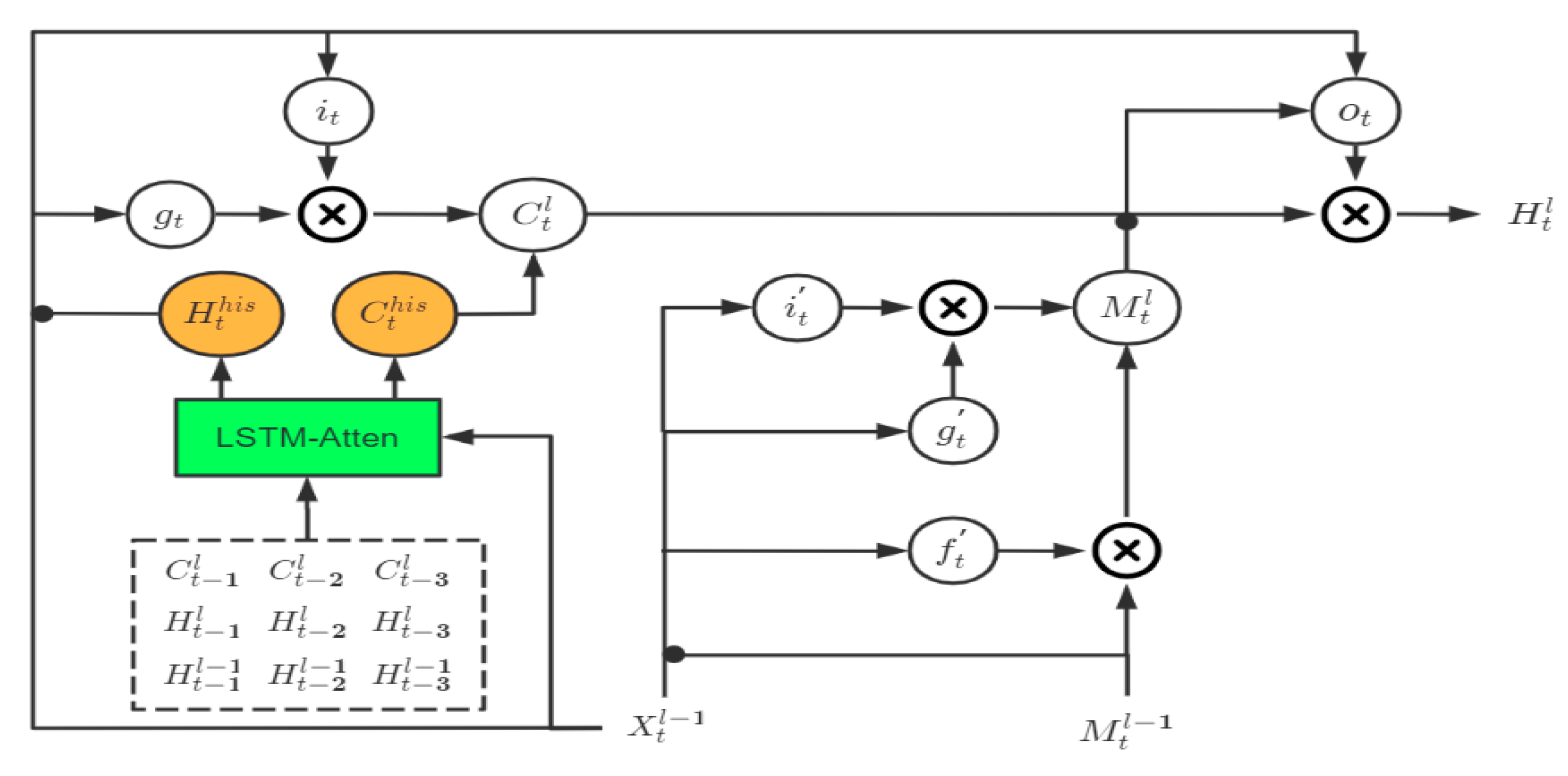
The GA-LSTM block is mainly inspired by the attention mechanism in natural language processing. It no longer only passively depends on the state of the previous moment, such as the ST-LSTM block and the MIM block, but constructs a mechanism that relies on the state information of multiple past moments and makes an automatic selection. As shown in
Figure 3 and
Figure 4 below, the historical state transition part of the ST-LSTM block and the MIM block in the sequential memory (the part covered by the dotted box in the figure) only depends on the state information at time t−1. The improvement of the MIM block relative to the ST-LSTM block is that, based on the assumption of differential stability, the state information is analyzed by using the differential information at time t−1 to perform stable information (corresponding to MIM-S in the figure) and unstable information (corresponding to MIM-N in the figure) decomposition. Compared with the single-time dependency of the ST-LSTM block and MIM block, we designed an LSTM-Atten module to process the state information of multiple moments in the past. The overall GA-LSTM block is shown in
Figure 5.
Here, the black dot denotes the concatenation operator. The input of the attention module LSTM-Atten includes the current input information
and the status information of the multiple past moments (3 moments as an example), including
,
,
,
,
,
,
,
, and
. Through the selection of the current input
, the outputs of the LSTM-Atten module are the expected historical state information
and the expected historical hidden state information
. The overall transfer equation of GA-LSTM is written as:
where LSTM-Atten denotes the attention operation based on the LSTM structure. We think that the selection is attention. If the active variable X can selectively extract the passive variable, we can think that the active variable X exerts attention on the passive variable C. When the passive variable C has a greater positive effect on the active variable X to complete a specific task, the passive variable C will be given greater attention when it is extracted, and vice versa; it will be smaller or even negative. From this point of view, the LSTM structure is an attention mechanism. The active variable is the input information
, the passive variable is the state information
and
. The active variable
selectively extracts the passive variable
and
to generate the
and
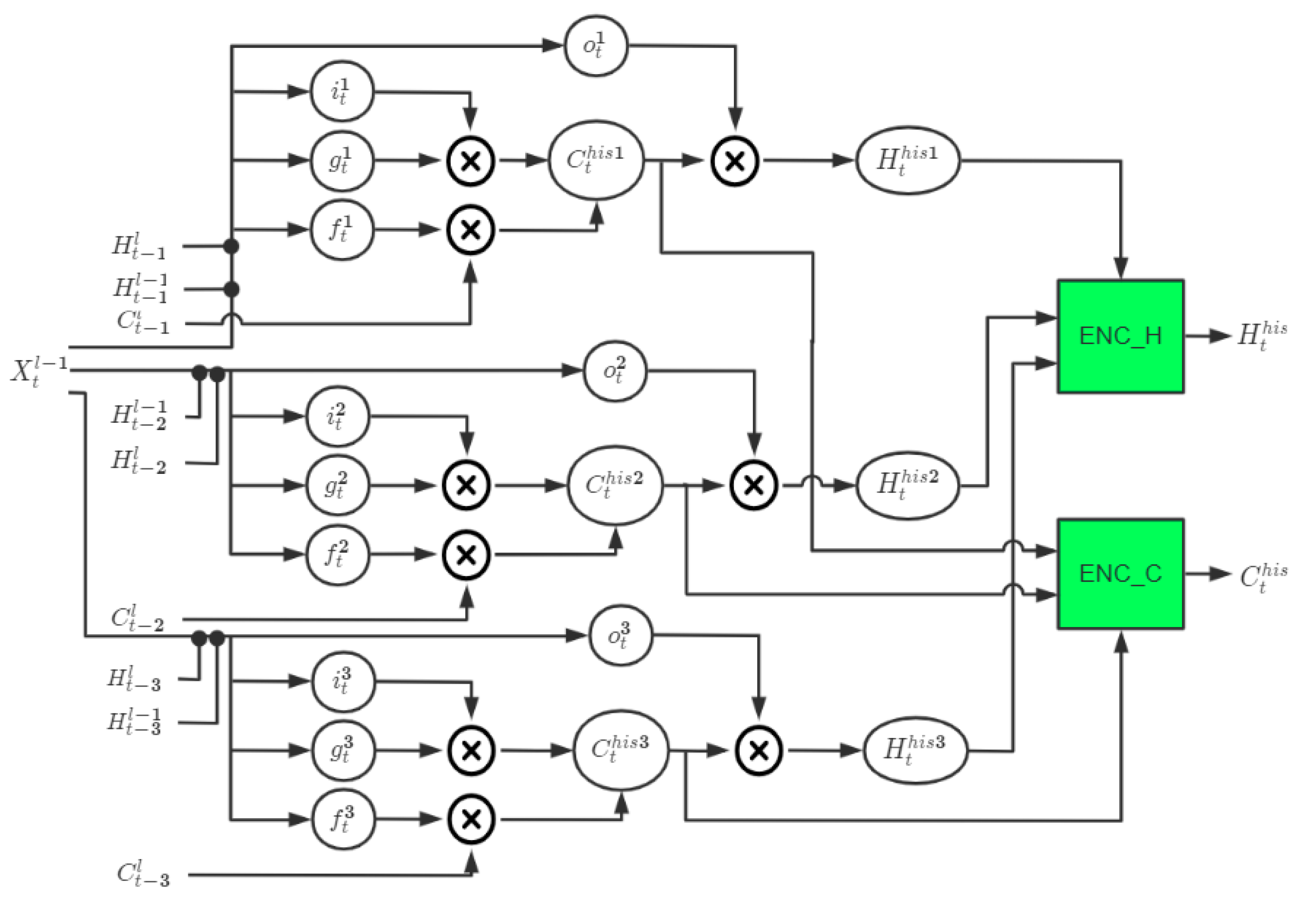
. Based on this understanding, we designed the LSTM-Atten module, using LSTM as the historical state information extraction operator integrated with the attention mechanism. The detailed structure of the LSTM-Atten module we designed is as follows (taking the extraction of historical state information from the past three moments as an example):
In
Figure 6, the black dot denotes the concatenation operator. Combined with the selection mechanism of the LSTM structure,
is used as the active variable, the state variables
and
at time t−1 are actively selectively extracted to obtain
and
, the state variables
and
at time t−2 are actively selectively extracted to obtain
and
, and the state variables
and
at time t−3 are actively selectively extracted to obtain
and
. Then, use the convolutional network ENC_H to synthesize the hidden state information
,
, and
, ENC_C to synthesize the state information
,
, and
. Automatically assign the attention weights to the state information at each moment to generate the weighted state information
and
of gated attention. The internal state transition equation of the LSTM-Atten module is written as:
where
and
denote the simple three-layer convolutional networks, respectively. Replacing the LSTM-Atten in Equation (4) with Equation (5), the state transition equation of the complete GA-LSTM block can be obtained.
Our proposed GA-LSTM is mainly reflected in two aspects: on the one hand, the LSTM structure is used to actively obtain the historical state information that matches the input information from multiple historical moments. On the other hand, two convolutional networks are used to automatically assign the attention weights to the historical state information matching the input, and to obtain the weighted gated attention state information, and .
4.2. Gated Attention Recurrent Neural Network
By stacking the GA-LSTM blocks, as shown in
Figure 7, we propose the Gated Attention Recurrent Neural Network (GARNN) for spatiotemporal prediction. The most prominent feature of this recurrent neural network is that it no longer only depends on the state of the previous moment, but on the state of the past multiple moments.
The GARNN network inputs a frame at each timestep and outputs the predicted frame of the next moment. The yellow arrow is the state transition path of the spatial memory unit, and the black arrow is the state transition path of the temporal memory unit.
Figure 7 shows the third layer of the GA-LSTM block at time t as an example. In addition to receiving the state information
and
at time
t − 1 (indicated by the black line), it also uses the state information
,
,
, and
at time
t − 2 and time
t − 3 (indicated by the blue line). In addition, inspired by the MIM model, the GARNN uses
that can, to a certain extent, learn the transient information in the temporal dimension, and uses
that can, to a certain extent, learn the transient information before and after the state transition. Adding this transient information helps to guide the extraction of the historical state information by input
, so the part of the red line in is added
Figure 7.
Furthermore, as shown in
Figure 7, due to the use of a four-layer stacked structure, there will be four pieces of input information at each timestep (take time t as an example, the input information at this time includes
,
,
, and
), the last three pieces of input information are the hidden state information of the previous layer. Usually, the hidden state has a higher number of channels (such as 64 or 128 channels), and the number of channels of the first input is just the number of channels of the original image. To be consistent, we let a simple convolutional network transform the input information
before entering the GARNN network. Similarly, the output of the last layer of the GA-LSTM block is transformed by another simple convolutional network to the same number of channels as the original input.
5. Experiments
5.1. Experiment Design
We evaluated the proposed GARNN model for spatiotemporal prediction using a real-life weather radar echo dataset, which was given in the form of a 120 × 120 × 1 grayscale image (for the convenience of observation, when the radar echo image is displayed, it is converted into a color image using the color scale) with a coverage of 240 km × 240 km. The interval of each radar echo frame was 6 min. During training, every 20 time-consecutive frames were used as a set of samples, the first 10 frames were input (the period is exactly 1 h), and the last 10 frames were predicted (the period is also 1 h). During the inference, 10 frames in the next hour were predicted, based on the last 10 frames that could be obtained at the current moment.
As shown in
Figure 8, we adopted a stacked recurrent neural network structure, which contains four-layer GA-LSTM units, and the number of feature channels of each gated structure in each GA-LSTM unit was 64. The model was trained with Mean Squared Error (MSE) as the loss function, using the Ranger optimizer, and the initial learning rate was set to 0.005. We set the mini-batch to eight, used the data-parallel mode for training, and set the time length to 3, extracting the historical state information of interest from the last 3 past moments each time. Additionally, we applied the layer normalization operation after the convolution of each gating operation of this model to reduce the covariate shift problem.
During the training and prediction, the image needs to be normalized to [0, 1], and then the mean of the squared differences of all the pixels was calculated as the MSE loss of the frame. The smaller the value, the better, indicating that the predicted image is closer to the ground truth image.
We usually pay more attention to the Critical Success Index (
CSI) indicator in practical applications. After specifying the precipitation threshold, the CSI indicator reflects the accuracy of the prediction results in precipitation forecasting, and a higher
CSI indicates a better precipitation forecasting accuracy. The
CSI is defined as:
where
TP corresponds to true positives;
FP corresponds to false positives; and
FN corresponds to false negatives; where positives can be considered as precipitation, and negatives can be considered as no precipitation.
5.2. Results
Figure 9 shows the comparison results of the GARNN model, the PredRNN model, and the ConvLSTM model on radar echo extrapolation prediction. As can be seen from the figure, relative to the ConvLSTM model, the PredRNN model and our proposed GARNN model predicted that the intensity attenuation of the generated echo was not apparent. The results of the PredRNN model show that it relied too much on spatial memory units, predicted that the echo changes in the generated images were small, and paid insufficient attention to the temporal memory units. The yellow echoes in the upper half of the Ground Truth images show a variation pattern of “dissipating gradually from the middle and finally dissipating completely in the upper right half.” The PredRNN model did not adequately capture this variation pattern, while the GARNN model captured it almost completely.
As shown in
Figure 10, the further the PredRNN model predicts, the greater the growth trend of MSE than the GARNN model. We speculate that the predictions of the PredRNN model are clearer than the GARNN model in the future, however, such clear details are not correct details, so the loss is too large, and the loss growth rate is hardly weakened. The GARNN model is relatively fuzzier, especially for the later predictions, and because it has learned the overall time dimension change characteristics, the overall MSE loss is smaller, and the loss growth rate is also lower. This can also be seen from the evaluation based on the CSI.
Combining the relationship between the radar and precipitation (according to our experience, the echo intensity threshold for determining precipitation is generally between [
8,
15] dBZ), we obtained three thresholds of 8 dBZ, 12 dBZ, and 15 dBZ for the CSI calculation. The overall mean value is shown in
Table 1, and the CSI value comparisons are shown in
Figure 11,
Figure 12 and
Figure 13.
As can be seen in the figures above, at the three thresholds of 8 dBZ, 12 dBZ, and 15 dBZ, the GARNN model had the most noticeable improvement compared to the PredRNN model at 8 dBZ, while the two were almost the same at 15 dBZ.
This is mainly because the GARNN model reduces the dependence on the spatial memory unit, the detail retention ability is not as strong as that of the PredRNN model, and there is a certain strength attenuation, however, it learns better the dynamic variations in the time dimension, so its CSI values are better.