Research on Evolutionary Game Analysis of Spatial Cooperation for Social Governance of Basin Water Pollution
Abstract
:1. Introduction
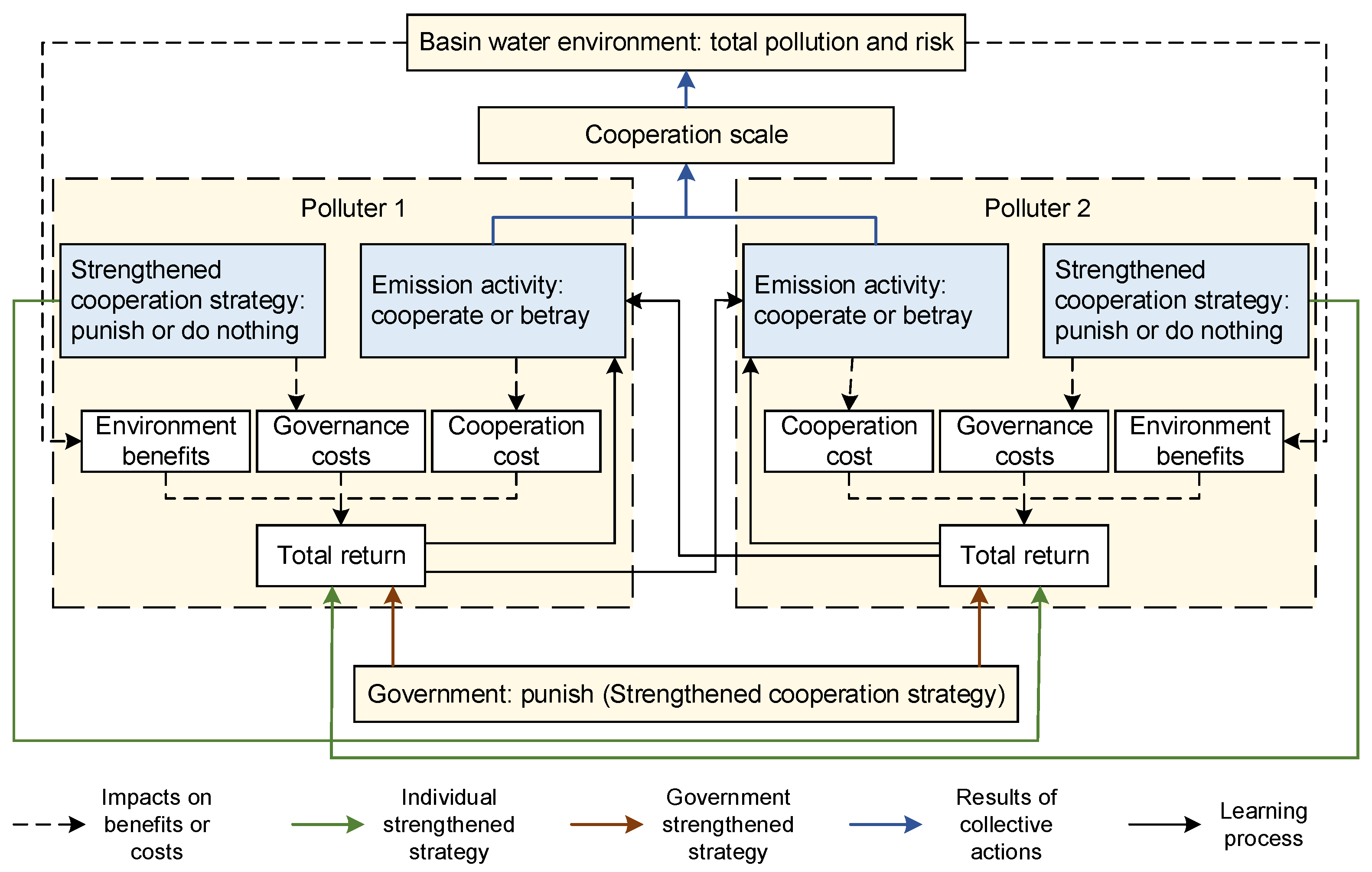
2. Materials and Methods
2.1. Environment Benefits from Pollution Governance
2.2. Decision Function for Pollutant Emission Behavior
2.3. Social Learning Strategy Update Based on Self-Organization
2.4. Strengthened Cooperation Strategy in the New Governance System
2.4.1. Cooperation Game under Individual Strengthened Cooperation Mechanism
2.4.2. Collective Cooperation Game under Government Intervention
2.5. Experiment Design and Evolutionary Process
3. Results
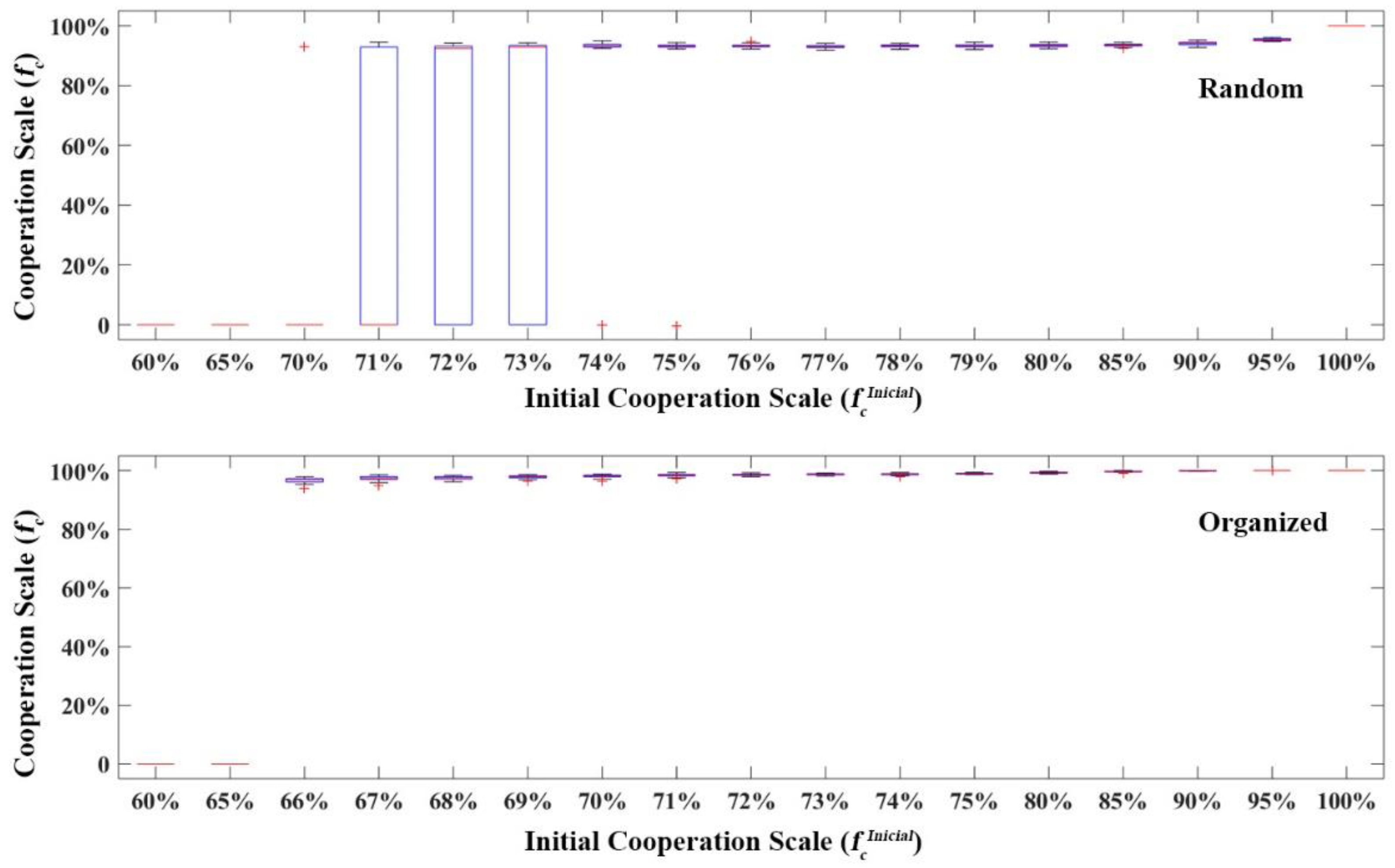
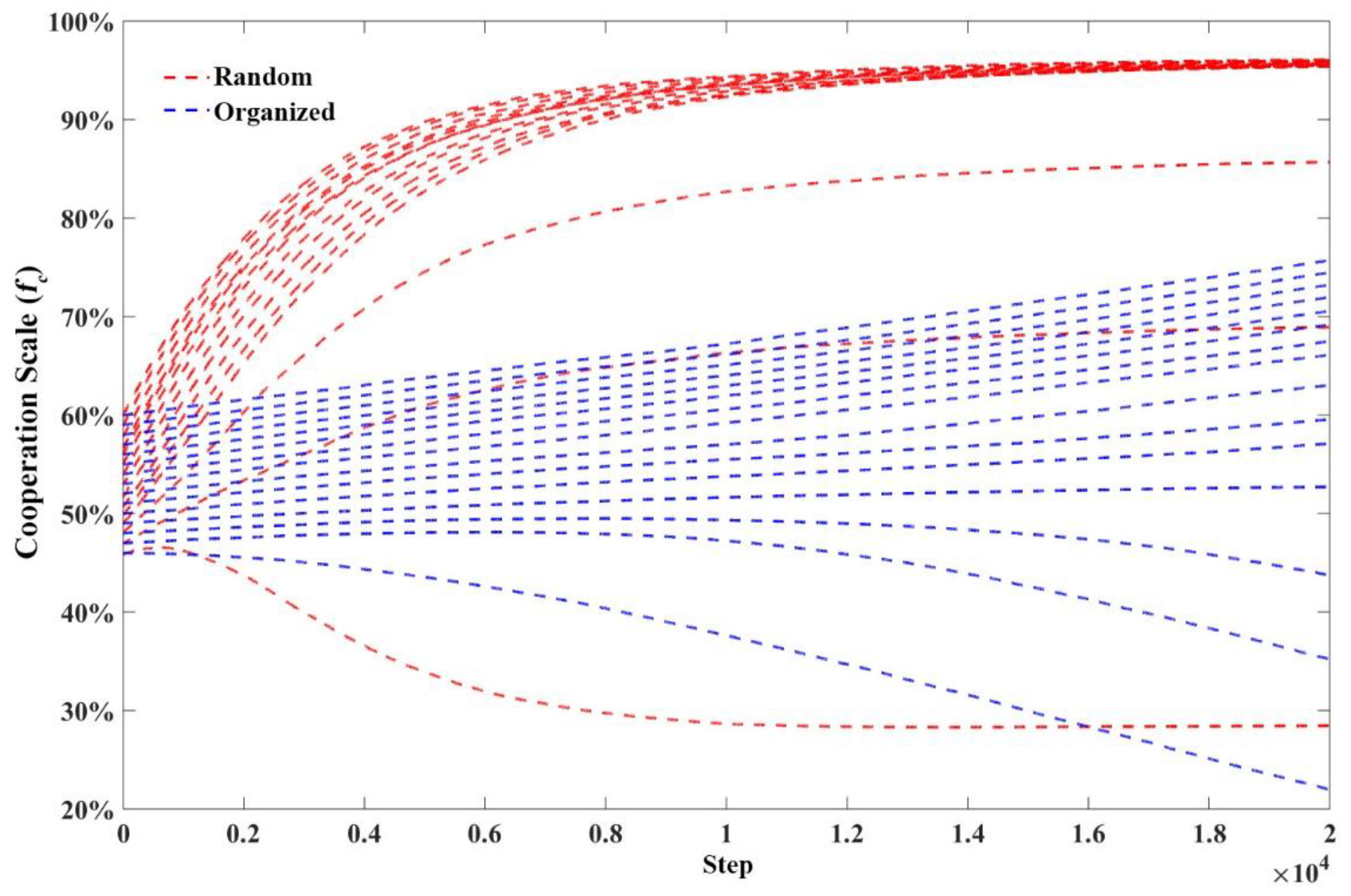
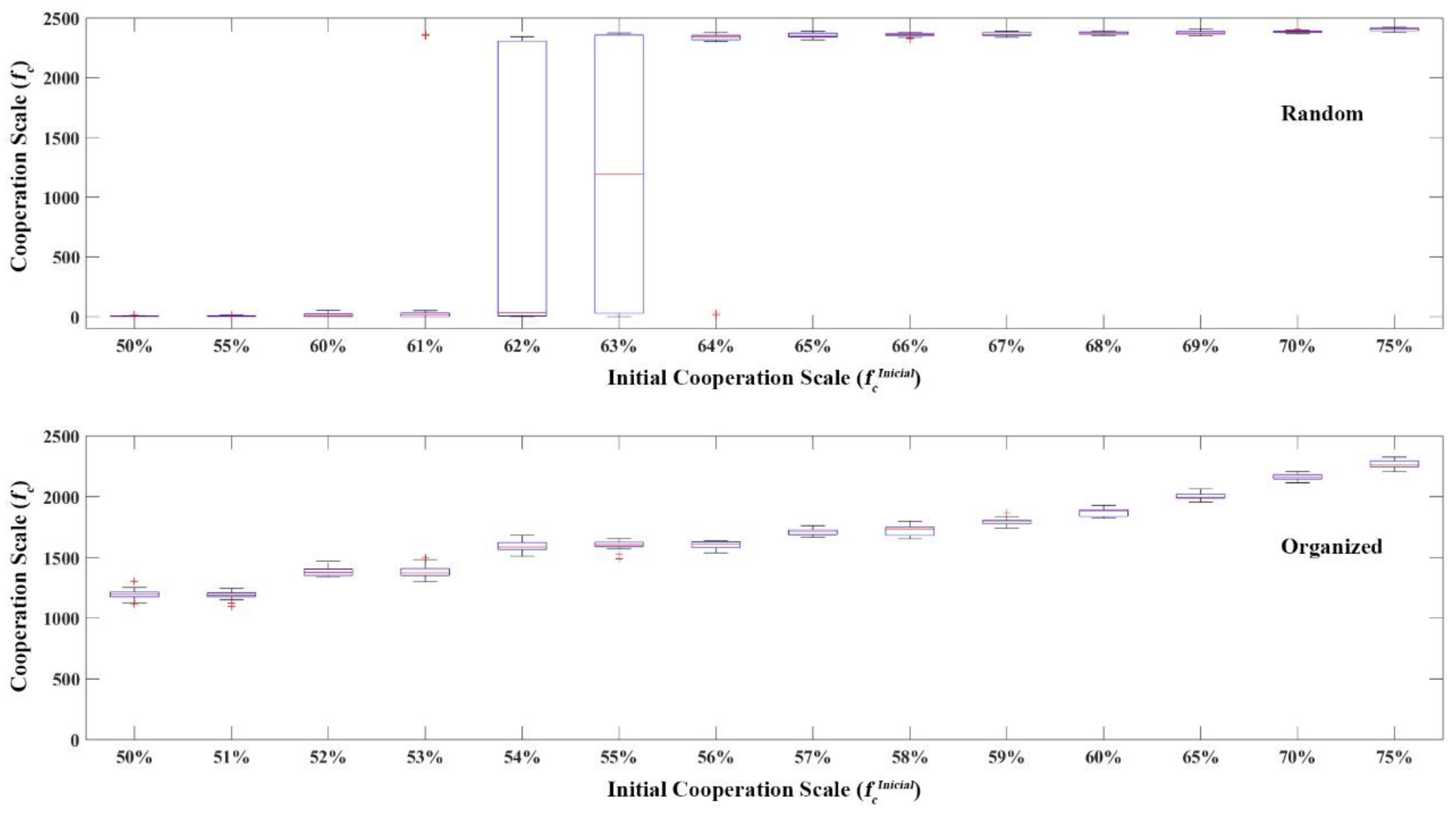
3.1. Spontaneous Cooperation Evolution Simulation
3.2. Cooperative Evolution Simulation under Strengthened Cooperation Mechanism
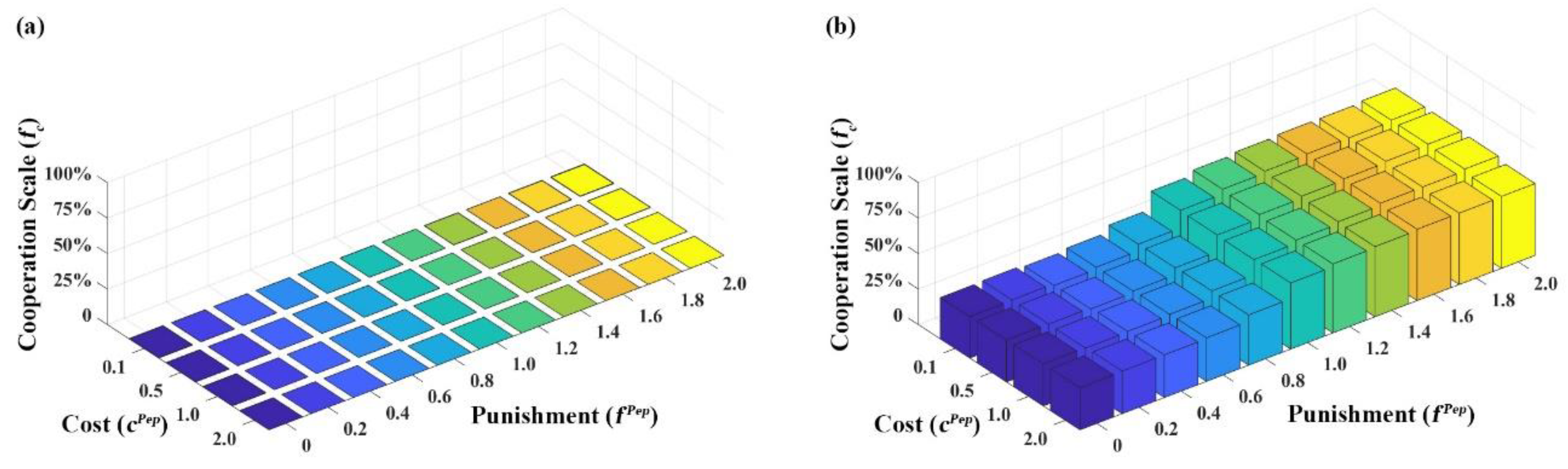
3.2.1. Cooperative Evolution Simulation under Individual Strengthened Mechanism
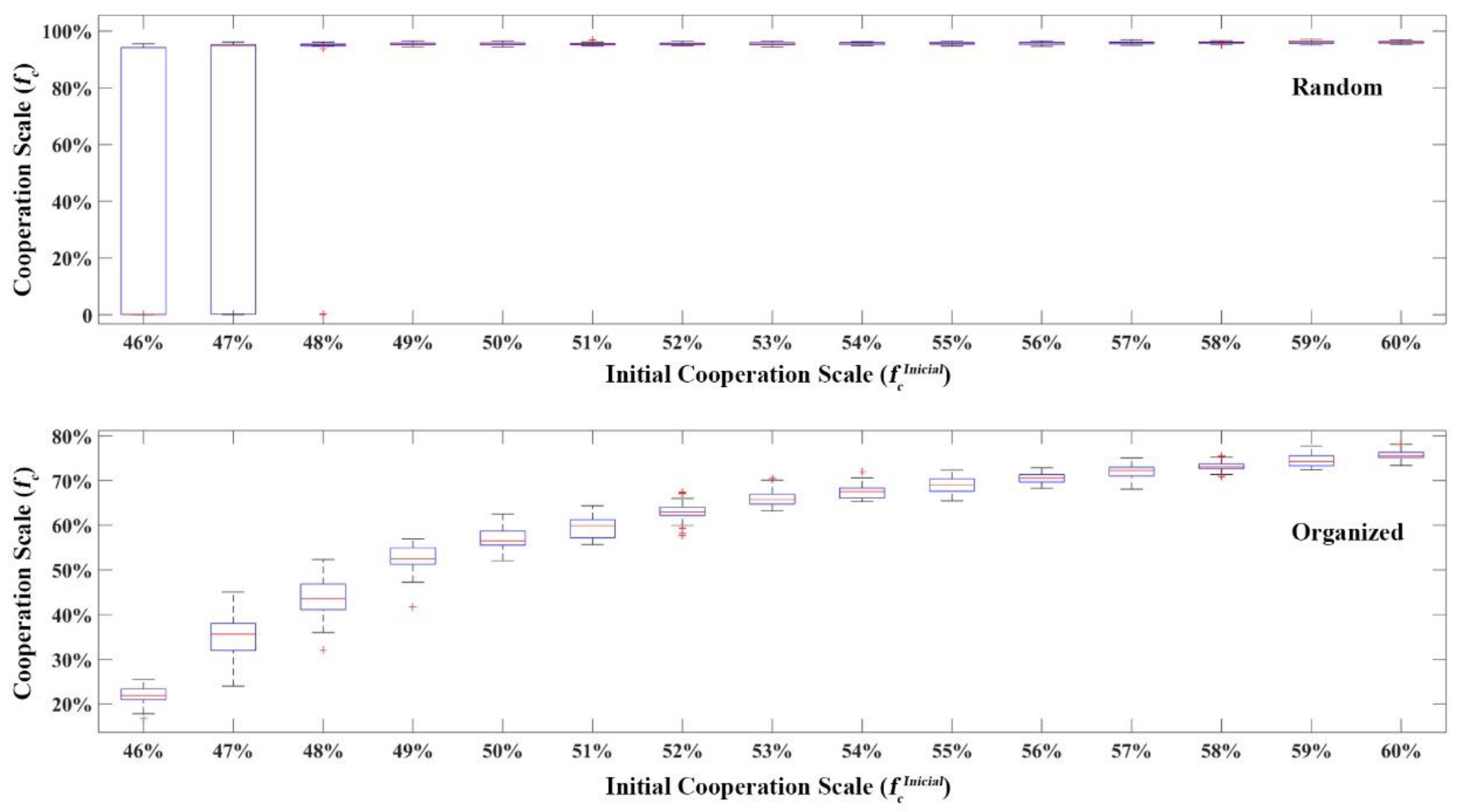
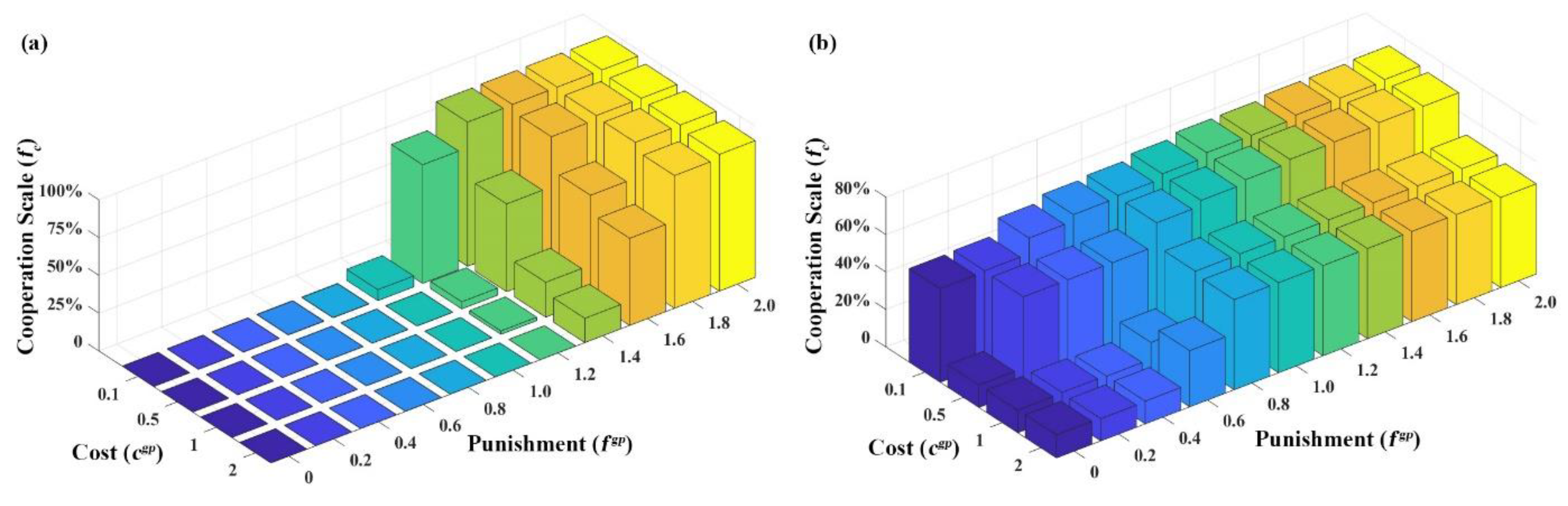
3.2.2. Cooperative Evolution Stimulation under Government Punishment Mechanism
Conditions for Government’s Punishment Strategy Implementation
Activation Conditions of Government Punishment Strategy
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, K.; Wang, P.; Zhang, R.; Lin, Z. Determination of Spatiotemporal Characteristics of Agricultural Non-Point Source Pollution of River Basins Using the Dynamic Time Warping Distance. J. Hydrol. 2020, 583, 124303. [Google Scholar] [CrossRef]
- Gao, B.; Han, L.; Hao, H.; Zhou, H. Pollution Characteristics of Mercury (Hg) in Surface Sediments of Major Basins, China. Ecol. Indic. 2016, 67, 577–585. [Google Scholar] [CrossRef]
- Shen, D. River Basin Water Resources Management in China: A Legal and Institutional Assessment. Water Int. 2009, 34, 484–496. [Google Scholar] [CrossRef]
- Wanhong, L.; Fang, L.; Fan, W.; Maiqi, D.; Tiansen, L. Industrial Water Pollution and Transboundary Eco-Compensation: Analyzing the Case of Songhua River Basin, China. Environ. Sci. Pollut. Res. 2020, 27, 34746–34759. [Google Scholar] [CrossRef]
- Jia, S.; Li, D. Evolution of Water Governance in China. J. Water Resour. Plan. Manag. 2021, 147, 04021050. [Google Scholar] [CrossRef]
- Ye, W.; Liu, L.; Zhang, B. Designing and Implementing Pollutant Emissions Trading Systems in China: A Twelve-Year Reflection. J. Environ. Manag. 2020, 261, 110207. [Google Scholar] [CrossRef]
- Tang, M.; Li, Z.; Hu, F.; Wu, B.; Zhang, R. Market Failure, Tradable Discharge Permit, and Pollution Reduction: Evidence from Industrial Firms in China. Ecol. Econ. 2021, 189, 107180. [Google Scholar] [CrossRef]
- Wang, K.-L.; Zhao, B.; Ding, L.-L.; Miao, Z. Government Intervention, Market Development, and Pollution Emission Efficiency: Evidence from China. Sci. Total Environ. 2021, 757, 143738. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, H.; Yu, Q.; Bi, J. Equity-Based Optimisation of Regional Water Pollutant Discharge Amount Allocation: A Case Study in the Tai Lake Basin. J. Environ. Plan. Manag. 2012, 55, 885–900. [Google Scholar] [CrossRef]
- Jiang, Y.; Hellegers, P. Joint Pollution Control in the Lake Tai Basin and the Stabilities of the Cost Allocation Schemes. J. Environ. Manag. 2016, 184, 504–516. [Google Scholar] [CrossRef]
- Tian, J.; Guo, S.; Liu, D.; Pan, Z.; Hong, X. A Fair Approach for Multi-Objective Water Resources Allocation. Water Resour. Manag. 2019, 33, 3633–3653. [Google Scholar] [CrossRef]
- Wang, B.; Huang, G.H.; Liu, L.; Li, W.; Xie, Y.L. Integrated Planning of Urban Water Resources and Water Pollution Control Management: Case of Urumqi, China. J. Water Resour. Plan. Manag. 2016, 142, 05016001. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, G.; Yu, T.; Shen, M.; Meng, W.; Ongley, E.D. Trans-Jurisdictional Pollution Control Options within an Integrated Water Resources Management Framework in Water-Scarce North-Eastern China. Water Policy 2011, 13, 624–644. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, J.; Zhou, N.; Zhang, T.; Zeng, H. Does the “10-Point Water Plan” Reduce the Intensity of Industrial Water Pollution? Quasi-Experimental Evidence from China. J. Environ. Manag. 2021, 295, 113048. [Google Scholar] [CrossRef]
- Tang, W.; Pei, Y.; Zheng, H.; Zhao, Y.; Shu, L.; Zhang, H. Twenty Years of China’s Water Pollution Control: Experiences and Challenges. Chemosphere 2022, 295, 133875. [Google Scholar] [CrossRef]
- Li, L.; Luo, H. Study of Game Theories Characters of Water Resources Management in China. China Popul. Resour. Environ. 2006, 16, 37–41. (In Chinese) [Google Scholar]
- Perez-Quesada, G.; Hendricks, N.P. Lessons from Local Governance and Collective Action Efforts to Manage Irrigation Withdrawals in Kansas. Agric. Water Manag. 2021, 247, 106736. [Google Scholar] [CrossRef]
- Luo, Y.; Wu, J.; Xu, Y. Can Self-Governance Tackle the Water Commons?—Causal Evidence of the Effect of Rural Water Pollution Treatment on Farmers’ Health in China. Ecol. Econ. 2022, 198, 107471. [Google Scholar] [CrossRef]
- Yeo, K.; Jung, Y. Cost Allocation of River Water Quality Management Based on the Separable Cost Remaining Benefit (SCRB) Method. J. Environ. Plan. Manag. 2016, 59, 1040–1053. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Wu, W.; Zhang, L.; Wang, L. Using Cooperative Game Model of Air Pollution Governance to Study the Cost Sharing in Yangtze River Delta Region. J. Environ. Manag. 2022, 301, 113896. [Google Scholar] [CrossRef]
- Li, H.; Guo, G. A Differential Game Analysis of Multipollutant Transboundary Pollution in River Basin. Phys. Stat. Mech. Its Appl. 2019, 535, 122484. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, R.; Yi, Y. Dynamic Optimal Control of Transboundary Pollution Abatement under Learning-by-Doing Depreciation. Complexity 2020, 2020, 3763684. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, G. Analyzing the Evolution of Cooperation among Different Parties in River Water Environment Comprehensive Treatment Public-Private Partnership Projects of China. J. Clean. Prod. 2020, 270, 121118. [Google Scholar] [CrossRef]
- Shi, G.-M.; Wang, J.-N.; Zhang, B.; Zhang, Z.; Zhang, Y.-L. Pollution Control Costs of a Transboundary River Basin: Empirical Tests of the Fairness and Stability of Cost Allocation Mechanisms Using Game Theory. J. Environ. Manag. 2016, 177, 145–152. [Google Scholar] [CrossRef]
- Van Soest, D.; Stoop, J.; Vyrastekova, J. Toward a Delineation of the Circumstances in Which Cooperation Can Be Sustained in Environmental and Resource Problems. J. Environ. Econ. Manag. 2016, 77, 1–13. [Google Scholar] [CrossRef]
- Sturm, B.; Weimann, J. Experiments in Environmental Economics and Some Close Relatives. J. Econ. Surv. 2006, 20, 419–457. [Google Scholar] [CrossRef]
- Levitt, S.D.; List, J.A. What Do Laboratory Experiments Measuring Social Preferences Reveal About the Real World? J. Econ. Perspect. 2007, 21, 153–174. [Google Scholar] [CrossRef]
- Rand, D.G.; Dreber, A.; Ellingsen, T.; Fudenberg, D.; Nowak, M.A. Positive Interactions Promote Public Cooperation. Science 2009, 325, 1272–1275. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Du, W.; Perc, M.; Cao, X.; Zhang, J. Resonance-like Cooperation Due to Transaction Costs in the Prisoner’s Dilemma Game. Phys. Stat. Mech. Its Appl. 2019, 521, 248–257. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M. Evolutionary Advantages of Adaptive Rewarding. New J. Phys. 2012, 14, 093016. [Google Scholar] [CrossRef]
- Yang, H.-X.; Chen, X. Promoting Cooperation by Punishing Minority. Appl. Math. Comput. 2018, 316, 460–466. [Google Scholar] [CrossRef]
- Nowak, M.A.; May, R.M. Evolutionary Games and Spatial Chaos. Nature 1992, 359, 826–829. [Google Scholar] [CrossRef]
- Nowak, M.A.; May, R.M. The Spatial Dilemmas of Evolution. Int. J. Bifurc. Chaos 1993, 3, 35–78. [Google Scholar] [CrossRef]
- Aoki, K.; Feldman, M.W. Evolution of Learning Strategies in Temporally and Spatially Variable Environments: A Review of Theory. Theor. Popul. Biol. 2014, 91, 3–19. [Google Scholar] [CrossRef]
- Nowak, M.A.; Tarnita, C.E.; Antal, T. Evolutionary Dynamics in Structured Populations. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 19–30. [Google Scholar] [CrossRef]
- Szolnoki, A.; Szabó, G.; Perc, M. Phase Diagrams for the Spatial Public Goods Game with Pool Punishment. Phys. Rev. E 2011, 83, 036101. [Google Scholar] [CrossRef]
- Perc, M.; Szolnoki, A. Self-Organization of Punishment in Structured Populations. New J. Phys. 2012, 14, 043013. [Google Scholar] [CrossRef]
- Chen, X.; Szolnoki, A.; Perc, M. Probabilistic Sharing Solves the Problem of Costly Punishment. New J. Phys. 2014, 16, 083016. [Google Scholar] [CrossRef]
- Yang, C.-L.; Zhang, B.; Charness, G.; Li, C.; Lien, J.W. Endogenous Rewards Promote Cooperation. Proc. Natl. Acad. Sci. USA 2018, 115, 9968–9973. [Google Scholar] [CrossRef]
- Sasaki, T.; Uchida, S. Rewards and the Evolution of Cooperation in Public Good Games. Biol. Lett. 2014, 10, 20130903. [Google Scholar] [CrossRef]
- Fu, M.; Guo, W.; Cheng, L.; Huang, S.; Chen, D. History Loyalty-Based Reward Promotes Cooperation in the Spatial Public Goods Game. Phys. Stat. Mech. Its Appl. 2019, 525, 1323–1329. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Z. The Public Goods Game with a New Form of Shared Reward. J. Stat. Mech. Theory Exp. 2016, 2016, 103201. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M.; Szabó, G. Topology-Independent Impact of Noise on Cooperation in Spatial Public Goods Games. Phys. Rev. E 2009, 80, 056109. [Google Scholar] [CrossRef]
- Perc, M.; Jordan, J.J.; Rand, D.G.; Wang, Z.; Boccaletti, S.; Szolnoki, A. Statistical Physics of Human Cooperation. Phys. Rep. 2017, 687, 1–51. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M. Reward and Cooperation in the Spatial Public Goods Game. EPL Europhys. Lett. 2010, 92, 38003. [Google Scholar] [CrossRef]
- Helbing, D.; Szolnoki, A.; Perc, M.; Szabó, G. Punish, but Not Too Hard: How Costly Punishment Spreads in the Spatial Public Goods Game. New J. Phys. 2010, 12, 083005. [Google Scholar] [CrossRef]
- Hardin, G. The Tragedy of the Commons. Science 1968, 162, 1243–1248. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010; ISBN 978-0-691-14275-3. [Google Scholar]
- Hauert, C.; Traulsen, A.; Brandt, H.; Nowak, M.A.; Sigmund, K. Via Freedom to Coercion: The Emergence of Costly Punishment. Science 2007, 316, 1905–1907. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y.; Nowak, M.A. Indirect Reciprocity Provides Only a Narrow Margin of Efficiency for Costly Punishment. Nature 2009, 457, 79–82. [Google Scholar] [CrossRef]
- Helbing, D.; Johansson, A. Evolutionary Dynamics of Populations with Conflicting Interactions: Classification and Analytical Treatment Considering Asymmetry and Power. Phys. Rev. E 2010, 81, 016112. [Google Scholar] [CrossRef]
- Helbing, D.; Szolnoki, A.; Perc, M.; Szabó, G. Evolutionary Establishment of Moral and Double Moral Standards through Spatial Interactions. PLoS Comput. Biol. 2010, 6, e1000758. [Google Scholar] [CrossRef]
- Nakamaru, M.; Iwasa, Y. The Coevolution of Altruism and Punishment: Role of the Selfish Punisher. J. Theor. Biol. 2006, 240, 475–488. [Google Scholar] [CrossRef]
- Szolnoki, A.; Szabó, G.; Czakó, L. Competition of Individual and Institutional Punishments in Spatial Public Goods Games. Phys. Rev. E 2011, 84, 046106. [Google Scholar] [CrossRef]
- Sheng, J.; Webber, M. Incentive-Compatible Payments for Watershed Services along the Eastern Route of China’s South-North Water Transfer Project. Ecosyst. Serv. 2017, 25, 213–226. [Google Scholar] [CrossRef]






| Experiments | Scenarios | Strengthened Cooperation Mechanism | Initial Strategy Distribution States | |||
|---|---|---|---|---|---|---|
| Experiment 1 | Scenario 1 | no | Random | 0–100% | N/A | N/A |
| Scenario 2 | no | Organized | 0–100% | N/A | N/A | |
| Experiment 2 | Scenario 3 | Individual strengthened mechanism | Random | 50% | 0.1, 0.5, 1.0, 2.0 | 0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0 |
| Scenario 4 | Individual strengthened mechanism | Organized | 50% | 0.1, 0.5, 1.0, 2.0 | 0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0 | |
| Experiment 3 | Scenario 5 | Government punishment mechanism | Random | 50% | 0.1, 0.5, 1.0, 2.0 | 0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0 |
| Scenario 6 | Government punishment mechanism | Organized | 50% | 0.1, 0.5, 1.0, 2.0 | 0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, M.; Chen, M.; Zhang, L.; Duan, Y.; Zhou, S. Research on Evolutionary Game Analysis of Spatial Cooperation for Social Governance of Basin Water Pollution. Water 2022, 14, 2564. https://doi.org/10.3390/w14162564
Bai M, Chen M, Zhang L, Duan Y, Zhou S. Research on Evolutionary Game Analysis of Spatial Cooperation for Social Governance of Basin Water Pollution. Water. 2022; 14(16):2564. https://doi.org/10.3390/w14162564
Chicago/Turabian StyleBai, Minghao, Meilin Chen, Liyuan Zhang, Yeqing Duan, and Shenbei Zhou. 2022. "Research on Evolutionary Game Analysis of Spatial Cooperation for Social Governance of Basin Water Pollution" Water 14, no. 16: 2564. https://doi.org/10.3390/w14162564
APA StyleBai, M., Chen, M., Zhang, L., Duan, Y., & Zhou, S. (2022). Research on Evolutionary Game Analysis of Spatial Cooperation for Social Governance of Basin Water Pollution. Water, 14(16), 2564. https://doi.org/10.3390/w14162564






