Study on Sustainable Well Water Pumping Technology to Melt Ice in Winter for the Middle Route of the South-to-North Water Diversion Project
Abstract
:1. Introduction
2. Data and Methods
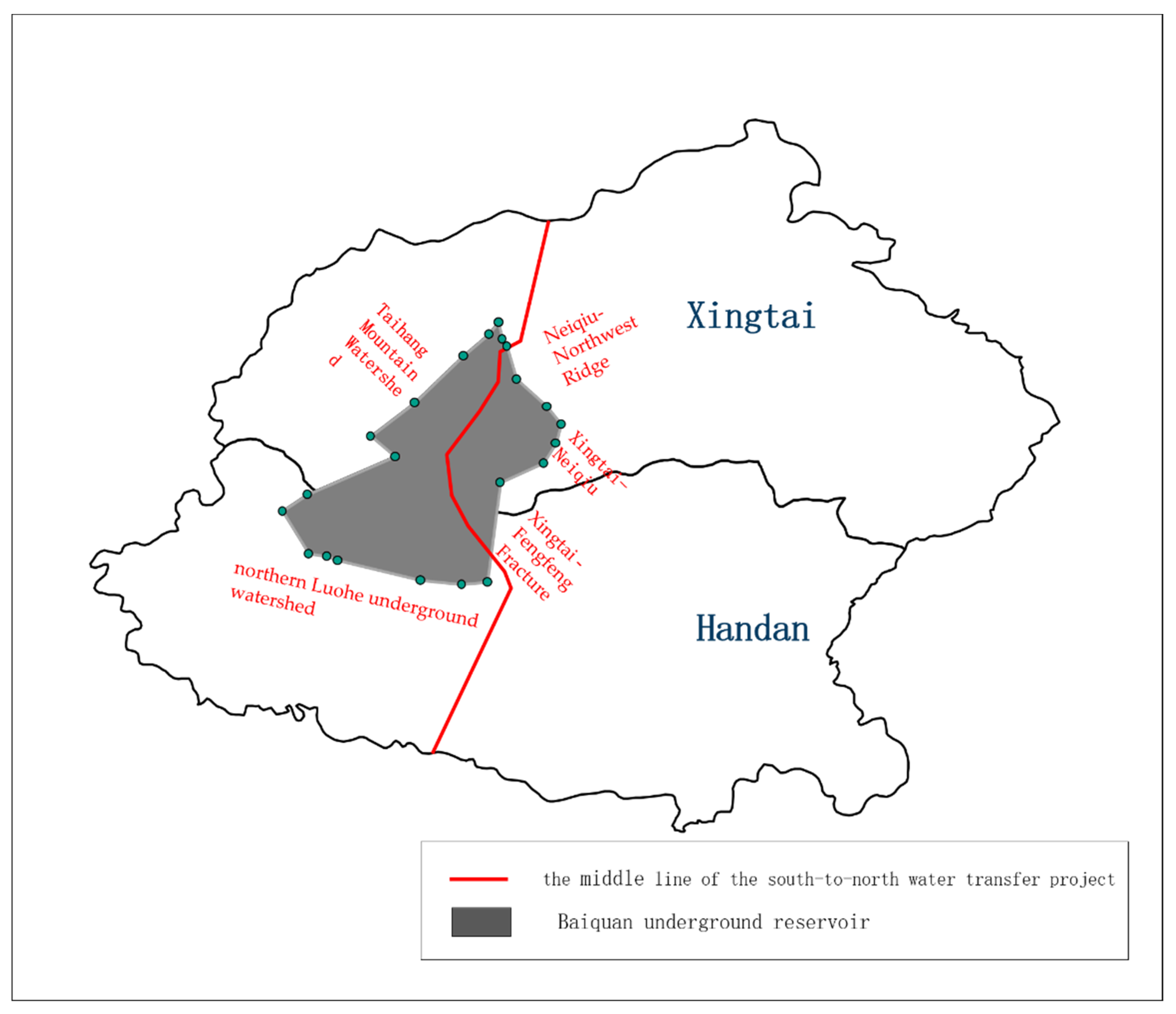
2.1. Study Area
2.2. Numerical Model
2.3. Model Construction
3. Results and Discussion
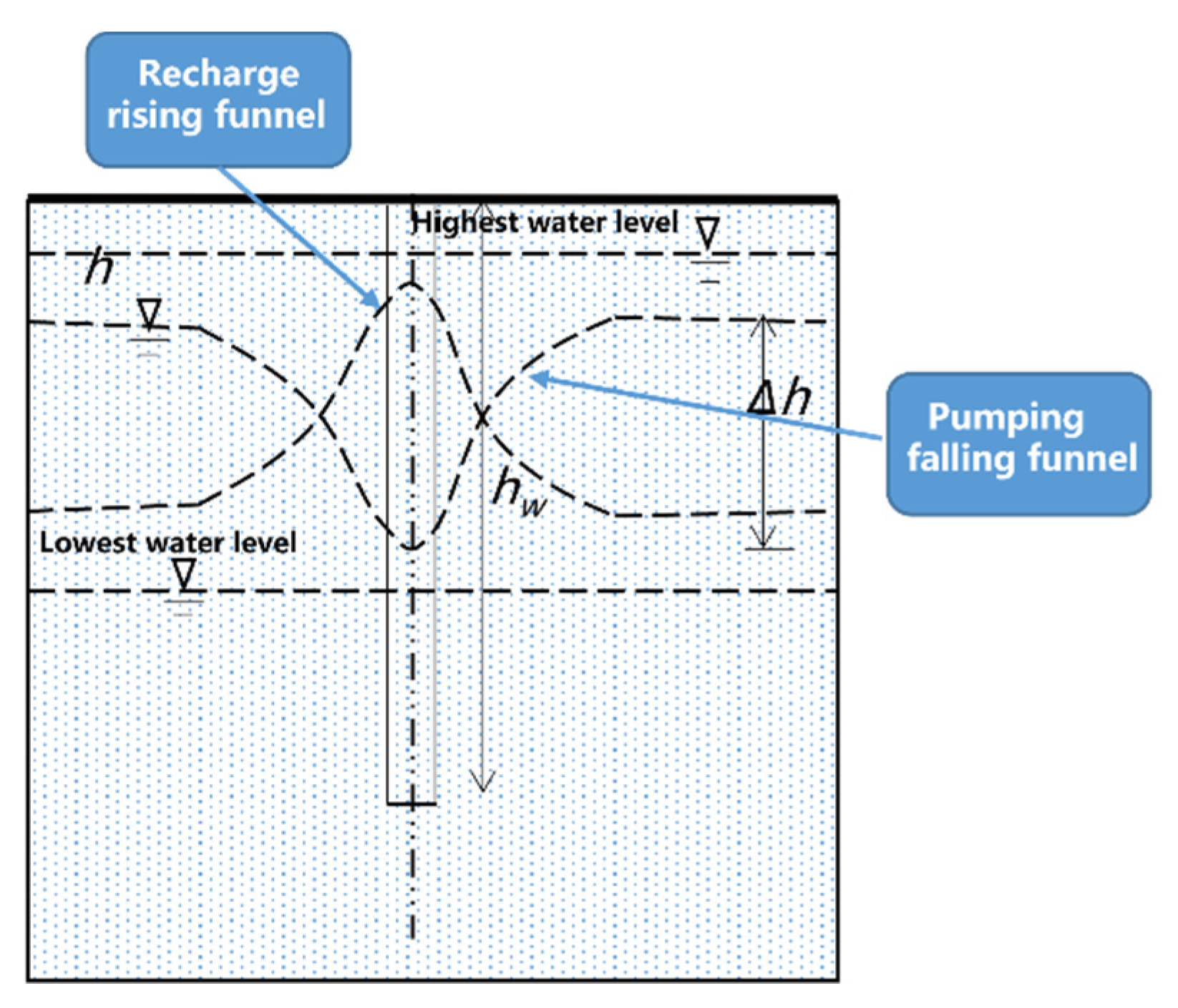
3.1. Analysis of Pumping and Recharge Characteristics of Underground Reservoirs
3.2. Determination of Ecological Pumping Capacity
3.3. Determination of Ecological Recharge Capacity
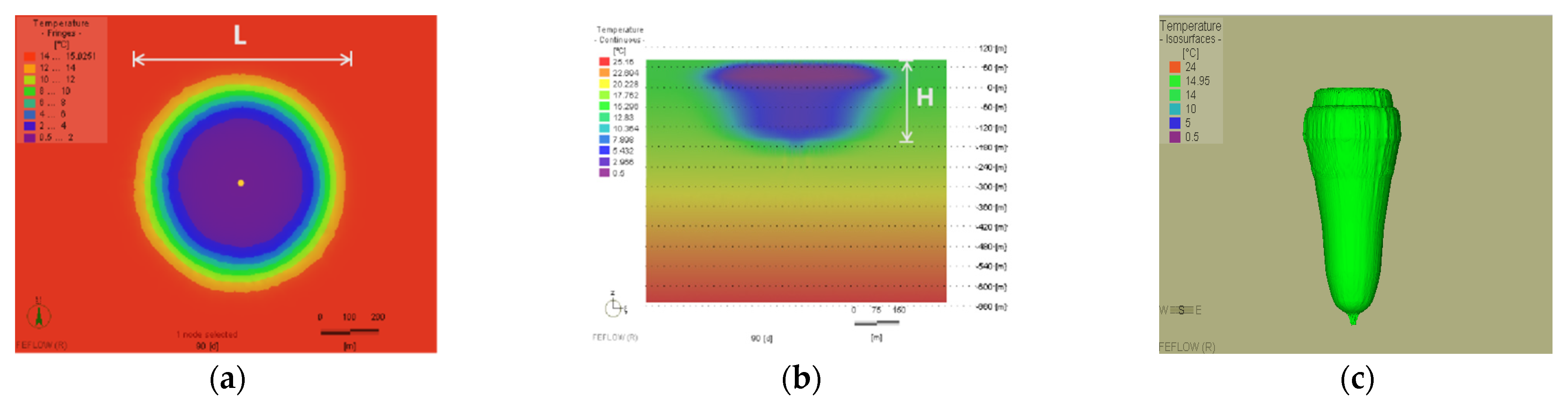
3.4. Analysis of Temperature Field Change Rule
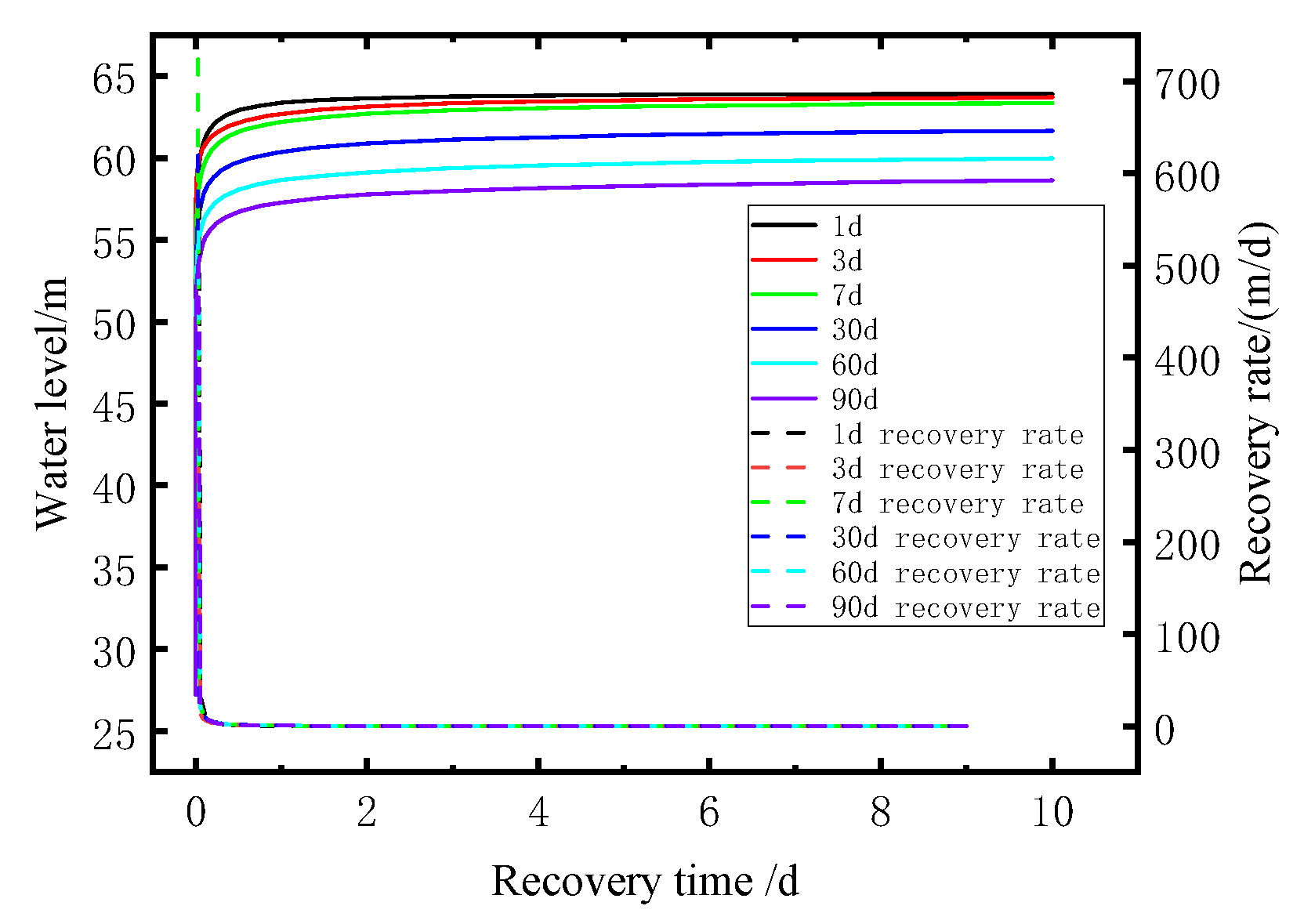
3.5. Temperature Field Recovery Analysis
3.6. Optimization of Pumping—Recharging Scheme
3.7. Discussion
4. Conclusions
- (1)
- Under the limitation of water level fluctuation, a quantitative estimation formula of pumping capacity and well depth, permeability coefficient, continuous pumping time and initial water level was established. After the pumping stopped, the water level recovered quickly, and a formula for calculating the recovery water level, the initial water level, and the duration of continuous pumping was established;
- (2)
- Under the limitation of water level fluctuation, a quantitative estimation formula of recharge capacity and well depth, permeability coefficient, continuous recharge time and initial water level was established. The quantitative estimation formula between the restored water level after recharging, the initial water level, and the continuous recharging time was established;
- (3)
- The variation characteristics of the temperature field after recharge were analyzed. It was affected by recharge flow rate, recharge water temperature, initial water level, well depth and specific heat of soil volume, but had no relation with permeability coefficient and soil thermal conductivity coefficient. The quantitative relationships between L, H, k, and the above influencing factors, were established;
- (4)
- Under different recharge flow rates, it was determined that the recharge water temperature in summer must be at least 14.8 °C to restore the recharge water temperature to the original temperature, before water pumping in winter, to ensure the sustainable operation of water pumping and ice melting;
- (5)
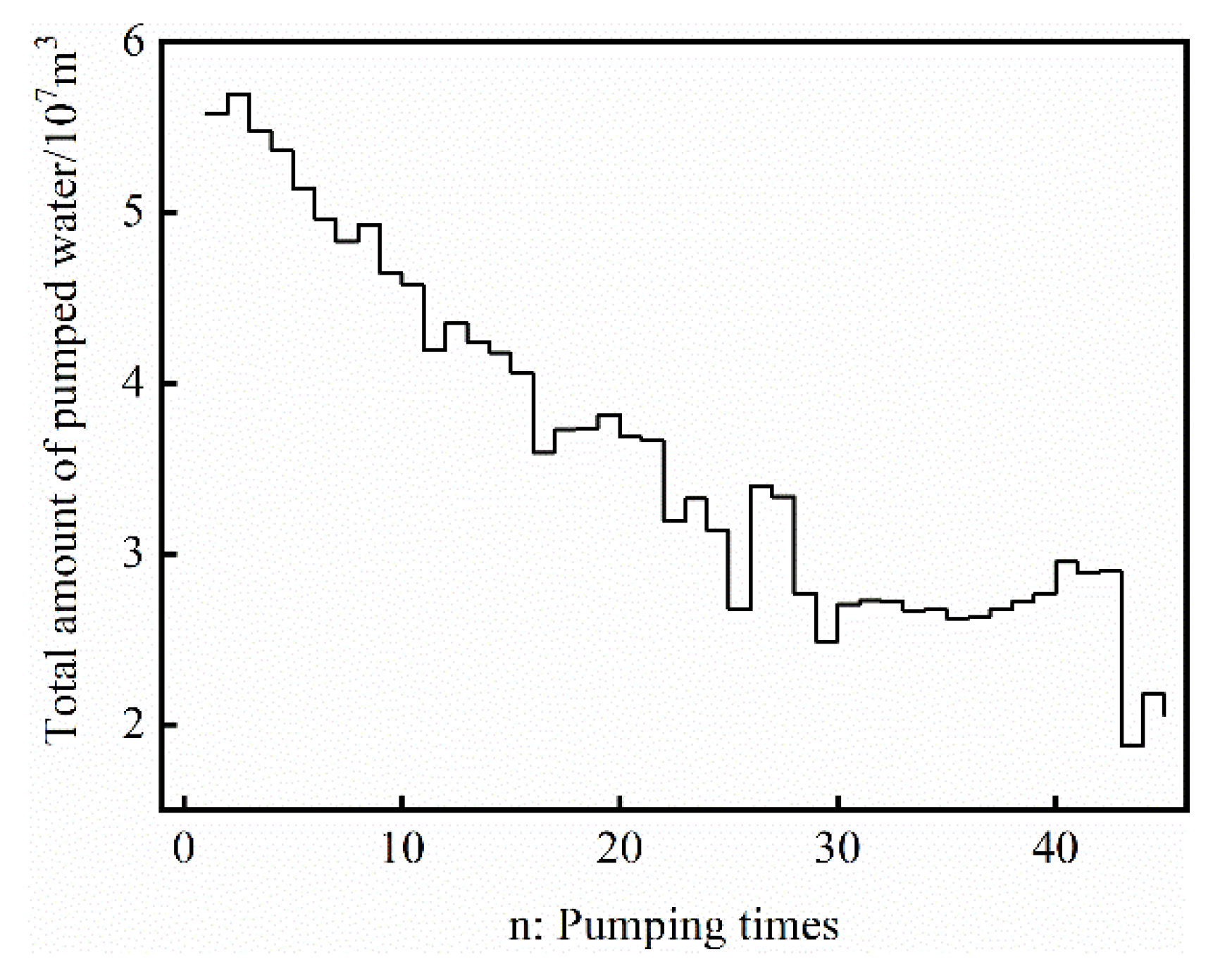
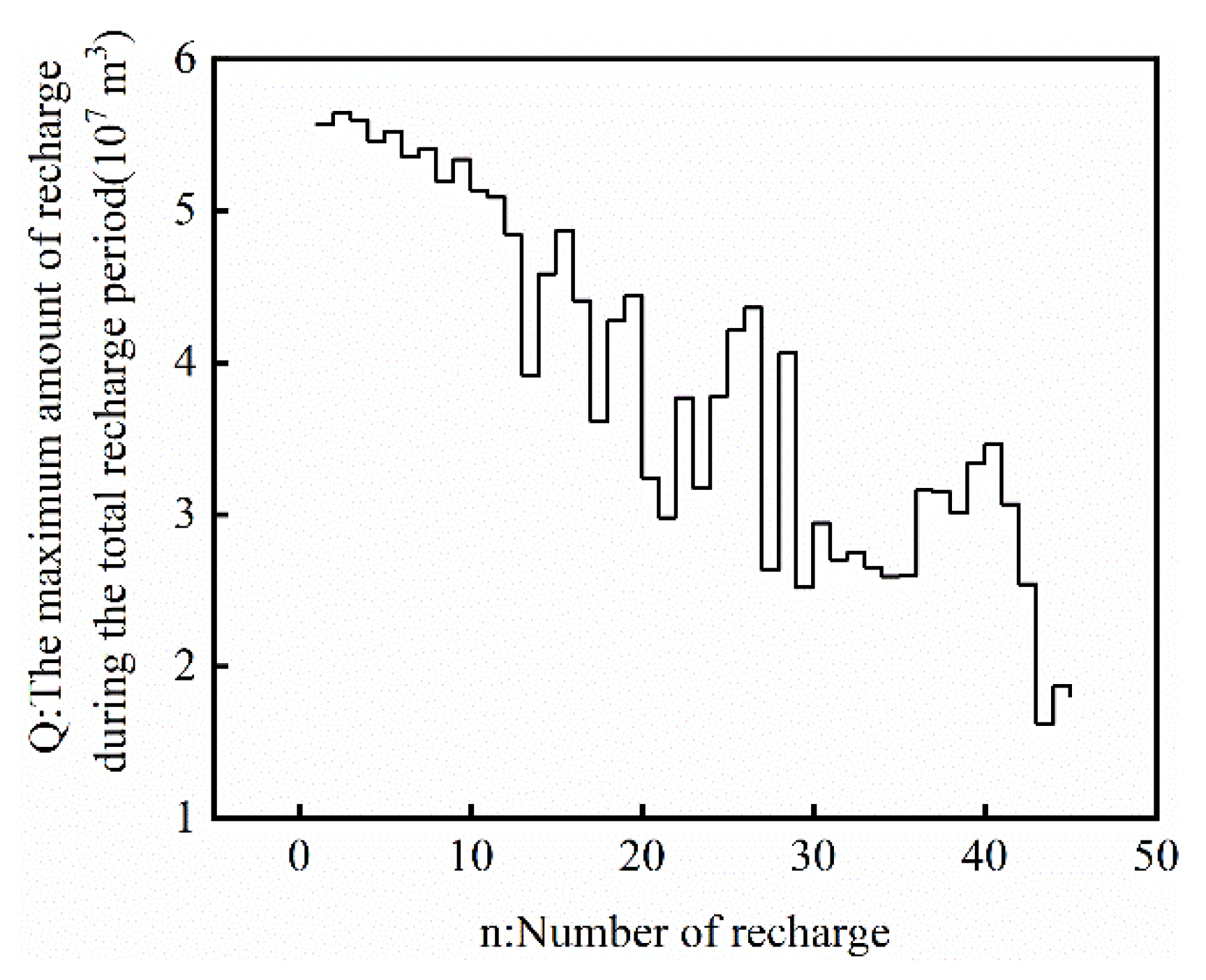
- A genetic algorithm was used to optimize the operation mode of single well recharge and pumping. When the number of pumping times was two, the pumping well was stopped for 1 day to restore the water level; the total amount of water pumped during the ice period reached the maximum, which was 5.69 × 107 m3. Compared with the continuous pumping during the ice period, the pumping volume was increased by 1.1 × 106 m3. When the number of recharges was two, and the recharge well was stopped for 1 day to restore the water level, the total amount of recharge during the recharge period reached the maximum, which was 5.64 × 107 m3. Compared with continuous recharge during the recharge period, the recharge amount was increased by 7 × 105 m3.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Maximum Pumping Flow (m3/s) | Well Depth (m) | Permeability Coefficient (m/d) | Initial Water Level (m) | Continuous Pumping Time (d) |
|---|---|---|---|---|
| 4.2 | 100 | 150 | 64 | 90 |
| 7.4 | 200 | 150 | 64 | 90 |
| 8.9 | 300 | 150 | 64 | 90 |
| 10.3 | 400 | 150 | 64 | 90 |
| 11.3 | 500 | 150 | 64 | 90 |
| 11.9 | 600 | 150 | 64 | 90 |
| 7.7 | 200 | 150 | 64 | 60 |
| 8.03 | 200 | 150 | 64 | 30 |
| 8.49 | 200 | 150 | 64 | 7 |
| 8.66 | 200 | 150 | 64 | 3 |
| 8.9 | 200 | 150 | 64 | 1 |
| 5.2 | 200 | 100 | 64 | 90 |
| 9.2 | 200 | 200 | 64 | 90 |
| 10.7 | 200 | 240 | 64 | 90 |
| 6.1 | 200 | 150 | 58 | 90 |
| 4.9 | 200 | 150 | 52 | 90 |
| 2.5 | 200 | 150 | 40 | 90 |
| 0.4 | 200 | 150 | 30 | 90 |
| 6.4 | 200 | 150 | 58 | 60 |
| 6.7 | 200 | 150 | 58 | 30 |
| 7.1 | 200 | 150 | 58 | 7 |
| 7.2 | 200 | 150 | 58 | 3 |
| 7.4 | 200 | 150 | 58 | 1 |
| 5.1 | 200 | 150 | 52 | 60 |
| 5.3 | 200 | 150 | 52 | 30 |
| 5.6 | 200 | 150 | 52 | 7 |
| 5.8 | 200 | 150 | 52 | 3 |
| 5.9 | 200 | 150 | 52 | 1 |
| 2.6 | 200 | 150 | 40 | 60 |
| 2.8 | 200 | 150 | 40 | 30 |
| 2.9 | 200 | 150 | 40 | 7 |
| 2.95 | 200 | 150 | 40 | 3 |
| 3 | 200 | 150 | 40 | 1 |
| 0.45 | 200 | 150 | 30 | 60 |
| 0.5 | 200 | 150 | 30 | 30 |
| 0.53 | 200 | 150 | 30 | 7 |
| 0.54 | 200 | 150 | 30 | 3 |
| 0.56 | 200 | 150 | 30 | 1 |
| Maximum Recharge Flow (m3/s) | Well Depth (m) | Permeability Coefficient (m/d) | Initial Water Level (m) | Continuous Recharge Time (d) |
|---|---|---|---|---|
| 4.2 | 100 | 150 | 27.7 | 90 |
| 7.4 | 200 | 150 | 27.7 | 90 |
| 8.9 | 300 | 150 | 27.7 | 90 |
| 10.3 | 400 | 150 | 27.7 | 90 |
| 11.3 | 500 | 150 | 27.7 | 90 |
| 11.9 | 600 | 150 | 27.7 | 90 |
| 7.7 | 200 | 150 | 27.7 | 60 |
| 8.03 | 200 | 150 | 27.7 | 30 |
| 8.49 | 200 | 150 | 27.7 | 7 |
| 8.66 | 200 | 150 | 27.7 | 3 |
| 8.9 | 200 | 150 | 27.7 | 1 |
| 5.2 | 200 | 100 | 27.7 | 90 |
| 9.2 | 200 | 200 | 27.7 | 90 |
| 10.7 | 200 | 240 | 27.7 | 90 |
| 6.1 | 200 | 150 | 33.7 | 90 |
| 4.9 | 200 | 150 | 39.7 | 90 |
| 2.5 | 200 | 150 | 51.7 | 90 |
| 0.4 | 200 | 150 | 61.7 | 90 |
| 6.4 | 200 | 150 | 33.7 | 60 |
| 6.7 | 200 | 150 | 33.7 | 30 |
| 7.1 | 200 | 150 | 33.7 | 7 |
| 7.2 | 200 | 150 | 33.7 | 3 |
| 7.4 | 200 | 150 | 33.7 | 1 |
| 5.1 | 200 | 150 | 39.7 | 60 |
| 5.3 | 200 | 150 | 39.7 | 30 |
| 5.6 | 200 | 150 | 39.7 | 7 |
| 5.8 | 200 | 150 | 39.7 | 3 |
| 5.9 | 200 | 150 | 39.7 | 1 |
| 2.6 | 200 | 150 | 51.7 | 60 |
| 2.8 | 200 | 150 | 51.7 | 30 |
| 2.9 | 200 | 150 | 51.7 | 7 |
| 2.95 | 200 | 150 | 51.7 | 3 |
| 3 | 200 | 150 | 51.7 | 1 |
| 0.45 | 200 | 150 | 61.7 | 60 |
| 0.5 | 200 | 150 | 61.7 | 30 |
| 0.53 | 200 | 150 | 61.7 | 7 |
| 0.54 | 200 | 150 | 61.7 | 3 |
| 0.56 | 200 | 150 | 61.7 | 1 |
References
- Lian, J.J.; Zhao, X. Research on spacing of double cable net ice stopper. South–North Water Divers. Water Sci. Technol. 2012, 10, 1–3. [Google Scholar]
- Mu, X.P.; Cao, P.; Chen, W.X.; Wu, Y.; Wen, R. Review on ice-free water transport technology and factors influencing the regulation of ice-water two-phase flow force in wide and shallow channels during glacial period. Water Power Energy Sci. 2016, 34, 132–136. [Google Scholar]
- Wang, F.; Wu, Y.H.; Ma, Y.J.; Zhang, G.Q. Application and discussion of pumping and deicing technology for Hongshanzui Cascade Hydropower Station. Henan Water Conserv. South–North Water Transf. 2009, 7, 111–112. [Google Scholar]
- ASHRAE. Geothermal Energy. In Ashrae Handbook HVAC Applications, American Society of Heating; Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, Georgia, 2003; pp. 11–28. [Google Scholar]
- IEA Heat Pump Centre. Ground-source Heat Pump Systems. In IEA Heat Pump Centre Newsletter; The Netherlands, 2005; pp. 23–24. Available online: https://www.osti.gov/etdeweb/biblio/420071 (accessed on 9 July 2022).
- Vieira, A.; Alberdi-Pagola, M.; Christodoulides, P.; Javed, S.; Loveridge, F.; Nguyen, F.; Cecinato, F.; Maranha, J.; Florides, G.; Prodan, I.; et al. Characterisation of Ground Thermal and Thermo-Mechanical Behaviour for Shallow Geothermal Energy Applications. Energies 2017, 10, 2044. [Google Scholar] [CrossRef]
- Liu, X.P.; Zhang, Z.S.; Chen, R. The Method of improving power Generation Capacity of cascade diversion hydropower stations. China Water Energy Electrif. 2007, 9, 38–43. [Google Scholar]
- Mitchell, M.S.; Spitler, J.D. Open-loop direct surface water cooling and surface water heat pump systems—A review. Hvac R Res. 2013, 19, 125–140. [Google Scholar]
- Huang, J.L.; Zong, Q.L.; Liu, Z.J.; Zhu, M.M.; Wang, Z.J.; Zhang, X.Y. Prototype test and analysis of water-melting ice-melting in water diversion channels in alpine regions. J. Shihezi Univ. 2014, 32, 392–396. [Google Scholar]
- Qin, Z.P.; Zong, Q.L.L.; Tian, Y.; Wu, S.J. Ice-pumping and ice-melting experiment of water diversion open channels in cold regions. J. Wuhan Univ. 2017, 50, 168–173. [Google Scholar]
- Zhu, M.M.; Liu, H.F.; Zong, Z.L. Experimental study on water temperature variation in water diversion channels in alpine regions. J. Shihezi Univ. 2015, 33, 239–243. [Google Scholar]
- Zheng, T.G.; Zong, Q.L.; Sun, S.K.; Wu, S.J. Attenuation law of water temperature along the process of pumping and melting ice channel in alpine region: Taking Hongshanzui Hydropower Station as an example. Adv. Water Sci. 2018, 29, 667–676. [Google Scholar]
- Wu, S.G.; Zong, Q.L.; Zheng, T.G.; Wang, Z.J.; Liu, Z.J. Three-dimensional simulation of water temperature changes in water diversion channels of multiple ice-melting wells in alpine regions and optimal arrangement of well groups. Chin. J. Agric. Eng. 2017, 33, 130–137. [Google Scholar]
- Wu, S.G. Process Simulation of Water Temperature Changes in Diversion Channels under the Condition of Pumping Water and Melting Ice; Shihezi University: Shihezi, China, 2017. [Google Scholar]
- Hao, G.Z. Analysis of drinking water protection in karst areas in western Xingtai City. In Proceedings of the Academic Exchange Conference on Building Technology and Management, Beijing, China, May 2016; pp. 199–200. [Google Scholar]
- Chen, T. Research on Optimization and Adjustment of Karst Water Source Protection Areas in Xingtai City; China University of Geosciences: Beijing, China, 2021. [Google Scholar]
- Si, P.Y. Research on Water Quality Evaluation and Algae Changes of Main Canals in the Middle Route of the South-to-North Water Diversion Project (Hebei Section); Hebei Agricultural University: Baoding, China, 2020. [Google Scholar]
- Sun, J.; Han, P.L.; Wang, C.; Xin, X.K.; Lei, J.S.; Yin, W. Comprehensive evaluation of the water quality of the main canals in the middle route of the South-to-North Water Diversion Project. South–North Water Divers. Water Conserv. Sci. Technol. 2019, 17, 102–112. [Google Scholar]
- Tang, W. Research on Water Conveyance Technology in Glacial Period by Recycling Geothermal Energy; Jinan University: Jinan, China, 2019. [Google Scholar]
- Jin, X.H.; Fan, Y.M.; Duan, H.; Yang, J.; Song, C.J.; Jia, Q.; Hu, Y.W. Spatial and temporal response analysis of groundwater level in Yinchuan Plain to unified water regulation in the Yellow River Basin. Chin. J. Water Resour. Hydraul. Eng. 2021, 32, 45–51. [Google Scholar]
- Wang, L.; Mao, H.T.; Yan, X.J.; Huang, F.; Lin. Influence of “prevent-intercept-conduct” seepage control in Pingyuan Reservoir on the groundwater level behind the dam. Chin. J. Water Resour. Hydraul. Eng. 2020, 31, 254–260. [Google Scholar]
- Shang, H.M.; Wang, W.K.; Duan, L.; Huo, C.Y. Simulation analysis of groundwater regulation based on ecological water level in the northern foot of the Tianshan Mountains. Soil Water Conserv. Res. 2014, 21, 144–147. [Google Scholar]
- Zhai, J.Q.; Liu, K.; Zhao, Y.; Dong, Y.Y.; Wang, L.Z.; Jiang, S. Research progress on groundwater level regulation methods and models in oasis in arid regions. Hydrology 2021, 41, 1–7. [Google Scholar]
- Cimmino, M.; Eslami-Nejad, P. A simulation model for solar assisted shallow ground heat exchangers in series arrangement. Energy Build. 2016, 157, 227–246. [Google Scholar] [CrossRef]
- Chen, W.F.; Du, S.H.; Chen, L.; Yuan, M.L. Correlation analysis of main controlling factors of groundwater temperature under the influence of water source heat pump. Chin. J. Water Resour. Water Eng. 2017, 28, 5. [Google Scholar]
- Chai, F.X.; Pan, S.B.; Shi, W.X.; Li, L. Karst groundwater simulation and scheme adjustment in Baiquan Springs, Xingtai. Hydrogeol. Eng. Geol. 2016, 43, 17–21. [Google Scholar]
- Borelli, M.; Pavlin, B. Approach to the problem of the underground water leakage from the storage in karst regions. In Dubrovnik Symposium; Hydrologie des Roches Fissures: Paris, France, 1965. [Google Scholar]
- Yang, W. Numerical Simulation of Groundwater in Western Jilin Based on Feflow; Jilin University: Changchun, China, 2007. [Google Scholar]
- Xue, Y.Q.; Xie, C.H. Numerical Simulation of Groundwater; Science Press: Beijing, China, 2007. [Google Scholar]
- Yuan, Z.Q. Evaluation of shallow geothermal resources and potential in Xingtai urban area. Green Sci. Technol. 2017, 10, 162–165. [Google Scholar]
- Lei, X.D.; Hu, S.B.; Li, J.; Yang, Q.H.; Han, Y.D.; Jiang, G.Z.; Zheng, J. Characteristics of thermophysical properties of bedrock formations in Beijing area. Adv. Geophys. 2018, 33, 1814–1823. [Google Scholar]
- Zheng, J.; Chen, X.; Zhang, Z.C. Hydrogeological parameters of dual medium in southern karst area estimated by pumping test method. Eng. Investig. 2014, 42, 42–46. [Google Scholar]
- Ren, Z.L.; Lu, M.; Sun, X.S. Numerical simulation of karst groundwater in Huixian Wetland. South–North Water Transf. Water Conserv. Sci. Technol. 2020, 18, 157–164. [Google Scholar]
- Joran, D.R.; Clauser, C.; Marquart, G.; Pechnig, R. Statistically reliable petrophysical properties of potential reservoir rocks for geothermal energy use and their relation to lithostratigraphy and rock composition: The NE Rhenish Massif and the Lower Rhine Embayment (Germany). Geothermics 2015, 53, 413–428. [Google Scholar] [CrossRef]
- Xin, S.L.; Wang, J.L.; Dou, H.P.; Wang, Y.; Zhang, J.; He, Y.Q. Experiment and analysis on influencing factors of rock thermophysical properties in buried hill reservoir. Miner. Rock 2014, 34, 102–107. [Google Scholar]
- Li, C.X.; Duan, W.G.; Lu, M.L.; Huang, M.H.; Teng, S.F. Research on water temperature and air temperature thresholds for the evolution of ice regime along the middle line of the South-to-North Water Diversion Project. Water Conserv. Sci. Cold Reg. Eng. 2022, 5, 4–8. [Google Scholar]
- Sun, J. Research on the Suitable Area of Groundwater Source Heat Pump in Shijiazhuang City and the Characteristic Change of Temperature Field of Aquifer; Hebei University of Geosciences: Shijiazhuang, China, 2020. [Google Scholar]


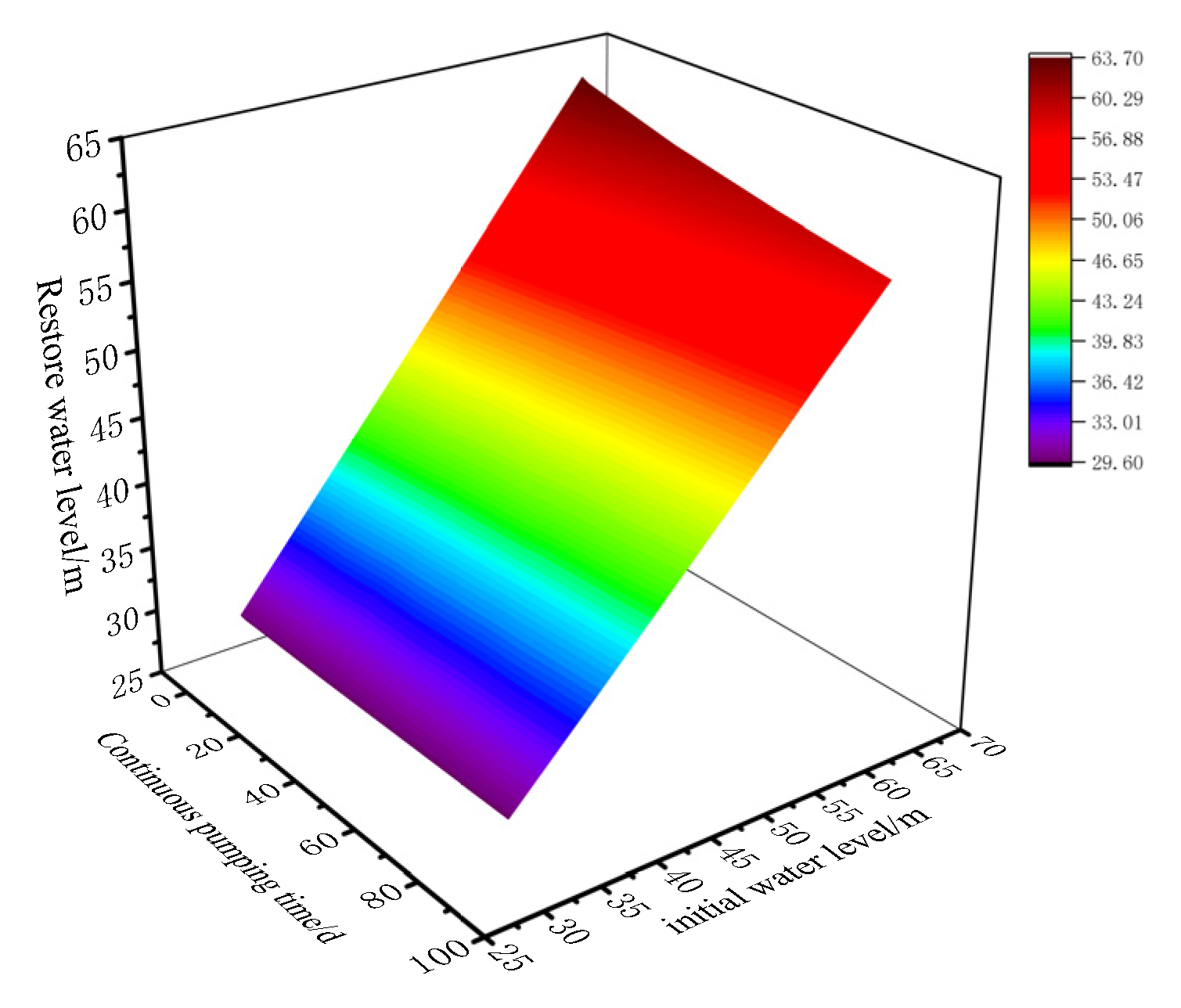


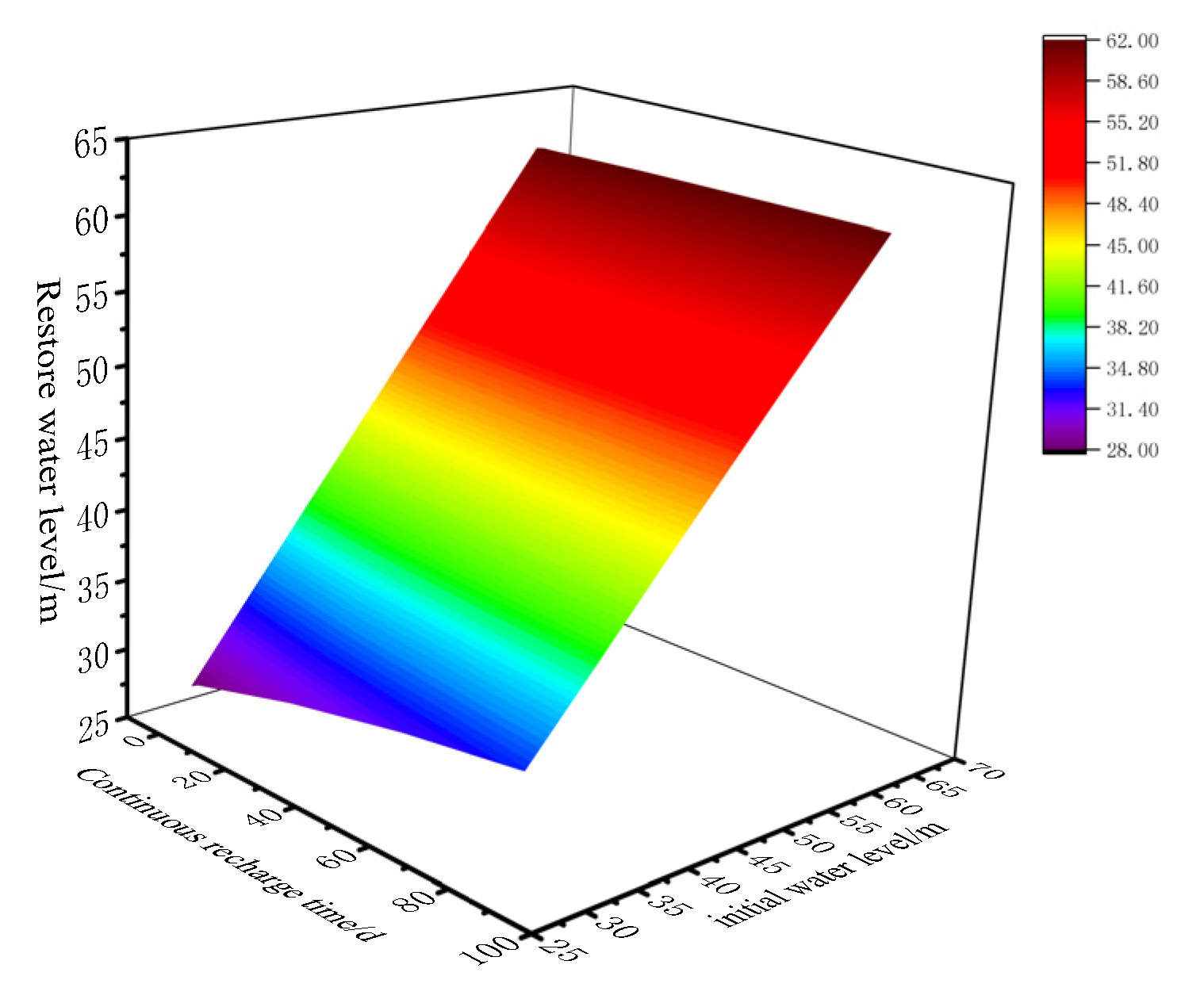
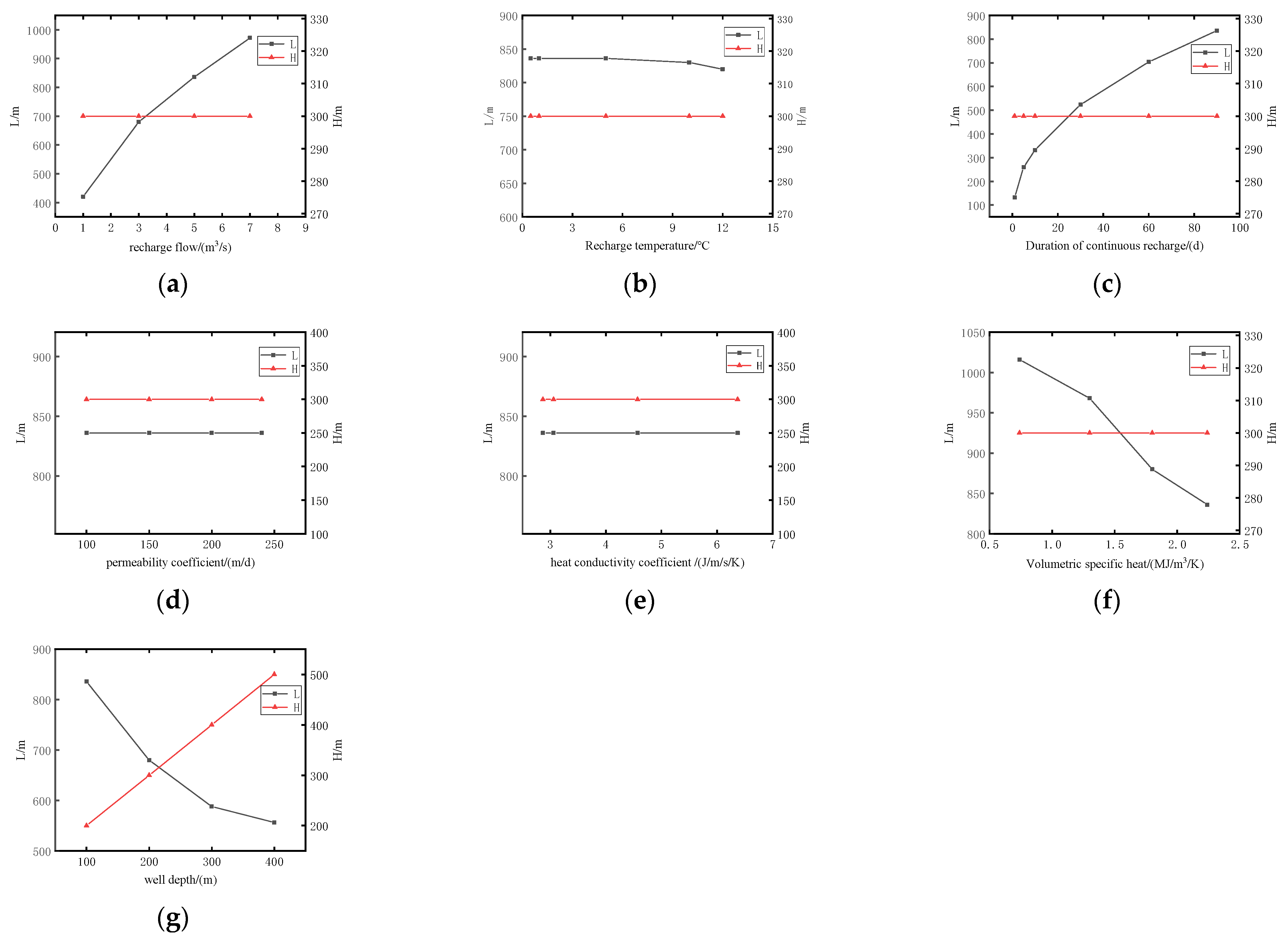
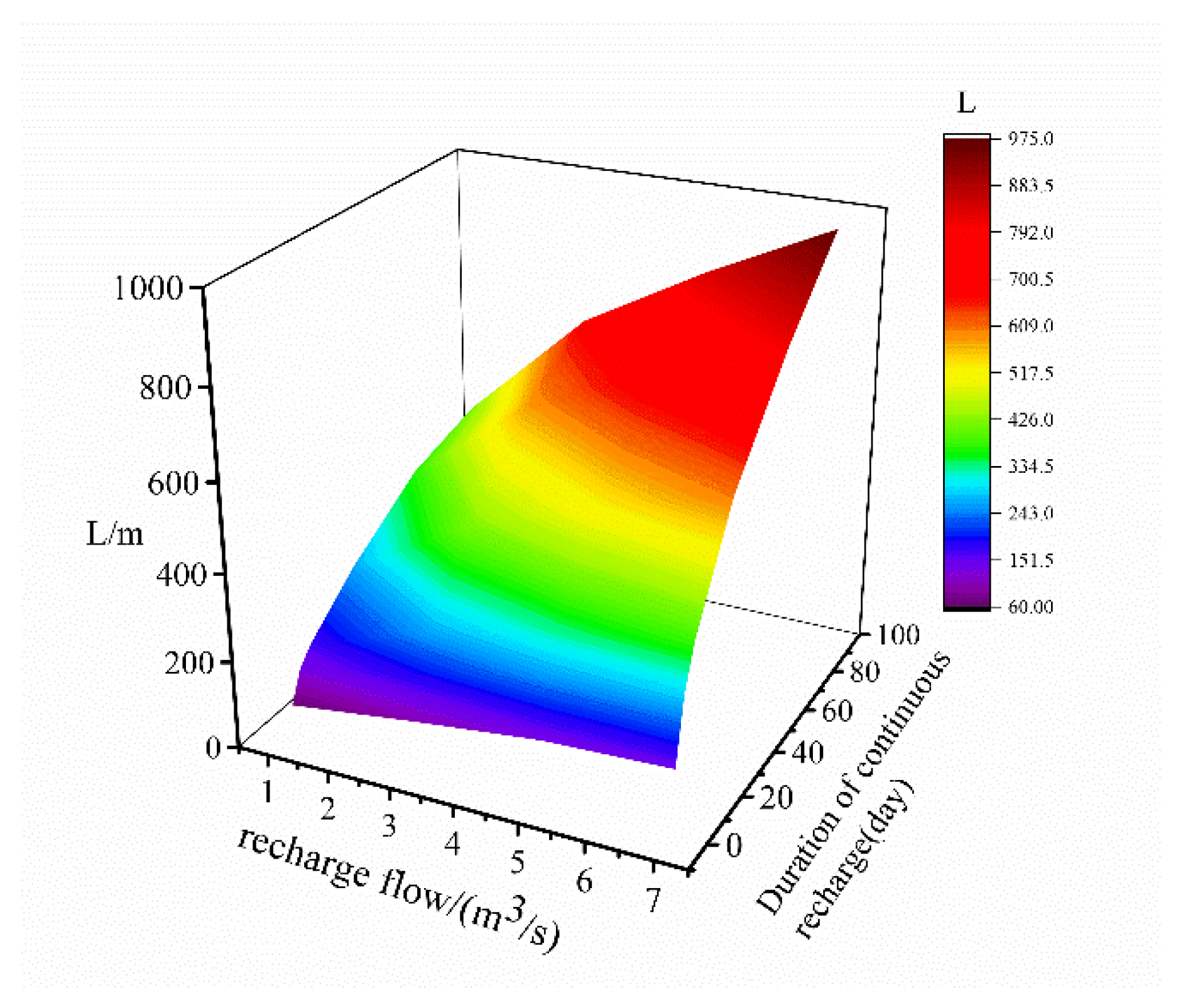

| Soil Type | Clay, Sandy Soil, Silt | Fine Sand | Medium Sand | Coarse Sand | Gravel | Fractured Limestone | Fractured Dolomite | Shale | |
|---|---|---|---|---|---|---|---|---|---|
| Parameter | |||||||||
| Permeability coefficient (m/d) | 0.1–5 | 3–15 | 8–25 | 20–50 | 50–300 | 10–240 | |||
| Storage coefficient | 0.16–0.2 | 0.2 | 0.21 | 0.24 | 0.26 | 0.05–0.5 | 0–0.05 | ||
| Specific volume heat of soil (106 J/m3/K) | 2.6 | 2.3–2.05 | 1.4–1.7 | 1.298–2.221 | 0.742–2.334 | 0.345–3.095 | |||
| Thermal conductivity of soil (J/m/s/K) | 1.05–1.1 | 1.8–2.4 | 1.82–2.85 | 2.865–5.873 | 3.833–6.327 | 1.195–2.369 | |||
| Specific heat of water (106 J/ m3/K) | 4.2 | ||||||||
| Water thermal conductivity (J/m/s/K) | 0.65 | ||||||||
| Parameter Name | Clay-Bearing Layer of Sand Gravel | Karst Extremely Strong Development Zone (Limestone, Dolomite) | Karst Medium Development Zone (Limestone, Dolomite) | Karst Weak Development Zone (Limestone, Dolomite) |
|---|---|---|---|---|
| Thickness of the strata (m) | 20 | 214 | 250 | 250 |
| Kx/Ky (m/d) | 10 | 150 | 75 | 35 |
| Kz (m/d) | 1 | 15 | 7.5 | 3.5 |
| Storage coefficient | 0.2 | |||
| Porosity | 0.22 | 0.3 | 0.2 | 0.08 |
| Specific heat of water (106 J/m3/K) | 4.2 | |||
| Water thermal conductivity (J/m/s/K) | 0.65 | |||
| Specific volume heat of soil (106 J/m3/K) | 2.34 | 2.24 | 1.83 | 1.3 |
| Thermal conductivity of soil (J/m/s/K) | 1.1 | 3.06 | 4.29 | 5.48 |
| Working Condition | Continuous Pumping Time (d) | Initial Water Level (m) | Permeability Coefficient (m/d) | Well Depth (m) |
|---|---|---|---|---|
| 1 | 90 | 64 | 150 | 100, 200, 300, 400, 500, 600 |
| 2 | 1 | 64, 58, 52, 40, 30 | 150 | 200 |
| 3 | 150 | 200 | ||
| 7 | 150 | 200 | ||
| 30 | 150 | 200 | ||
| 60 | 150 | 200 | ||
| 90 | 150 | 200 | ||
| 3 | 90 | 64 | 100, 200, 240 | 200 |
| Working Status | Working Condition | Initial Water Level (m) | Continuous Pumping/Recharge Time (d) |
|---|---|---|---|
| After pumping | 1 | 64 | 1, 3, 7, 30, 60, 90 |
| 2 | 58 | 1, 3, 7, 30, 60, 90 | |
| 3 | 52 | 1, 3, 7, 30, 60, 90 | |
| 4 | 40 | 1, 3, 7, 30, 60, 90 | |
| 5 | 30 | 1, 3, 7, 30, 60, 90 | |
| After recharge | 1 | 27.7 | 1, 3, 7, 30, 60, 90 |
| 2 | 33.7 | 1, 3, 7, 30, 60, 90 | |
| 3 | 39.7 | 1, 3, 7, 30, 60, 90 | |
| 4 | 51.7 | 1, 3, 7, 30, 60, 90 | |
| 5 | 61.7 | 1, 3, 7, 30, 60, 90 |
| Working Condition | Continuous Recharge Time (d) | Initial Water Level (m) | Permeability Coefficient (m/d) | Well Depth (m) |
|---|---|---|---|---|
| 1 | 90 | 27.7 | 150 | 100, 200, 300, 400, 500, 600 |
| 2 | 1 | 27.7, 33.7, 39.7, 51.7, 61.7 | 150 | 200 |
| 3 | 150 | 200 | ||
| 7 | 150 | 200 | ||
| 30 | 150 | 200 | ||
| 60 | 150 | 200 | ||
| 90 | 150 | 200 | ||
| 3 | 90 | 27.7 | 100, 200, 240 | 200 |
| Working Condition | Recharge Flow (m3/s) | Recharge Water Temperature (°C) | Continuous Recharge Time (d) | Initial Water Level (m) | Permeability Coefficient (m/d) | Thermal Conductivity of Soil (J/(∙m∙s∙K)) | Specific Volume Heat of Soil (MJ/(m3∙K)) | Well Depth (m) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1, 3, 5, 7 | 0.5 | 90 | 27.7 | 150 | 3.06 | 2.24 | 200 |
| 2 | 5 | 0.5, 1, 5, 10, 12 | 90 | 27.7 | 150 | 3.06 | 2.24 | 200 |
| 3 | 5 | 0.5 | 90 | 27.7 | 100, 200, 240 | 3.06 | 2.24 | 200 |
| 4 | 5 | 0.5 | 90 | 27.7 | 150 | 2.87, 4.57, 6.37 | 2.24 | 200 |
| 5 | 5 | 0.5 | 90 | 27.7 | 150 | 3.06 | 0.74, 1.3, 1.8 | 200 |
| 6 | 3 | 0.5 | 90 | 27.7 | 150 | 3.06 | 2.24 | 100, 200, 300, 400 |
| 7 | 5 | 0.5 | 30, 60, 90 | 27.7 | 150 | 3.06 | 2.24 | 200 |
| Continuous Pumping Time ti (d) | Pumping Capacity qi (m3/s) | Initial Water Level hi (m) | |
|---|---|---|---|
| i = 1 | 57 | 7.57 | 64 |
| i = 2 | 32 | 6.99 | 59.93 |
| Continuous Recharge Time di (d) | Recharge Capability ci (m3/s) | Initial Water Level Hi (m) | |
|---|---|---|---|
| i = 1 | 58 | 7.56 | 27.7 |
| i = 2 | 31 | 6.99 | 31.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Lian, J.; Zhao, X. Study on Sustainable Well Water Pumping Technology to Melt Ice in Winter for the Middle Route of the South-to-North Water Diversion Project. Water 2022, 14, 2550. https://doi.org/10.3390/w14162550
Zhang Y, Lian J, Zhao X. Study on Sustainable Well Water Pumping Technology to Melt Ice in Winter for the Middle Route of the South-to-North Water Diversion Project. Water. 2022; 14(16):2550. https://doi.org/10.3390/w14162550
Chicago/Turabian StyleZhang, Yuning, Jijian Lian, and Xin Zhao. 2022. "Study on Sustainable Well Water Pumping Technology to Melt Ice in Winter for the Middle Route of the South-to-North Water Diversion Project" Water 14, no. 16: 2550. https://doi.org/10.3390/w14162550




