Joint Modelling of Flood Hydrograph Peak, Volume and Duration Using Copulas—Case Study of Sava and Drava River in Croatia, Europe

Abstract

Morphodynamic changes in the riverbed may be accelerated by the climate change-induced effects, mostly through the increase of the frequency of extreme climatic events such as floods. This can lead to scouring of the riverbed around the bridge substructure and consequently reduces its overall stability. In order to better understand hydromorphological processes at the local scale, the influence of floods on bridge scour requires a detailed analysis of several interacting flood hydrograph characteristics. This paper presents a multivariate analysis of the annual maximum (AM) flood discharge data at four gauging stations on the Drava and Sava Rivers in Croatia (Europe). As part of the hydrograph analysis, multiple baseflow separation methods were tested. Flood volumes and durations were derived after extracting the baseflow from measured discharge data. Suitable marginal distribution functions were fitted to the peak discharge (Q), flood volume (V) and duration (D) data. Bivariate copula analyses were conducted for the next pairs: peak discharge and volume (Q–V), hydrograph volume and duration (V–D) and peak discharge and hydrograph duration (Q–D). The results of the bivariate copula analyses were used to derive joint return periods for different flood variable combinations, which may serve as a preliminary analysis for the pilot bridges of the R3PEAT project where the aim is to investigate the influences on the riverbed erosion around bridges with installed scour countermeasures. Hence, a design hydrograph was derived that could be used as input data in the hydraulic model for the investigation of the bridge scour dynamics within the project and a preliminary methodology is proposed to be applied. The results indicate that bivariate frequency analysis can be very sensitive to the selected baseflow separation methodology. Therefore, future studies should test multiple baseflow separation methods and visually inspect the performance.

1. Introduction

Extreme climatic events such as floods may induce morphodynamic changes in the riverbed, which can lead to scouring around the substructure of the bridge, affecting its overall stability [1]. Due to its effect on stability, local scour at bridge piers in a river has been studied extensively and described as a function of flow characteristics, fluid properties, bed material characteristics, sediment bed geometry, and the geometry of the pier and footing [2,3], with scour holes reaching their maximum depth during floods [4].

Flooding is one of the most common hazards on Earth, it is considered, along with scour, to be the prevailing cause (66%) of bridge failures in Europe and North America [5] and is defined as multivariate stochastic events with mutually correlated characteristics, such as peak discharge (Q), corresponding hydrograph volume (V) and hydrograph duration (D) [6]. Because of its multivariate nature, the reliability of the univariate analysis of flood events is uncertain and the results of such analysis cannot provide a complete assessment of flood severity [7,8], so the joint distribution properties of flood characteristics should be examined in the scour development analysis. Hence, this kind of analysis is often limited and does not account for the multivariate characteristics of flood hydrographs. It is clear that longer-duration floods with larger volumes can accelerate erosion processes at scour compared to events with shorter durations and smaller volumes. Therefore, not only consideration of the peak discharges but also hydrograph volumes and durations are essential to ensure the safety of these structures.

Research in recent years has focused on bivariate and multivariate flood frequency analysis assuming that the flood variables conform to the same type of marginal probability distribution [9], which is often not the case [8]. Therefore, to eliminate undesirable assumptions, copula functions were introduced as an alternative to the traditional multivariate functions, as they are flexible enough to separately select univariate marginal distributions and their joint dependence structure [10].

Apart from application in flood frequency analysis [6,11,12,13,14,15,16,17,18,19,20,21,22,23,24], copulas have found their application in low flow modelling [25], extreme drought modelling [26,27,28], groundwater modelling [15] and modelling of hydroclimatic case studies [29] with De Michele and Salvadori [30] writing the first paper on copulas in hydrology that inspired other authors in adjacent years to further explore its implementation in hydrological practice. Additionally, Tootoonchi et al. [31] recently presented a systematic literature review on copulas, along with the necessary requirements, limitations and decision support framework, for hydroclimatic applications.

The aforementioned studies applied the two- and three-variable copula functions combining the influence of peak discharge, volume, and duration (bivariate and trivariate copula analysis) based on river discharge data, which play a critical role in sediment transport and deposition [32] representing an important part of scour development analysis. In addition, Plumb et al. [33] acknowledge that the effects of hydrograph shape and changes in the flow regime should be examined in the scour development analysis, and a recent review of scour near bridges [34] indicates that flow magnitude is the main factor influencing scour depth development and indicates hydrograph duration and shape (i.e., related to volume) should be considered in the analysis.

As a part of the ongoing R3PEAT project (UIP-2019-04-4046; www.grad.hr/r3peat, accessed on 1 June 2022), which explores influences on the riverbed erosion around the structure of bridges with installed scour countermeasures crossing large rivers in Croatia, a multivariate analysis of flood events will be conducted on the hydrological data of the Drava and Sava River. The importance of multivariate analysis of flood events and scour development analysis on the Drava River is related to the evaluation of the long-term effects of hydropower dams and interrupted sediment continuum as well as the changing hydromorphological conditions. On the Sava River, it represents an extension of the research already conducted for the upper (Slovenian) part of the Sava River [16,17,35,36] to the sections of the Sava River in Croatia, where few similar hydrological studies exist [37,38,39,40] and none of them consider joint modelling of flood characteristics (Q, D, V). Additionally, tributaries with large water yields (and some smaller tributaries with torrential flows) may have an impact on increasing the peak hydrograph along the river segments. Therefore, joint probability analyses for floods should be performed to better explain the contribution of these processes (see, for example, the study by Gilja et al. [38] on the Sava River on the confluences of two tributaries, Kupa and Una using bivariate copulas). Moreover, the pilot bridges of the R3PEAT project located in the middle course of both Drava and Sava Rivers require detailed multivariate analysis of flood events as input for scour development analysis.

The aim of this paper is to conduct a comprehensive multivariate analysis of the selected flood events on two lowland rivers in Croatia (i.e., Sava and Drava Rivers) in order to make preparations for future scour analysis within the R3PEAT project by extracting annual maximum (AM) series of discharge data (Q) for several gauging stations on the Drava and Sava Rivers in Croatia. Several baseflow separation methods have been applied to the discharge data, and have been evaluated, to derive the corresponding flood hydrograph duration (D) and volume (V). Furthermore, an appropriate marginal distribution for each derived hydrologic variable (Q, D, V) was defined based on the results of statistical tests. Additionally, a bivariate copula analysis for the three pairs: peak discharge and volume (Q–V), hydrograph volume and duration (V–D) and peak discharge and hydrograph duration (Q–D) were conducted and the most suitable copula function was selected for each pair. Finally, joint return period pairs were calculated. Copulas from Archimedean (Gumbel–Hougaard, Clayton), extreme value (Galambos, Huesler–Reiss, Tawn) and elliptical (Normal) copula families were used in this study. Hence, the main novelty of this study is the fact that several baseflow separation techniques were tested and an optimal method for the rivers that are significantly influenced by hydropower operation was selected. Moreover, the preliminary methodology of applying joint dependence modelling for the bridge scour is proposed with an example of the design hydrograph definition that could be used as input to the hydraulic model in order to investigate bridge scour dynamics.

2. Data and Methods

2.1. Study Area and Data

Two large lowland rivers in Croatia (Figure 1), the Drava River and the Sava Rivers, were selected as case study examples.

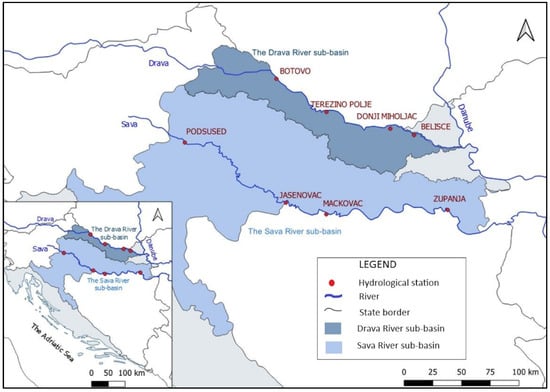
Figure 1. Location of the observed gauging stations on the Drava River and the Sava River in Croatia.

The Drava River rises in Italy and flows through four countries (Austria, Slovenia, Croatia, and Hungary) until it joins the Danube River, of which it is the fourth largest and longest tributary (725 km). With a total catchment area of 41,238 km² and its most important tributary—the Mura River—it connects the Alpine region with the Pannonian region. The Drava River can be divided into three sections by river regime: the upper part which exhibits the Alpine nival-pluvial regime characterized by the construction of numerous dams and reservoirs, which are mainly used for hydroelectric production; the middle part affected by the tributaries (from 255,050 rkm to 53,800 rkm in Croatia); the lower part that stretches to the confluence with the Danube River and is under the influence of the Danube River backwater effect [41]. Prior to the hydro-regulation of the Drava River, the frequency of flood events was quite high. Nowadays, changes in the hydrological regime of the Drava River in Croatia can be described as predominantly influenced by anthropogenic factors and more recently attributed to climate change [42]. Moreover, Bonacci and Oskorus [43] reported the reduction of minimum and average discharges and all characteristic water levels of the lower Drava River, which agrees with similar results of other authors who conclude that the discharge analysis of the Drava River shows a negative trend [44,45]. Additionally, the analysis of the highest flood events in the period before and after the construction of large reservoirs for hydropower plants shows similar results [46].

Four gauging stations were selected in the Drava River section in Croatia: Botovo, Terezino polje, Donji Miholjac and Belisce. Other gauging stations in the middle part of the Drava River do not have discharge measurements due to the built accumulations (hydropower plants), and due to the backwater influence of the Danube River at some gauging stations in the lower part of the Drava River. The largest tributary of the Drava River, the Mura River, is upstream from the selected stations. Other tributaries along the selected river section, such as Bednja, Plitivica, Karašica and Vučica, have a lower water yield and a smaller influence on the peak discharge. Daily discharge time series with several data gaps in the period 1962–2019, resulted in a total of 46 to 47 flood events (depending on the analyzed station). These events were used in this study and the main characteristics of the annual maximum (AM) series samples of the flood variables (i.e., discharge (Q), flood hydrograph duration (D) and hydrograph volume (V)) were extracted (Table 1).

Table 1. Basic properties of the observed annual maximum series of hydrological variables: peak discharge (maximum—Q_max; mean—Q_mean and standard deviation—Q_sd), hydrograph duration (maximum—D_max; mean—D_mean and standard deviation—D_sd) and hydrograph volume (maximum—V_max; mean—V_mean and standard deviation—V_sd) for gauging stations on the Drava and Sava River.

River	Station	Watershed Area [km2]	Period; Years of Data	Qmax; Qmean; Qsd (m3/s)	Dmax; Dmean; Dsd (day)	Vmax; Vmean; Vsd (106 m3)
Drava	Botovo	31,038.0	1962–2019; 47	2551; 1430; 464.6	58; 25; 10.3	1408; 558; 299.4
	Terezino polje	33,916.0	1962–2019; 47	2778; 1379; 493.5	62; 26; 11.1	1511; 563; 315.8
	Donji Miholjac	37,142.0	1962–2019; 46	2140; 1269; 371.5	56; 27; 10.2	1367; 530; 282.3
	Belisce	38,500.0	1962–2019; 46	2035; 1242; 326.9	57; 25; 10.2	1355; 508; 273.0
Sava	Podsused	12,316.0	1951–2019; 55	3038; 1648; 488.1	59; 25; 12.2	1195; 560; 221.7
	Jasenovac	38,953.0	1951–2019; 53	2759; 1884; 371.1	113; 55; 20.8	4059; 1975; 850.5
	Mackovac	40,838.0	1951–2019; 53	3100; 1803; 393.7	129; 54; 23.4	5600; 2020; 1015.5
	Zupanja	62,891.0	1951–2019; 54	5317; 2679; 657.4	174; 63; 29.0	6274; 2956; 1326.5

Additionally, the Sava River represents the longest right tributary of the Danube River (990 km), forming in the Slovenian town Radovljica at the confluence of the Sava Dolinka River and Sava Bohinjka River, from where it flows through four countries (Slovenia, Croatia, Bosnia and Herzegovina and Serbia) until it joins the Danube in Belgrade, Serbia. It is the largest tributary of the Danube River in terms of the size of the catchment area (95,419 km²), and together Sava and Danube form a large part of the Black Sea drainage basin area. The upstream part of the Sava River exhibits the Alpine nival-pluvial regime, which changes along the downstream Sava River into the Peripannonian pluvial-nival regime, while in the middle course of the Sava River near the town of Jasenovac it gradually changes into the Pannonian pluvial-nival regime [38,47]. Hydrological research on the part of the Sava River that flows through Croatia mainly focused on the changes in floods at the Zagreb gauging station, where it was concluded that the discharge regime is under the influence of engineering works carried out as part of the flood protection system of the Zagreb city area [48,49,50,51,52]. Moreover, Segota and Filpcic [53] reported that the discharge regime at the Zagreb gauging station is linked to scientifically observed climate changes, while Oresic et al. [54] extended that conclusion to the middle section of the Sava River in the 1931–2010 period. Additionally, the analysis of flood waves along the middle course showed strong variability on multiple scales [55,56] and a preliminary approach to clustering of flood hydrograph shapes was conducted at gauging station Zagreb [57].

The gauging station network at the middle course of the Sava River was practically lost during the war (1991–1995) and post-war period, which is mainly shown in the discontinuity of the hydrological data of around ten years. This analysis was conducted on the daily discharge data of four gauging stations (i.e., Podsused, Jasenovac, Mackovac and Zupanja) for the 1951–2019 period with several data gaps, resulting in a total of 53 to 55 AM flood events (depending on the analyzed station) (Table 1). The watershed area of the observed stations on the Drava River ranges from 31,038 to 38,500 km² and the Sava River has a wider range, from 12,316 to 62,891 km², due to the large tributaries from Bosnia and Herzegovina. The mean AM discharge values for the Drava River stations range from 1430 m³/s at GS Botovo to 1242 m³/s at GS Belisce. However, the mean AM discharge series on the Sava River stations show a wider range of values, from 1648 m³/s at GS Podsused to 2679 m³/s at GS Zupanja. In addition, there is a considerable range in observed mean AM duration and volume data, influenced by tributaries (especially right tributaries with large water yield e.g., Una, Vrbas, Bosna, Drina) and the Middle Sava flood protection system retention areas located upstream of GS Jasenovac. It can be seen that the operation of the hydropower plants has an influence on the formation of the hydrograph, since the peak discharge values of the Drava River do not increase with the catchment area (Table 1). This is in agreement with a previous study conducted by Potočki et al. [46].

2.2. Flood Characteristics

A flood event can be described by three variables: peak discharge (Q), hydrograph volume (V) and hydrograph duration (D). The annual maximum (AM) method was applied to daily discharge time series data at four gauging stations on the Drava River (Botovo, Terezino polje, Donji Miholjac, Belisce) and the Sava River (Podsused, Jasenovac, Mackovac, Zupanja) resulting in a range of 46 to 55 AM events.

Duration of the flood hydrograph events is defined as the number of days between the starting and ending days of the observed flood event. In order to define the duration of the flood event, one must choose between a specific threshold method and a baseflow separation technique [6]. In the scope of this study, we used several automated baseflow separation methods to define flood hydrograph duration and volume (Figure 2). The proposed baseflow separation methods were applied because they can be automated using the R programming language, are easily accessible, are free to obtain and operate, and are widely used in hydrological practice [17,58].

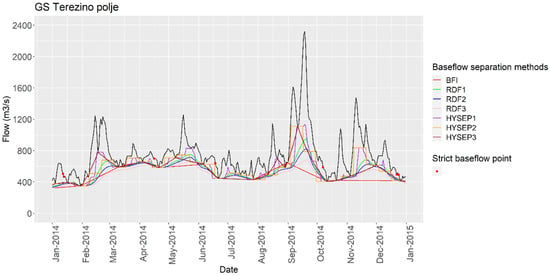
Figure 2. Example of the applied baseflow separation methods and strict baseflow points at gauging station Terezino polje on the Drava River for the year 2014.

Three automatic baseflow separation methods (Table 2) were used to separate direct runoff from baseflow using the R programming language packages “lfstat” and “ EcoHydrRology” and the R code for HYSEP automated method for baseflow separation. The baseflow index (BFI) method, recursive digital filter (RDF) method (i.e., three different values for the parameter alpha (α) were tested) and HYSEP baseflow separation method (i.e., three-curve fitting methods (sliding interval, fixed interval, local minimum) were tested) were applied and afterwards evaluated using the baseflow evaluation criterion described by Xie et al. [59]—based on the work of Brutsaert [60] and Cheng et al. [61]. Hence, the Nash–Sutcliffe efficiency (NSE) criterion for baseflow was used. Therefore, the performance of all tested BFI methods has been evaluated.

The BFI method was first developed by Gustard et al. [62] for flow separation in several catchments in the United Kingdom (UK) and it is also used by the World Meteorological Organization (WMO). Additionally, Koffler and Laaha [63] created an R package “lfstat” in 2012 to help automate the baseflow separation procedure which consists of four main steps:

• Divide the mean daily discharge data into non-overlapping blocks of N days and calculate the minima for each of these blocks, and let them be called Q₁, Q₂, Q₃, … Q_i.
• Consider in turn (Q₁, Q₂, Q₃), (Q₂, Q₃, Q₄), … (Q_{i − 1}, Q_i, Q_{i + 1}), etc.
• In each case, if 0.9·Q_i < Q_{i − 1} and 0.9·Q_i < Q_{i + 1}, then the central value is an ordinate for the baseflow line. Continue the procedure until a derived set of baseflow ordinates QB₁, QB₂, QB₃, … QB_n is provided with different time periods between them.
• Apply linear interpolation between each QB_i value and estimate each daily value of QB₁ … Q₁.
• If QBi > Qi, then set QBi = Qi.

The recursive digital filter method with the R software package “EcoHydrRology” was developed by Lyne and Hollick [64] and consists of parameter α estimation, where α is the recession parameter [64,65,66,67,68]. Afterwards, a certain number of passes is applied to identify the runoff and the baseflow parts of the hydrograph. According to the recommendations [64,69], the value of alpha can be defined as 0.900, 0.925 or 0.950 and the number of passes can be set to 3 (one forward, one backward and another forward).

Table 2. Overview of the baseflow separation methods applied and tested in this study.

Baseflow Separation Method	Acronym	Reference
Baseflow index method	BFI	Gustard et al. [61]; Koffler and Laaha [63]
Recursive digital filter method	RDF1	Lyne and Hollick [64]
	RDF2
	RDF3
Sliding interval method	HYSEP1	Sloto and Crouse [70]; Source code available at: https://github.com/USGS-R/DVstats/blob/main/R/hysep.R, accessed on 1 June 2022
Fixed interval method	HYSEP2
Local minimum method	HYSEP3

Table 2. Overview of the baseflow separation methods applied and tested in this study.

Baseflow Separation Method	Acronym	Reference
Baseflow index method	BFI	Gustard et al. [61]; Koffler and Laaha [63]
Recursive digital filter method	RDF1	Lyne and Hollick [64]
	RDF2
	RDF3
Sliding interval method	HYSEP1	Sloto and Crouse [70]; Source code available at: https://github.com/USGS-R/DVstats/blob/main/R/hysep.R, accessed on 1 June 2022
Fixed interval method	HYSEP2
Local minimum method	HYSEP3

The HYSEP automated method for baseflow separation was implemented by Sloto and Crouse [70] and recently converted to an R code provided by the United States Geological Survey (USGS). It allows the use of three curve fitting methods of hydrograph separation [71]:

• The sliding interval method (HYSEP1) finds the lowest discharge in one-half of the interval minus 1 day before and after the day being considered and assigns it to that day.
• The fixed interval method (HYSEP2) assigns the lowest discharge in each interval to all days in that interval starting with the first day of the period of record.
• The local minimum method (HYSEP3) checks each day to determine if it is the lowest discharge in one-half of the interval minus 1 day before and after the day is considered. If it is, then it is a local minimum and is connected by straight lines to adjacent local minimums.

The evaluation of the mentioned baseflow separation methods was performed by applying the baseflow evaluation criterion [59,60,61] with conforming to the four rules proposed and explained by Xie et al. [59]:

• Erase all data points of daily streamflow with $\frac{d_y}{d_t}\ge 0$, where $\frac{d_{y_i}}{d_t}=\frac{y_{i+1}-y_{i-1}}{2}$ that represents the slope of the curve between two consecutive points.
• Eliminate the previous 2 points before points with $\frac{d_y}{d_t}\ge 0$, as well as the next three points.
• Eliminate 5 points after major events that were identified by flood peaks greater than the 90th quantile of all streamflow observations [61].
• Exclude data points followed by a data point with smaller $\frac{d_y}{d_t}$, namely $\frac{d^{2}y}{d{x}^2}\ge 0$.

After implementing the four rules, the remaining daily streamflow points are considered strict baseflow points, which were used as the baseflow reference to evaluate the accuracies of different baseflow separation methods by calculating the NSE:

$$NSE=1-\frac{{{\displaystyle \sum }}_{t=t_1,t_2,\dots ,t_n}{\left(Q_m^t-Q_0^t\right)}^2}{{{\displaystyle \sum }}_{t=t_1,t_2,\dots ,t_n}{\left(Q_0^t-\overline{Q_0}\right)}^2} ,$$

(1)

where t₁, t₂, …, t_n represent the date of the nth strict baseflow point, $Q_m^t$ is the baseflow estimated from a baseflow separation method in date t, $Q_0^t$ is the value of the strict baseflow point in date t, $\overline{Q_0}$ is the mean value of all strict baseflow points. The NSE ranges from −∞ to 1, where an NSE value of 1 indicates a perfect match of the baseflow estimated from the baseflow separation method and the strict baseflow points.

Finally, the flood hydrograph volume (V) is estimated by the equation:

$$V={{\displaystyle \sum }}_{j=e}^s{q}_j-\frac{D}{2}\left(q_s+q_e\right),$$

(2)

where q_s and q_e are the daily discharge values on the starting and ending dates of the flood event, q_j denotes the jth day daily discharge value, and D represents the duration of the flood event.

To evaluate the stationarity of the derived hydrological variables (Q, D, V) the nonparametric Mann–Kendall (MK) test [72,73] was performed and the Ljung–Box test [74] was selected to test the serial correlation of the data. Prior to the introduction of the univariate or multivariate copula distribution framework, analyzed flood characteristics should be tested for stationarity and independence [6,10]. Both tests were performed using R software, where the MK test has a null hypothesis H₀ assuming there is no trend in the sample, and the null hypothesis for the Ljung–Box test is that the time series are not autocorrelated. The significance level of 0.05 was used in this study.

2.3. Marginal Probability Distributions

By defining the three variables describing the flood event (Q, V, D), a univariate frequency analysis was conducted by fitting marginal probability distributions to each variable separately. Several studies have been conducted with the aim to find the best-modelled families of univariate distributions, with some recommending parametric distributions [75,76,77,78], while others select different families (e.g., nonparametric distributions) [79,80]. In order to determine the best-fitting univariate distribution for Q, V and D, six parametric distributions were fitted and compared in the scope of this study: Gumbel (GUM), Pearson 3 (P3), generalized extreme value (GEV), generalized logistics (GLO), log-normal (LN), and log-Pearson 3 (LP3). Parametric distribution function parameters were estimated with the method of L-moments [81]. The best-fitting distribution function for each variable was evaluated based on graphical Q-Q plots and the statistical Anderson–Darling (AD) test, which is included in the R package “ADGof” [82].

2.4. Copulas

Copulas can be defined as transfer functions that connect marginal distributions and the multivariate joint distribution [83]. To assess the dependence between the pairs of considered variables three correlation coefficients were calculated and a graphical presentation of dependence was shown by Chi-plots [84,85] and K-plots [86]. Knowing that Kendall’s correlation coefficient τ is more insensitive to ties in data [14], it was selected over Spearman’s ρ and Pearson’s correlation coefficient, which measures only linear dependence between pairs of variables [16].

Several copulas from different copula families were used in this study: two Archimedean copulas (Gumbel–Hougaard, Clayton), three extreme-value copulas (Galambos, Huesler–Reiss, Tawn) and one elliptical copula (Normal), since these are frequently used families in hydrology [15,17,76]. Their characteristics are provided in Table 3.

Table 3. Properties of the applied copula functions [16,87].

Copula Family	Copula	Cθ (u, v)
Archimedean	Gumbel–Hougaard	$\exp (-{({\left(-\ln u\right)}^{\theta }+{\left(-\ln v\right)}^{\theta })}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.})$, θ ∈ [ 1, ∞)
	Clayton	${\left[u^{-\theta }+v^{-\theta }-1\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.}$, θ ∈ [ −1, ∞) \ {0}
Extreme value	Galambos	$u·\exp (-{({\left(-\ln u\right)}^{\theta }+{\left(-\ln v\right)}^{\theta })}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.})$, θ ∈ [ 0, ∞)
	Huesler–Reiss	$\exp \left[-\tilde{u}\Phi \left\{\frac{1}{\theta }+\frac{\theta }{2}\ln \left(\frac{\tilde{u}}{\tilde{v}}\right)\right\}-\tilde{v}\Phi \left\{\frac{1}{\theta }+\frac{\theta }{2}\ln \left(\frac{\tilde{u}}{\tilde{v}}\right)\right\}\right]$, θ ∈ [ 0, ∞)
	Tawn	$uv·\exp (-{({\left(-\ln u\right)}^{\theta }+{\left(-\ln v\right)}^{\theta })}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.})$, θ ∈ [ 0;1]
Elliptical	Normal	${{\displaystyle \int }}_{-\infty }^{{\Phi }^{-1}\left(u\right)}{{\displaystyle \int }}_{-\infty }^{{\Phi }^{-1}\left(v\right)}\frac{1}{2\pi \ast \sqrt{\left(1-{\theta }^2\right)}}\exp \left\{-\frac{s^2-2\theta st+t^2}{2\left(1-{\theta }^2\right)}\right\}\mathrm{d}s\mathrm{d}t$, θ ∈ [ −1;1]

Selected copulas were fitted to the AM samples using the R package “Copula”. The Cramér–von Mises test S_n was used to check the adequacy of the selected copula functions, and the parameters of all copulas were estimated using the method of moments with the use of the Kendall correlation coefficient [14,16,88]. The best-fitted copula function was then selected using the model selection criterion (i.e., function xvCopula), which is based on the k-fold cross-validation and is also implemented in the R package “Copula” [89,90,91].

Additionally, using the best-fitted copula, two joint primary return periods were calculated, T_and and T_or [92,93], where T_and represents the return period where both u and v are exceeded, and T_or where only u or v is exceeded [16,87,94,95]. T_and and T_or return periods are defined by equations where u and v are marginal distributions:

$$T_{u,v}^{AND}=\frac{1}{1-\left(u+v-C\left(u,v\right)\right)}$$

(3)

$$T_{u,v}^{OR}=\frac{1}{1-C\left(u,v\right)}$$

(4)

3. Results and Discussion

This section presents the results of the applied baseflow separation methods, marginal distribution selection, copula model definition, and joint return periods calculations for the selected pairs of variables using copulas. Additionally, a preliminary methodology is proposed for the use of copula analysis results in bridge scour analysis.

3.1. Selection of Baseflow Separation Method for Computing Flood Hydrograph Characteristics

Three baseflow separation methods (i.e., the BFI method, RDF method and HYSEP) were applied to the daily discharge time series data for each station on the Drava River (Botovo, Terezino polje, Donji Miholjac, Belisce) and the Sava River (Podsused, Jasenovac, Mackovac, Zupanja). Each baseflow separation method was applied by changing some of its parameters, resulting in seven different sub-methods (Table 2). These methods were evaluated by comparing the strict baseflow points derived from the four rules proposed by Xie et al. [59]. Results of each baseflow separation method using the NSE values were compared and ranked as shown in Table 4. Results show that the HYSEP1 method (sliding interval) performs the best for all stations on the Drava River and the Sava River (Table 4).

Table 4. Evaluation of 7 baseflow separation methods using the Nash–Sutcliffe efficiency criterion.

River	Station	Evaluation Results	BFI	RDF1	RDF2	RDF3	HYSEP1	HYSEP2	HYSEP3
Drava	Botovo	NSE	−0.216	0.325	0.119	−0.224	0.350	0.324	0.216
		Rank	6	2	5	7	1	3	4
	Terezino polje	NSE	−0.189	0.337	0.118	−0.248	0.407	0.367	0.238
		Rank	6	3	5	7	1	2	4
	Donji Miholjac	NSE	−0.109	0.361	0.149	−0.207	0.440	0.413	0.237
		Rank	6	3	5	7	1	2	4
	Belisce	NSE	−0.277	0.266	0.023	−0.378	0.387	0.313	0.164
		Rank	6	3	5	7	1	2	4
Sava	Podsused	NSE	−0.003	0.444	0.290	0.039	0.530	0.525	0.264
		Rank	7	3	4	6	1	2	5
	Jasenovac	NSE	0.220	0.615	0.499	0.313	0.654	0.624	0.488
		Rank	7	3	4	6	1	2	5
	Mackovac	NSE	0.188	0.627	0.507	0.315	0.678	0.650	0.480
		Rank	7	3	4	6	1	2	5
	Zupanja	NSE	0.319	0.687	0.581	0.402	0.693	0.662	0.531
		Rank	7	2	4	6	1	3	5

Incorrect ranking values excluded from the analysis by visual inspection are shown as bold.

Additionally, a visual inspection of the results was performed as an expert knowledge approach for each station to confirm the selection of the appropriate baseflow separation method, since the performed evaluation criterion has not yet been tested at gauging stations that have a complex flood regime under the influence of upstream retention areas, which is mainly the case at the middle course of the Sava River (Jasenovac, Mackovac, Zupanja GS). The visual inspection results have shown the overestimation of the baseflow points derived from the HYSEP method. Therefore, the HYSEP method was completely excluded from the analysis for the Jasenovac, Mackovac, Zupanja GS and the RDF1 method was applied to the observed data, as it is the next best method according to the NSE ranking. Therefore, it is clear that visual interpretation of the results should be conducted in order to identify potential spurious results as in the case of this study. It can be seen that some of the methods (e.g., BFI or RDF3 for the Drava River) do not yield optimal results. Hence, in most of the studies that focus on the investigation of the flood hydrograph characteristics or applying copula functions for bivariate or trivariate analysis only one baseflow separation method is tested. It is clear that multiple methods should be tested and the optimal one should be selected. Otherwise, the use of a non-optimal method could yield significant differences in the derived V and D variables, which can result in under- or overestimation of the joint return periods (Table 5). It can be seen that the difference among tested methods can be quite significant ranging from a few percentages to a difference of an order of magnitude. This applies both for hydrograph duration (D) as well for the hydrograph volume (V) (Table 5). To sum up, it is clear that multiple baseflow separation methods should be tested in relation to conducting the bivariate flood frequency analysis.

Table 5. Example of derived AM samples for flood hydrograph duration and flood hydrograph volume for seven different baseflow separation methods on the Terezino Polje GS on the Drava River.

Year	Peak Date	Peak Value	Variable	BFI	RDF1	RDF2	RDF3	HYSEP1	HYSEP2	HYSEP3
1962	6 June 1962	1367	D (day)	39	39	39	245	26	21	26
			V (106 m3)	1327	1041	1192	4700	414	328	505
1963	15 March 1963	1683	D (day)	30	31	31	151	21	21	21
			V (106 m3)	970	846	923	2533	684	789	807
1964	29 October 1964	1932	D (day)	40	69	69	69	25	23	25
			V (106 m3)	1683	1618	1831	2132	788	842	875
1965	6 August 1965	2471	D (day)	29	29	29	37	29	22	29
			V (106 m3)	1119	980	1020	1200	998	1001	1121
1966	23 August 1966	2525	D (day)	53	62	62	104	62	25	52
			V (106 m3)	2047	1608	1763	2986	1404	1173	2086
1967	4 June 1967	1398	D (day)	24	50	50	161	9	9	9
			V (106 m3)	486	933	1027	2678	267	205	248
1968	18 June 1968	811	D (day)	45	50	68	137	12	20	12
			V (106 m3)	815	641	884	1958	161	221	160
1969	22 May 1969	979	D (day)	41	41	41	41	18	12	18
			V (106 m3)	860	656	741	847	213	176	182
1970	14 August 1970	1390	D (day)	52	52	100	100	14	14	14
			V (106 m3)	1228	855	1173	1367	353	324	354
1971	25 March 1971	717	D (day)	36	99	99	239	18	18	18
			V (106 m3)	444	922	1058	2181	203	165	214
1972	19 July 1972	2882	D (day)	57	58	58	119	36	16	36
			V (106 m3)	2415	1925	2093	2748	1511	978	2040
1973	30 September 1973	1749	D (day)	49	49	78	78	27	24	27
			V (106 m3)	1729	1272	1635	1871	906	827	1085
1974	23 October 1974	1192	D (day)	47	29	61	61	15	15	15
			V (106 m3)	1214	347	1030	1160	290	336	298
1975	5 July 1975	2578	D (day)	50	70	70	121	50	25	50
			V (106 m3)	1932	1607	1776	2613	1174	879	1964
1976	29 April 1976	1108	D (day)	35	73	125	125	18	13	14
			V (106 m3)	630	867	1380	1684	290	316	259
1977	11 April 1977	1137	D (day)	26	26	86	107	14	21	14
			V (106 m3)	384	307	1193	1556	224	335	229
1978	14 June 1978	1226	D (day)	36	36	88	251	26	25	26
			V (106 m3)	932	731	1535	3533	319	365	394
1979	22 November 1979	1428	D (day)	29	45	77	77	45	24	45
			V (106 m3)	822	803	1121	1285	710	447	1028
1980	16 October 1980	1593	D (day)	27	30	70	112	30	21	30
			V (106 m3)	1367	1248	1863	2562	1002	930	1439
1981	22 July 1981	1259	D (day)	49	50	67	67	29	22	29
			V (106 m3)	822	645	762	840	502	517	632
1982	10 October 1982	1190	D (day)	40	48	48	48	24	21	24
			V (106 m3)	1026	835	922	1025	520	589	632
1983	27 May 1983	862	D (day)	29	72	72	185	12	21	12
			V (106 m3)	404	646	713	2046	142	164	140
1984	24 May 1984	1223	D (day)	41	41	94	94	21	22	21
			V (106 m3)	995	777	1431	1713	296	421	290
1985	11 May 1985	1414	D (day)	45	45	45	83	16	22	12
			V (106 m3)	1141	969	1119	1891	396	474	272
1986	19 June 1986	1370	D (day)	20	53	53	154	46	25	29
			V (106 m3)	496	718	787	3564	661	492	672
1987	8 August 1987	1331	D (day)	31	31	31	66	21	12	21
			V (106 m3)	659	572	616	1031	410	263	450
1988	9 June 1988	1058	D (day)	27	27	70	70	27	18	27
			V (106 m3)	396	352	637	723	357	338	398
1989	8 July 1989	1772	D (day)	35	39	39	71	22	25	22
			V (106 m3)	1174	1059	1147	1855	800	649	925
1990	4 November 1990	1321	D (day)	32	47	47	99	25	23	25
			V [(06 m3)	712	747	800	1832	519	479	625
2003	4 November 2003	947	D (day)	28	28	36	91	16	16	16
			V (106 m3)	401	389	450	1124	309	323	322
2004	28 June 2004	1155	D (day)	92	92	92	200	76	23	76
			V (106 m3)	2551	1353	1553	3473	842	400	1998
2005	27 August 2005	1585	D (day)	36	36	36	36	36	24	36
			V (106 m3)	1109	916	985	1062	772	574	1113
2006	2 June 2006	1185	D (day)	31	124	124	169	17	25	17
			V (106 m3)	699	1802	2031	2868	287	385	231
2007	21 September 2007	749	D (day)	32	63	70	70	8	10	8
			V (106 m3)	428	718	830	947	102	107	100
2008	9 June 2008	780	D (day)	78	85	139	139	26	20	26
			V (106 m3)	1367	964	1437	1706	228	227	279
2009	29 June 2009	1129	D (day)	43	32	43	43	32	24	31
			V (106 m3)	1240	706	982	1080	570	496	879
2010	22 September 2010	1634	D (day)	38	49	49	82	31	18	31
			V (106 m3)	1095	937	1006	1585	762	639	994
2011	22 June 2011	789	D (day)	68	68	103	103	54	20	54
			V (106 m3)	1182	773	1127	1323	590	337	990
2012	9 November 2012	1637	D (day)	82	82	82	116	31	25	30
			V (106 m3)	2310	1393	1559	2380	770	736	1063
2013	11 May 2013	1313	D (day)	65	65	140	221	33	24	29
			V (106 m3)	2021	1359	2222	3825	358	337	436
2014	18 September 2014	2322	D (day)	41	43	76	76	30	18	30
			V (106 m3)	2209	1696	2459	2738	968	879	1114
2015	18 October 2015	1357	D (day)	35	35	35	105	35	25	35
			V (106 m3)	1087	867	931	1415	755	579	1087
2016	4 May 2016	1045	D (day)	22	22	55	104	8	8	8
			V (106 m3)	385	332	596	1464	197	176	160
2017	22 September 2017	1424	D (day)	39	44	44	44	44	25	44
			V (106 m3)	874	761	818	879	671	655	984
2018	2 November 2018	1335	D (day)	46	63	63	86	30	24	30
			V (106 m3)	1061	877	966	1169	631	640	834
2019	21 November 2019	1513	D (day)	45	51	51	51	43	25	37
			V (106 m3)	1659	1284	1431	1624	896	572	1485

3.2. Selection of Marginal Probability Distributions for Q, D and V Series

After the baseflow separation was conducted, the annual maximum (AM) method was applied to the daily discharge time series at all stations, resulting in samples of peak discharges (Q) with corresponding hydrograph volumes (V) and durations (D) (Table 1).

The Mann–Kendall test was performed to test for stationarity (Table 6). The results indicate that the null hypothesis cannot be rejected at a significance level of 0.05 for all stations except Belisce GS (Q variable) on the Drava River and Podsused GS (D, V variables) on the Sava River. Additionally, the computed Z-values for the Belisce (Q) and Podsused (D, V) GS are outside the critical values (±1.96), which can indicate a significant negative trend at the Belisce GS and a significant positive trend at the Podsused GS. Therefore, both stations were excluded from further analysis due to these results. A negative trend was also observed for the Q variable for the most downstream station on the Drava River and a positive trend was detected for V and variables for the most upstream station on the Sava River. Hence, the trend for the GS Podsused could be explained by the construction of several hydropower plants in the lower Sava River reach in Slovenia in the period from 2000 until 2015. Other GS located on the Sava River are less influenced by the operation of hydropower plants. On the other hand, the negative trend on Belisce GS is in line with the previous analysis of changes in discharges and water levels made by Tadic and Brlekovic [96] and it could be partially also attributed to climate change.

Table 6. The Mann–Kendall and Ljung–Box test results for Q, V and D variables.

River	Station		Mann–Kendall Test			Ljung–Box Test
		Variable	Test Statistic (S)	Z Value	p-Value	Test Statistic (Q)	p-Value
Drava	Botovo	Q	−44	−0.394	0.693	0.417	0.518
		D	143	1.304	0.192	0.297	0.586
		V	65	0.587	0.557	0.893	0.345
	Terezino polje	Q	−121	−1.101	0.271	1.292	0.256
		D	−1	0.000	1.000	0.064	0.801
		V	−86	−0.780	0.436	0.394	0.530
	Donji Miholjac	Q	−135	−1.269	0.205	1.125	0.289
		D	−137	−1.290	0.197	0.508	0.476
		V	−117	−1.098	0.272	0.322	0.571
	Belisce	Q	−221	−2.083	0.037	2.053	0.152
		D	−30	−0.275	0.783	2.017	0.156
		V	−94	−0.881	0.379	1.297	0.255
Sava	Podsused	Q	187	1.350	0.177	0.409	0.522
		D	448	3.248	0.001	0.241	0.623
		V	301	2.178	0.029	0.025	0.874
	Jasenovac	Q	151	1.151	0.250	0.058	0.810
		D	144	1.098	0.272	0.861	0.354
		V	122	0.928	0.353	1.157	0.282
	Mackovac	Q	76	0.576	0.565	0.012	0.911
		D	85	0.645	0.519	0.041	0.840
		V	34	0.253	0.800	0.004	0.949
	Zupanja	Q	−162	−1.201	0.230	1.531	0.216
		D	−28	−0.202	0.840	1.168	0.280
		V	−115	−0.851	0.395	0.043	0.837

Significant negative/positive trends are shown in bold.

Additionally, the Ljung–Box test was applied to test for autocorrelation in the data (Table 6) and the results show that the null hypothesis cannot be rejected at a significance level of 0.05 for all stations analyzed. Therefore, the flood peak discharge, hydrograph volume and hydrograph duration can be considered independent random variables.

Selection of the appropriate marginal distribution for the three flood variables was performed using the Anderson–Darling test and graphical Q-Q plots. Table 7 shows the basic properties of the selected variables.

Table 7. Selected distribution functions as marginal distributions of flood peak discharge, hydrograph duration, and hydrograph volume.

River	Station	Q	D	V
Drava	Botovo	GEV	GEV	Pearson 3
	Terezino polje	GLO	GEV	Pearson 3
	Donji Miholjac	Pearson 3	GLO	Pearson 3
Sava	Jasenovac	log-Pearson 3	Pearson 3	log-Pearson 3
	Mackovac	GLO	log-Pearson 3	log-Pearson 3
	Zupanja	GLO	GLO	log-Pearson 3

According to the results of the Anderson–Darling test, no distribution functions could be rejected from the analysis with the selected significance level of 0.05. The results of the AD test show that for the V at the Drava River stations Pearson 3 is the most appropriate marginal distribution function, and at the Sava River stations, it is the log-Pearson 3 distribution. The final selection of the best-fitted marginal distribution function was conducted visually using the QQ plots with the consideration of the AD test statistics as shown in the example of the Botovo GS on the Drava River (Figure 3). The results shown in Table 7 indicate that Pearson and log-Pearson type 3 distributions are the most suitable for describing hydrograph volumes. On the other hand, more diverse results were obtained for the Q and D variables (Table 7).

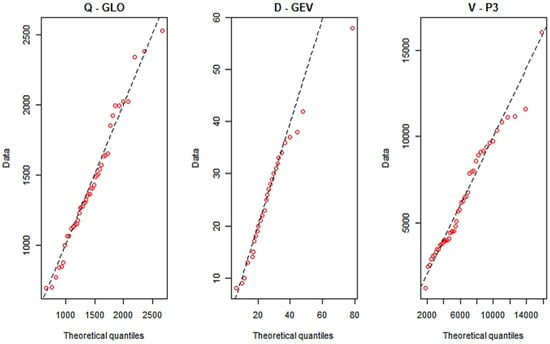
Figure 3. Example of QQ plots for the selected marginal distributions for the Botovo GS on the Drava River.

3.3. Copula Model Estimation

To assess the dependence between pairs of variables (Q, D and V) Kendall’s correlation coefficient was calculated (Table 8). The correlation coefficient for the pair Q–D is notably lower than for other pairs, which is consistent with several previous studies [15,16,76,77]. Kendall’s correlation coefficients ranged from 0.09 to 0.72 for all stations. Similarly, as in other studies, the dependence between Q and V was stronger than the correlation between V and D (Table 8).

Table 8. Kendall correlation coefficient values for pairs of analyzed flood variables.

River	Gauging Station	Sample Size	Q–D	Q–V	V–D
Drava	Botovo	47	0.23	0.61	0.56
	Terezino polje	47	0.36	0.72	0.56
	Donji Miholjac	46	0.27	0.70	0.44
Sava	Jasenovac	53	0.21	0.49	0.47
	Mackovac	54	0.15	0.36	0.56
	Zupanja	54	0.09	0.31	0.55

Q—hydrograph peak discharge; D—hydrograph duration; V—hydrograph volume.

Graphical dependence between pairs of variables is shown using Chi-plots and K-plots. An example of this can be seen in Figure 4 for the Jasenovac GS on the Sava River. The independence of the variables on the Chi-plots is indicated by the events being in the range between the confidence intervals [84,85]. All pairs of variables appear to be interdependent, with the least dependence between the Q–D pair. Moreover, K-plots show independence between the observed variables when the events are on the x = y line [16]. In this example, all events are above the line x = y, indicating positive dependence. The graphical results are consistent with the conclusions drawn from the calculation of Kendall’s correlation coefficient.

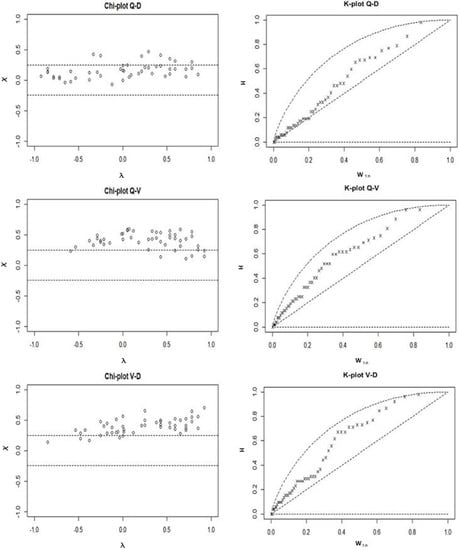
Figure 4. Example of dependence assessment for the Jasenovac GS on the Sava River.

The best matching copula is estimated using the R function “xvcopula” from the package “Copula”. It is based on k-fold cross-validation and the highest test statistic indicates the best fit. The adequacy of the selected copula functions was evaluated using the Cramér–von Mises test (S_n) applied with the R package “Copula” (Table 9) at a 0.05 significance level. The stations on the Drava River have the same best copula function for the Q–D (Huesler–Reiss) and V–D (Normal) pairs. Moreover, different copulas show the best fit for the Q–V pair. While for the Sava River, the results are more diverse, and no dominant copula function could be identified in this case. Moreover, it can be seen that none of the tested copulas could be rejected by the selected statistical test and taking into consideration the significance level of 0.05.

Table 9. Results of Cramér–von Mises test for estimation of copula parameters.

River	Station	Q–D			Q–V			V–D
		Copula	Sn	p-Value	Copula	Sn	p-Value	Copula	Sn	p-Value
Drava	Botovo	Huesler–Reiss	0.038	0.937	Huesler–Reiss	0.033	0.078	Normal	0.023	0.471
	Terezino polje	Huesler–Reiss	0.020	0.809	Gumbel	0.021	0.381	Normal	0.017	0.873
	Donji Miholjac	Huesler–Reiss	0.020	0.895	Normal	0.022	0.369	Normal	0.022	0.674
Sava	Jasenovac	Gumbel	0.031	0.251	Normal	0.022	0.538	Tawn	0.033	0.413
	Mackovac	Tawn	0.035	0.166	Tawn	0.020	0.873	Gumbel	0.035	0.052
	Zupanja	Huesler–Reiss	0.040	0.067	Tawn	0.043	0.055	Normal	0.018	0.793

3.4. Joint Return Periods

In the next step, with the consideration of the selected best-fitted marginal distributions and copula functions two joint return periods were calculated. Joint return periods T_and and T_or were calculated using best-fitting copulas for each pair of variables (i.e., Q–D, Q–V, and V–D). Different T_and (T_and (Q₁₀, V₁₀), T_and (Q₁₀₀, V₁₀₀), T_and (Q₁₀, V₁₀₀), T_and (Q₁₀₀, V₁₀) and T_or (T_or (Q₁₀, V₁₀), Tor (Q₁₀₀, V₁₀₀), T_or (Q₁₀, V₁₀₀) and T_or (Q₁₀₀, V₁₀) were calculated for all stations on the Drava River and the Sava River (Table 10). According to Salvadori et al. [92], which is in accordance with the results of the analysis, the relationship between univariate and primary (bivariate) return periods can be written as: $T_{u,v}^{OR}<T^{UNI}<T_{u,v}^{AND}$. The results show that the corresponding peak discharge, hydrograph duration and hydrograph volume values for a return period of 10 years ($T^{UNI}$) are in the range 1778.1–2054.7 m³/s, 38.7–39.4 days and 920.9–970.2 10⁶ m³ for stations on the Drava River, and in the range 2278.8–3450.0 m³/s, 83.2–98.9 days and 3185.8–4821.4 10⁶ m³ for stations on the Sava River, respectively. To get the values of the observed flood variables for the future scour analysis around bridges for a fixed value of the OR and AND return periods ($T_{u,v}^{OR}, T_{u,v}^{AND})$, different combinations of variables can be selected. It can be seen that the specific design discharge values (e.g., Q₁₀) decrease with increasing catchment area while different results can be obtained for higher return periods (Table 10).

Table 10. Comparison of different return periods for variable pairs Q–D, Q–V, and V–D.

	Drava			Sava
Return Period	Botovo	Terezino Polje	Donji Miholjac	Jasenovac	Mackovac	Zupanja
Q10 (m3/s)	2054.7	1967.4	1778.1	2382.8	2278.8	3450.0
Q10 (m3/s/km2)	0.0662	0.0580	0.0479	0.0612	0.0558	0.0549
D10 (day)	38.7	40.8	39.4	83.2	86.4	98.9
V10 (106 m3)	970.2	999.3	920.9	3185.8	3366.2	4821.4
V10 (m3/km2)	31,258.3	29,464.3	24,793.0	81,786.2	82,429.3	76,662.3
Q100 (m3/s)	2910.9	3296.2	2411.4	2858.8	3199.2	5060.176
Q100 (m3/s/km2)	0.0938	0.0972	0.0649	0.0734	0.0783	0.0805
D100 (day)	51.5	59.9	58.5	111.6	127.5	157.0
V100 (106 m3)	1554.0	1674.2	1483.7	4554.1	5617.7	7451.7
V100 (m3/km2)	50,068.7	49,362.8	39,945.4	116,912.3	137,560.2	118,485.4
	Huesler–Reiss	Huesler–Reiss	Huesler–Reiss	Gumbel	Tawn	Huesler–Reiss
TAND (Q10D10)	30	22	26	28	36	51
TOR (Q10D10)	6	7	6	6	6	6
TAND (Q100D100)	364	238	303	329	462	835
TOR (Q100D100)	58	63	60	59	56	53
TAND (Q10D100)	148	114	131	151	226	271
TOR (Q10D100)	10	10	10	10	9	9
TAND (Q100D10)	148	114	131	151	226	271
TOR (Q100D10)	10	10	10	10	9	9
	Huesler–Reiss	Gumbel	Normal	Normal	Tawn	Tawn
TAND (Q10V10)	14	13	15	21	21	23
TOR (Q10V10)	8	8	8	7	7	6
TAND (Q100V100)	147	127	193	375	224	256
TOR (Q100V100)	76	82	68	58	64	62
TAND (Q10V100)	100	100	102	128	121	136
TOR (Q10V100)	10	10	10	10	10	10
TAND (Q100V10)	100	100	102	128	121	136
TOR (Q100V10)	10	10	10	10	10	10
	Normal	Normal	Normal	Tawn	Gumbel	Normal
TAND (V10D10)	20	19	24	19	15	19
TOR (V10D10)	7	7	6	7	7	7
TAND (V100D100)	316	312	479	199	156	306
TOR (V100D100)	59	60	56	67	74	60
TAND (V10D100)	118	117	145	109	102	116
TOR (V10D100)	10	10	10	10	10	10
TAND (V100D10)	118	117	145	109	102	116
TOR (V100D10)	10	10	10	10	10	10

3.5. Preliminary Methodology for the Bridge Scour Analysis Using Copulas

The results presented in Section 3.4 can be further used as input data for the bridge scour analysis. In the scope of this study, a preliminary methodology is presented that will be further applied in the following research steps within the scope of the R3PEAT project. At least two different options can be used to apply the bivariate flood frequency results (Section 3.4) in order to define the design hydrograph:

-

a relatively simple option using a typical hydrograph (TH) method (e.g., as cited by Yue et al. [97]);

-

a slightly more sophisticated approach following the methodology proposed by Brunner et al. [98].

The TH method is the most frequently used in engineering applications and involves the selection of the so-called typical flood hydrograph. In many cases, this is an extreme flood event or some other typical flood event (i.e., hydrograph). In the next steps of the TH method, the selected typical flood hydrograph is multiplied by the design discharge values. Most often, the method is used only with the univariate flood frequency analysis while it can be easily upgraded using the bivariate flood frequency analysis using copula functions as shown in this section. Hence, this means that both Q and V (or Q and D or V and D) are used together with a typical flood hydrograph in order to derive the so-called design flood hydrograph. Figure 5 shows an example of the design hydrograph derived with the consideration of the TH method where both Q and V variables were set to be equal to the Q₁₀₀ and V₁₀₀, respectively. At the same time, this hydrograph corresponds to the bivariate return periods T_AND and T_OR 256 years and 62 years, respectively (Table 10). Therefore, this design hydrograph can be used further as input to the hydraulic model for the bridge scour analysis.

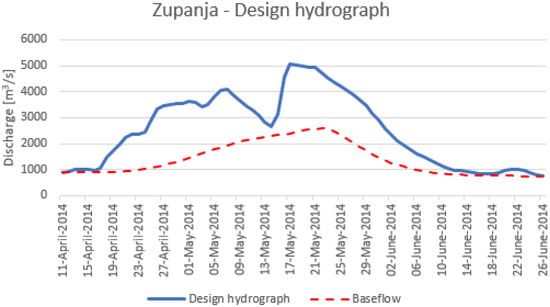
Figure 5. Example of design hydrograph for the Zupanja GS on the Sava River that was constructed based on the measured AM flood hydrograph from the year 2014. The surface runoff volume corresponds to the V₁₀₀ (i.e., 7454 × 10⁶ m³) while peak discharge corresponds to Q₁₀₀ (i.e., 5060 m³/s). At the same time, the design hydrograph corresponds to the bivariate return periods T_AND and T_OR 256 years and 62 years, respectively.

The alternative approach follows the methodology developed by Brunner et al. [98] and is composed of multiple steps such as classification of events (e.g., rain on snow, flash floods), data normalization, use of the probability density function to describe the shape of the selected flood hydrograph, etc. A detailed description of the methodology is provided by Brunner et al. [98]. As a result of the methodology, the design flood hydrograph is defined with the consideration of the bivariate return periods.

The selected design hydrograph using either the TH method or methodology proposed by Brunner et al. [98] is then used as input data to the hydraulic model, which is needed to investigate the bridge scour dynamics and obtain detailed hydraulic properties for specific river cross-sections such as water velocity, shear stress. The unsteady flow simulations should be used in order to analyze the impact of the entire flood hydrograph on the bridge scour dynamics. The hydraulic simulation requires adequate information about cross-sections, roughness, and most important hydro-technical objects (e.g., dams) and should be thoroughly calibrated and evaluated based on the historical flood events. Afterwards, applying the design hydrographs can yield useful information about the bridge scour dynamics for specific cases. It is recommended to test multiple scenarios (i.e., different design hydrographs).

The described methodology can be further extended in order to capture some of the variability in the flood generation process. For example, in the scope of the TH method multiple typical flood hydrographs can be selected, which results in multiple input data for the hydraulic model, which then yields several different scenarios that can be investigated and compared. Similar steps can be done in the scope of the methodology proposed by Brunner et al. [98]. Both TH and Brunner et al.’s [98] methods are proposed to be used as part of the methodology for the design hydrograph estimation in Slovenia [99,100].

4. Conclusions

In this paper, detailed bivariate copula flood frequency analyses were conducted using data from four gauging stations on the Drava River and four gauging stations on the Sava River. For each river, one gauging station was excluded from the copula analysis due to the non-stationarity of the observed data samples. The analysis was conducted using several copula functions while the most suitable marginal distribution and copulas were selected based on different statistical tests and graphical data representation. Different joint return periods T_and and T_or were calculated using the best-fitting copulas (and marginal distributions) for each pair of variables (i.e., Q–D, Q–V and V–D).

Several conclusions can be drawn based on the results presented in this study:

• The HYSEP1 baseflow separation method can be regarded as an appropriate choice for baseflow separation for stations on the Drava River. In order to apply the baseflow evaluation criterion proposed by Xie et al. [59] at the stations in the middle part of the Sava River, additional analyses should be performed, or the proposed rules should be modified to correspond to the complex flood regime that prevails there. This indicates the importance of the visual inspection of the results, especially in the case of rivers where there are significant effects of dam operation and/or flood protection systems on flood hydrograph characteristics. Additionally, some of the tested baseflow separation methods did not yield useful results. Hence, it is advised that further studies that deal with flood hydrograph characteristics test multiple baseflow separation methods since extracted V and D variables can be highly sensitive to the selection of the baseflow separation methods. The differences among tested methods can yield V and D values that differ by an order of magnitude. Hence, this can lead to over- or under-estimation of the design variables.
• The Huesler–Reiss copula from the extreme-value family of copulas was selected as the most suitable copula for modelling peak discharges and hydrograph durations at all stations of the Drava River, while the most appropriate copula for modelling hydrograph volumes and hydrograph durations seems to be the Normal copula from the elliptical family of copulas. On the other hand, for the Sava River, more diverse results were obtained indicating non-uniform flow characteristics along the Sava River in Croatia.
• Different combinations of variables Q, D and V derived from the bivariate copula results for each station can eventually be computed if there is a need in practical applications (e.g., design, scour analysis, etc.). Hence, a preliminary methodology for the implication of the bivariate flood frequency analysis using copulas for the bridge scour analysis is proposed. As an example, the design hydrograph for one station on the Sava River is derived.

The objective of this study was to contribute to the better description of some of the most important variables related to flood events in order to better understand them and, in future, to apply the copula frequency approach to determine the probabilities of occurrence of different pairs of flood variables, which should be of great interest for scour analysis connected to the R3PEAT project. In addition, the presented methodology can also be used as an example for other similar case studies. To sum up, the main scientific contribution of this study is that multiple baseflow separation methods were tested, which is not usually the case in studies dealing with multivariate flood frequency analysis. Additionally, a preliminary methodology is proposed that could be used for the bridge scour analysis using copula functions. Moreover, the presented methodology could be applied to other rivers with different characteristics since multiple methods have been tested at each stage and the most suitable method (e.g., baseflow separation, marginal distribution, copula function) was selected at every conducted step.