Freeze-Thaw Effect on Riverbank Stability
Abstract
:1. Introduction
2. Slope Stability Analysis and Modeling
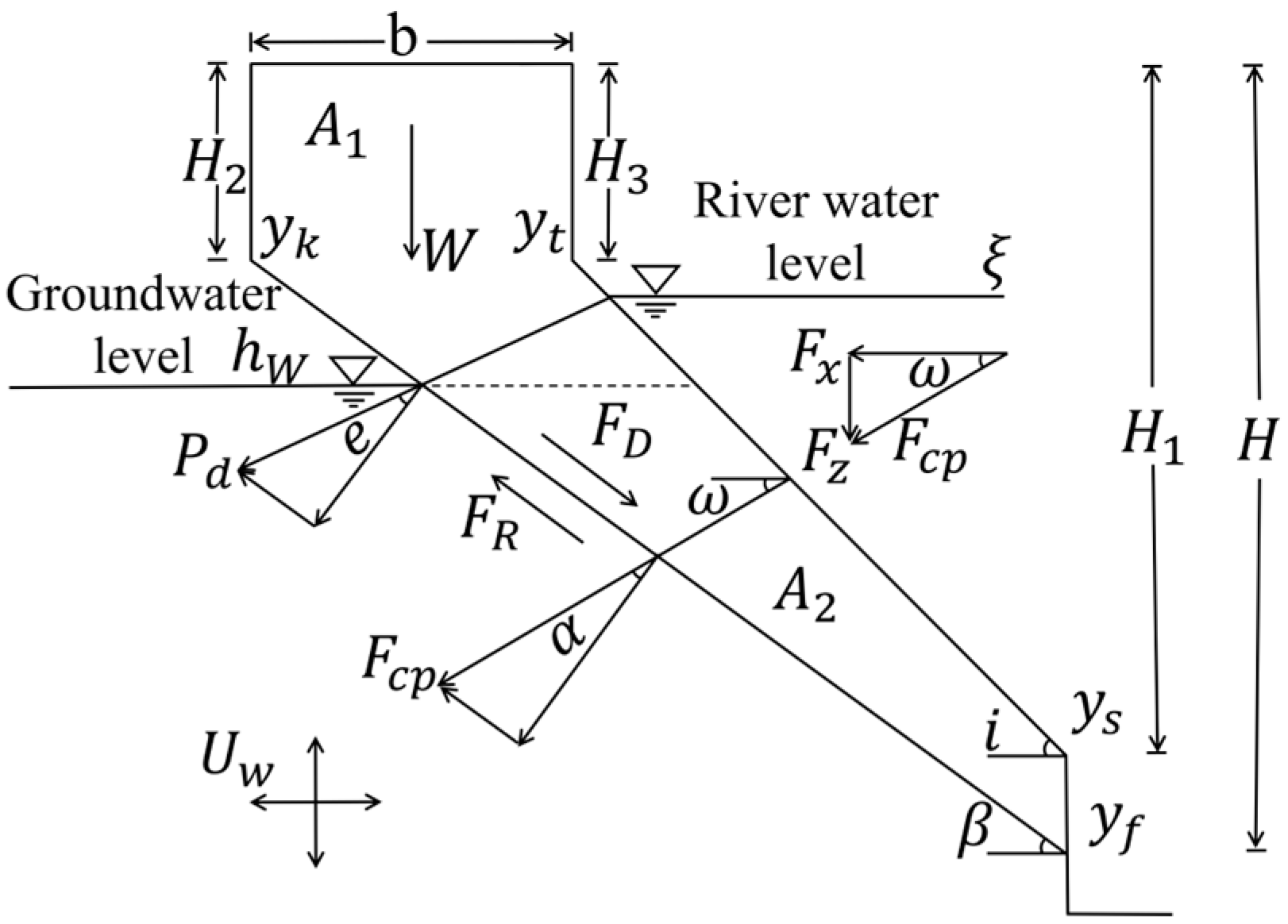
2.1. Bank Stability Mechanics
Forces on the Potential Sliding Mass
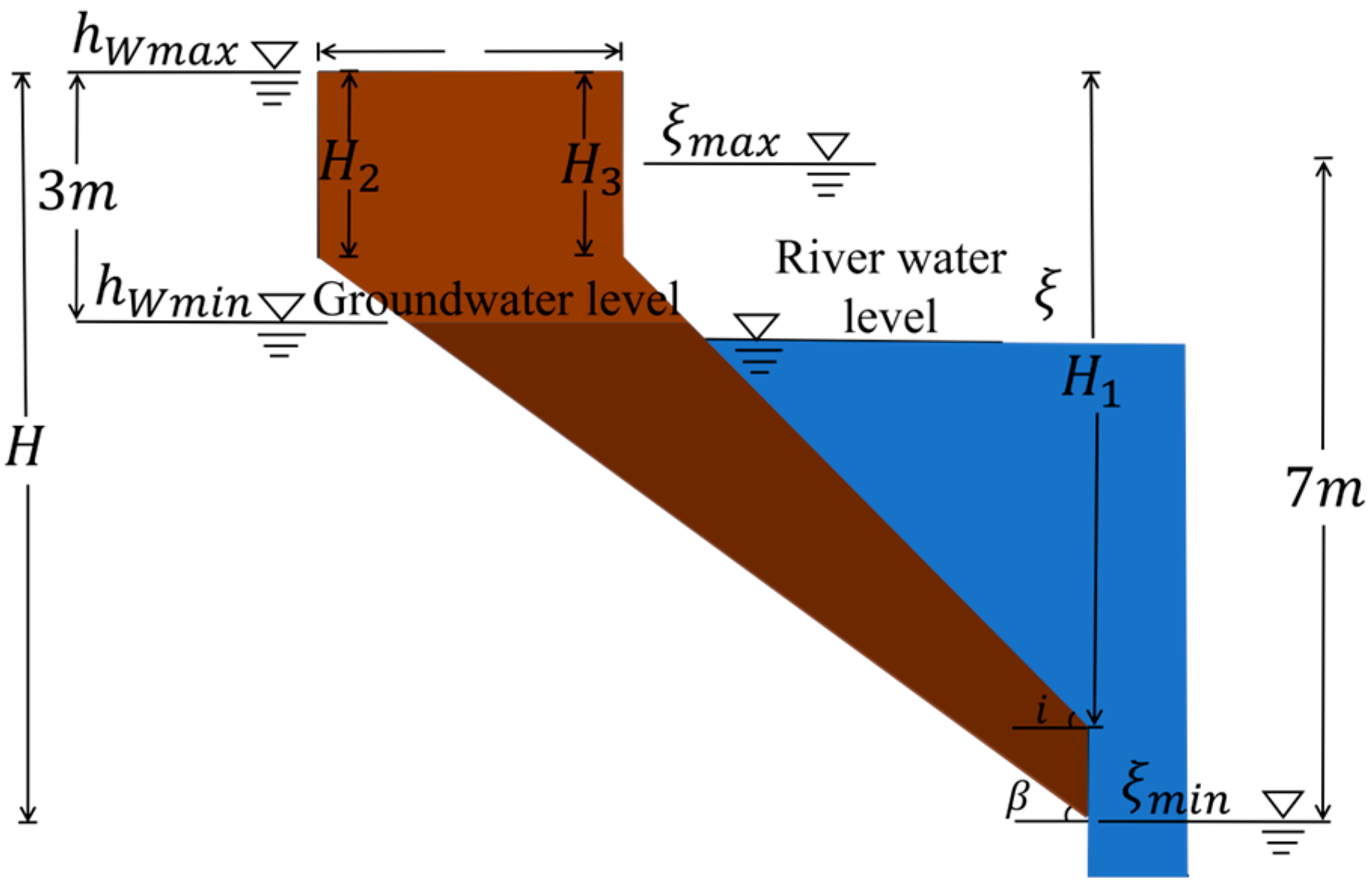
2.2. Modeling Bank Slope Instability
3. Model Application and Analysis
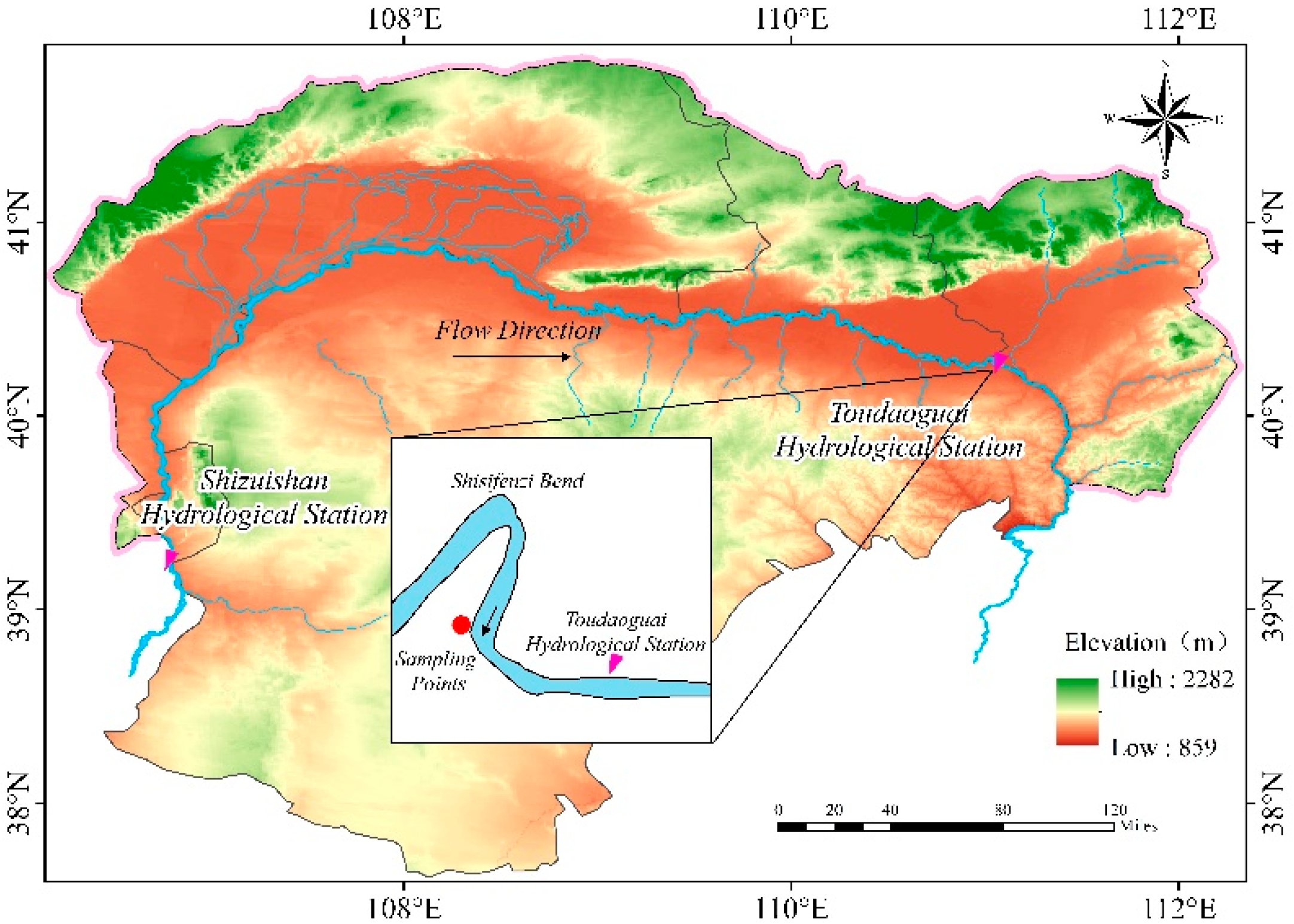
3.1. Study Site
3.2. Bank Stability Analysis
3.3. Factors Affecting Bank Stability
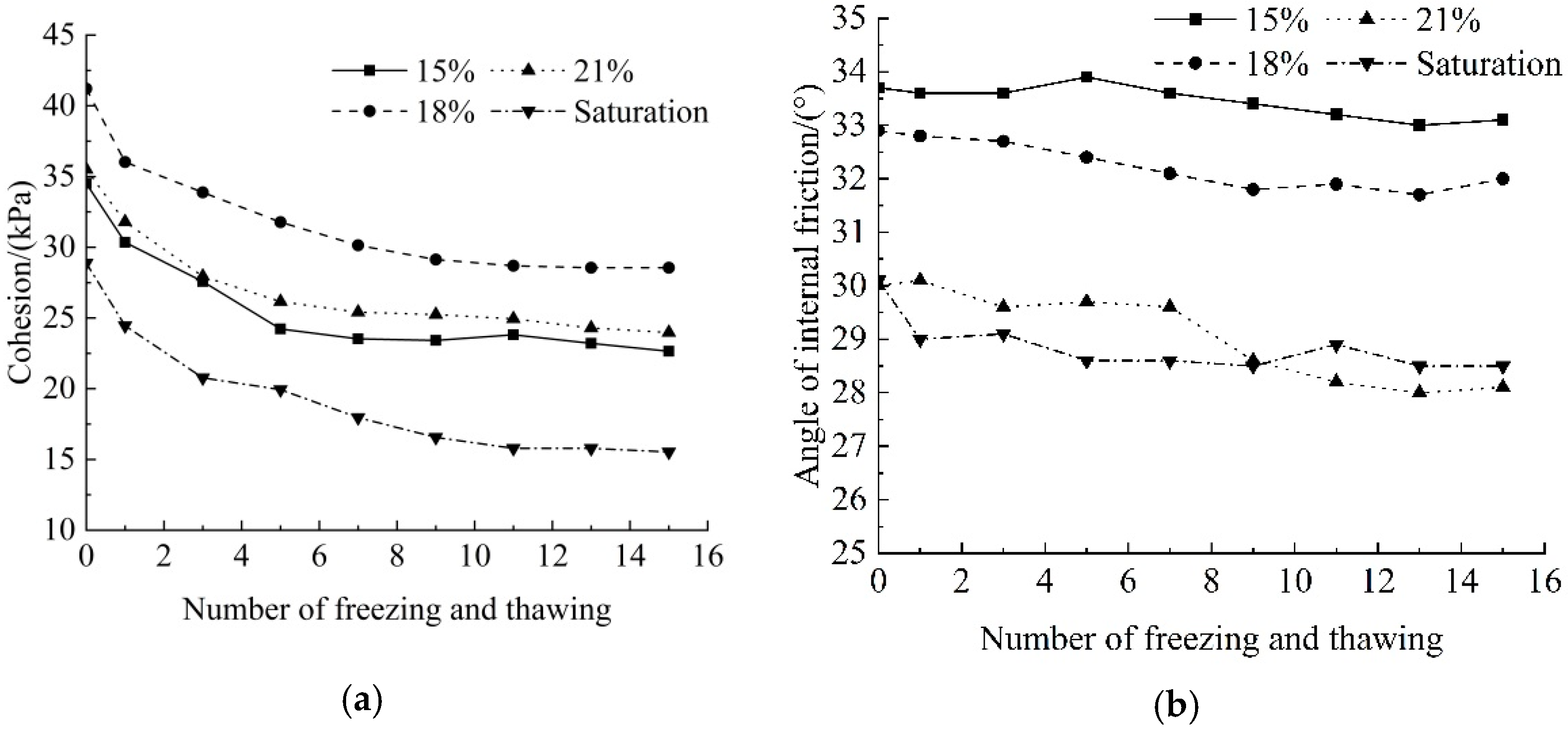
3.3.1. Freeze-Thaw Effect
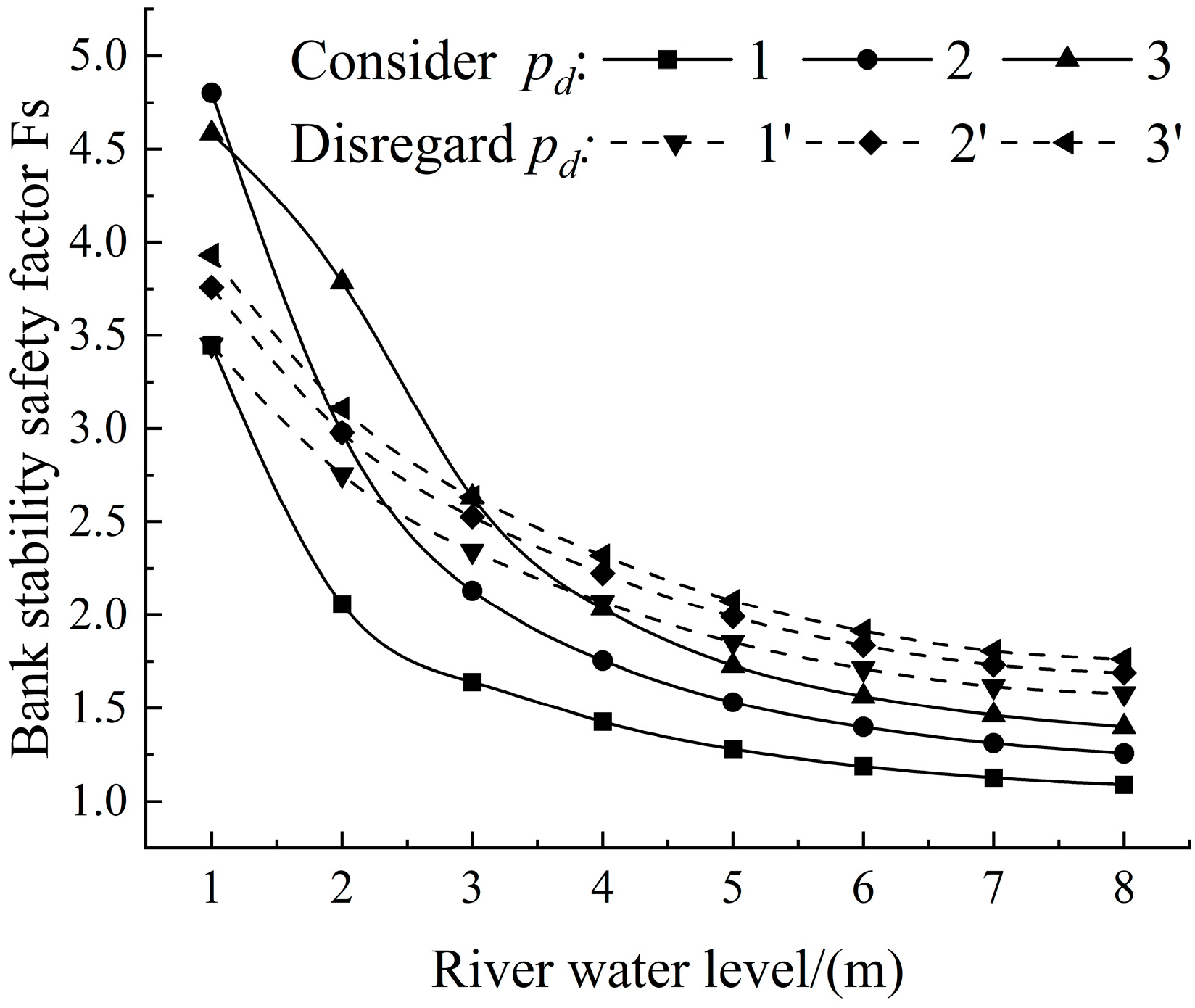
3.3.2. Effect of Infiltration Water Pressure
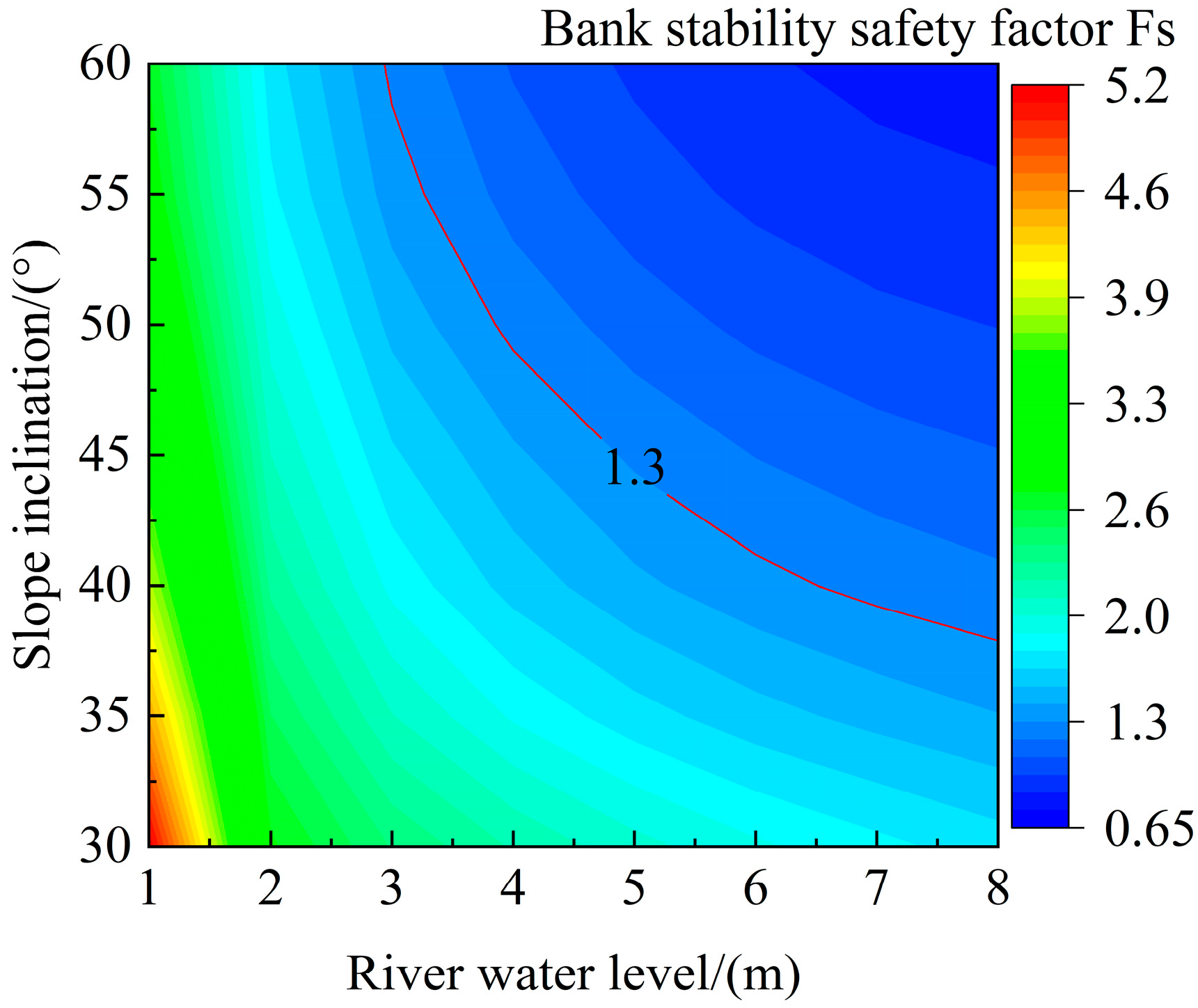
3.3.3. Effect of Bank Slope
4. Conclusions
- (1)
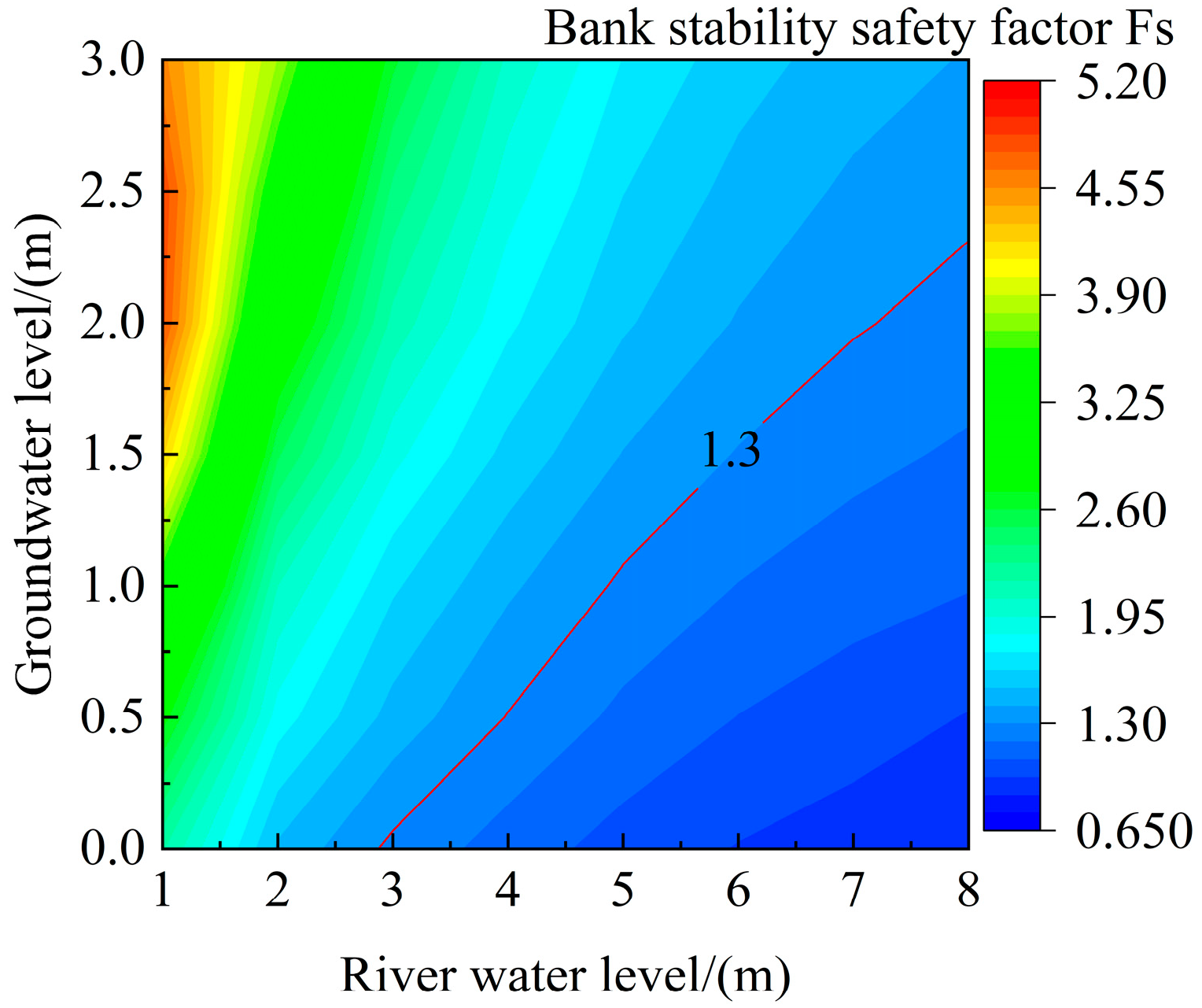
- When the river water level is constant, the safety factor of bank stability decreases with the rising groundwater level. When the groundwater level is constant, the safety coefficient of bank stability declines with the decreasing river water level, with a trend of thawing period < dry period < low water period < flooding period < wet period.
- (2)
- The freeze-thaw action significantly changes the mechanical properties of the bank material, leading to a 24.35–29.13% reduction in the safety factor of bank stability, indicating the important effect of the freeze-thaw in reducing the bank stability.
- (3)
- When the groundwater level is lower than the river water level, the infiltration water pressure mainly shows an inhibitory effect on the bank stability. The safety factor of bank stability will increase. By contrast, when the groundwater level is higher, the infiltration water pressure plays a destabilizing role.
- (4)
- When the river water level is below 4 m, there is a possibility of bank collapse under different bank slope angles, and the safety factor decreases with larger bank slope angles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hooke, J.M. An analysis of the processes of river bank erosion. J. Hydrol. 1979, 42, 39–62. [Google Scholar] [CrossRef]
- Chen, D.; Duan, J.G. Modeling width adjustment in meandering channels. J. Hydrol. 2006, 321, 59–76. [Google Scholar] [CrossRef]
- Henshaw, A.J.; Thorne, C.R.; Clifford, N.J. Identifying causes and controls of river bank erosion in a British upland catchment. Catena 2012, 100, 107–119. [Google Scholar] [CrossRef]
- Xia, J.Q.; Zong, Q.L.; Deng, S.S.; Xu, Q.X.; Lu, J.Y. Seasonal variations in composite riverbank stability in the Lower Jingjiang Reach, China. J. Hydrol. 2014, 519, 3664–3673. [Google Scholar] [CrossRef]
- Xia, J.Q.; Zong, Q.L. Mechanism of Bank Failure in Jingjiang Section of Yangtze River and Its Numerical Simulation; Science Press: Beijing, China, 2015; pp. 155–167. (In Chinese) [Google Scholar]
- Lu, Y.; Lu, Y.J.; Zhang, X.N. Influence of river water level landing on slope stability. Adv. Water Science. 2008, 19, 389–393. (In Chinese) [Google Scholar]
- Guo, Y.; Shen, W. Monitoring and Experiment on the Effect of Freeze-Thaw on Soil Cutting Slope Stability. Procedia Environ. Sci. 2011, 10, 1115–1121. [Google Scholar] [CrossRef]
- Xie, H.; Yu, K.Z. Analysis of factors affecting bank stability in construction of Yangtze River dry embankment protection project. People’s Yangtze River. 2006, 37, 93–94+101. (In Chinese) [Google Scholar]
- Hoomehr, S.; Akinola, A.; Wynn-Thompson, T.; Garnand, W.; Eick, M.J. Water Temperature, pH, and Road Salt Impacts on the Fluvial Erosion of Cohesive Streambanks. Water 2018, 10, 302. [Google Scholar] [CrossRef]
- Xu, W.; He, S.L. Analysis of influencing factors of riverbank collapse. Regul. Huai River. 2019, 4, 22–24. (In Chinese) [Google Scholar]
- Osman, A.M.; Thorne, C.R.; Member, A. Riverbank stability analysis. I: Theory. J. Hydraul. Eng. 1988, 114, 134–150. [Google Scholar] [CrossRef]
- Zhang, X.N.; Jiang, C.F.; Ying, Q.; Chen, C.Y. Review of research on bank collapse in natural rivers. Adv. Sci. Technol. Water Resour. 2008, 28, 80–83. (In Chinese) [Google Scholar]
- Zhang, X.N.; Jiang, C.F.; Chen, C.Y.; Ying, Q. Analysis of influencing factors of river bank failure. J. River Sea Univ. (Nat. Sci. Ed.) 2009, 37, 36–40. (In Chinese) [Google Scholar]
- Zhang, F.Z.; Chen, X.P. Study on the effect of river scour on seepage and deformation of embankment. Geotechnics 2011, 32, 441–447. (In Chinese) [Google Scholar]
- Simon, A.; Curini, A.; Darby, S.E.; Langendoen, E.J. Bank and near-bank processes in an incised channel. Geomorphology 2000, 35, 193–217. [Google Scholar] [CrossRef]
- Couper, P. Effects of silt–clay content on the susceptibility of river banks to subaerial erosion. Geomorphology 2003, 56, 95–108. [Google Scholar] [CrossRef]
- Chiang, S.W.; Tsai, T.L.; Yang, J.H. Conjunction effect of stream water level and groundwater flow for riverbank stability analysis. Environ. Earth Sci. 2011, 62, 707–715. [Google Scholar] [CrossRef]
- Karmaker, T.; Dutta, S. Erodibility of fine soil from the composite river bank of Brahmaputra in India. Hydrol. Processes. 2011, 25, 104–111. [Google Scholar] [CrossRef]
- Kimiaghalam, N.; Goharrokhi, M.; Clark, S.P.; Ahmari, H. A comprehensive fluvial geomorphology study of riverbank erosion on the Red River in Winnipeg, Manitoba, Canada. J. Hydrol. 2015, 529, 1488–1498. [Google Scholar] [CrossRef]
- Thoron, C.R.; Tovey, N.K. Stability of composite riverbanks. Earth Surf. Processes Landf. 1981, 6, 469–484. [Google Scholar] [CrossRef]
- Wang, Y.G.; Kuang, S.F. Study of critical collapse height of river banks. J. Water Resour. 2007, 10, 1158–1165. (In Chinese) [Google Scholar]
- Wang, J.; Zong, Q.L.; Yue, H.Y.; Liu, Z.X. Effects of alternating wet and dry on the mechanical properties of shoreland soils in a typical section of the Jingjiang River section of the Yangtze River. J. Agric. Eng. 2019, 35, 144–152. (In Chinese) [Google Scholar]
- Wang, X.D.; Li, S.Y.; Sun, Y.F.; Zhang, C.B.; Liu, G.W. Influence of freeze–thaw cycling on the soil mechanical properties of open-pit mine dump under different moisture contents. Environ. Earth Sci. 2021, 80, 279. [Google Scholar] [CrossRef]
- Simon, A.; Collison, A.J.C. Pore-water pressure effects on the detachment of cohesive streambeds: Seepage forces and matric suction. Earth Surf. Processes Landf. 2001, 26, 1421–1442. [Google Scholar] [CrossRef]
- Tang, L.Y.; Li, G.; Li, Z.; Jin, L.; Yang, G.S. Shear properties and pore structure characteristics of soil–rock mixture under freeze–thaw cycles. Bull. Eng. Geol. Environ. 2021, 80, 3233–3249. [Google Scholar] [CrossRef]
- Darby, S.E.; Thorne, C.R. Development and testing of riverbank-stability analysis. J. Hydraul. Eng. 1996, 122, 443–454. [Google Scholar] [CrossRef]
- Samadi, A.; Davoudi, M.H.; Amiri-Tokaldany, E. Experimental study of cantilever failure in the upper part of cohesive riverbanks. Res. J. Environ. Sci. 2011, 5, 444–460. [Google Scholar] [CrossRef]
- Wang, Y.G.; Kuang, S.F. Research on bank collapse types and collapse modes. Sediment Res. 2014, 1, 13–20. [Google Scholar]
- Rinaldi, M.; Casagli, N. Stability of streambanks formed in partially saturated soils and effect of negative pore water pressures: The Sieve River (Italy). Geomorphology 1999, 26, 253–277. [Google Scholar] [CrossRef]
- Deng, S.; Xia, J.Q.; Zhou, M.R.; Li, J.; Zhu, Y.H. Coupled modeling of bank retreat processes in the Upper Jingjiang Reach, China. Earth Surf. Processes Landf. 2018, 43, 2863–2875. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Wang, W.D.; Zhang, Y.B. Improvement of transfer coefficient method under the consideration of hydrodynamic pressure. Eng. Fail. Anal. 2021, 124, 1167–1170. [Google Scholar] [CrossRef]
- Amiri-tokaldany, E.; Darby, S.E.; Tosswell, P. Bank stability analysis for predicting reach-scale land loss and sediment yield. J. Am. Water Resour. Assoc. 2003, 39, 897–909. [Google Scholar] [CrossRef]
- Amiri-tokaldany, E.; Darby, S.E.; Tosswell, P. Coupling bank stability and bed deformation models to predict equilibrium bed topography in river bends. J. Hydraul. Eng. 2007, 113, 1167–1170. [Google Scholar] [CrossRef]
- Lai, Y.G.; Thomas, R.E.; Ozeren, Y.; Simon, A.; Greimann, B.P.; Wu, K. Modeling of multilayer cohesive bank erosion with a coupled bank stability and mobile-bed model. Geomorphology 2015, 243, 116–129. [Google Scholar] [CrossRef]
- Li, C.; Quan, D.; Zhang, Y.; Shi, X.H.; Guo, Z.Y. Characteristics of water-sand movement process and evolution trend of the Yellow River (Inner Mongolia section). J. Soil Water Conserv. 2020, 34, 41–46+53. (In Chinese) [Google Scholar]
- Li, Y.; Su, H.F.; Wang, L. Advances in shore slope stability research. Constr. Technol. 2017, 46, 1225–1229. (In Chinese) [Google Scholar]
- Simon, A. Mass Wasting Algorithms in an Alluvial Channel Model. In Proceedings of the 5th Federal Inter-Agency Sedimentation Conference, Las Vegas, NV, USA, 22–29 August 1991. [Google Scholar]
- Zhang, X.N.; Jiang, C.F.; Chen, C.Y.; Ying, Q. Types and characteristics of river bank failure. Prog. Water Resour. Hydropower Sci. Technol. 2008, 28, 66–70. (In Chinese) [Google Scholar]
- Xia, J.Q.; Zong, Q.L.; Xu, Q.X.; Deng, C.Y. Characteristics of binary structure riverbank soils and bank failure mechanism in the lower Jingjiang River. Adv. Water Sci. 2013, 24, 810–820. (In Chinese) [Google Scholar]
- Ran, R.; Liu, Y.F. Analysis of the influence of reservoir bank slope morphology on its stability using BSTEM model. Groundwater 2011, 33, 162–165. (In Chinese) [Google Scholar]
- Yang, Z.; Li, C.; Ji, H.L.; Sun, C.; Shi, Z.F. Study on the characteristics of temperature and humidity changes in the embankment soil of the Yellow River during the freeze-thaw period and the influencing factors. Arid. Zone Resour. Environ. 2021, 35, 76–83. (In Chinese) [Google Scholar]




| Natural Specific Weight, (kN/m3) | Saturated Specific Weight, (kN/m3) | Dry Density, (g/cm3) | Experimental Values | Valid Values | |||
|---|---|---|---|---|---|---|---|
| 18.1 | 19.3 | 33.55 | 1.58 | 35.5 | 30 | 24.85 | 27 |
| 0 | −0.5 | −1 | −1.5 | −2.0 | −2.5 | −3.0 | ||
|---|---|---|---|---|---|---|---|---|
| −1 | + | + | + | + | + | + | + | |
| −2 | + | + | + | + | + | + | + | |
| −3 | - | + | + | + | + | + | + | |
| −4 | - | - | + | + | + | + | + | |
| −5 | - | - | - | + | + | + | + | |
| −6 | - | - | - | - | + | + | + | |
| −7 | - | - | - | - | + | + | + | |
| −8 | - | - | - | - | - | + | + | |
| Parameters | Thawing Period | Dry Period | Wet Period | Flooding Period | Low Flow Period |
|---|---|---|---|---|---|
| 16.8 | 16.8 | 24.85 | 24.85 | 24.85 | |
| /° | 25.2 | 25.2 | 27 | 27 | 27 |
| /m | 0 | −3 | −3 | −0.5 | −0.5 |
| /m | −5 | −5 | −1.5 | −1.5 | −4 |
| Safety factor | 0.75 | 1.26 | 4.16 | 2.14 | 1.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Yang, Z.; Shen, H.T.; Mou, X. Freeze-Thaw Effect on Riverbank Stability. Water 2022, 14, 2479. https://doi.org/10.3390/w14162479
Li C, Yang Z, Shen HT, Mou X. Freeze-Thaw Effect on Riverbank Stability. Water. 2022; 14(16):2479. https://doi.org/10.3390/w14162479
Chicago/Turabian StyleLi, Chao, Zhen Yang, Hung Tao Shen, and Xianyou Mou. 2022. "Freeze-Thaw Effect on Riverbank Stability" Water 14, no. 16: 2479. https://doi.org/10.3390/w14162479
APA StyleLi, C., Yang, Z., Shen, H. T., & Mou, X. (2022). Freeze-Thaw Effect on Riverbank Stability. Water, 14(16), 2479. https://doi.org/10.3390/w14162479






