Impact of Boundary Conditions Dynamics on Groundwater Budget in the Campania Region (Italy)
Abstract
:1. Introduction
2. Materials and Methods
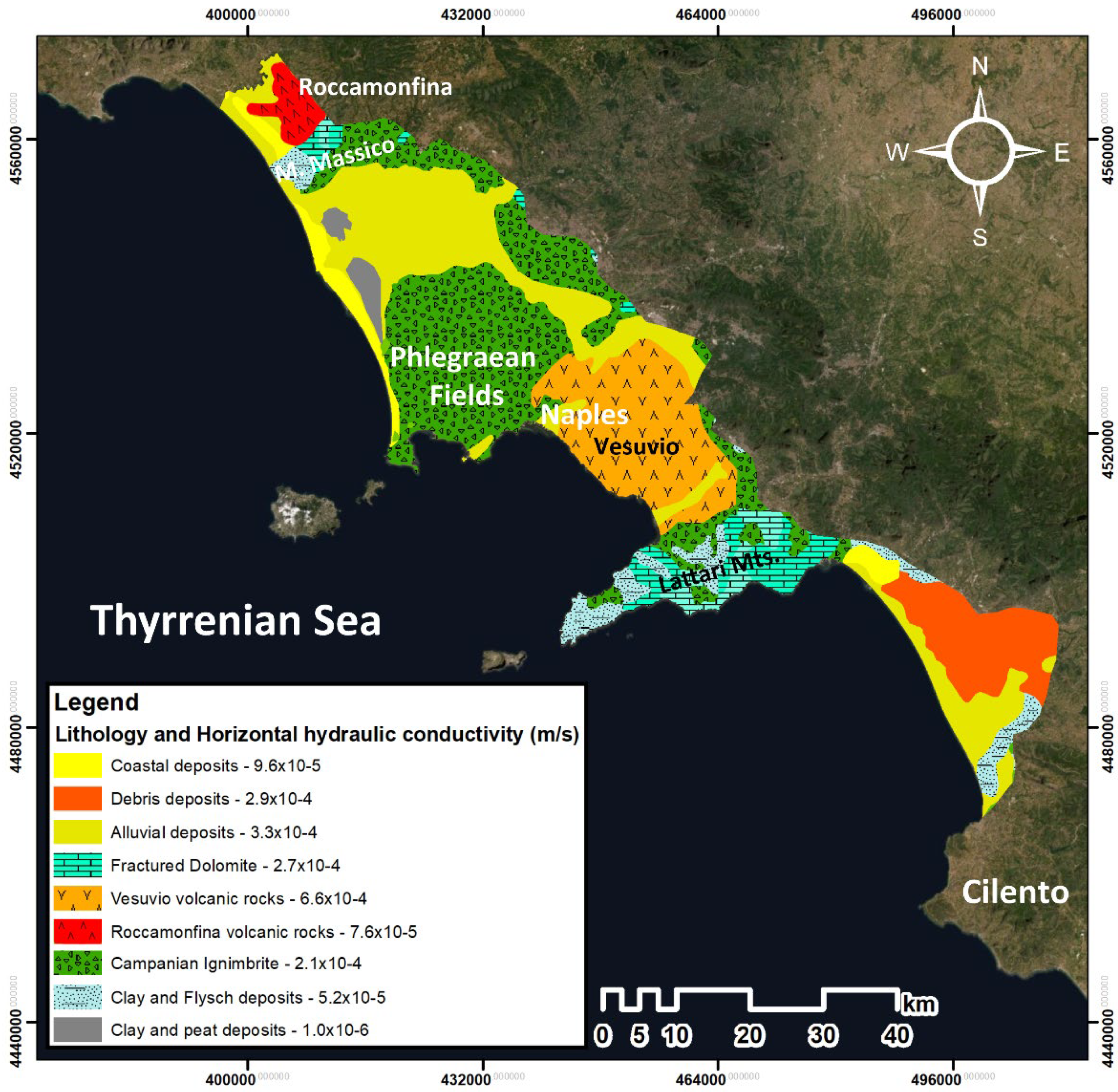
2.1. The Study Area
2.2. Field Characterization and Boundary Conditions
2.3. Numerical Modelling
- constant head at the fractured aquifers BC (scenario S1);
- uniform extinction depth BC (scenario S2);
- constant Tyrrhenian Sea level BC (scenario S3);
- constant river levels BC (scenario S4).
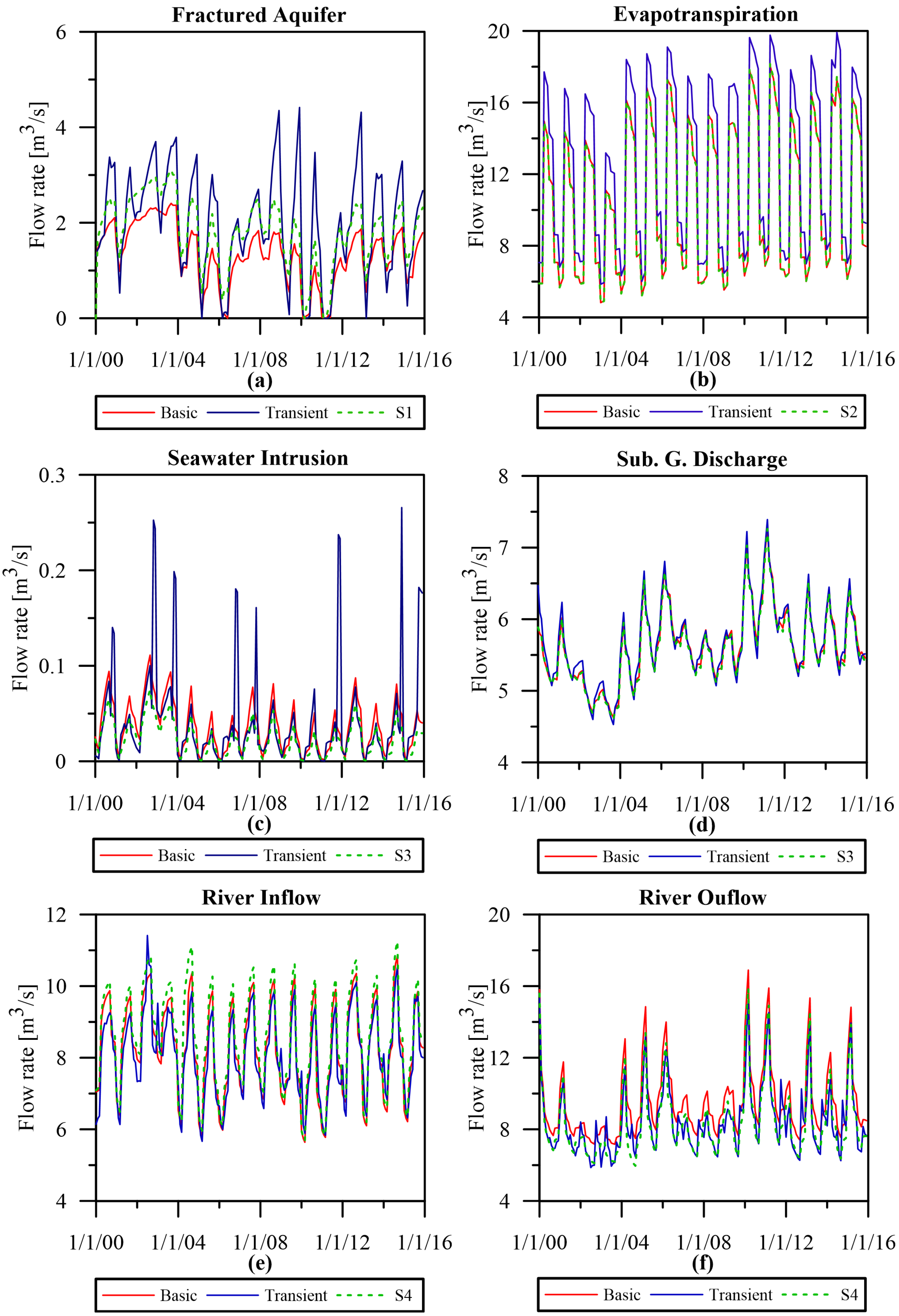
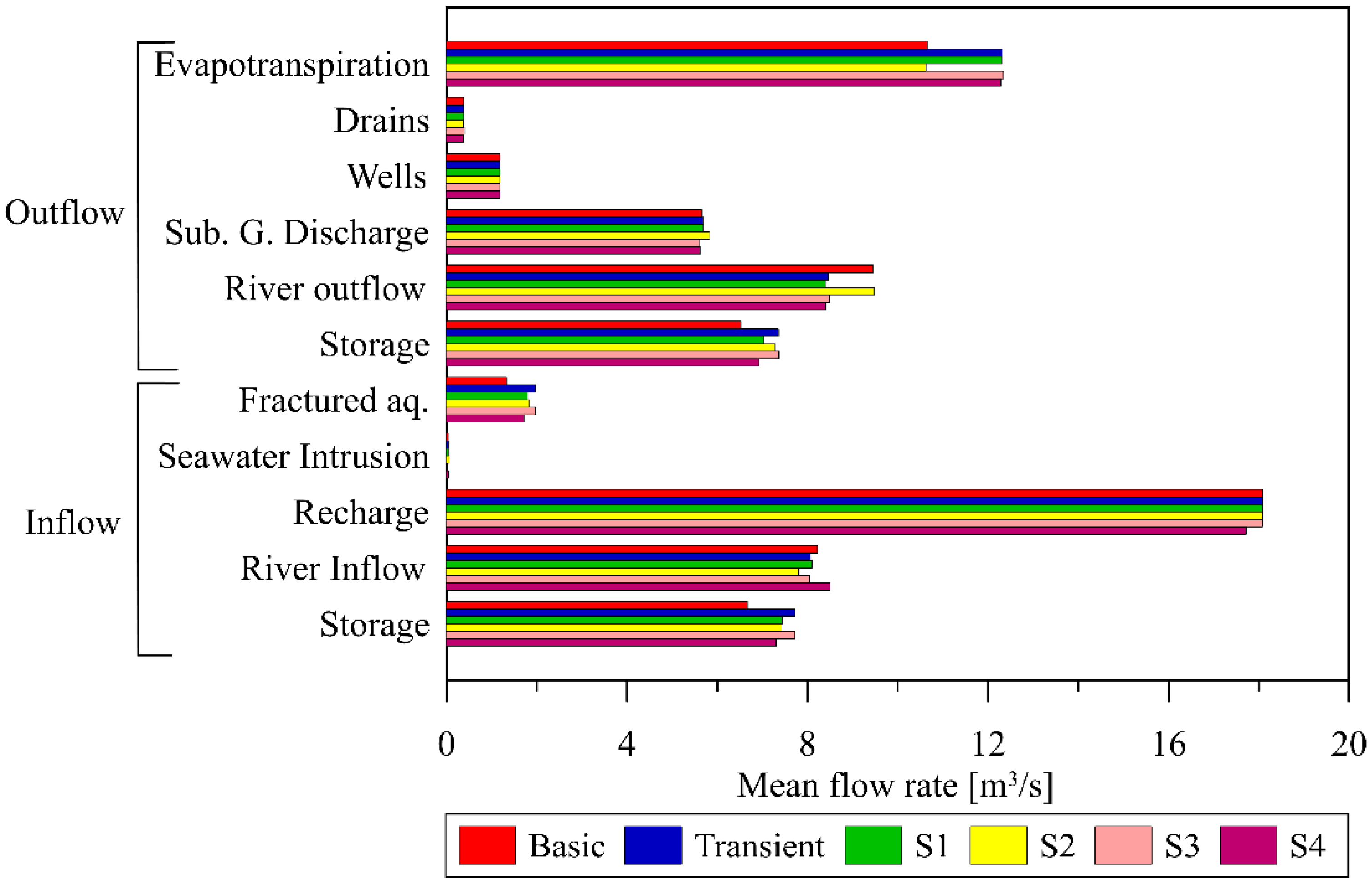
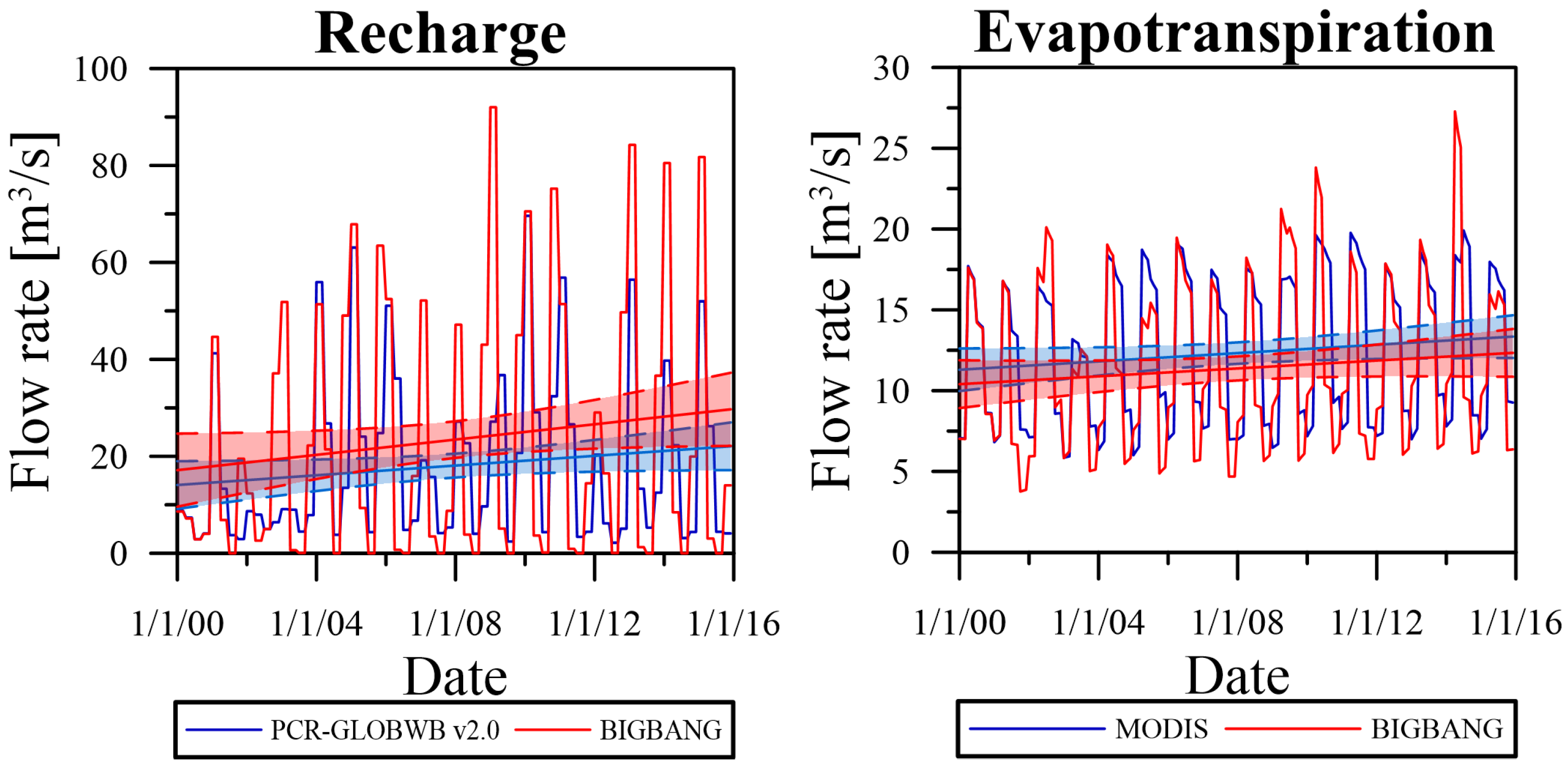
3. Results and Discussion
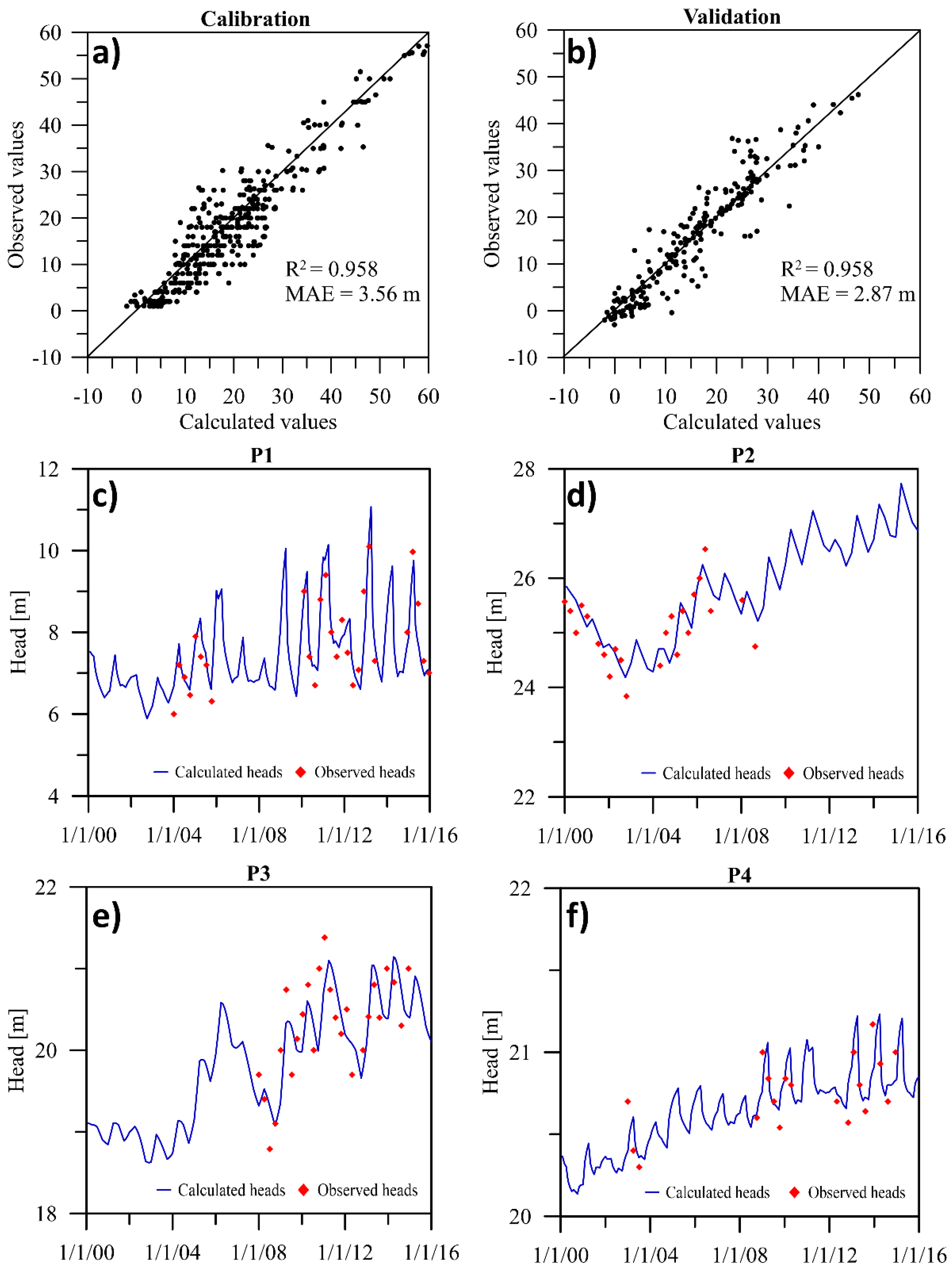
3.1. Flow Model Performance
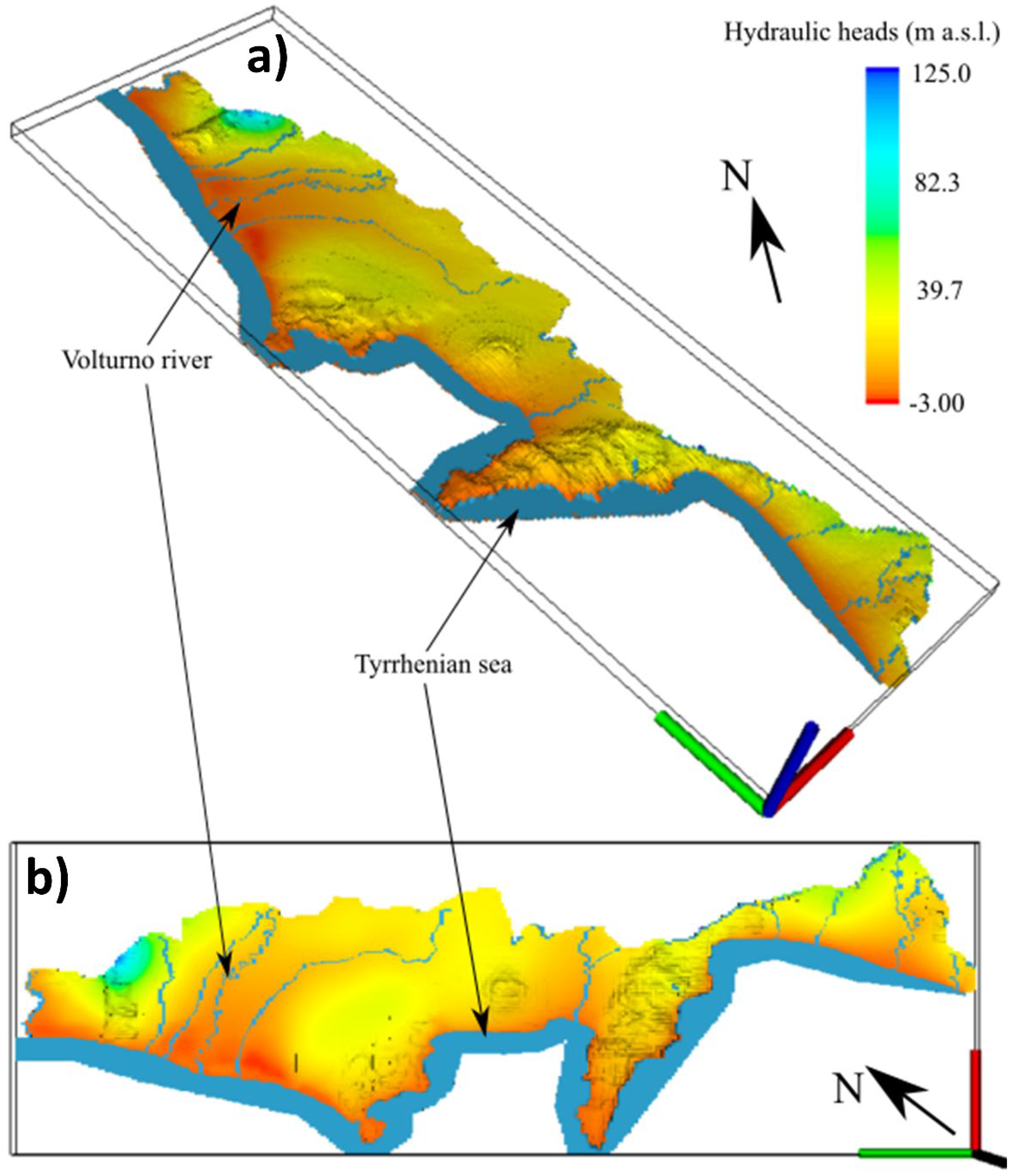
3.2. Water Fluxes Trends and Comparative Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blondel, J.; Aronson, J. Biology and Wildlife of the Mediterranean Region, 1st ed.; Oxford University Press: Oxford, UK, 1999; p. 328. [Google Scholar]
- Lionello, P.; Scarascia, L. The relation between climate change in the Mediterranean region and global warming. Reg. Environ. Chang. 2018, 18, 1481–1493. [Google Scholar] [CrossRef]
- Cramer, W.; Guiot, J.; Fader, M.; Garrabou, J.; Gattuso, J.P.; Iglesias, A.; Xoplaki, E. Climate change and interconnected risks to sustainable development in the Mediterranean. Nat. Clim. Chang. 2018, 8, 972–980. [Google Scholar] [CrossRef] [Green Version]
- Hallegatte, S. Strategies to adapt to an uncertain climate change. Global. Environ. Chang. 2009, 19, 240–247. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V.P., Zhai, A., Pirani, S.L., Connors, C., Péan, S., Berger, N., Caud, Y., Chen, L., Goldfarb, M.I., Gomis, M., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; in press. [Google Scholar] [CrossRef]
- FitzGerald, D.M.; Fenster, M.S.; Argow, B.A.; Buynevich, I.V. Coastal impacts due to sea-level rise. Earth Planet. Sci. 2008, 36, 601–647. [Google Scholar] [CrossRef] [Green Version]
- Carrasco, A.R.; Ferreira, Ó.; Roelvink, D. Coastal lagoons and rising sea level: A review. Earth Sci. 2016, 154, 356–368. [Google Scholar] [CrossRef] [Green Version]
- Benjamin, J.; Rovere, A.; Fontana, A.; Furlani, S.; Vacchi, M.; Inglis, R.H.; Gehrels, R. Late Quaternary sea-level changes and early human societies in the central and eastern Mediterranean Basin: An interdisciplinary review. Quat. Int. 2017, 449, 29–57. [Google Scholar] [CrossRef] [Green Version]
- Erostate, M.; Huneau, F.; Garel, E.; Ghiotti, S.; Vystavna, Y.; Garrido, M.; Pasqualini, V. Groundwater dependent ecosystems in coastal Mediterranean regions: Characterization, challenges and management for their protection. Water Res. 2020, 172, 115461. [Google Scholar] [CrossRef]
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Erturk, A.; Ekdal, A.; Gurel, M.; Karakaya, N.; Guzel, C.; Gonenc, E. Evaluating the impact of climate change on groundwater resources in a small Mediterranean watershed. Sci. Tot. Environ. 2014, 499, 437–447. [Google Scholar] [CrossRef] [PubMed]
- Butscher, C.; Huggenberger, P. Modeling the temporal variability of karst groundwater vulnerability, with implications for climate change. Environ. Sci. Technol. 2009, 43, 1665–1669. [Google Scholar] [CrossRef] [Green Version]
- Oude Essink, G.H.P.; Van Baaren, E.S.; De Louw, P.G. Effects of climate change on coastal groundwater systems: A modeling study in the Netherlands. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Mastrocicco, M.; Gervasio, M.P.; Busico, G.; Colombani, N. Natural and anthropogenic factors driving groundwater resources salinization for agricultural use in the Campania plains (Southern Italy). Sci. Total Environ. 2021, 758, 144033. [Google Scholar] [CrossRef]
- Allen, D.M.; Mackie, D.C.; Wei, M. Groundwater and climate change: A sensitivity analysis for the Grand Forks aquifer, southern British Columbia, Canada. Hydrogeol. J. 2004, 12, 270–290. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, W. A review of regional groundwater flow modeling. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Aghlmand, R.; Abbasi, A. Application of MODFLOW with boundary conditions analyses based on limited available observations: A case study of Birjand plain in East Iran. Water 2019, 11, 1904. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.J.; Johnston, R.H. Regional Aquifer-System Analysis Program of the US Geological Survey, 1978–1992; US Government Printing Office: Denver, CO, USA, 1994; p. 126. [Google Scholar] [CrossRef]
- Coelho, C.D.; Faria, A.C.S.; Marques, E.A.G. Comparative analysis of different boundary conditions and their influence on numerical hydrogeological modeling of Palmital watershed, southeast Brazil. J. Hydrol. 2017, 12, 210–219. [Google Scholar] [CrossRef]
- Bastani, M.; Harter, T. Effects of upscaling temporal resolution of groundwater flow and transport boundary conditions on the performance of nitrate-transport models at the regional management scale. Hydrogeol. J. 2020, 28, 1299–1322. [Google Scholar] [CrossRef] [Green Version]
- Cushman, J.H.; Bennethum, L.S.; Hu, B.X. A primer on upscaling tools for porous media. Adv. Water Resour. 2002, 25, 1043–1067. [Google Scholar] [CrossRef]
- Dentz, M.; Le Borgne, T.; Englert, A.; Bijeljic, B. Mixing, spreading and reaction in heterogeneous media: A brief review. J. Contam. Hydrol. 2011, 120, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Scheibe, T.D.; Murphy, E.M.; Chen, X.; Rice, A.K.; Carroll, K.C.; Palmer, B.J.; Wood, B.D. An analysis platform for multiscale hydrogeologic modeling with emphasis on hybrid multiscale methods. Groundwater 2015, 53, 38–56. [Google Scholar] [CrossRef] [PubMed]
- Hellwig, J.; de Graaf, I.E.M.; Weiler, M.; Stahl, K. Large-scale assessment of delayed groundwater responses to drought. Water Resour. Res. 2020, 56, e2019WR025441. [Google Scholar] [CrossRef] [Green Version]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.A.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef] [Green Version]
- Rau, G.C.; Cuthbert, M.O.; Post, V.E.A.; Daniel Schweizer, D.; Acworth, R.I.; Andersen, M.S.; Blum, P.; Carrara, E.; Rasmussen, T.C.; Ge, S. Future-proofing hydrogeology by revising groundwater monitoring practice. Hydrogeol. J. 2020, 28, 2963–2969. [Google Scholar] [CrossRef]
- De Vita, P.; Fusco, F.; Tufano, R.; Cusano, D. Seasonal and event-based hydrological and slope stability modeling of pyroclastic fall deposits covering slopes in Campania (Southern Italy). Water 2018, 10, 1140. [Google Scholar] [CrossRef] [Green Version]
- Corniello, A.; Ducci, D.; Ruggieri, G.; Iorio, M. Complex groundwater flow circulation in a carbonate aquifer: Mount Massico (Campania Region, Southern Italy). Synergistic hydrogeological understanding. J. Geochem. Explor. 2018, 190, 253–264. [Google Scholar] [CrossRef]
- Mastrocicco, M.; Busico, G.; Colombani, N.; Vigliotti, M.; Ruberti, D. Modelling actual and future seawater intrusion in the Variconi coastal wetland (Italy) due to climate and landscape changes. Water 2019, 11, 1502. [Google Scholar] [CrossRef] [Green Version]
- Lancia, M.; Petitta, M.; Zheng, C.; Saroli, M. Hydrogeological insights and modelling for sustainable use of a stressed carbonate aquifer in the Mediterranean area: From passive withdrawals to active management. J. Hydrol. 2020, 32, 100749. [Google Scholar] [CrossRef]
- Brancaccio, L.; Cinque, A.; Romano, P.; Rosskopf, C.; Russo, F.; Santangelo, N.; Santo, A. Geomorphology and neotectonic evolution of a sector of the Tyrrhenian flank of the southern Apennines (Region of Naples, Italy). Z. Geomorphol. 1991, 82, 47–58. [Google Scholar]
- Pappone, G.; Alberico, I.; Amato, V.; Aucelli, P.P.C.; Di Paola, G. Recent evolution and present-day conditions of the Campanian Coastal plains (South Italy): The case history of Sele River Coastal plain. WIT Trans. Ecol. Envir. 2011, 149, 15–27. [Google Scholar] [CrossRef]
- Ruberti, D.; Vigliotti, M. Land use and landscape pattern changes driven by land reclamation in a coastal area: The case of Volturno delta plain, Campania region, southern Italy. Environ. Earth Sci. 2017, 76, 694. [Google Scholar] [CrossRef]
- ISPRA. National Geological Database. 2021. Available online: http://sgi2.isprambiente.it/viewersgi2/ (accessed on 10 October 2021).
- Corniello, A.; Ducci, D. Hydrogeochemical characterization of the main aquifer of the “Litorale Domizio-Agro Aversano NIPS” (Campania—Southern Italy). J. Geochem. Explor. 2014, 137, 1–10. [Google Scholar] [CrossRef]
- Allocca, V.; Coda, S.; De Vita, P.; Di Rienzo, B.; Ferrara, L.; Giarra, A.; Mangoni, O.; Stellato, L.; Trifuoggi, M.; Arienzo, M. Hydrogeological and hydrogeochemical study of a volcanic-sedimentary coastal aquifer in the archaeological site of Cumae (Phlegraean Fields, southern Italy). J. Geochem. Explor. 2018, 185, 105–115. [Google Scholar] [CrossRef]
- Stellato, L.; Coda, S.; Arienzo, M.; De Vita, P.; Di Rienzo, B.; D’Onofrio, A.; Ferrara, L.; Marzaioli, F.; Trifuoggi, M.; Allocca, V. Natural and anthropogenic groundwater contamination in a coastal volcanic-sedimentary aquifer: The case of the archaeological site of Cumae (Phlegraean Fields, Southern Italy). Water 2020, 12, 3463. [Google Scholar] [CrossRef]
- AppEEARS Team. Application for Extracting and Exploring Analysis Ready Samples (AppEEARS); Ver. 2.54.1. NASA EOSDIS Land Processes Distributed Active Archive Center (LP DAAC); USGS/Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2020. Available online: https://lpdaacsvc.cr.usgs.gov/appeears (accessed on 10 October 2021).
- Running, S.; Mu, Q.; Zhao, M.; Moreno, A. MOD16A2GF MODIS/Terra Net Evapotranspiration Gap-Filled 8-Day L4 Global 500m SIN Grid V006. NASA EOSDIS Land Processes DAAC. 2019. Available online: https://doi.org/10.5067/MODIS/MOD16A2GF.006 (accessed on 10 October 2021).
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Rem. Sens Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Shah, N.; Nachabe, M.; Ross, M. Extinction depth and evapotranspiration from ground water under selected land covers. Groundwater 2007, 45, 329–338. [Google Scholar] [CrossRef]
- Sutanudjaja, E.H.; van Beek, R.; Wanders, N.; Wada, Y.; Bosmans, J.H.C.; Drost, N.; van der Ent, R.J.; de Graaf, I.E.M.; Hoch, J.M.; de Jong, K.; et al. PCR-GLOBWB 2: A 5 arcmin global hydrological and water resources model. Geosci. Model Dev. 2018, 11, 2429–2453. [Google Scholar] [CrossRef] [Green Version]
- Harbaugh, A.W. MODFLOW-2005, the US Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; U.S. Geological Survey Techniques and Methods 6-A16; US Department of the Interior; US Geological Survey: Reston, VA, USA, 2005; p. 253. [Google Scholar]
- Reimann, T.; Hill, M.E. MODFLOW-CFP: A New Conduit Flow Process for MODFLOW-2005. Groundwater 2009, 47, 321–325. [Google Scholar] [CrossRef]
- Hill, M.C. The practical use of simplicity in developing ground water models. Groundwater 2006, 44, 775–781. [Google Scholar] [CrossRef]
- Doherty, J. PEST-Model-Independent Parameter Estimation. Version 12. Watermark Computing. Australia. 2010. Available online: http://www.pesthomepage.org/ (accessed on 10 October 2021).
- De Vita, P.; Allocca, V.; Celico, F.; Fabbroncino, S.; Cesaria, M.; Monacelli, G.; Musilli, I.; Piscopo, V.; Scalise, A.R.; Summa, G.; et al. Hydrogeology of continental southern Italy. J. Maps 2018, 14, 230–241. [Google Scholar] [CrossRef] [Green Version]
- Russo, G.; Viggiani, C.; Viggiani, G. Geotechnical design and construction issues for Lines 1 and 6 of the Naples Underground/Geotechnische Planung und Ausführung der U-Bahnlinien 1 und 6 in Neapel. Geomech. Tunnelbau 2012, 5, 300–311. [Google Scholar] [CrossRef]
- de Graaf, I.E.; van Beek, R.L.; Gleeson, T.; Moosdorf, N.; Schmitz, O.; Sutanudjaja, E.H.; Bierkens, M.F. A global-scale two-layer transient groundwater model: Development and application to groundwater depletion. Adv. Water Resour. 2017, 102, 53–67. [Google Scholar] [CrossRef]
- Fan, Y.; Li, H.; Miguez-Macho, G. Global patterns of groundwater table depth. Science 2013, 339, 940–943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Braca, G.; Bussettini, M.; Ducci, D.; Lastoria, B.; Mariani, S. Evaluation of national and regional groundwater resources under climate change scenarios using a GIS-based water budget procedure. Rend. Fis. Acc. Lincei 2019, 30, 109–123. [Google Scholar] [CrossRef]
- Brakkee, E.; Van Huijgevoort, M.H.; Bartholomeus, R.P. Improved understanding of regional groundwater drought development through time series modelling: The 2018–2019 drought in the Netherlands. Hydrol. Earth Syst. Sci. 2022, 26, 551–569. [Google Scholar] [CrossRef]
- Ruggieri, G.; Allocca, V.; Borfecchia, F.; Cusano, D.; Marsiglia, P.; De Vita, P. Testing Evapotranspiration Estimates Based on MODIS Satellite Data in the Assessment of the Groundwater Recharge of Karst Aquifers in Southern Italy. Water 2021, 13, 118. [Google Scholar] [CrossRef]
- Allocca, V.; Manna, F.; De Vita, P. Estimating annual groundwater recharge coefficient for karst aquifers of the southern Apennines (Italy). Hydrol. Earth Syst. Sci. 2014, 18, 803–817. [Google Scholar] [CrossRef] [Green Version]
- Allocca, V.; De Vita, P.; Manna, F.; Nimmo, J.R. Groundwater recharge assessment at local and episodic scale in a soil mantled perched karst aquifer in southern Italy. J. Hydrol. 2015, 529, 843–853. [Google Scholar] [CrossRef]
- De Vita, P.; Allocca, V.; Manna, F.; Fabbrocino, S. Coupled decadal variability of the North Atlantic Oscillation, regional rainfall and karst spring discharges in the Campania region (southern Italy). Hydrol. Earth Syst. Sci. 2012, 16, 1389–1399. [Google Scholar] [CrossRef] [Green Version]
- Colombani, N.; Gaiolini, M.; Busico, G.; Postacchini, M. Quantifying the impact of evapotranspiration at the aquifer scale via groundwater modelling and MODIS data. Water 2021, 13, 950. [Google Scholar] [CrossRef]
- Lehr, C.; Lischeid, G. Efficient screening of groundwater head monitoring data for anthropogenic effects and measurement errors. Hydrol. Earth Syst. Sci. 2020, 24, 501–513. [Google Scholar] [CrossRef] [Green Version]
| Dataset | Parameter | Repository | URL |
|---|---|---|---|
| Soil | Grain size distribution | ISRIC | https://maps.isric.org/ accessed on 17 July 2022 |
| Geology | Aquifer thickness | ISPRA | http://sgi2.isprambiente.it/viewersgi2 accessed on 17 July 2022 |
| Hydrogeology | Hydraulic conductivity | ISPRA | http://sgi2.isprambiente.it/viewersgi2 accessed on 17 July 2022 |
| CORINE Land Cover | Land use | COPERNICUS | https://land.copernicus.eu/pan-european/corine-land-cover accessed on 17 July 2022 |
| SEALEVELEURPHYL4MY008068 | Sea levels | CMEMS | https://doi.org/10.48670/moi-00141 accessed on 13 June 2022 |
| Hydrometric station dependent | Rivers stages | CFM | http://centrofunzionale.regione.campania.it/#/pages/sensori/archivio-idrometrici accessed on 17 July 2022 |
| MYD16A3GF | Evapotranspiration | MODIS | https://doi.org/10.5067/MODIS/MOD16A2GF.006 accessed on 10 May 2022 |
| PCRGLOBWB 2 | Recharge | UU-HYDRO | https://github.com/UU-Hydro/PCR-GLOBWB_model accessed on 12 June 2022 |
| BIGBANG40 | Evapotranspiration | ISPRA | https://groupware.sinanet.isprambiente.it/bigbang-data/library/bigbang40/grids/it_evapotraspirazione_ae accessed on 17 July 2022 |
| BIGBANG40 | Recharge | ISPRA | https://groupware.sinanet.isprambiente.it/bigbang-data/library/bigbang40/grids/it_ricarica_degli_acquiferi_gr accessed on 17 July 2022 |
| Material | Ss (m−1) | Sy (-) |
|---|---|---|
| Clayey and calcareous clayey units | 0.001 | 0.2 |
| Debris, alluvial, fluviolacusters and fluvioglacial deposits | 1 × 10−4 | 0.33 |
| Lavas, ignibrites, pyroclastics | 1 × 10−5 | 0.21 |
| Organogenic, neritic, and platform limestone | 1 × 10−5 | 0.14 |
| River | Criv (m2/s) | |
| Garigliano | from 0.021 to 0.235 | |
| Savone | from 0.017 to 0.058 | |
| Agnena | from 0.001 to 0.033 | |
| Volturno | from 0.009 to 0.044 | |
| Regi Lagni | from 0.007 to 0.072 | |
| Sarno | from 0.007 to 0.040 | |
| Picentino | from 0.009 to 0.011 | |
| Tusciano | from 0.011 to 0.019 | |
| Sele | from 0.014 to 0.116 | |
| Calore | from 0.060 to 0.086 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaiolini, M.; Colombani, N.; Busico, G.; Rama, F.; Mastrocicco, M. Impact of Boundary Conditions Dynamics on Groundwater Budget in the Campania Region (Italy). Water 2022, 14, 2462. https://doi.org/10.3390/w14162462
Gaiolini M, Colombani N, Busico G, Rama F, Mastrocicco M. Impact of Boundary Conditions Dynamics on Groundwater Budget in the Campania Region (Italy). Water. 2022; 14(16):2462. https://doi.org/10.3390/w14162462
Chicago/Turabian StyleGaiolini, Mattia, Nicolò Colombani, Gianluigi Busico, Fabrizio Rama, and Micòl Mastrocicco. 2022. "Impact of Boundary Conditions Dynamics on Groundwater Budget in the Campania Region (Italy)" Water 14, no. 16: 2462. https://doi.org/10.3390/w14162462






