A Peridynamic Differential Operator-Based Model for Quantifying Spatial Non-Local Transport Behavior of Pollutants in Heterogeneous Media
Abstract
:1. Introduction
2. Model Development
2.1. A Brief Review of PDDO
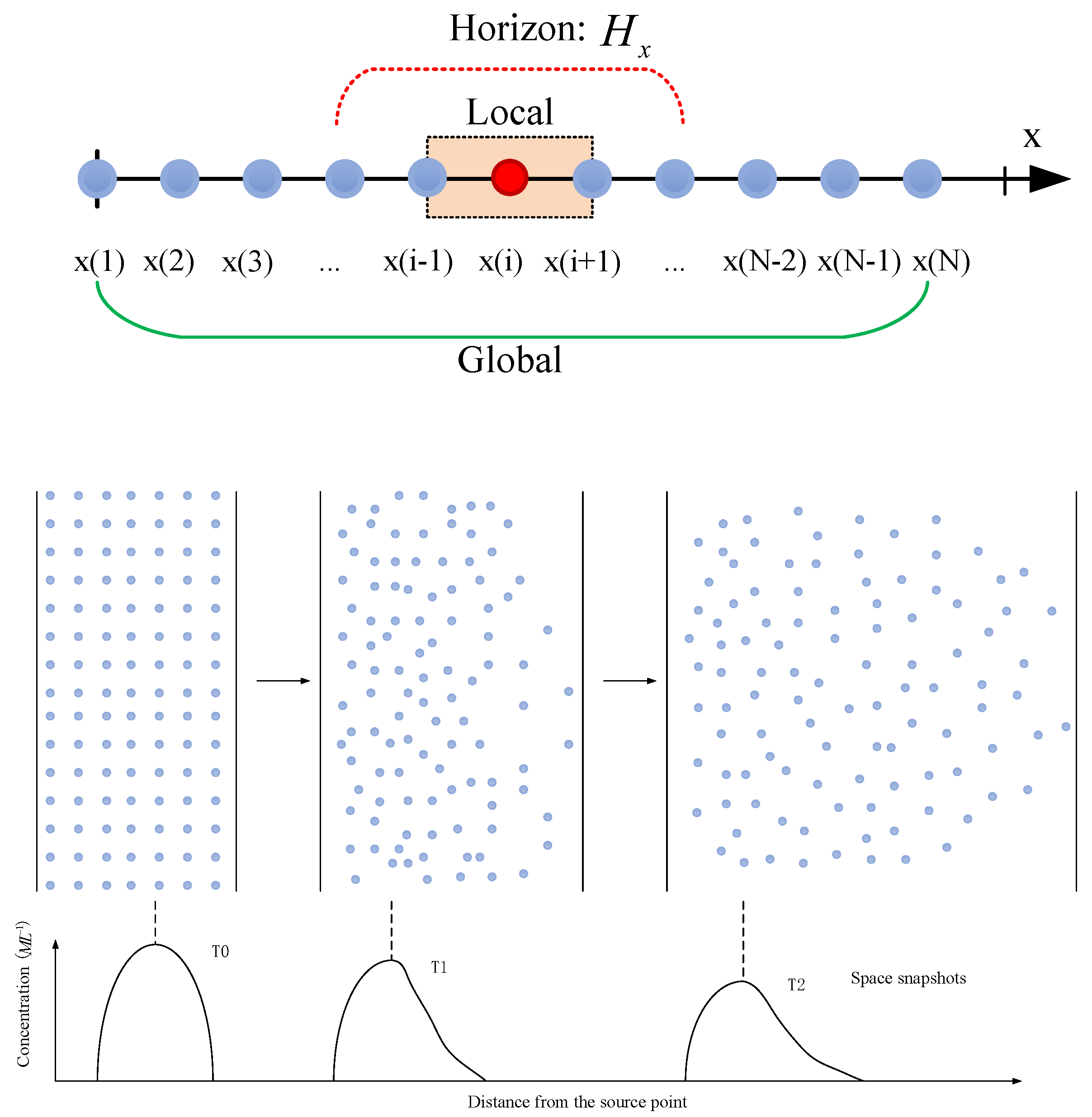
2.2. PDDO-Based Model
2.3. Numerical Algorithm of the PDDO-Based Model
3. Results
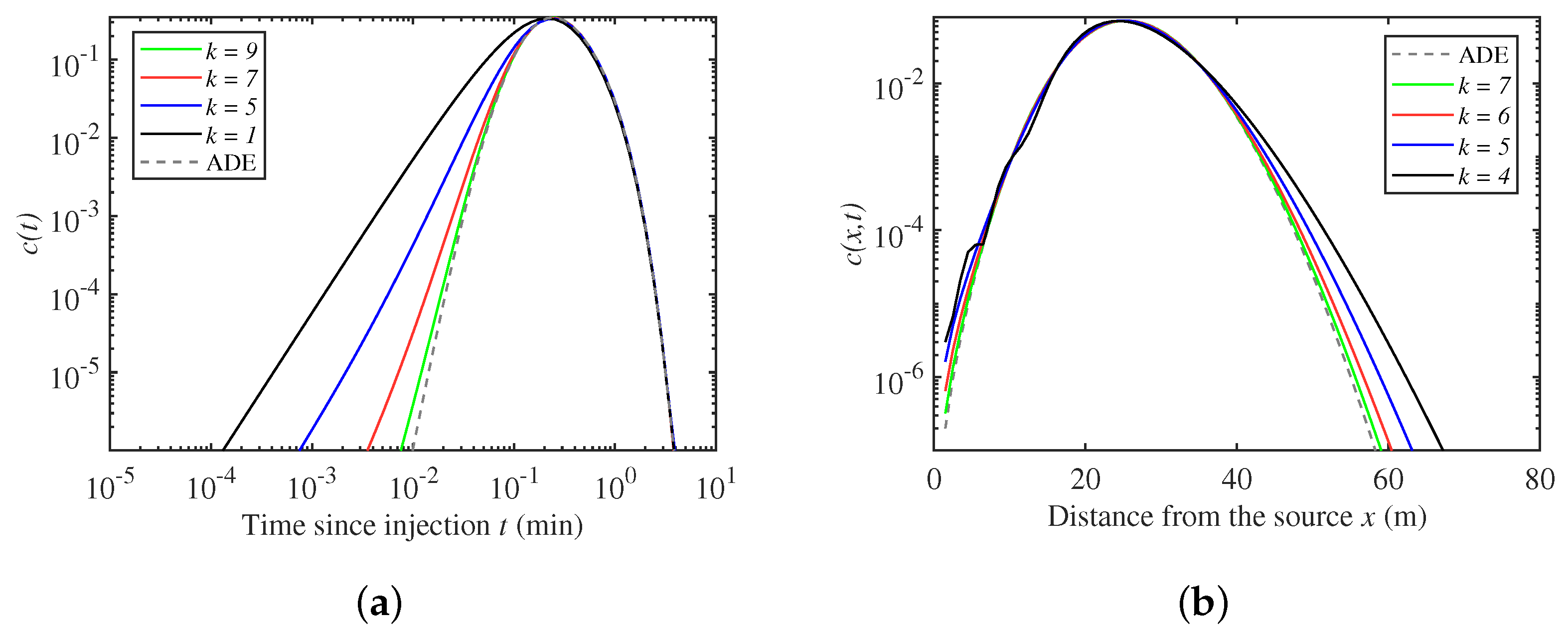
3.1. Analytical Solution of PDDO Model
3.2. One-Dimensional Results of the PDDO-Based Model
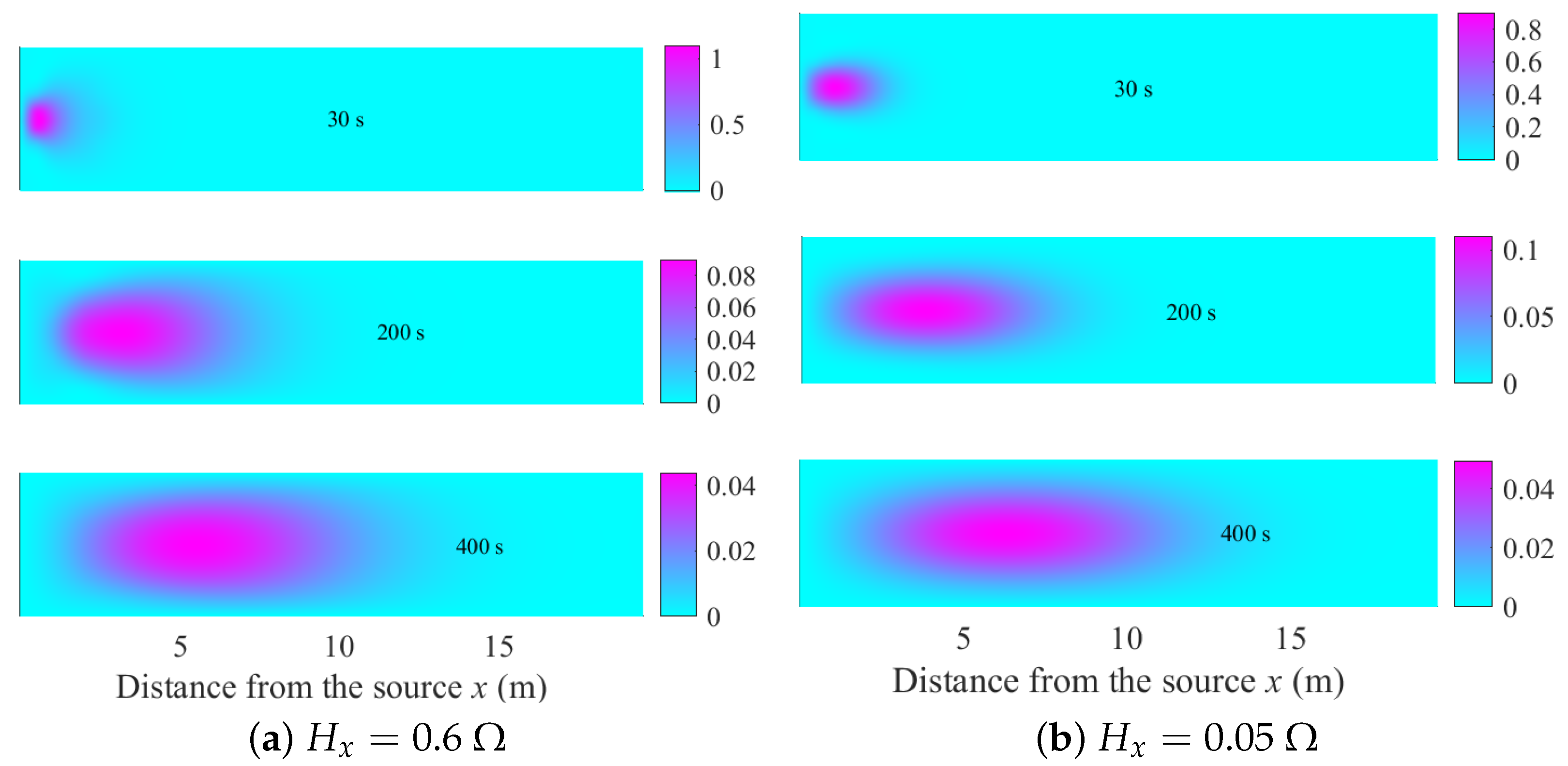
3.3. Two-Dimensional Results of the PDDO-Based Model
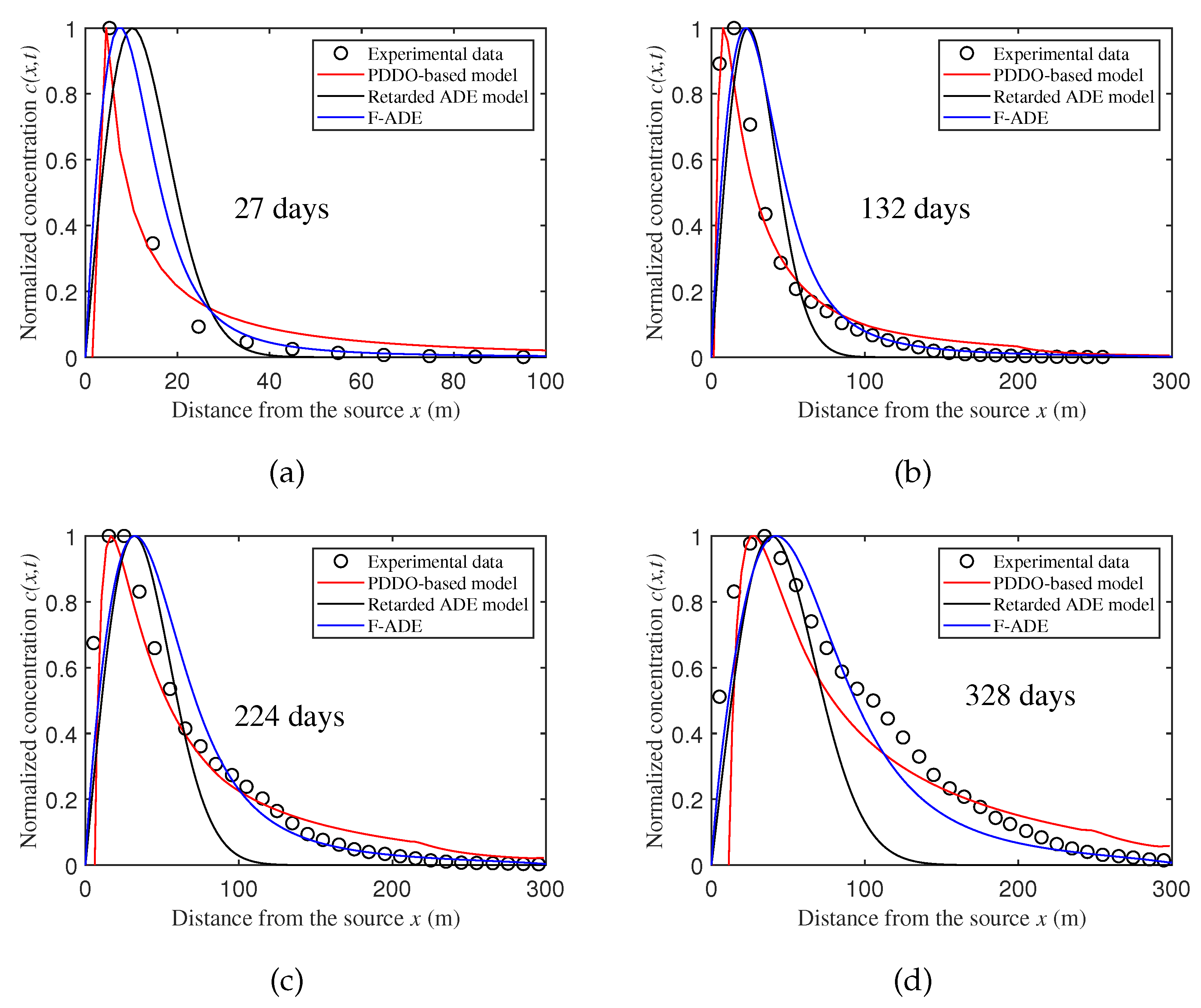
3.4. Applications
4. Discussion
Diffusion Regime of the PDDO-Based Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodarzi, D.; Mohammadian, A.; Pearson, J.; Abolfathi, S. Numerical modelling of hydraulic efficiency and pollution transport in waste stabilization ponds. Ecol. Eng. 2022, 182, 106702. [Google Scholar] [CrossRef]
- Allen, D.T.; Cohen, Y.; Kaplan, I.R. Intermedia Pollutant Transport: Modeling and Field Measurements; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Goodarzi, D.; Abolfathi, S.; Borzooei, S. Modelling solute transport in water disinfection systems: Effects of temperature gradient on the hydraulic and disinfection efficiency of serpentine chlorine contact tanks. J. Water Process. Eng. 2020, 37, 101411. [Google Scholar] [CrossRef]
- Qi, Y.; Zhou, P.; Wang, J.; Ma, Y.; Wu, J.; Su, C. Groundwater Pollution Model and Diffusion Law in Ordovician Limestone Aquifer Owe to Abandoned Red Mud Tailing Pit. Water 2022, 14, 1472. [Google Scholar] [CrossRef]
- Ghiasi, B.; Noori, R.; Sheikhian, H.; Zeynolabedin, A.; Sun, Y.; Jun, C.; Hamouda, M.; Bateni, S.M.; Abolfathi, S. Uncertainty quantification of granular computing-neural network model for prediction of pollutant longitudinal dispersion coefficient in aquatic streams. Sci. Rep. 2022, 12, 4610. [Google Scholar] [CrossRef]
- Valari, M.; Menut, L. Transferring the heterogeneity of surface emissions to variability in pollutant concentrations over urban areas through a chemistry-transport model. Atmos. Environ. 2010, 44, 3229–3238. [Google Scholar] [CrossRef]
- Ho, Q.N.; Fettweis, M.; Spencer, K.L.; Lee, B.J. Flocculation with heterogeneous composition in water environments: A review. Water Res. 2022, 213, 118147. [Google Scholar] [CrossRef]
- Kachiashvili, K.; Gordeziani, D.; Melikdzhanian, D. Mathematical models of Pollutants Transport with Allowance for Many Affecting Pollution Sources. Proceeding of the Urban Drainage Modeling Symposium, Orlando, FL, USA, 20–24 May 2001; pp. 692–702. [Google Scholar]
- Zhang, Y.; Sun, H.; Stowell, H.H.; Zayernouri, M.; Hansen, S.E. A review of applications of fractional calculus in Earth system dynamics. Chaos Solitons Fractals 2017, 102, 29–46. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional calculus: Theory and applications. Mathematics 2018, 6, 145. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Ke, S.; Zhang, S.; Shao, J.; Chen, H. Reactive transport modeling of pollutants in heterogeneous layered paddy soils: A) Cadmium migration and vertical distributions. J. Contam. Hydrol. 2020, 235, 103735. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Kitanidis, P.K.; Roberts, P.V. Analysis of one-dimensional solute transport through porous media with spatially variable retardation factor. Water Resour. Res. 1990, 26, 437–446. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Kitanidis, P.K.; Roberts, P.V. Macrodispersion of sorbing solutes in heterogeneous porous formations with spatially periodic retardation factor and velocity field. Water Resour. Res. 1992, 28, 1517–1529. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Kitanidis, P.K.; Roberts, P.V. Generalized Taylor-Aris moment analysis of the transport of sorbing solutes through porous media with spatially-periodic retardation factor. Transp. Porous Media 1992, 7, 163–185. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Impact of spatially variable collision efficiency on the transport of biocolloids in geochemically heterogeneous porous media. Water Resour. Res. 2018, 54, 3841–3862. [Google Scholar] [CrossRef]
- Chakraborty, J.; Das, S. Molecular perspectives and recent advances in microbial remediation of persistent organic pollutants. Environ. Sci. Pollut. Res. 2016, 23, 16883–16903. [Google Scholar] [CrossRef] [PubMed]
- Yin, M.; Zhang, Y.; Ma, R.; Tick, G.R.; Bianchi, M.; Zheng, C.; Wei, W.; Wei, S.; Liu, X. Super-diffusion affected by hydrofacies mean length and source geometry in alluvial settings. J. Hydrol. 2020, 582, 124515. [Google Scholar] [CrossRef]
- Sun, L.; Qiu, H.; Wu, C.; Niu, J.; Hu, B.X. A review of applications of fractional advection–dispersion equations for anomalous solute transport in surface and subsurface water. Wiley Interdiscip. Rev. Water 2020, 7, e1448. [Google Scholar] [CrossRef]
- Zilitinkevich, S. Non-local turbulent transport: Pollution dispersion aspects of coherent structure of connective flows. WIT Trans. Ecol. Environ. 1970, 9, 53–60. [Google Scholar]
- Mihailović, D.T.; Alapaty, K.; Sakradžija, M. Development of a nonlocal convective mixing scheme with varying upward mixing rates for use in air quality and chemical transport models. Environ. Sci. Pollut. Res. Int. 2008, 15, 296–302. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, D.; Yin, M.; Sun, H.; Wei, W.; Li, S.; Zheng, C. Nonlocal transport models for capturing solute transport in one-dimensional sand columns: Model review, applicability, limitations and improvement. Hydrol. Process. 2020, 34, 5104–5122. [Google Scholar] [CrossRef]
- Masciopinto, C.; Passarella, G.; Caputo, M.C.; Masciale, R.; De Carlo, L. Hydrogeological Models of Water Flow and Pollutant Transport in Karstic and Fractured Reservoirs. Water Resour. Res. 2021, 57, e2021WR029969. [Google Scholar] [CrossRef]
- Madenci, E.; Barut, A.; Futch, M. Peridynamic differential operator and its applications. Comput. Methods Appl. Mech. Eng. 2016, 304, 408–451. [Google Scholar] [CrossRef]
- Madenci, E.; Barut, A.; Dorduncu, M. Peridynamic Differential Operator for Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef] [Green Version]
- Madenci, E.; Roy, P.; Behera, D. Advances in Peridynamics; Spring: Tucson, AZ, USA, 2022. [Google Scholar]
- Clark, M.M. Transport Modeling for Environmental Engineers and Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Draxler, R.R.; Taylor, A.D. Horizontal dispersion parameters for long-range transport modeling. J. Appl. Meteorol. Climatol. 1982, 21, 367–372. [Google Scholar] [CrossRef] [Green Version]
- Nezhad, M.M.; Javadi, A.A. Stochastic finite-element approach to quantify and reduce uncertainty in pollutant transport modeling. J. Hazard. Toxic Radioact. Waste 2011, 15, 208–215. [Google Scholar] [CrossRef]
- Chen, J.; Zhuang, B.; Chen, Y.; Cui, B. Diffusion control for a tempered anomalous diffusion system using fractional-order PI controllers. ISA Trans. 2018, 82, 94–106. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Li, Z.; Zhang, Y.; Chen, W. Fractional and fractal derivative models for transient anomalous diffusion: Model comparison. Chaos Solitons Fractals 2017, 102, 346–353. [Google Scholar] [CrossRef]
- Egan, B.A.; Mahoney, J.R. Numerical modeling of advection and diffusion of urban area source pollutants. J. Appl. Meteorol. Climatol. 1972, 11, 312–322. [Google Scholar] [CrossRef] [Green Version]
- Union, J.I.G. Advection diffusion equation models in near-surface geophysical and environmental sciences. J. Ind. Geophys. Union 2013, 17, 117–127. [Google Scholar]
- Buske, D.; Vilhena, M.; Moreira, D.; Tirabassi, T. An analytical solution of the advection-diffusion equation considering non-local turbulence closure. Environ. Fluid Mech. 2007, 7, 43–54. [Google Scholar] [CrossRef]
- Farhane, M.; Alehyane, O.; Souhar, O. Three-dimensional analytical solution of the advection-diffusion equation for air pollution dispersion. Anziam J. 2022, 64, 40–53. [Google Scholar]
- Laaouaoucha, D.; Farhane, M.; Essaouini, M.; Souhar, O. Analytical model for the two-dimensional advection-diffusion equation with the logarithmic wind profile in unstable conditions. Int. J. Environ. Sci. Technol. 2022, 19, 6825–6832. [Google Scholar] [CrossRef]
- Li, Z.; Sun, H.; Sibatov, R.T. An investigation on continuous time random walk model for bedload transport. Fract. Calc. Appl. Anal. 2019, 22, 1480–1501. [Google Scholar] [CrossRef]
- Hilfer, R. Fractional diffusion based on Riemann-Liouville fractional derivatives. J. Phys. Chem. B 2000, 104, 3914–3917. [Google Scholar] [CrossRef] [Green Version]
- Gu, X.; Zhang, Q.; Madenci, E. Refined bond-based peridynamics for thermal diffusion. Eng. Comput. 2019, 36, 2557–2587. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Das, B.S. Moment Analysis for Subsurface Hydrologic Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]


| Time (Days) | (m/day) | (m/day) | (m/day) | (m/day) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 27 | 60 | ||||||||
| 132 | 0.018 | 10 | 1.4 | 10 | 0.18 | 20 | 10 | 1 | 65 |
| 224 | 70 | ||||||||
| 328 | 80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Gu, X.; Zhang, Q. A Peridynamic Differential Operator-Based Model for Quantifying Spatial Non-Local Transport Behavior of Pollutants in Heterogeneous Media. Water 2022, 14, 2455. https://doi.org/10.3390/w14162455
Li T, Gu X, Zhang Q. A Peridynamic Differential Operator-Based Model for Quantifying Spatial Non-Local Transport Behavior of Pollutants in Heterogeneous Media. Water. 2022; 14(16):2455. https://doi.org/10.3390/w14162455
Chicago/Turabian StyleLi, Tianyi, Xin Gu, and Qing Zhang. 2022. "A Peridynamic Differential Operator-Based Model for Quantifying Spatial Non-Local Transport Behavior of Pollutants in Heterogeneous Media" Water 14, no. 16: 2455. https://doi.org/10.3390/w14162455
APA StyleLi, T., Gu, X., & Zhang, Q. (2022). A Peridynamic Differential Operator-Based Model for Quantifying Spatial Non-Local Transport Behavior of Pollutants in Heterogeneous Media. Water, 14(16), 2455. https://doi.org/10.3390/w14162455






