1. Introduction
An excess of nutrients such as phosphates and nitrates in drinking water is undesirable since they are responsible for the eutrophication phenomenon, that is, the growth of algae and aquatic plants that are considered a type of water pollution and affect the quality of aquatic resources [
1,
2,
3,
4,
5,
6,
7]. The removal of these nutrients from water is carried out using physical, chemical, and biological treatment methods. In general, these techniques consume a large amount of chemicals, are expensive, require sludge handling and regeneration processes, and are not applicable in low-income communities [
6,
7,
8].
Currently, water treatment requires new pollutant-removal techniques and, with it, the search for new natural materials with adsorbent and refractory properties that could be used to create granular media for potable and residual water treatments. These new materials should be equally inexpensive, easily accessible, malleable, and most importantly, be environmentally friendly.
Oxidic lithological materials (MLOs) belong to the terrestrial lithosphere. They cannot be classified as “soils” due to their monophasic profile. They are basically composed of amphoteric aluminum and iron oxides as well as Mn and Ti and some other crystalline phases, with chemical and physical properties that allow for use in the preparation of calcined adsorbent media with good thermal and mechanical resistance [
9]. These oxides have surfaces suitable for ion adsorption due to their pH-dependent charge variability [
8,
10,
11,
12]. The oxidic groups can be deprotonated or protonated, depending on medium pH, thus modifying the surface charges of the particles, and are able to generate the adsorption of both cations and anions, as presented in the following reactions [
12,
13,
14,
15,
16]:
The chemical and mineralogical characteristics of these materials have previously been reported in the literature [
9,
12,
14,
16,
17], evidencing the richness in metals that form the amphoteric oxides of variable charge and that of other minerals that confer refractory and mechanical resistance properties, allowing for the manufacture of these adsorbent substrates.
These materials have been used for the manufacture of adsorbent beds and for water-softening processes via the adsorption of Ca
+2 and Mg
+2 ions [
11,
18] which participate in a cationic exchange reaction. The adsorption of heavy metal ions such as Cu and Zn has been studied previously [
9,
12,
13,
14,
19,
20]. These metallic species participate in a specific adsorption reaction called chemisorption. The adsorption of anions on these calcined substrates has also been studied, specifically the adsorption of dichromate [
21], on similar substrates made with lithological materials with different mineralogy.
Building on the research identified above, the aim of this study was to evaluate the adsorption of phosphate and nitrate ions on a calcined adsorbent substrate of variable charge made of oxidic lithological material.
2. Materials and Methods
2.1. Oxidic Lithological Material
The oxidic lithological material was collected from a natural deposit (UTM coordinates 252020.60 E, 944936.78 N). The samples were collected manually with the help of pallets and pickaxes. They were kept in sealed bags and taken to the laboratory. A crushing process was applied to a subsample using a rubber hammer so as not to destroy the mineral structures—then sieved with a Tyler (Mentor, OH, USA) sieve, to obtain three particle-size fractions of 850 μm (coarse fraction), 425 μm (medium fraction), and 250 μm (fine fraction).
2.2. Chemical Analysis
The pH was measured in a 1:2.5 mass ratio of soil:water, according to the French standard AFNOR NF X-31-103 [
22] by mixing 10 g of the sample with 25 mL of distilled water. The mixture was stirred for one hour, then let to settle for 30 min. The pH of the supernatant was measured using an OAKTON (Vernon Hills, IL, USA) eco Test pH2 model pH tester, previously calibrated with buffer solutions of pH 4 and 7. The cation exchange capacity (CEC) was estimated in cmol (+) kg
−1, from the amount of cations adsorbed by the soil from a neutral solution of ammonium acetate. The exchange sites of the lithological material were saturated with an excess of ammonium acetate, then washed with alcohol to remove the excess. The remaining ammonium occupying the change sites was displaced by leaching the soil with a NaCl solution, which was quantified in the extract by titration with NaOH [
23]. Therefore, the CEC was calculated using Equation (1):
The electrical conductivity (EC) was determined in a 1:2.5 mass ratio of soil:water [
22], by weighing 20 g of dry soil and mixing it with 50 mL of distilled water. Afterwards, it was stirred for one hour, and then the suspension was left to settle for half an hour. The supernatant was extracted and filtered. Finally, the temperature and conductivity of the filtrated solution was measured using an OAKTON (Vernon Hills, IL, USA) CON 510 model conductivity meter.
The specific surface area and average pore volume of the calcined materials were determined using N2 adsorption–desorption measurements at a temperature of −196 °C, previously treated at 400 °C under vacuum for 12 h, using a Micromeritics ASAP 2010 Surface Area and Porosity Analyzer (Norcross, GA, USA).
The mineralogical phases were determined via X-ray diffraction using a Malvern Panalytical B.V. Diffractometer model CUBIX3 (Almelo, Overijssel, The Netherlands). The powder samples were processed on sample holders at room temperature. The diffractograms were taken using Cu-Kα radiation (λ = 1.54184 Å) in the 2θ range of 2–70° with a step of 0.04° and a counting time of 1 s per step and were analyzed using the X’Pert High Score Plus software (Malvern Panalytical B.V., Almelo, Overijssel, The Netherlands).
The differential thermal analysis (DTA) measurements were performed using the device METTLER TOLEDO model TGA/A851 thermobalance (Columbus, OH, USA). About 10 mg of sample was used for each measurement, in the temperature range from 25 to 1000 °C, with a heating rate of 10 K min−1 in air flow (50 mL min−1).
2.3. Preparation of the Adsorbent Substrate and Activation of Positive Surface Charges
The preparation of the adsorbent substrate, as well as the heat treatment, were described by Millán et al. [
9]. The generation of positive surface charges, or the activation process, was carried out on the calcined substrates with each particle-size fraction via acid treatment with HCl and H
2SO
4 over 12 h, and then they were washed out with distillate water until neutral pH was achieved, and finally, they were dried in an oven for another 12 h. The packed column was filled with the acidic solution until it reached a level of 20 cm above the bed. The first 15 mL of effluent was discarded. Aliquots of 40 mL of effluent were collected (average flow was 60 mL min
−1) and titrated with 0.01 N NaOH in the presence of phenolphthalein. The effluent concentration was calculated for each aliquot until it was equal to that of the acid solution at the inlet of the column. Finally, the excess acid was removed by washing with distilled water.
2.4. Adsorption Studies
The adsorption experiments were carried out using glass columns for chromatographic separation of 2.5 cm diameter and 70 cm length, with a closing valve to control the flux of effluent. Standard solutions of phosphates and nitrates were prepared from pro-analysis grade reagents. A 200 ppm and 100 ppm phosphate standard solution were prepared from KH2PO4, and a 30 ppm nitrate standard solution from a KNO3 standard solution. A mass of 150 g of the substrate was introduced into the column up to 30 cm height. The column was then slowly filled with the anion solution, avoiding air bubble formation, and it was allowed to stand for 30 min to equilibrate the system. The first 15 mL of effluent was discarded. Then, 40 mL aliquots, using a graduated cylinder, were collected, keeping a constant liquid height of 20 cm above the bed during the test so as not to alter the hydrostatic pressure on the substrate column. Next, the concentration of the species studied in each of the collected aliquots was determined. Percolation stopped when the concentration of the effluent was equal to the concentration at the inlet of the column.
Nitrates were spectrophotometrically analyzed using the 4500 NO
3− B method [
24], by measuring the absorbance of the samples at 215 nm using a Genesys 10S UV-Vis model (Thermo Fisher Scientific Inc., Madrid, Spain), in 1 cm-wide quartz cuvettes. Solutions of 1, 3, 6, 10, 15, 20, 25, 30, and 35 ppm of nitrates were prepared from a 200 ppm stock solution. A blank solution was also prepared using distilled water. Subsequently, a spectral scan was carried out to determine the optimal wavelength for the absorbance measurement, which turned out to be 215 nm.
Phosphate ions were also spectrophotometrically analyzed using the molybdenum blue method using a 4500 P-E [
24]. The said method was based on the formation of the blue phosphomolybdic complex, and its absorbance was measured at 880 nm, using a Genesys 10S UV-Vis spectrophotometer (Thermo Fisher Scientific Inc., Madrid, Spain) with plastic cells. A 100 ppm phosphate standard solution was prepared as phosphorus from KH PO
4 (0.4390 g L
−1). From this phosphate standard solution, dilutions were made to prepare the calibration standards of 0.15, 0.30, 0.60, 1.00, 1.30 and 1.50 ppm as phosphorus.
2.5. Adsorption Isotherm Modeling
Adsorption isotherm models describe a mathematical relation between the behavior of the adsorbate–adsorbent interaction and provide information on the adsorption capacity of the studied adsorbent [
25,
26,
27]. The adsorption equilibria data were studied by analyzing the Langmuir and Freundlich isotherm models’ feasibility. The best fit between the isotherm function and the experimental data was verified by carrying out linear regressions of the isotherm linear equation.
The Langmuir isotherm is a valid theoretical model for adsorption in a monolayer on a completely homogeneous surface with a finite number of identical and equivalent sites of adsorption and with a negligible interaction between the molecules. The non-linear and linear form of the Langmuir isotherm are described in Equations (2) and (3) [
25,
26,
27,
28]:
where
= the amount adsorbed per adsorbent weight unit, C
e = the equilibrium concentration of adsorbate in solution after adsorption,
= the constant of Langmuir, and b
A = the adsorption amount corresponding to the monolayer coverage.
The Freundlich adsorption isotherm is an empirical model describing the reversible and non-ideal adsorption process. It can be used for multilayer adsorption on heterogeneous sites, assuming non-uniform sites and adsorption energies [
8,
25,
26,
27,
28]. The mathematical model of the Freundlich adsorption isotherm is represented by Equation (4), and its linearized form by Equation (5):
In Equations (4) and (5), KA = Freundlich’s constant related to adsorption capacity, and n = a constant related to adsorption intensity or energetic homogeneity of active sites of adsorption. n may take values near unity or greater. The greater the value of n, the greater the energetic homogeneity in the adsorption active sites.
For the construction of the isotherms, adsorption batch tests were carried out in 100 mL beakers, varying the masses of adsorbent substrate in each beaker (1, 2, 5, 8, 12, and 16 g), keeping the adsorbate volume constant (50 mL) and its initial concentration constant. The mixture was left to stand for 24 h in isothermal conditions (20 ± 1 °C) and periodically mixed. At the end of this period, the equilibrium concentration (Ce) of the ion in the solution was measured.
2.6. Adsorption Kinetic Modeling
In adsorption, as a time-dependent process, it is necessary to know its speed for the evaluation of adsorbents. Adsorption kinetic models express the relationship between the amount of retained adsorbate and time, allowing the prediction of reaction pathways and possible adsorption mechanisms [
25,
29]. There are different mathematical models for the description of adsorption kinetics. The adsorption kinetic data were studied by analyzing the pseudo-first-order and pseudo-second-order models’ feasibility. The best fit between the model and the experimental data was verified by carrying out linear regressions of the linearized kinetic equation.
The pseudo-first-order Lagergren model is mathematically described by Equation (6) [
29,
30,
31]:
where K
1 is the first-order adsorption kinetic constant (min
−1),
is the equilibrium adsorption capacity (mg g
−1), and
is the amount of adsorbate retained at any time t (mg g
−1). Equation (6) is solved by integrating it and taking as boundary conditions t = 0 with
= 0 and t = t with
=
(Equation (7)), and the parameters k
1 and
are determined by the linearized form of the pseudo-first-order model, shown in Equation (8) [
30,
31]:
The pseudo-second-order kinetics model proposed by Blanchard et al. [
32] is generally used to describe second-order chemisorption and ion-exchange adsorption mechanisms that occur on the adsorbent surface [
10,
25,
30,
32]. The differential form corresponding to this model is given by Equation (9), after integrating it with the boundary conditions q (t = 0) = 0 and q (t = t) = q
e, rearranging the linearized expression (Equation (10)) [
8,
30,
31,
32,
33]:
where K
2 is the second-order rate constant (g mg
−1 min
−1), t is the time (min), and
and
represent the adsorption capacities (mg g
−1) at equilibrium and at time t, respectively.
The adsorption kinetics test was carried out in 100 mL glass containers where 50 mL of the ion solution at a concentration of 50 ppm was mixed with 2 g of activated adsorbent, keeping the temperature constant (20 ± 1 °C) and periodically mixing it. For the kinetic analysis, samples of the supernatant were taken at time intervals of 5, 10, 30, 60, 120, 240, 360, 720, and 1440 min, and the concentration of the residual ion in each aliquot was measured.
3. Results and Discussion
3.1. pH, Electrical Conductivity (EC), and Cation Exchange Capacity (CEC)
Table 1 shows the pH, EC, and CEC values found in the three particle-size fractions of the untreated lithological material, i.e., raw material. As shown, the pH values of the three particle-size fractions are similar to the value reported in the literature for this lithological material, which indicates a marked acid character [
9].
Similarly, the conductivity values are in the same order of magnitude as those reported by Millán et al. [
9], indicating that the material is poorly soluble, i.e., there are no soluble salts. The cation exchange capacity is low, comparable to kaolinite, and agrees with that reported in the literature for the case of gibbsite and amorphous goethite [
34]. Furthermore, the absence of organic matter in the lithological material considerably reduces the CEC.
3.2. BET Surface Area Studies
Table 2 shows N
2 absorption analysis for calcined adsorbent substrate. Specific surfaces have relatively low values, comparative to kaolinite (which range between 5 and 20 m
2 g
−1) [
35], which is the limiting factor for the adsorption capacity. According to the microporosity results, the fine fraction could present better adsorbent properties; it has pores and micropores with greater volume and, of course, a larger micropore area.
3.3. RX Diffraction
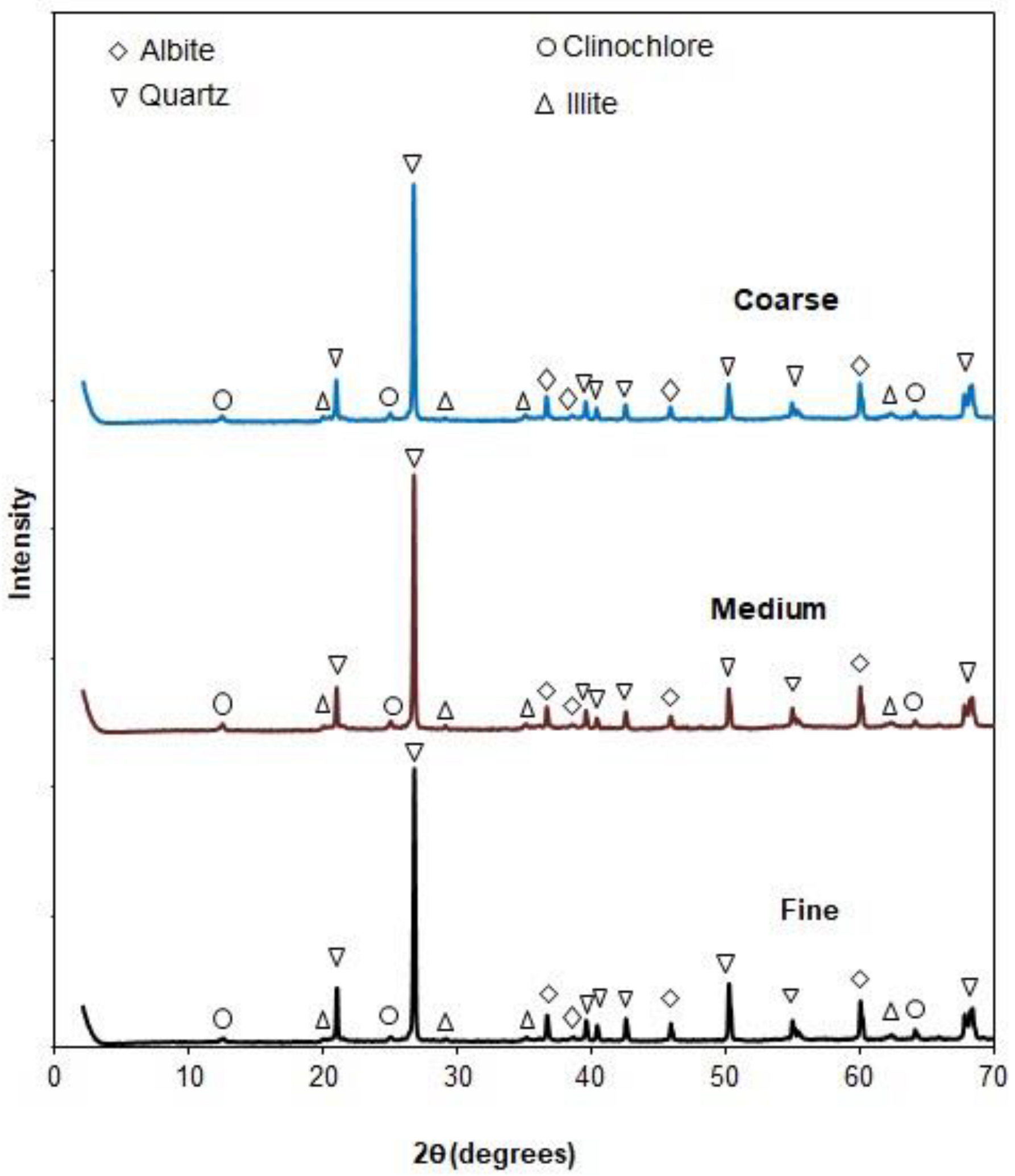
Figure 1 shows the X-ray diffractograms for the three particle-size fractions of the lithological material studied. All three diffractograms are similar, indicating a similar mineralogical composition in each of the fractions, consisting mainly of quartz, illite, albite, and clinochlore. These results indicate the presence of minerals of iron, aluminum, and silicon that are parts of the material. The diffractograms of calcined and non-calcined substrate were reported in the literature [
9], showing no change in the mineral composition of the material owing to the thermal treatment, evidencing the refractory nature of the lithological material.
3.4. Differential Thermal Analysis (DTA)
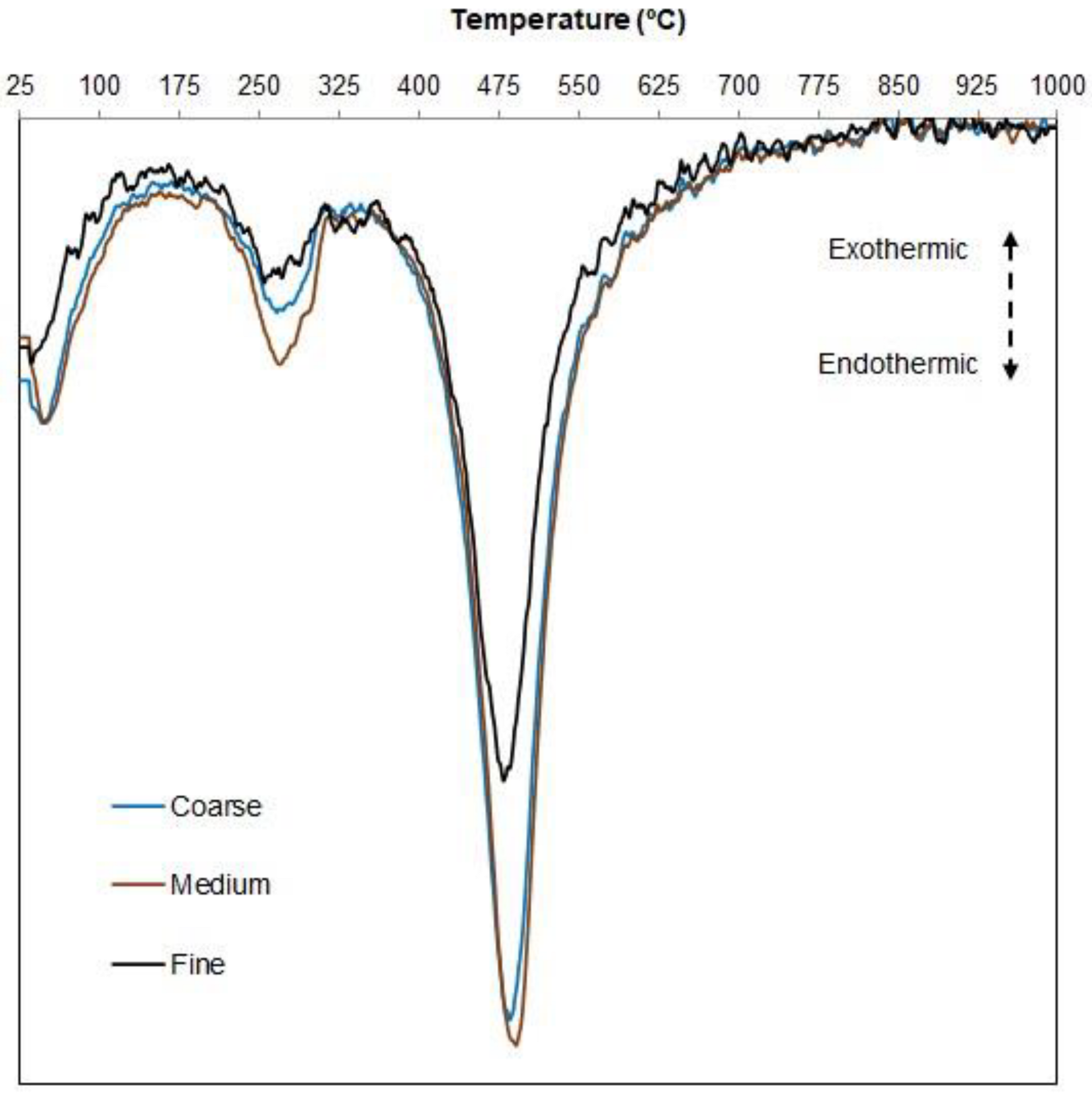
Figure 2 shows the DTA curves in the range of 25 to 1000 °C, identifying the main endothermic peaks of each one of the fine, medium, and coarse fractions of the lithological material.
The curves of each fraction show a weak endothermic peak at approximately 250–300 °C, owing to a loss of lattice water [
34,
36,
37]. A broad endothermic peak between 400 and 600 °C is visible where the transformation α–β of quartz and the dehydroxylation of the illite may be overlapping [
36,
37,
38].
No loss of adhesion water is observed, and the absence of kaolinite is evidenced by the lack of the exothermic peak near 980 °C corresponding to the alumina reach spinel or mullite formation, [
22,
34,
36,
38]. These results confirm the presence of minerals of iron, aluminum, and silicon in the fractions of the lithological material, observed in the studies via X-ray diffraction.
3.5. Protonation Reaction on the Calcined Substrate; Activation Reaction
The calcined substrates were subjected to a protonation reaction with acidic solutions of HCl and H
2SO
4 0.01 N in order to increase the positive surface charge density that favors anionic adsorption.
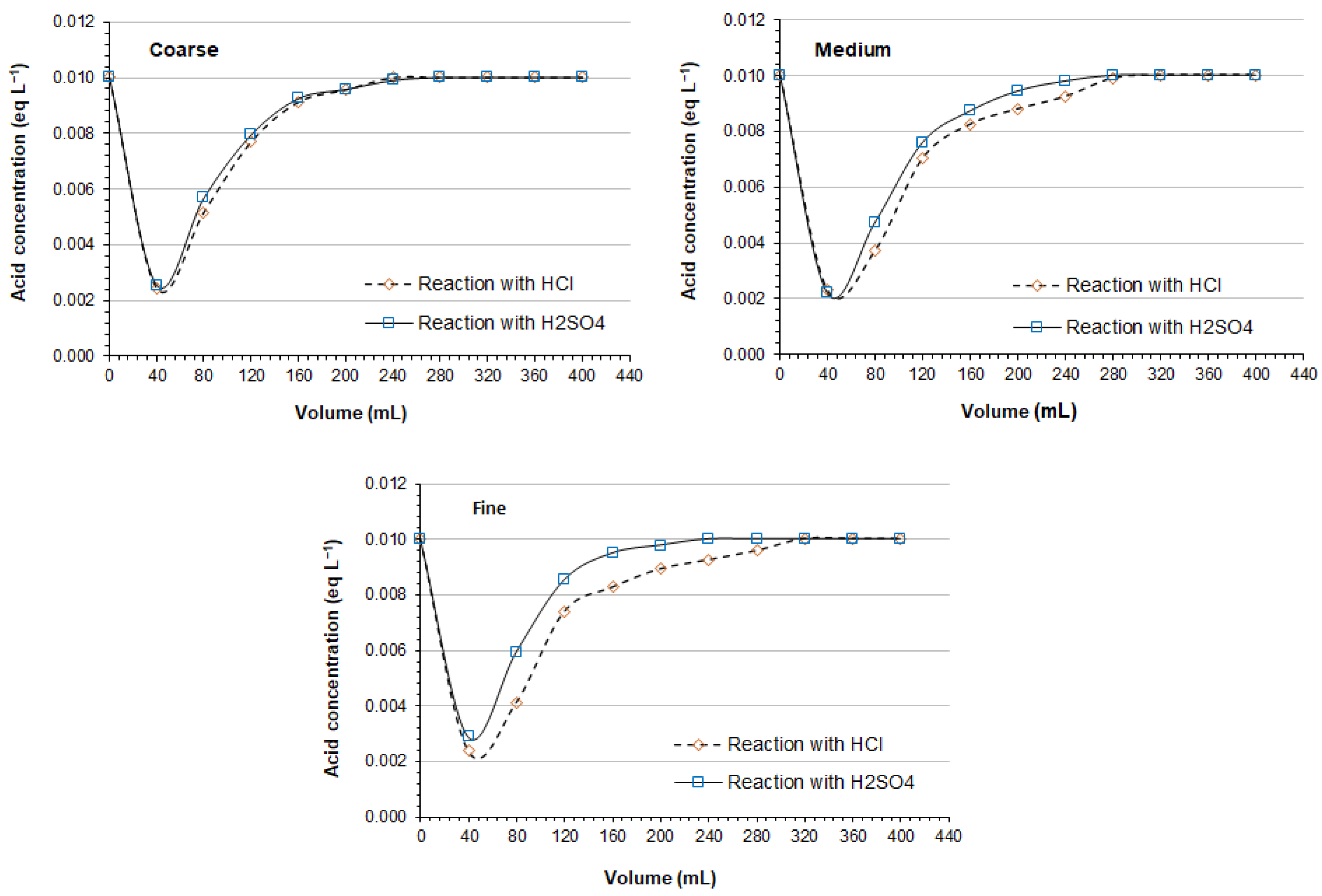
Figure 3 shows the evolution of the protonation reaction on the calcined substrates made from the three particle-size fractions studied.
Initially, the protonation reaction is rapid, as it is seen in the first 40 mL collected at the exit of the column, obtaining a decrease in the concentration of acids of approximately 8 meq L−1. When the percolation flowed at a rate of 60 mL min−1, then about 0.9 min (54 s) would have passed for the recollection of the aliquot, which resulted in the reaction rate of about 8 × 10−3 meq s−1.
The progress of the protonation reaction is similar to the calcined substrates prepared from the course fraction and medium fractions. It can be seen that the protonation reactions with both acids display similar behaviors. When using HCl, the highest yields are achieved with the medium and fine fractions, around 28.6%, while with the coarse fraction, 26.6% is obtained. On the other hand, when using H2SO4, the middle fraction presents the highest percentage of reaction (27.5%), and the fine and coarse fractions reach 25.1% activation.
The results show better performance when HCl was used as it allowed a higher protonation number of active sites for ion exchange. Some of these positively charged active sites can be occupied by the chloride and sulphate ions from HCl and H2SO4, respectively, interfering in the adsorption reaction of other anions such as phosphate.
3.6. Phosphate Ion Adsorption
Table 3 shows the mass-balance of phosphate in the column experiments with the substrates non-activated and treated with both HCl and H
2SO
4. The results indicate that the protonation process favored the retention of the anions due to the surface being positively charged, which presents an opportunity for phosphate ion sorption [
3,
4,
5,
17,
31,
39].
The results obtained using fine and coarse fractions show better performance of the adsorption reaction of phosphate ions on the surface activated with HCl, which was quantified between 25.4 and 25.6%. In the case of the medium fraction, the increase in adsorption performance reached 29.9%.
The best efficiency of phosphate adsorption with the HCl-activated substrates is related to the higher generation of active sites, obtained with this acid in the protonation tests [
3,
4,
5,
39,
40].
Similar adsorption capacities were obtained when using ecological adsorbents such as protonated biochar, the yield varying between 0.025 and 2.59 mg g
−1 depending on the conditions of preparation, activation, metal content, and surface characteristics [
40,
41].
When using modified materials with high surface areas, the retention capacity of phosphate ions increases notably, as has been reported for carbonaceous sorbents (graphene oxide and carbon nanotubes) with adsorption between 7.42 and 45.95 mg g
−1 (46–251 m
2 g
−1), depending on surface charge, functional groups, pore characteristics, surface area, and the modification element [
42,
43,
44]. Furthermore, when using metal-doped zeolites, maximum adsorptions are obtained that vary between 21.84 and 129.2 mg g
−1 (227–914 m
2 g
−1) and that depend on the introduction of active sites into mesoporous silicas by metal coordination or protonation and metal doping [
5,
45]. These materials require complex and expensive production techniques that limit the applications of these materials in the wastewater treatment field.
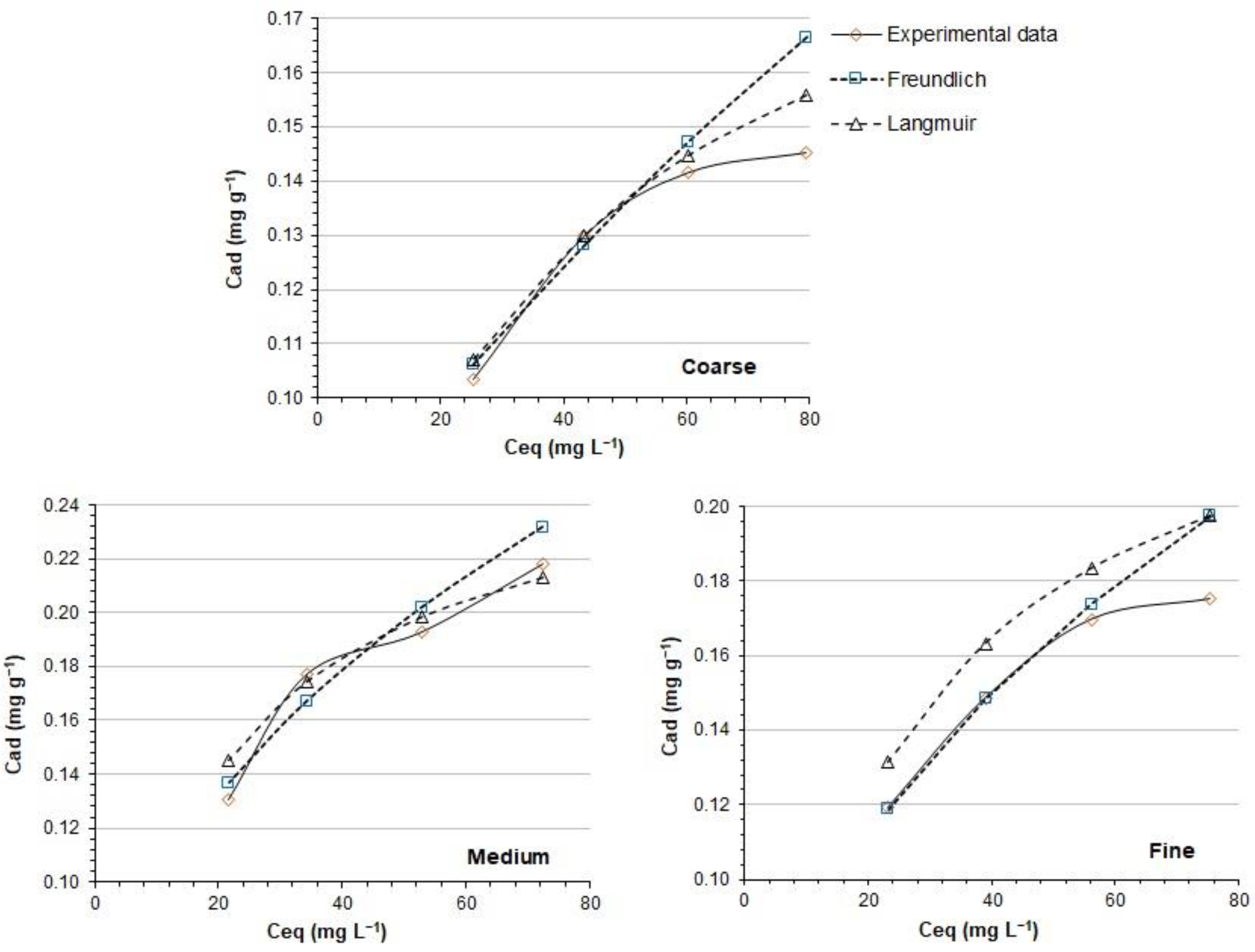
3.7. Phosphate Isotherms
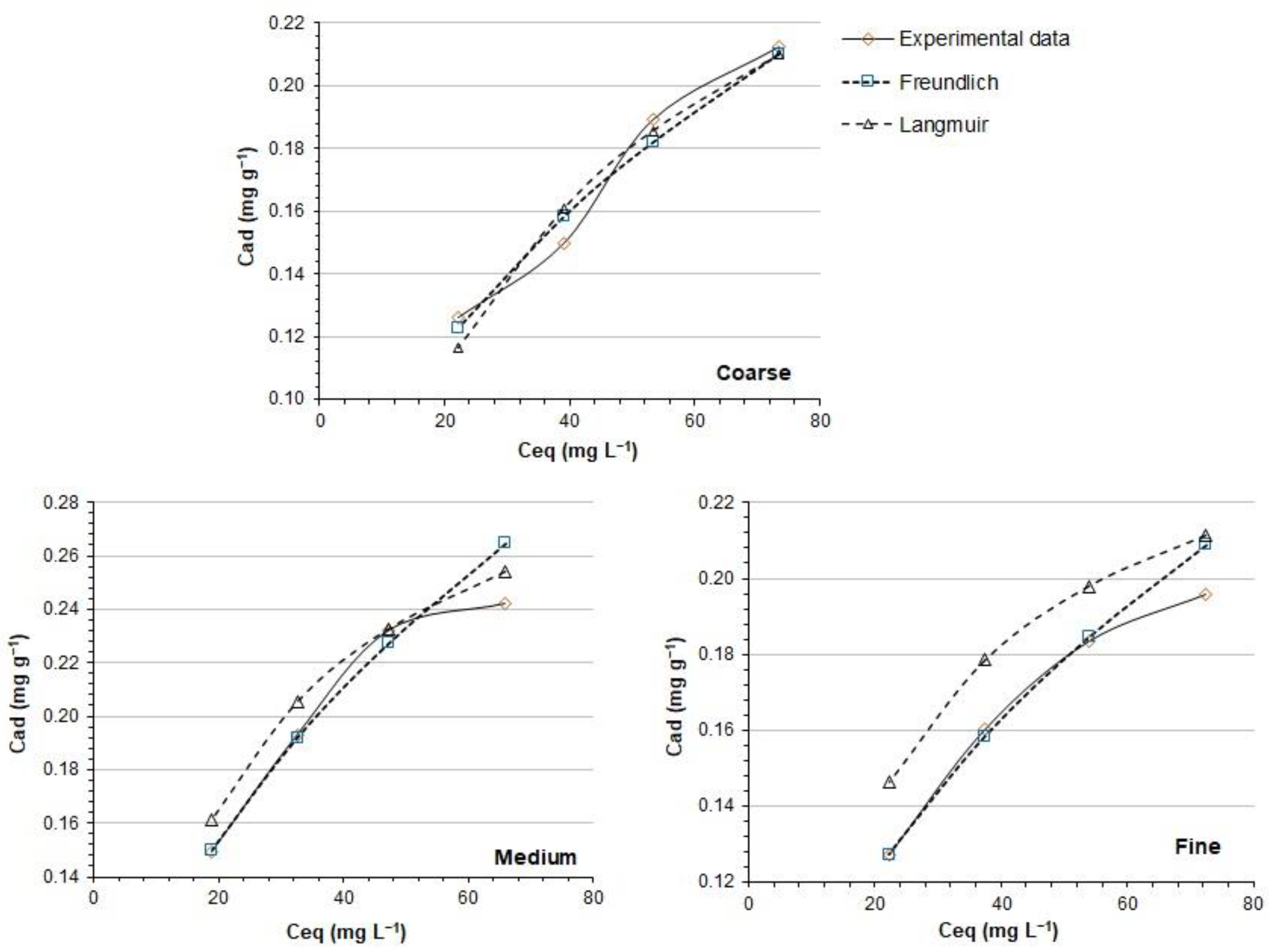
Figure 4 and
Figure 5 show the adsorption isotherms for the phosphate ions on the adsorbent substrates prepared with the three particle-size fractions of the oxidic lithological material. The adsorption of phosphate ions, at the established concentration range, fits well with the Freundlich and Langmuir models. The former conforms to experimental data at low concentrations, while the latter does the same at high concentrations. Furthermore, an increase in the equilibrium concentration follows an increase in the amount of adsorbate retained on the adsorbent material.
The isotherm profile indicates a high affinity between phosphate ions and the activated surface of the adsorbent substrate and shows evidence of specific adsorption with the formation of a covalence between phosphate ions and the Fe and Al—as well as Ti and Mn—oxides and surfaces [
7,
8,
31].
Table 4 shows the parameters of the linear adjustment of the Freundlich and Langmuir models. Linear adjustments in all cases are acceptable values showing a good fit with the experimental data, so the models could predict adsorbed concentrations with some accuracy. In general, the r values for the Freundlich model look a little better.
n values are low, under 0.500, which indicates low energetic homogeneity on the substrate surface. The active sites for the adsorption are not equivalent; therefore, active sites with less energetic requirement are occupied first, etc. However, energetic heterogeneity in such a kind of substrate is expected; the topology and chemical composition of the surface also show non-homogeneity [
27,
28,
46].
The Freundlich and Langmuir models pursue the same objective; however, the Langmuir model has limitations when used to describe the adsorption process on non-homogeneous surfaces [
25,
26,
27,
41]. This model was developed for gas adsorption on homogeneous surfaces; therefore, the model might fail when adsorption takes place on irregular surfaces and in an aqueous phase. Furthermore, the Langmuir model assumes the formation of a monolayer on a homogeneous surface where all the available sites for adsorption are equivalent and the ΔH
ad is independent of the degree of surface coverage, θ [
5,
45]. An example is the adsorption of phosphates on various materials with homogeneous surfaces such as zeolites and protonated mesoporous metal oxide, where the Langmuir isotherm presents a better fit to the adsorption process than the Freundlich isotherm [
33,
36].
However, on a non-homogeneous or irregular surface as in the case of the calcined substrates, the adsorption sites are non-equivalent and the ΔH
ad varies from one place to another. Consequently, those places which lead to more stable bonding are first occupied. The interaction between adsorbed molecules might affect the affinity between the adsorbate and adsorbent, and as θ increases, ΔH
ad decreases. Furthermore, the repulsion increases between the adsorbed molecules, which at the same time causes the mobility of the molecules through the surface, and different places can be occupied. As a result, physisorbed layers can be formed over the chemisorbed layer [
26,
27,
28,
45,
46].
For the adsorption from the aqueous phase on non-homogeneous or irregular surfaces such as the calcined substrate surface, the Freundlich model fits better because of its empiric nature, the model does not assume energetic homogeneity in the active sites, and there are no limits in the adsorption charge [
47]. The isotherm gives an expression that defines the surface heterogeneity and the exponential distribution of active sites and their energies. Moreover, the regression coefficients for the Freundlich fitting are a slightly high when HCl is used for the activation reaction.
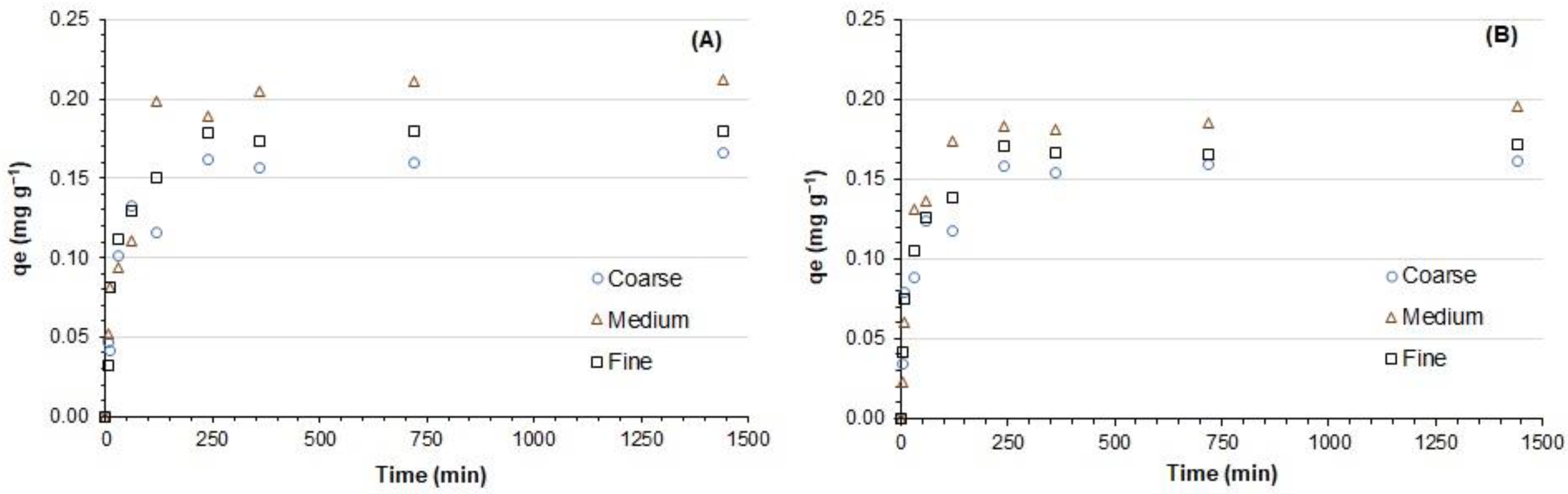
3.8. Phosphate Kinetic
The performance of an adsorbent material can be evaluated through the adsorption rate. Generally, adsorbents have different equilibrium times in the adsorption process due to various adsorption mechanisms and the structural characteristics of the materials, such as pore size and surface charge. The kinetic adsorption profiles of phosphate ions on the three fractions activated with HCl and H
2SO
4 are shown in
Figure 6. The phosphate adsorption capacity is carried out in two stages. The retention of ions increases rapidly during the first 120 min, being the middle fraction with which the highest retention is obtained. This is probably due to the greater availability of free sorption sites on the protonated surfaces of the adsorbents [
40]. Subsequently, phosphate adsorption follows a second, slower phase, until the adsorbents reach saturation after 360 min.
To study the adsorption dynamics, pseudo-first-order and pseudo-second-order kinetic models were applied.
Table 5 shows the parameters of the linear adjustment of the kinetic models. The pseudo-first-order model does not fit the experimental data because it provides values of adsorption capacity at equilibrium, which are different from those determined experimentally (q
e, exp). In contrast, the pseudo-second-order kinetic model leads to q
e values consistent with those obtained experimentally, presenting high fit coefficients (r > 0.99), which demonstrates the viability of this model.
These results support the hypothesis that the adsorption of phosphate ions on the fractions of lithological material is a specific adsorption (chemisorption) or involves the exchange of electrons between the phosphate ions and the protonated surface of the adsorbents [
8,
25,
32,
39]. However, more studies are needed to elucidate the phosphate adsorption mechanism. Similar results have been reported for the adsorption of phosphates on zeolites, carbonaceous materials, and activated clay, where the experimental data are satisfactorily represented by the pseudo-second-order kinetic model [
8,
39,
40,
41].
3.9. Nitrate Ion Adsorption
Table 6 shows the mass-balance of nitrate in the experimental column with the substrates treated with both HCl and H
2SO
4. The results show better performance for the adsorption reaction for the bed activated with HCl, especially for the bed prepared with the medium fraction of the material, where the adsorption of nitrates was 68% higher than the corresponding bed treated with H
2SO
4.
The adsorbed amount was generally small. Nitrate ions can be leached into soils without difficulty since they are not retained by colloids; therefore, they are the primary contaminants of groundwater in agricultural areas where nitrogen fertilizers are used [
2,
48].
However, the adsorption of nitrate ions was somewhat favored on the HCl-activated substrate. Adsorption on the H2SO4-treated bed was reduced by more than 50%, possibly due to competition with sulphate ions for the active sites.
In the case of adsorption with the activated substrate in an acidic media, chloride and sulfate ions coming from HCl and H
2SO
4, respectively, can compete with nitrate ions for the active sites since they have a higher affinity with the active surface (as they do with phosphate ions) than nitrates ions themselves. In studies carried out on the adsorption of nitrates on steel slag activated with HCl, the strong acid environment produced the dissociation of the active sites on the surface of the adsorbent, and chloride ions of the acid inhibited the adsorption of nitrate [
10].
In contrast, the adsorption process would be affected by the high ionic strength caused by coexisting ions. In previous studies on the adsorption of anions by activated clay and different soil colloidal materials, it has been observed that the adsorption of anions decreases in the following order: H
2PO
4− > SO
42− > Cl
− > NO
3− due to the different molecular dimensions, charge density, and degrees of hydration [
8,
39,
49].
Other ecological adsorbents such as biochar have a better nitrate retention capacity than the calcined fractions of the lithological material. The adsorption range can vary between 0.05 and 10.85 mgNO
3− g
−1, depending on the raw material, pH, and temperature of biochar production [
41,
50,
51,
52].
When using clay-modified adsorbents, variable adsorption capacities are obtained between 0.85 and 23.22 mg g
−1 [
53], depending on the experimental conditions (contact time, pH, initial concentration of nitrates, amount, and granulometry of the adsorbent). In our study, another factor that could influence the low retention of nitrates was the contact time, since the experiments were carried out in continuous flow.
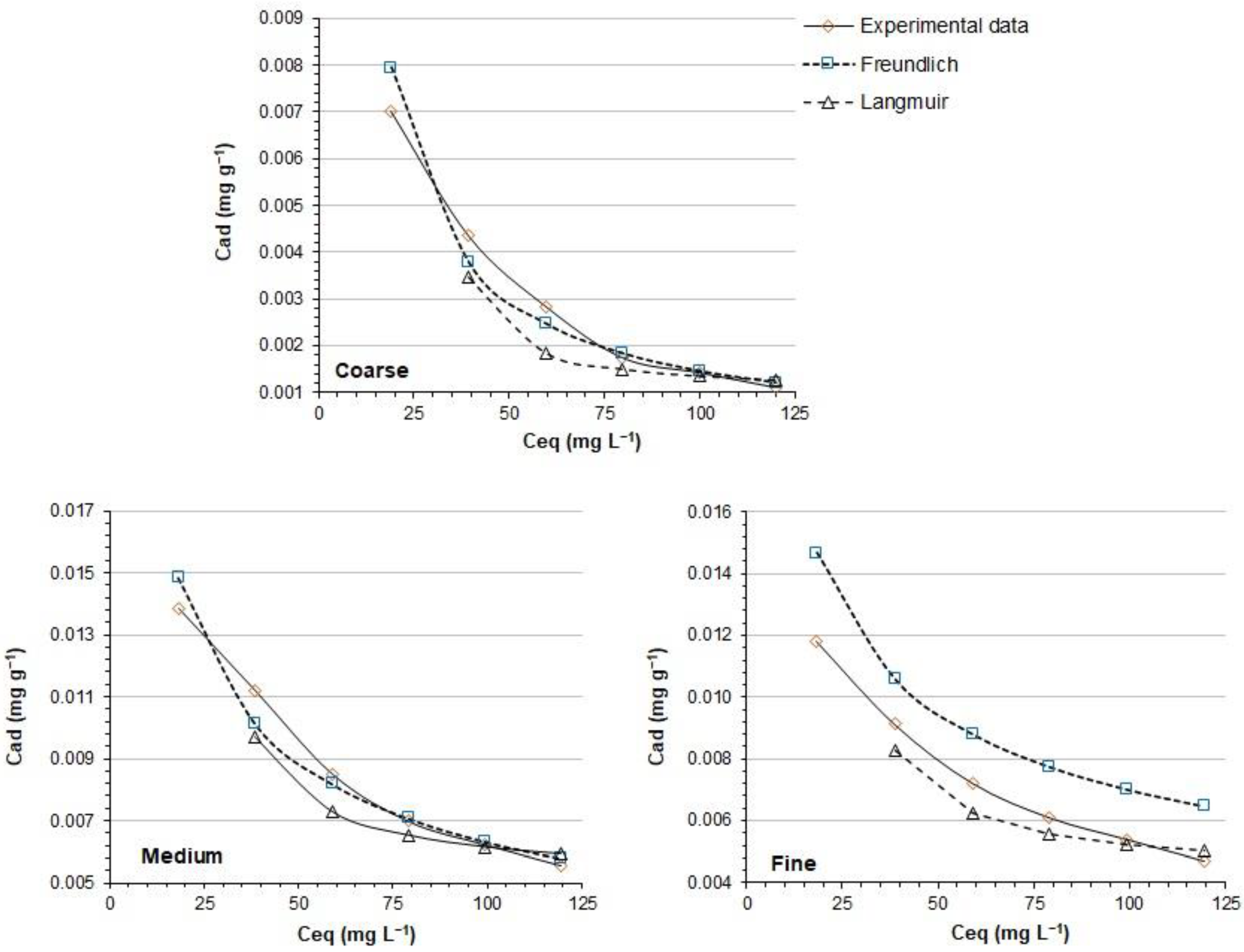
3.10. Nitrate Isotherms
Figure 7 and
Figure 8 show the nitrate adsorption equilibria, described by the models and the experimental data, for the beds prepared with the different particle-size fractions, whose positive charges were generated using HCl. The behavior of nitrate adsorption shows that as the equilibrium concentration increases, the number of adsorbed ions decreases. Furthermore, the low order of magnitude of the retained adsorbate amount (q
eq) compared to that obtained in the balance of phosphate ions indicates that there is a low affinity of the adsorbent bed for nitrates.
The low affinity shown by the fractions of the lithological material for the retention of nitrate ions, together with the low concentration of the adsorption experiments (4.8 × 10
−4 M) and the presence of coexisting ions in the activated substrates, possibly affect the nitrate adsorption process, obtaining a reverse course for the adsorption isotherm. Research indicates that the adsorption of nitrates on different types of soil is affected by the concentration of the ion in solution. For concentrations below 3 × 10
−2 M, anionic exclusion or negative adsorption can occur [
54,
55]. Negative capacities for the adsorption of phosphate and ammonium ions have been reported when different types of biochar were used [
40].
The application of the mathematical models of the Freundlich and Langmuir isotherms is not feasible, because the linearization leads to negative values for the constant related to adsorption intensity (n) for the Freundlich case and the adsorption amount corresponding to the monolayer coverage (bA) for the Langmuir case, which would not represent an adsorption process.
4. Conclusions
The selected lithological material has refractory and adsorbent characteristics due to the presence of amphoteric metal oxides of variable charge, which makes it suitable for the preparation of such substrates. It is a moderately acidic lithological material, very slightly soluble and with a low cation exchange capacity, similar to those characteristics reported for the case of amphoteric oxides and kaolinite. The XRD analysis shows that there are no significant differences in the composition of the three fractions with respect to the mineralogical composition present.
The protonation reaction of the substrate with HCl shows better performance in relation to the protonation reaction with H2SO4 and produces a higher density of positive surface charges and favors the anionic adsorption reaction. Column adsorption experiments with standard solutions indicate the substrates prepared with the fine and medium fractions of the lithological material have a higher adsorption capacity than the coarse fraction for phosphate.
Phosphate adsorption on the different substrates better fit the Freundlich mathematical model and the pseudo-second-order kinetic model, suggesting a chemisorption process. In the case of the adsorption of nitrate ions, the substrate does not have affinity for the retention of these ions.
The presence of amphoteric iron and aluminum oxides of variable charges in the studied fractions of the oxidic lithological material allows their use in the preparation of adsorbent beds for phosphate retention in natural waters, which can be effective as an innovative technique and is sustainable for the elimination of other ions dissolved in water.
Author Contributions
Conceptualization, J.G.P., F.C.M. and L.C.G.; methodology, J.G.P., F.C.M., L.C.G., E.L. and A.M.; software, J.G.P., F.C.M. and E.L.; validation, J.G.P., F.C.M., E.L., S.N. and A.M.; formal analysis, J.G.P., F.C.M., L.C.G., E.L., I.R. and J.C.C.; investigation, J.G.P., F.C.M., A.M., E.L., S.N. and J.I.D.; resources, J.G.P., F.C.M., L.C.G. and A.C.R.; data curation, J.G.P., F.C.M., E.L. and J.I.D.; writing—original draft preparation, J.G.P., F.C.M. and L.C.G.; writing—review and editing, J.G.P., F.C.M., L.C.G., J.C.C. and J.I.D.; visualization, A.C.R. and I.R.; supervision, A.C.R. and I.R.; project administration, A.C.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used and analyzed during the current study are avail-able from the corresponding author on reasonable request.
Acknowledgments
The authors give thanks to the Universidad Nacional de Chimborazo for supporting this work through the research projects program.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Payen, S.; Falconer, S.; Carlson, B.; Yang, W.; Ledgard, S. Eutrophication and Climate Change Impacts of a Case Study of New Zealand beef to the European Market. Sci. Total Environ. 2020, 710, 136120. [Google Scholar] [CrossRef]
- Singh, A.; Tripathi, A.; Kumar, A.; Singh, V. Nitrate and Phosphate Contamination in Ground Water of Varanasi, Uttar Pradesh, India. J. Ind. Res. Technol. 2012, 2, 26–32. [Google Scholar]
- Vicente-Martínez, Y.; Caravaca, M.; Soto-Meca, A.; Martín-Pereira, M.Á.; García-Onsurbe, M.d.C. Adsorption Studies on Magnetic Nanoparticles Functionalized with Silver to Remove Nitrates from Waters. Water 2021, 13, 1757. [Google Scholar] [CrossRef]
- Fanfan, L.; Yungen, L.; Yan, W.; Silin, Y.; Rong, M. Preparation of Structured Biochar, its Adsorption Capacity of N and P and its Characterization. Water Sci. Technol. 2022, 85, 2443–2462. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, Y.; Li, D. Adsorptive Removal of Phosphate from Water using Mesoporous Materials: A Review. J. Environ. Manag. 2017, 193, 470–482. [Google Scholar] [CrossRef]
- Liang, Q.; Fu, X.; Wang, P.; Li, X.; Zheng, P. Dynamic Adsorption Characteristics of Phosphorus Using MBCQ. Water 2022, 14, 508. [Google Scholar] [CrossRef]
- Fan, T.; Wang, M.; Wang, X.; Chen, Y.; Wang, S.; Zhan, H.; Chen, X.; Lu, A.; Zha, S. Experimental Study of the Adsorption of Nitrogen and Phosphorus by Natural Clay Minerals. Adsorp. Sci. Technol. 2021, 2021, 4158151. [Google Scholar] [CrossRef]
- Wang, Y.; He, H.; Zhang, N.; Shimizu, K.; Lei, Z.; Zhang, Z. Efficient Capture of Phosphate from Aqueous Solution using Acid Activated Akadama Clay and Mechanisms Analysis. Water Sci. Technol. 2018, 78, 1603–1614. [Google Scholar] [CrossRef]
- Millán, F.; Prato, J.G.; García, O.; Díaz, I.; Sánchez, M. Adsorción de Iones Cu2+ y Zn2+ por Materiales Litológicos de Carga Variable Provenientes de Suelos del Estado Mérida, Venezuela. Rev. Técnica Fac. Ing. Univ. Zulia 2013, 36, 195–201. [Google Scholar]
- Yang, L.; Yang, M.; Xu, P.; Zhao, X.; Bai, H.; Li, H. Characteristics of Nitrate Removal from Aqueous Solution by Modified Steel Slag. Water 2017, 9, 757. [Google Scholar] [CrossRef] [Green Version]
- Prato, J.G.; González-Ramírez, L.C.; Pérez, M.C.; Rodríguez, M.E. Adsorción de la Dureza del Agua sobre Lechos de Rocas Volcánicas de Ecuador. Inf. Tecnol. 2021, 32, 51–60. [Google Scholar] [CrossRef]
- Xu, R.K.; Qafoku, N.P.; Van Ranst, E.; Li, J.Y.; Jiang, J. Adsorption Properties of Subtropical and Tropical Variable Soils: Implication from Climate Change and Biochard Amendment. Adv. Agron. 2016, 135, 1–58. [Google Scholar]
- Gu, S.; Kang, X.; Wang, L.; Lichtfouse, E.; Wang, C. Clay Mineral Adsorbents for Heavy Metal Removal from Wastewater: A Review. Environ. Chem. Lett. 2019, 17, 629–654. [Google Scholar] [CrossRef]
- Millán, F.; Prato, J.G.; González, L.C.; Márquez, A.; Djabayan, P. Cu (II) Chemisorption on Calcined Substrates made with an Oxidic Refractory Variable Charges Lithological Material. Rev. Técnica Fac. Ing. Univ. Zulia 2019, 32, 10–18. [Google Scholar] [CrossRef] [Green Version]
- Qafoku, N.P.; Van Ranst, E.; Noble, A.; Baert, G. Variable Charge Coils: Their Mineralogy, Chemistry and Management. Adv. Agron. 2004, 84, 159–214. [Google Scholar]
- Prato, J.G.; Millán, F.; González, L.C.; Ríos, I.; Márquez, A.; Sánchez, J.; Palomares, A.E.; Díaz, J.I. Evaluación de Materiales Litológicos Oxídicos como Adsorbentes para el Tratamiento de Efluentes y Aguas Residuales. Novasinergia 2021, 4, 93–110. [Google Scholar]
- Wang, Y.; Jiang, J.; Xu, R.K.; Tiwari, D. Phosphate Adsorption at Variable Charge Soils/water Interfaces as Influenced by Ionic Strength. Aust. J. Soil Res. 2009, 47, 529–536. [Google Scholar] [CrossRef]
- Prato, J.G.; Millán, F.; Ríos, A.; González-Ramírez, L.C. Uso de Materiales Litológicos Oxídicos para la Reducción de la Dureza en Aguas Naturales. Inf. Technol. 2022, 33, 145–156. [Google Scholar] [CrossRef]
- Xu, R.; Wang, Y.; Tiwari, D.; Wang, H. Effect of Ionic Strength on Adsorption of As(III) and As(V) on variable charge soils. J. Environ. Sci. 2009, 21, 927–932. [Google Scholar] [CrossRef]
- Agarwal, M.; Singh, K. Heavy Metal Removal from Wastewater using Various Adsorbents: A Review. J. Water Reuse Desal. 2017, 7, 387–419. [Google Scholar]
- Márquez, A.; Millán, F.; Prato, J.G.; La Cruz, C. Adsorción de Iones Cr(VI) sobre Lechos Adsorbentes Calcinados con Superficie de Carga Variable Químicamente Modificada. Rev. Técnica Fac. Ing. Univ. Zulia 2020, 43, 72–81. [Google Scholar] [CrossRef]
- Pansu, M.; Gautheyrou, J. Handbook of Soil Analysis; Springer: Berlin/Heidelberg, Germany, 2006; pp. 551–656. [Google Scholar]
- McKean, S.J. Manual de Análisis de Suelo y Tejido Vegetal; Centro Internacional de Agricultura Tropical: Bogotá, Colombia, 1993; pp. 95–99. [Google Scholar]
- Rice, E.W.; Baird, R.D.; Eaton, A.D. Standard Methods for the Examination of Water and Wastewater, 23rd ed.; American Public Health Association, American Water Works Association, Water Environment Federation: Washington, DC, USA, 2017. [Google Scholar]
- Márquez, C.O.; García, V.J.; Guaypatin, J.R.; Fernández-Martínez, F.; Ríos, A.C. Cationic and Anionic Dye Adsorption on a Natural Clayey Composite. Appl. Sci. 2021, 11, 5127. [Google Scholar] [CrossRef]
- Foo, K.Y.; Hameed, B.H. Insights into the Modeling of Adsorption Isotherm Systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Al-Ghouti, M.A.; Da’ana, D.A. Guidelines for the use and Interpretation of Adsorption Isotherm Models: A Review. J. Hazard. Mater. 2020, 393, 122383. [Google Scholar] [CrossRef]
- Kalam, S.; Abu-Khamsin, S.A.; Kamal, M.S.; Shirish Patil, S. Surfactant Adsorption Isotherms: A Review. ACS Omega 2021, 6, 32342–32348. [Google Scholar] [CrossRef]
- Tran, H.N.; You, S.J.; Hosseini-Bandegharaei, A.; Chao, H.P. Mistakes and Inconsistencies Regarding Adsorption of Contaminants from Aqueous Solutions: A Critical Review. Water Res. 2017, 120, 88–116. [Google Scholar] [CrossRef]
- Plazinski, W.; Rudzinski, W.; Plazinska, A. Theoretical Models of Sorption Kinetics Including a Surface Reaction Mechanism: A Review. Adv. Colloid Interface Sci. 2009, 152, 2–13. [Google Scholar] [CrossRef]
- Guaya, D.; Valderrama, C.; Farran, A.; Armijos, C.; Cortina, J.L. Simultaneous Phosphate and Ammonium Removal from Aqueous Solution by a Hydrated Alumium Oxide Modified Natural Zeolite. Chem. Eng. J. 2015, 271, 204–213. [Google Scholar] [CrossRef] [Green Version]
- Blanchard, G.; Maunaye, M.; Martin, G. Removal of Heavy Metals from Waters by Means of Natural Zeolites. Water Res. 1984, 18, 1501–1507. [Google Scholar] [CrossRef]
- Ho, Y.S. Review of Second-order Models for Adsorption Systems. J. Hazard. Mater. 2006, 136, 681–689. [Google Scholar] [CrossRef] [Green Version]
- Tan, K.H. Principles of Soil Chemistry, 4th ed.; CRC Press: Boca Raton, FL, USA, 2011; pp. 133–241. [Google Scholar]
- Kwon, S.; Hwang, H.; Lee, Y. Effect of Pressure Treatment on the Specific Surface Area in Kaolin Group Minerals. Crystals 2019, 9, 528. [Google Scholar] [CrossRef] [Green Version]
- Manoharan, C.; Sutharsan, P.; Dhanapandian, S.; Venkatachalapathy, R. Characteristics of Some Clay Materials from Tamilnadu, India, and their Possible Ceramic Uses. Ceramica 2012, 58, 412–418. [Google Scholar] [CrossRef] [Green Version]
- Húlan, T.; Trník, A.; Medved, I. Kinetics of Thermal Expansion of Illite-based Ceramics in the Dehydroxylation Region during Heating. J. Therm. Anal. Calorim. 2017, 127, 291–298. [Google Scholar] [CrossRef]
- Gasparini, E.; Serena, C.; Tarantino, S.C.; Ghigna, P.; Pia Riccardi, M.; Cedillo-González, E.I.; Siligardi, C.; Zema, M. Thermal Dehydroxylation of Kaolinite under Isothermal Conditions. Appl. Clay Sci. 2013, 80–81, 417–425. [Google Scholar] [CrossRef]
- Rahman, M.A.; Lamb, D.; Kunhikrishnan, A.; Rahman, M.M. Kinetics, Isotherms and Adsorption–Desorption Behavior of Phosphorus from Aqueous Solution Using Zirconium–Iron and Iron Modified Biosolid Biochars. Water 2021, 13, 3320. [Google Scholar] [CrossRef]
- Munar-Florez, D.A.; Varón-Cárdenas, D.A.; Ramírez-Contreras, N.E.; García-Núñez, J.A. Adsorption of Ammonium and Phosphates by Biochar Produced from Oil Palm Shells: Effects of Production Conditions. Result. Chem. 2021, 3, 100119. [Google Scholar] [CrossRef]
- Frišták, V.; Pipíška, M.; Turčan, V.; Bell, S.M.; Laughinghouse, H.D., IV; Ďuriška, L.; Soja, G. Preparation and Characterization of Novel Magnesium Composite/Walnut Shells-Derived Biochar for As and P Sorption from Aqueous Solutions. Agriculture 2021, 11, 714. [Google Scholar] [CrossRef]
- Luo, X.; Wang, X.; Bao, S.; Liu, X.; Zhang, W.; Fang, T. Adsorption of Phosphate in Water using One-step Synthesised Zirconium-loaded Reduced Graphene Oxide. Sci. Rep. 2016, 6, 38824. [Google Scholar] [CrossRef] [Green Version]
- Mahdavi, S.; Akhzari, D. The Removal of Phosphate from Aqueous Solutions using Two Nano-structures: Copper Oxide and Carbon Tubes. Clean Technol. Environ. Policy 2016, 18, 817–827. [Google Scholar] [CrossRef]
- Almanassra, I.W.; Al-Ansari, T.; Kochkodan, V.; Mckay, G.; Ali Atieh, M. Review of Phosphate Removal from Water by Carbonaceous Sorbents. J. Environ. Manag. 2021, 287, 112245. [Google Scholar] [CrossRef]
- Adamson, A.; Gast, A. Physical Chemistry of Surfaces, 6th ed.; John and Wiley and Sons: Hoboken, NJ, USA, 1997; pp. 1–808. [Google Scholar]
- Kang, J.K.; Kim, J.H.; Kim, S.B.; Lee, S.H.; Choi, J.W.; Lee, C.G. Ammonium-functionalized Mesoporous Silica MCM-41 for Phosphate Removal from Aqueous Solutions. Desalination Water Treat. 2016, 53, 10839–10849. [Google Scholar] [CrossRef]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and Interpretation of Adsorption Isotherms. J. Chem. 2017, 2017, 3039817. [Google Scholar] [CrossRef]
- Goss, M.; Goorahoo, D. Nitrate Contamination of Groundwater: Measurement and Prediction. Fertil. Res. 1995, 42, 331–338. [Google Scholar] [CrossRef]
- Hong, B.D.; Lee, K.S.; Lee, D.S.; Rhie, J.H.; Bae, H.S.; Seo, I.H.; Song, S.G.; Chung, D.Y. Competitive Adsorption and Subsequent Desorption of Sulfate in the Presence of Various Anions in Soils. Korean J. Soil Sci. Fert. 2016, 49, 541–547. [Google Scholar] [CrossRef] [Green Version]
- Chintala, R.; Mollinedo, J.; Schumacher, T.E.; Papiernik, S.K.; Malo, D.D.; Clay, D.E.; Kumar, S.; Gulbrandson, D.W. Nitrate Sorption and Desorption in Biochars from Fast Pyrolysis. Microporous Mesoporous Mater. 2013, 179, 250–257. [Google Scholar] [CrossRef]
- Gai, X.; Wang, H.; Liu, J.; Zhai, L.; Liu, S.; Ren, T.; Liu, H. Effects of Feedstock and Pyrolysis Temperature on Biochar Adsorption of Ammonium and Nitrate. PLoS ONE 2014, 9, e113888. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fidel, R.B.; Laird, D.A.; Spokas, K.A. Sorption of Ammonium and Nitrate to Biochars is Electrostatic and pH-dependent. Sci. Rep. 2018, 8, 17627. [Google Scholar] [CrossRef]
- Lazaratoua, C.V.; Vayenasb, D.V.; Papoulis, D. The Role of Clays, Clay Minerals and Clay-based Materials for Nitrate Removal from Water Systems: A Review. Appl. Clay Sci. 2020, 185, 105377. [Google Scholar] [CrossRef]
- Haan, F.A.M. The negative Adsorption of Anions (anion exclusion) in Systems Interacting Double Layers. J. Phys. Chem. 1964, 68, 2970–2977. [Google Scholar] [CrossRef]
- Mouat, M.C.H. Negative Adsorption of Phosphate by Plant Roots. N. Z. J. Agric. Res. 1983, 26, 489–492. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).