An Integrated Bayesian and Machine Learning Approach Application to Identification of Groundwater Contamination Source Parameters
Abstract
:1. Introduction
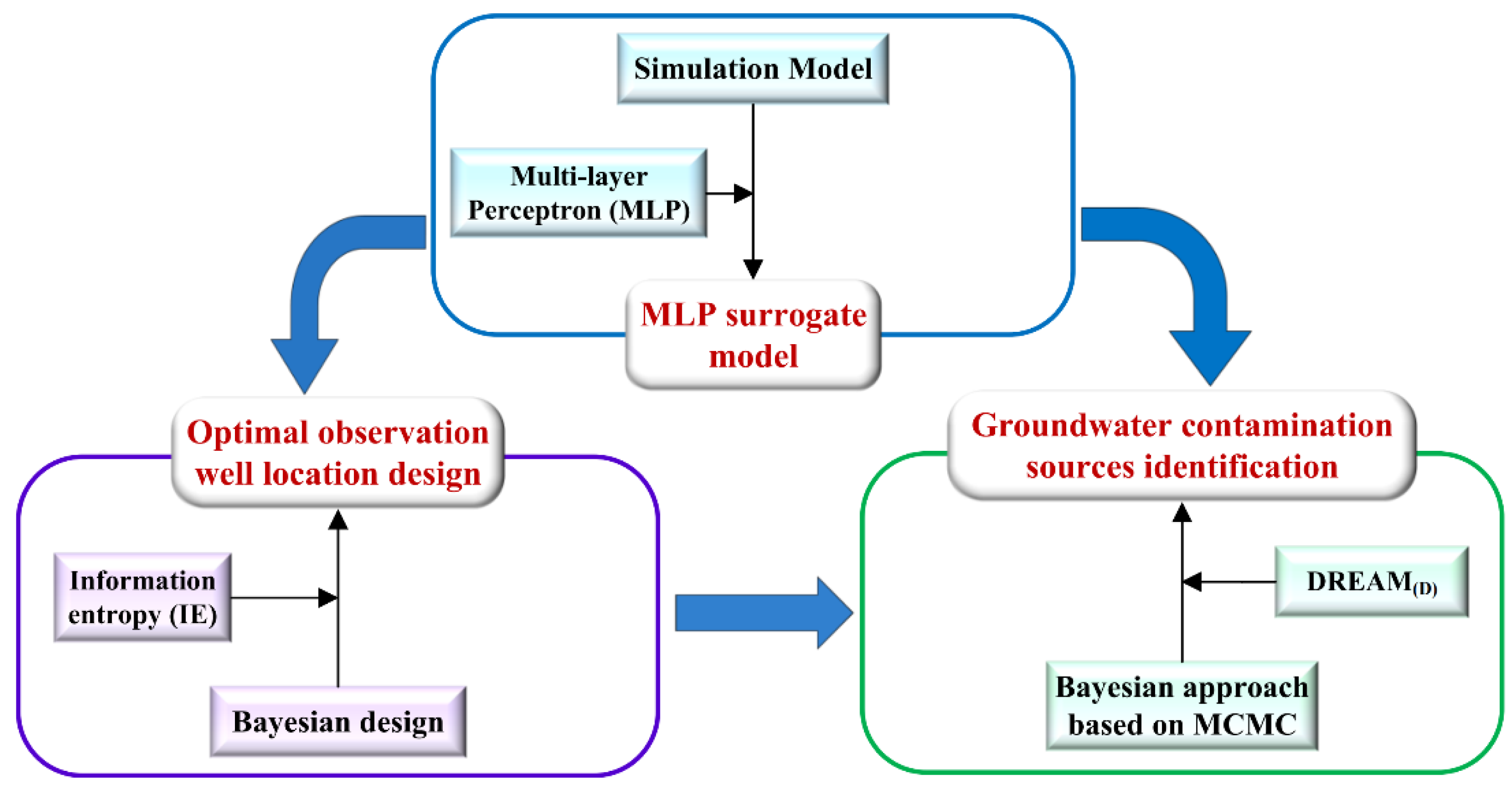
2. Theoretical Framework
2.1. Simulation Model
2.2. Optimal Observation Well Location Design
2.3. Parameter Identification
2.3.1. Bayesian Inversion
2.3.2. MCMC
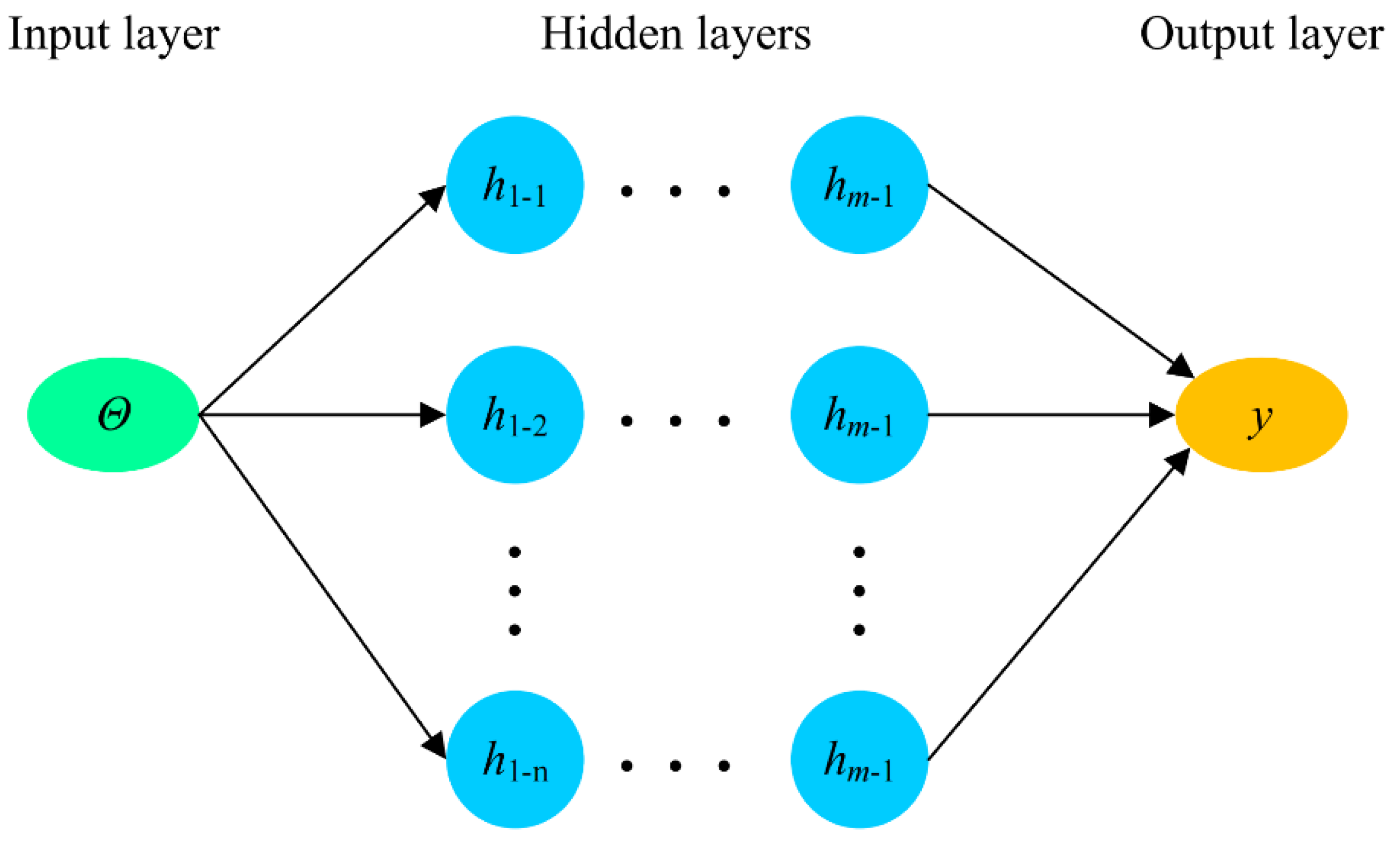
2.4. Multi-Layer Perceptron
3. Numerical Applications
3.1. Case studies
3.1.1. Case 1
3.1.2. Case 2
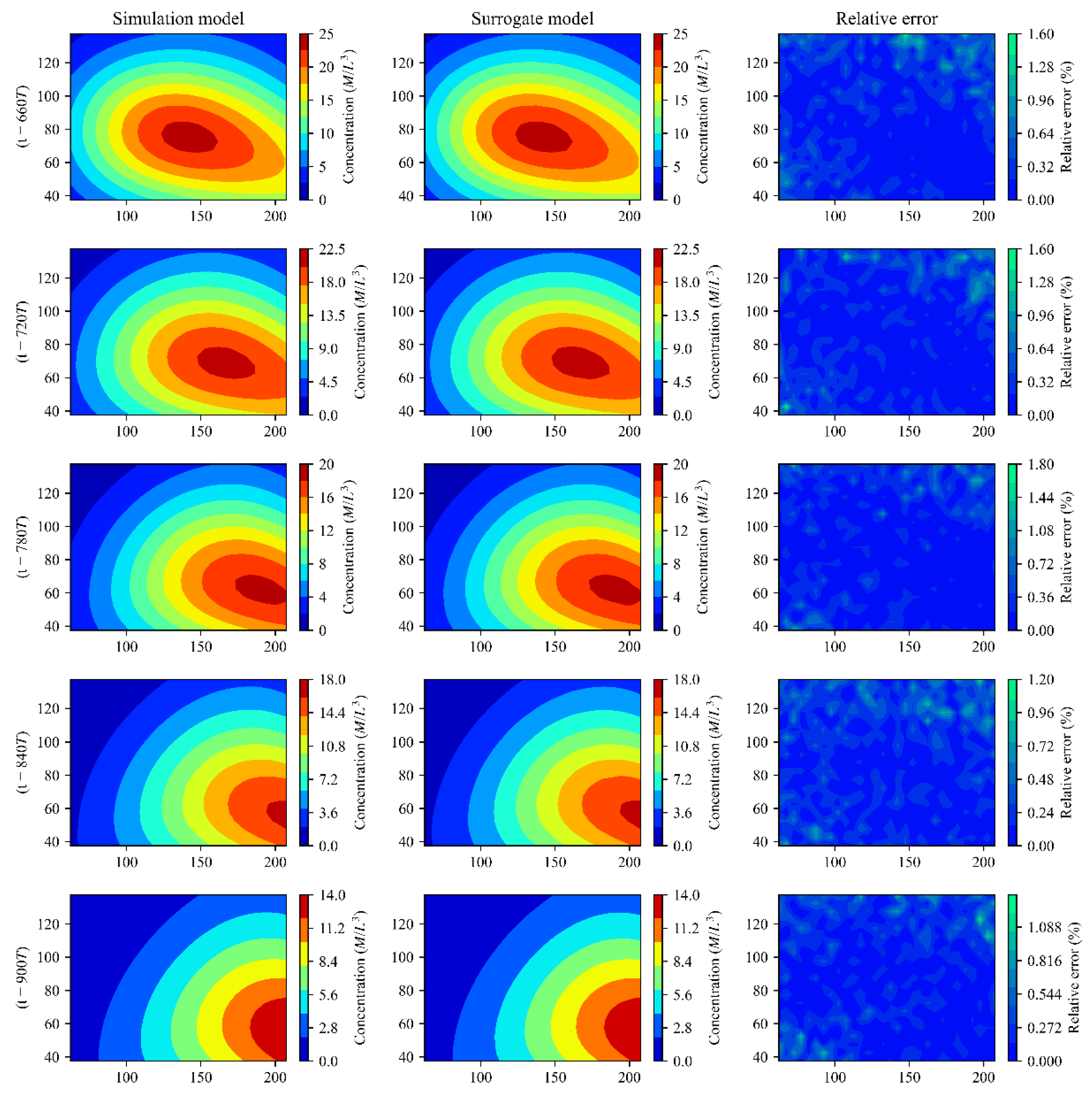
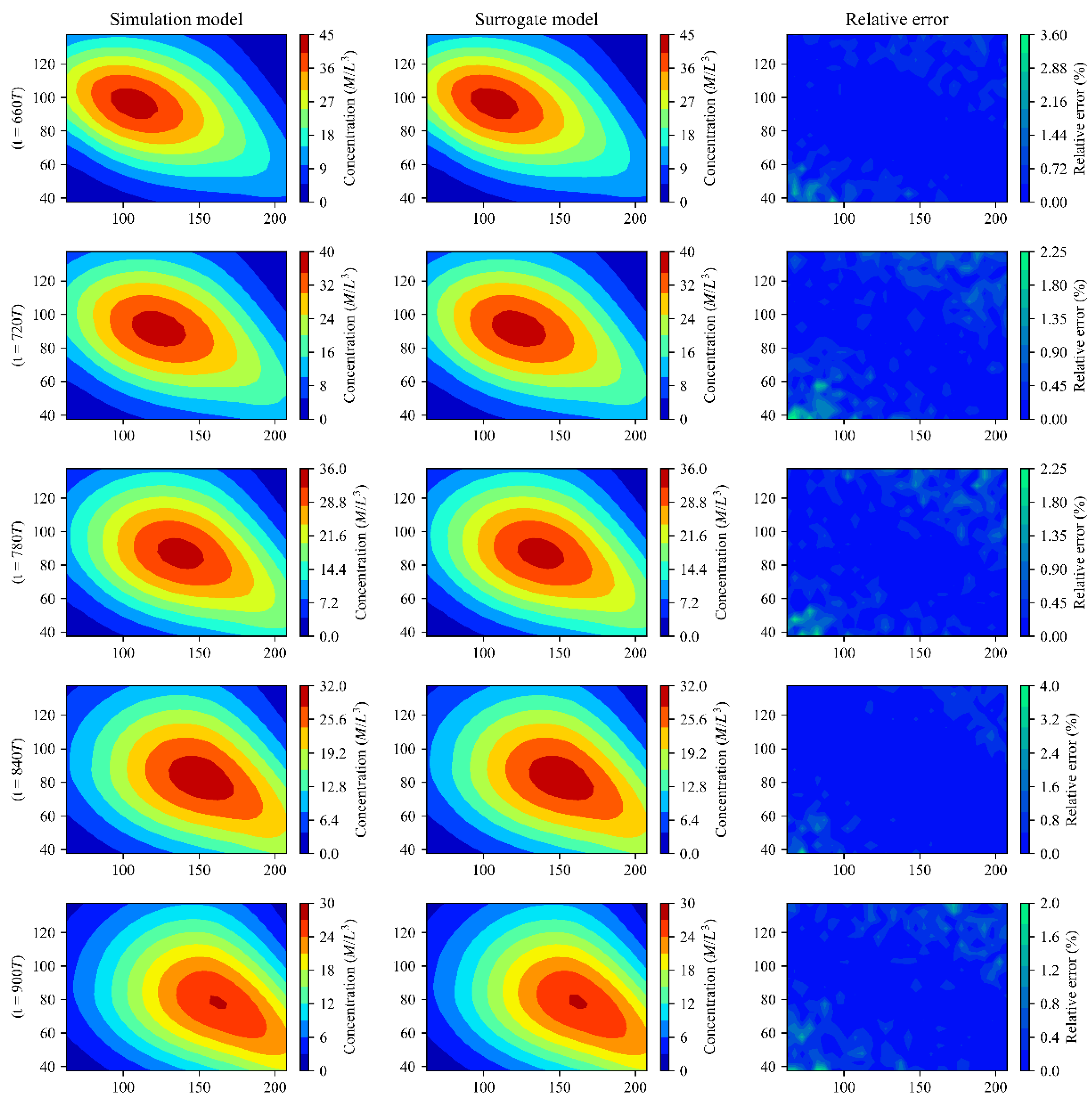
3.2. Application of the Surrogate Model
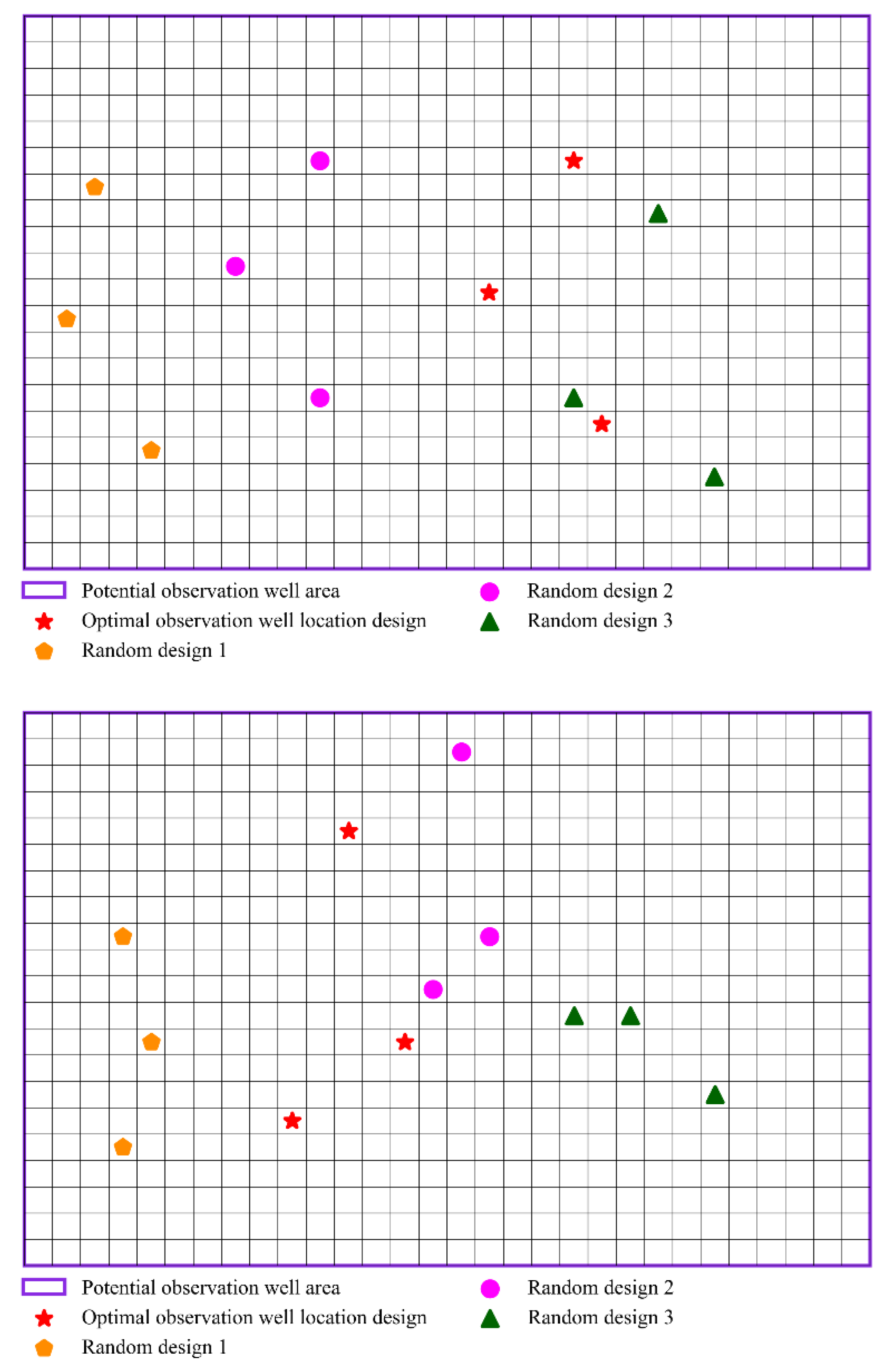
3.3. Optimal Observation Well Location Design for Case Studies
3.4. Computational Time Analysis
4. Results and Discussion
4.1. Analysis of the Surrogate Model
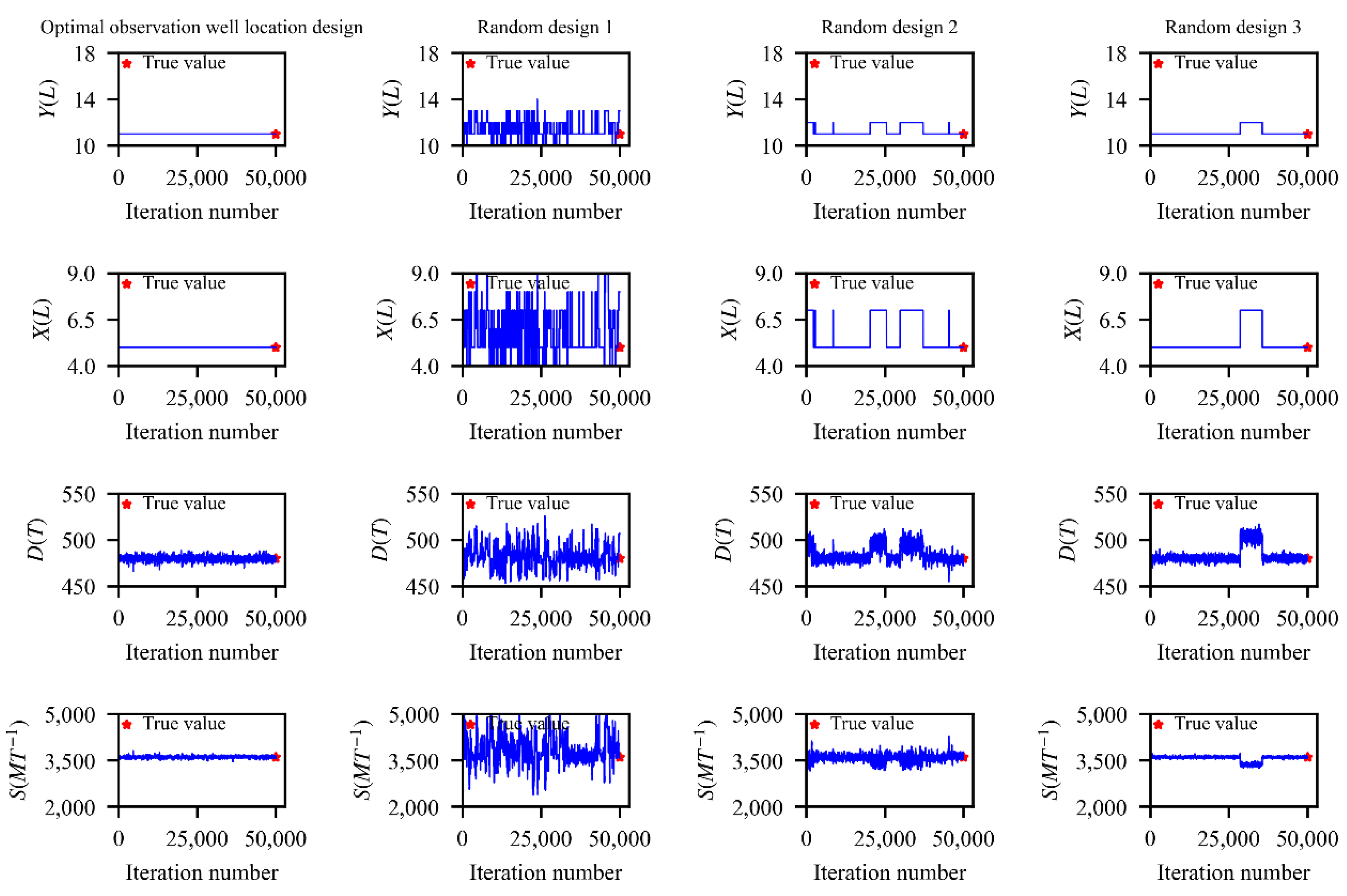
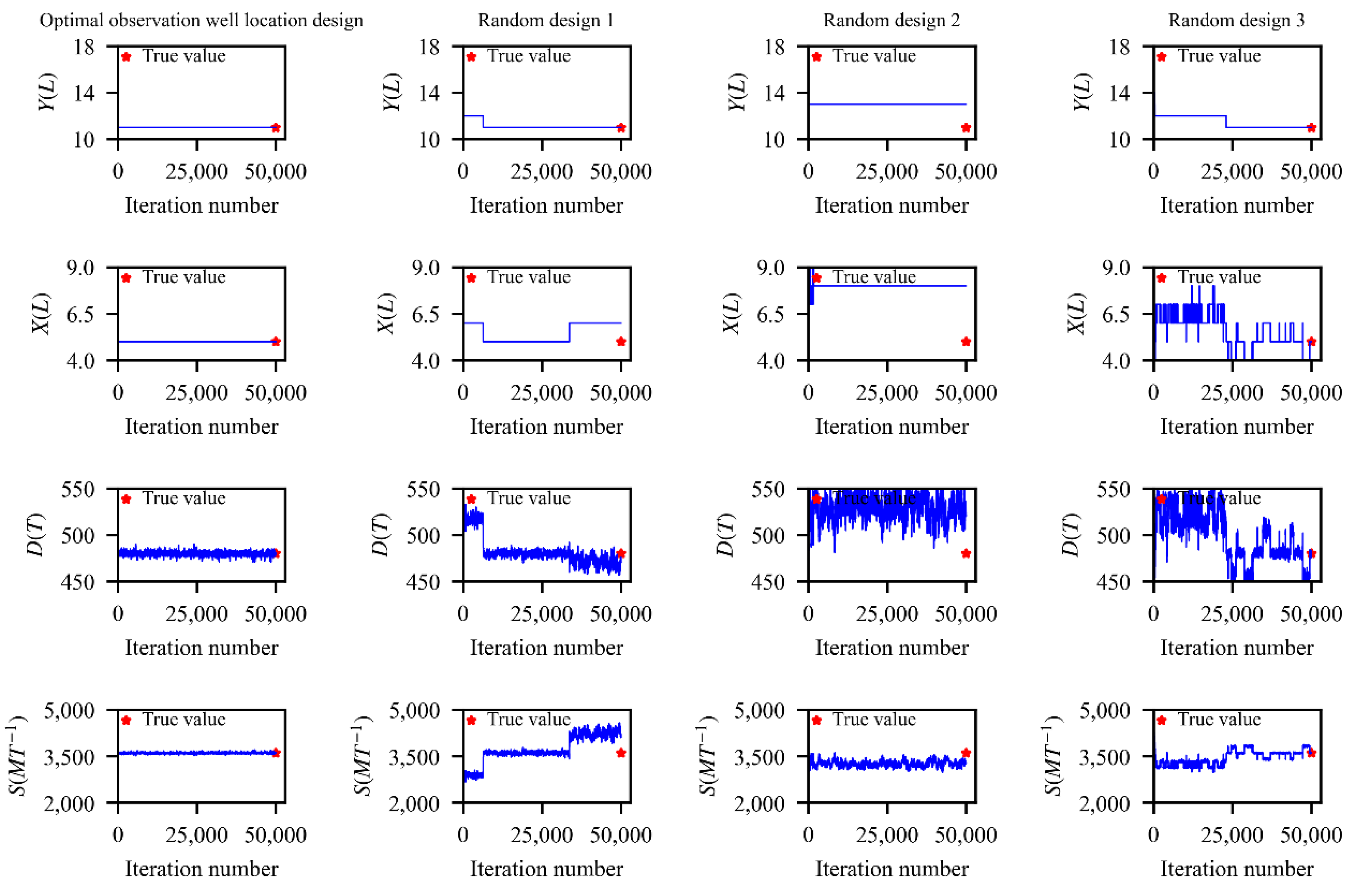
4.2. Analysis of the Optimal Observation Well Locations
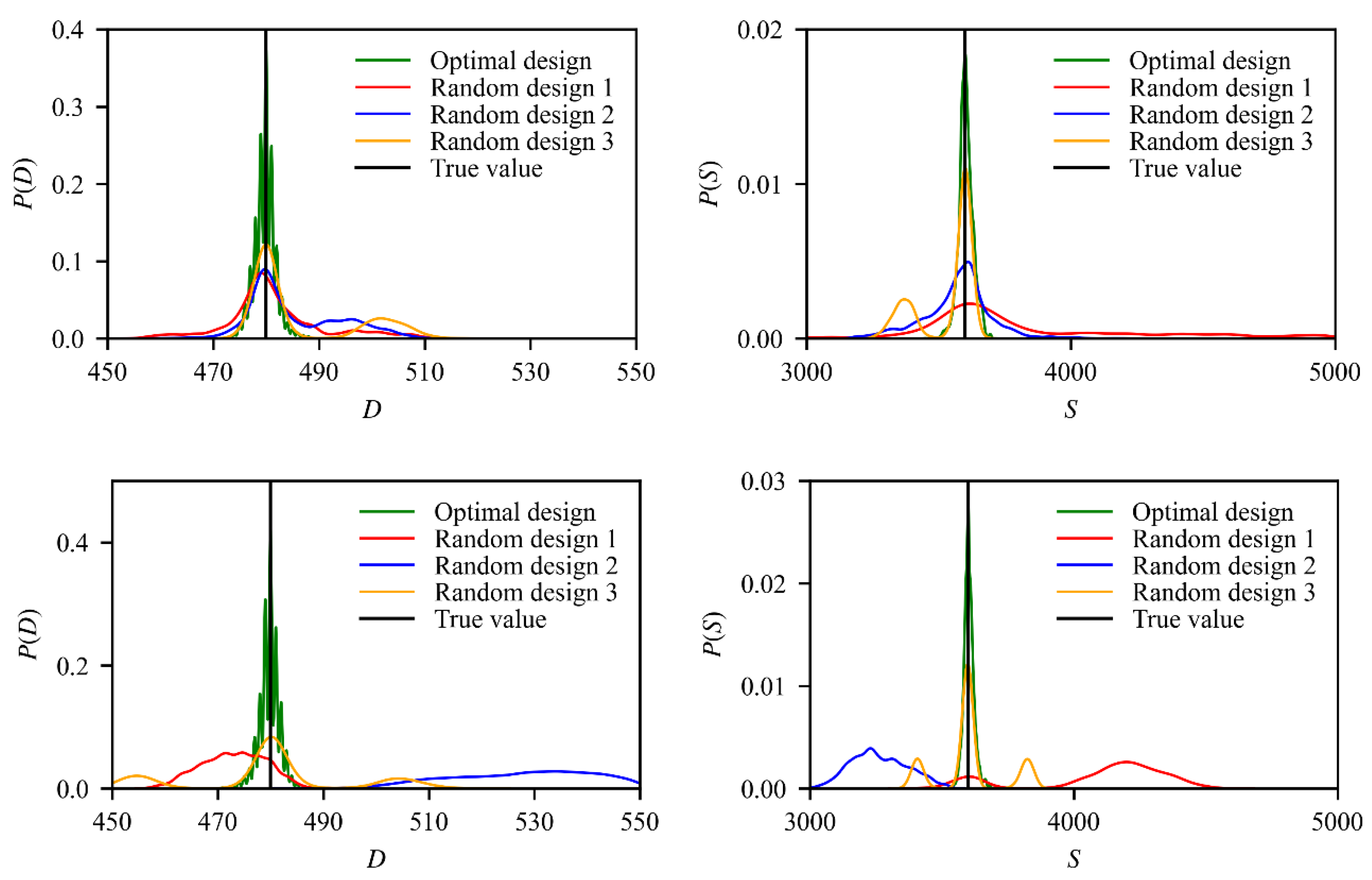
4.3. Analysis of the Parameter Identification Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Egbueri, J.C.; Agbasi, J.C. Combining data-intelligent algorithms for the assessment and predictive modeling of groundwater resources quality in parts of southeastern Nigeria. Environ. Sci. Pollut. Res. 2022, 1–25. [Google Scholar] [CrossRef]
- Egbueri, J.C.; Unigwe, C.O.; Omeka, M.E.; Ayejoto, D.A. Urban groundwater quality assessment using pollution indicators and multivariate statistical tools: A case study in southeast Nigeria. Int. J. Environ. Anal. Chem. 2021, 4, 1–27. [Google Scholar] [CrossRef]
- Egbueri, J.C. Groundwater quality assessment using pollution index of groundwater (PIG), ecological risk index (ERI) and hierarchical cluster analysis (HCA): A case study. Groundw. Sustain. Dev. 2019, 10, 100292. [Google Scholar] [CrossRef]
- Omeka, M.E.; Egbueri, J.C. Hydrogeochemical assessment and health-related risks due to toxic element ingestion and dermal contact within the nnewi-awka urban areas, Nigeria. Environ. Geochem. Health 2022, 1–29. [Google Scholar] [CrossRef]
- Ayvaz, M.T. A hybrid simulation–optimization approach for solving the areal groundwater pollution source identification problems. J. Hydrol. 2016, 538, 161–176. [Google Scholar] [CrossRef]
- Datta, B. Optimal unknown pollution source characterization in a contaminated groundwater aquifer—Evaluation of a developed dedicated software tool. J. Geosci. Environ. Prot. 2014, 2, 41. [Google Scholar] [CrossRef]
- Zeng, L.; Shi, L.; Zhang, D.; Wu, L. A sparse grid based Bayesian method for contaminant source identification. Adv. Water Resour. 2012, 37, 1–9. [Google Scholar] [CrossRef]
- Atmadja, J.; Bagtzoglou, A.C. State of the art report on mathematical methods for groundwater pollution source identification. Environ. Forensics 2001, 2, 205–214. [Google Scholar] [CrossRef]
- Datta, B.; Chakrabarty, D.; Dhar, A. Identification of unknown groundwater pollution sources using classical optimization with linked simulation. J. Hydro-Environ. Res. 2011, 5, 25–36. [Google Scholar] [CrossRef]
- Sun, A.Y.; Painter, S.L.; Wittmeyer, G.W. A constrained robust least squares approach for contaminant release history identification. Water Resour. Res. 2006, 42, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Amirabdollahian, M.; Datta, B. Identification of pollutant source characteristics under uncertainty in contaminated water resources systems using adaptive simulated anealing and fuzzy logic. Int. J. GEOMATE 2014, 6, 757–762. [Google Scholar] [CrossRef]
- Huang, L.; Wang, L.; Zhang, Y.; Xing, L.; Hao, Q.; Xiao, Y.; Yang, L.; Zhu, H. Identification of groundwater pollution sources by a SCE-UA algorithm-based simulation/optimization model. Water 2018, 10, 193. [Google Scholar] [CrossRef] [Green Version]
- Jha, M.K.; Datta, B. Linked simulation-optimization based dedicated monitoring network design for unknown pollutant source identification using dynamic time warping distance. Water Resour. Manag. 2014, 28, 4161–4182. [Google Scholar] [CrossRef]
- Butera, I.; Tanda, M.G. A geostatistical approach to recover the release history of groundwater pollutants. Water Resour. Res. 2003, 39, WR002314. [Google Scholar] [CrossRef]
- Gzyl, G.; Zanini, A.; Frączek, R.; Kura, K. Contaminant source and release history identification in groundwater: A multi-step approach. J. Contam. Hydrol. 2014, 157, 59–72. [Google Scholar] [CrossRef]
- Yan, X.; Dong, W.; An, Y.; Lu, W. A Bayesian-based integrated approach for identifying groundwater contamination sources. J. Hydrol. 2019, 579, 124160. [Google Scholar] [CrossRef]
- Alapati, S.; Kabala, Z.J. Recovering the release history of a groundwater contaminant using a non-linear least-squares method. Hydrol. Process. 2000, 14, 1003–1016. [Google Scholar] [CrossRef]
- Bagtzoglou, A.C.; Atmadja, J. Marching-jury backward beam equation and quasi-reversibility methods for hydrologic inversion: Application to contaminant plume spatial distribution recovery. Water Resour. Res. 2003, 39, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Woodbury, A.D.; Ulrych, T.J. Minimum relative entropy inversion: Theory and application to recovering the release history of a groundwater contaminant. Water Resour. Res. 1996, 32, 2671–2681. [Google Scholar] [CrossRef]
- Neupauer, R.M.; Borchers, B.; Wilson, J.L. A Comparison of Two Methods for Recovering the Release History of a Groundwater Contamination Source. Water Resour. Res. 2000, 36, 2469–2475. [Google Scholar] [CrossRef]
- Skaggs, T.H.; Kabala, Z.J. Recovering the release history of a groundwater contaminant. Water Resour. Res. 1994, 30, 71–79. [Google Scholar] [CrossRef]
- Ma, X.; Zabaras, N. An efficient Bayesian inference approach to inverse problems based on an adaptive sparse grid collocation method. Inverse Probl. 2009, 25, 35013–35027. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, L.; Chen, C.; Chen, D.; Wu, L. Efficient Bayesian experimental design for contaminant source identification. Water Resour. Res. 2015, 51, 576–598. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Q.; Chen, D.; Wu, L.; Zeng, L. Surrogate-Based Bayesian Inverse Modeling of the Hydrological System: An Adaptive Approach Considering Surrogate Approximation Error. Water Resour. Res. 2020, 56, e2019WR025721. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Morse, B.S.; Pohll, G.; Huntington, J.; Rodriguez, R. Stochastic capture zone analysis of an arsenic-contaminated well using the generalized likelihood uncertainty estimator (GLUE) methodology. Water Resour. Res. 2003, 39, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Rojas, R.; Feyen, L.; Dassargues, A. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging. Water Resour. Res. 2008, 44, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Blasone, R.S.; Vrugt, J.A.; Madsen, H.; Rosbjerg, D.; Robinson, B.A.; Zyvoloski, G.A. Generalized likelihood uncertainty estimation (GLUE) using adaptive Markov Chain Monte Carlo sampling. Adv. Water Resour. 2008, 31, 630–648. [Google Scholar] [CrossRef] [Green Version]
- Montanari, A. Large sample behaviors of the generalized likelihood uncertainty estimation (GLUE) in assessing the uncertainty of rainfall-runoff simulations. Water Resour. Res. 2005, 41, 1–13. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- An, Y.; Lu, W.; Cheng, W. Surrogate model application to the identification of optimal groundwater exploitation scheme based on regression kriging method—A case study of Western Jilin Province. Int. J. Environ. Res. Public Health 2015, 12, 8897–8918. [Google Scholar] [CrossRef] [Green Version]
- Haario, H.; Saksman, E.; Tamminen, J. Adaptive proposal distribution for random walk Metropolis algorithm. Comput. Stat. 1999, 14, 375–395. [Google Scholar] [CrossRef]
- Haario, H.; Saksman, E.; Tamminen, J. An adaptive Metropolis algorithm. Bernoulli 2001, 7, 223–242. [Google Scholar] [CrossRef] [Green Version]
- Haario, H.; Laine, M.; Mira, A.; Saksman, E. DRAM: Efficient adaptive MCMC. Stat. Comput. 2006, 16, 339–354. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F.; Diks, C.G.H.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J. DREAM (D): An adaptive Markov Chain Monte Carlo simulation algorithm to solve discrete, noncontinuous, and combinatorial posterior parameter estimation problems. Hydrol. Earth Syst. Sci. 2011, 15, 3701–3713. [Google Scholar] [CrossRef] [Green Version]
- Laloy, E.; Rogiers, B.; Vrugt, J.A.; Mallants, D.; Jacques, D. Efficient posterior exploration of a high-dimensional groundwater model from two-stage Markov chain Monte Carlo simulation and polynomial chaos expansion. Water Resour. Res. 2013, 49, 2664–2682. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Jin, X. Characterization of groundwater contaminant source using Bayesian method. Stoch. Environ. Res. Risk Assess. 2013, 27, 867–876. [Google Scholar] [CrossRef]
- Datta, B.; Chakrabarty, D.; Dhar, A. Optimal dynamic monitoring network design and identification of unknown groundwater pollution sources. Water Resour. Manag. 2009, 23, 2031–2049. [Google Scholar] [CrossRef]
- Prakash, O.; Datta, B. Sequential optimal monitoring network design and iterative spatial estimation of pollutant concentration for identification of unknown groundwater pollution source locations. Environ. Monit. Assess. 2013, 185, 5611–5626. [Google Scholar] [CrossRef] [PubMed]
- Michalak, A.M.; Kitanidis, P.K. A method for enforcing parameter nonnegativity in Bayesian inverse problems with an application to contaminant source identification. Water Resour. Res. 2003, 39, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Huan, X.; Marzouk, Y.M. Simulation-based optimal Bayesian experimental design for nonlinear systems. J. Comput. Phys. 2013, 232, 288–317. [Google Scholar] [CrossRef] [Green Version]
- An, Y.; Yan, X.; Lu, W.; Qian, H.; Zhang, Z. An improved Bayesian approach linked to a surrogate model for identifying groundwater pollution sources. Hydrogeol. J. 2022, 30, 601–616. [Google Scholar] [CrossRef]
- Mo, S.; Zabaras, N.; Shi, X.; Wu, J. Deep autoregressive neural networks for high-dimensional inverse problems in groundwater contaminant source identification. Water Resour. Res. 2019, 55, 3856–3881. [Google Scholar] [CrossRef] [Green Version]
- Xing, Z.; Qu, R.; Zhao, Y.; Fu, Q.; Ji, Y.; Lu, W. Identifying the release history of a groundwater contaminant source based on an ensemble surrogate model. J. Hydrol. 2019, 572, 501–516. [Google Scholar] [CrossRef]
- Ruck, D.W.; Rogers, S.K.; Kabrisky, M.; Maybeck, P.S.; Oxley, M.E. Comparative analysis of backpropagation and the extended Kalman filter for training multilayer perceptrons. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 686–691. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, The U.S. Geological Survey Modular Groundwater Model—The GroundWater Flow Process; U.S. Geological Survey Techniques and Methods 6-A16; U.S. Geological Survey: Reston, VA, USA, 2005.
- Zheng, C.; Wang, P.P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide; U.S. Army Corps of Engineers—Engineer Research and Development Center: Vicskburg, MS, USA, 1999. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Agirre-Basurko, E.; Ibarra-Berastegi, G.; Madariaga, I. Regression and multilayer perceptron-based models to forecast hourly O3 and NO2 levels in the Bilbao area. Environ. Model. Softw. 2006, 21, 430–446. [Google Scholar] [CrossRef]
- Egbueri, J.C.; Agbasi, J.C. Performances of MLR, RBF-NN, and MLP-NN in the evaluation and prediction of water resources quality for irrigation purposes under two modeling scenarios. Geocarto Int. 2022, 1–28. [Google Scholar] [CrossRef]
- Noriega, L. Multilayer Perceptron Tutorial; School of Computing, Staffordshire University: Stoke-on-Trent, UK, 2005. [Google Scholar]
- Zhao, Y.; Lu, W.; Xiao, C. A Kriging surrogate model coupled in simulation–optimization approach for identifying release history of groundwater sources. J. Contam. Hydrol. 2016, 185, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]

| Parameters | Values | Unit |
|---|---|---|
| Hydraulic conductivity, K | 18.00 | LT−1 |
| Porosity, n | 0.30 | - |
| Longitudinal dispersivity, αL | 12.00 | L |
| Transverse dispersivity, αT | 3.60 | L |
| Parameters | True Values | Prior Ranges | Unit |
|---|---|---|---|
| S | 3600 | [2000, 5000] | MT−1 |
| D | 480 | [450, 550] | T |
| X | 11 | [10, 18] | L |
| Y | 5 | [4, 9] | L |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, Y.; Zhang, Y.; Yan, X. An Integrated Bayesian and Machine Learning Approach Application to Identification of Groundwater Contamination Source Parameters. Water 2022, 14, 2447. https://doi.org/10.3390/w14152447
An Y, Zhang Y, Yan X. An Integrated Bayesian and Machine Learning Approach Application to Identification of Groundwater Contamination Source Parameters. Water. 2022; 14(15):2447. https://doi.org/10.3390/w14152447
Chicago/Turabian StyleAn, Yongkai, Yanxiang Zhang, and Xueman Yan. 2022. "An Integrated Bayesian and Machine Learning Approach Application to Identification of Groundwater Contamination Source Parameters" Water 14, no. 15: 2447. https://doi.org/10.3390/w14152447





