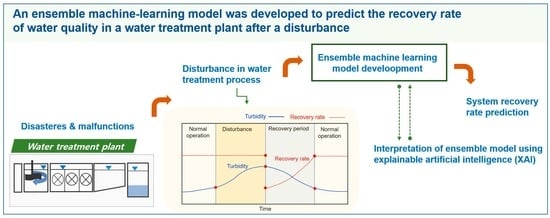
Prediction and Interpretation of Water Quality Recovery after a Disturbance in a Water Treatment System Using Artificial Intelligence
Abstract
:1. Introduction
2. Materials and Methods
2.1. Pilot Plant Operation
2.2. Model Development
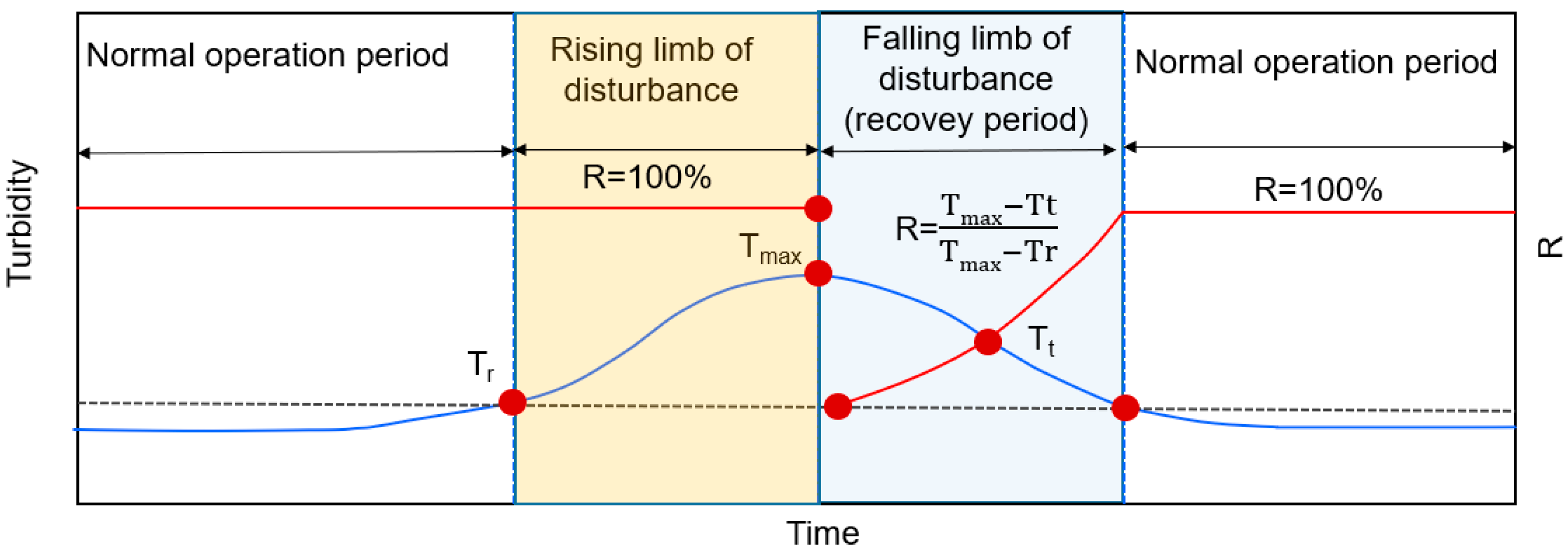
2.2.1. Definition of the Recovery Rate
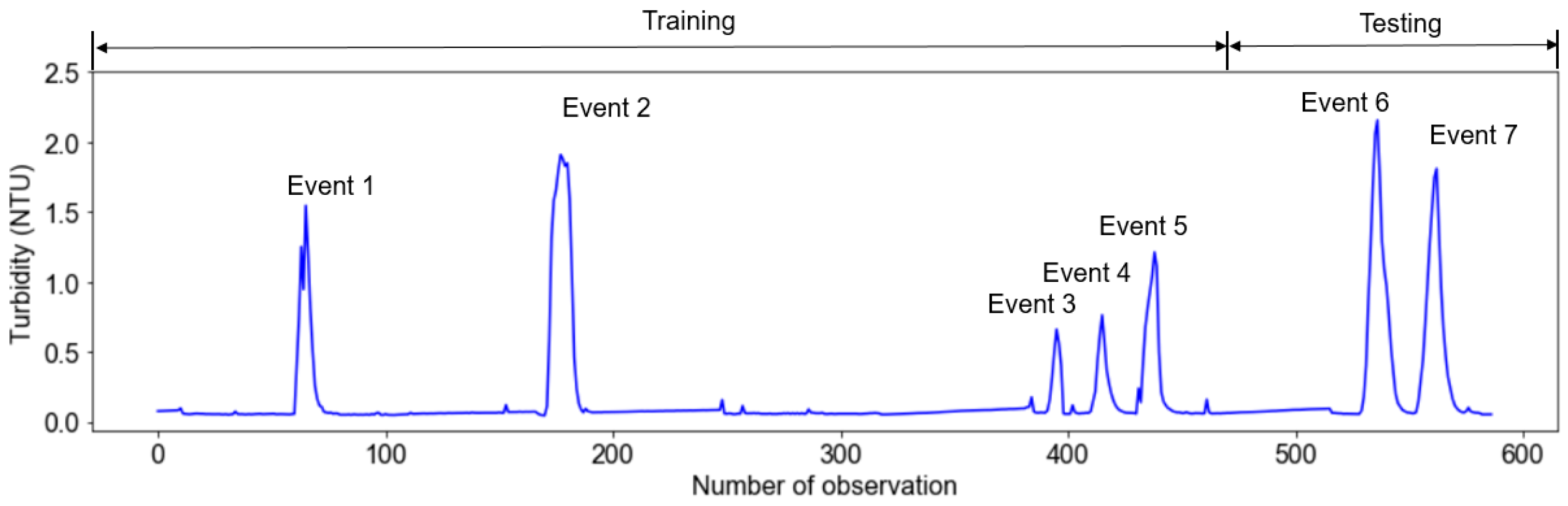
2.2.2. Operation Scenario
2.2.3. Data Split for the Training and Testing of the Model
2.2.4. Input Variables
2.2.5. Pretreatment of the Input Variable
2.2.6. Post-Treatment of Machine Learning Results
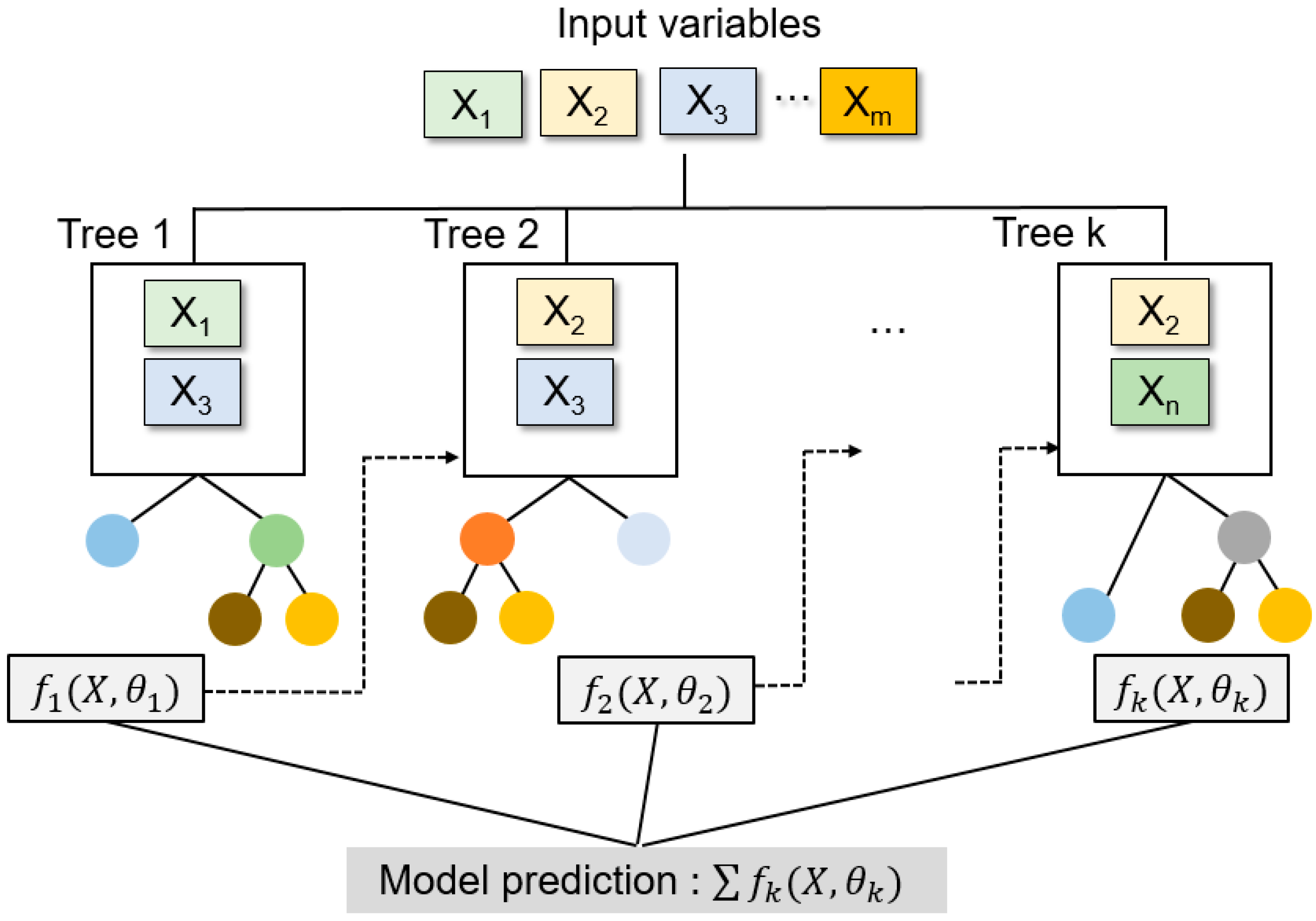
2.3. Machine Learning Model Selection
2.4. Model Evaluation
2.5. XAI for Model Interpretation
3. Results and Discussion
3.1. Water Quality of the Pilot Plant
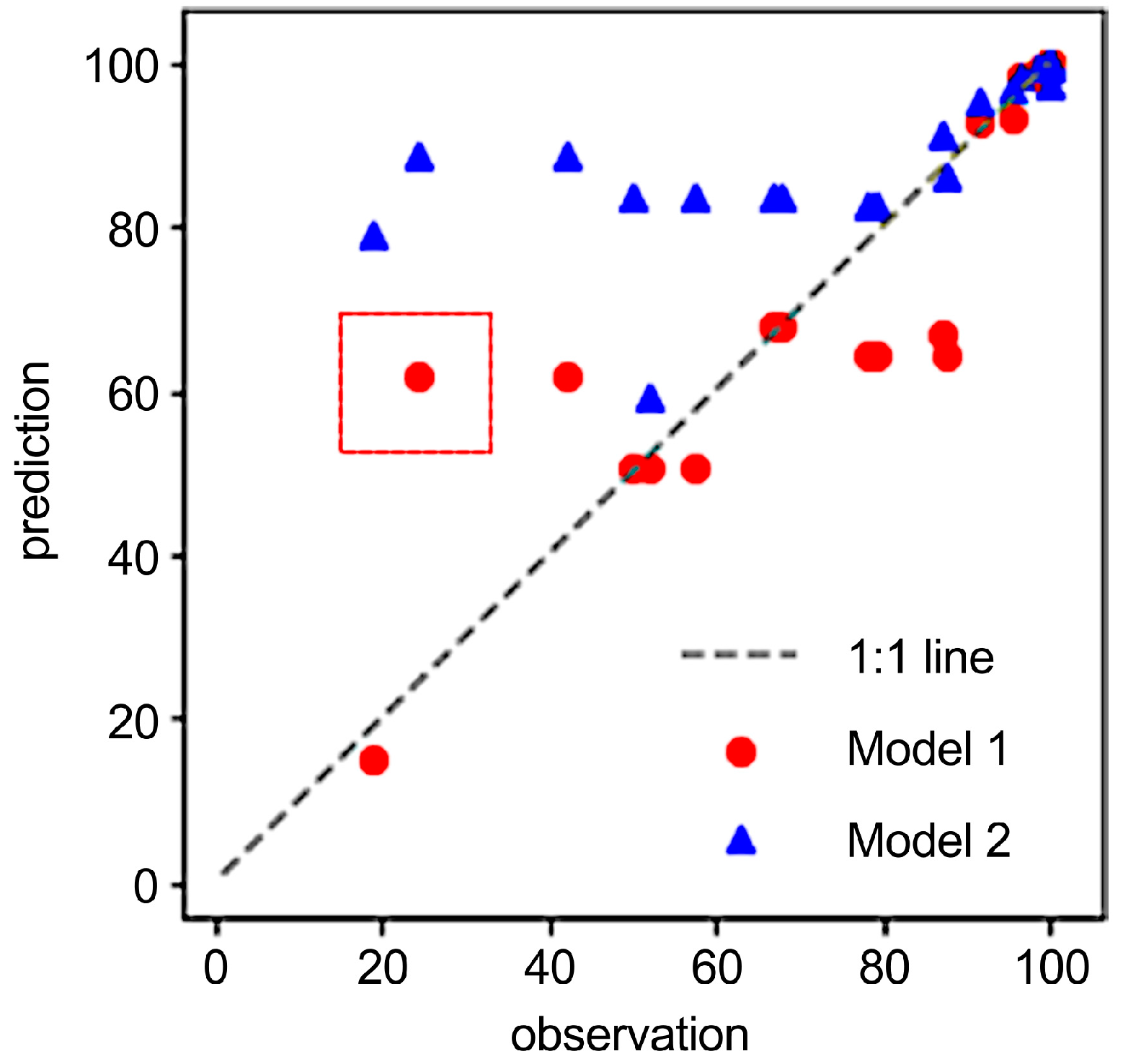
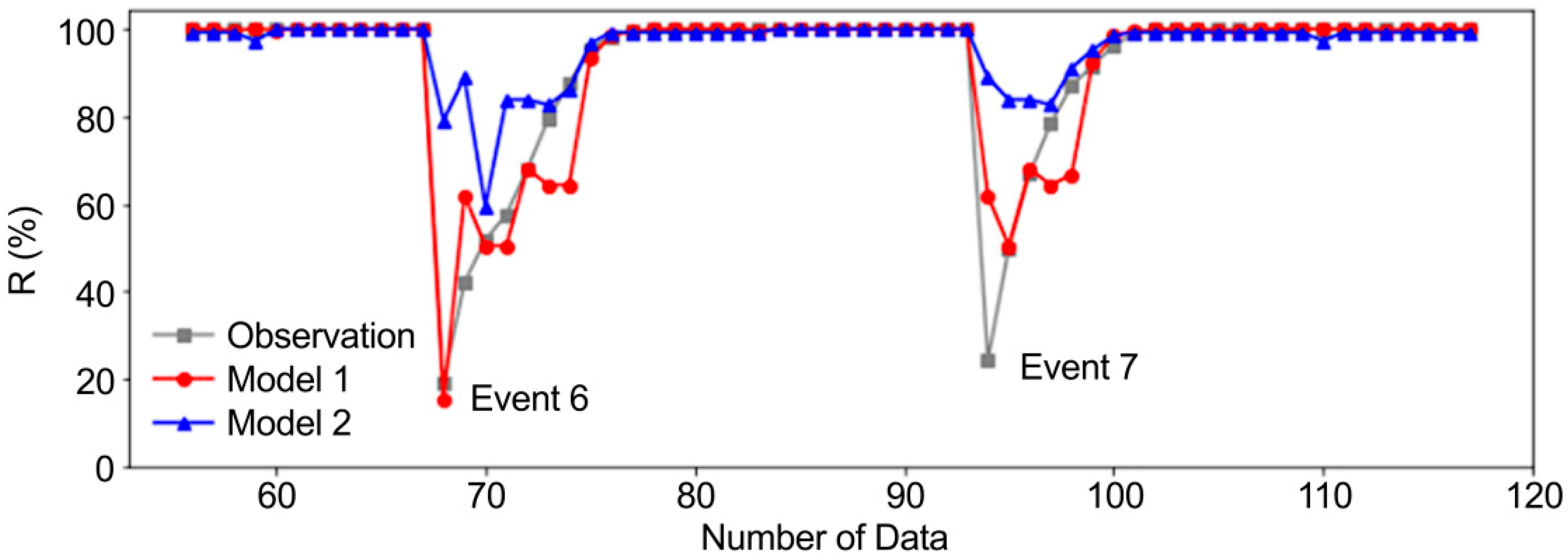
3.2. Model Prediction of Recovery Rate
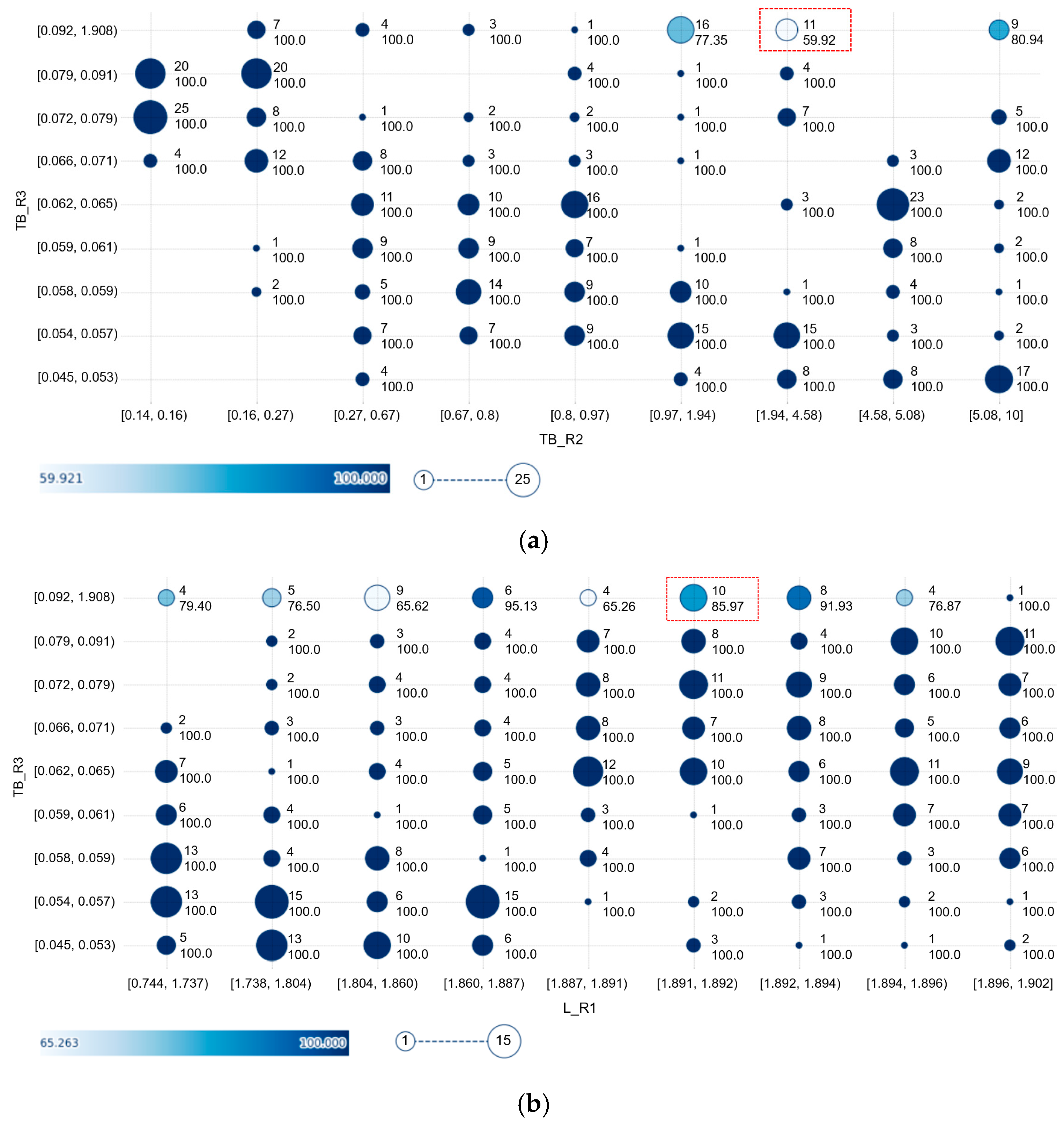
3.3. Explainable Artificial Intelligence for Model Interpretation
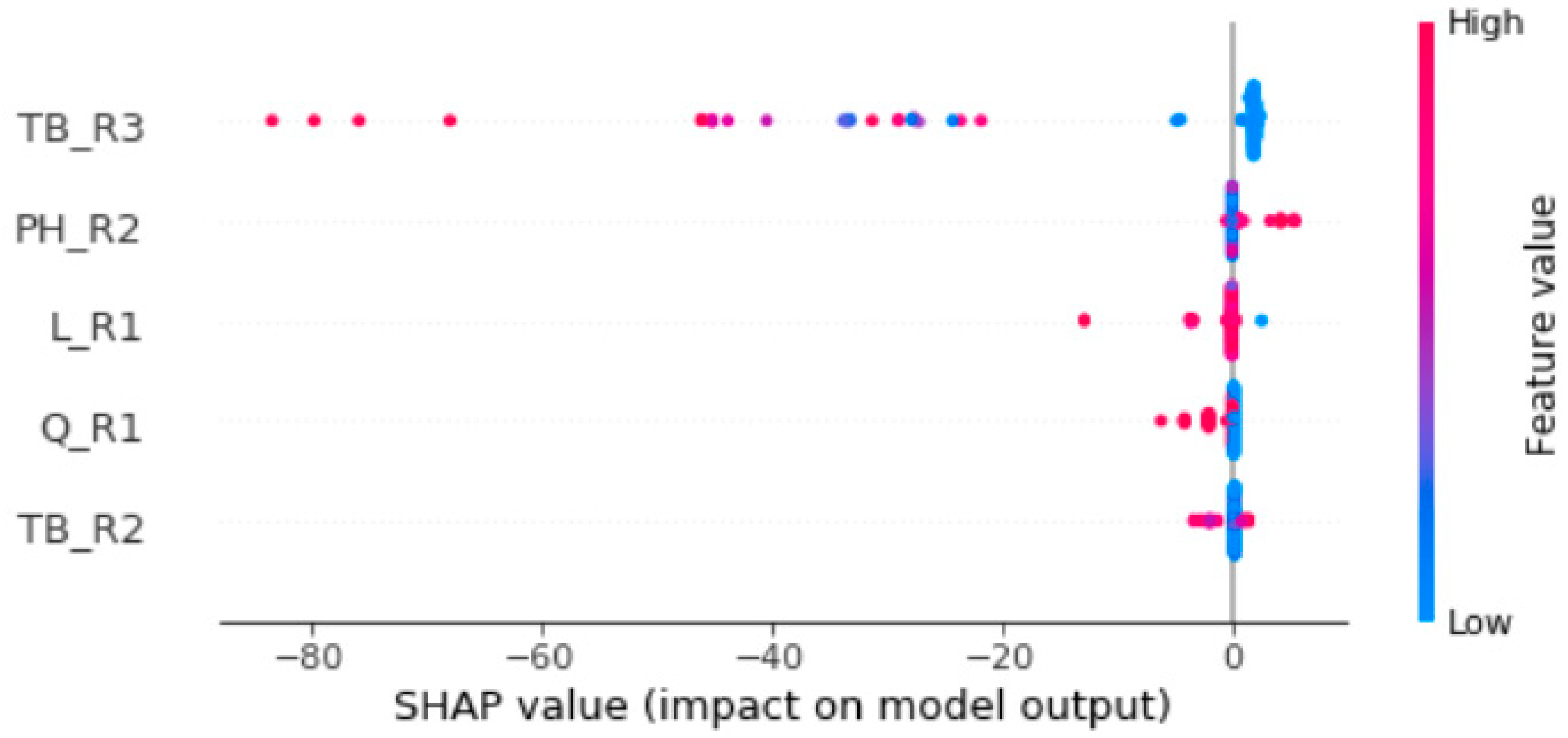
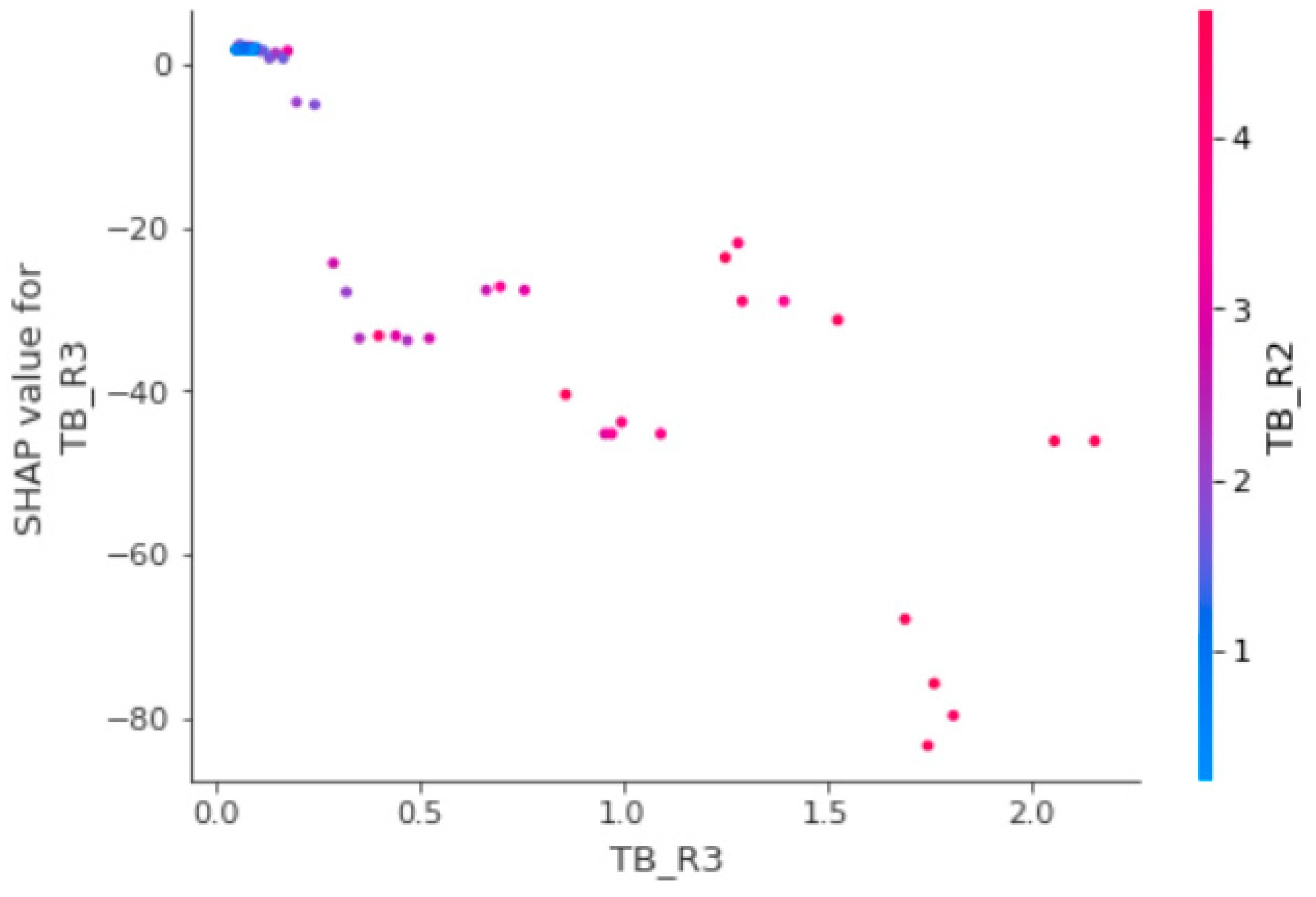
3.3.1. SHAP
3.3.2. Exploratory Data Analysis with SHAP
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Davis, C.A. Water system service categories, post-earthquake interaction, and restoration strategies. Earthq. Spectra 2014, 30, 1487–1509. [Google Scholar] [CrossRef]
- Matthews, J.C. Disaster resilience of critical water infrastructure systems. J. Struct. Eng. 2016, 142, C6015001. [Google Scholar] [CrossRef]
- WHO. Emergencies and Disasters in Drinking Water Supply and Sewage Systems: Guidelines for Effective Response; Pan American Health Organization: Washington, DC, USA, 2002; pp. 5–12. [Google Scholar]
- Park, J.; Park, J.-H.; Choi, J.-S.; Joo, J.C.; Park, K.; Yoon, H.C.; Park, C.Y.; Lee, W.H.; Heo, T.-Y. Ensemble model development for the prediction of a disaster index in water treatment systems. Water 2020, 12, 3195. [Google Scholar] [CrossRef]
- Shamsuzzoha, M.; Kormoker, T.; Ghosh, R.C. Implementation of water safety plan considering climatic disaster risk reduction in Bangladesh: A study on Patuakhali Pourashava water supply system. Procedia Eng. 2018, 212, 583–590. [Google Scholar] [CrossRef]
- Gaya, M.S.; Zango, M.U.; Yusuf, L.A.; Mustapha, M.; Muhammad, B.; Sani, A.; Tijjani, A.; Wahab, N.A.; Khairi, M.T.M. Estimation of turbidity in water treatment plant using Hammerstein-Wiener and neural network technique. Indones. J. Electr. Eng. Comput. Sci. 2017, 5, 666–672. [Google Scholar] [CrossRef]
- Iglesias, C.; Martínez Torres, J.; García Nieto, P.J.; Alonso Fernández, J.R.; Díaz Muñiz, C.; Piñeiro, J.I.; Taboada, J. Turbidity prediction in a river basin by using artificial neural networks: A case study in northern Spain. Water Resour. Manag. 2014, 28, 319–331. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Pei, J.; Deng, M. An ensemble risk assessment model for urban rainstorm disasters based on random forest and deep belief nets: A case study of Nanjing, China. Nat. Hazards 2021, 107, 2671–2692. [Google Scholar] [CrossRef]
- Santos, L.B.L.; Londe, L.R.; de Carvalho, T.J.; Menasché, D.S.; Vega-Oliveros, D.A. Towards Mathematics, Computers and Environment: A Disasters Perspective; Springer: Berlin/Heidelberg, Germany, 2019; pp. 185–215. [Google Scholar]
- Inoue, J.; Yamagata, Y.; Chen, Y.; Poskitt, C.M.; Sun, J. Anomaly detection for a water treatment system using unsupervised machine learning. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 1058–1065. [Google Scholar]
- Abba, S.I.; Pham, Q.B.; Usman, A.G.; Linh, N.T.T.; Aliyu, D.S.; Nguyen, Q.; Bach, Q.-V. Emerging evolutionary algorithm integrated with kernel principal component analysis for modeling the performance of a water treatment plant. J. Water Process Eng. 2020, 33, 101081. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Gitis, V.; Hankins, N. Water treatment chemicals: Trends and challenges. J. Water Process Eng. 2018, 25, 34–38. [Google Scholar] [CrossRef]
- Ghaffarian, S.; Emtehani, S. Monitoring urban deprived areas with remote sensing and machine learning in case of disaster recovery. Climate 2021, 9, 58. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Kerle, N.; Kuffer, M.; Ghaffarian, S. Post-disaster recovery assessment with machine learning-derived land cover and land use information. Remote Sens. 2019, 11, 1174. [Google Scholar] [CrossRef] [Green Version]
- Ghandehari, S.; Montazer-Rahmati, M.M.; Asghari, M. A comparison between semi-theoretical and empirical modeling of cross-flow microfiltration using ANN. Desalination 2011, 277, 348–355. [Google Scholar] [CrossRef]
- Li, L.; Rong, S.; Wang, R.; Yu, S. Recent advances in artificial intelligence and machine learning for nonlinear relationship analysis and process control in drinking water treatment: A review. Chem. Eng. J. 2021, 405, 126673. [Google Scholar] [CrossRef]
- O’Reilly, G.; Bezuidenhout, C.C.; Bezuidenhout, J.J. Artificial neural networks: Applications in the drinking water sector. Water Supply 2018, 18, 1869–1887. [Google Scholar] [CrossRef]
- Zhang, K.; Achari, G.; Li, H.; Zargar, A.; Sadiq, R. Machine learning approaches to predict coagulant dosage in water treatment plants. Int. J. Syst. Assur. Eng. Manag. 2013, 4, 205–214. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Lu, H.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Z.; Sassoubre, L.; Yu, G.; Liao, C.; Hu, Q.; Wang, Y. Improving the robustness of beach water quality modeling using an ensemble machine learning approach. Sci. Total Environ. 2021, 765, 142760. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Sutton, C.D. Classification and regression trees, bagging, and boosting. Handb. Stat. 2005, 24, 303–329. [Google Scholar]
- Dunnington, D.W.; Trueman, B.F.; Raseman, W.J.; Anderson, L.E.; Gagnon, G.A. Comparing the Predictive performance, interpretability, and accessibility of machine learning and physically based models for water treatment. ACS ES&T Eng. 2020, 1, 348–356. [Google Scholar]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on explainable artificial intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Lee, W.H.; Kim, K.T.; Park, C.Y.; Lee, S.; Heo, T.-Y. Interpretation of ensemble learning to predict water quality using explainable artificial intelligence. Sci. Total Environ. 2022, 832, 15507. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Shin, Y.; Kim, T.; Hong, S.; Lee, S.; Lee, E.; Hong, S.; Lee, C.; Kim, T.; Park, M.S.; Park, J.; et al. Prediction of chlorophyll-a concentrations in the Nakdong River using machine learning methods. Water 2020, 12, 1822. [Google Scholar] [CrossRef]
- Uddameri, V.; Silva, A.L.B.; Singaraju, S.; Mohammadi, G.; Hernandez, E.A. Tree-based modeling methods to predict nitrate exceedances in the Ogallala aquifer in Texas. Water 2020, 12, 1023. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Wang, Y.; Zhang, K.; Hu, M.; Weng, Q.; Zhang, H. Spatial heterogeneity modeling of water quality based on random forest regression and model interpretation. Environ. Res. 2021, 202, 111660. [Google Scholar] [CrossRef]
- Zhang, D.; Qian, L.; Mao, B.; Huang, C.; Huang, B.; Si, Y. A data-driven design for fault detection of wind turbines using random forests and XGboost. IEEE Access 2018, 6, 21020–21031. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- XGBoost. Available online: https://pypi.org/project/xgboost/ (accessed on 1 July 2021).
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hellen, N.; Marvin, G. Explainable AI for safe water evaluation for public health in urban settings. In Proceedings of the International Conference on Innovations in Science, Engineering and Technology (ICISET), Chittagong, Bangladesh, 26–27 February 2022; pp. 1–6. [Google Scholar]
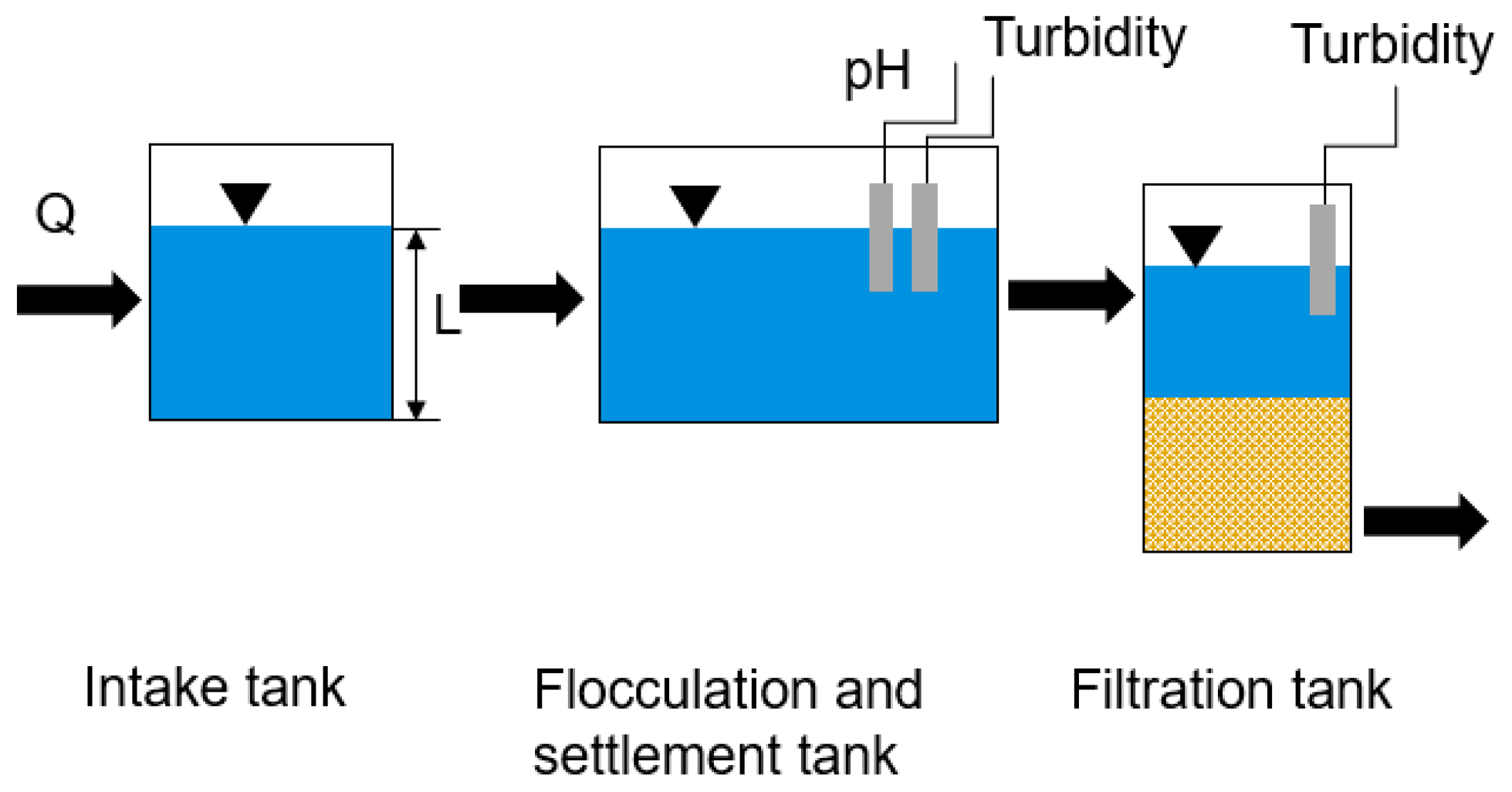

| Reactor | Observed Input Variable |
|---|---|
| Intake tank (17.96 m3) | Flow rate (Q_R1, m3/d), Water level (L_R1, m) |
| Flocculation and settlement tank (25.15 m3) | Turbidity (TB_R2, NTU), pH (PH_R2) |
| Filtration tank (1.44 m3) | Turbidity (TB_R3, NTU) |
| Event No. | Period of Coagulant Suspension | Observation Period |
|---|---|---|
| 1 | 10:30–16:30, 23 September 2020 | Period 1: 01:00 21 September 2020–23:00 27 September 2020 |
| 2 | 06:30–16:30, 29 September 2020 | Period 2: 01:00 29 September 2020–22:00 5 January 2021 |
| 3 | 14:37–19:37, 22 February 2021 | Period 3: 01:00 13 February 2021–22:00 28 February 2021 |
| 4 | 09:21–15:21, 24 February 2021 | |
| 5 | 08:24–15:24, 25 February 2021 | |
| 6 | 09:34–17:35, 3 March 2021 | Period 4: 00:00 3 March 2021–22:00 5 March 2021 |
| 7 | 10:29–19:29, 4 March 2021 |
| Variables | Min | Max | Average | Standard Deviation | |
|---|---|---|---|---|---|
| Independent variables | Q_R1(m3/d) | 0 | 15.345 | 7.188 | 5.135 |
| L_R1(m) | 0.744 | 1.902 | 1.832 | 0.159 | |
| TB_R2(NTU) | 0.144 | 10.000 | 1.852 | 1.912 | |
| pH _R2 | 5.531 | 8.712 | 7.151 | 0.998 | |
| TB_R3(NTU) | 0.045 | 2.156 | 0.175 | 0.342 | |
| Dependent variable | R | 1.659 | 100.00 | 97.312 | 12.813 |
| Hyperparameter | Optimal Value | |
|---|---|---|
| Model 1 | Model 2 | |
| n estimator | 50 | 50 |
| Max depth | 2 | 2 |
| Learning rate | 0.2 | 0.1 |
| Model | NSE | RMSE | RSR |
|---|---|---|---|
| Model 1 (with pretreatment) | 0.861 | 5.266 | 0.373 |
| Model 2 (without pretreatment) | 0.467 | 10.308 | 0.730 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Ahn, J.; Kim, J.; Yoon, Y.; Park, J. Prediction and Interpretation of Water Quality Recovery after a Disturbance in a Water Treatment System Using Artificial Intelligence. Water 2022, 14, 2423. https://doi.org/10.3390/w14152423
Park J, Ahn J, Kim J, Yoon Y, Park J. Prediction and Interpretation of Water Quality Recovery after a Disturbance in a Water Treatment System Using Artificial Intelligence. Water. 2022; 14(15):2423. https://doi.org/10.3390/w14152423
Chicago/Turabian StylePark, Jungsu, Juahn Ahn, Junhyun Kim, Younghan Yoon, and Jaehyeoung Park. 2022. "Prediction and Interpretation of Water Quality Recovery after a Disturbance in a Water Treatment System Using Artificial Intelligence" Water 14, no. 15: 2423. https://doi.org/10.3390/w14152423