A Dynamic Modeling Approach to Predict Water Inflow during Karst Tunnel Excavation
Abstract
:1. Introduction
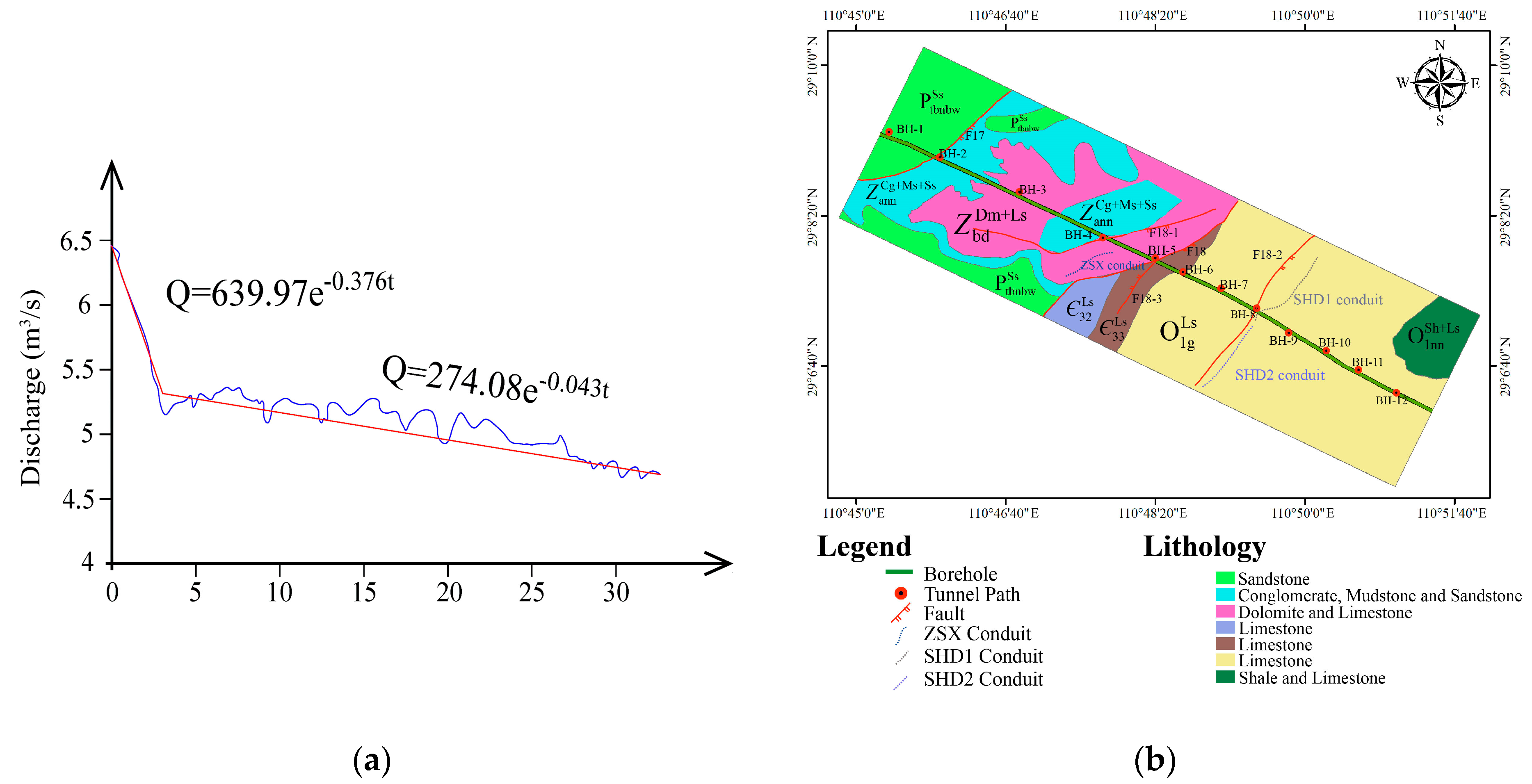
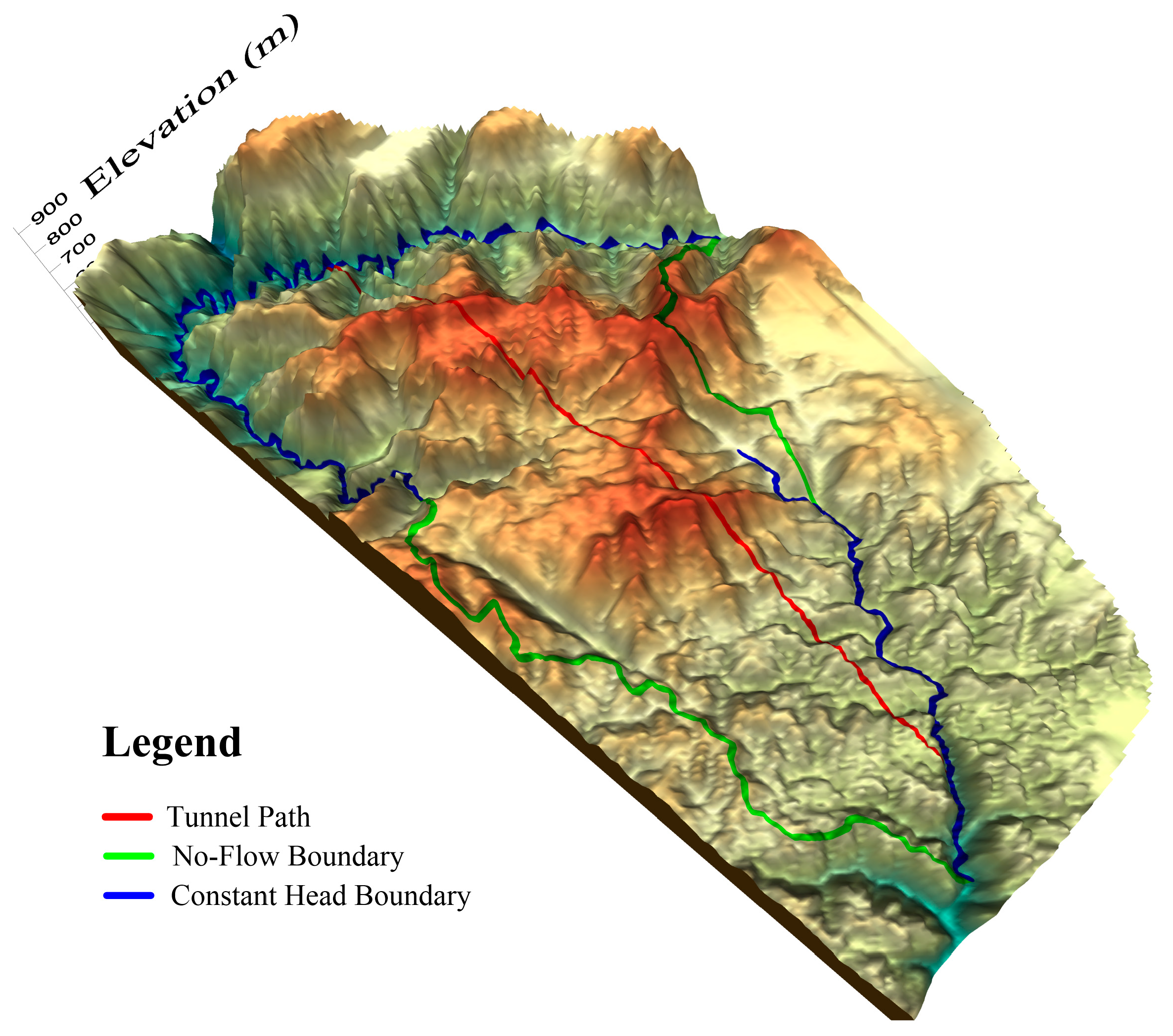
2. Overview of the Study Area
3. Modeling Approach
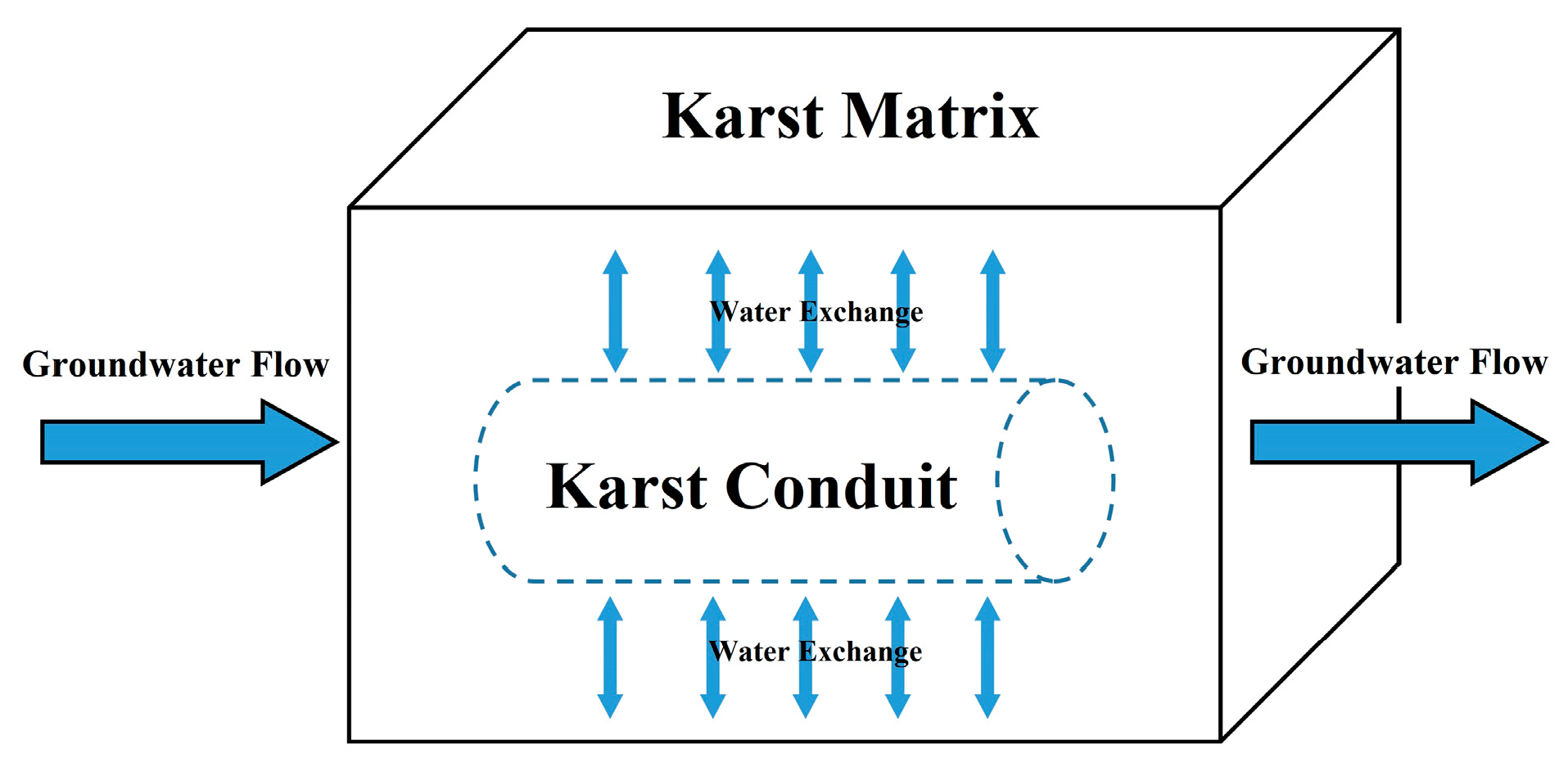
3.1. CFP Model
3.2. Boundary Conditions
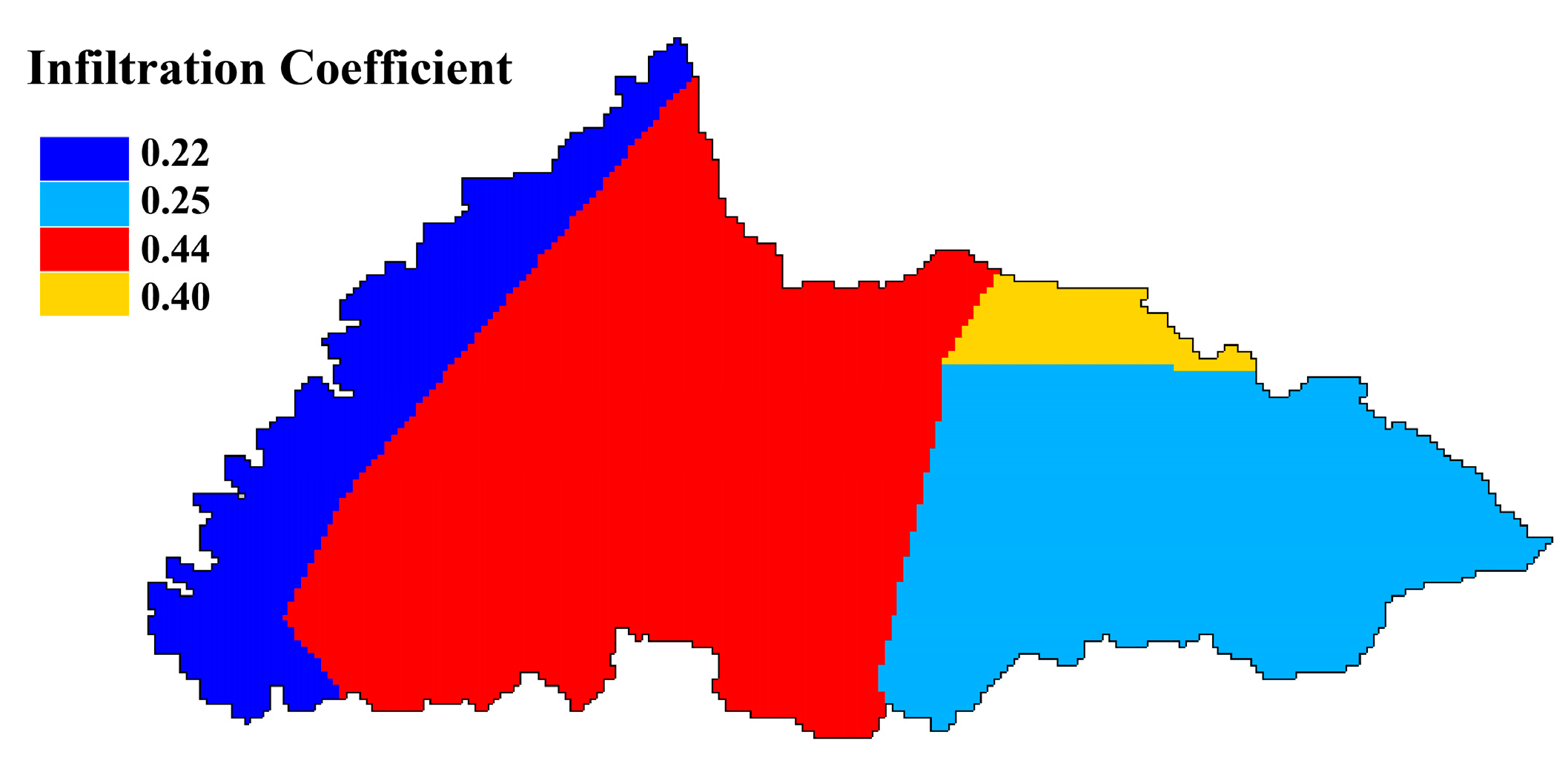
3.3. Aquifer Hydraulic Properties
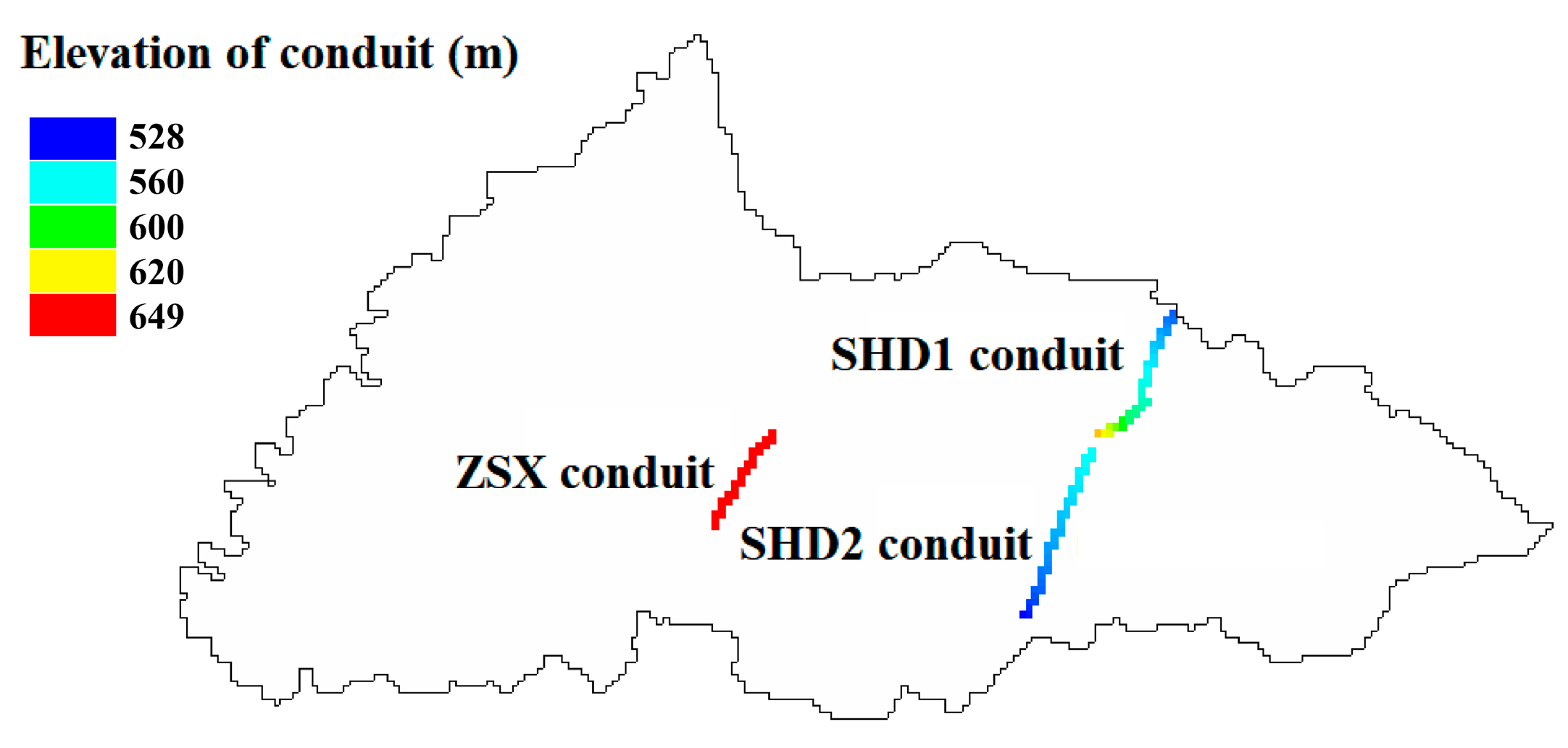
3.4. Conduit Parameter
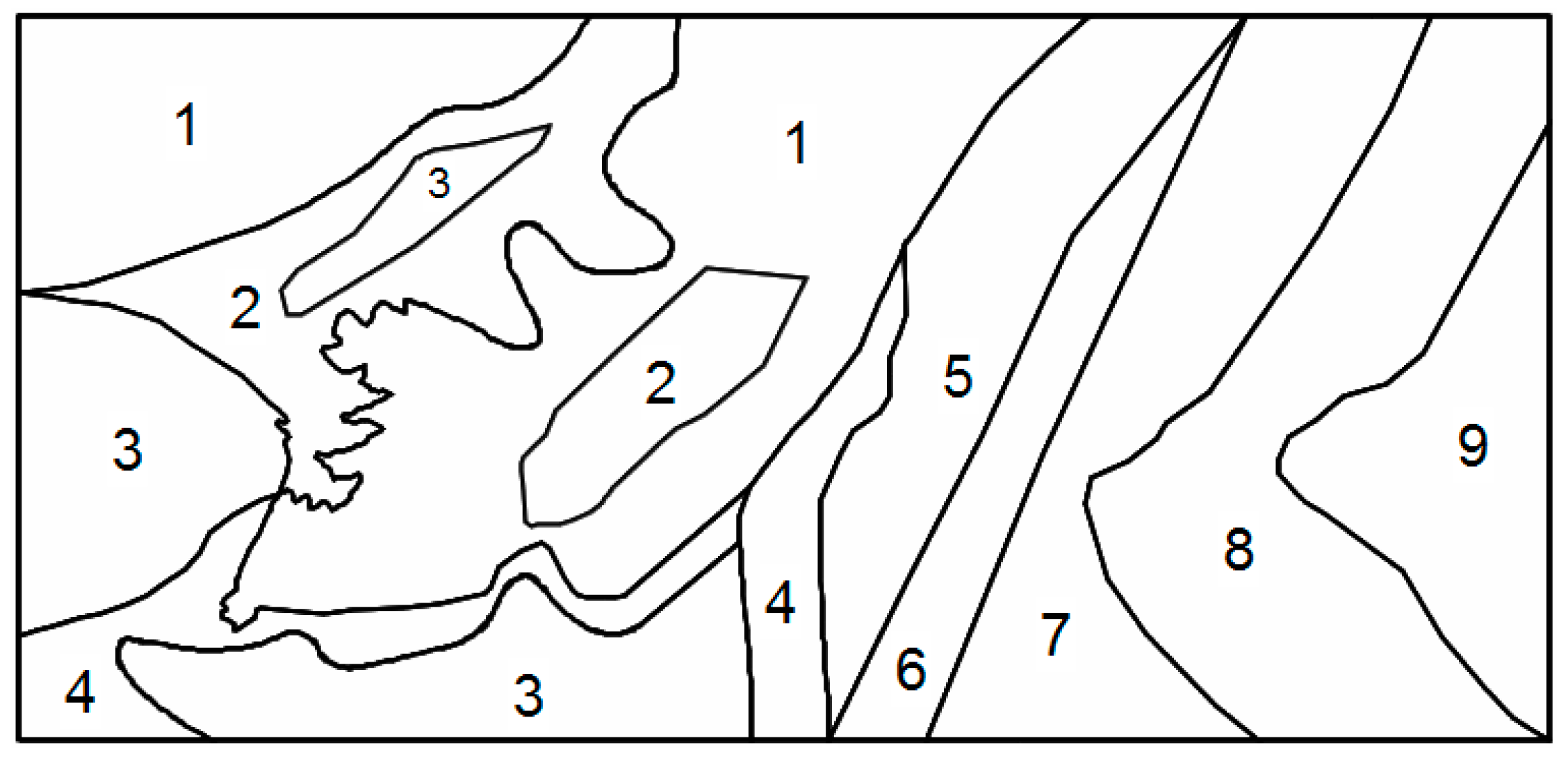
3.5. Model Representation
3.6. Dynamic Excavation
4. Results and Discussion
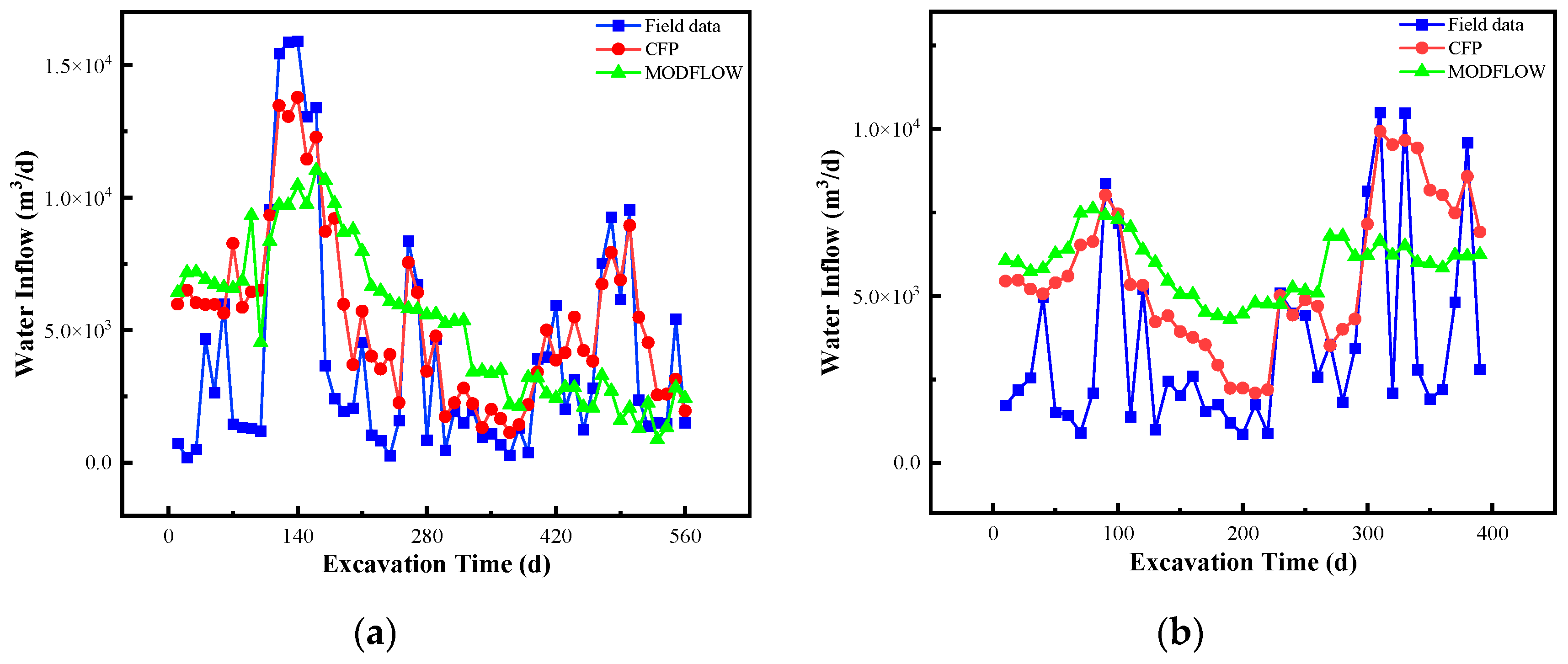
4.1. Model Calibration
4.2. Water Inflow Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, N.; Shen, S.L.; Zhou, A.; Arulrajah, A. Tunneling Induced Geohazards in Mylonitic Rock Faults with Rich Groundwater: A Case Study in Guangzhou. Tunn. Undergr. Space Technol. 2017, 74, 262–272. [Google Scholar] [CrossRef]
- Zhang, N.; Zheng, Q.; Elbaz, K.; Xu, Y.S. Water Inrush Hazards in the Chaoyang Tunnel, Guizhou, China: A Preliminary Investigation. Water 2020, 12, 1083. [Google Scholar] [CrossRef]
- Yang, W.; Fang, Z.; Yang, X.; Shi, S.; Wang, J.; Wang, H.; Bu, L.; Li, L.; Zhou, Z.; Li, X. Experimental Study of Influence of Karst Aquifer on the Law of Water Inrush in Tunnels. Water 2018, 10, 1211. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Teng, T.; Zhu, L.; He, M.; Ren, J.; Dong, X.; Liu, F. Evaluation of the Non-Darcy Effect of Water Inrush from Karst Collapse Columns by Means of a Nonlinear Flow Model. Water 2018, 10, 1234. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Chen, D.; Wang, J.; Bi, Y.; Liu, S.; Zhong, G.; Wang, C. Evolution Pattern and Matching Mode of Precursor Information about Water Inrush in a Karst Tunnel. Water 2021, 13, 1579. [Google Scholar] [CrossRef]
- Li, S.C.; Zhou, Z.Q.; Li, L.P.; Xu, Z.H.; Zhang, Q.Q.; Shi, S.S. Risk Assessment of Water Inrush in Karst Tunnels Based on Attribute Synthetic Evaluation System. Tunn. Undergr. Space Technol. 2013, 38, 50–58. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Shao, J.; Zhang, W.; Wu, X.; Zhu, X. New Type of Similar Material for Simulating the Processes of Water Inrush from Roof Bed Separation. ACS Omega 2020, 5, 30405–30415. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Z. Spatial Prediction of Loose Aquifer Water Abundance Mapping Based on a Hybrid Statistical Learning Approach. Earth Sci. Inform. 2021, 14, 1349–1365. [Google Scholar] [CrossRef]
- Hwang, J.H.; Lu, C.C. A Semi-Analytical Method for Analyzing the Tunnel Water Inflow. Tunn. Undergr. Space Technol. 2007, 22, 39–46. [Google Scholar] [CrossRef]
- Chiu, Y.C.; Chia, Y. The Impact of Groundwater Discharge to the Hsueh-Shan Tunnel on the Water Resources in Northern Taiwan. Hydrogeol. J. 2012, 20, 1599–1611. [Google Scholar] [CrossRef]
- Shi, W.H.; Yang, T.H.; Liu, H.L.; Yang, B. Numerical Modeling of Non-Darcy Flow Behavior of Groundwater Outburst through Fault Using the Forchheimer Equation. J. Hydrol. Eng. 2018, 23, 04017062. [Google Scholar] [CrossRef]
- Chen, D.; Xu, M.; Zeng, K.; Zhao, R. Analysis of the dynamic change process of water inflow in karst tunnel simulated by SWMM model—Take Zhongba Tunnel as an example. Ground Water 2014, 36, 82–84. (In Chinese) [Google Scholar]
- Wang, J.H.; Li, S.C.; Li, L.P.; Xu, Z.H. Dynamic evolution characteristics and prediction of water inflow of karst piping-type water inrush of tunnels. Chin. J. Geotech. Eng. 2018, 40, 1880–1888. (In Chinese) [Google Scholar]
- Li, S.C.; He, P.; Li, L.P.; Shi, S.S.; Zhang, Q.Q.; Zhang, J.; Hu, J. Gaussian Process Model of Water Inflow Prediction in Tunnel Construction and Its Engineering Applications. Tunn. Undergr. Space Technol. 2017, 69, 155–161. [Google Scholar] [CrossRef]
- Zhang, P.X.; Huang, Z.; Liu, S.; Xu, T.S. Study on the Control of Underground Rivers by Reverse Faults in Tunnel Site and Selection of Tunnel Elevation. Water 2019, 11, 889. [Google Scholar] [CrossRef] [Green Version]
- Goldscheider, N.; Drew, D. Methods in Karst Hydrogeology, 1st ed.; Taylor and Francis: London, UK, 2007; pp. 33–47. [Google Scholar]
- Kovács, A.; Perrochet, P.; Király, L.; Jeannin, P.Y. A Quantitative Method for the Characterisation of Karst Aquifers Based on Spring Hydrograph Analysis. J. Hydrol. 2005, 303, 152–164. [Google Scholar] [CrossRef] [Green Version]
- Shoemaker, W.B.; Kuniansky, E.L.; Birk, S.; Bauer, S.; Swain, E.D. Documentation of a Conduit Flow Process (CFP) for MODFLOW-2005. U.S. Geol. Surv. Tech. Methods 2008, 6, 50. [Google Scholar]
- Chang, Y.; Wu, J.; Jiang, G.; Kang, Z. Identification of the Dominant Hydrological Process and Appropriate Model Structure of a Karst Catchment through Stepwise Simplification of a Complex Conceptual Model. J. Hydrol. 2017, 548, 75–87. [Google Scholar] [CrossRef]
- Xia, Q.; Xu, M.; Zhang, H.; Zhang, Q.; Xiao, X.X. A Dynamic Modeling Approach to Simulate Groundwater Discharges into a Tunnel from Typical Heterogenous Geological Media during Continuing Excavation. KSCE J. Civ. Eng. 2018, 22, 341–350. [Google Scholar] [CrossRef]
- Zhao, L.J.; Xia, R.Y.; Yang, Y.; Shao, J.L.; Cao, J.W.; Fan, L.J. Research on Numerical Simulation of Karst Conduit Media Based on CFP: A Case Study of Zhaidi Karst Underground River Subsystem of Guilin. Acta Geosci. Sin. 2018, 39, 225–232. (In Chinese) [Google Scholar]
- Chen, N.; Gunzburger, M.; Hu, B.; Wang, X.; Woodruff, C. Calibrating the Exchange Coefficient in the Modified Coupled Continuum Pipe-Flow Model for Flows in Karst Aquifers. J. Hydrol. 2012, 414, 294–301. [Google Scholar] [CrossRef]
- Yi, L.X.; Xia, R.Y.; Wang, Z.; Lu, H.P.; Zhao, L.J. Infiltration coefficient of precipitation in karst peak-cluster depression area: A case study of Zhaidi karst underground river basin. Arsologica Sin. 2017, 36, 512–517. (In Chinese) [Google Scholar]
- Borghi, A.; Renard, P.; Cornaton, F. Can One Identify Karst Conduit Networks Geometry and Properties from Hydraulic and Tracer Test Data? Adv. Water Resour. 2016, 90, 99–115. [Google Scholar] [CrossRef] [Green Version]
- Panagopoulos, G. Application of MODFLOW for Simulating Groundwater Flow in the Trifilia Karst Aquifer, Greece. Environ. Earth Sci. 2012, 67, 1877–1889. [Google Scholar] [CrossRef]
- Fernandez, G.; Moon, J. Excavation-Induced Hydraulic Conductivity Reduction around a Tunnel--Part 1: Guideline for Estimate of Ground Water Inflow Rate. Tunn. Undergr. Space Technol. 2010, 25, 560–566. [Google Scholar] [CrossRef]
- Li, Z.; He, C.; Yang, S.Z.; Wang, B.; Wang, J.Y. Experimental study on tunnel inflow without considering the influence of excavation disturbance. Chin. J. Geotech. Eng. 2016, 35, 2499–2506. (In Chinese) [Google Scholar]
- Winston, R.B. ModelMuse version 4: A graphical user interface for MODFLOW 6. U.S. Geol. Surv. Tech. Methods 2019, 5036, 10. [Google Scholar]
- Poeter, E.P.; Hill, M.C. UCODE, a Computer Code for Universal Inverse Modeling. Comput. Geosci. 1999, 25, 457–462. [Google Scholar] [CrossRef]
- Hill, M.C.; Tiedeman, C.R. Effective Groundwater Model Calibration: With Analysis of Data, Sensitivities, Predictions, and Uncertainty, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 96–107. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Harbaugh, A.W. Zonebudget Version 3.01, A Computer Program for Computing Subregional Water Budgets for MODFLOW Ground-Water Flow Models. US Geol. Surv. Groundw. Softw. 2009, 46, 90–392. [Google Scholar]
- Bailly-Comte, V.; Martin, J.B.; Jourde, H.; Screaton, E.J.; Pistre, S.; Langston, A. Water Exchange and Pressure Transfer between Conduits and Matrix and Their Influence on Hydrodynamics of Two Karst Aquifers with Sinking Streams. J. Hydrol. 2010, 386, 55–66. [Google Scholar] [CrossRef]
- Binet, S.; Joigneaux, E.; Pauwels, H.; Albéric, P.; Fléhoc, C.; Bruand, A. Water Exchange, Mixing and Transient Storage between a Saturated Karstic Conduit and the Surrounding Aquifer: Groundwater Flow Modeling and Inputs from Stable Water Isotopes. J. Hydrol. 2017, 544, 278–289. [Google Scholar] [CrossRef] [Green Version]
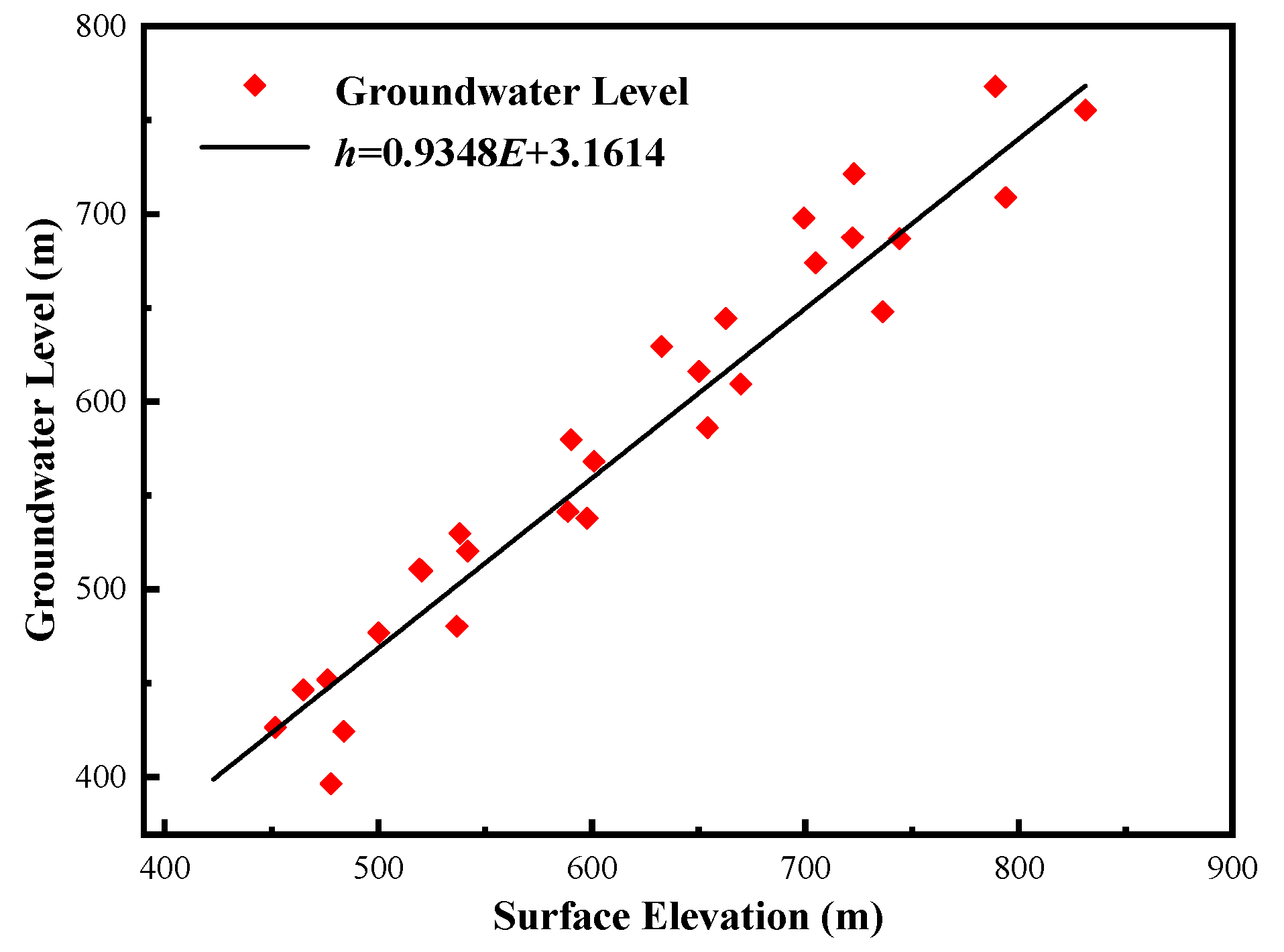

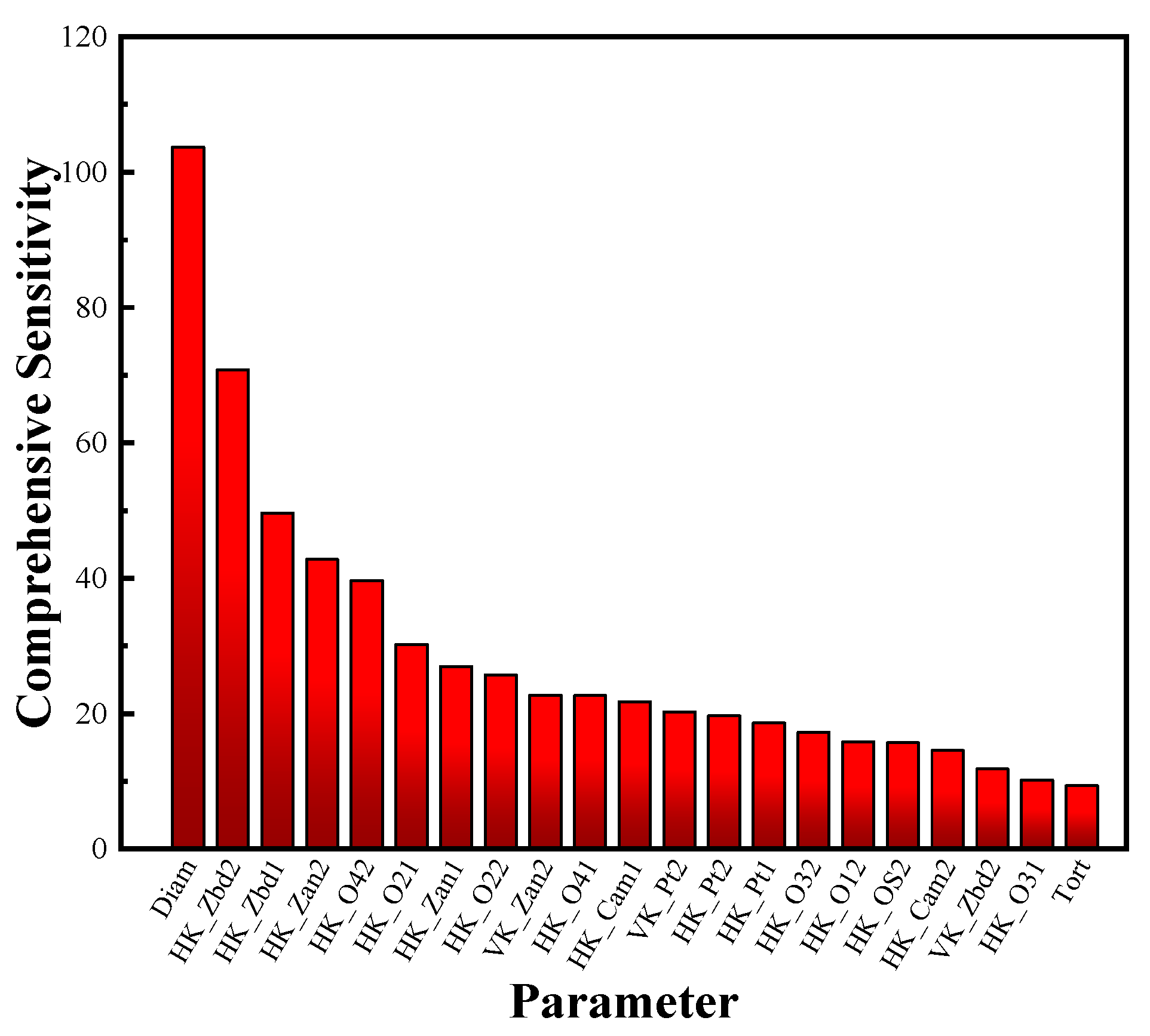
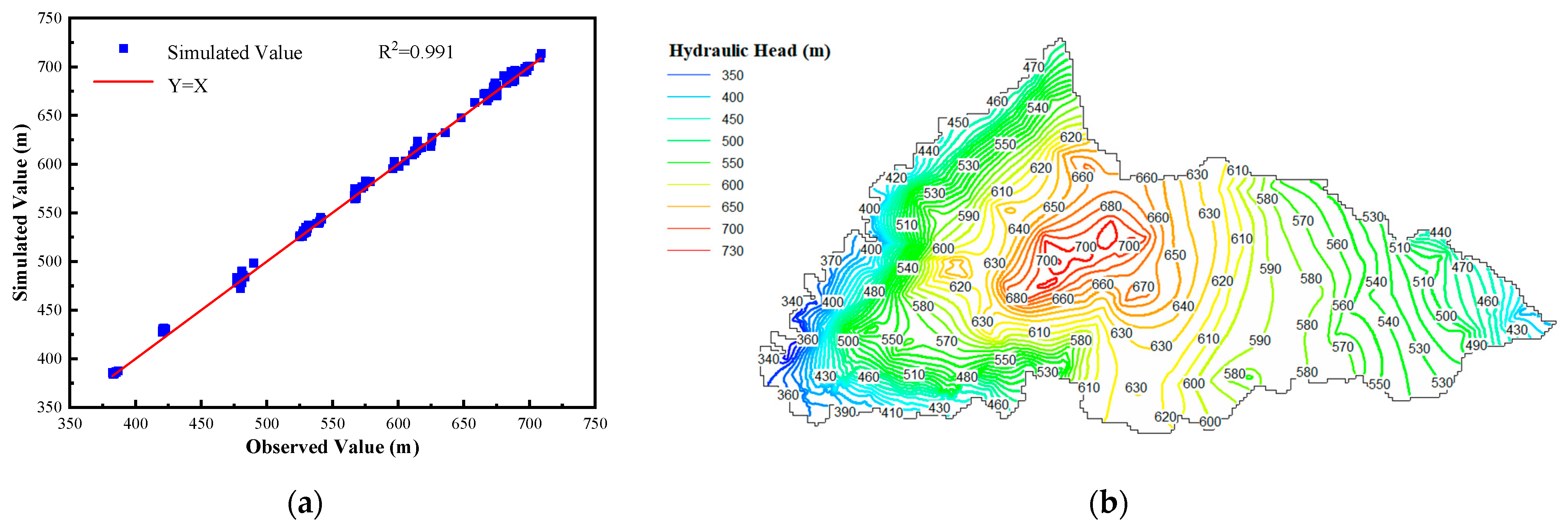
| Tunnel Section | Mileage | Section Length (m) | Excavation Days (d) |
|---|---|---|---|
| 1 | DK234+506-DK237+400 | 2894 | 580 |
| 2 | DK237+400-DK240+060 | 2660 | 540 |
| 3 | DK240+060-DK241+848 | 1788 | 360 |
| 4 | DK241+848-DK243+535 | 1687 | 341 |
| Parameters | ZSX Conduit | SHD1 Conduit | SHD2 Conduit | Unit | Explanation |
|---|---|---|---|---|---|
| DIAMETER | 1.5 | 1.0 | 1.0 | (m) | Conduit diameter |
| TORTUOSITY | 1.1 | 1.1 | 1.1 | - | Conduit tortuosity |
| RHEIGHT | 0.0001 | 0.0001 | 0.0001 | (m) | Conduit wall roughness |
| LCRITREY | 2000 | 2000 | 2000 | - | Reynolds number |
| TCRITREY | 4000 | 4000 | 4000 | - | Reynolds number |
| K_EXCHANGE | 25 | 25 | 25 | (m2·d−1) | Exchange coefficient |
| Precipitation (mm) | Duration (h) | Maximum Intensity (mm·h−1) | Average Intensity (mm·h−1) | Proportion of Concentrated Recharge | ||
|---|---|---|---|---|---|---|
| ZSX Conduit | SHD1 Conduit | SHD2 Conduit | ||||
| 114.2 | 42 | 21.6 | 2.719 | 0.571 | 0.536 | 0.554 |
| 64.4 | 36 | 10.8 | 1.79 | 0.440 | 0.422 | 0.432 |
| 64 | 63 | 12.6 | 1.02 | 0.128 | 0.137 | 0.184 |
| 355.2 | 142 | 23.2 | 2.501 | 0.518 | 0.476 | 0.503 |
| 216.8 | 58 | 13.2 | 3.576 | 0.677 | 0.636 | 0.652 |
| 34.8 | 16 | 15.6 | 2.175 | 0.473 | 0.442 | 0.492 |
| Hydraulic Conductivity | Initial Value (m·d−1) | Calibrated Value (m·d−1) |
|---|---|---|
| HK_Zbd2 | 0.4 | 0.667 |
| HK_Zbd1 | 0.13 | 0.125 |
| HK_Zan2 | 0.1 | 0.413 |
| HK_O42 | 0.2 | 0.137 |
| HK_O21 | 0.3 | 0.3 |
| HK_Zan1 | 0.4 | 0.16 |
| HK_O22 | 0.3 | 0.37 |
| VK_Zan2 | 0.01 | 0.011 |
| HK_O41 | 0.1 | 0.177 |
| HK_Cam1 | 0.3 | 0.284 |
| VK_Pt2 | 0.01 | 0.011 |
| HK_Pt2 | 0.1 | 0.457 |
| HK_Pt1 | 0.25 | 0.5 |
| HK_O32 | 0.4 | 0.403 |
| HK_O12 | 0.1 | 0.15 |
| HK_OS2 | 0.4 | 0.2 |
| HK_Cam2 | 0.2 | 0.25 |
| VK_Zbd2 | 0.04 | 0.04 |
| HK_O31 | 0.2 | 0.2 |
| HK_O11 | 0.1 | 0.141 |
| VK_O22 | 0.01 | 0.037 |
| HK_OS1 | 0.2 | 0.21 |
| VK_OS2 | 0.04 | 0.093 |
| VK_O42 | 0.02 | 0.02 |
| VK_Zbd1 | 0.16 | 0.63 |
| VK_O12 | 0.01 | 0.015 |
| HK_Zan3 | 0.01 | 0.01 |
| VK_Cam2 | 0.04 | 0.025 |
| VK_O32 | 0.04 | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Wu, Z.; Huang, T.; Peng, D. A Dynamic Modeling Approach to Predict Water Inflow during Karst Tunnel Excavation. Water 2022, 14, 2380. https://doi.org/10.3390/w14152380
Bai Y, Wu Z, Huang T, Peng D. A Dynamic Modeling Approach to Predict Water Inflow during Karst Tunnel Excavation. Water. 2022; 14(15):2380. https://doi.org/10.3390/w14152380
Chicago/Turabian StyleBai, Yang, Zheng Wu, Tao Huang, and Daoping Peng. 2022. "A Dynamic Modeling Approach to Predict Water Inflow during Karst Tunnel Excavation" Water 14, no. 15: 2380. https://doi.org/10.3390/w14152380
APA StyleBai, Y., Wu, Z., Huang, T., & Peng, D. (2022). A Dynamic Modeling Approach to Predict Water Inflow during Karst Tunnel Excavation. Water, 14(15), 2380. https://doi.org/10.3390/w14152380