A CNN-LSTM Model Based on a Meta-Learning Algorithm to Predict Groundwater Level in the Middle and Lower Reaches of the Heihe River, China
Abstract
:1. Introduction
- (1)
- Aiming to resolve the problem that the existing methods are not effective for long-term prediction of groundwater level, and the insufficient modeling ability of various influencing factors. In this paper, a deep learning network structure of hybrid CNN-LSTM is designed, in which the CNN module can effectively extract the multivariate features that affect the groundwater level, and the LSTM module has natural advantages for long-term time series prediction. Therefore, the network structure can effectively solve the above problems.
- (2)
- For deep learning models, large-scale training data are usually needed as a support, and the real groundwater prediction problem usually lacks sufficient samples. In this study, a meta-learning algorithm is added to the CNN-LSTM network structure, so that the model can train a meta-learner with fewer training samples to complete the task of groundwater level prediction. To the authors’ knowledge, there is no single paper that applies meta-learning to groundwater level prediction, and our study provides support for the expansion of meta-learning algorithm applications.
- (3)
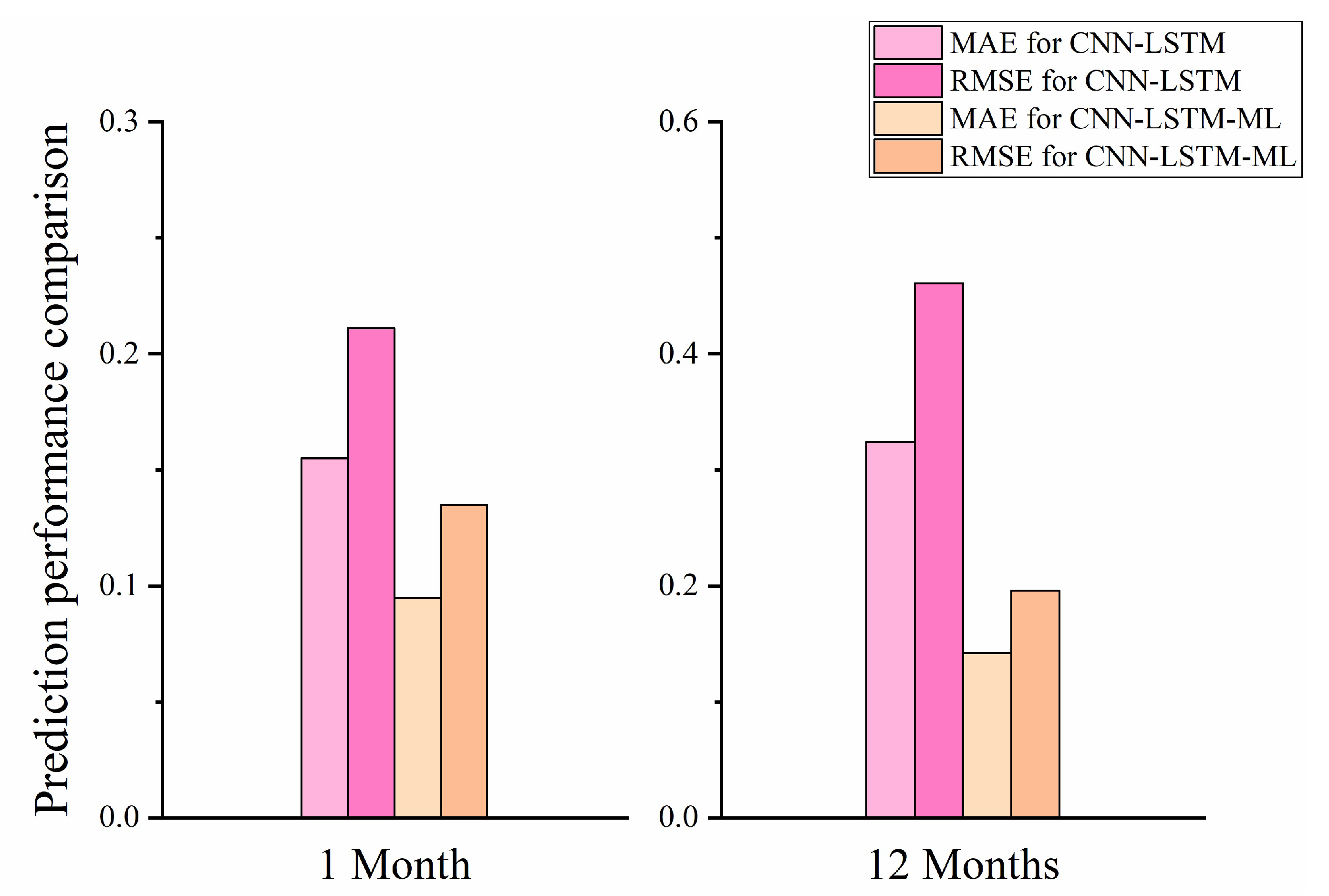
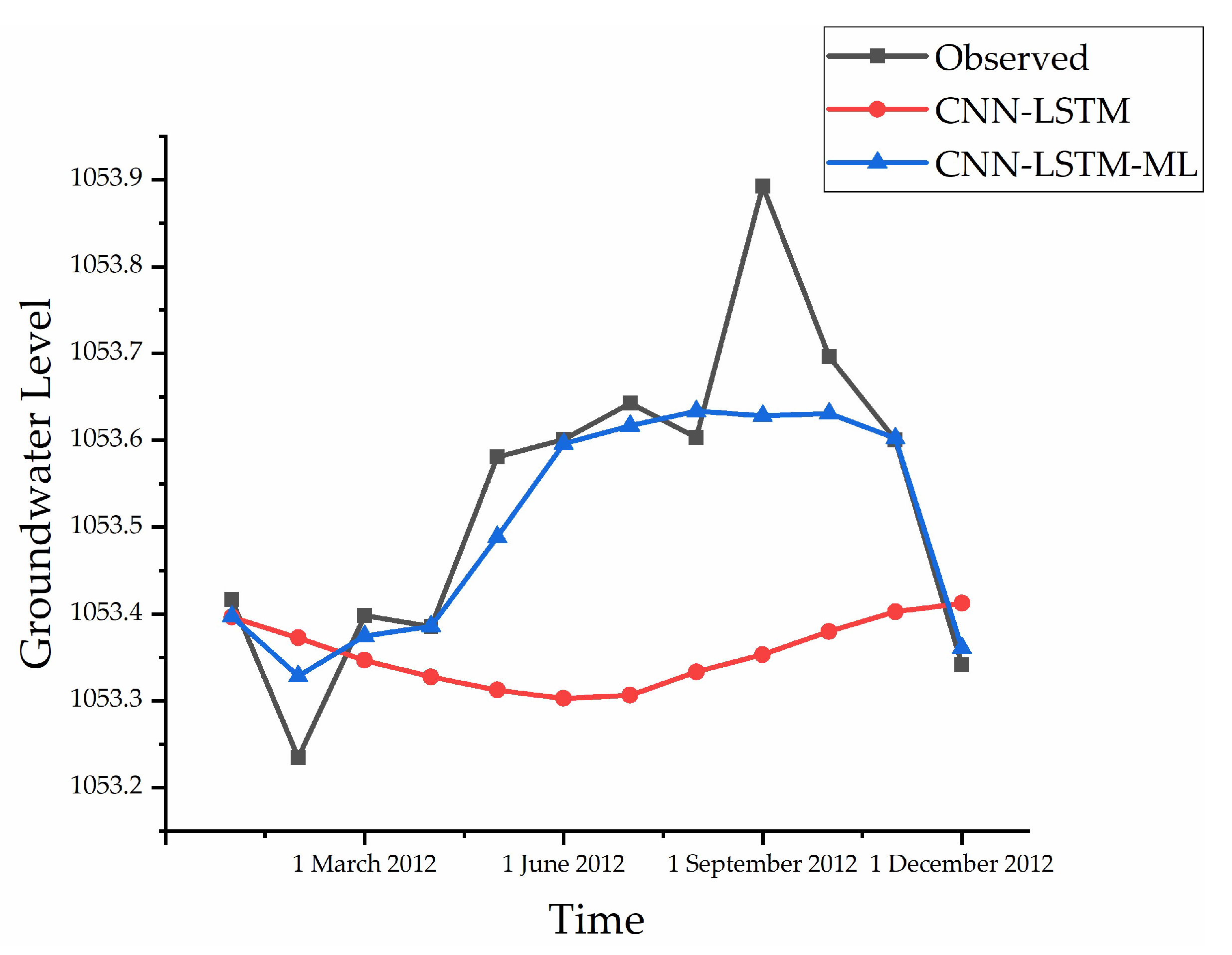
- To verify the performance of the CNN-LSTM-ML, this study is conducted on a real groundwater level dataset in the middle and lower reaches of the Heihe River. Experimental results show that in short-term prediction (1 month), the MAE of CNN-LSTM-ML is 11.7% lower than that of the multiple regression method. In long-term prediction (12 months), the RMSE of CNN-LSTM-ML is 5% lower than that of LSTM. At the same time, the model can still maintain a high prediction accuracy even when the training samples are reduced. All in all, the proposed model can accurately predict groundwater levels, which can help relevant government departments manage water resources and make evidence-based decisions.
2. Materials and Methods
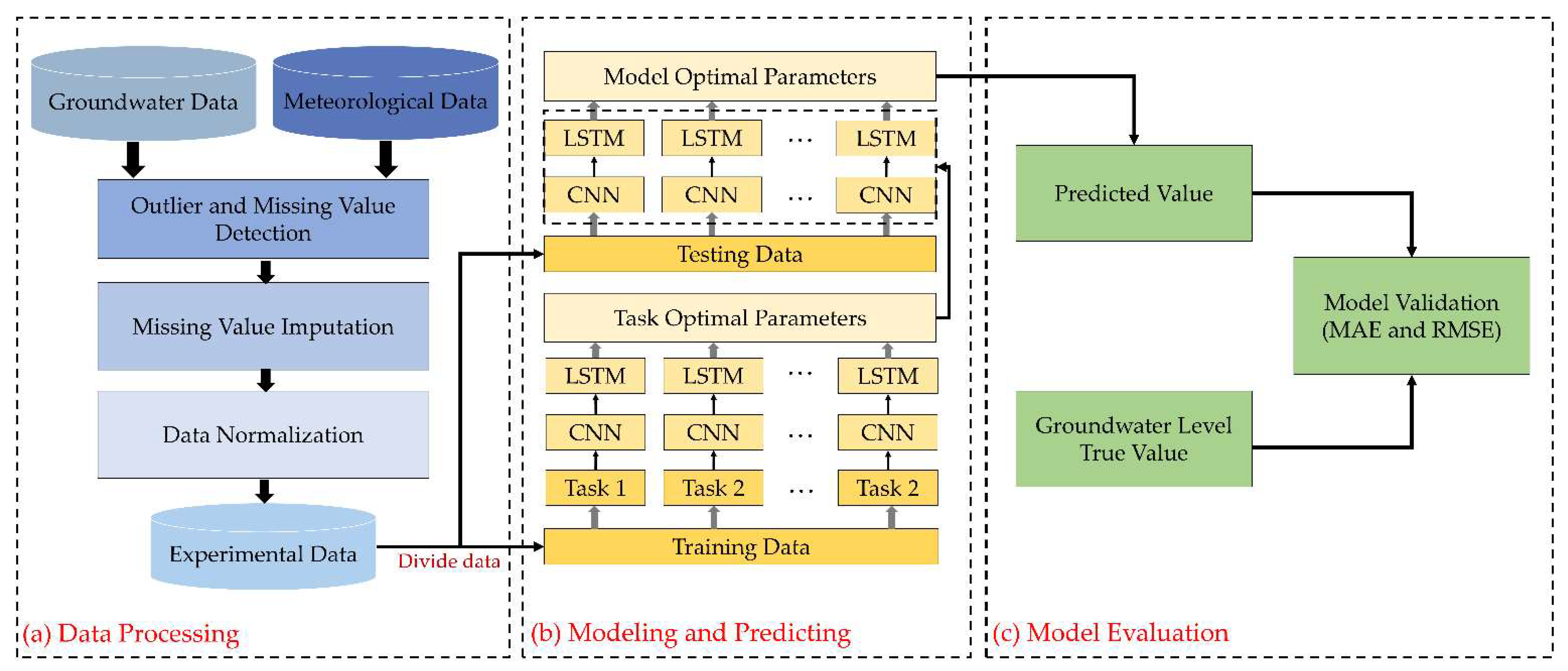
2.1. Groundwater Level Prediction Process
2.2. Study Area and Data Processing
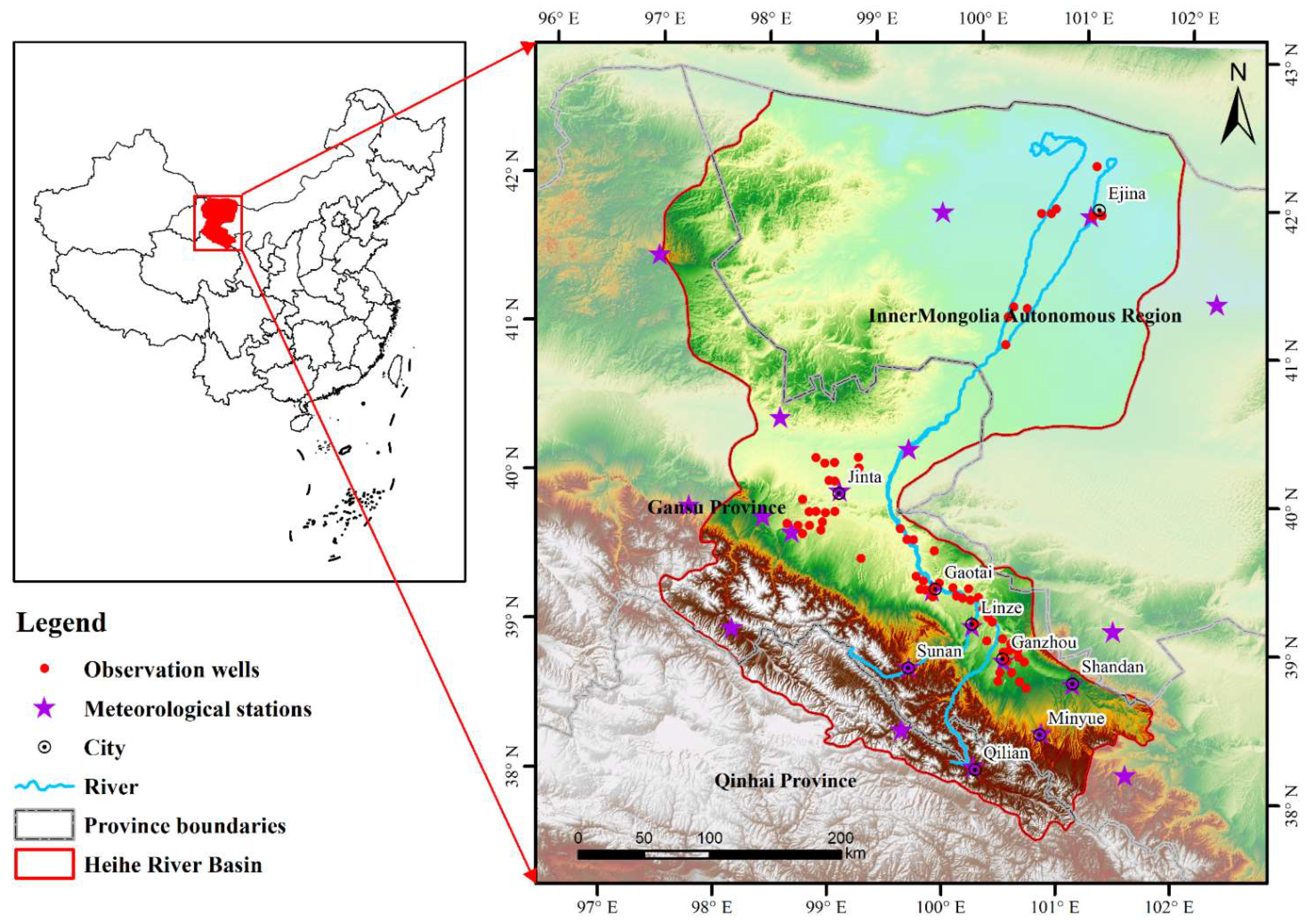
2.2.1. Study Area and Data
2.2.2. Missing Data Processing
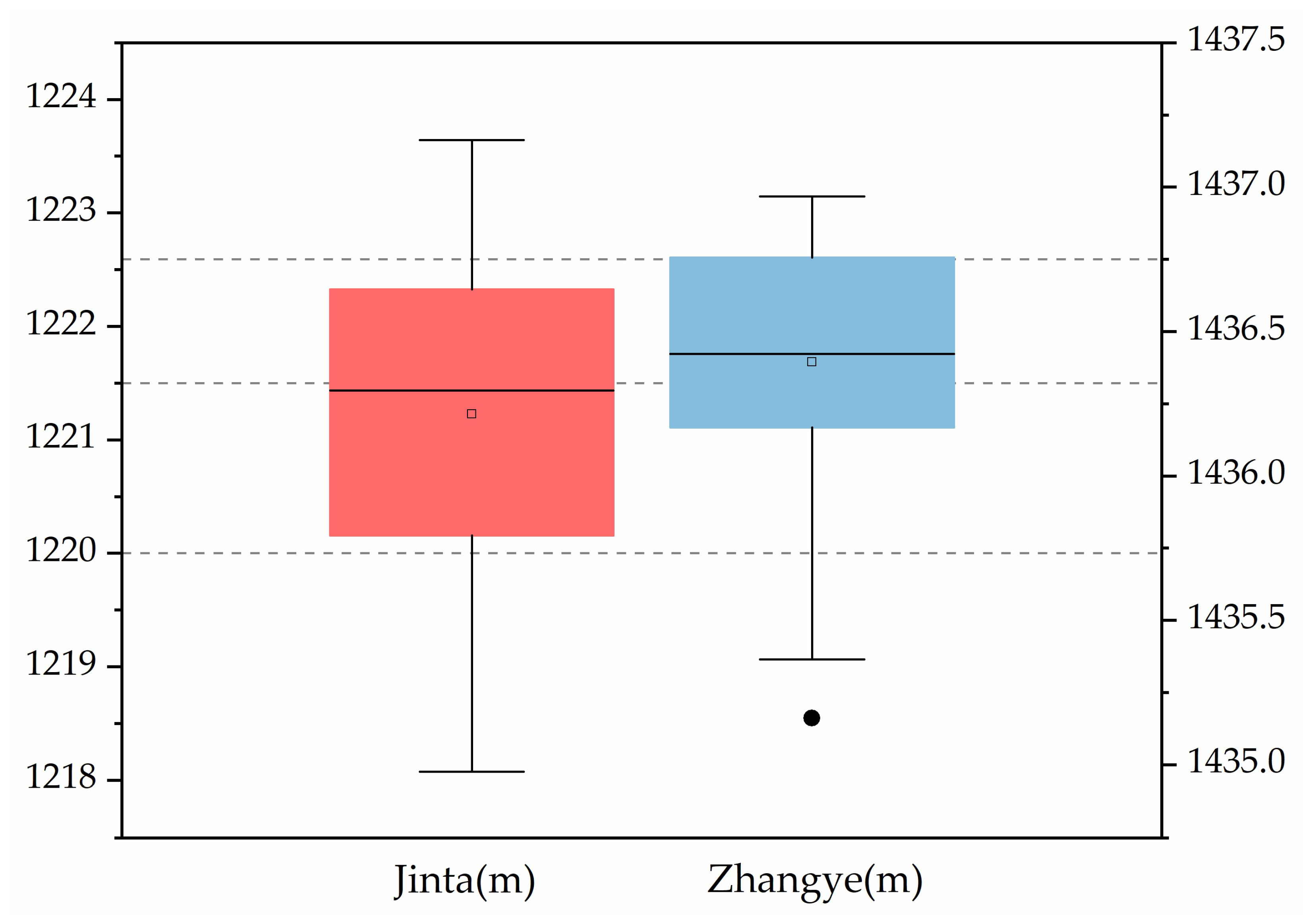
2.2.3. Outlier Data Processing
2.2.4. Data Normalization
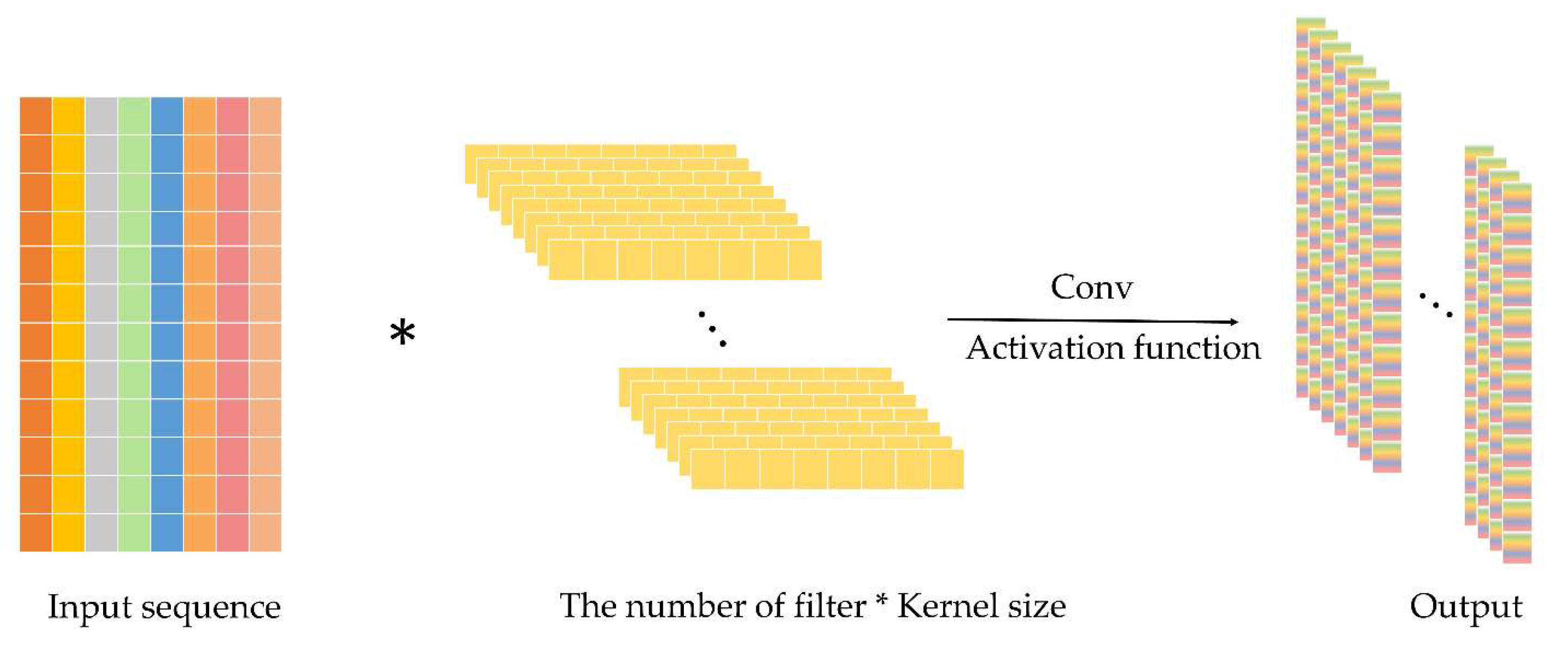
2.3. Convolutional Neural Network (CNN)
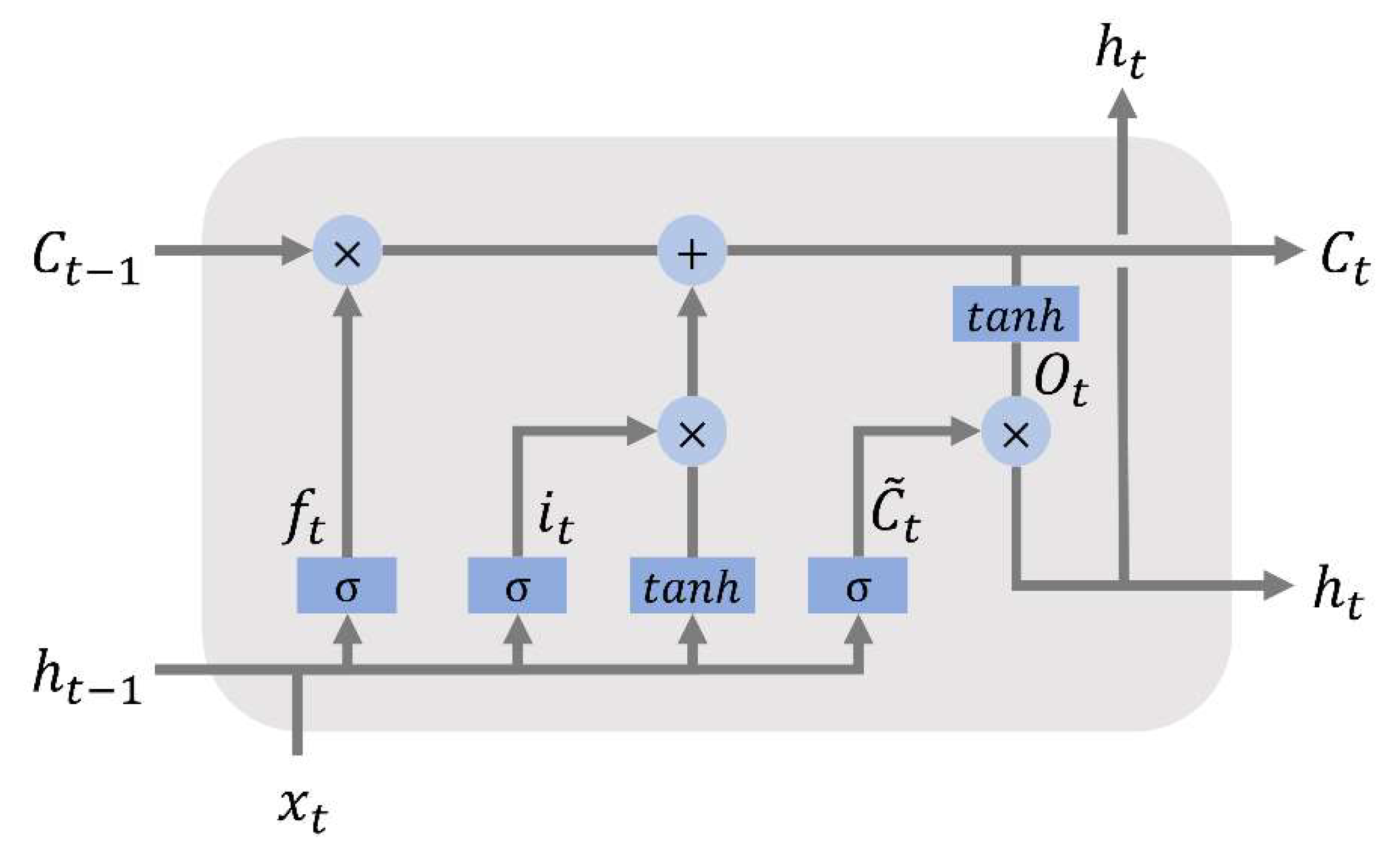
2.4. Long-Short Term Memory (LSTM) Network
2.5. Meta-Learning Algorithm
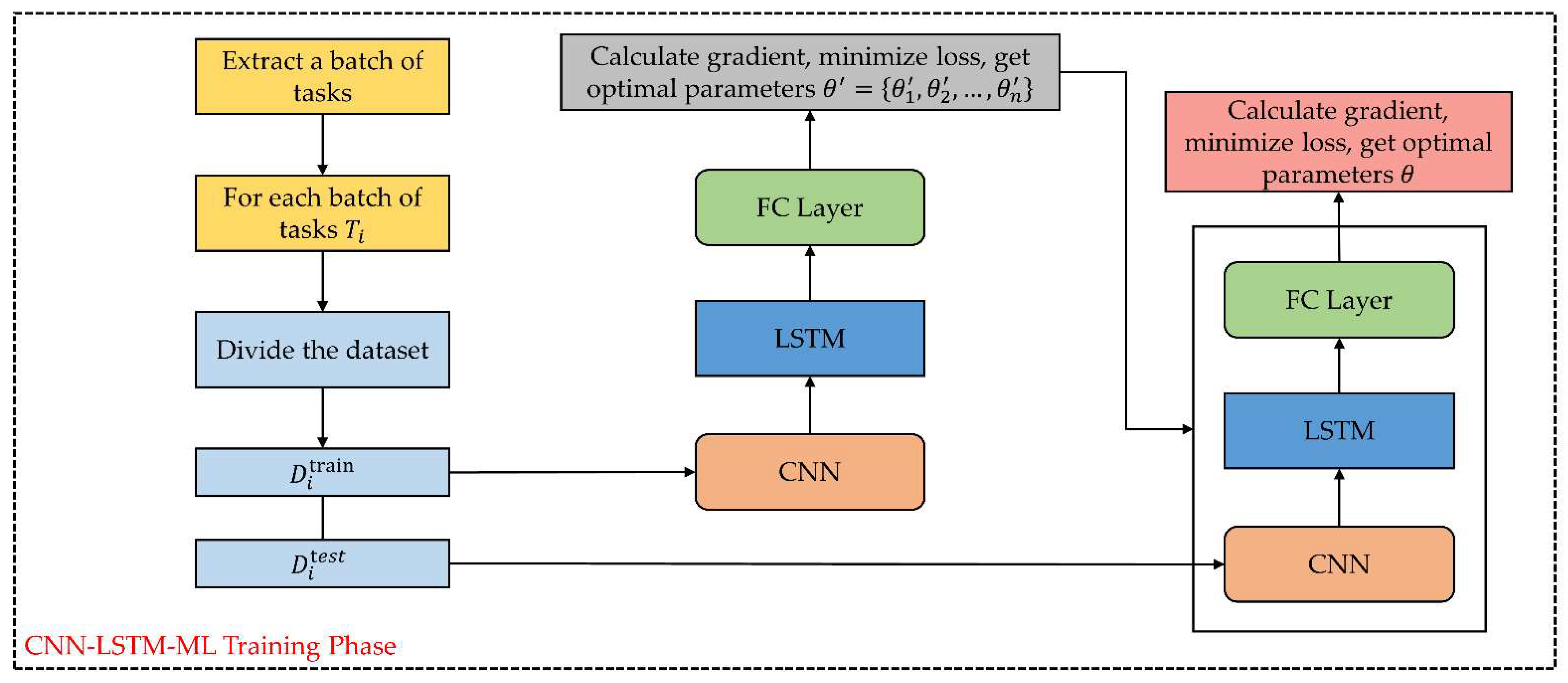
2.6. CNN-LSTM-ML Prediction Model
2.6.1. Problem Definition
2.6.2. Model Structure
2.6.3. CNN-LSTM-ML Meta-Training and Fine-Tune Testing
| Algorithm 1 CNN-LSTM-ML Meta-Training |
| Require: Distribution of tasks , Step size hyperparameters , 1: Random Initialization parameters 2: While not done do 3: Sample a batch of tasks from i.e., 4: for all do 5: Set up training set for each task in 6: Calculate using and in Equation (15) 7: Calculate adapted parameters with gradient descent: 8: Set up test set for each task in for the meta-update 9: end for 10: Update using each and in Equation (15) 11: end while |
| Algorithm 2 CNN-LSTM-ML Fine-tune Testing |
| Require: Distribution of tasks , Step size hyperparameters 1: Well-trained parameters 2: While not done do 3: Sample a task from i.e., 4: Set up training set for each task in 5: Calculate using and in Equation (15) 6: Calculate adapted parameters with gradient descent: 7: Set up test set for each task in for the prediction 8: Calculate prediction values 9: end while |
2.6.4. Model Evaluation
3. Results
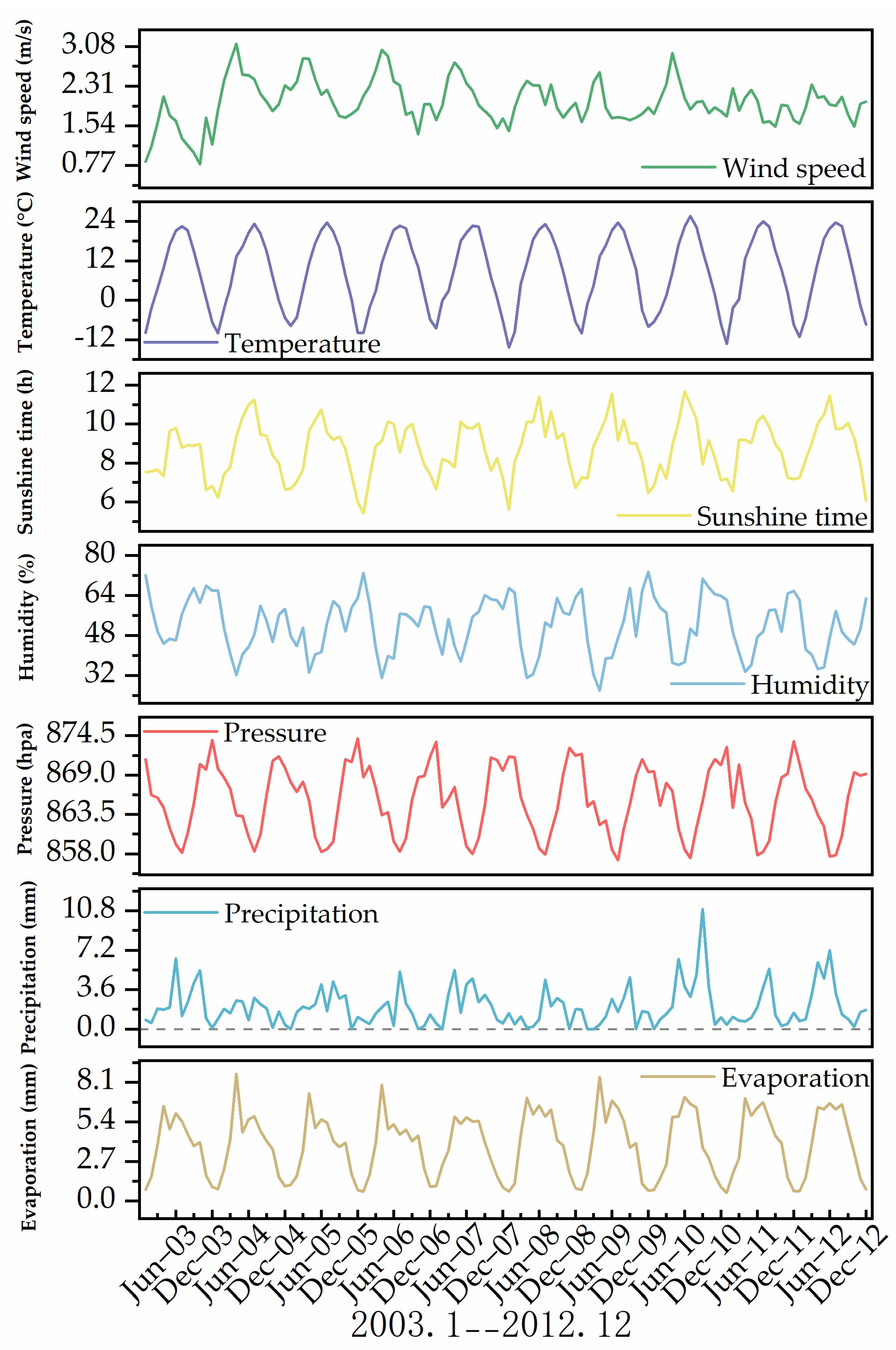
3.1. Meteorological Factor Time Series
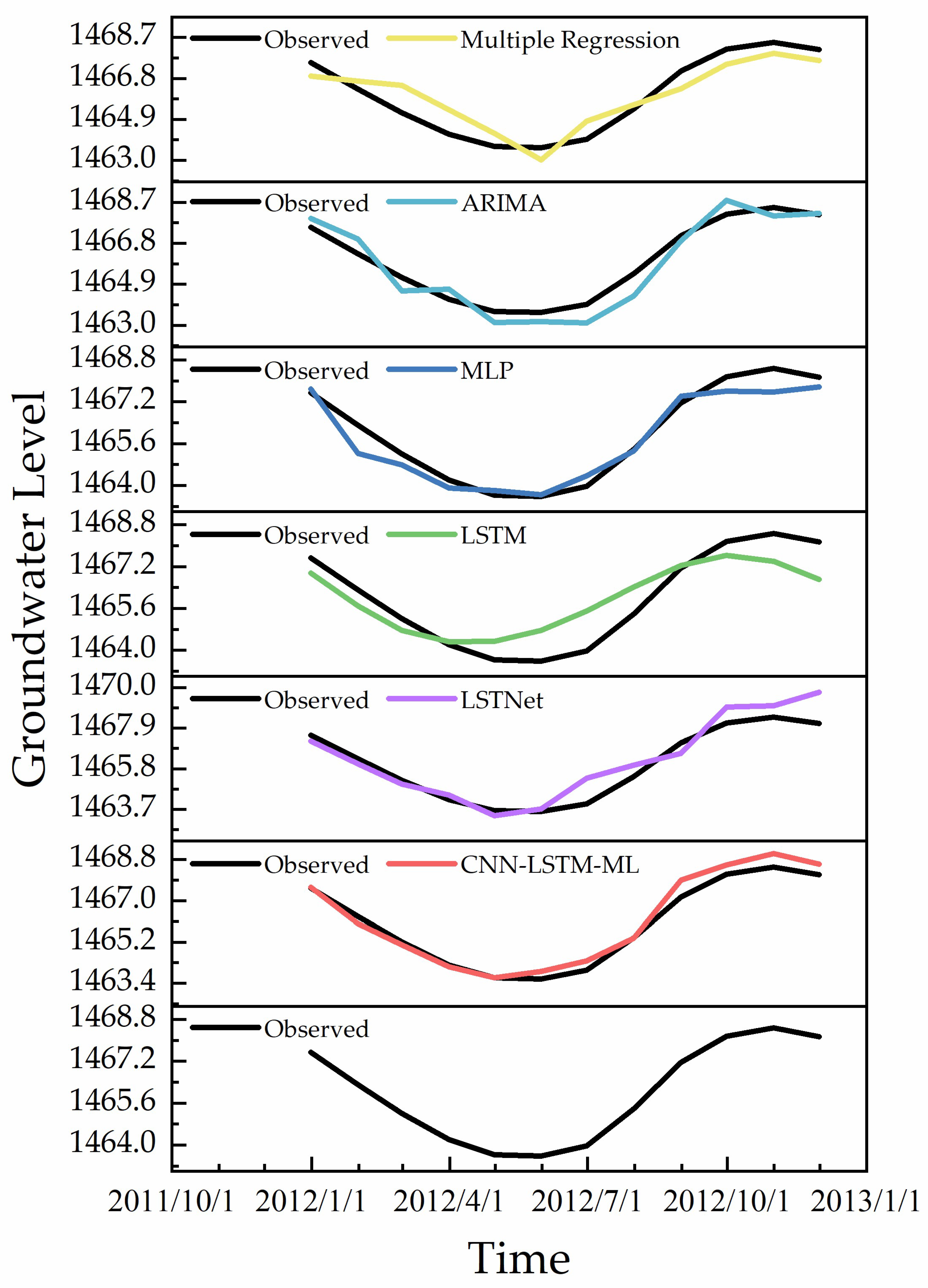
3.2. Prediction Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taylor, R.G.; Scanlon, B.; Doll, P.; Rodell, M.; van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef] [Green Version]
- UNESCO. The Groundwater Resources of the World are Suffering the Effects of Poor Governance, Experts Say. Available online: http://www.unesco.org/new/en/media-services/single-view/news/worlds_groundwater_resources_are_suffering_from_poor_gove/ (accessed on 22 March 2022).
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Li, P.Y.; Qian, H.; Howard, K.W.F.; Wu, J.H. Building a new and sustainable “Silk Road economic belt”. Environ. Earth Sci. 2015, 74, 7267–7270. [Google Scholar] [CrossRef]
- Ostad-Ali-Askari, K.; Shayannejad, M. Quantity and quality modelling of groundwater to manage water resources in Isfahan-Borkhar Aquifer. Environ. Dev. Sustain. 2021, 23, 15943–15959. [Google Scholar] [CrossRef]
- Neshat, A.; Pradhan, B.; Pirasteh, S.; Shafri, H.Z.M. Estimating groundwater vulnerability to pollution using a modified DRASTIC model in the Kerman agricultural area, Iran. Environ. Earth Sci. 2014, 71, 3119–3131. [Google Scholar] [CrossRef]
- Sajedi-Hosseini, F.; Malekian, A.; Choubin, B.; Rahmati, O.; Cipullo, S.; Coulon, F.; Pradhan, B. A novel machine learning-based approach for the risk assessment of nitrate groundwater contamination. Sci. Total Environ. 2018, 644, 954–962. [Google Scholar] [CrossRef] [Green Version]
- Shekhar, S.; Purohit, R.; Kaushik, Y. Technical paper included in the special session on Groundwater in the 5th Asian Regional Conference of INCID. In Groundwater Management in NCT Delhi; Vigyan Bhawan: New Delhi, India, 2009; pp. 23–35. [Google Scholar]
- Richey, A.S.; Thomas, B.F.; Lo, M.H.; Famiglietti, J.S.; Swenson, S.; Rodell, M. Uncertainty in global groundwater storage estimates in a Total Groundwater Stress framework. Water Resour. Res. 2015, 51, 5198–5216. [Google Scholar] [CrossRef]
- Dalin, C.; Wada, Y.; Kastner, T.; Puma, M.J. Groundwater depletion embedded in international food trade. Nature 2017, 543, 700–704. [Google Scholar] [CrossRef] [Green Version]
- Konikow, L.F.; Kendy, E. Groundwater depletion: A global problem. Hydrogeol. J. 2005, 13, 317–320. [Google Scholar] [CrossRef]
- Chen, W.; Li, H.; Hou, E.K.; Wang, S.Q.; Wang, G.R.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C.; et al. GIS-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef] [Green Version]
- Cavelan, A.; Golfier, F.; Colombano, S.; Davarzani, H.; Deparis, J.; Faure, P. A critical review of the influence of groundwater level fluctuations and temperature on LNAPL contaminations in the context of climate change. Sci. Total Environ. 2022, 806, 150412. [Google Scholar] [CrossRef] [PubMed]
- Fu, G.B.; Crosbie, R.S.; Barron, O.; Charles, S.P.; Dawes, W.; Shi, X.G.; Niel, T.V.; Li, C. Attributing variations of temporal and spatial groundwater recharge: A statistical analysis of climatic and non-climatic factors. J. Hydrol. 2019, 568, 816–834. [Google Scholar] [CrossRef]
- Klove, B.; Ala-Aho, P.; Bertrand, G.; Gurdak, J.J.; Kupfersberger, H.; Kvaerner, J.; Muotka, T.; Mykra, H.; Preda, E.; Rossi, P.; et al. Climate change impacts on groundwater and dependent ecosystems. J. Hydrol. 2014, 518, 250–266. [Google Scholar] [CrossRef]
- Latif, Y.; Ma, Y.; Ma, W. Climatic trends variability and concerning flow regime of Upper Indus Basin, Jehlum, and Kabul river basins Pakistan. Theor. Appl. Climatol. 2021, 144, 447–468. [Google Scholar] [CrossRef]
- Latif, Y.; Ma, Y.; Ma, W.; Muhammad, S.; Adnan, M.; Yaseen, M.; Fealy, R. Differentiating Snow and Glacier Melt Contribution to Runoff in the Gilgit River Basin via Degree-Day Modelling Approach. Atmosphere 2020, 11, 1023. [Google Scholar] [CrossRef]
- Latif, Y.; Yaoming, M.; Yaseen, M. Spatial analysis of precipitation time series over the Upper Indus Basin. Theor. Appl. Climatol. 2018, 131, 761–775. [Google Scholar] [CrossRef] [Green Version]
- Latif, Y.; Yaoming, M.; Yaseen, M.; Muhammad, S.; Wazir, M.A. Spatial analysis of temperature time series over the Upper Indus Basin (UIB) Pakistan. Theor. Appl. Climatol. 2020, 139, 741–758. [Google Scholar] [CrossRef] [Green Version]
- Winter, T.C. Relation of streams, lakes, and wetlands to groundwater flow systems. Hydrogeol. J. 1999, 7, 28–45. [Google Scholar] [CrossRef]
- Lyu, H.; Wu, T.T.; Su, X.S.; Wang, Y.Q.; Wang, C.; Yuan, Z.J. Factors controlling the rise and fall of groundwater level during the freezing-thawing period in seasonal frozen regions. J. Hydrol. 2022, 606, 127442. [Google Scholar] [CrossRef]
- Delinom, R.M.; Assegaf, A.; Abidin, H.Z.; Taniguchi, M.; Suherman, D.; Lubis, R.F.; Yulianto, E. The contribution of human activities to subsurface environment degradation in Greater Jakarta Area, Indonesia. Sci. Total Environ. 2009, 407, 3129–3141. [Google Scholar] [CrossRef] [PubMed]
- Lamb, S.E.; Haacker, E.M.K.; Smidt, S.J. Influence of Irrigation Drivers Using Boosted Regression Trees: Kansas High Plains. Water Resour. Res. 2021, 57, e2020WR028867. [Google Scholar] [CrossRef]
- Gerke, H.H.; Koszinski, S.; Kalettka, T.; Sommer, M. Structures and hydrologic function of soil landscapes with kettle holes using an integrated hydropedological approach. J. Hydrol. 2010, 393, 123–132. [Google Scholar] [CrossRef]
- Goldman, M.; Neubauer, F.M. Groundwater exploration using integrated geophysical techniques. Surv. Geophys. 1994, 15, 331–361. [Google Scholar] [CrossRef]
- Owen, R.J.; Gwavava, O.; Gwaze, P. Multi-electrode resistivity survey for groundwater exploration in the Harare greenstone belt, Zimbabwe. Hydrogeol. J. 2006, 14, 244–252. [Google Scholar] [CrossRef]
- Allafta, H.; Opp, C.; Patra, S. Identification of Groundwater Potential Zones Using Remote Sensing and GIS Techniques: A Case Study of the Shatt Al-Arab Basin. Remote Sens. 2021, 13, 112. [Google Scholar] [CrossRef]
- Celik, R.; Aslan, V. Evaluation of hydrological and hydrogeological characteristics affecting the groundwater potential of Harran Basin. Arab. J. Geosci. 2020, 13, 1–13. [Google Scholar] [CrossRef]
- Rahmati, O.; Samani, A.N.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab. J. Geosci. 2015, 8, 7059–7071. [Google Scholar] [CrossRef]
- Castrillo, M.; Garcia, A.L. Estimation of high frequency nutrient concentrations from water quality surrogates using machine learning methods. Water Res. 2020, 172, 115490. [Google Scholar] [CrossRef] [Green Version]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Perez-Garcia, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Naganna, S.R.; Sa’adi, Z.; Samui, P.; Ghorbani, M.A.; Salih, S.Q.; Shahid, S. Hourly River Flow Forecasting: Application of Emotional Neural Network Versus Multiple Machine Learning Paradigms. Water Resour. Manag. 2020, 34, 1075–1091. [Google Scholar] [CrossRef]
- Khalil, B.; Broda, S.; Adamowski, J.; Ozga-Zielinski, B.; Donohoe, A. Short-term forecasting of groundwater levels under conditions of mine-tailings recharge using wavelet ensemble neural network models. Hydrogeol. J. 2015, 23, 121–141. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Groundwater-level prediction using multiple linear regression and artificial neural network techniques: A comparative assessment. Hydrogeol. J. 2013, 21, 1865–1887. [Google Scholar] [CrossRef]
- Adhikary, S.; Rahman, M.; Das Gupta, A. A Stochastic Modelling Technique for Predicting Groundwater Table Fluctuations with Time Series Analysis. Int. J. Appl. Sci. Eng. Res. 2012, 1, 238–249. [Google Scholar]
- Mirzavand, M.; Ghazavi, R. A Stochastic Modelling Technique for Groundwater Level Forecasting in an Arid Environment Using Time Series Methods. Water Resour. Manag. 2015, 29, 1315–1328. [Google Scholar] [CrossRef]
- Patle, G.T.; Singh, D.K.; Sarangi, A.; Rai, A.; Khanna, M.; Sahoo, R.N. Time Series Analysis of Groundwater Levels and Projection of Future Trend. J. Geol. Soc. India 2015, 85, 232–242. [Google Scholar] [CrossRef]
- Gholami, V.; Chau, K.W.; Fadaee, F.; Torkaman, J.; Ghaffari, A. Modeling of groundwater level fluctuations using dendrochronology in alluvial aquifers. J. Hydrol. 2015, 529, 1060–1069. [Google Scholar] [CrossRef]
- Muller, J.; Park, J.; Sahu, R.; Varadharajan, C.; Arora, B.; Faybishenko, B.; Agarwal, D. Surrogate optimization of deep neural networks for groundwater predictions. J. Glob. Optim. 2021, 81, 203–231. [Google Scholar] [CrossRef]
- Sahu, R.K.; Muller, J.; Park, J.; Varadharajan, C.; Arora, B.; Faybishenko, B.; Agarwal, D. Impact of Input Feature Selection on Groundwater Level Prediction From a Multi-Layer Perceptron Neural Network. Front. Water 2020, 2, 573034. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, F.; Aravena, R.; Bobee, B. Artificial neural network modeling of water table depth fluctuations. Water Resour. Res. 2001, 37, 885–896. [Google Scholar] [CrossRef]
- Bowes, B.D.; Sadler, J.M.; Morsy, M.M.; Behl, M.; Goodall, J.L. Forecasting Groundwater Table in a Flood Prone Coastal City with Long Short-term Memory and Recurrent Neural Networks. Water 2019, 11, 1098. [Google Scholar] [CrossRef] [Green Version]
- Jeong, J.; Park, E. Comparative applications of data-driven models representing water table fluctuations. J. Hydrol. 2019, 572, 261–273. [Google Scholar] [CrossRef]
- Jeong, J.; Park, E.; Chen, H.L.; Kim, K.Y.; Han, W.S.; Suk, H. Estimation of groundwater level based on the robust training of recurrent neural networks using corrupted data. J. Hydrol. 2019, 582, 124512. [Google Scholar] [CrossRef]
- Supreetha, B.S.; Shenoy, N.; Nayak, P. Lion Algorithm-Optimized Long Short-Term Memory Network for Groundwater Level Forecasting in Udupi District, India. Appl. Comput. Intell. Soft Comput. 2020, 2020, 8685724. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.F.; Zhu, Y.; Zhang, X.P.; Ye, M.; Yang, J.Z. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Afzaal, H.; Farooque, A.A.; Abbas, F.; Acharya, B.; Esau, T. Groundwater Estimation from Major Physical Hydrology Components Using Artificial Neural Networks and Deep Learning. Water 2019, 12, 5. [Google Scholar] [CrossRef] [Green Version]
- Lahivaara, T.; Malehmir, A.; Pasanen, A.; Karkkainen, L.; Huttunen, J.M.J.; Hesthaven, J.S. Estimation of groundwater storage from seismic data using deep learning. Geophys. Prospect. 2019, 67, 2115–2126. [Google Scholar] [CrossRef] [Green Version]
- Lai, G.K.; Chang, W.C.; Yang, Y.M.; Liu, H.X. Acm/Sigir In Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks. In Proceedings of the 41st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Fei-Fei, L.; Fergus, R.; Perona, P.; Ieee Computer, S.; Ieee Computer, S. A Bayesian approach to unsupervised one-shot learning of object categories. In Proceedings of the 9th IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; pp. 1134–1141. [Google Scholar]
- Li, F.F.; Fergus, R.; Perona, P. One-shot learning of object categories. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 594–611. [Google Scholar]
- Malik, A.; Bhagwat, A. Modelling groundwater level fluctuations in urban areas using artificial neural network. Groundw. Sustain. Dev. 2021, 12, 100484. [Google Scholar] [CrossRef]
- Fort, S. Gaussian prototypical networks for few-shot learning on omniglot. arXiv 2017, arXiv:1708.02735. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese Neural Networks for One-Shot Image Recognition; ICML Deep Learning Workshop: Lille, France, 2015; pp. 1–8. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Processing Syst. 2017, 30, 1–13. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Cheng, G.D.; Li, X.; Zhao, W.Z.; Xu, Z.M.; Feng, Q.; Xiao, S.C.; Xiao, H.L. Integrated study of the water-ecosystem-economy in the Heihe River Basin. Natl. Sci. Rev. 2014, 1, 413–428. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Liu, Q.H.; Wang, W.Z.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific Objectives and Experimental Design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Zhongjing, W. Groundwater Simulation Data in the Middle Reaches of Heihe (2003–2012); National Tibetan Plateau Data, C., Ed.; National Tibetan Plateau Data Center: Beijing, China, 2016. [Google Scholar]
- Dong, Y.R.; Peng, C.Y.J. Principled missing data methods for researchers. Springerplus 2013, 2, 222. [Google Scholar] [CrossRef] [Green Version]
- Gnauck, A. Interpolation and approximation of water quality time series and process identification. Anal. Bioanal. Chem. 2004, 380, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Kulesh, M.; Holschneider, M.; Kurennaya, K. Adaptive metrics in the nearest neighbours method. Phys. D Nonlinear Phenom. 2008, 237, 283–291. [Google Scholar] [CrossRef]
- Lepot, M.; Aubin, J.B.; Clemens, F. Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water 2017, 9, 796. [Google Scholar] [CrossRef] [Green Version]
- Schwertman, N.C.; Owens, M.A.; Adnan, R. A simple more general boxplot method for identifying outliers. Comput. Stat. Data Anal. 2004, 47, 165–174. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Yin, C.Y.; Zhang, S.; Wang, J.; Xiong, N.N. Anomaly Detection Based on Convolutional Recurrent Autoencoder for IoT Time Series. IEEE Trans. Syst. Man Cybern.-Syst. 2022, 52, 112–122. [Google Scholar] [CrossRef]
- Zhang, Y.; Wallace, B. A sensitivity analysis of (and practitioners’ guide to) convolutional neural networks for sentence classification. arXiv 2015, arXiv:1510.03820. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ke, J.T.; Zheng, H.Y.; Yang, H.; Chen, X.Q. Short-term forecasting of passenger demand under on-demand ride services: A spatio-temporal deep learning approach. Transp. Res. Part C-Emerg. Technol. 2017, 85, 591–608. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Chen, W.H.; Wu, X.M.; Chen, P.C.Y.; Liu, J.M. LSTM network: A deep learning approach for short-term traffic forecast. Iet Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.C.; Deng, F.; Cai, Y.Y.; Chen, J. Long short-term memory—Fully connected (LSTM-FC) neural network for PM2.5 concentration prediction. Chemosphere 2019, 220, 486–492. [Google Scholar] [CrossRef]
- Geng, C.X.; Huang, S.J.; Chen, S.C. Recent Advances in Open Set Recognition: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3614–3631. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in a ssessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Zhu, S.C. Visual interpretability for deep learning: A survey. Front. Inf. Technol. Electron. Eng. 2018, 19, 27–39. [Google Scholar] [CrossRef] [Green Version]
- Chorowski, J.K.; Bahdanau, D.; Serdyuk, D.; Cho, K.; Bengio, Y. Attention-based models for speech recognition. Adv. Neural Inf. Process. Syst. 2015, 28, 1–19. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Shan, C.H.; Zhang, J.B.; Wang, Y.J.; Xie, L. Ieee In Attention-based end-to-end speech recognition on voice search. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 4764–4768. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–15. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. In Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Yin, W.; Schütze, H.; Xiang, B.; Zhou, B. Abcnn: Attention-based convolutional neural network for modeling sentence pairs. Trans. Assoc. Comput. Linguist. 2016, 4, 259–272. [Google Scholar] [CrossRef]
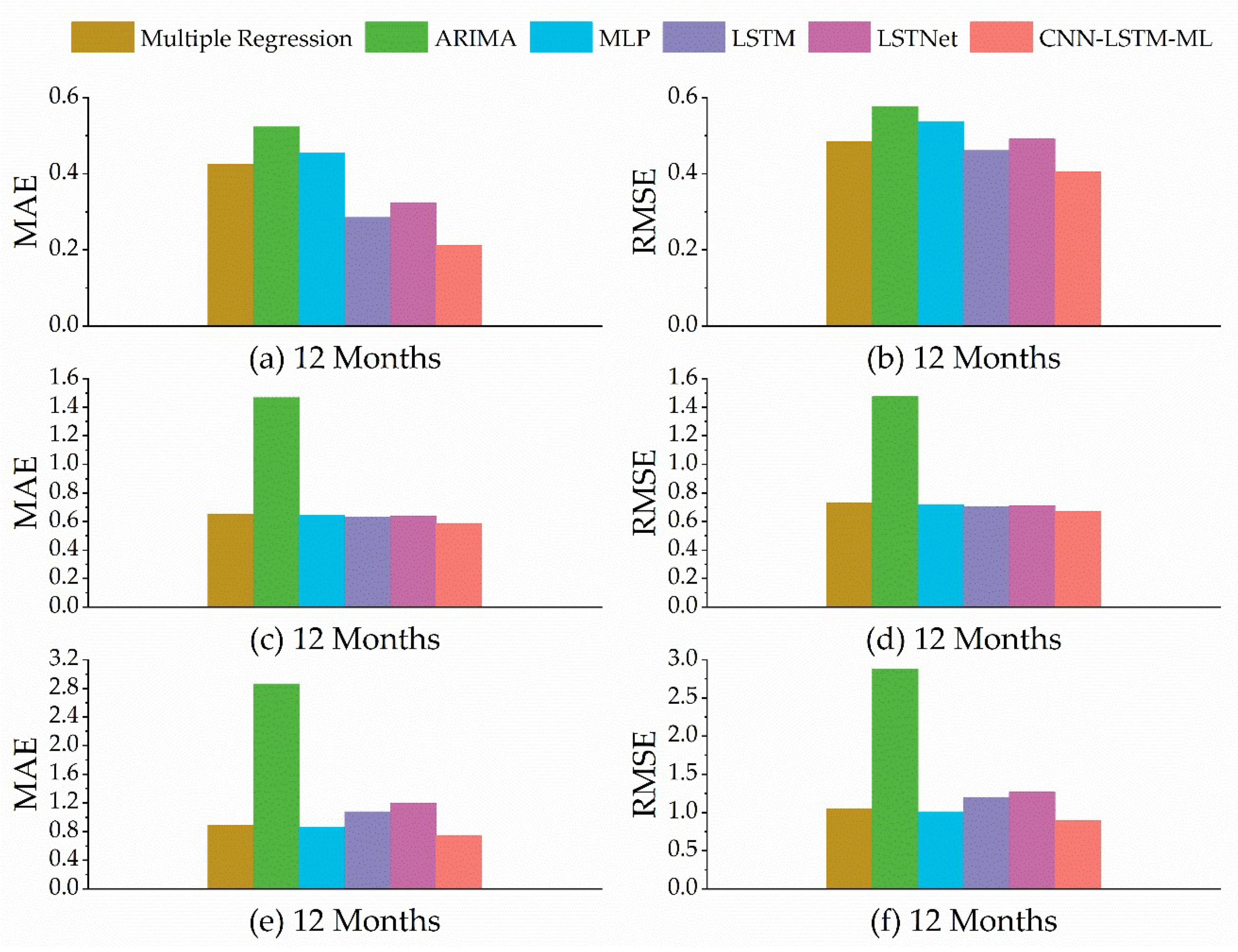
| Month | CNN-LSTM-ML | LSTNet | LSTM | MLP | ARIMA | Multiple Regression | |
|---|---|---|---|---|---|---|---|
| 1 | 0.095 | 0.123 | 0.116 | 0.109 | 0.154 | 0.212 | |
| 2 | 0.111 | 0.154 | 0.135 | 0.143 | 0.176 | 0.205 | |
| MAE | 4 | 0.105 | 0.141 | 0.139 | 0.154 | 0.209 | 0.249 |
| 6 | 0.124 | 0.152 | 0.158 | 0.172 | 0.223 | 0.269 | |
| 8 | 0.122 | 0.168 | 0.147 | 0.221 | 0.238 | 0.331 | |
| 10 | 0.136 | 0.187 | 0.165 | 0.193 | 0.244 | 0.348 | |
| 12 | 0.142 | 0.201 | 0.171 | 0.256 | 0.251 | 0.357 | |
| 1 | 0.135 | 0.172 | 0.163 | 0.155 | 0.21 | 0.389 | |
| 2 | 0.154 | 0.202 | 0.187 | 0.196 | 0.248 | 0.376 | |
| RMSE | 4 | 0.148 | 0.195 | 0.191 | 0.237 | 0.267 | 0.462 |
| 6 | 0.172 | 0.194 | 0.206 | 0.266 | 0.292 | 0.505 | |
| 8 | 0.175 | 0.226 | 0.201 | 0.301 | 0.304 | 0.571 | |
| 10 | 0.183 | 0.245 | 0.224 | 0.298 | 0.315 | 0.603 | |
| 12 | 0.196 | 0.287 | 0.246 | 0.429 | 0.337 | 0.642 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, Z. A CNN-LSTM Model Based on a Meta-Learning Algorithm to Predict Groundwater Level in the Middle and Lower Reaches of the Heihe River, China. Water 2022, 14, 2377. https://doi.org/10.3390/w14152377
Yang X, Zhang Z. A CNN-LSTM Model Based on a Meta-Learning Algorithm to Predict Groundwater Level in the Middle and Lower Reaches of the Heihe River, China. Water. 2022; 14(15):2377. https://doi.org/10.3390/w14152377
Chicago/Turabian StyleYang, Xingyu, and Zhongrong Zhang. 2022. "A CNN-LSTM Model Based on a Meta-Learning Algorithm to Predict Groundwater Level in the Middle and Lower Reaches of the Heihe River, China" Water 14, no. 15: 2377. https://doi.org/10.3390/w14152377






