1. Introduction
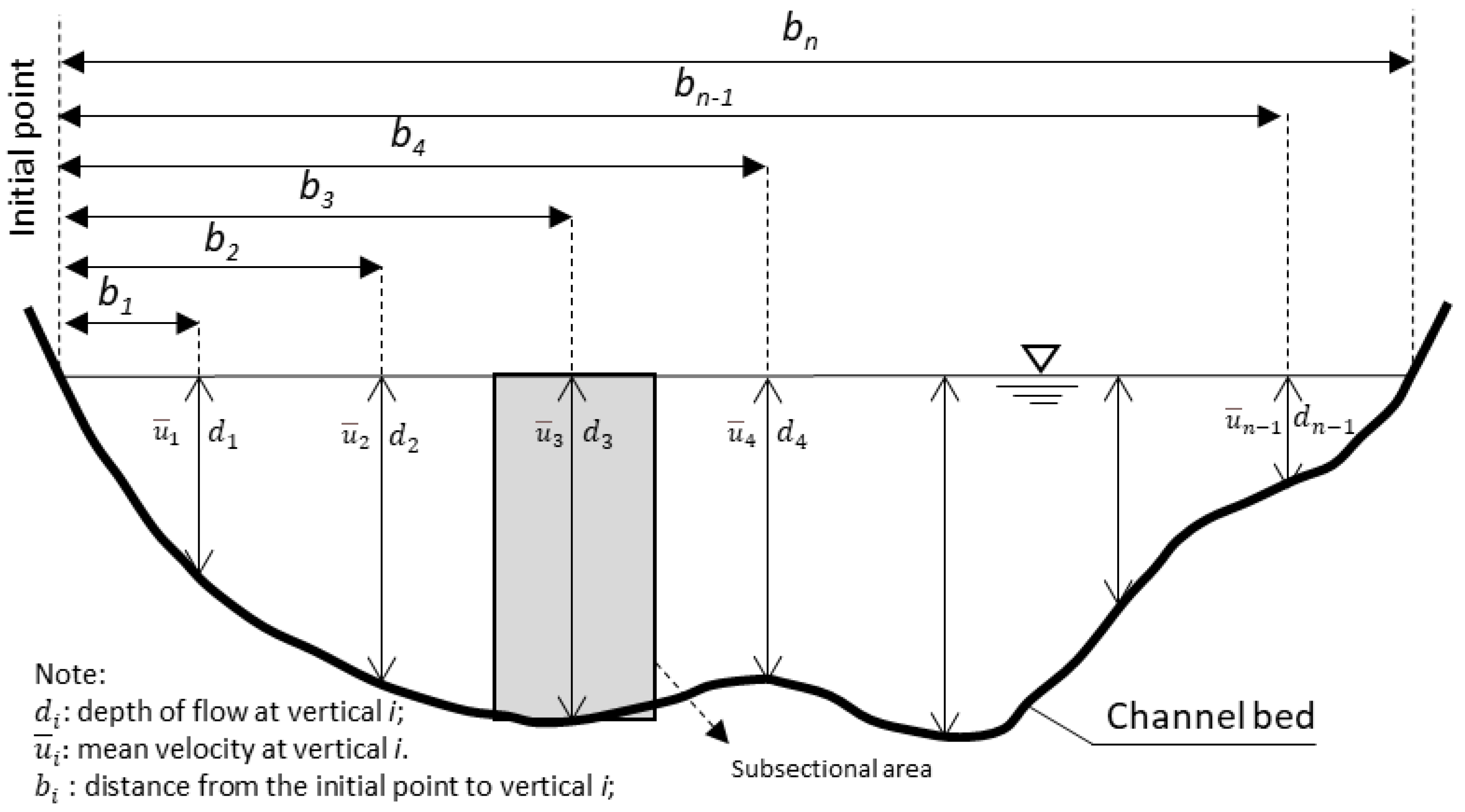
Conventional methods of river discharge measurement apply the velocity-area principle [
1] for field measurements while the mid-section method [
2] is used to calculate the streamflow. The conventional method involves dividing a river cross-section into several subsections. In each subsection, the mean velocity and water depth are measured along the vertical to obtain the discharge of the subsection. The streamflow is the sum of the discharge measurements of all subsections. The conventional method is usually a contact method, requiring a current meter, a sounding weight, and hydrologists on site making this method costly, time-consuming, and labor-intensive. This method is not suitable for tidal streams and during the high water.
Many instruments have been invented with the goal of improving conventional methods, allowing for the rapid and accurate measurement of flow velocity and water depth. An acoustic Doppler current profiler (ADCP) which applies the Doppler effect is a relatively new instrument and has been widely considered as a method used to replace mechanical current meters for velocity measurement. Simpson [
3] used a broad-band ADCP that is much faster for accurately measuring tidally affected flow than conventional methods. Boiten [
4] applied ADCPs to measure discharges in open channels, according to the velocity-area principle. Costa et al. [
5,
6] used a boat-mounted ADCP to measure discharge for converting surface-velocity to mean velocity. Muste et al. [
7] analyzed velocity profiles collected by ADCPs to propose complementary software for better support of hydraulic investigation requirements. Chauhan et al. [
8] showed that the relative error of the discharge measurement is very small with the ADCP compared to the conventional method. Oberg and Mueller [
9] showed that ADCP streamflow measurements are unbiased when compared to the discharges obtained by current meter, stable rating curves, salt-dilution, and acoustic velocity meter. Flener et al. [
10] used the multidimensional spatial flow patterns measured by an ADCP installed on a remotely-controlled boat to monitor a spring flood. Ground penetration radar [
11,
12], lidar [
13], pressure sensors, and sonar systems [
14,
15] have been developed to replace the conventional sounding weights during water depth measurement. Although these modern instruments are costlier, they can be applied to provide data when conventional instruments cannot, with the extra benefits of reducing the overall cost and time required [
10,
16].
It is better to not put hydrologists and equipment in contact with the water, given concerns for personal safety and efficiency. The US Geological Survey [
16] has also suggested that in the future gaging stations can use remote sensing outside the flow of water to measure water stages, cross-section, and velocity, and so on. In the past and currently, floats are most often used for surface velocity measurements. The principal sources of error inherent in determining surface velocity in this way are wind and flow conditions. With the recent development of new technology, non-contact instruments [
5,
6] used for measuring surface flow velocity and to estimate discharge have gradually been developed, among which, surface velocity radar (SVR, [
17,
18,
19,
20]) and particle image velocimetry (PIV, [
21]) are the main ones. The most important issue when applying surface velocity to estimate discharge is the choice of a surface-velocity coefficient. In a natural channel a surface-velocity coefficient of 0.85 or 0.86 is typically used to compute mean flow velocity [
2]. However, the surface-velocity coefficient varies with the positions of the verticals from the river bank. Generally, the closer to the bank, the larger the surface-velocity coefficient. In addition, with higher water flow the maximum velocity will occur below the water surface, so the surface-velocity coefficient will also become larger. The velocity distributions can be used to determine the surface-velocity coefficient. The logarithmic distribution [
22,
23] and probabilistic velocity distribution [
24] are commonly used to determine the surface-velocity coefficient. The mean velocity of the vertical can be estimated by the surface-velocity coefficient and surface velocity, and then the velocity-area principle can be used to estimate streamflow.
Although using surface velocity to estimate river discharge is quite efficient, it is still necessary to select surface-velocity coefficients for all verticals to accurately estimate the streamflow; however, it is always a difficult task to determine the best coefficients. Therefore, this study proposes a method which uses the average surface velocity and only one surface velocity coefficient to efficiently and accurately estimate streamflow.
3. Case Study: Study Sites and Data Collection Methods
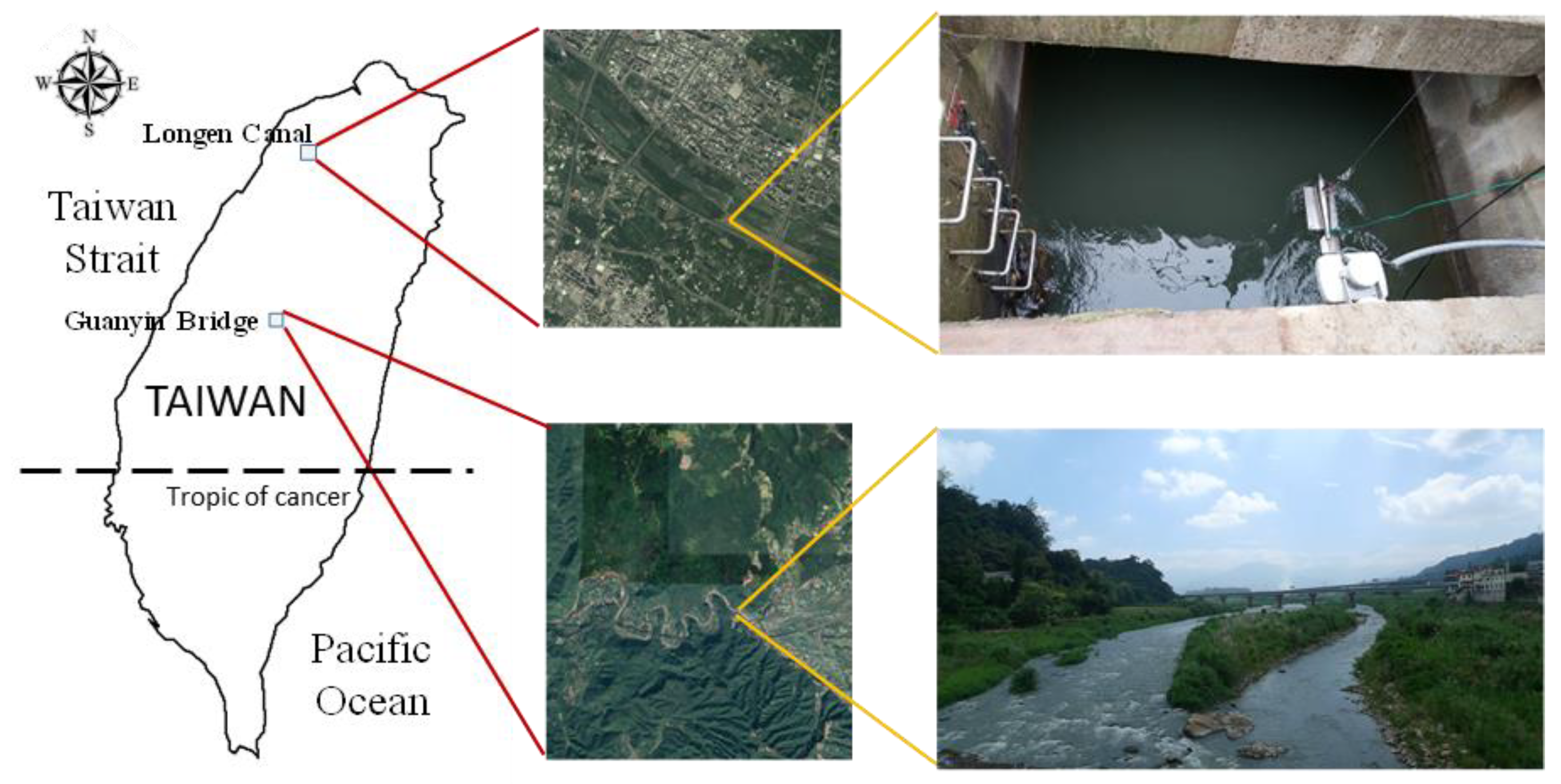
This study applied field data collected in a natural river and an artificial channel to verify the proposed approach. The study sites are located along Nankang River at Guanyin Bridge in central Taiwan and along Longen Channel in Hsinchu, northern Taiwan (
Figure 3).
The Nangang Creek serves as the main tributary of the Wu River, with a length of about 37.4 km and a catchment area of about 438.14 km2. It originates from the western foothills of the Hehuan Mountain at an elevation of 3417 m. Wu River is one of the most important rivers in Taiwan, providing vast amounts of water for industrial, agricultural and domestic uses. Thus, the Third River Management Office set up a gauge station at the Guanyin Bridge for the purposes of water resources and flood management.
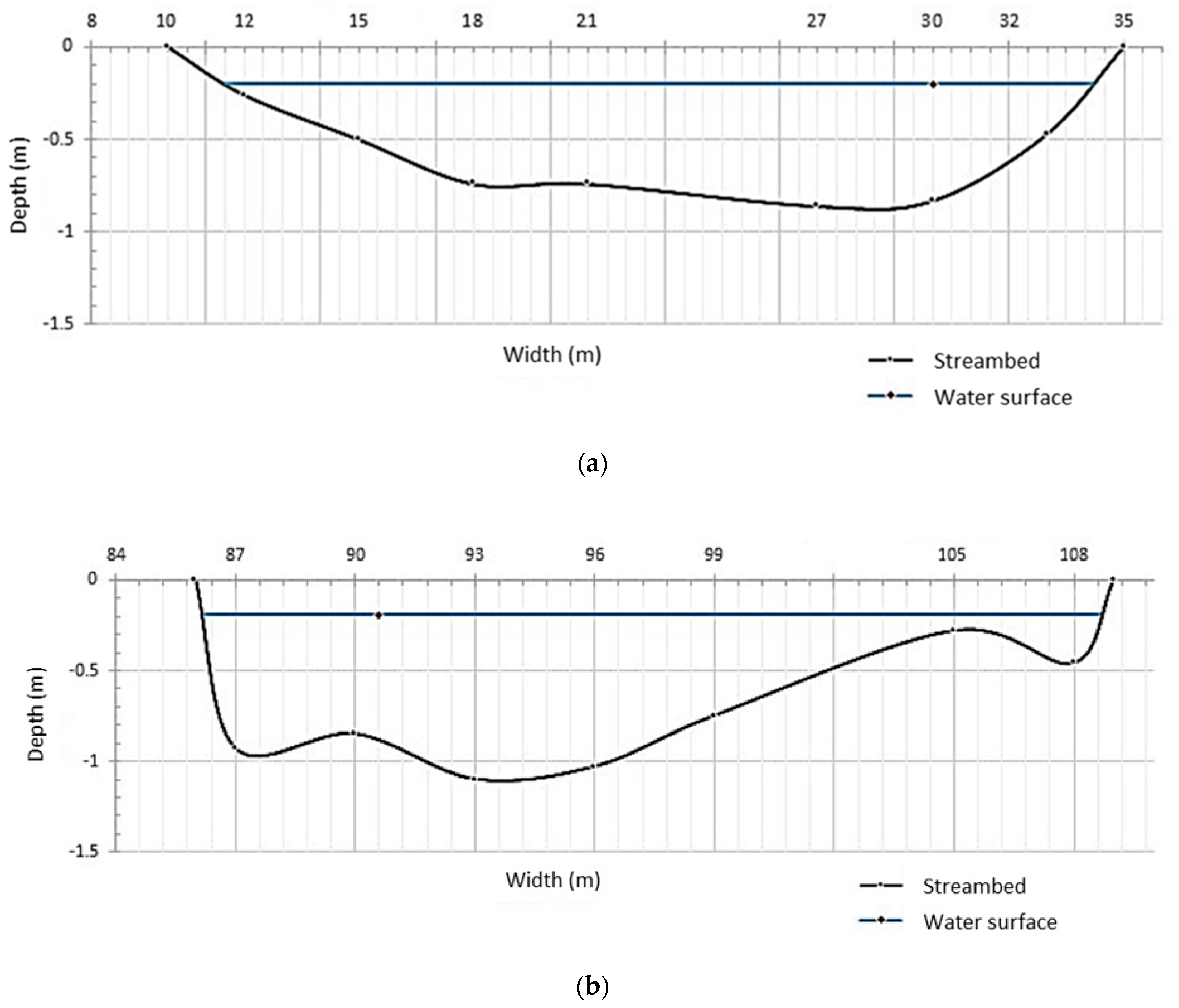
The Nangang Creek at the Guanyin Bridge, where the measurements were taken, is located near the geographical center of Taiwan, with water flowing from east to west. The channel of Nangang Creek near the Guanyin Bridge is divided into left and right channels. As shown in
Figure 4, both the two channels are considered rectangular in cross-section, particularly during the periods of high water, while the left channel is narrower in width and shallower in depth. The collision of tectonic plates has uplifted the terrain of Taiwan over time, while floods brought by typhoons always wash the riverbeds, causing riverbeds to become unstable and change shape frequently. An electromagnetic current meter was used to estimate the water discharge at the Guanyin Bridge. The distance between two successive verticals was 3 m. The velocity observations were made based on the water depth of each vertical. When the water depth was greater than 0.6 m, the two-point method was used, while when the water depth was less than 0.6 m, the six-tenths depth method was used. This study also used a vehicle-mounted SVR unit to measure the surface velocity at each vertical (
Figure 5a). A total 23 discharge measurements were made in 2018.
The water in Longen Channel comes from Longen Weir in the middle reach of the Touqian River. Its main function is to divert water from the Touqian River for irrigation and domestic use purposes. The measurement location in Longen Channel was about 1 km downstream from the water intake location. The channel at this location was formed by a box culvert with no place for mounting instruments. Therefore, the top of the box culvert was opened about 1 m wide to allow for discharge measurements. The cross-section of Lungen Channel is rectangular with a width of 2.6 m. Due to the narrow width, the SVR unit can be easily affected by the side walls. With slow water flow, the water surface is very calm, which also makes the SVR unit unable to measure the surface velocity. Therefore, an Argonaut SW acoustic Doppler Flowmeter (Sontek, San Diego, CA, USA) was used to measure the velocity profile, and then a probabilistic velocity distribution equation was used to estimate the surface velocity. The SW Flowmeter was a pulsed Doppler Current profiling system designed for measuring water velocity profiles using three acoustic beams (
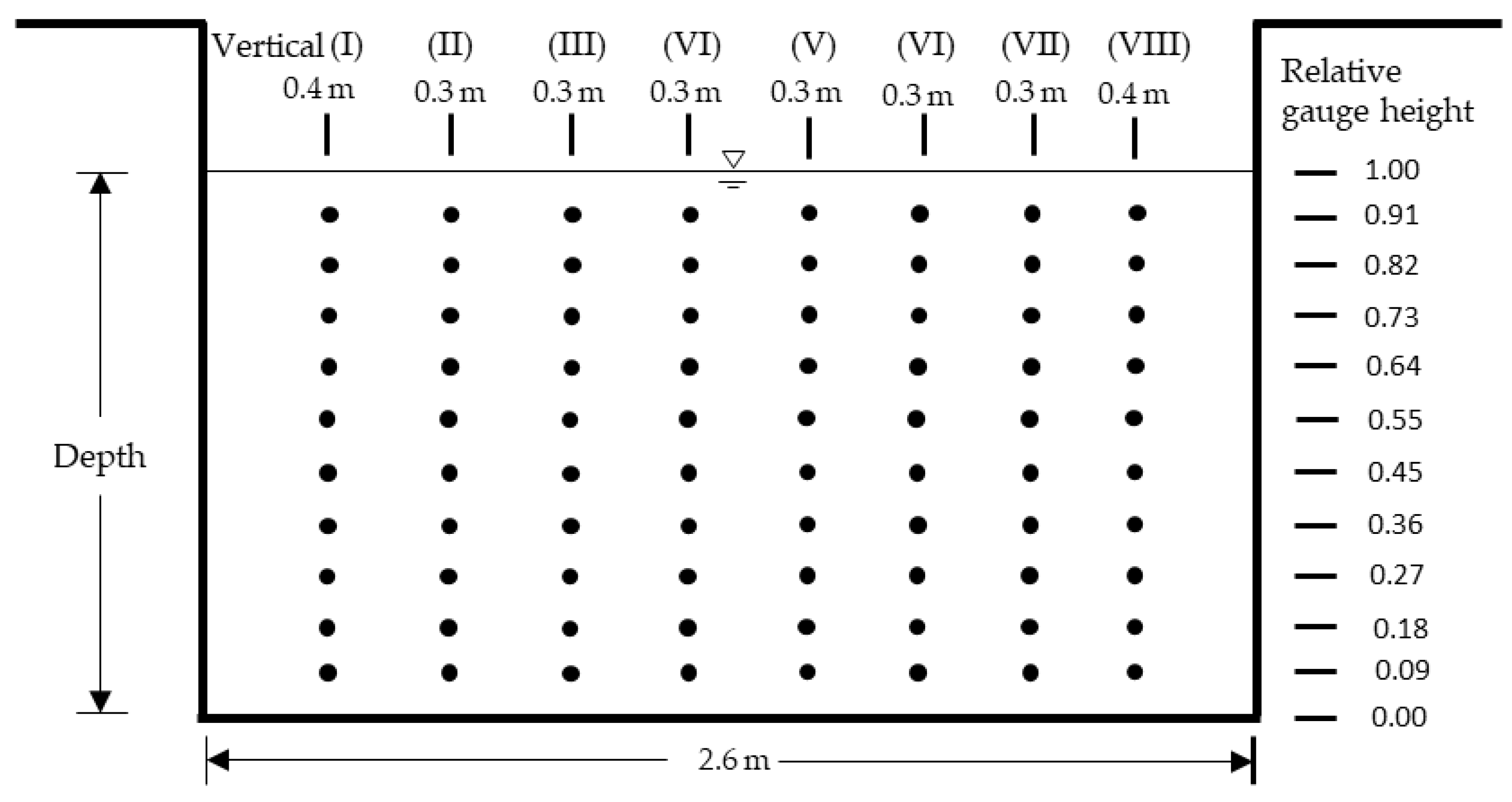
Figure 5b). The slanted beams, Beams 1 and 2, measure the water velocity in two dimensions, and the down-looking beam measures water depth. An SW Flowmeter is usually mounted in a channel bottom. In this study, the SW Flowmeter was installed under the sounding weight, so that the velocity profile was measured from top to bottom. The velocity observation locations in Longen Channel are shown in
Figure 6. The velocity distribution was measured on eight vertical lines, the distance between the verticals was 0.3 m, and the velocity was measured at ten points on each vertical.
Table 1 shows the discharge and water depth measurements of eight runs during different water stages having covered the upper and lower water supply capability of Longen Channel. Based on
Figure 6, the velocity measurements of Run 4 in
Table 1 are shown in
Figure 7.
4. Results and Discussion
The discharge measurement in the natural channel at the Guanyin Bridge was taken by the conventional two-point method for the water depth and the mean vertical velocity. Meanwhile, owing to the limitations caused by the channel width, the discharge measurement at the Longen Channel was taken from the vertical velocity profile for the mean velocity. The mid-section method was then applied to both the natural and the artificial channels. The mean cross-sectional velocity can be observed by the discharge divided by the cross-sectional area.
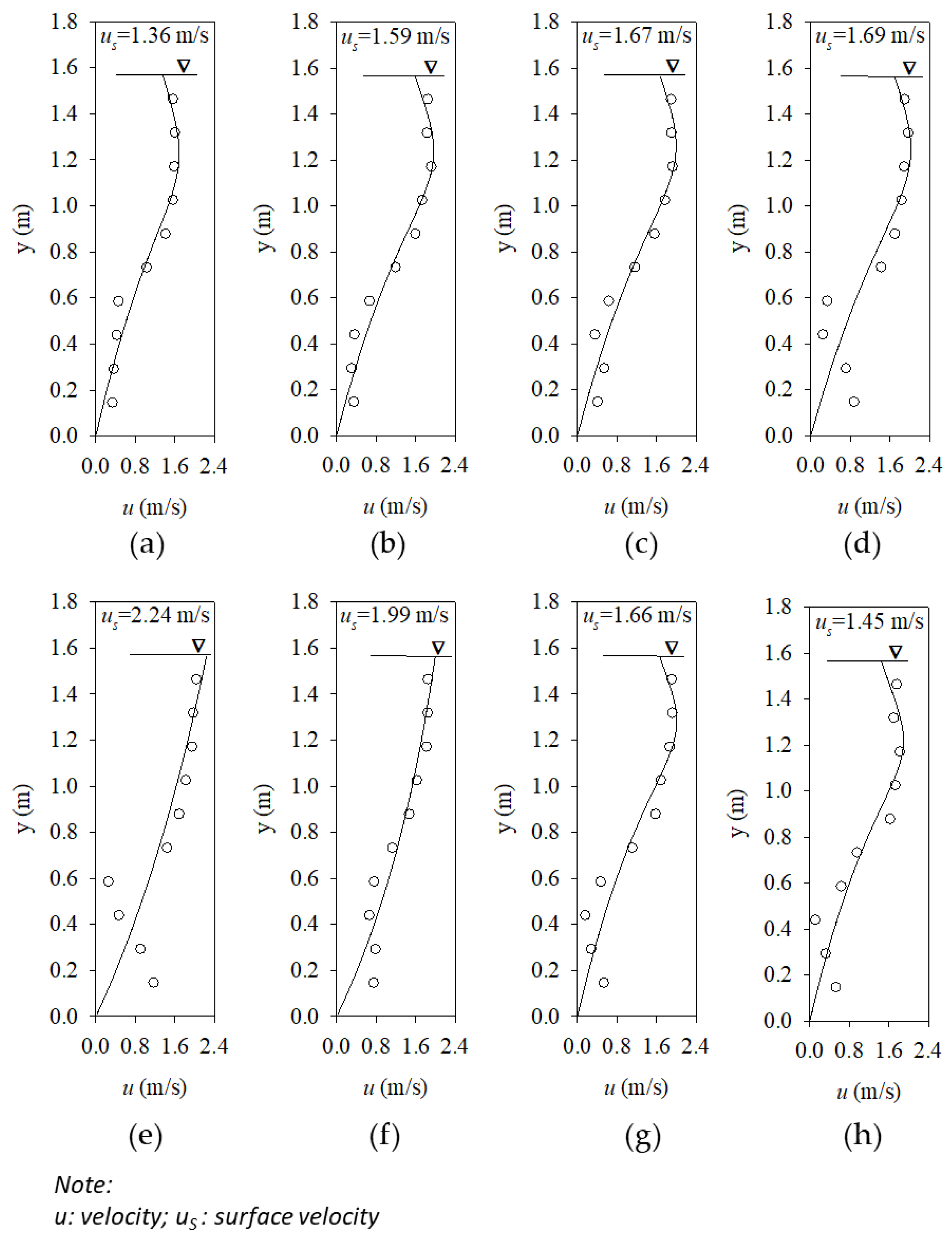
Figure 7 shows the vertical velocity profile of the Longen Channel on 8 March 2019 when the discharge was 3.80 m
3/s. The flow pattern of the Longen Channel was quite similar to a large-scale hydraulic flume in a laboratory. In
Figure 7, it is obvious that the flow patterns of Longen Channel were very different from those of natural rivers. Most of the maximum velocities on the verticals occurred at a depth of about 1/4 water depth from the water surface, while the surface velocity was relatively small. It also shows that the maximum velocities of the verticals excluding verticals (e) and (f) did not occur on the water surface. Experimental studies have been shown from considerations of momentum transfer that the velocity in an open channel should decrease toward the channel bed. In a very wide channel the velocity decreases toward the bed and walls, and theoretically the maximum occurs at the water surface. The Longen Channel is a small artificial flume; therefore, depression of the maximum velocities below the water surface was observed. The flow pattern cannot be described by a logarithmic distribution. The circle in
Figure 7 is the actual velocity measurement on each vertical, and the line is the velocity distributions based on (11) indicating that vertical maximum velocity does not always occur on the water surface. It also shows that the velocity profile data of the Longen Channel is difficult to describe using conventional velocity distribution theories, such as logarithm velocity distribution. However, (11) can simulate velocity profiles effectively, regardless of whether the maximal velocity occurs on or below the water surface. Therefore, the surface velocities on the verticals could also obtained precisely by using (11). In addition, using the nonlinear regression method,
M,
h and
umax can also be obtained from (11) with the vertical velocity and water depth. Thus, the mean vertical velocity (
) on each vertical can be estimated. Therefore (11) can be used to accurately estimating the mean velocity of the vertical for obtaining reliable discharge.
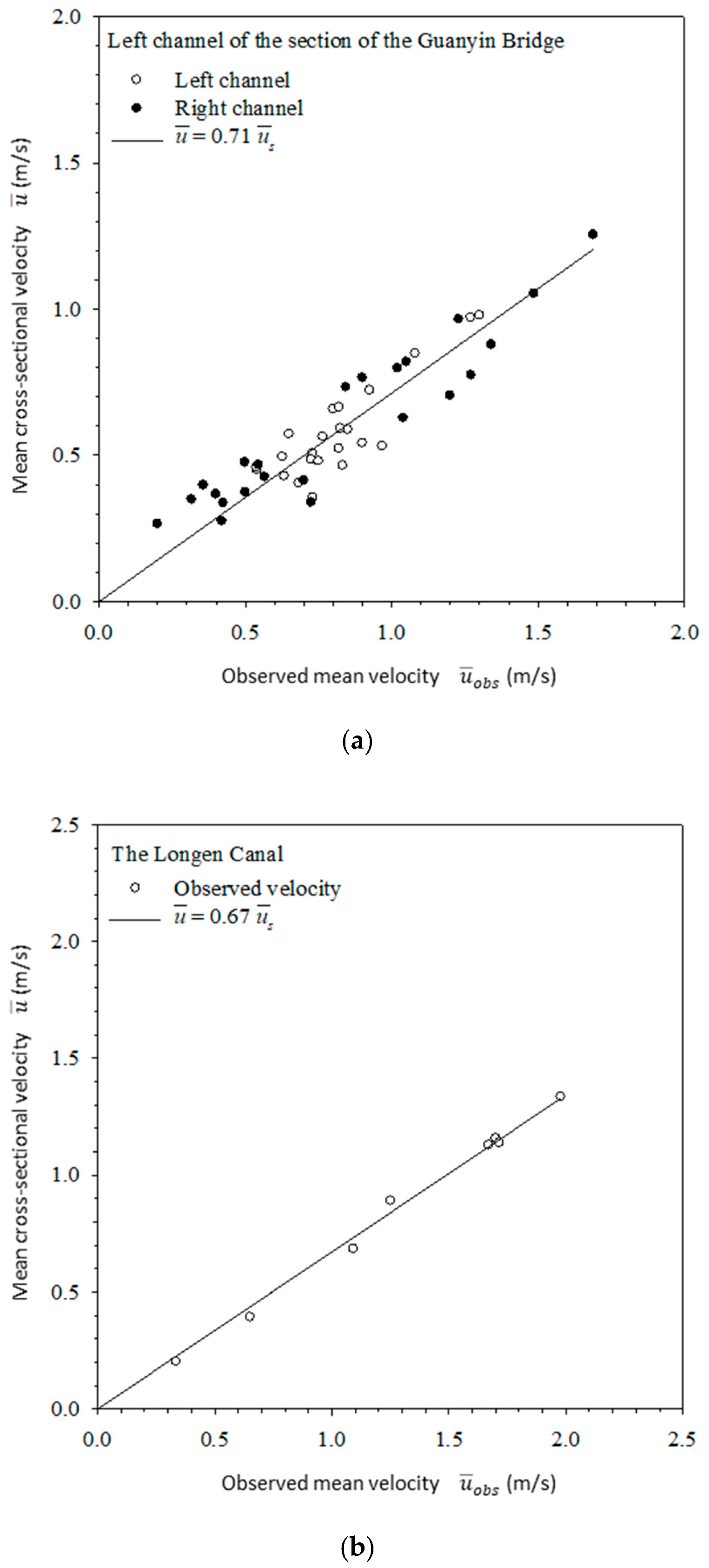
Figure 8 shows the relationship of the mean surface velocity and mean velocity of Nankang River at Guanyin Bridge and at Longen Channel. The surface velocity of the natural river was directly measured by SVR, while surface velocities of artificial channels were estimated by the probabilistic velocity distribution equation. All the points, including those in the left and right channels, distribute closely on the two sides of the regression. The relationships of the mean surface velocity and the mean velocity of the cross section in the left and right channels in
Figure 8a do not show much difference.
When all the points were combined, all the points fall on the periphery of the regression line, and when the mean surface velocity increases, the data tends to approach the regression line. This means that as the water depth increases, the width of the cross-section increases even more making the shape of the cross-section approach the shape of a rectangle. Hence, the relationship between the mean surface velocity and the mean velocity was stable.
Figure 8b shows an artificial rectangular channel with all the points falling near the regression line. This means that the relationship between
and
of the artificial rectangular channel is very stable. It reveals that the mean cross-sectional velocity and mean surface velocity in both the natural and the artificial channels have correlation coefficients of 0.92 and 0.99, respectively. As the artificial channel is confined with the concrete bed and walls, the velocity is less affected by natural factors; and thus, it performs better than the natural channel.
Figure 8 demonstrates that the relationship between the mean surface velocity and the mean velocity of natural rivers and artificial channels is quite stable, forming a linear relationship through the origin.
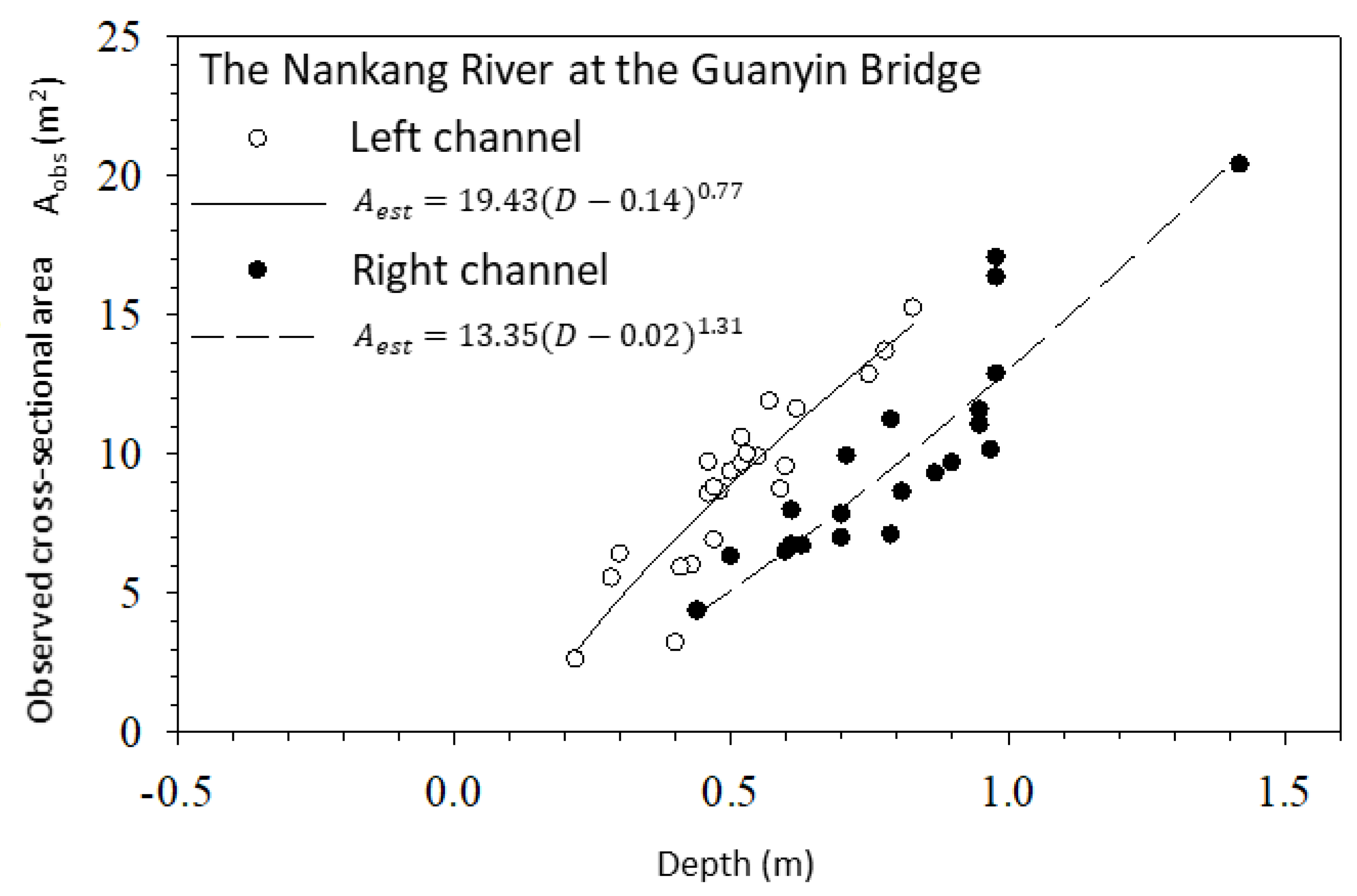
Nangang Creek is a mountain river at Guanyin Bridge, with steep slopes and continuous erosion and sediment deposition. When a flood occurs, the river course will initially be deepened, although the river course will be silted back in as the water recedes. However, the data from 2018 show that the water stage did not change much during the study; nevertheless, the flow and cross-sectional area of the river have changed greatly over time due to erosion and deposition along the river. Thus, it is impossible to estimate the water cross-sectional area based on the water stage. In order to quickly estimate the cross-sectional area, the water depths of the left and right channels at 30 m and 91 m from the initial point were used to establish the relationship between water depth and cross-sectional area (
Figure 9). The points (dots and open circles) in the figure represent observed data in the right and left channels, respectively, while the lines represent the depth-cross-sectional area rating curves obtained by nonlinear regression. The nonlinear regression method was applied to relate the water depth and the cross-sectional area with the coefficients given from the observations. The points did not deviate too far from the regression lines. The correlation coefficients of the left and right channels were 0.94 and 0.90, respectively, suggesting that the regression equations are quite useful for making estimations of cross-sectional area by using depths.
As the shape of the artificial channel is rectangular, the cross-sectional area can be obtained easily from the water depth and the width of the channel. Therefore, the cross-sectional area of the Longen Canal can be quickly and accurately estimated by the water depth of each run and the width of the channel.
After the two relationships: (1) between mean cross section and mean surface velocity, and (2) between water depth and cross-sectional area were established, the estimated discharge could be quickly obtained with mean surface velocity and water depth. The estimated discharge with the mean surface velocity and water depth were:
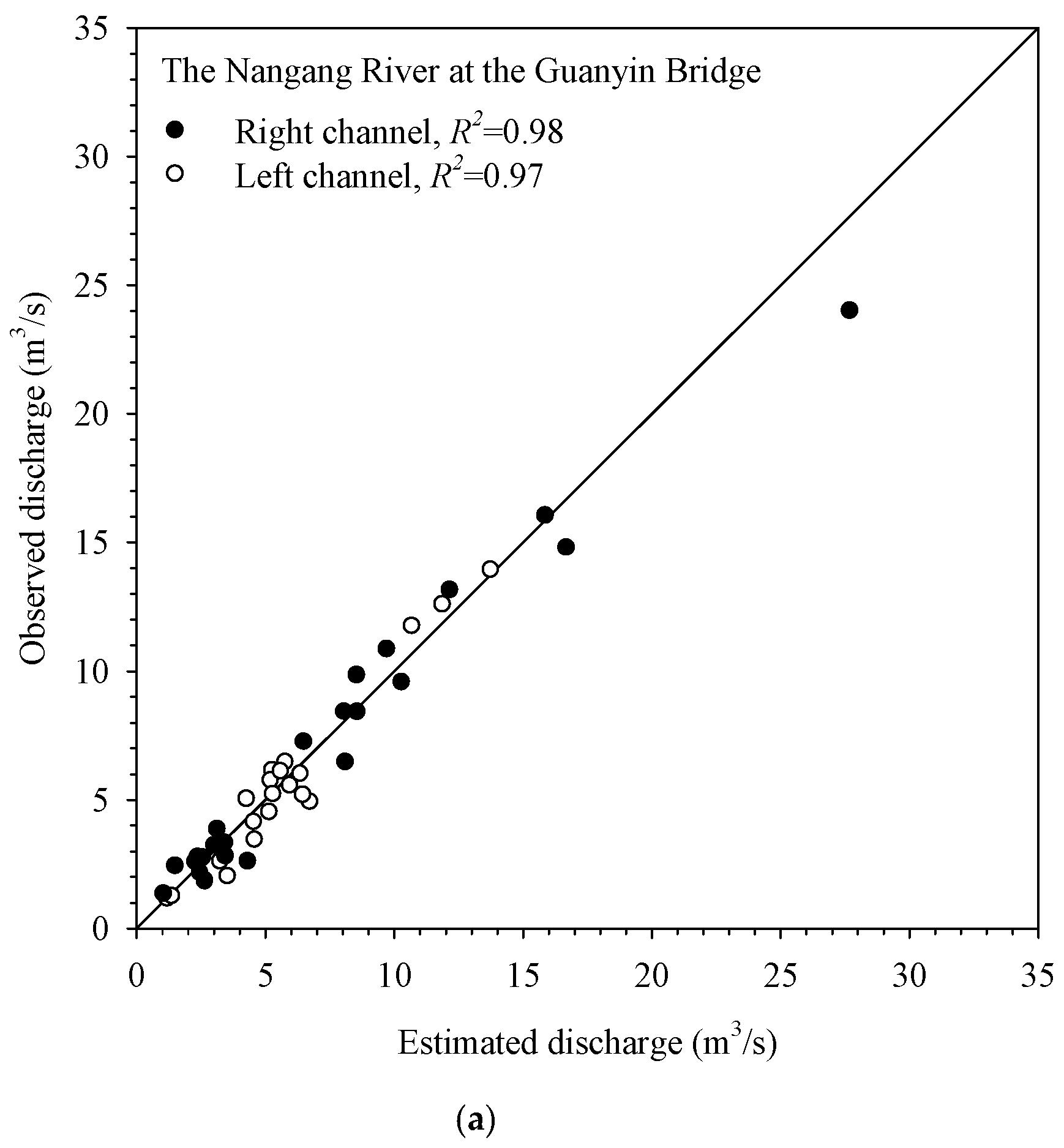
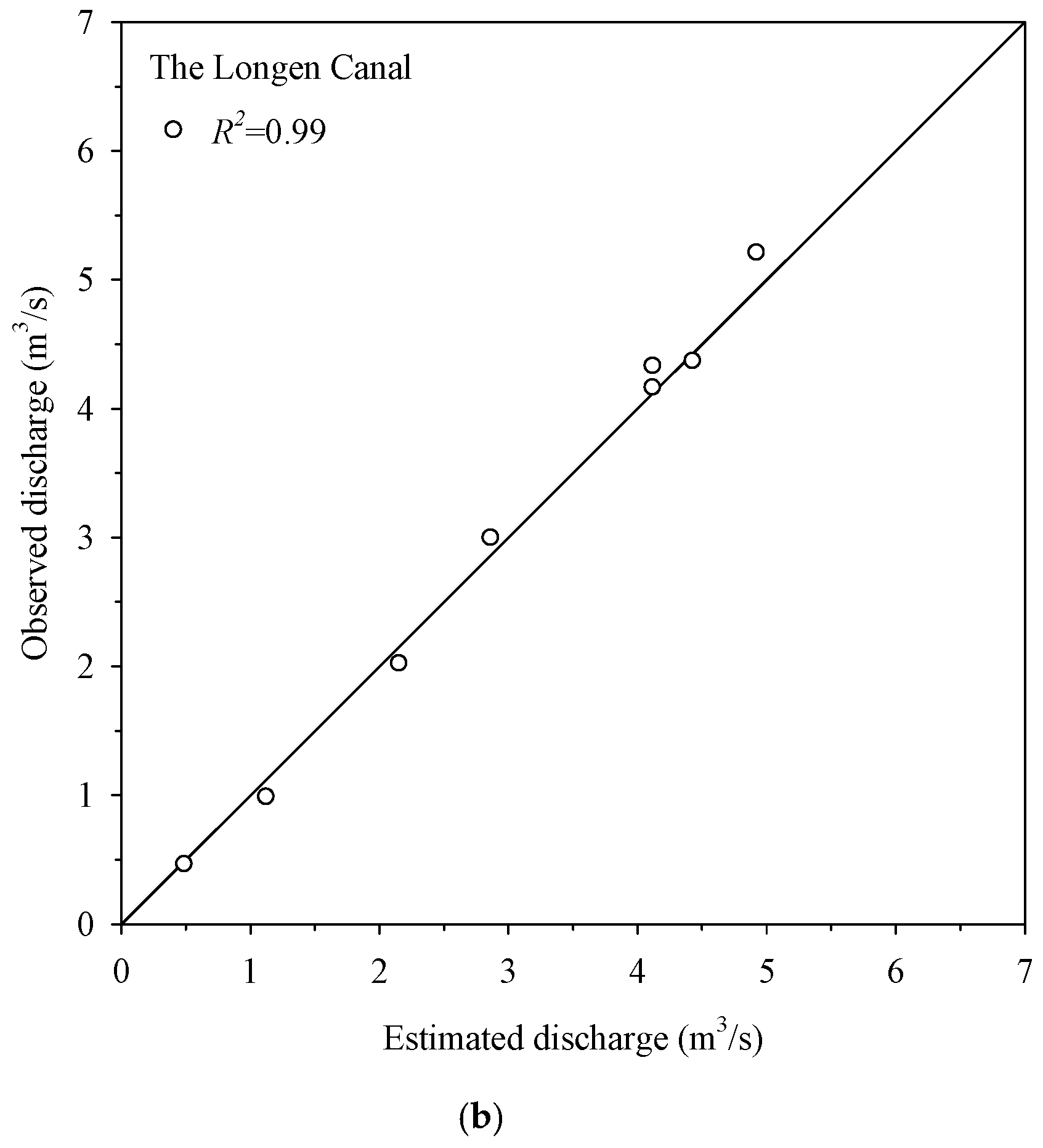
Figure 10 illustrates the accuracy of the discharge measurement using the mean surface velocity. The
x- and
y-axes represent the discharge measured by the mean surface velocity and the conventional method, respectively. This figure also shows that the natural channel cross-section was close to a rectangle; however, the estimation of the cross-sectional area of the natural channel was not as accurate as that of the artificial channel. As a result, the measurement of the artificial channel was better than that of the natural channel, but all points fall on the 45-degree agreement line, which demonstrates that the streamflow measured by both the conventional and the proposed methods were close to each other with less than 1% error on average.
A strong correlation (R2 > 0.97) between the above two methods demonstrates the accuracy and reliability of using the mean surface velocity method for discharge measurement in both the natural rivers and artificial channels. Therefore, the authors concluded the measurement of river discharge can be obtained promptly and accurately using the proposed approach, which only requires one to measure the surface velocity to obtain the mean surface velocity, and estimate the cross-sectional area based on the water depth (or water stage).
5. Conclusions
The conventional methods for discharge measurement consume more labor and time than the proposed approach. Particularly, it is more risky when taking discharge measurement during the high water. The proposed approach applies the relationship between the mean cross-sectional velocity and the mean surface velocity as a constant in each cross section if the cross section does not change too much. Once the constant of the relationship is found, the discharge can be easily estimated based on the constant, the mean surface velocity, and the cross-sectional area. The mean surface velocity can be obtained through the SVR or other means; and the cross-sectional area can be estimated by water depth (or stage) or other means. Nowadays, the surface velocity radar (SVR) has become a popular instrument, which makes the surface velocity measurement easy, reliable and accurate.
The data collection from a natural stream and an artificial channel was used to demonstrate the proposed approach. Two case studies were conducted at two locations with many session runs at different times with low to intermediate flows. Both conventional and the proposed methods were conducted for flow measurements. The results show the feasibility of measuring streamflow with an accuracy of less than 1% difference on average comparing the proposed and the conventional methods. Moreover, the strong correlation coefficient (>0.97) of the observed discharge and the estimated discharge suggests the reliability of the proposed approach for streamflow measurement in both the natural and artificial channels. In previous studies, the conventional methods required extra coefficients (velocity profile or surface velocity coefficient) of each subsection for determining the mean velocity in each subsection, involving more time and labor cost. In this study, we proposed that the mean surface velocity to estimate streamflow can provide an opportunity to improve the conventional methods in streamflow measurement and maintain the accuracy of discharge measurement.
This approach can substantially reduce the uncertainty involved in determining surface velocity coefficients that are employed in conventional methods, while maintaining the accuracy of discharge measurement. Compared with the conventional methods, the proposed approach saves more labor and time cost. As it is a non-contact method, it can also reduce the risk to human life and measuring instruments when taking measurements in the natural environment. The proposed approach can be applied in both natural and artificial channels for flow measurement. Based on the measurement sessions implemented in this study, we conclude that the proposed approach can provide reliable and accurate streamflow measurement from low to intermediate flows. The constancy of the relationship between the mean cross-sectional velocity and the mean surface velocity suggests that this approach might also be applied for high water conditions, which would need further tests in the future.