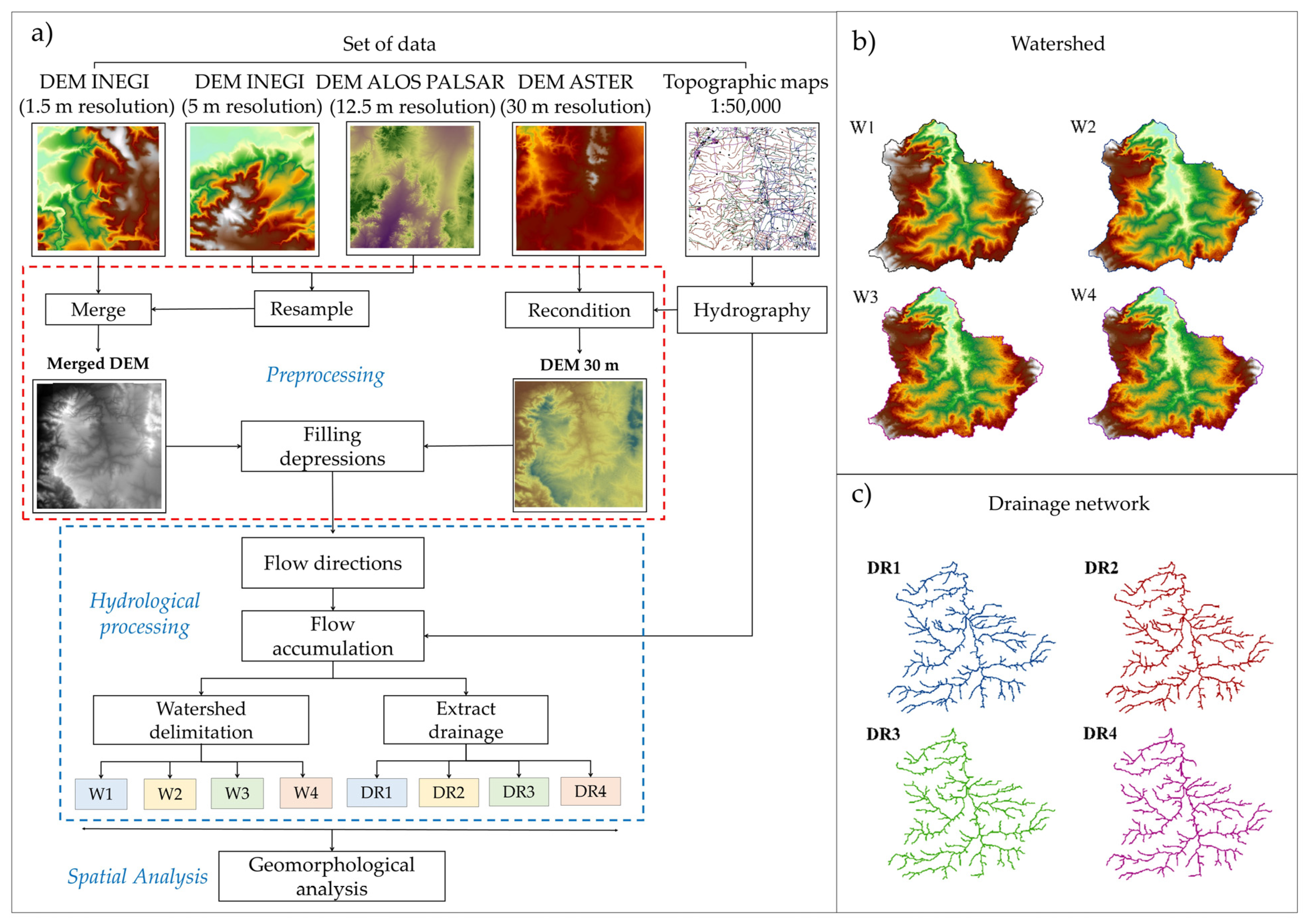
Scientific literature reports that DEM resolution should be as high as possible (<5 m) [
37,
41,
42]; however, in countries where available DEM are of coarse resolution (most of the terrestrial surface), other alternatives are required. On the other hand, it is stated that the implications of some algorithms used in the hydrological processing of the DEMs are negligible [
15]. Therefore, both DEM resolution and processing algorithms SIG should be considered a significant influence on the characterization of the watershed, and consequently, on the hydrological behavior of the water. Pre-treated DEMs (merged DEM and reconditioned DEM 30 m) were subjected to the processing algorithms.
3.1. Comparative of Fill DEMs
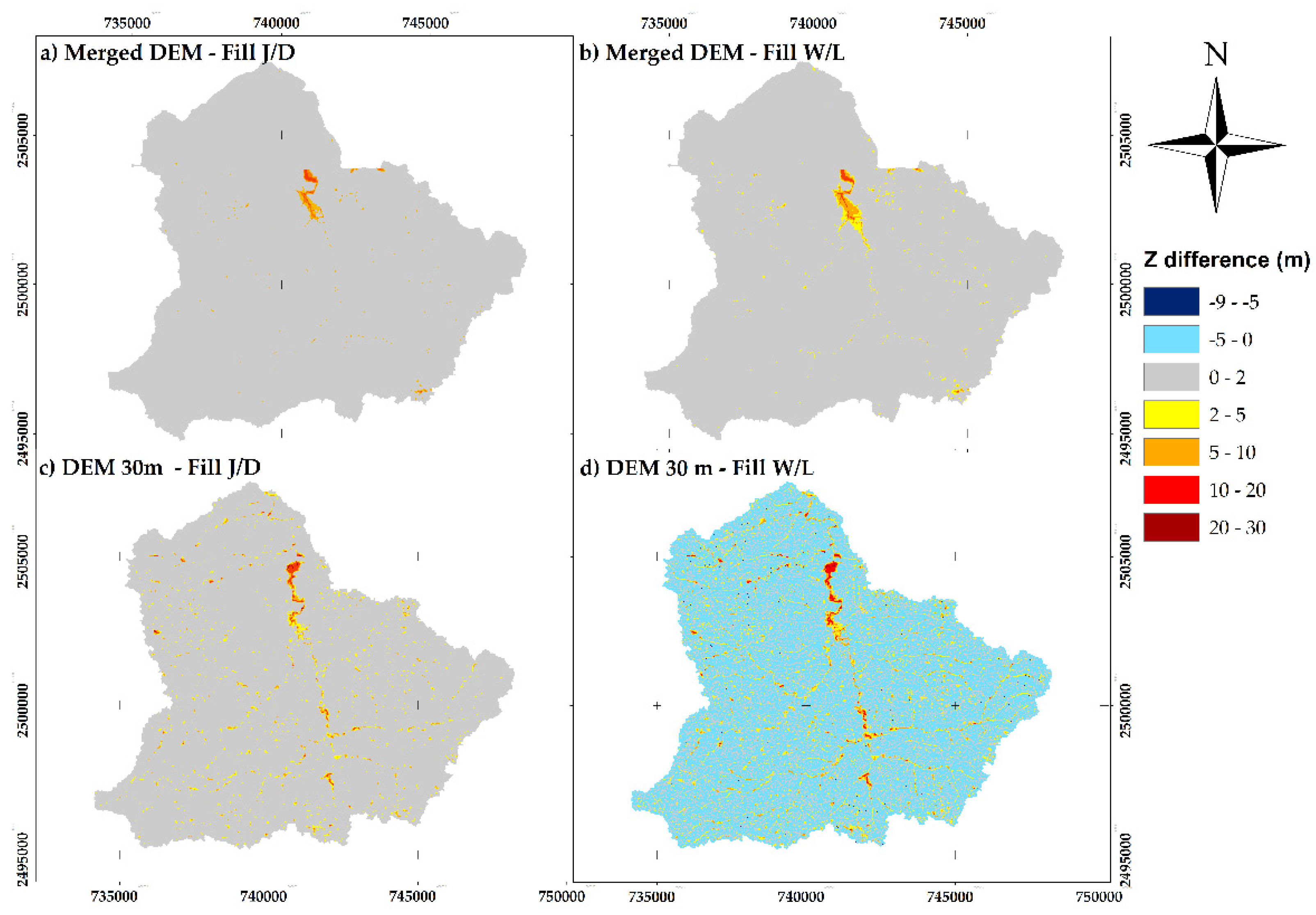
The watershed obtained with the most excellent area derived from the DEM dataset process was designated as the surface extent for analyzing the results in the fill and flow direction raster. To exhibit divergences between the J/D and W/L fill algorithms, the difference in elevation between each cell of pre-treated DEMs against the fill DEMs was determined for each resolution (
Figure 3).
Histograms of elevation differences expressed were determined in percentage, including the minimum and maximum variations; the data found are summarized in
Table 3. The differences in elevation show mostly values close to zero (0–2 m); however, important differences in the fill DEM 30 m were detected when using the algorithm of W/L, in both negative and positive values (56.2% of the cell range from −2 to 0 m), the product of a DEM smoothing. SAGA GIS generated a DEM smoothing within the same cell-filling tool for this algorithm. The W/L algorithm induces the highest elevation changes for two reasons: the slope gradient (in this research, a gradient of 0.1° was applied) and the smoothing (implicit in the SAGA GIS). In agreement with Engelhardt et al. [
6], smoothing originates flattening of local topographic characteristics, changes in both slopes and water dividing lines and also affects the calculation of flow direction. The maximum increase in the elevations of some cells (19–27.2 m), showing a more significant effect over the DEM 30 m (
Table 3). According to the results, the less affected raster by the filling is the merged DEM; the smoothing does not affect this resolution. Meanwhile, the J/D algorithm elevates cells without considering the slope, where cells with the same elevation can be presented. It is noticeable that the original topography suffers alterations on a coarse resolution.
Fill DEMs with the same resolution reveal a change in elevation similar, though not identical. Contrary to Pardo-Igúzquiza’s [
15] report that the methodologies of J/D and W/L produce the same result; in this research, it is evidenced that significant differences are caused by fill algorithms; the impact increases by decreasing the DEM resolution (
Table 3). The difference increases by employing a higher slope gradient in the W/L algorithm. It is worth mentioning that the fill DEM is the foundation of the following processes and variations have a significant impact.
The impact of the filling can be observed on the watershed slopes by assessing the obtained average slopes and the area percentages regarding the relief type (listed in
Table 4) in agreement with the IGAC classification [
86]. The main variation occurs on the flat and lightly flat relief, again due to resolution and slope gradient. The difference between the mean slopes of the watershed is approximately 1% for the two resolutions. Some of the geomorphological parameters that are directly influenced by the relief slope are the concentration time (
Tc), the mean slope of the main channel (
S) and the slope of the hillsides of the watershed.
Table 4 shows that in the highest resolution DEM (merged DEM), the relief of the watershed is predominantly flat (average of 68.9%). In case the DEM of 30 m prevails, there is a lightly flat and inclined relief of 70.7%. The relief was verified with a field visit, finding that the study site corresponds to a light flat. Flat reliefs are more susceptible to changes by smoothing or aggregation due to changes in the appearance of slopes [
41]. The slope variations directly affect the water speed travel (in advance and recession), the hypsometric curve, the hydrographs, the flood peak times, the soil erosion, and consequently the runoff estimates and the flow design that support the waterworks safety. At the sub-basin scale, the effects of slopes on hillsides and channels propagate in surface and subsurface runoff [
21,
28,
87,
88].
3.3. Geomorphometric Parameterization
The geomorphological parameters were determined to understand that the estimates of tributary areas and flow concentrations depend on the routing algorithms [
89,
90] and the DEM resolution [
44,
91]. Based on flow routing algorithms D8, D∞, and MFD, the watershed area (
A) and perimeter (
P) were obtained (see
Table 6). The watershed areas W1, W2, W3, and W4, correspond to the four scenarios illustrated in
Figure 2b. The range of values for the area was 100.381 km
2 to 103.524 km
2 and the average area of the watershed was 101.544 km
2. According to the classification of Faustino and Jimenez [
92], the watershed is classified as a micro-basin. The area value provided by the MFD algorithm over the fill DEM of W/L reaches 1.9% more than the average area—it was the most scattered. There is a greater difference in the estimated areas over a coarse resolution. On the other side, the average perimeter was 74.514 km, with a maximum variation of 19.351 km, representing approximately 26% of the difference. The perimeter directly affects the shape parameters that define the form of the watershed and provide an idea of the behavior of the runoff.
Achieving the highest accuracy in quantifying the watershed area is vital since it influences the estimates of most theoretical hydrological models. Wooding [
93] and Lee [
87] referred to the direct influence of the area in hydrological investigations. Similarly, dos Santos and Fewtrell expressed that the discrepancies in the watershed area impact simulations for estimating rainwater and sediment distribution.
Comparing areas of each scenario manifest the MFD algorithm overestimation in delimitation since it includes adjacent areas of other watersheds.
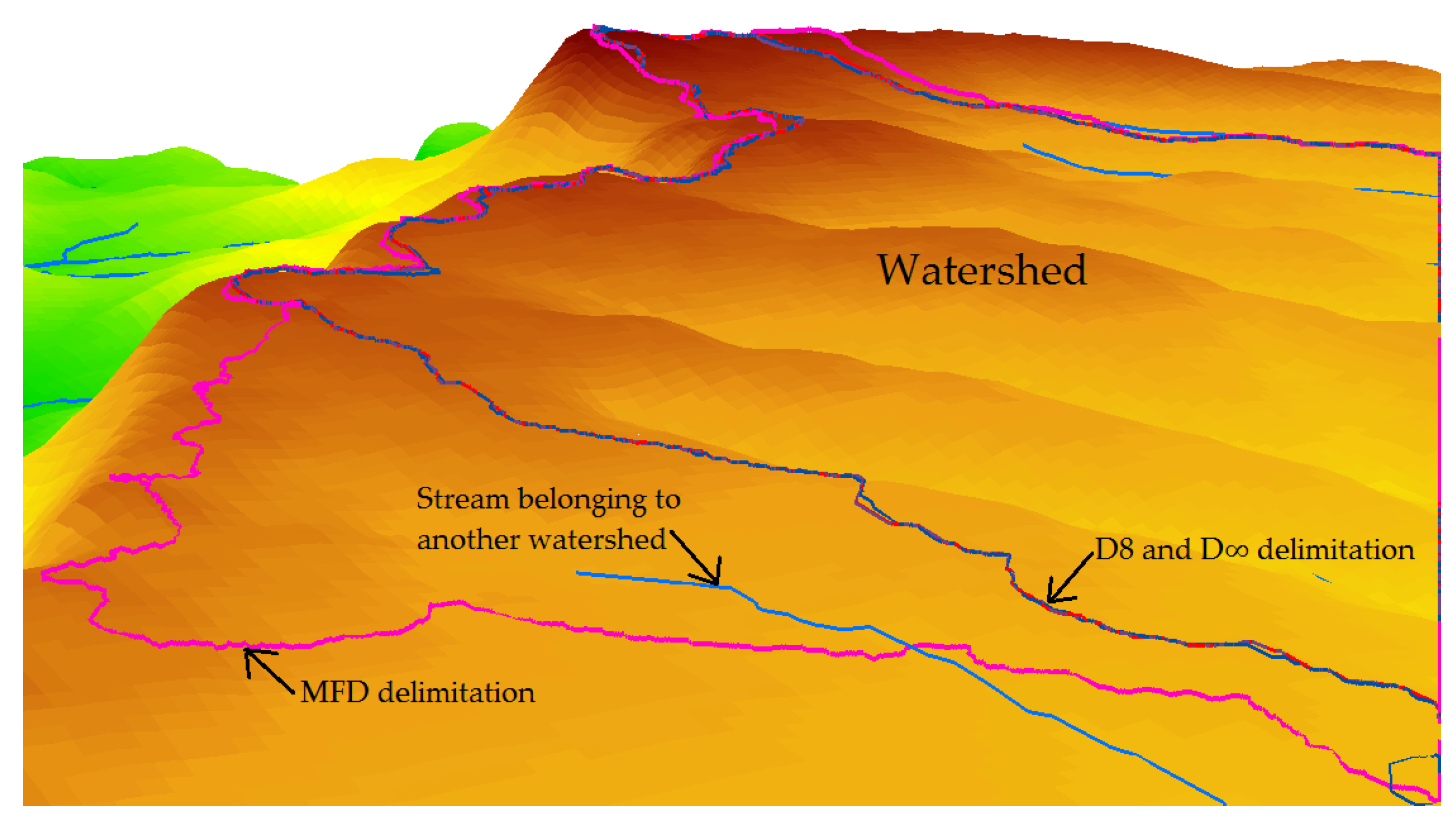
Figure 5 displays some watershed boundaries of the merged DEM where the D8 and D∞ algorithms delineation were similar, contrasting with the delineation executed by the MFD algorithm. The MFD algorithm exhibited greater discrepancy and overestimation in concave hillsides, while in convex hillsides, the delimitation approaches the other algorithms. These findings are consistent with Seibert [
46] and Huang [
73] about unrealistic dispersion generated by multidirectional algorithms.
Meanwhile, the drainage network was generated with the accumulated flow obtained by the D8 and KRA algorithms. The stream order of the watershed in this research was estimated at five. The geomorphometrics quantification results are summarized in
Table 7. The average length of the main flow channel (
Lc) was 20.665 km, with a maximum variation of 1.445 km (approximately 7%). The average slope of the main channel (
Sc) resulted in 1.21%, with a maximum difference of 0.167%. The values of
Lc and
Sc affect the concentration time
Tc, generating a maximum variation between the scenarios of 0.398 h (24 min). This significant difference may disturb the peak flood time estimated, and thereby the safety of the areas adjacent to the main channel. In general, the shape parameters show minimum variations, the value compactness coefficient (
Kc >1.54) indicates a lobular watershed [
91], and the circulatory ratio value (
Rc ranging from 0.24 to 0.26) implies low relief and an almost impermeable surface [
1,
78]. Nevertheless, the low value in the elongation ratio (
Re) indicates that the watershed is on an undulating or steep relief [
79], discordant with the slope analysis and
Rc; the contradiction is probably due to the high sinuosity of the mean channel. The shape parameters imply almost symmetrical hydrograms at the watershed outlet. Regarding drainage parameters, no significant variations were found between the variables, except in drainage density (
Dd), concentration time (
Tc) and texture ratio (
T). Based on the drainage parameters obtained, the watershed presents a rapid response to runoff.
Important variations are denoted by analyzing each network concerning the stream order (see
Table 8). Drainage networks were similar for the same resolution, whereas the results with different resolutions show that the drainage density exhibit the greatest difference. The largest differences are presented in stream order 2, with a maximum of 21 channels and a length of 13.8 km. Furthermore, the stream order 5, particularly for the D8 algorithm (DEM 30 m), the number and length of the channels are nearly half of those displayed in the other scenarios. In general, the lower resolution (DEM 30 m) exhibited the greatest variability. Variations imply that the number of sub-basins is different in each scenario, including the geomorphometric characteristics of each one. In investigations of non-urban watersheds where the unit of analysis is the sub-basin for estimates of water travel times (e.g., [
21,
28,
29,
87,
88,
94]), it is logical that the results are affected by the DEM resolution and also for the algorithms of the hydrological processing used. Similarly, the unit base for estimations in urban flood assessment studies is the sub-basin [
37,
95].
3.4. Drainage Networks Analysis
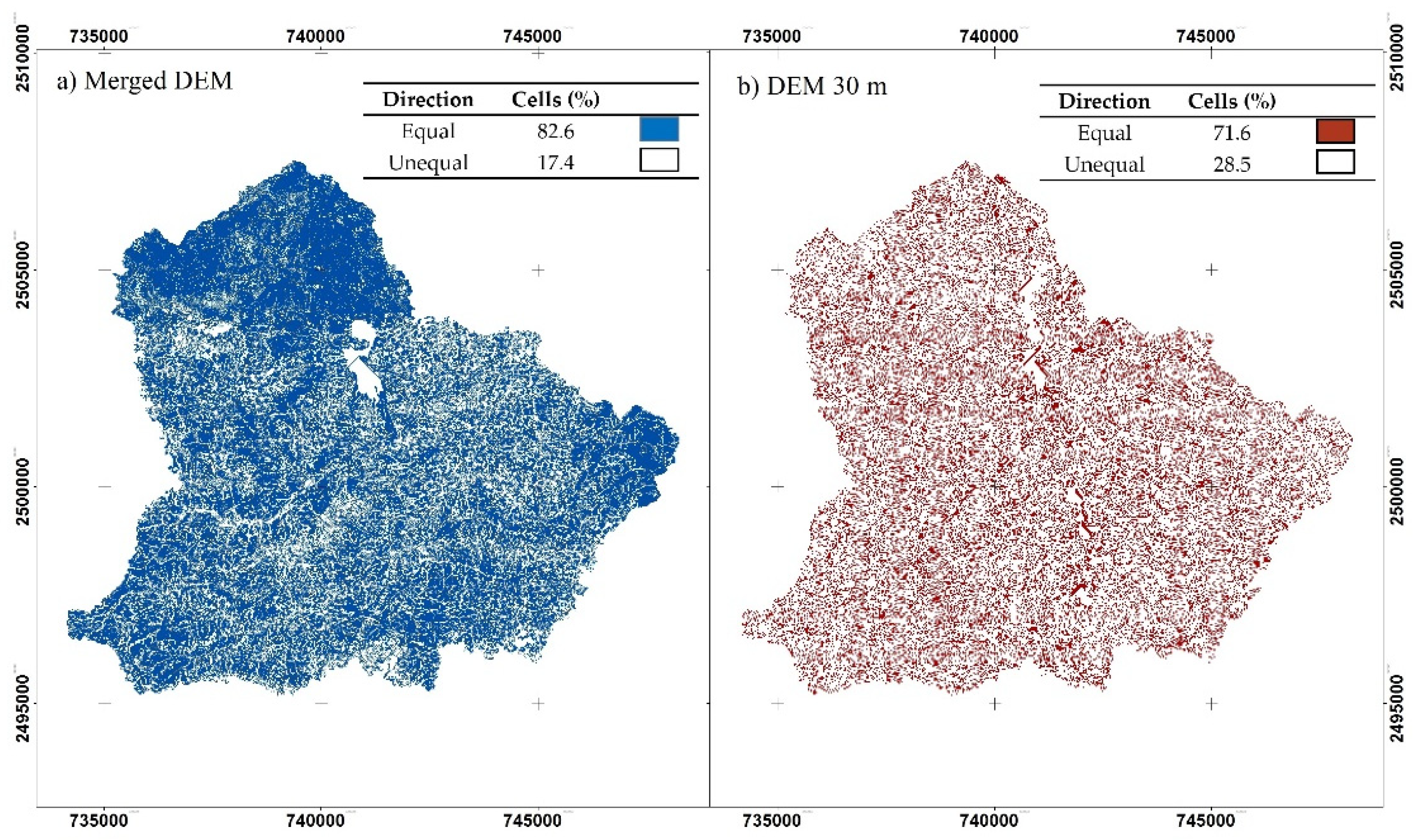
Output raster maps display the difference in each stage process (filling, flow direction, and flow accumulated), which were reflected in the drainage networks and generated uncertainty [
8,
13,
35,
96]. To reduce uncertainty due to drainage network discrepancies, the plane distances between control points and each channel network in the four scenarios were calculated. Sixty control points were acquired, distributed as follows: 11, 16, 13, 8, and 12 points, corresponding to current orders 1, 2, 3, 4, and 5, respectively. The drainage networks were analyzed for each stream order, to expose the impact of algorithms and resolutions. Results in
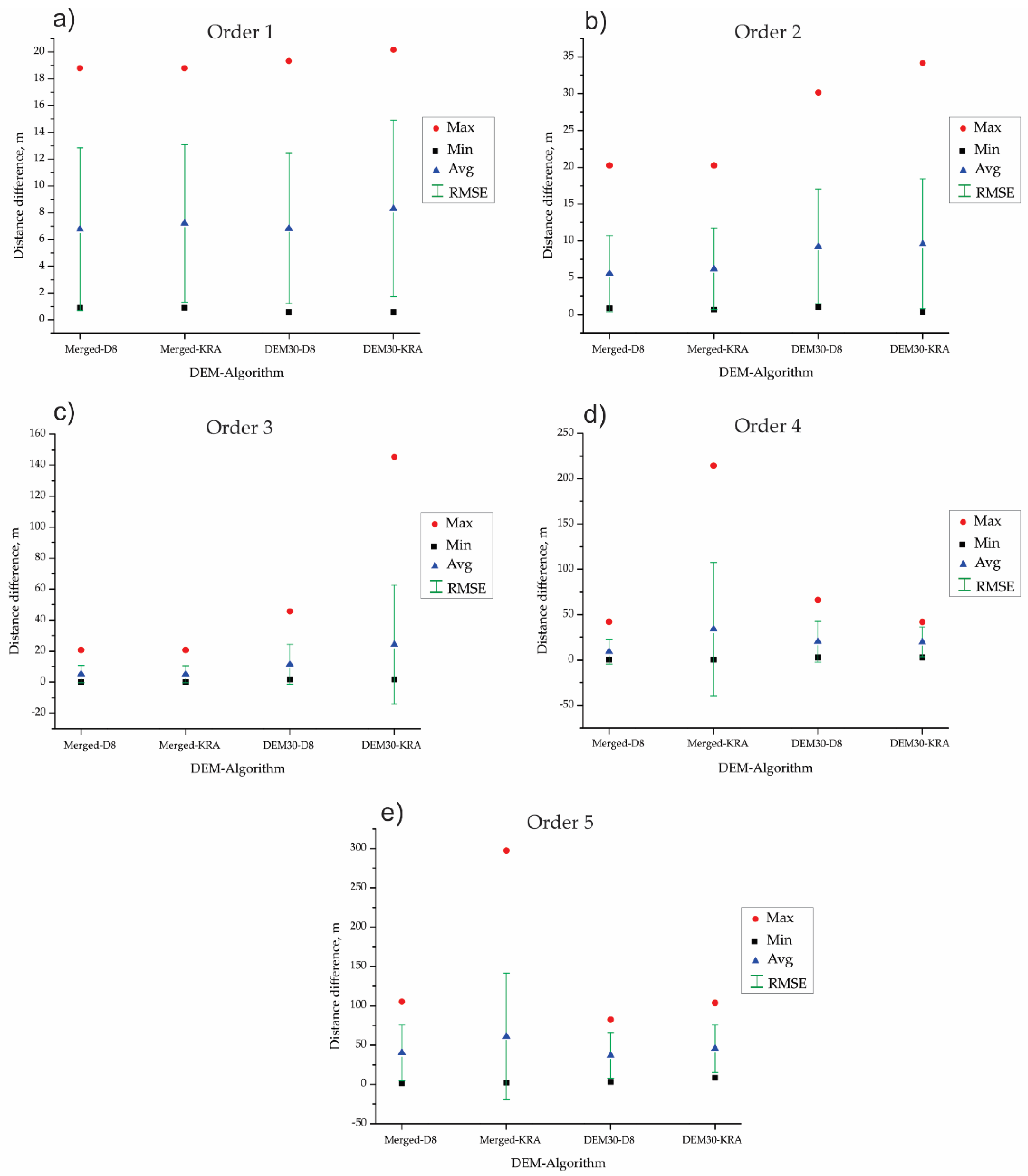
Figure 6 show the maximum, the minimum, average, and the root mean square error distances between the control points and the nearest channel for each scenario. Overall, a significant susceptibility to DEM resolution was found in modeling by mesh-based routing algorithms, in agreement with Li [
44]. The higher accuracy was observed in the merged DEM in comparison with DEM 30 m, except for stream orders 4 and 5 (
Figure 6d,e, respectively). The differences in distance for channels of the stream order 1 were similar in the four sceneries (
Figure 6a), despite reaching a maximum of 20 m; furthermore, resolutions or processing algorithms in stream order 1 exhibited no appreciable advantages or disadvantages. In the case of the channels of stream order 2 (
Figure 6b), no important divergence was perceived for merged DEM, whereas, in the lower resolution DEM 30 m, the distances were more remarkable and increased for the KRA algorithm. Similarly, in channels of stream order 3 (
Figure 6c), the distances increased with the decrease in DEM resolution and the distances were more remarkable for the KRA algorithm (maximum 145 m). On the contrary, channels of stream orders 4 and 5 (
Figure 6d,e) showed greater separation for the higher resolution (merged DEM); with a maximum distance higher than 200 m. The KRA routing algorithm on the DEM filled with the W/L algorithm presented the highest distance differences in the drainage networks (300 m for stream order 5).
Comparative raster maps were generated to visualize differences between stream orders of drainage networks. The automatic methods identified different stream orders from reality channels and presented variations of orders even for the same resolution (
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11). Accordingly, algorithms are another variable to consider in DEM-based automatic methods. The variations in shape and length of the channels observed in
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11 were reflected in the quantifications of the geomorphological parameters in
Table 7 andescription by stream order in
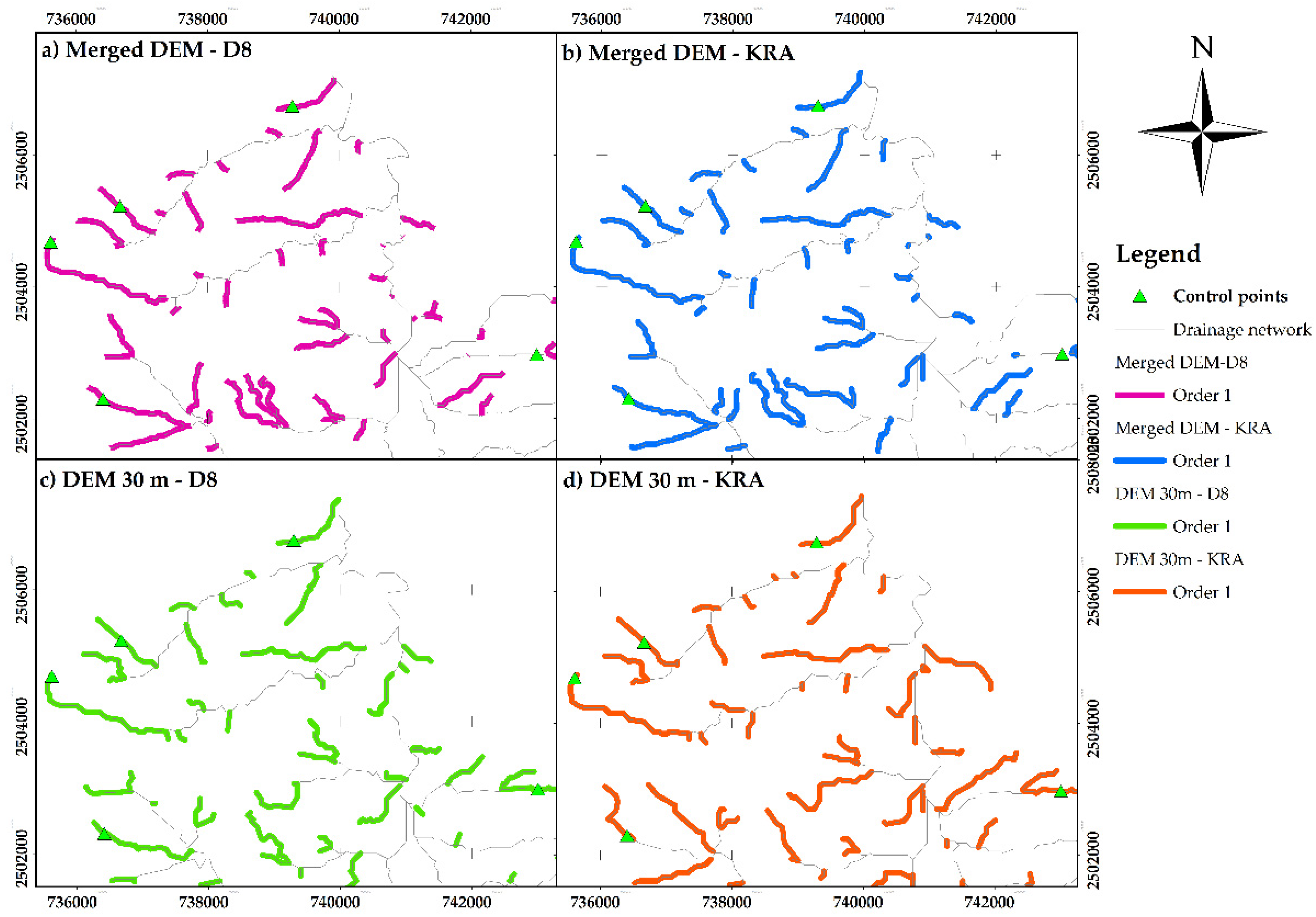
Table 8. To visualize some control points (five) of stream order 1, it was considered a part of the watershed (
Figure 7); the differences in shape, location, and length of the channels between the two resolutions used are significant.
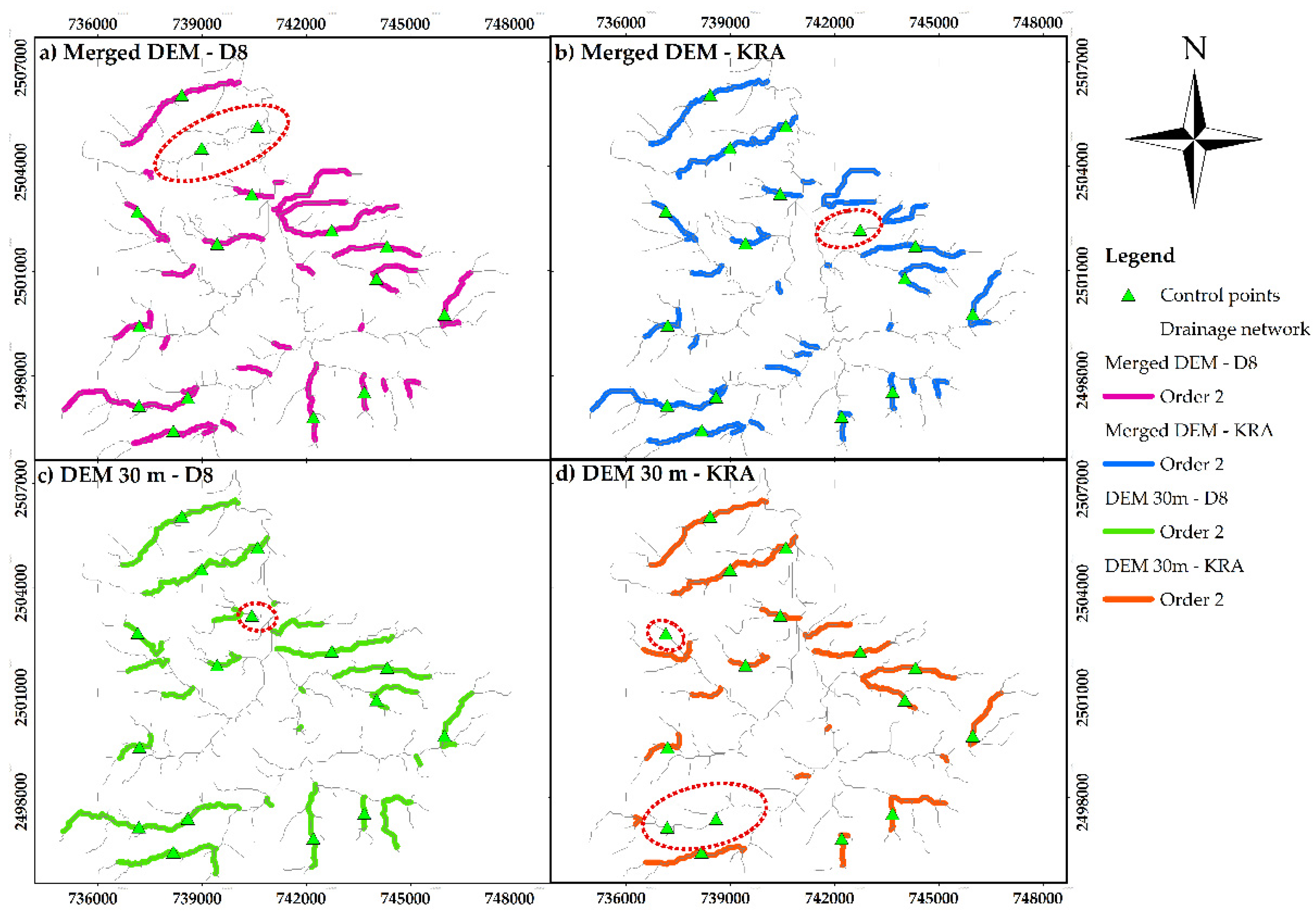
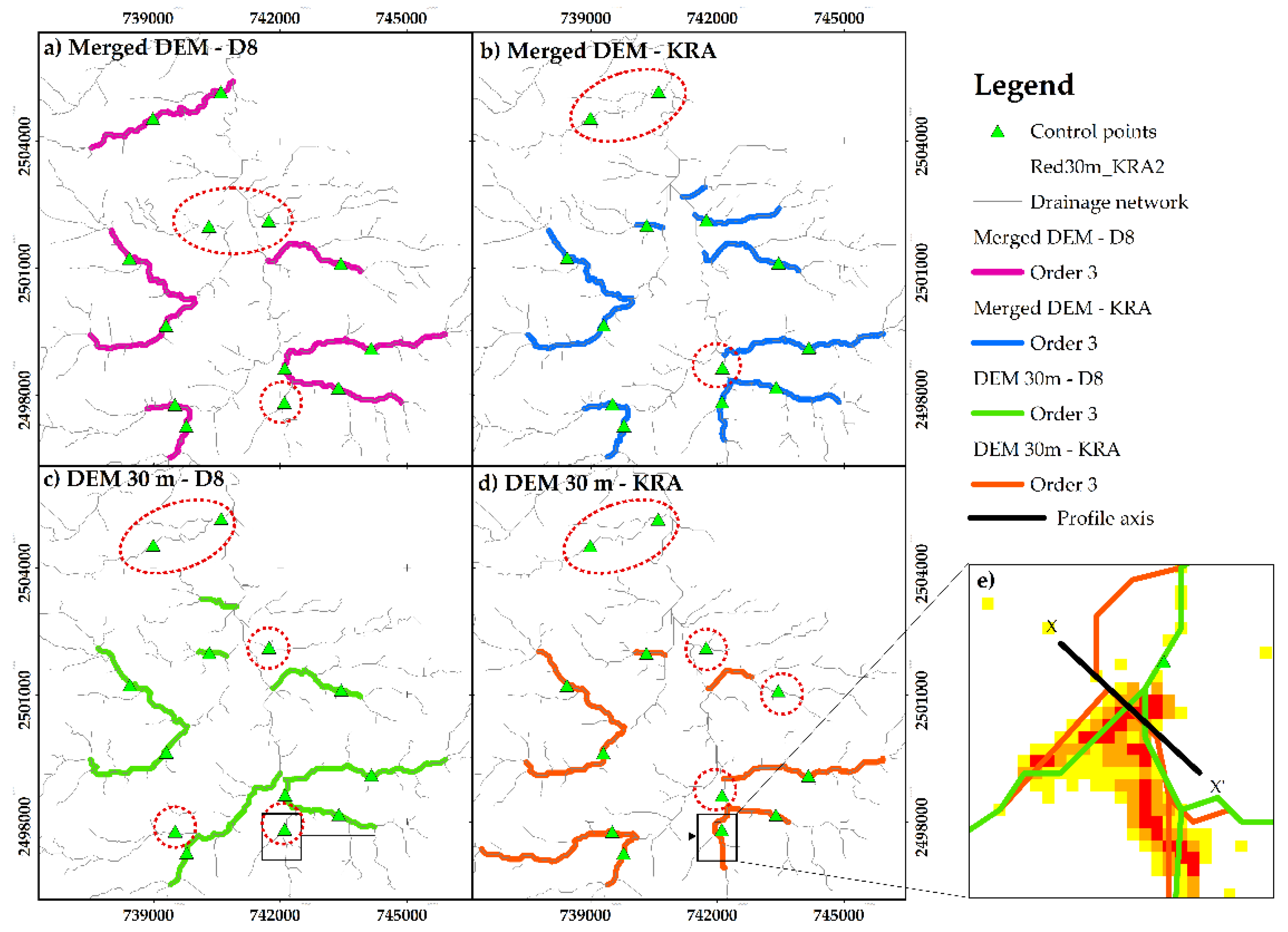
Regarding the stream order 2, the areas marked with a red dashed line within
Figure 8 exhibit channels with erroneous stream order, demonstrating that routing and fill algorithms affect them significantly. The most critical differences in the number and length of channels resulted from applying the KRA algorithm to the filled DEM with the W/L algorithm, which corresponds with
Table 7 and
Table 8.
The accumulative length of the stream order 3 channels in
Table 8 showed a small difference between D8 and KRA algorithms on a single resolution (0.1587 km in the merged DEM and 0.5852 km over the DEM 30 m). However, reviewing the channels of order 3 concerning the control points, the location of the channels was different in each scenario (see
Figure 9). Some channels were identified under another order. The area marked within
Figure 9c,d corresponds to the higher magnification image in
Figure 9e, with the X-X’ axis. Cells most affected by the fill algorithms were included in
Figure 9e.
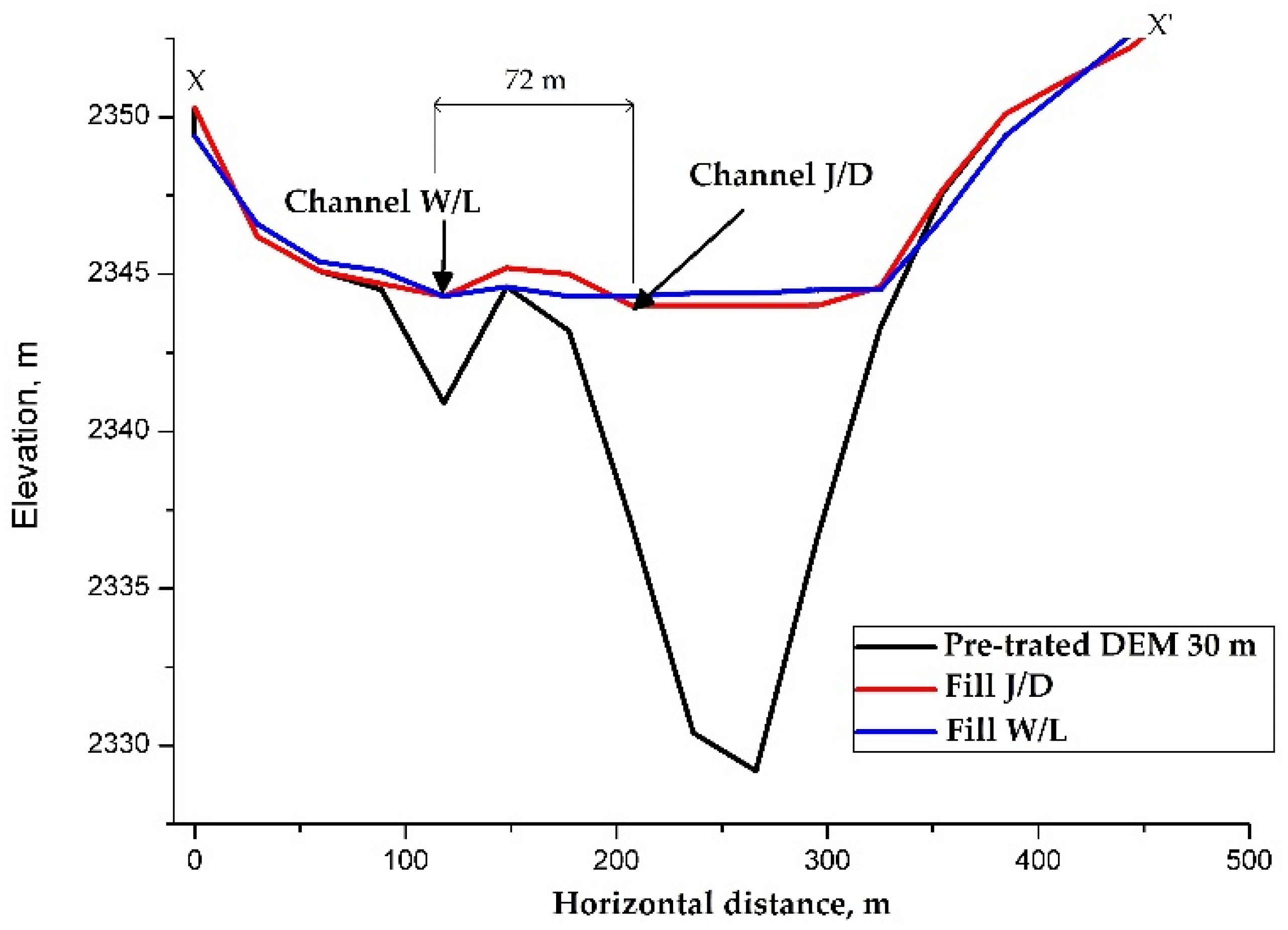
Figure 12 exhibits the topographic profiles of the X-X’ axis corresponding to the pre-treated DEM 30 m, fill DEM by the J/D algorithm and fill DEM by the W/L algorithm. The elevation change by the fill algorithms and the slope gradient of the W/L algorithm was evidenced. The location of the channels generated by the flow routing algorithms (channel W/L and channel J/D) was included in
Figure 12, highlighting the horizontal distance separating the channels (approximately 72 m). The main reason for the distance difference between the drainage networks was that the lowest point location was established at a different site in each filled DEM. Additionally, the two resulting channels in the DEM 30 m were considerably distant from the real channel. It is noteworthy that Habtezion [
97] noted that the areas filled and slopes modified were induced a greater arrangement of channels, which simultaneously contributes to underestimating or overestimating the saturation zones.
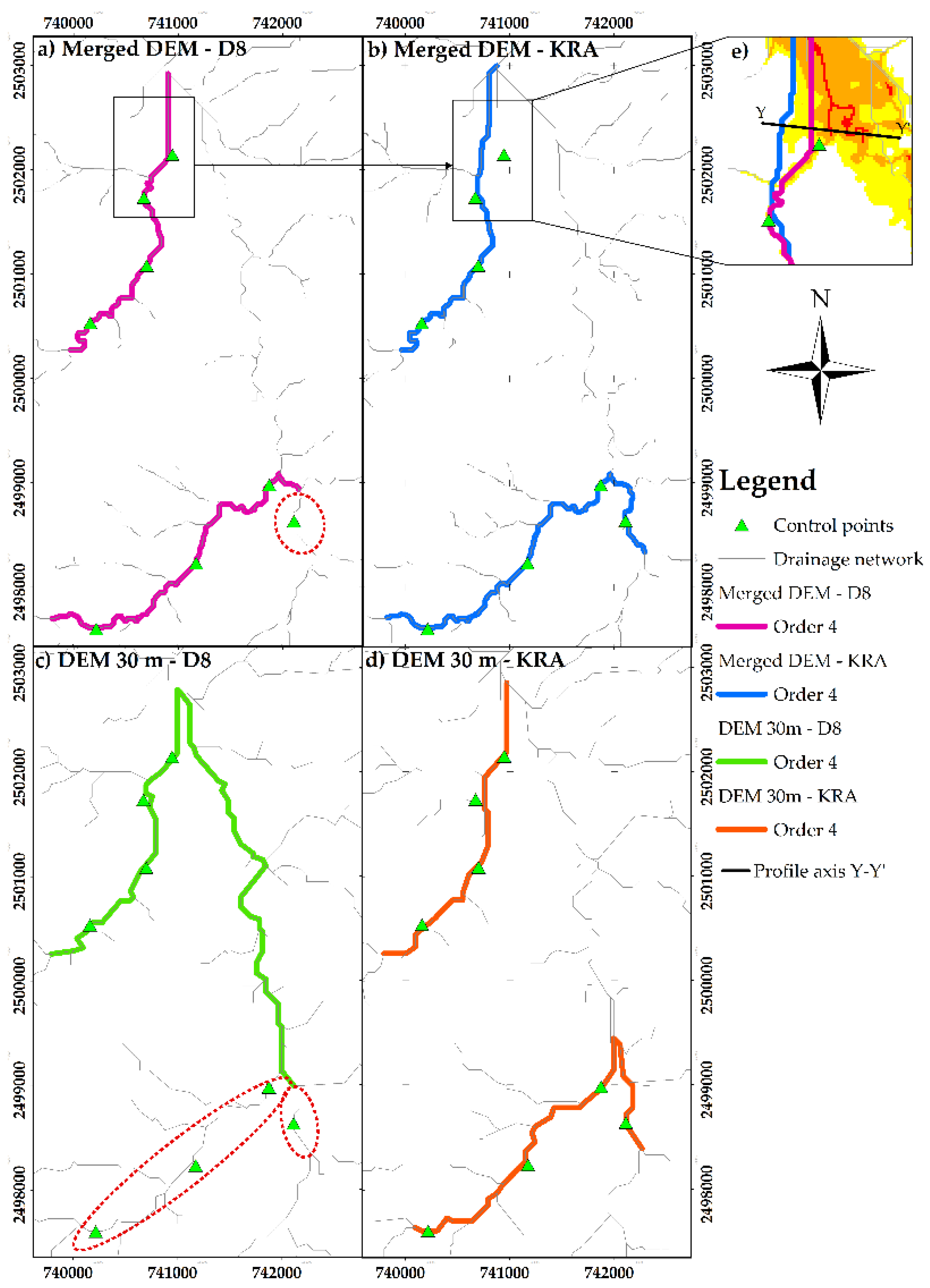
On the other hand, the channels of stream order 4 showed an important difference in the location over the merged DEM (
Figure 10a,b). The same issues were repeated as in the previous orders. Again, the marked area within
Figure 10a,b can be observed at higher magnification in
Figure 10e; the Y-Y’ axis and cells filled by the W/L and J/D algorithms are displayed.
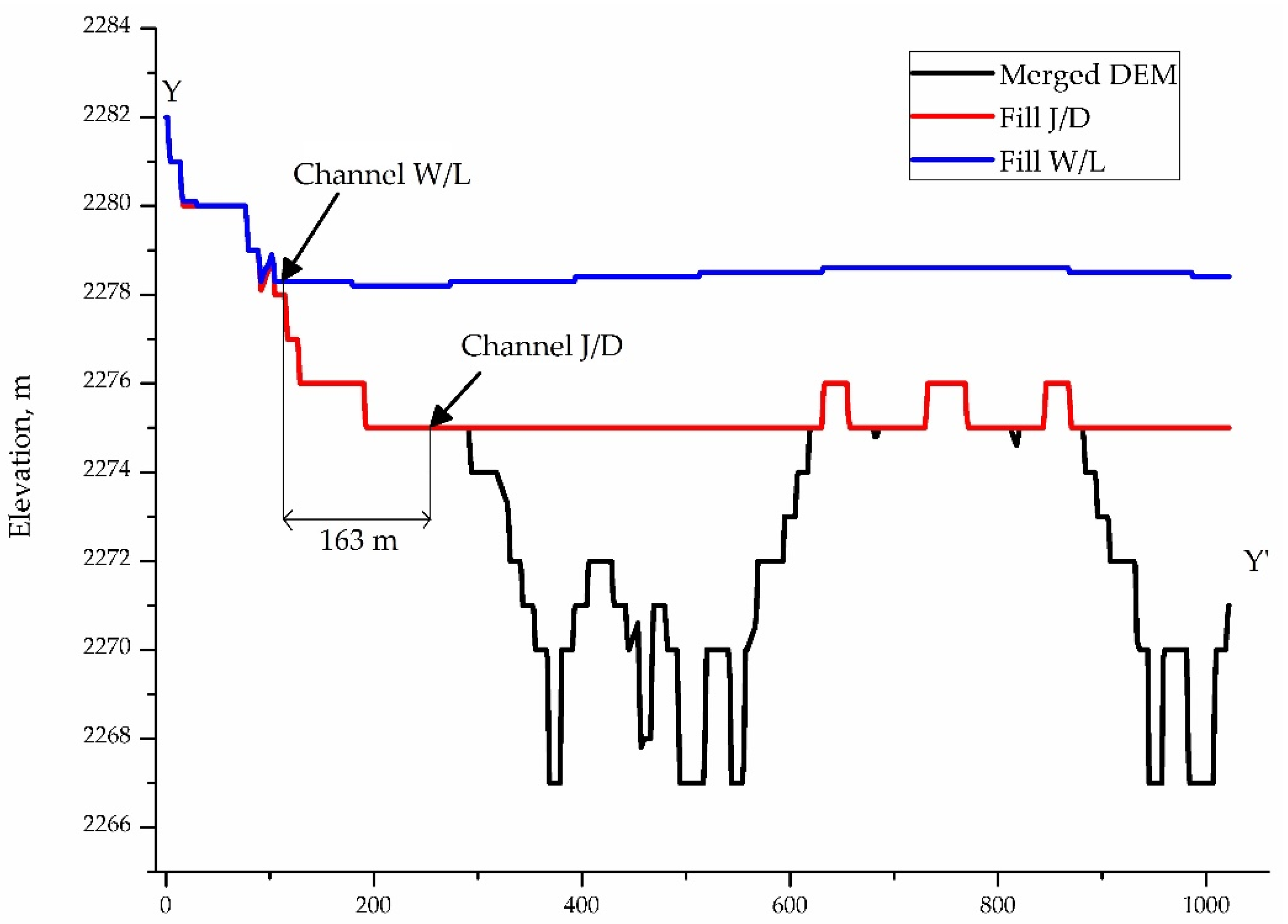
Figure 13 shows the Y-Y’ axis topographic profiles corresponding to the merged DEM, fill DEM W/L, fill DEM J/D, with W/L and J/D channels. The elevation increases, realized with the W/L algorithm (blue line), were the most significant due to the slope gradient (0.1°). The channel separation was similar to the previous stream order, the distance extended from channel W/L to channel J/D, up to approximately 163 m. Furthermore, the channel obtained in the W/L fill DEM with the KRA algorithm was the furthest from the real channel; this circumstance was potentially attributed to the filling process.
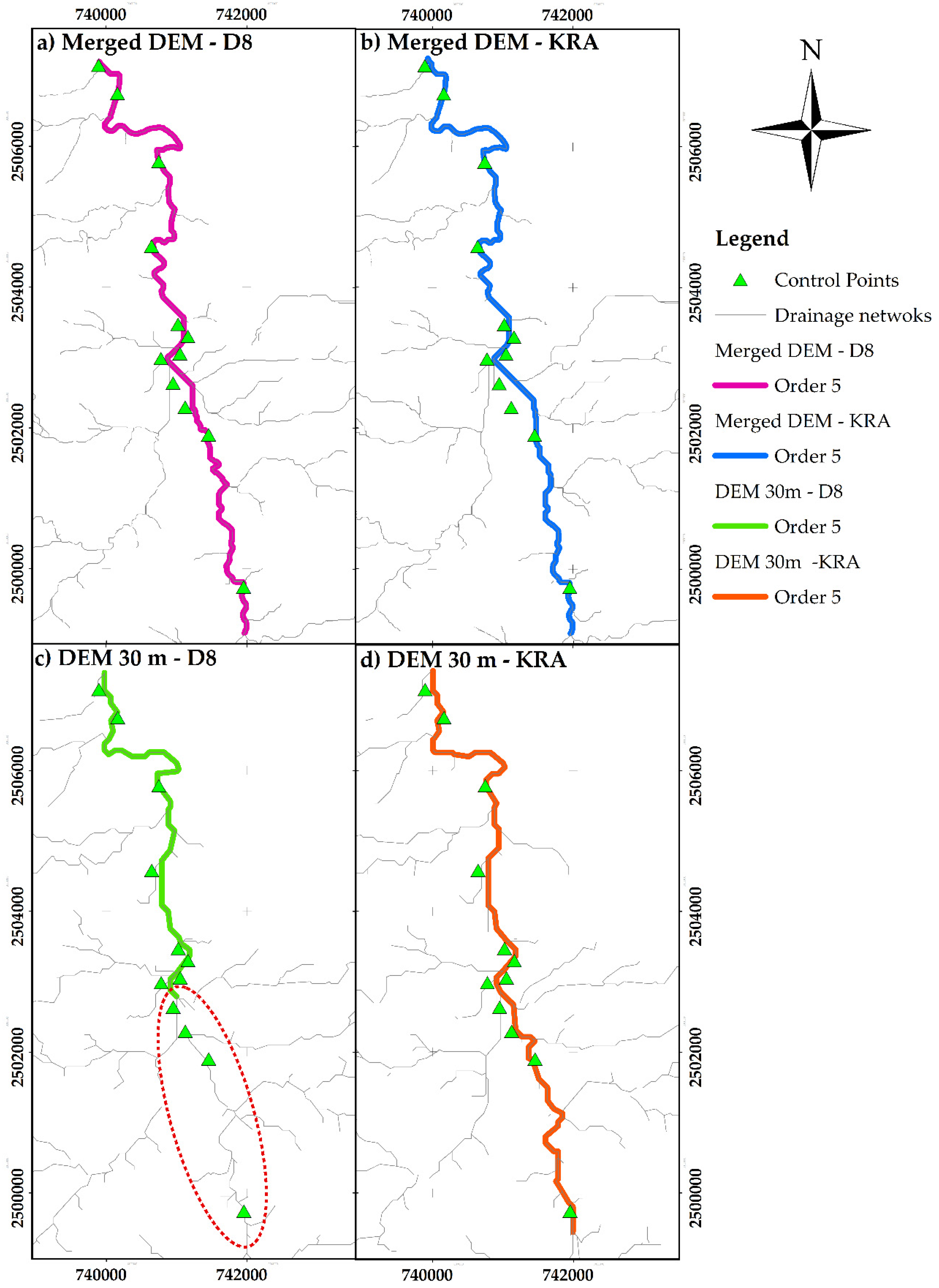
Channels of stream order 5 exhibited the most significant separation concerning the control points, as shown in
Figure 11; the drainage network obtained by the KRA algorithm was the furthest. It is essential to highlight that the reduced length of the channels of stream order 5 resulted in the DEM 30 m with algorithm D8 (
Figure 11c); this difference could be attributed to the routing algorithm. Furthermore, the most important location variations of the channels coincided with the filled areas. The issue areas identified in the maps were examined, and the channels presented direction changes at close distances and narrow sections. Another factor identified in the issue areas was the existence of plain terrains adjacent to the channels upstream of the sites with the highest cell fill.
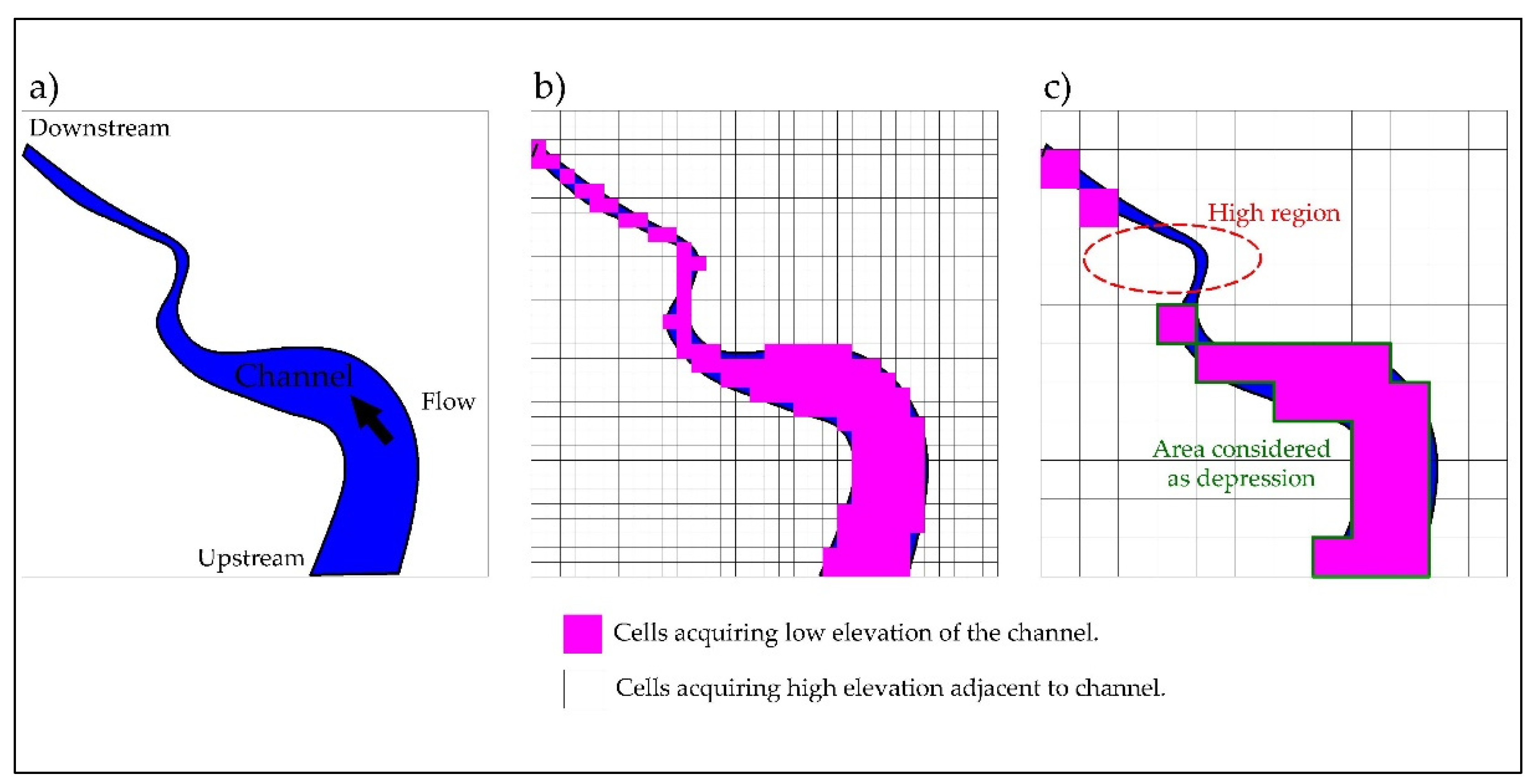
To illustrate the allocation of the elevations in a DEM; a hypothetical channel is provided in
Figure 14a, together with a raster elevation data set (
Figure 14b,c). The channel (blue area) exhibits direction changes at close distances and section narrowing (
Figure 14a). In the higher resolution DEM (
Figure 14b), the flow (magenta cells) in the natural channel was recognized due to less or equal cell size to the channel width, despite the section narrowing. In contrast, in a lower resolution DEM (
Figure 14c), the cells acquired the dominant elevation, which is the elevation of the terrain adjacent to the channel (with cells). The area marked with a red dashed line within
Figure 14c indicates the assigned cells with a higher elevation than the channel (
Figure 14c).
Consequently, the cells upstream of the narrowing of the channel were considered with lower elevation (depressions). From the above analysis, it can be argued that the coarse DEM is not representative of a relief since it establishes non-real depressions. It is worth mentioning that the problem expanded when adjacent plain terrains existed. The filling process modified the topography in depressions, which was increasing by employing a slope gradient, such as the W/L algorithm (
Figure 3b,d). Recently, Erdbrügger [
41] also verified that the areas with the most significant discrepancy in drainage networks coincided with the sites modified by fill algorithms. It seems that the assumption that DEM-based automatic approaches are more consistent and objective than the manual approach [
6] can be re-examined.