Next Article in Journal
Evaluation and Spatial Equilibrium Analysis of High-Quality Development Level in Mainland China Considering Water Constraints
Previous Article in Journal
Seasonal Differences in the Hydrochemical Characteristics of Karst Wetlands and the Associated Mechanisms in Huixian, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 14
Issue 15
10.3390/w14152363
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of the Digital Elevation Model and Hydrological Processing Algorithms on the Geomorphological Parameterization

by
Sandra Dávila-Hernández
1,
Julián González-Trinidad
1,2,*,
Hugo Enrique Júnez-Ferreira
1,2,
Carlos Francisco Bautista-Capetillo
1,2,*,
Heriberto Morales de Ávila
1,
Juana Cázares Escareño
1,
Jennifer Ortiz-Letechipia
1,
Cruz Octavio Robles Rovelo
1,2 and
Enrique A. López-Baltazar
3
1
Doctorado en Ciencias de la Ingeniería UAE, Universidad Autónoma de Zacatecas, Campus UAZ Siglo XXI, Carretera Zacatecas-Guadalajara Km. 6, Ejido La Escondida, Zacatecas 98160, Mexico
2
Licenciatura en Ciencia y Tecnología del Agua LUMAT, Universidad Autónoma de Zacatecas, Campus UAZ Siglo XXI, Carretera Zacatecas-Guadalajara Km. 6, Ejido La Escondida, Zacatecas 98160, Mexico
3
Maestría en Ciencias e Ingeniería de los Materiales, UAI, Universidad Autónoma de Zacatecas, Zacatecas 98000, Mexico
*
Authors to whom correspondence should be addressed.
Water 2022, 14(15), 2363; https://doi.org/10.3390/w14152363
Submission received: 5 July 2022 / Revised: 23 July 2022 / Accepted: 25 July 2022 / Published: 30 July 2022
(This article belongs to the Section Hydrology)
Browse Figures
Versions Notes

Abstract

:
Hydrological cycle research requires a detailed analysis of the involved parameters to understand watershed behavior comprehensively. In recent decades, both Geographic Information Systems (GIS) and Digital Elevation Models (DEMs) were implemented and took a substantial role in watershed geomorphological parameterization; however, the variability of these instruments remains a challenge, together with high-resolution DEMs being unavailable, requiring digital processing to improve resolution. This research aims to merge DEMs and evaluate GIS geoprocessing algorithms to determine drainage networks and the geomorphological parametrization of a semiarid watershed. DEMs with resolutions of 1.5, 5, 12.5, and 30 m, the Jenson/Domingue (J/D) and Wang/Liu (W/L) fill algorithms; and D8, D, KRA, and MFD flow routing algorithms were used. One of the research findings proved that the divergences of the drainage networks are mainly attributed to filling algorithms and not flow routing algorithms; the shifts between the networks obtained in the processes reach horizontal distances up to 300 m. Since the water movement within the watershed depends on geomorphological characteristics, it is suggested that DEM-based hydrological studies specify both the resolution and the algorithms used in the parametrization to validate the rigidity of the research, improving estimate areas of high hydrological risk.

1. Introduction

One of the most important components for understanding the behavior of natural resources in a watershed is geomorphometry. Through mathematical measurements and terrestrial surface processing, geomorphometry allows for knowing how drainage patterns function, as well as water conservation, sediment production, and the soil erosion state within a hydrological system [1,2,3,4]. With the geomorphological data, it is possible to generate hazard and flood risk maps [5], estimate flows for hydraulic purposes, and to analyze anthropogenic activity effects [6]. The hydrological, geomorphological and ecological processes of an environment are susceptible to the topographic surface [7,8,9]. In particular, the hydrological response of the watershed is significantly controlled by geomorphological parameters [10,11]. The surface and sub-surface runoff dynamics are intimately linked to the slopes and drainage networks of the watershed channels; the geomorphology mainly impacts the catchment area, the travel times, and the flow hydrogram changes [12]. Therefore, determining geomorphological parameters is crucial to generating accurate maps and modeling the water redistribution within the watershed [13].
Initially, the terrain configuration was achieved through collaborator mapping, followed by field studies [14]. After this, techniques such as photogrammetry based on analog restorers were added. Years later, the use of DEM derived from implementing GIS and remote sensors became popular [4,15,16,17]. These advances were driven by the existing databases that provide DEM from practically anywhere on the planet. Advanced technology was incorporated to obtain surface information, including digital photogrammetry, Light Detection and Ranging (LiDAR), and laser scanners. Digital algorithms can be added to these advances to process information more quickly and accurately [1,2,5]. The evolution in geomorphometric characterization allowed for important progress in the determination of the physical parameters of the watershed, thereby achieving a better understanding of the behavior of the hydrological cycle.
The geomorphometric characterization was carried out by traditional approaches (as conventional topographic surveys, geodesics, among others) [14], geoprocessing, and two-dimensional modeling with high-resolution data [12]. Geoprocessing-based methods generally used a raster DEM as a base source ranging from medium to coarse resolution, depending on availability, followed by the geomorphometric characterization of the watershed [18]; this processing is usually carried out using GIS with different algorithms. The processes based on DEMs are widely selected and various research works applied this approach, using programs such as ArcGIS (e.g., [1,13,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]) and SAGA GIS (e.g., [7,15,34,35,36]). It is worth mentioning that only few studies use high-resolution data, and they correspond to small study areas [12,15,35,37,38]. In many regions around the world, there are no high-resolution DEMs [17,39,40], and producing high-resolution topography presents various difficulties, such as economic or technical disadvantages, the processing time, inaccessibility, and remoteness from study areas, among others.
The literature agrees that DEM resolution is vital for hydrological modeling [5,12,37,39,41,42,43,44], as well as the susceptibility of the results in consideration of the flow fill and routing algorithms [45,46,47]. Most studies are limited to the systematic use of the tools available for hydrological geoprocessing, and just a few assess the effectiveness of these methodologies. Some studies analyze routines from a computational cost approach [46], while others evaluate basin scale dispersions [47]. Still, the sequels at the sub-basin scale or channel orders are not explicitly determined. This research details the relevance of DEM resolution as the hydrological geoprocesses within the GIS environment simultaneously. The aims of this research were: (1) assess the efficiency of the Jenson/Domingue (J/D) and Wang/Liu (W/L) fill algorithms, the flow routing algorithms D8, D∞, MFD, and KRA for watershed delimitation and drainage network generation; and (2) analyze the effect produced by the DEM with resolutions of 30 m and 1.5 m (merged) on the geomorphological parameterization of a watershed.

2. Methodology

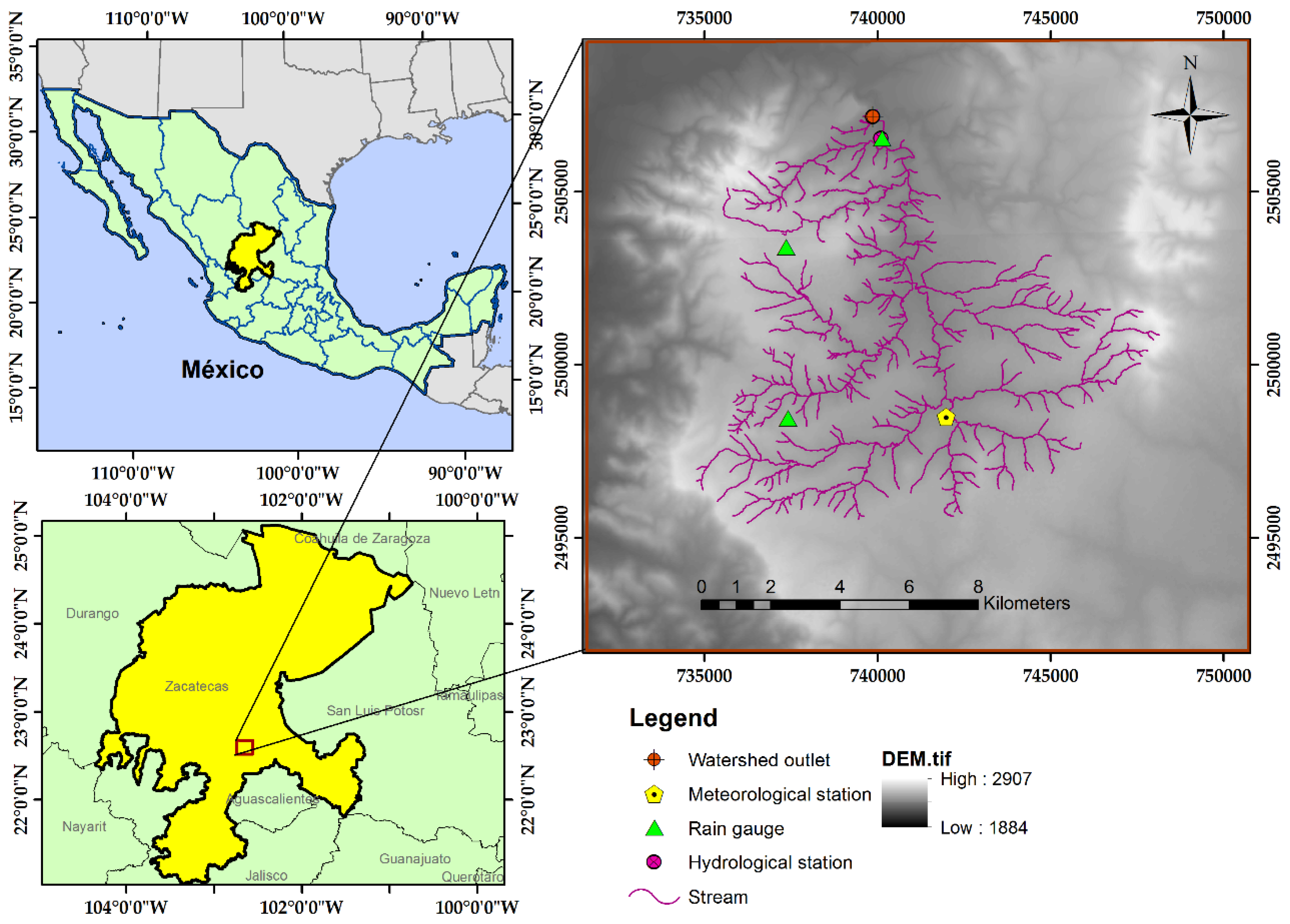
2.1. Study Site

The watershed “Chilitas” is located in the center of Mexico, in the state of Zacatecas, 20 km south of the capital; it has an approximate area of 100 km2, as illustrated in Figure 1. The geographic coordinates of the centroid are approximately 22°39′17″ N and 102°39′57″ W, datum WGS84. It is a rural watershed with a population minor to 500 inhabitants distributed in two towns; no sewage is discharged into the streams and there are practically no reservoirs over the streams or appreciable depressions. Regarding the use and soil covering, 62.4% of the surface is natural pasture, 18.6% is dedicated to annual seasonal agriculture, 9.3% is crasicaule scrub, 4.2% is for annual agricultural watering, 3.6% is secondary shrub vegetation, 0.43% is urban construction, and less than 0.03% is pine forest. The predominant soil type is phaeozem, with 61.8% of the surface, followed by kastañozem with 32.5%, and 3.7% leptosol [48]. The climate is semi-arid, with rains in the summer, mainly from June to September [49]. The average maximum and minimum temperatures are 29 °C and −2.8 °C, respectively, with a mean precipitation of 428 mm per year; the values were obtained by the weather station installed in the watershed and were cross-match referenced with data from [50]. The study area features four rain gauges and two hydrometric stations (Figure 1). It is assumed that the watershed is possibly one of the groundwater recharge sites of the “Benito Juarez” aquifer, one of the most important aquifers in the region, hence the interest of study.

2.2. Data Set Used

DEMs with resolutions of 1.5, 5, 12.5, and 30 m were used; the literature recommends high resolutions [5,12]. Resolutions of 1.5 and 5 m DEMs were obtained from the National Institute of Statistics and Geography (INEGI, Mexico) [51]; the high resolution without cost was the primary requirement. The DEM of Phased Array type L-band Synthetic Aperture Radar (PALSAR) produced by the Advanced Land Observing Satellite (ALOS) with 12.5 m resolution was employed to complete a DEM that covered the entire study area with the higher resolution without cost. INEGI DEMs were derived from airborne sensors and remote satellite data. The Phased Array type L-band Synthetic Aperture Radar (PALSAR) DEM produced by the Advanced Land Observing Satellite (ALOS) with 12.5 m resolution completed a DEM that covered the whole study area with a higher resolution without cost. The Advanced Space Thermal Reflection and Emission Radiometer (ASTER) Global Digital Elevation Model third version (GDEM3) (freely available), with DEM 30 m resolution, was used as a reference due to less elevation void area than other DEMs of equal resolution.
The hydrographic map in vector format of the area was obtained from the topographic maps scale 1:50,000, a product of INEGI derived from digital photogrammetry [52]. Control points were measured in the field with a dual-frequency Topcon (Hiper Lite) GPS receiver with two antennas at a static relative position to the riverbed centers. The points were initially identified with satellite images and then verified in the field. The 60 control point positions were used to evaluate the effectiveness of the results in the generation of drainage networks.

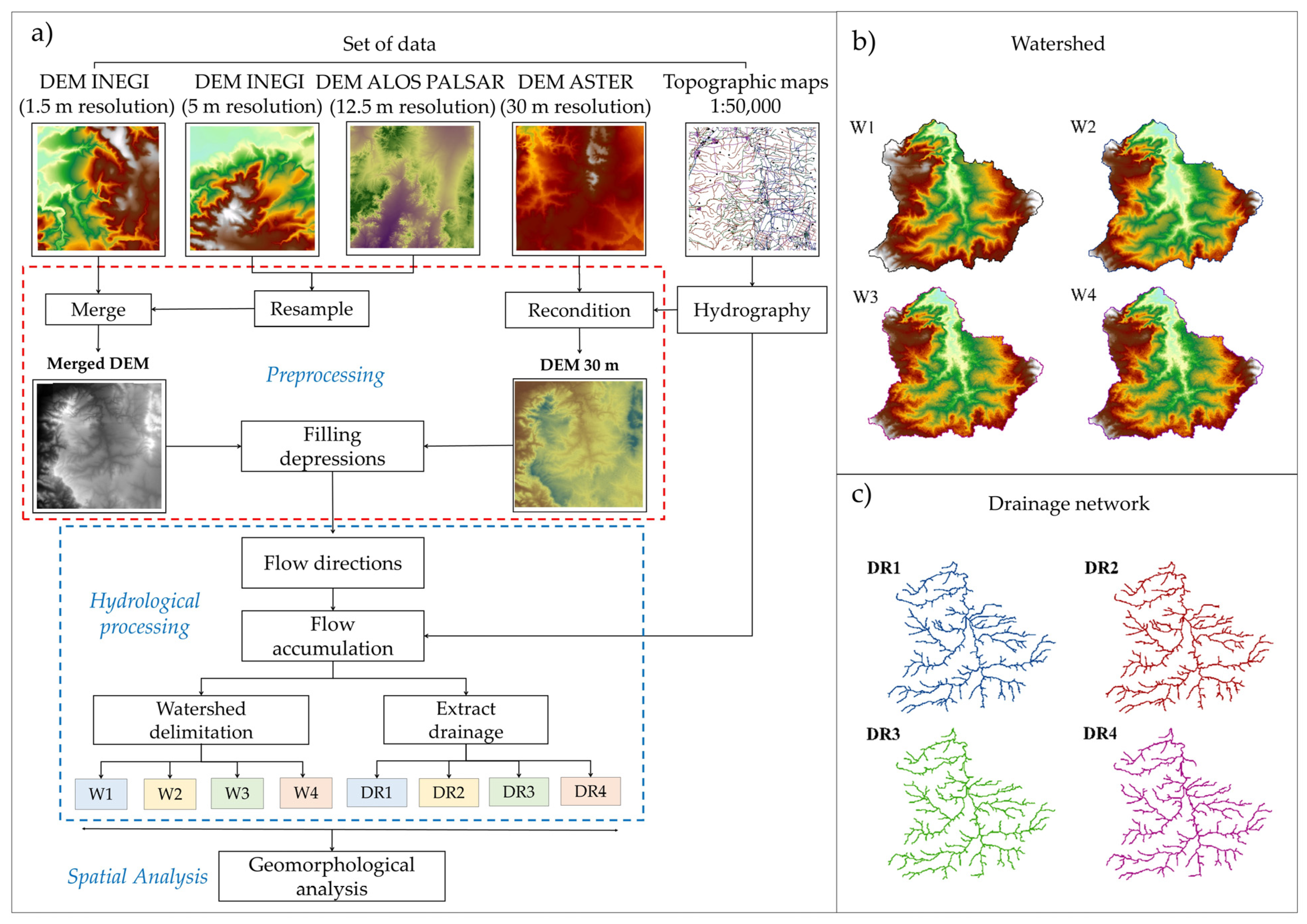
2.3. Geomorphological Parameterization

The methodology for geomorphology parameterization in a GIS environment is resumed in Figure 2, which was developed using ArcGIS version 10.5 and SAGA GIS version 2.3.2 (free software) [7,15,18,30,33,36,37,53].

2.3.1. Preprocessing

This research proposed merging DEMs to achieve the highest resolution freely available from the study area. As illustrated in the area marked with a red dashed line within Figure 2a, two preprocesses to the DEMs were applied. In the first preprocess, the 1.5, 5, and 12.5 m resolution DEMs were used to obtain the DEM called “merged DEM”; the second preprocess was applied to the 30 m resolution DEM to get the DEM called “DEM 30 m”. The preprocesses were carried out in ArcGIS software version 10.5. To achieve the merged DEM, the 5 and 12.5 m DEMs were resampled to a cell size of 1.5 m, thus standardizing the cell sizes; then the DEMs were merged with the 1.5 m DEM. It is worth mentioning that the use of resampled DEMs dos not imply that the level of detail of the DEM is increased; the zones that initially had a larger cell size continue to be areas that represent entities of the surface of 5 and 12.5 m.
On the other hand, in attention to the vector hydrographic network extracted from the topographic map, the 30 m DEM was reconditioned by considering that a lower spatial resolution implies fewer cells per unit area; this preprocess is indicated in the area marked with a red dashed line in Figure 2a. Reconditioned DEMs were utilized in previous studies [39], ensuring that the lowest cells of the DEMs are located in the course indicated by the hydrography.

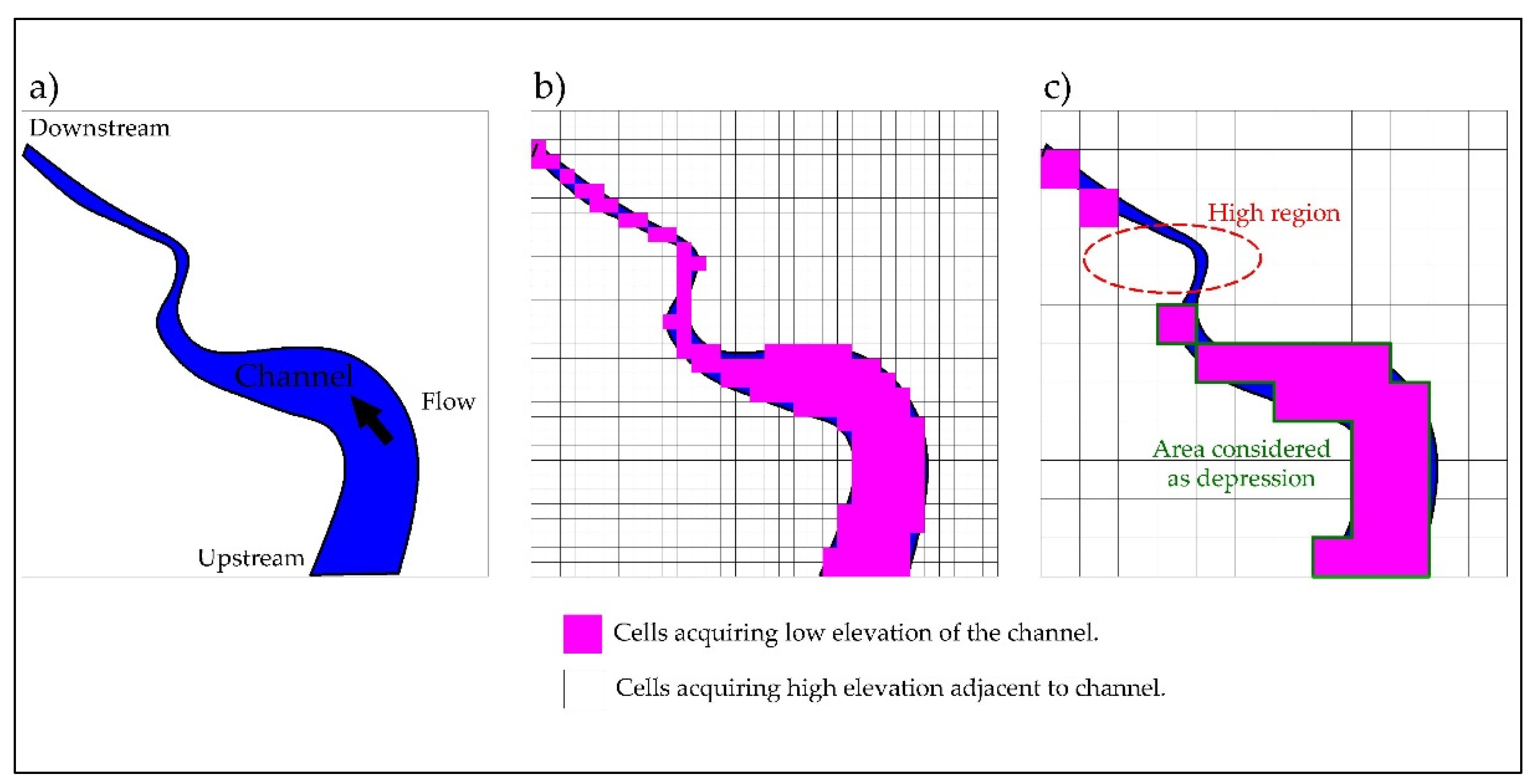
Filling Depressions

Depressions in DEM are generally considered obstacles to hydrological analysis [15,43,54,55]. Depressions (sinks) are cells surrounded by others with higher elevation; this scenario does not offer defined flow continuity or direction and is presented in most DEMs [38,39,56,57,58,59,60,61].
Although not all depressions should be labeled as errors, there are surfaces naturally dominated by descents and endorheic areas [15,38,42,62,63]. Therefore, not all DEMs with a fill process should be “corrected”. However, to ensure hydrological connectivity by flow routing algorithms, most methods to delimit basins and define drainage networks are based on DEMs without depressions [24,45,64,65,66,67,68].
The study area has no domain of either natural or anthropogenic depressions; the first phase is to eliminate the sinks remaining with a DEM fill processing. This research examines the methodologies proposed by Jenson and Domingue (J/D) [66] and Wang and Liu (W/L) [59] to perform the filling with the help of ArcGIS and SAGA GIS software.
The J/D algorithm performs a series of iterations to fill the cells within each sink to the lowest elevation of the depression-contributing area [66]. It is one of the most widely used algorithms for hydrological processing software, for example, ArcGIS [57], HEC GEO-HMS [69], and GRASS GIS [70]. Possible drawbacks of the J/D algorithm are smoothing if applied excessively and loss of representative information from the original DEM in trouble-free areas [59].
The W/L algorithm identifies and fills cells by considering, if required, preservation of the downstream slope along the flow path [59], thus avoiding zero slopes between the filled cells [56].

2.3.2. Hydrological Processing

The following stages are required to establish a catchment area and drainage network channels of a watershed in environment GIS (the area marked with a blue dashed line within Figure 2a exhibits the hydrological process).

Flow Directions

Each cell directs the flow to one or more of the eight adjacent cells; the cells with the greatest slope are selected. This procedure can present variations in consideration of the GIS or the fill algorithm. Flow directions in ArcGIS are determined by applying the eight-direction or deterministic 8 (D8) method, which is one of the oldest and most used algorithms [61]. D8 is a unidirectional flow routing algorithm (single-flow direction method), which tracks each cell separately within the DEM to the limits [26,66]. If one or more downstream cells have the same elevation value in several directions, the flow is directed according to the most probable orientation [71]. It is worth mentioning that some authors consider D8 inadequate since generating dispersion in the flow and contributing areas is indefinite in the DEM [72,73,74]. On the other hand, the W/L algorithm simultaneously fills depressions and identifies the optimal spill path between the cells in SAGA GIS. Therefore, based on the elevation delivered by the W/L filling process, it is revealed to which of the eight neighboring cells the flow is directed [56,60]. For both methods, a raster map is obtained, in which each cell indicates the numeric value corresponding to the flow direction.

Flow Accumulation

The catchment zone, known as flow accumulation, is the most crucial parameter for hydrological processing [8,60]. Flow accumulation algorithms provide a structured representation of terrestrial flow, the watershed for quantifying runoff [47]. The flow accumulation of a cell constitutes the amount of water mass that comes from upstream cells that are eventually contributors [24,73,74]. The methods used to generate a grid of catchment areas differ according to the flow routing algorithm. A raster map is obtained showing the accumulated flow for each cell; it was determined by the accumulation of the weight of all cells flowing into each cell downstream [39,56,60].
Cells with high flow accumulation are considered to be flow concentration areas [57] and can be used to identify streams. Unidirectional flow routing algorithms D8 and Kinematic Routing (KRA) [58] were used to determine the drainage network. D8 sends the entire water mass from a cell to a unique adjacent cell with a lower elevation [73]. KRA assumes that the flow originates in the center of the source pixel and travels kinematically as a source point. Similar to a ball rolling through the DEM, without restricting its position to the center of the cells, and without angular limitations and the flow rolls through the DEM [58].
Three flow routing algorithms were used in the delimitation of the watershed, the D8 algorithm and the algorithms of two-dimensional flow Deterministic infinity (D∞) [31] and the divergent flow called Multiple Flow Direction (MFD) [72] were included. The D∞ algorithm considers that the topographic surface is composed of interconnected overlapping triangular faces; the water mass flows from the center of a cell to the two adjacent cells with the greatest decrease [31,60,73]. The MFD algorithm delivers the water mass to more than one adjacent cell, achieving a dispersed flow pattern [72].

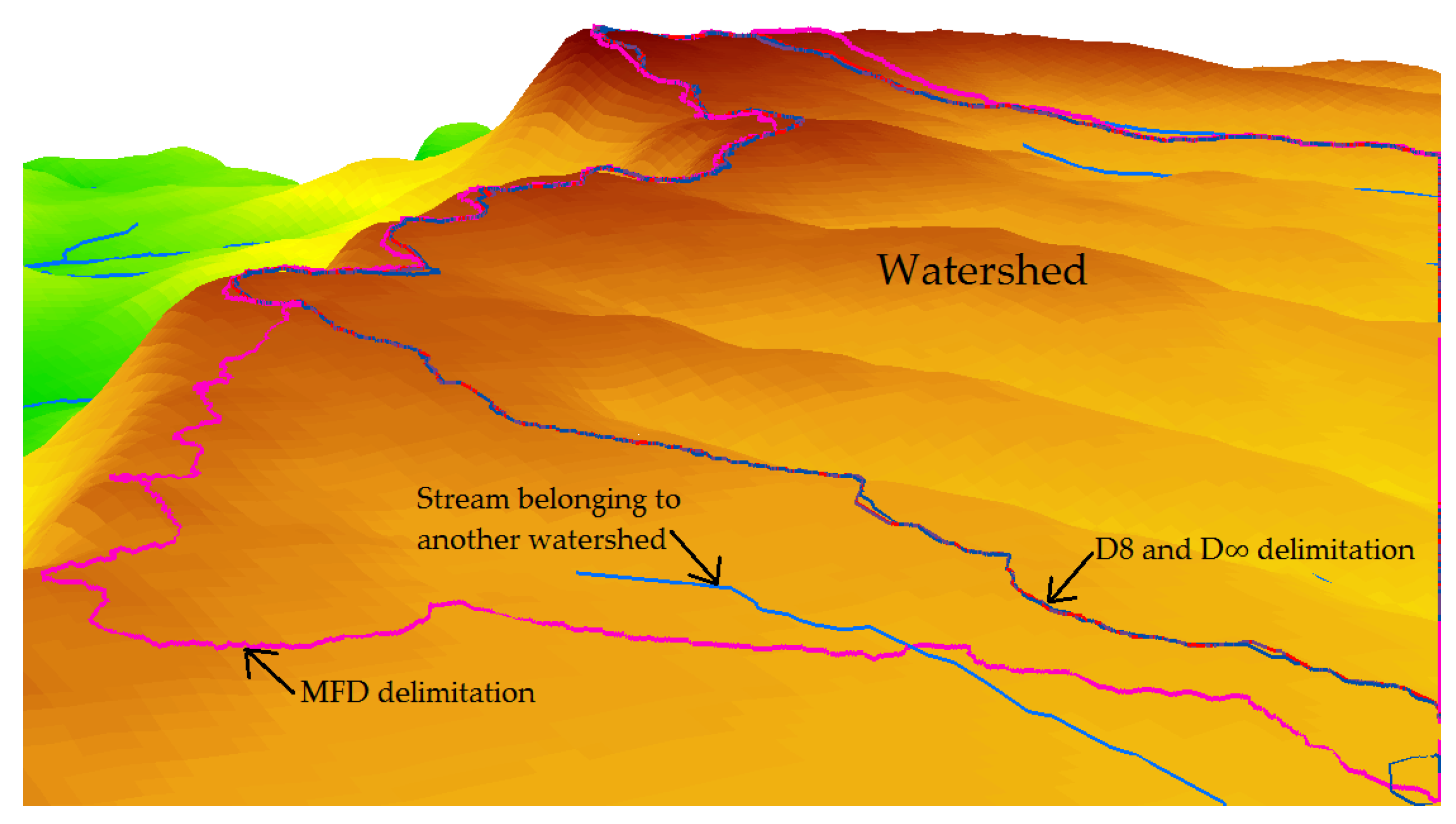
Determination of Drainage Network and Watershed Delimitation

The drainage network is determined by applying map algebra on the raster map of the accumulated flow. It is necessary to define a threshold for quantifying the flow accumulation value; therefore, multiple networks can be generated. A viable criterion for determining the threshold is to use known data, such as a hydrographic network, prior measured areas, or high spatial resolution images of the study area [17,39].
Concerning the delimitation of the watershed, the outlet must be established to determine the flow contribution area. Afterward, the desired flow routing algorithm is applied to quantify the contributing area to the indicated site. The result is the watershed water dividing line, from which it is possible to measure diverse geomorphological parameters.

Geomorphological Parameters Quantification

The parameters considered in this study are summarized in Table 1 and Table 2. Basic parameters of the watershed are achieved with spatial analysis tools within a GIS environment. The mean slope of the main channel and the remaining parameters are calculated by the equations listed in Table 1 and Table 2.

3. Results and Discussions

Scientific literature reports that DEM resolution should be as high as possible (<5 m) [37,41,42]; however, in countries where available DEM are of coarse resolution (most of the terrestrial surface), other alternatives are required. On the other hand, it is stated that the implications of some algorithms used in the hydrological processing of the DEMs are negligible [15]. Therefore, both DEM resolution and processing algorithms SIG should be considered a significant influence on the characterization of the watershed, and consequently, on the hydrological behavior of the water. Pre-treated DEMs (merged DEM and reconditioned DEM 30 m) were subjected to the processing algorithms.

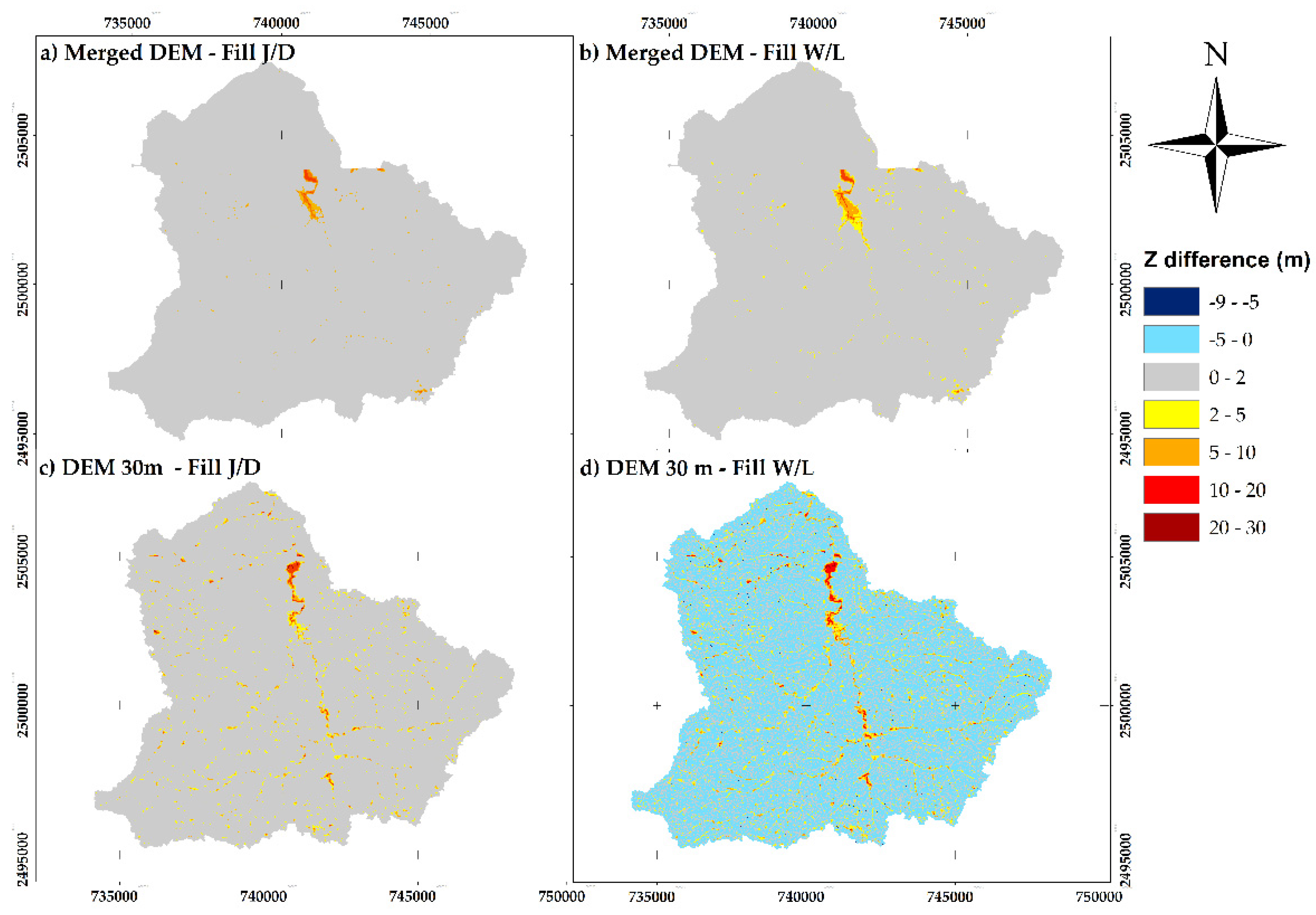
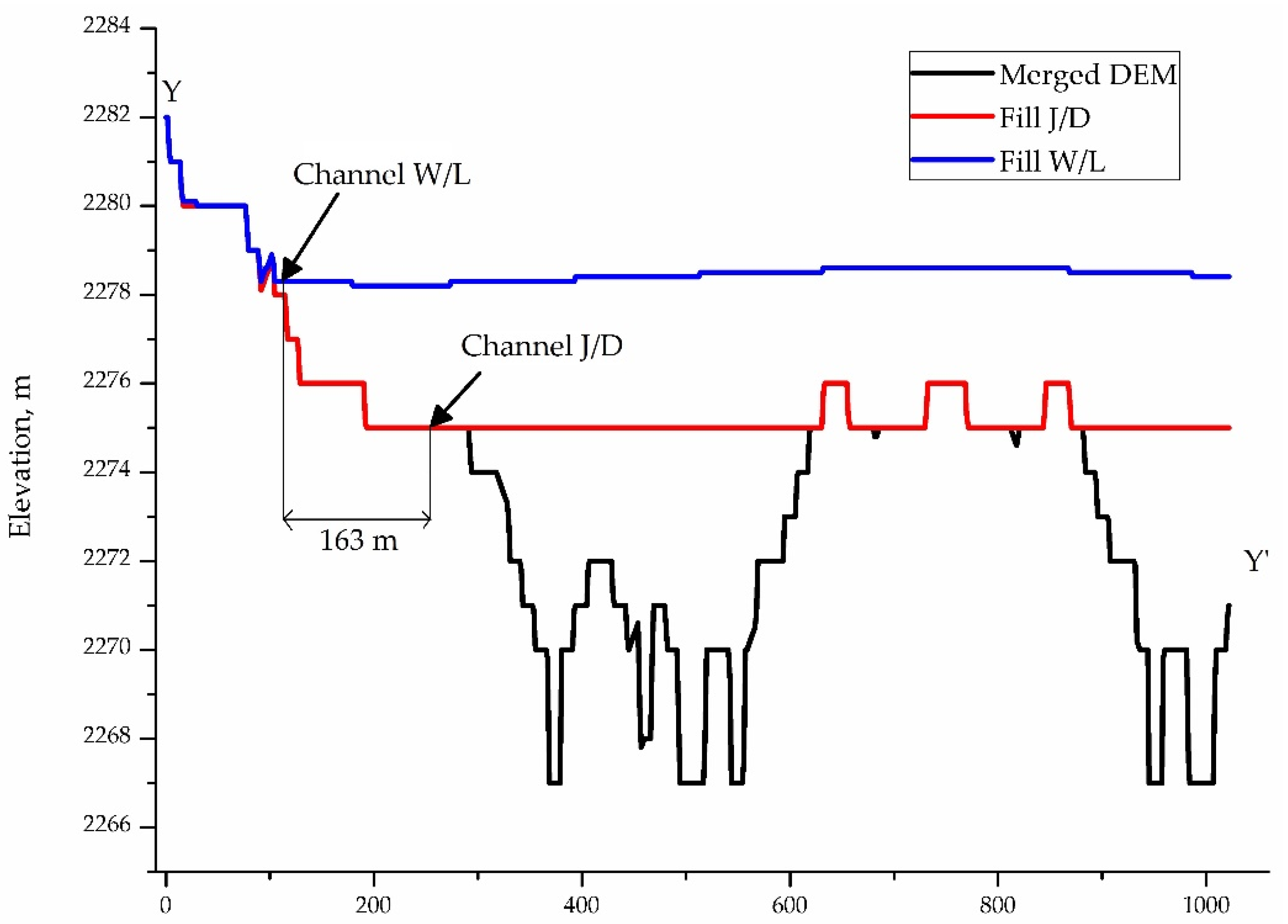
3.1. Comparative of Fill DEMs

The watershed obtained with the most excellent area derived from the DEM dataset process was designated as the surface extent for analyzing the results in the fill and flow direction raster. To exhibit divergences between the J/D and W/L fill algorithms, the difference in elevation between each cell of pre-treated DEMs against the fill DEMs was determined for each resolution (Figure 3).
Histograms of elevation differences expressed were determined in percentage, including the minimum and maximum variations; the data found are summarized in Table 3. The differences in elevation show mostly values close to zero (0–2 m); however, important differences in the fill DEM 30 m were detected when using the algorithm of W/L, in both negative and positive values (56.2% of the cell range from −2 to 0 m), the product of a DEM smoothing. SAGA GIS generated a DEM smoothing within the same cell-filling tool for this algorithm. The W/L algorithm induces the highest elevation changes for two reasons: the slope gradient (in this research, a gradient of 0.1° was applied) and the smoothing (implicit in the SAGA GIS). In agreement with Engelhardt et al. [6], smoothing originates flattening of local topographic characteristics, changes in both slopes and water dividing lines and also affects the calculation of flow direction. The maximum increase in the elevations of some cells (19–27.2 m), showing a more significant effect over the DEM 30 m (Table 3). According to the results, the less affected raster by the filling is the merged DEM; the smoothing does not affect this resolution. Meanwhile, the J/D algorithm elevates cells without considering the slope, where cells with the same elevation can be presented. It is noticeable that the original topography suffers alterations on a coarse resolution.
Fill DEMs with the same resolution reveal a change in elevation similar, though not identical. Contrary to Pardo-Igúzquiza’s [15] report that the methodologies of J/D and W/L produce the same result; in this research, it is evidenced that significant differences are caused by fill algorithms; the impact increases by decreasing the DEM resolution (Table 3). The difference increases by employing a higher slope gradient in the W/L algorithm. It is worth mentioning that the fill DEM is the foundation of the following processes and variations have a significant impact.
The impact of the filling can be observed on the watershed slopes by assessing the obtained average slopes and the area percentages regarding the relief type (listed in Table 4) in agreement with the IGAC classification [86]. The main variation occurs on the flat and lightly flat relief, again due to resolution and slope gradient. The difference between the mean slopes of the watershed is approximately 1% for the two resolutions. Some of the geomorphological parameters that are directly influenced by the relief slope are the concentration time (Tc), the mean slope of the main channel (S) and the slope of the hillsides of the watershed.
Table 4 shows that in the highest resolution DEM (merged DEM), the relief of the watershed is predominantly flat (average of 68.9%). In case the DEM of 30 m prevails, there is a lightly flat and inclined relief of 70.7%. The relief was verified with a field visit, finding that the study site corresponds to a light flat. Flat reliefs are more susceptible to changes by smoothing or aggregation due to changes in the appearance of slopes [41]. The slope variations directly affect the water speed travel (in advance and recession), the hypsometric curve, the hydrographs, the flood peak times, the soil erosion, and consequently the runoff estimates and the flow design that support the waterworks safety. At the sub-basin scale, the effects of slopes on hillsides and channels propagate in surface and subsurface runoff [21,28,87,88].

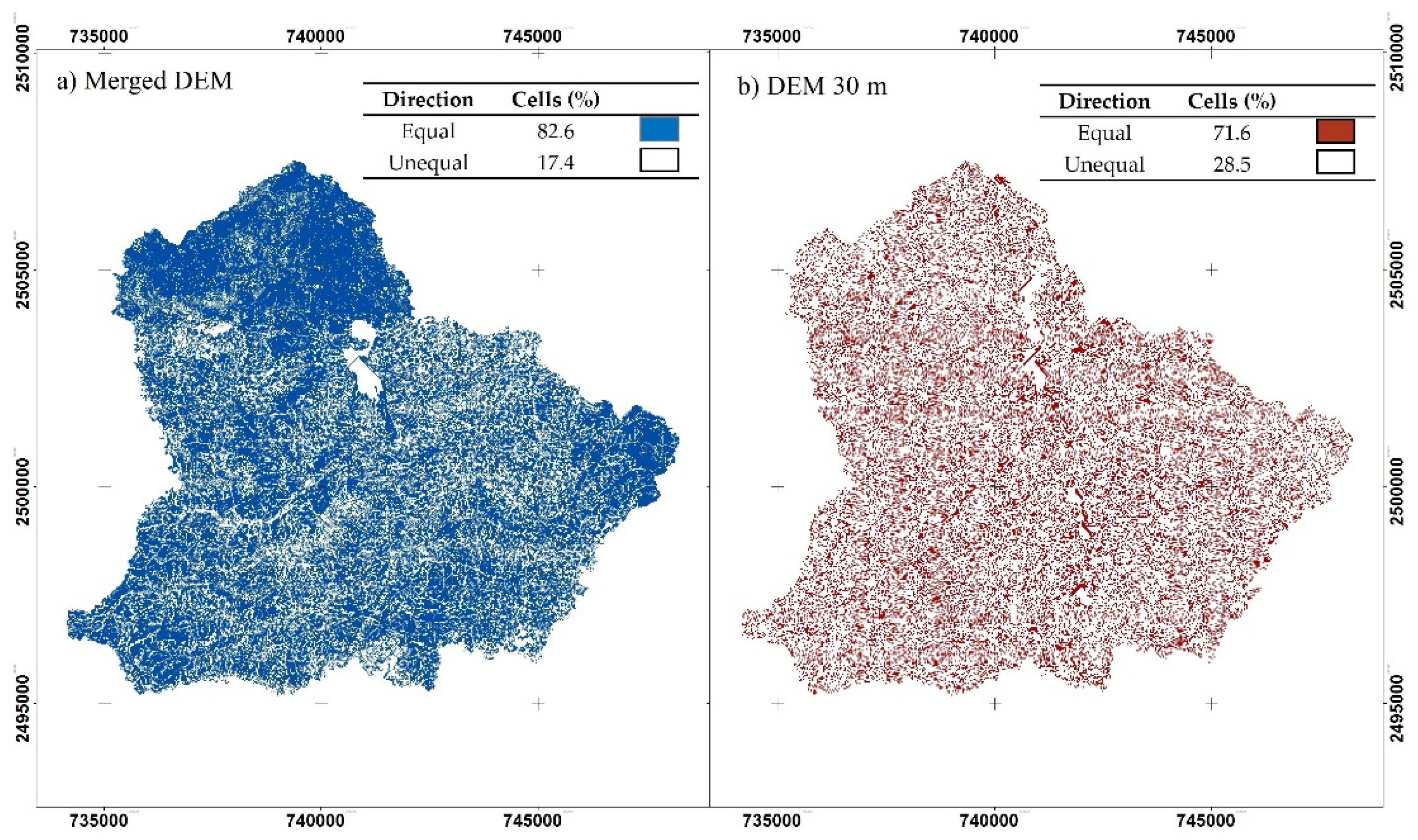
3.2. DEM Comparison Flow Direction

Flow directions influence the quantification of flow accumulation [46], parallel to delineating the watershed and drainage networks. The results of the flow directions raster were compared between DEM resolutions (see Table 5). There is an apparent difference between the flow directions of the two resolutions. The north (N) flow direction prevailed and the average maximum difference was 9.6%.
Raster maps were generated to analyze the differences in the direction of each cell, post the filling process. Figure 4 displays the areas with significant unequal directions (white zones) that coincide with the sites where the fill algorithms mainly affected the original DEM (flat reliefs). Flat reliefs were pointed out by Nardi et al. as generators of technical issues for identifying channels [45]. In the DEM 30 m (Figure 4b), 28.5% of the total area displayed unequal flow direction patterns, while the merged DEM (Figure 4a) resulted in 17.5% of the area with distinct flow directions. Engelhardt et al. [6] compared directions between original DEMs and smoothed or aggregated DEMs and found that resolution affects further than the type of algorithm selected, which coincides with the results of this investigation.

3.3. Geomorphometric Parameterization

The geomorphological parameters were determined to understand that the estimates of tributary areas and flow concentrations depend on the routing algorithms [89,90] and the DEM resolution [44,91]. Based on flow routing algorithms D8, D∞, and MFD, the watershed area (A) and perimeter (P) were obtained (see Table 6). The watershed areas W1, W2, W3, and W4, correspond to the four scenarios illustrated in Figure 2b. The range of values for the area was 100.381 km2 to 103.524 km2 and the average area of the watershed was 101.544 km2. According to the classification of Faustino and Jimenez [92], the watershed is classified as a micro-basin. The area value provided by the MFD algorithm over the fill DEM of W/L reaches 1.9% more than the average area—it was the most scattered. There is a greater difference in the estimated areas over a coarse resolution. On the other side, the average perimeter was 74.514 km, with a maximum variation of 19.351 km, representing approximately 26% of the difference. The perimeter directly affects the shape parameters that define the form of the watershed and provide an idea of the behavior of the runoff.
Achieving the highest accuracy in quantifying the watershed area is vital since it influences the estimates of most theoretical hydrological models. Wooding [93] and Lee [87] referred to the direct influence of the area in hydrological investigations. Similarly, dos Santos and Fewtrell expressed that the discrepancies in the watershed area impact simulations for estimating rainwater and sediment distribution.
Comparing areas of each scenario manifest the MFD algorithm overestimation in delimitation since it includes adjacent areas of other watersheds. Figure 5 displays some watershed boundaries of the merged DEM where the D8 and D∞ algorithms delineation were similar, contrasting with the delineation executed by the MFD algorithm. The MFD algorithm exhibited greater discrepancy and overestimation in concave hillsides, while in convex hillsides, the delimitation approaches the other algorithms. These findings are consistent with Seibert [46] and Huang [73] about unrealistic dispersion generated by multidirectional algorithms.
Meanwhile, the drainage network was generated with the accumulated flow obtained by the D8 and KRA algorithms. The stream order of the watershed in this research was estimated at five. The geomorphometrics quantification results are summarized in Table 7. The average length of the main flow channel (Lc) was 20.665 km, with a maximum variation of 1.445 km (approximately 7%). The average slope of the main channel (Sc) resulted in 1.21%, with a maximum difference of 0.167%. The values of Lc and Sc affect the concentration time Tc, generating a maximum variation between the scenarios of 0.398 h (24 min). This significant difference may disturb the peak flood time estimated, and thereby the safety of the areas adjacent to the main channel. In general, the shape parameters show minimum variations, the value compactness coefficient (Kc >1.54) indicates a lobular watershed [91], and the circulatory ratio value (Rc ranging from 0.24 to 0.26) implies low relief and an almost impermeable surface [1,78]. Nevertheless, the low value in the elongation ratio (Re) indicates that the watershed is on an undulating or steep relief [79], discordant with the slope analysis and Rc; the contradiction is probably due to the high sinuosity of the mean channel. The shape parameters imply almost symmetrical hydrograms at the watershed outlet. Regarding drainage parameters, no significant variations were found between the variables, except in drainage density (Dd), concentration time (Tc) and texture ratio (T). Based on the drainage parameters obtained, the watershed presents a rapid response to runoff.
Important variations are denoted by analyzing each network concerning the stream order (see Table 8). Drainage networks were similar for the same resolution, whereas the results with different resolutions show that the drainage density exhibit the greatest difference. The largest differences are presented in stream order 2, with a maximum of 21 channels and a length of 13.8 km. Furthermore, the stream order 5, particularly for the D8 algorithm (DEM 30 m), the number and length of the channels are nearly half of those displayed in the other scenarios. In general, the lower resolution (DEM 30 m) exhibited the greatest variability. Variations imply that the number of sub-basins is different in each scenario, including the geomorphometric characteristics of each one. In investigations of non-urban watersheds where the unit of analysis is the sub-basin for estimates of water travel times (e.g., [21,28,29,87,88,94]), it is logical that the results are affected by the DEM resolution and also for the algorithms of the hydrological processing used. Similarly, the unit base for estimations in urban flood assessment studies is the sub-basin [37,95].

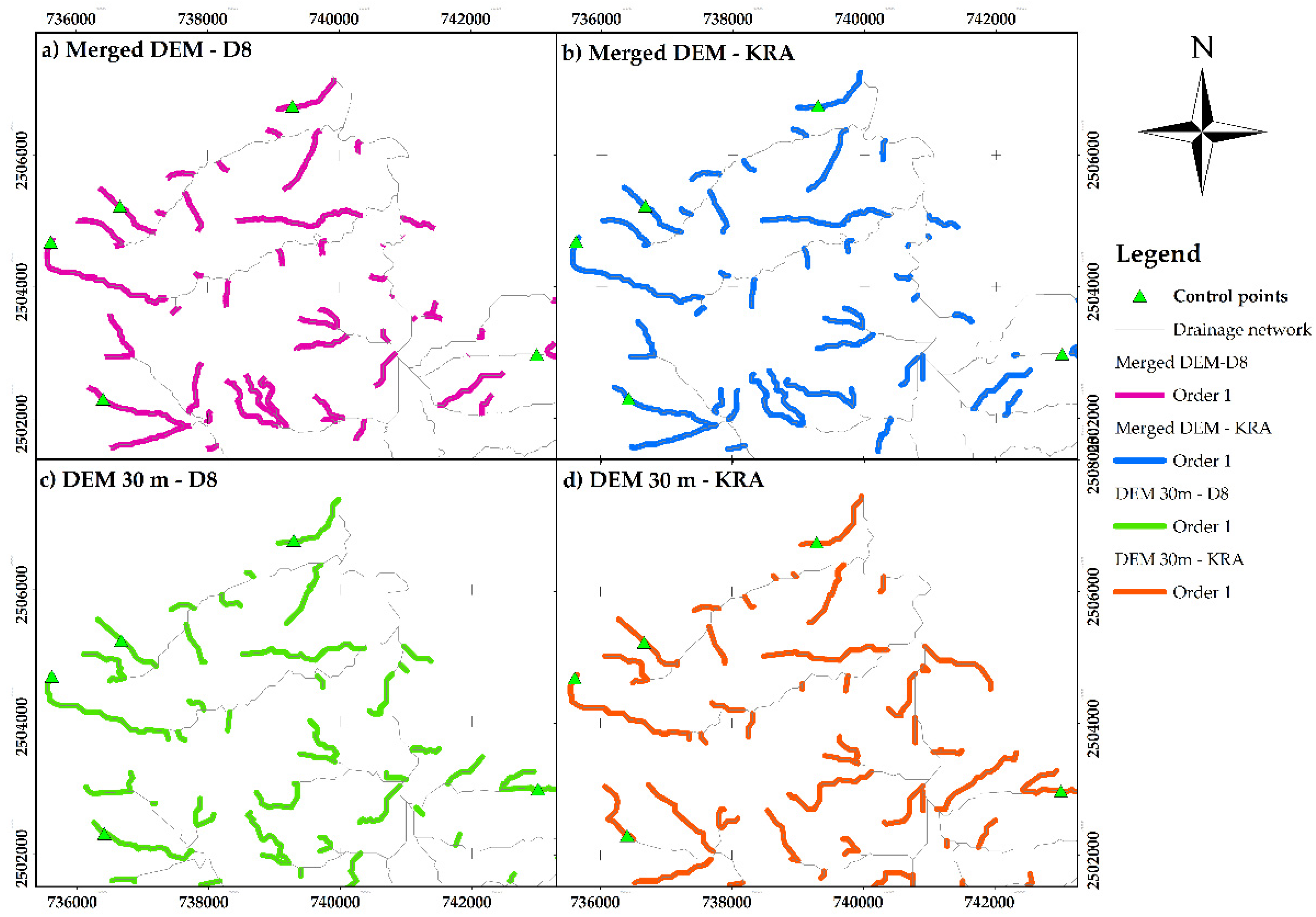
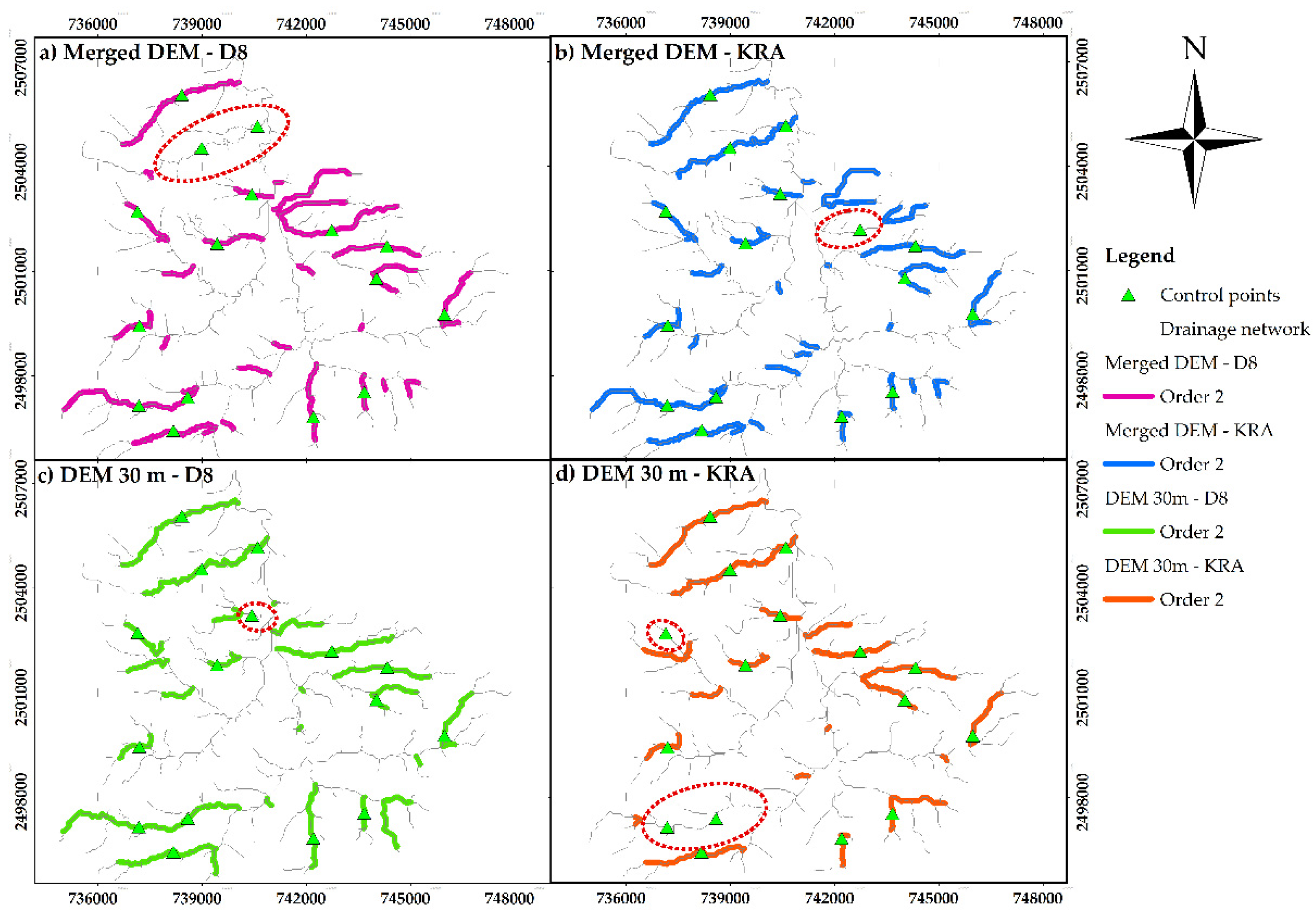
3.4. Drainage Networks Analysis

Output raster maps display the difference in each stage process (filling, flow direction, and flow accumulated), which were reflected in the drainage networks and generated uncertainty [8,13,35,96]. To reduce uncertainty due to drainage network discrepancies, the plane distances between control points and each channel network in the four scenarios were calculated. Sixty control points were acquired, distributed as follows: 11, 16, 13, 8, and 12 points, corresponding to current orders 1, 2, 3, 4, and 5, respectively. The drainage networks were analyzed for each stream order, to expose the impact of algorithms and resolutions. Results in Figure 6 show the maximum, the minimum, average, and the root mean square error distances between the control points and the nearest channel for each scenario. Overall, a significant susceptibility to DEM resolution was found in modeling by mesh-based routing algorithms, in agreement with Li [44]. The higher accuracy was observed in the merged DEM in comparison with DEM 30 m, except for stream orders 4 and 5 (Figure 6d,e, respectively). The differences in distance for channels of the stream order 1 were similar in the four sceneries (Figure 6a), despite reaching a maximum of 20 m; furthermore, resolutions or processing algorithms in stream order 1 exhibited no appreciable advantages or disadvantages. In the case of the channels of stream order 2 (Figure 6b), no important divergence was perceived for merged DEM, whereas, in the lower resolution DEM 30 m, the distances were more remarkable and increased for the KRA algorithm. Similarly, in channels of stream order 3 (Figure 6c), the distances increased with the decrease in DEM resolution and the distances were more remarkable for the KRA algorithm (maximum 145 m). On the contrary, channels of stream orders 4 and 5 (Figure 6d,e) showed greater separation for the higher resolution (merged DEM); with a maximum distance higher than 200 m. The KRA routing algorithm on the DEM filled with the W/L algorithm presented the highest distance differences in the drainage networks (300 m for stream order 5).
Comparative raster maps were generated to visualize differences between stream orders of drainage networks. The automatic methods identified different stream orders from reality channels and presented variations of orders even for the same resolution (Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11). Accordingly, algorithms are another variable to consider in DEM-based automatic methods. The variations in shape and length of the channels observed in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 were reflected in the quantifications of the geomorphological parameters in Table 7 andescription by stream order in Table 8. To visualize some control points (five) of stream order 1, it was considered a part of the watershed (Figure 7); the differences in shape, location, and length of the channels between the two resolutions used are significant.
Regarding the stream order 2, the areas marked with a red dashed line within Figure 8 exhibit channels with erroneous stream order, demonstrating that routing and fill algorithms affect them significantly. The most critical differences in the number and length of channels resulted from applying the KRA algorithm to the filled DEM with the W/L algorithm, which corresponds with Table 7 and Table 8.
The accumulative length of the stream order 3 channels in Table 8 showed a small difference between D8 and KRA algorithms on a single resolution (0.1587 km in the merged DEM and 0.5852 km over the DEM 30 m). However, reviewing the channels of order 3 concerning the control points, the location of the channels was different in each scenario (see Figure 9). Some channels were identified under another order. The area marked within Figure 9c,d corresponds to the higher magnification image in Figure 9e, with the X-X’ axis. Cells most affected by the fill algorithms were included in Figure 9e.
Figure 12 exhibits the topographic profiles of the X-X’ axis corresponding to the pre-treated DEM 30 m, fill DEM by the J/D algorithm and fill DEM by the W/L algorithm. The elevation change by the fill algorithms and the slope gradient of the W/L algorithm was evidenced. The location of the channels generated by the flow routing algorithms (channel W/L and channel J/D) was included in Figure 12, highlighting the horizontal distance separating the channels (approximately 72 m). The main reason for the distance difference between the drainage networks was that the lowest point location was established at a different site in each filled DEM. Additionally, the two resulting channels in the DEM 30 m were considerably distant from the real channel. It is noteworthy that Habtezion [97] noted that the areas filled and slopes modified were induced a greater arrangement of channels, which simultaneously contributes to underestimating or overestimating the saturation zones.
On the other hand, the channels of stream order 4 showed an important difference in the location over the merged DEM (Figure 10a,b). The same issues were repeated as in the previous orders. Again, the marked area within Figure 10a,b can be observed at higher magnification in Figure 10e; the Y-Y’ axis and cells filled by the W/L and J/D algorithms are displayed.
Figure 13 shows the Y-Y’ axis topographic profiles corresponding to the merged DEM, fill DEM W/L, fill DEM J/D, with W/L and J/D channels. The elevation increases, realized with the W/L algorithm (blue line), were the most significant due to the slope gradient (0.1°). The channel separation was similar to the previous stream order, the distance extended from channel W/L to channel J/D, up to approximately 163 m. Furthermore, the channel obtained in the W/L fill DEM with the KRA algorithm was the furthest from the real channel; this circumstance was potentially attributed to the filling process.
Channels of stream order 5 exhibited the most significant separation concerning the control points, as shown in Figure 11; the drainage network obtained by the KRA algorithm was the furthest. It is essential to highlight that the reduced length of the channels of stream order 5 resulted in the DEM 30 m with algorithm D8 (Figure 11c); this difference could be attributed to the routing algorithm. Furthermore, the most important location variations of the channels coincided with the filled areas. The issue areas identified in the maps were examined, and the channels presented direction changes at close distances and narrow sections. Another factor identified in the issue areas was the existence of plain terrains adjacent to the channels upstream of the sites with the highest cell fill.
To illustrate the allocation of the elevations in a DEM; a hypothetical channel is provided in Figure 14a, together with a raster elevation data set (Figure 14b,c). The channel (blue area) exhibits direction changes at close distances and section narrowing (Figure 14a). In the higher resolution DEM (Figure 14b), the flow (magenta cells) in the natural channel was recognized due to less or equal cell size to the channel width, despite the section narrowing. In contrast, in a lower resolution DEM (Figure 14c), the cells acquired the dominant elevation, which is the elevation of the terrain adjacent to the channel (with cells). The area marked with a red dashed line within Figure 14c indicates the assigned cells with a higher elevation than the channel (Figure 14c).
Consequently, the cells upstream of the narrowing of the channel were considered with lower elevation (depressions). From the above analysis, it can be argued that the coarse DEM is not representative of a relief since it establishes non-real depressions. It is worth mentioning that the problem expanded when adjacent plain terrains existed. The filling process modified the topography in depressions, which was increasing by employing a slope gradient, such as the W/L algorithm (Figure 3b,d). Recently, Erdbrügger [41] also verified that the areas with the most significant discrepancy in drainage networks coincided with the sites modified by fill algorithms. It seems that the assumption that DEM-based automatic approaches are more consistent and objective than the manual approach [6] can be re-examined.

4. Conclusions

This research proved that merging DEMs is feasible to achieve a more satisfactory base data condition in geoprocessing, particularly in regions where high-resolution data are lacking, and furthermore, to assessed the hydrological processing algorithms most widely used in the watershed geomorphological parametrization. Therefore, the following conclusions are obtained.
The research suggests conducting a thorough analysis of the DEM used in geoprocessing to identify and differentiate between natural depressions or possible errors generated by the cell size of the DEM, as non-real depressions were manifested as narrowing and changes in channel direction at close distances.
Choosing the fill algorithm in treating DEM is fundamental, as it significantly influences the lower elevation cell locations to identify drainage networks. Moreover, the slope gradient does not guarantee an improvement because it considerably modifies the original DEM topography. The most significant discrepancies in drainage networks from this research can be associated with the variations of the filling process since they correspond with the most noticeable elevation change places in a range of 2 to 30 m.
The 1.5 resolution-merged DEM generated in this research presented better deportment than the DEM of 30 m in the drainage network for the stream orders from 1 to 3 since its variations remained below 20 m, with a root mean square error between 3 and 6 m. In contrast, channels with 4 and 5 stream orders shift away from the existing network over 50 and 300 m—the maximum range; this can be attributed mainly to the topography change affected by the gradient slope of the W/L algorithm. This research suggests not to use a slope gradient for the filling of depressions, and it is recommended to carry out a reconditioning before being merged to the lower resolution DEM if reliable hydrology vector information of the zone is available.
The D8 and D∞ algorithms estimated the watershed area and perimeter more accurately, exhibiting a difference of less than 1%; however, the MFD algorithm manifested area overestimations of the order of 2%, because it showed problems in identifying the water dividing line in topography concave forms. Concerning the main channel length, the D8 and KRA algorithms present a difference of 1.4 km, impacting the estimation of the concentration time, with a difference of 24 min; this variation considerably affects the watershed peak discharge response.
The research proved that the drainage network divergences are mainly attributed to filling algorithms (J/D and W/L) and not flow routing algorithms (D8 and KRA). Therefore, it is suggested that DEM-based hydrological studies specify both the resolution and the algorithms employed in obtaining the geomorphological parameters to validate the rigidity of the study since the surface movement of water in the watershed directly depends on the characteristics of the topography, consequently in estimating floods and high hydrological risk delineation.
Recommendations and approaches for future work: to obtain the slopes on the original DEM and not on the DEM modified by the filling algorithms; identify issue zones (e.g., plains adjacent to channels, changes of direction, and narrowing); and, if possible, reform the base DEM, by merging with direct or indirect survey product DEMs.

Author Contributions

Conceptualization: S.D.-H., J.G.-T. and H.E.J.-F.; methodology, software, validation, and writing: S.D.-H. and J.G.-T.; resources and supervision: H.E.J.-F., C.F.B.-C., J.G.-T. and C.O.R.R.; investigation: S.D.-H.; writing—original draft: S.D.-H.; writing—review and editing: S.D.-H., J.G.-T., H.E.J.-F., C.F.B.-C., H.M.d.Á., J.C.E., J.O.-L., C.O.R.R. and E.A.L.-B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in the article.

Acknowledgments

The authors express their gratitude to the Universidad Autónoma de Zacatecas (UAZ) for financing the scholarship of the doctoral students and to the Consejo Zacatecano de Ciencia y Tecnología e Inovación (COZCyT). We deeply appreciate the recommendation and professional comments from the reviewers and the editor.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Altaf, F.; Meraj, G.; Romshoo, S.A. Morphometric Analysis to Infer Hydrological Behaviour of Lidder Watershed, Western Himalaya, India. Geogr. J. 2013, 2013, 1–14. [Google Scholar] [CrossRef]
  2. Beven, K. Searching for the Holy Grail of Scientific Hydrology: Qt= H(SR)A as closure. Hydrol. Earth Syst. Sci. 2006, 3, 769–792. [Google Scholar] [CrossRef] [Green Version]
  3. Krishnamurthy, J.; Srinivas, G.; Jayaraman, V.; Chandrasekhar, M.G. Influence of Rock Types and Structures in Development of Drainage Network in Typical Hardrock Terrain. Int. J. Appl. Earth Obs. Geoinf. 1996, 3/4, 252–259. [Google Scholar]
  4. Pareta, K.; Pareta, U. Quantitative morphometric analysis of a watershed of Yamuna basin, India using ASTER (DEM) data and GIS. Int. J. Geomat. Geosci. 2011, 2, 248. [Google Scholar]
  5. Costabile, P.; Costanzo, C.; Ferraro, D.; Macchione, F.; Petaccia, G. Performances of the New HEC-RAS Version 5 for 2-D Hydrodynamic-Based Rainfall-Runoff Simulations at Basin Scale: Comparison with a State-of-the Art Model. Water 2020, 12, 2326. [Google Scholar] [CrossRef]
  6. Engelhardt, B.M.; Weisberg, P.J.; Chambers, J.C.; Huston, M. Influences of watershed geomorphology on extent and composition of riparian vegetation. J. Veg. Sci. 2012, 23, 127–139. [Google Scholar] [CrossRef]
  7. García, A.; Acosta, J.; Chávez, E.; Yuli Posadas, R.; Bulege, W. Use of Hydrogeomorphic Indexes in SAGA-GIS for the Characterization of Flooded Areas in Madre de Dios, Peru. Int. J. Appl. Eng. Res. 2017, 12, 9078–9086. [Google Scholar]
  8. Pilesjö, P.; Hasan, A. A Triangular Form-based Multiple Flow Algorithm to Estimate Overland Flow Distribution and Accumulation on a Digital Elevation Model. Trans. GIS 2014, 18, 108–124. [Google Scholar] [CrossRef] [Green Version]
  9. Tesfa, T.K.; Tarboton, D.G.; Watson, D.W.; Schreuders, K.A.T.; Baker, M.E.; Wallace, R.M. Extraction of hydrological proximity measures from DEMs using parallel processing. Environ. Model. Softw. 2011, 26, 1696–1709. [Google Scholar] [CrossRef]
  10. Diakakis, M. A method for flood hazard mapping based on basin morphometry: Application in two catchments in Greece. Nat. Hazards 2010, 56, 803–814. [Google Scholar] [CrossRef]
  11. Huang, P.-C.; Lee, K.T. Influence of topographic features and stream network structure on the spatial distribution of hydrological response. J. Hydrol. 2021, 603, 126856. [Google Scholar] [CrossRef]
  12. Costabile, P.; Costanzo, C.; De Bartolo, S.; Gangi, F.; Macchione, F.; Tomasicchio, G. Hydraulic Characterization of River Networks Based on Flow Patterns Simulated by 2-D Shallow Water Modeling: Scaling Properties, Multifractal Interpretation, and Perspectives for Channel Heads Detection. Water Resour. Res. 2019, 55, 7717–7752. [Google Scholar] [CrossRef]
  13. López-Vicente, M.; Navas, A. Routing runoff and soil particles in a distributed model with GIS: Implications for soil protection in mountain agricultural landscapes. Land Degrad. Dev. 2010, 21, 100–109. [Google Scholar] [CrossRef] [Green Version]
  14. Vozinaki, A.-E.K.; Morianou, G.G.; Alexakis, D.D.; Tsanis, I.K. Comparing 1D and combined 1D/2D hydraulic simulations using high-resolution topographic data: A case study of the Koiliaris basin, Greece. Hydrol. Sci. J. 2016, 62, 642–656. [Google Scholar] [CrossRef]
  15. Pardo-Igúzquiza, E.; Dowd, P.A. The mapping of closed depressions and its contribution to the geodiversity inventory. Int. J. Geoheritage Parks 2021, 9, 480–495. [Google Scholar] [CrossRef]
  16. Patel, D.P.; Gajjar, C.A.; Srivastava, P.K. Prioritization of Malesari mini-watersheds through morphometric analysis: A remote sensing and GIS perspective. Environ. Earth Sci. 2012, 69, 2643–2656. [Google Scholar] [CrossRef]
  17. Chen, H.; Liang, Q.; Liu, Y.; Xie, S. Hydraulic correction method (HCM) to enhance the efficiency of SRTM DEM in flood modeling. J. Hydrol. 2018, 559, 56–70. [Google Scholar] [CrossRef] [Green Version]
  18. Prieto, A.; Pinedo, A.; Vázquez, Q.; Valles, A.; Rascón, R.; Martinez, S.; Villarreal, G. A Multivariate Geomorphometric Approach to Prioritize Erosion-Prone Watersheds. Sustainability 2019, 11, 5140. [Google Scholar] [CrossRef] [Green Version]
  19. Brunda, G.S.; Nyamathi, S.J. Derivation and Analysis of Dimensionless Hydrograph and S Curve for Cumulative Watershed Area. Aquat. Procedia 2015, 4, 964–971. [Google Scholar] [CrossRef]
  20. Burke, L.; Sugg, Z. Hydrologic Modeling of Watersheds Discharging Adjacent to the Mesoamerican Reef; World Resources Institute: Washington, DC, USA, 2006; p. 36. [Google Scholar]
  21. Chang, C.-H.; Lee, K.T. Analysis of geomorphologic and hydrological characteristics in watershed saturated areas using topographic-index threshold and geomorphology-based runoff model. Hydrol. Processes 2008, 22, 802–812. [Google Scholar] [CrossRef]
  22. Goñi, M.; López, J.J.; Gimena, F.N. Geomorphological instantaneous unit hydrograph model with distributed rainfall. Catena 2019, 172, 40–53. [Google Scholar] [CrossRef]
  23. Ji, P.; Yuan, X.; Liang, X.-Z. Do Lateral Flows Matter for the Hyperresolution Land Surface Modeling? J. Geophys.Res. Atmos. 2017, 122, 12077–12092. [Google Scholar] [CrossRef]
  24. O’Callaghan, J.F.; Mark, D.M.J.C. The extraction of drainage networks from digital elevation data. Comput. Vis.Graph. Image Processing 1984, 28, 323–344. [Google Scholar] [CrossRef]
  25. Orlandini, S.; Moretti, G. Determination of surface flow paths from gridded elevation data. Water Resour. Res. 2009, 45, 1–14. [Google Scholar] [CrossRef] [Green Version]
  26. Orlandini, S.; Moretti, G.; Franchini, M.; Aldighieri, B.; Testa, B. Path-based methods for the determination of nondispersive drainage directions in grid-based digital elevation models. Water Resour. Res. 2003, 39, 1–8. [Google Scholar] [CrossRef] [Green Version]
  27. Orlandini, S.; Moretti, G.; Gavioli, A. Analytical basis for determining slope lines in grid digital elevation models. Water Resour. Res. 2014, 50, 526–539. [Google Scholar] [CrossRef] [Green Version]
  28. Sabzevari, T.; Noroozpour, S. Effects of hillslope geometry on surface and subsurface flows. Hydrogeol. J. 2014, 22, 1593–1604. [Google Scholar] [CrossRef]
  29. Sabzevari, T.; Saghafian, B.; Talebi, A.; Ardakanian, R. Time of concentration of surface flow in complex hillslopes. J. Hydrol. Hydromech. 2013, 61, 269–277. [Google Scholar] [CrossRef] [Green Version]
  30. Sadeghi, S.H.; Moradi Dashtpagerdi, M.; Moradi Rekabdarkoolai, H.; Schoorl, J.M. Sensitivity analysis of relationships between hydrograph components and landscapes metrics extracted from digital elevation models with different spatial resolutions. Ecol. Indic. 2021, 121, 107025. [Google Scholar] [CrossRef]
  31. Tarboton, D.G. A new method for the determination of flow directions and upslope areas in grid digital elevation models. Water Resour. Res. 1997, 33, 309–319. [Google Scholar] [CrossRef] [Green Version]
  32. Tarboton, D.G.; Bras, R.L. Rodriguez-Iturbe, On the extraction of channel networks from digital elevation data. Hydrol. Processes 1991, 5, 81–100. [Google Scholar] [CrossRef]
  33. Zhu, Q.; Abdelkareem, M. Mapping Groundwater Potential Zones Using a Knowledge-Driven Approach and GIS Analysis. Water 2021, 13, 579. [Google Scholar] [CrossRef]
  34. López-Vicente, M.; García-Ruiz, R.; Guzmán, G.; Vicente-Vicente, J.L.; Van Wesemael, B.; Gómez, J.A. Temporal stability and patterns of runoff and runon with different cover crops in an olive orchard (SW Andalusia, Spain). Catena 2016, 147, 125–137. [Google Scholar] [CrossRef] [Green Version]
  35. López-Vicente, M.; Pérez-Bielsa, C.; López-Montero, T.; Lambán, L.J.; Navas, A. Runoff simulation with eight different flow accumulation algorithms: Recommendations using a spatially distributed and open-source model. Environ. Model. Softw. 2014, 62, 11–21. [Google Scholar] [CrossRef] [Green Version]
  36. Szumińska, D.; Czapiewski, S.; Goszczyński, J. Changes in Hydromorphological Conditions in an Endorheic Lake Influenced by Climate and Increasing Water Consumption, and Potential Effects on Water Quality. Water 2020, 12, 1348. [Google Scholar] [CrossRef]
  37. Muthusamy, M.; Casado, M.R.; Butler, D.; Leinster, P. Understanding the effects of Digital Elevation Model resolution in urban fluvial flood modelling. J. Hydrol. 2021, 596, 126088. [Google Scholar] [CrossRef]
  38. Seleem, O.; Heistermann, M.; Bronstert, A. Efficient Hazard Assessment for Pluvial Floods in Urban Environments: A Benchmarking Case Study for the City of Berlin, Germany. Water 2021, 13, 2476. [Google Scholar] [CrossRef]
  39. Mardhel, V.; Pinson, S.; Allier, D. Description of an indirect method (IDPR) to determine spatial distribution of infiltration and runoff and its hydrogeological applications to the French territory. J. Hydrol. 2021, 592, 125609. [Google Scholar] [CrossRef]
  40. Pham, H.T.; Marshall, L.; Johnson, F.; Sharma, A. A method for combining SRTM DEM and ASTER GDEM2 to improve topography estimation in regions without reference data. Remote Sens. Environ. 2018, 210, 229–241. [Google Scholar] [CrossRef]
  41. Erdbrügger, J.; van Meerveld, I.; Bishop, K.; Seibert, J. Effect of DEM-smoothing and -aggregation on topographically-based flow directions and catchment boundaries. J. Hydrol. 2021, 602, 126717. [Google Scholar] [CrossRef]
  42. Grimm, K.; Tahmasebi Nasab, M.; Chu, X. TWI Computations and Topographic Analysis of Depression-Dominated Surfaces. Water 2018, 10, 663. [Google Scholar] [CrossRef] [Green Version]
  43. Haile, A.; Rientjes, T. Effects of LiDAR DEM resolution in flood modelling: A model sensitivity study for the city of Tegucigalpa, Honduras. ISPRS WG 2005, 3, 168–173. [Google Scholar]
  44. Li, J.; Chen, H.; Xu, C.-Y.; Li, L.; Zhao, H.; Huo, R.; Chen, J. Joint Effects of the DEM Resolution and the Computational Cell Size on the Routing Methods in Hydrological Modelling. Water 2022, 14, 797. [Google Scholar] [CrossRef]
  45. Nardi, F.; Grimaldi, S.; Santini, M.; Petroselli, A.; Ubertini, L. Hydrogeomorphic properties of simulated drainage patterns using digital elevation models: The flat area issue / Propriétés hydro-géomorphologiques de réseaux de drainage simulés à partir de modèles numériques de terrain: La question des zones planes. Hydrol. Sci. J. 2010, 53, 1176–1193. [Google Scholar] [CrossRef]
  46. Seibert, J.; McGlynn, B.L. A new triangular multiple flow direction algorithm for computing upslope areas from gridded digital elevation models. Water Resour. Res. 2007, 43, 1–8. [Google Scholar] [CrossRef] [Green Version]
  47. Tarboton, D.G.; Baker, M.E. Towards an algebra for terrain-based flow analysis. In Modeling and Visualizing the Natural Environment: Innovations in GIS 13; CRC Press: Boca Raton, FL, USA, 2008; Volume 13, pp. 167–194. [Google Scholar]
  48. INEGI. SIATL: Simulador de Flujos de Agua de Cuencas Hidrográficas. Available online: https://antares.inegi.org.mx/analisis/red_hidro/siatl/ (accessed on 23 May 2022).
  49. INEGI. Marco Geoestadístico Municipal 2005 Versión 1.0 (Conteo de Población y Vivienda 2005). Available online: https://www.inegi.org.mx/app/biblioteca/ficha.html?upc=702825292850 (accessed on 23 May 2022).
  50. CONAGUA. Sistema de Información Hidrológica (SIH). Available online: https://sih.conagua.gob.mx/ (accessed on 31 May 2022).
  51. INEGI. Relieve Continental. Available online: https://www.inegi.org.mx/temas/relieve/continental/#Descargas (accessed on 23 May 2022).
  52. INEGI. Topografía (Mapas). Available online: https://www.inegi.org.mx/temas/topografia/ (accessed on 23 May 2022).
  53. Chymyrov, A. Comparison of different DEMs for hydrological studies in the mountainous areas. Egypt. J. Remote Sens. Space Sci. 2021, 24, 587–594. [Google Scholar] [CrossRef]
  54. Chu, X. Delineation of Pothole-Dominated Wetlands and Modeling of Their Threshold Behaviors. J. Hydrol. Eng. 2015, 22, D5015003. [Google Scholar] [CrossRef]
  55. Tahmasebi Nasab, M.; Singh, V.; Chu, X. SWAT Modeling for Depression-Dominated Areas: How Do Depressions Manipulate Hydrologic Modeling. Water 2017, 9, 58. [Google Scholar] [CrossRef] [Green Version]
  56. Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Boehner, J. SAGA-GIS Module Library Documentation (v2.1.3). Available online: https://saga-gis.sourceforge.io/saga_tool_doc/2.1.3/a2z.html (accessed on 23 May 2022).
  57. ESRI. ArcGIS Desktop Help 10.5. Available online: https://desktop.arcgis.com/es/quick-start-guides/latest/arcgis-location-referencing-quick-start-guide.htm (accessed on 23 May 2022).
  58. Lea, N.J. An Aspect-Driven Kinematic Routing Algorithm. In Overland Flow: Hydraulics and Erosion Mechanics; Parson, A.J., Abrahams, A.D., Eds.; Taylor & Francis: London, UK, 1992; pp. 393–407. [Google Scholar]
  59. Wang, L.; Liu, H. An efficient method for identifying and filling surface depressions in digital elevation models for hydrologic analysis and modelling. Int. J. Geogr. Inf. Sci. 2006, 20, 193–213. [Google Scholar] [CrossRef]
  60. Olaya, V. A gentle introduction to SAGA GIS; The SAGA User Group eV: Gottingen, Germany, 2004; Volume 208, pp. 1–216. [Google Scholar]
  61. Pardo-Igúzquiza, E.; Valsero, J.J.D.; Dowd, P.A.J.A.C. Automatic detection and delineation of karst terrain depressions and its application in geomorphological mapping and morphometric analysis. Acta Carsologica 2013, 42, 17–24. [Google Scholar] [CrossRef] [Green Version]
  62. Wang, N.; Chu, X. A New Algorithm for Delineation of Surface Depressions and Channels. Water 2019, 12, 7. [Google Scholar] [CrossRef] [Green Version]
  63. Wang, N.; Chu, X.; Zhang, X. Functionalities of surface depressions in runoff routing and hydrologic connectivity modeling. J. Hydrol. 2021, 593, 125870. [Google Scholar] [CrossRef]
  64. Barnes, R.; Lehman, C.; Mulla, D. An efficient assignment of drainage direction over flat surfaces in raster digital elevation models. Comput. Geosci. 2014, 62, 128–135. [Google Scholar] [CrossRef] [Green Version]
  65. Garbrecht, J.; Martz, L.W. TOPAZ, An Automated Digital Landscape Analysis Tool for Topographic Evaluation, Drainage Identification, Watershed Segmentation, and Subcatchment Parameterization: Overview; ARS-NAWQL 95-1; US Department of Agriculture, Agricultural Research Service: El Reno, OK, USA, 1996.
  66. Jenson, S.K.; Domingue, J.O. Extracting topographic structure from digital elevation data for geographic information system analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
  67. Marks, D.; Dozier, J.; Frew, J. Automated basin delineation from digital elevation data. Geo-Processing 1984, 2, 299–311. [Google Scholar]
  68. Martz, L.W.; Garbrecht, J. The treatment of flat areas and depressions in automated drainage analysis of raster digital elevation models. Hydrol. Processes 1998, 12, 843–855. [Google Scholar] [CrossRef]
  69. USACE. Geospatial Hydrologic Modelling Extension HEC-GeoHMS, User’s Manual, version 1.1; United States Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2003. [Google Scholar]
  70. Team, G.D. GRASS GIS 7.8.8dev Reference Manual. Available online: https://grass.osgeo.org/grass78/manuals/ (accessed on 23 May 2022).
  71. Greenlee, D.D. Raster and vector processing for scanned linework. Photogramm. Eng. Remote Sens. 1987, 53, 1383–1387. [Google Scholar]
  72. Freeman, T.G. Calculating catchment area with divergent flow based on a regular grid. Comput. Geosci. 1991, 17, 413–422. [Google Scholar] [CrossRef]
  73. Huang, P.-C.; Lee, K.T. Distinctions of geomorphological properties caused by different flow-direction predictions from digital elevation models. Int. J. Geogr. Inf. Sci. 2015, 30, 168–185. [Google Scholar] [CrossRef]
  74. Tarboton, D.G. Terrain analysis using digital elevation models in hydrology. In Proceedings of the 23rd ESRI international users conference, San Diego, CA, USA, 7–11 July 2003. [Google Scholar]
  75. Horton, R.E. Erosional Development of Streams and Their Drainage Basins; Hydrophysical Approach to Quantitative Morphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef] [Green Version]
  76. Strahler, A.N. Transactions American Geophysical Union. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef] [Green Version]
  77. Gravelius, H. Grundrifi der gesamten Gewcisserkunde. Band I: Flufikunde. Compendium of Hydrology I. Rivers. 1914. [Google Scholar]
  78. Miller, V.C. A Quantitative Geomorphic Study of Drainage Basin Characteristics in the Clinch Mountain Area Virginia and Tennessee; Columbia University: New York, NY, USA, 1953. [Google Scholar]
  79. Schumm, S.A. Evolution of Drainage Systems and Slopes in Badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
  80. Horton, R.E. Drainage-basin characteristics. Trans. Am. Geophys. Union 1932, 13, 350–361. [Google Scholar] [CrossRef]
  81. Kirpich, Z.P. Time of concentration of small agricultural watersheds. Civ. Eng. 1940, 10, 362. [Google Scholar]
  82. Smith, K.G. Standards for grading texture of erosional topography. Am. J. Sci. 1950, 248, 655–668. [Google Scholar] [CrossRef]
  83. Faniran, A. The index of drainage intensity: A provisional new drainage factor. Austral. J. Sci 1968, 31, 326–330. [Google Scholar]
  84. Monsalve Sáenz, G. Hidrología en la Ingeniería; Alfaomega: Bogotá, Colombia, 1999. [Google Scholar]
  85. Romero Díaz, M.A.; López Bermúdez, F. Morfometria de redes fluviales: Revision critica de los parámetros más utilizados y aplicación al Alto Guadalquivir. Pap. De Geogr. 1987, 12, 47–62. [Google Scholar]
  86. IGAC. Estudio General de Suelos y Zonificación de Tierras de Boyacá Tomo I.; Instituto Geográfico Agustín Codazzi: Bogota, Colombia, 2005. [Google Scholar]
  87. Lee, K.T.; Chang, C.-H. Incorporating subsurface-flow mechanism into geomorphology-based IUH modeling. J. Hydrol. 2005, 311, 91–105. [Google Scholar] [CrossRef]
  88. Sabzevari, T.; Noroozpour, S.; Pishvaei, M.H. Effects of geometry on runoff time characteristics and time-area histogram of hillslopes. J. Hydrol. 2015, 531, 638–648. [Google Scholar] [CrossRef]
  89. dos Santos, P.; Tavares, A. Basin Flood Risk Management: A Territorial Data-Driven Approach to Support Decision-Making. Water 2015, 7, 480–502. [Google Scholar] [CrossRef] [Green Version]
  90. Fewtrell, T.J.; Duncan, A.; Sampson, C.C.; Neal, J.C.; Bates, P.D. Benchmarking urban flood models of varying complexity and scale using high resolution terrestrial LiDAR data. Phys. Chem. Earth Parts A/B/C 2011, 36, 281–291. [Google Scholar] [CrossRef]
  91. Sellers, C.; Corbelle-Rico, E.; Buján, S.; Miranda, D. Morfología interpretativa de alta resolución usando datos lídar en la cuenca hidrográfica del río Paute en Ecuador; Universidade de Santiago de Compostela, Servizo de Publicacións e Intercambio Científico: Santiago de Compostela, España, 2016; pp. 225–258. [Google Scholar]
  92. Faustino, J.; Jiménez, F. Manejo de cuencas hidrográficas; Centro Agronómico Tropical de Investigación y Enseñanza: Turrialba, Costa Rica, 2000. [Google Scholar]
  93. Wooding, R.A. A hydraulic model for the catchment-stream problem: I. Kinematic-wave theory. J. Hydrol. 1965, 3, 254–267. [Google Scholar] [CrossRef]
  94. Sabzevari, T.; Fattahi, M.H.; Mohammadpour, R.; Noroozpour, S. Prediction of surface and subsurface flow in catchments using the GIUH. J. Flood Risk Manag. 2013, 6, 135–145. [Google Scholar] [CrossRef]
  95. Zhang, H.; Cheng, X.; Jin, L.; Zhao, D.; Feng, T.; Zheng, K. A Method for Dynamical Sub-Watershed Delimitating by No-Fill Digital Elevation Model and Defined Precipitation: A Case Study of Wuhan, China. Water 2020, 12, 486. [Google Scholar] [CrossRef]
  96. Liu, H.; Kiesel, J.; Hörmann, G.; Fohrer, N. Effects of DEM horizontal resolution and methods on calculating the slope length factor in gently rolling landscapes. Catena 2011, 87, 368–375. [Google Scholar] [CrossRef]
  97. Habtezion, N.; Tahmasebi Nasab, M.; Chu, X. How does DEM resolution affect microtopographic characteristics, hydrologic connectivity, and modelling of hydrologic processes. Hydrol. Processes 2016, 30, 4870–4892. [Google Scholar] [CrossRef]
Water 14 02363 g001 550
Figure 1. Location of the study site.
Figure 1. Location of the study site.
Water 14 02363 g001
Water 14 02363 g002 550
Figure 2. Workflow chart of geomorphological parameterization: (a) flow diagram of the general methodology in GIS environments for geomorphological analysis; (b) watershed assessment derived from the different delimitations; and (c) assessment of drainage networks for each scenario.
Figure 2. Workflow chart of geomorphological parameterization: (a) flow diagram of the general methodology in GIS environments for geomorphological analysis; (b) watershed assessment derived from the different delimitations; and (c) assessment of drainage networks for each scenario.
Water 14 02363 g002
Water 14 02363 g003 550
Figure 3. Difference of cell elevation in pre-treated DEMs against fill DEMs: (a) merged DEM–fill DEM J/D, (b) merged DEM–fill DEM W/L, (c) DEM 30 m–fill DEM J/D, and (d) DEM 30 m–fill DEM W/L.
Figure 3. Difference of cell elevation in pre-treated DEMs against fill DEMs: (a) merged DEM–fill DEM J/D, (b) merged DEM–fill DEM W/L, (c) DEM 30 m–fill DEM J/D, and (d) DEM 30 m–fill DEM W/L.
Water 14 02363 g003
Water 14 02363 g004 550
Figure 4. Differences in flow directions: (a) merged DEM and (b) DEM 30 m.
Figure 4. Differences in flow directions: (a) merged DEM and (b) DEM 30 m.
Water 14 02363 g004
Water 14 02363 g005 550
Figure 5. Accomplished delimitations by the D8, D∞, and MFD algorithms over the merged DEM, including part of the hydrography.
Figure 5. Accomplished delimitations by the D8, D∞, and MFD algorithms over the merged DEM, including part of the hydrography.
Water 14 02363 g005
Water 14 02363 g006 550
Figure 6. Comparison between the control points and nearest channels of each drainage network: (a) distances of stream order 1, (b) distances of stream order 2, (c) distances of stream order 3, (d) distances of stream order 4, and (e) distances of stream order 5.
Figure 6. Comparison between the control points and nearest channels of each drainage network: (a) distances of stream order 1, (b) distances of stream order 2, (c) distances of stream order 3, (d) distances of stream order 4, and (e) distances of stream order 5.
Water 14 02363 g006
Water 14 02363 g007 550
Figure 7. Drainage networks, control points, and channels of stream order 1.
Figure 7. Drainage networks, control points, and channels of stream order 1.
Water 14 02363 g007
Water 14 02363 g008 550
Figure 8. Drainage networks, control points, and channels of stream order 2.
Figure 8. Drainage networks, control points, and channels of stream order 2.
Water 14 02363 g008
Water 14 02363 g009 550
Figure 9. Drainage networks, control points, channels of stream order 3, and X-X’ axis over filled cells.
Figure 9. Drainage networks, control points, channels of stream order 3, and X-X’ axis over filled cells.
Water 14 02363 g009
Water 14 02363 g010 550
Figure 10. Drainage networks, control points, channels of stream order 4 and Y-Y’ axis over filled cells.
Figure 10. Drainage networks, control points, channels of stream order 4 and Y-Y’ axis over filled cells.
Water 14 02363 g010
Water 14 02363 g011 550
Figure 11. Drainage networks, control points, and channels of stream order 5.
Figure 11. Drainage networks, control points, and channels of stream order 5.
Water 14 02363 g011
Water 14 02363 g012 550
Figure 12. X-X’ axis topographic profiles from DEM 30 m.
Figure 12. X-X’ axis topographic profiles from DEM 30 m.
Water 14 02363 g012
Water 14 02363 g013 550
Figure 13. Y-Y’ axis topographic profiles from merged DEM.
Figure 13. Y-Y’ axis topographic profiles from merged DEM.
Water 14 02363 g013
Water 14 02363 g014 550
Figure 14. Allocation of elevations on DEMs and depression identification: (a) planar view of a hypothetical channel; (b) high-resolution DEM; and (c) low-resolution DEM.
Figure 14. Allocation of elevations on DEMs and depression identification: (a) planar view of a hypothetical channel; (b) high-resolution DEM; and (c) low-resolution DEM.
Water 14 02363 g014
Table
Table 1. System of methods and principles used for the computation of the geomorphometric parameters of basic and shape.
Table 1. System of methods and principles used for the computation of the geomorphometric parameters of basic and shape.
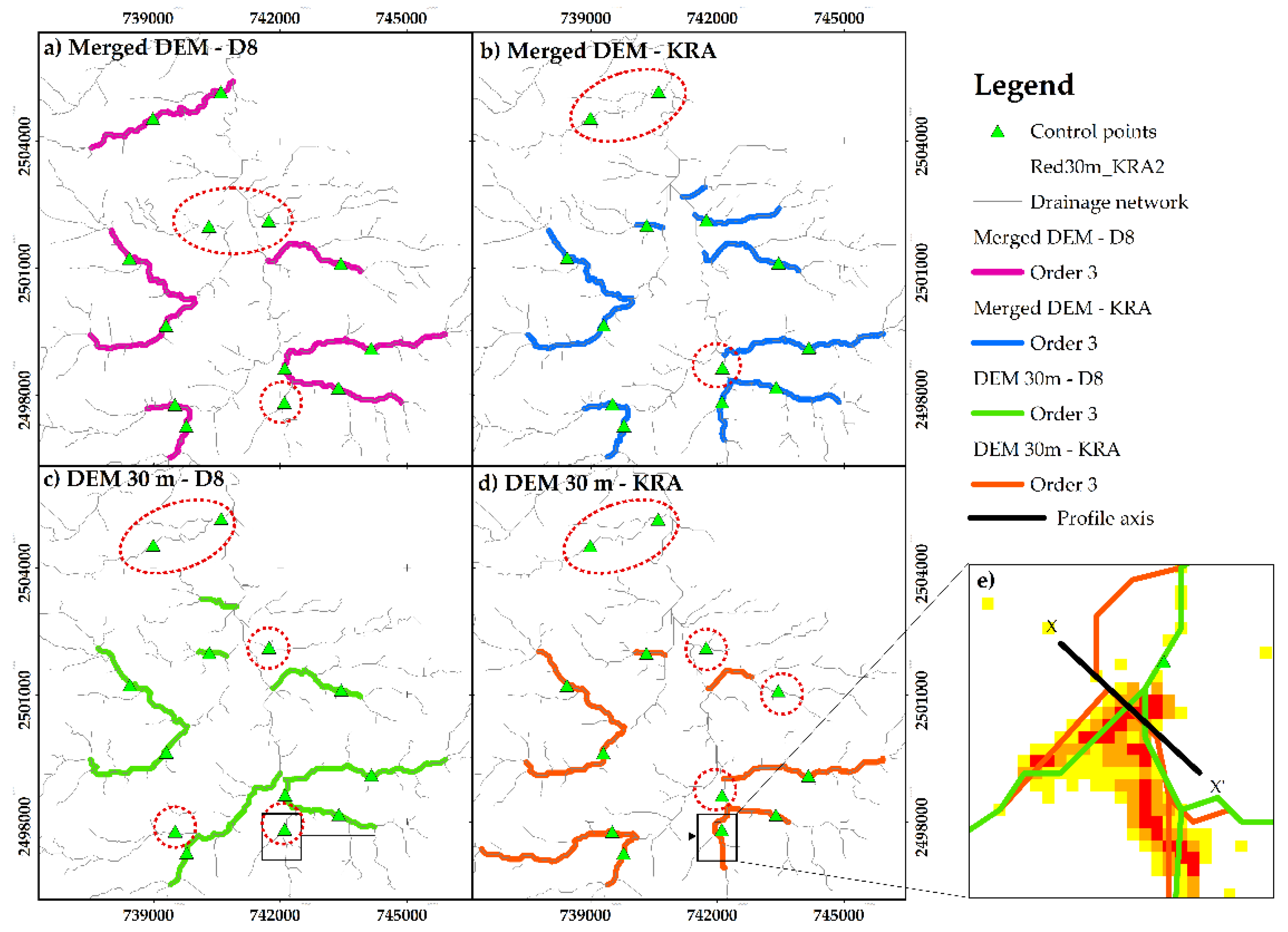
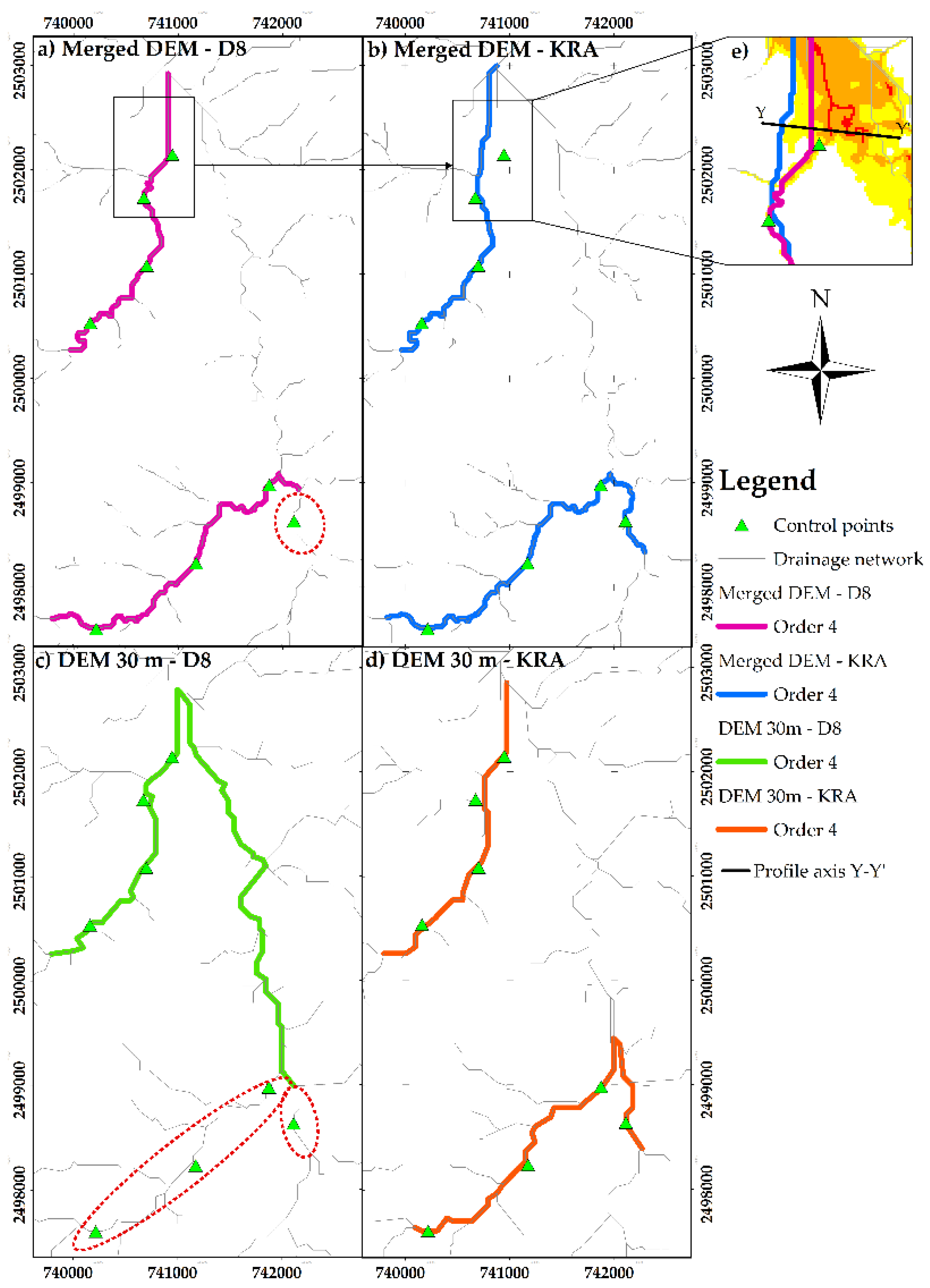
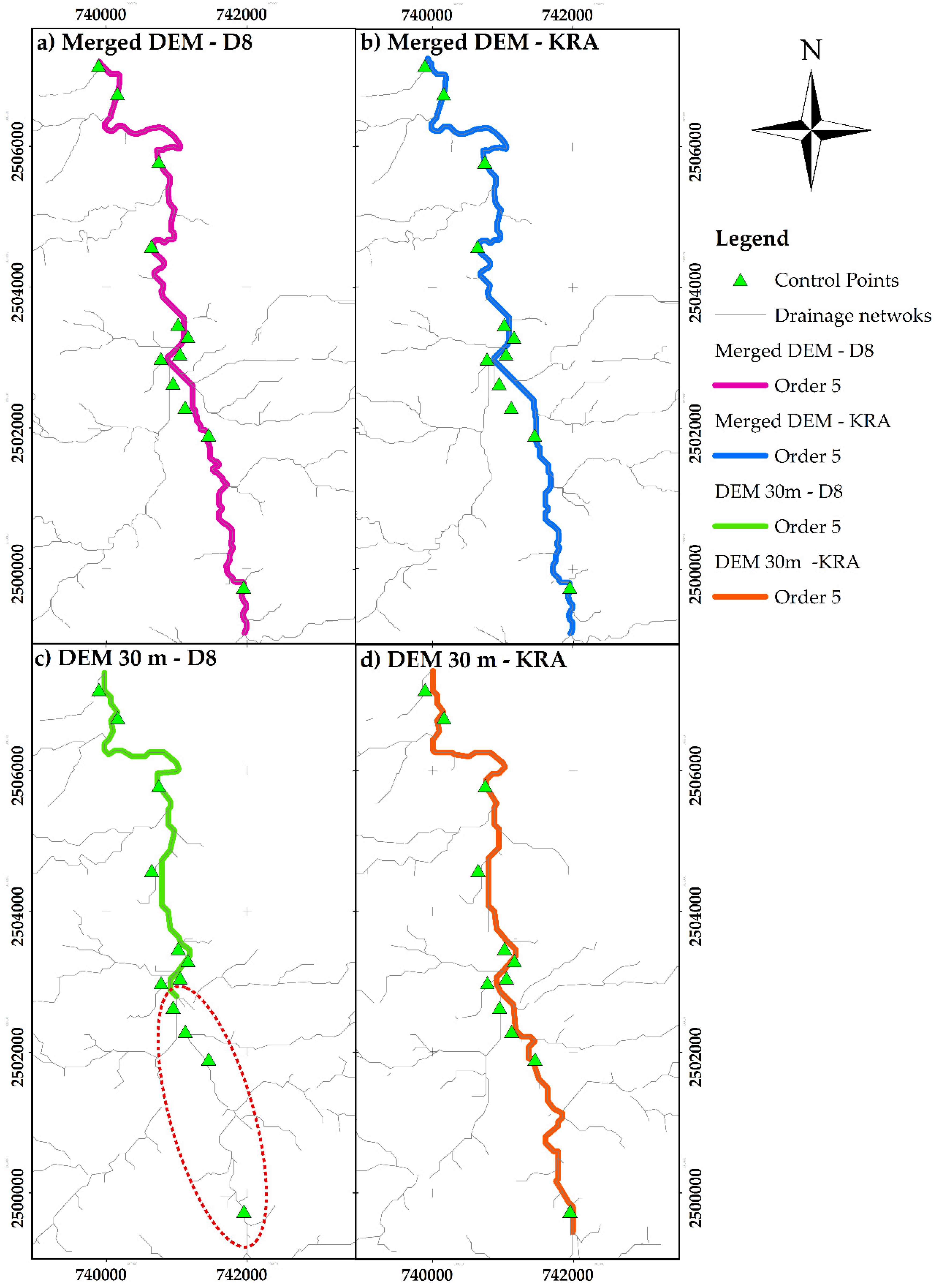
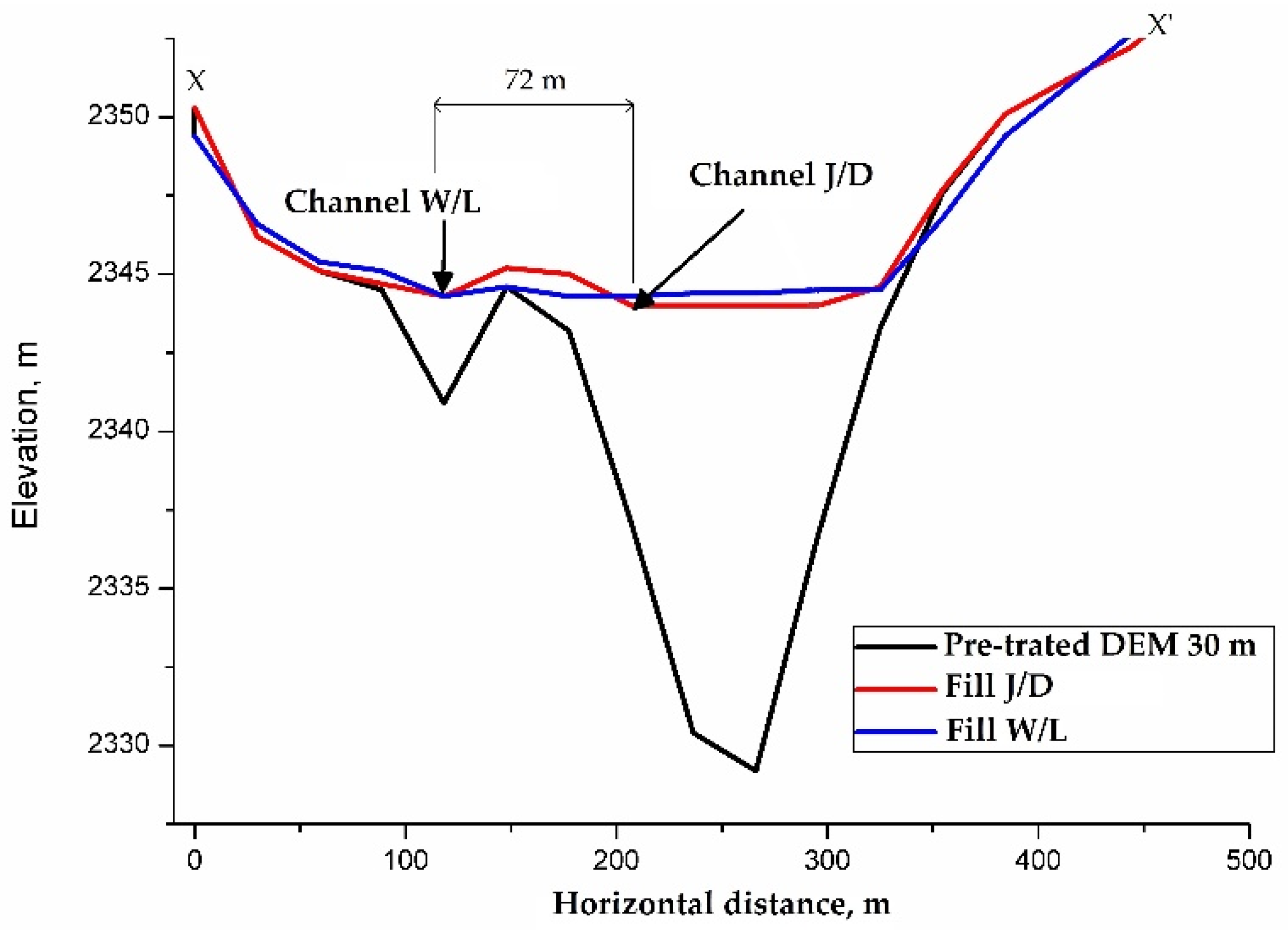
No.NameEquationReference
Basic parameters
(1)Area (A)A = Watershed surface area (km2)[75]
(2)Perimeter (P)P = Watershed perimeter (km)[75]
(3)Main channel length (Lc)Lc = Main flow channel length (km)[75]
(4)Stream order (u)u = Stream order (unitless)[76]
(5)All number of flow channels (Nu)Nu = Number of flow channels [75]
(6)All channel lengths (Lu)Lu = Length of all the flow channels in the watershed (km)[75]
(7)Mean slope of the main channel (Sc) S c = ( H m a x − H m i n L c ) 100 (%)[75]
Shape parameters
(8)Compactness coefficient (Kc) K c = P 2 π A (unitless)[77]
(9)Circularity ratio (Rc) R c = 4 π A P 2 (unitless)[78]
(10)Elongatio ratio (Re) R e = 1.128 A L (unitless)[79]
Table
Table 2. System of methods and principles used for computation of geomorphometric parameters related to drainage.
Table 2. System of methods and principles used for computation of geomorphometric parameters related to drainage.
No.NameEquationReference
Drainage parameters
(11)Stream frequency (Fu) F u = N u / A (channels/km2)[80]
(12)Drainage density (Dd) D d = L u / A (km/km2)[75]
(13)Overland flow length (Lof) L o f = 1 / 2 D d (km)[75]
(14)Constant channel maintenance (C) C = A / L u = 1 / D d (km)[79]
(15)Concentration time (Tc) T c = 0.066 ( L c S c ) 0.77 (h)[81]
(16)Texture ratio (T)T = Nu/P (channels/km)[82]
(17)Drainage intensity (Di) D i = F u / D d (unitless)[83]
(18)Average extent of runoff (E) E = A / 4 L u (km)[84]
(19)Torrential coefficient (Ct) C t = N u 1 / A (channels/km2)[85]
Table
Table 3. Percentage of elevation variation between the pre-treated DEMs and the fill DEMs.
Table 3. Percentage of elevation variation between the pre-treated DEMs and the fill DEMs.
Elevation Difference
(m)		Cells Percentage (%)
Fill Merged DEMFill DEM 30 m
J/DW/LJ/DW/L
<−20009.8
−2 to 000056.2
0 to 299.198.396.526.3
>20.91.73.57.7
Min. value (m)0.00.00.0−9.0
Max. value (m)19.019.429.427.2
Table
Table 4. Area percentage regarding the relief type and mean slope of the watershed.
Table 4. Area percentage regarding the relief type and mean slope of the watershed.
Relief TypeRange Slope
(%)		Watershed Area (%)
Fill Merged DEMFill DEM 30 m
J/DW/LJ/DW/L
Flat0–368.969.018.721.7
Lightly flat3–71.01.041.844.3
Lightly inclined7–120.00.128.926.1
Strongly undulating12–2520.620.710.27.7
Strongly inclined25–508.78.40.40.2
Steep50–750.70.70.00.0
Very steep>750.00.00.00.0
Mean slope of the watershed 7.207.086.596.04
Table
Table 5. Cell percentage according to flow directions.
Table 5. Cell percentage according to flow directions.
Flow DirectionCells Percentage (%)
Merged DEMDEM 30 mMax Difference
J/DW/LJ/DW/L
E24.223.014.113.710.5
SE0.81.510.39.39.6
S23.323.214.515.18.8
SW0.61.18.89.08.3
W21.021.511.914.69.6
NW0.81.510.09.79.1
N28.326.618.918.39.9
NE0.91.611.510.310.6
Table
Table 6. Watershed area and perimeter calculation.
Table 6. Watershed area and perimeter calculation.
DEMFill AlgorithmRouting AlgorithmArea (km2)Perimeter (km)
Merged DEMJ/DD8 (W1)101.06972.699
W/LD8100.76771.946
MFD102.82089.133
D∞ (W2)100.91472.531
DEM 30 mJ/DD8 (W3)101.09972.375
W/LD8100.38170.385
MFD103.52477.261
D∞ (W4)101.77669.782
Max difference3.14419.351
Table
Table 7. Quantitative geomorphometry.
Table 7. Quantitative geomorphometry.
Subclassification SymbolUnitsMerged DEM DEM 30 m Max Difference
D8 (W1)KRA (W2)D8 (W3)KRA (W4)
Basic parametersLckm21.380221.1426 20.204319.93491.445
Sc%1.1271.1491.2741.2940.167
Shape parametersKcunitless2.0402.0372.0311.9510.089
Rcunitless0.2400.2410.2430.2630.022
Reunitless0.5300.5360.5610.5710.040
Drainage parametersFuchannels/km23.1363.2212.9482.9280.293
Lofkm0.8700.8870.8200.7950.092
Ckm0.5750.5630.6100.6290.065
Ddkm/km21.7401.7751.6391.5910.184
Tch3.9233.8603.5823.5250.398
Tno. channels/km24.3604.4814.1174.2700.363
Diunitless1.8031.8151.7981.8410.042
Ekm0.1440.1410.1530.1570.016
Ctunitless1.5731.595|1.4841.5520.122
Table
Table 8. Quantification of number and lengths channels.
Table 8. Quantification of number and lengths channels.
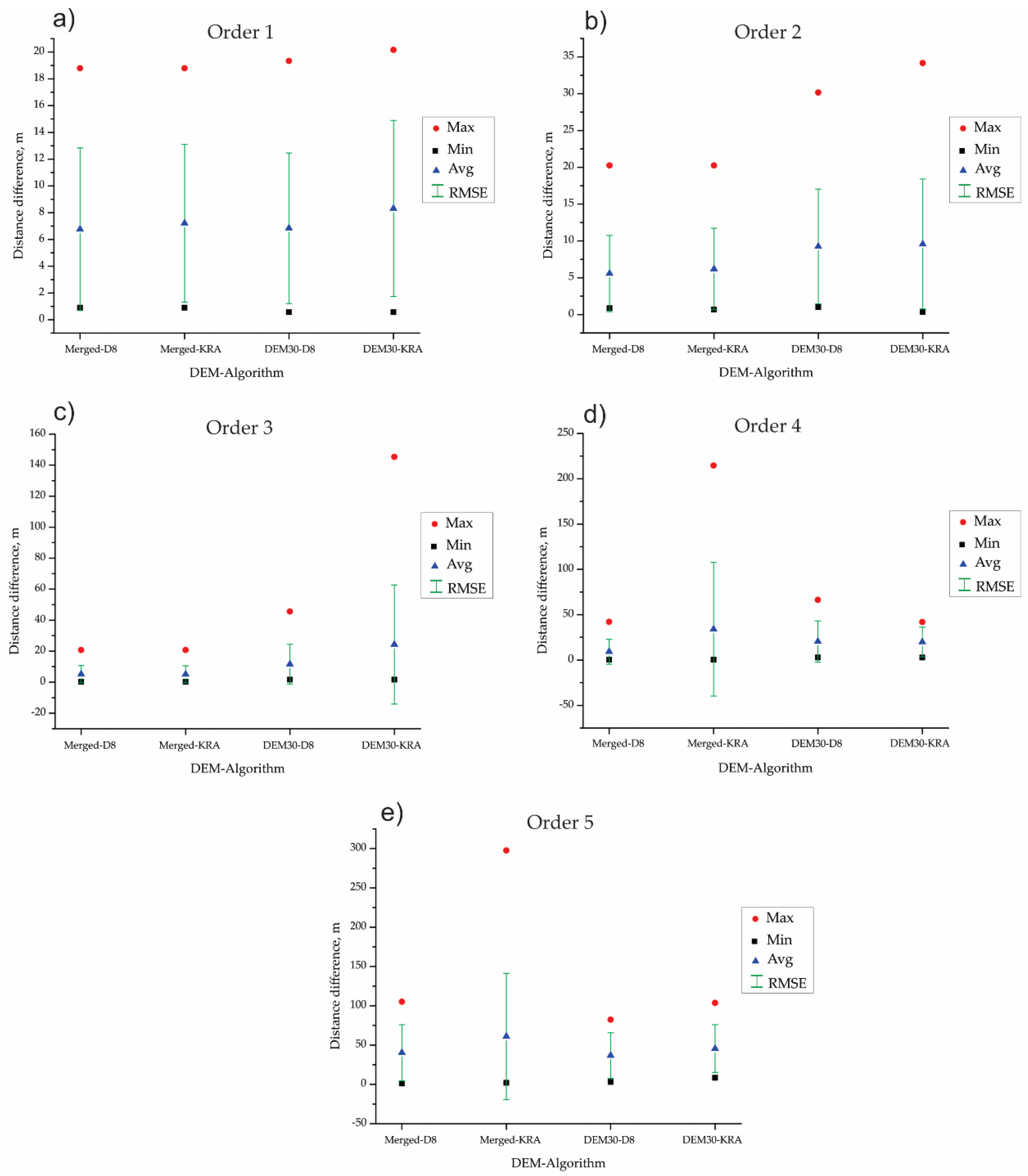
Order Merged DEMDEM 30 m MeanMax Difference
D8KRA D8 KRA
1No. Channels15916115015815711
Length (km)84.871786.017382.234587.762385.22155.53
2No. Channels7880745972.821
Length (km)46.487348.238146.781434.439143.986513.8
3No. Channels4647454044.57
Length (km)25.454725.29622.318621.733423.70073.72
4No. Channels1215181715.56
Length (km)7.36988.07197.93447.55757.73340.7
5No. Channels2222112419.813
Length (km)11.660311.46276.440410.39359.98925.22
All Number of Flow Channels (Nu)317325298298309.527
All Channel Lengths (Lu), in km175.8438179.086165.7092161.8858170.631217.2
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Dávila-Hernández, S.; González-Trinidad, J.; Júnez-Ferreira, H.E.; Bautista-Capetillo, C.F.; Morales de Ávila, H.; Cázares Escareño, J.; Ortiz-Letechipia, J.; Robles Rovelo, C.O.; López-Baltazar, E.A. Effects of the Digital Elevation Model and Hydrological Processing Algorithms on the Geomorphological Parameterization. Water 2022, 14, 2363. https://doi.org/10.3390/w14152363

AMA Style

Dávila-Hernández S, González-Trinidad J, Júnez-Ferreira HE, Bautista-Capetillo CF, Morales de Ávila H, Cázares Escareño J, Ortiz-Letechipia J, Robles Rovelo CO, López-Baltazar EA. Effects of the Digital Elevation Model and Hydrological Processing Algorithms on the Geomorphological Parameterization. Water. 2022; 14(15):2363. https://doi.org/10.3390/w14152363

Chicago/Turabian Style

Dávila-Hernández, Sandra, Julián González-Trinidad, Hugo Enrique Júnez-Ferreira, Carlos Francisco Bautista-Capetillo, Heriberto Morales de Ávila, Juana Cázares Escareño, Jennifer Ortiz-Letechipia, Cruz Octavio Robles Rovelo, and Enrique A. López-Baltazar. 2022. "Effects of the Digital Elevation Model and Hydrological Processing Algorithms on the Geomorphological Parameterization" Water 14, no. 15: 2363. https://doi.org/10.3390/w14152363

APA Style

Dávila-Hernández, S., González-Trinidad, J., Júnez-Ferreira, H. E., Bautista-Capetillo, C. F., Morales de Ávila, H., Cázares Escareño, J., Ortiz-Letechipia, J., Robles Rovelo, C. O., & López-Baltazar, E. A. (2022). Effects of the Digital Elevation Model and Hydrological Processing Algorithms on the Geomorphological Parameterization. Water, 14(15), 2363. https://doi.org/10.3390/w14152363

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop