1. Introduction
Hydropower is a type of renewable energy with flexible operation and mature technology, which is clean, low carbon, and has been favored by countries all over the world [
1,
2]. With more than 9000 hydropower dams registered across all continents, it supplies almost 70% of all renewable energy globally [
3,
4,
5]. As of the end of 2019, the world’s total installed hydropower capacity stood at about 1308 GW. Clean electricity generation from hydropower achieved a record 4306 TWh in 2019, the single greatest contribution from a renewable energy source in history. Fifty countries added hydropower capacity in 2019. Those with the highest individual increases in installed capacity were Brazil (4.92 GW), China (4.17 GW), and Laos (1.89 GW). The 11,233 MW Belo Monte project in Brazil became fully operational in 2019, while other major projects include the 1285 MW Xayaburi project in Laos, followed by the 990 MW Wunonglong and 920 MW Dahuaqiao projects in China [
6].
China’s total installed hydropower capacity climbed to 300 GW, accounting for 27% of the world’s installed hydropower capacity and 17% of China’s total installed power capacity [
7]. In 2015, China implemented a new round of power industry reform and established a medium- and long-term electricity market [
8]. Since 2017, China has organized and promoted the construction of spot markets in eight regions, including Southern China (starting from Guangdong Province) and Sichuan Province as the first batch of pilot projects [
9,
10]. It has been a developing trend for hydropower plants to participate in both the contract market and the day-ahead market [
11,
12]. Medium- and long-term contracts can lock the electricity price to avoid the risk of price fluctuation, but the price is generally low. The day-ahead market has created high profit opportunities for hydropower plants involved in the transaction, but the price volatility and uncertainty are strong, so there is a large profit risk. Because of the limitations of runoff, storage capacity, installed capacity, and other factors of hydropower plants, as well as the complex hydraulic and electric coupling relationship between cascade hydropower plants [
13], there is a close internal relationship between the contract market and the day-ahead market of power distribution. Medium- and long-term contracts signed by the hydropower generation company (HGenCo) are required be physically settled, which may affect the total revenue of the HGenCo and bidding space of the day-ahead market. Hence, how to determine the power generation of the cascade hydropower plants that participates in the contract market and day-ahead market to obtain the maximum benefit is an extremely difficult problem for the HGenCo.
Because the power output of hydropower plants is limited by reservoir inflow and storage capacity [
14], it is difficult to directly apply research on the participation of other types of power plants in the electricity market [
15,
16,
17] to the present problem. Scholars have carried out some research on the participation of hydropower plants in the electricity market, and most of them can be broadly divided into two categories: (1) The first category is the optimal decomposition of yearly or monthly contracted electricity. For example, Lu et al. [
18] proposed a long-term optimal operation method for cascade hydropower plants considering the allocation of power generation in multiple markets and the uncertainty of multiple variables. Li et al. [
19] developed an information gap decision-making theory-based method for optimal medium-term stochastic cascade hydropower operation in a multimarket environment, which considers the hydrological and economic uncertainties. Shrestha et al. [
20] studied the optimal management of hydropower resources in the medium term to maximize the expected revenue of a Nordic hydropower producer. Luo et al. [
21] developed an optimal scheduling model for long-term generation schedules of a cascade hydropower plant, which takes into account the uncertainty of multiple market prices. Chen et al. [
12] proposed an integrated solution methodology based on a multi-core parallel tabu genetic algorithm to provide the optimal assignment of bilateral contracts, considering the simulation of a hydro-dominated market. (2) The second category is the trading and dispatching strategy of hydropower plants in the day-ahead spot market. Yuan et al. [
22] proposed an efficient method to solve the benefit-based optimal self-scheduling of several cascaded hydro plants in a pool-based day-ahead electricity market. Conejo et al. [
23] addressed the self-scheduling of a hydro generating company to maximize the benefit from selling energy in the day-ahead market. Pousinho et al. [
24] established a stochastic mixed-integer linear programming (MILP) model to maximize the expected total benefit of a HGenCo in the pool-based day-ahead market. Kongelf et al. [
25] proposed a stochastic MILP approach to formulate a coordinated planning problem for a hydropower producer, considering the uncertainty of portfolio size in multiple electricity markets. However, there are few studies on the decomposition of monthly contracted electricity for cascade hydropower plants connected with the bidding in the day-ahead spot market.
The optimal decomposition of monthly contract electricity is part of the mid- and long-term optimal operation problem of cascade hydropower plants, which is a typical nonlinear programming (NLP) problem with multiple variables, high dimensionality, and complex constraints. At present, the methods of solving such an NLP problem can be divided into three categories: dynamic programming (DP) and its improved algorithm [
26], intelligent algorithms represented by particle swarm optimization algorithm [
27], and the mathematical programming methods [
28,
29]. The model constructed in this paper struggles to meet the requirement of having no aftereffect because it takes into account the uncertainty of the day-ahead market clearing price and involves the coupling relationship between monthly contract electricity and day-ahead market trading electricity. Thus, DP would be a hindrance in formulating the present problem as a multi-stage optimization problem. The intelligent algorithms would struggle to effectively handle the complex operation constraints and cannot guarantee a global optimal solution within finite iterations. The computational efficiency of NLP algorithm is affected by the initial solution and easily falls into the local optimal solution, and therefore are also unsuitable for solving the present problem. Among mathematical programming methods, the MILP approach becomes more and more mature and has been widely used in in the field of optimal reservoir operation due to its good performance in addressing complex constraints and producing stable calculation results [
30,
31,
32].
Aiming at the above problems, this paper emphasizes on the optimal decomposition model for the monthly contract electricity of cascade hydropower plants considering the bidding space in the day-ahead spot market. In this model, the generation benefits of cascade hydropower plant participating in both the monthly contract market and the day-ahead spot market are maximized. The uncertainty of the day-ahead market clearing price is modeled by a scenario analysis technique. An efficient and novel method, coupling a successive approximation (SA) approach and a MILP approach is then proposed to solve the proposed model. The rationality and validity of the proposed model and method are verified by an example of monthly contracted electricity decomposition plan of a cascade hydropower plant in China. The major contributions of this paper are clarified as follows: (1) An optimal scheduling model for cascade hydropower plants participating in both the monthly contract market and the day-ahead spot market is established, considering the uncertainty of the day-ahead market electricity price. This model mirrors the real-life situation of cascade hydropower plants participating in China’s electricity market. (2) SA along with a MILP approach is developed to solve this complex issue, which guarantees an optimal or near-optimal solution and significantly improves the solving efficiency.
The organization of the remaining parts of this paper is shown as follows. The mathematical formulation of this problem is established in
Section 2.
Section 3 provides the solution technique for the optimization model. The optimization results of the case study are presented and discussed in
Section 3. Finally, conclusions are drawn in
Section 4.
2. Mathematical Formulation
2.1. Problem Description
According to the trading rules of the electricity market, each hydropower plant signs the monthly electricity contract for the next month with the power purchasing user in the current month, and the contract stipulates the amount of electricity to be traded and the settlement price. In order to improve the consumption of renewable energy sources like hydropower, hydropower plants are allowed to participate in the day-ahead market according to the market situation and their own power generation capacity by self-scheduling during their operation within a month. In this case, the hydropower plant only declares the electricity quantity, not the price, and uses the market clearing price as the settlement price for the electricity quantity traded in the day-ahead market (i.e., as the price-taker). According to the settlement rules, the trading electricity in the day-ahead market will be settled the next day, while the monthly contract electricity will be settled at the beginning of the next month. Therefore, the monthly contracted electricity that has been agreed in advance by the hydropower plants can still bide in the day-ahead market, but the imbalanced portion of the monthly contracted electricity will be compensated to the power purchasing user according to the market rules or the contract agreement. At present, the medium- and long-term market is the energy market, and the power generation curves of the power plants are not agreed. Therefore, the power market operation institution or the power grid dispatching center will require the hydropower plants to report the water level process for the next month, the daily electricity generation, and the monthly and day-ahead market combined transaction electricity at the end of the month. To get more benefits, it is necessary for cascade hydropower plants to optimize the decomposition scheme for monthly contract electricity and the trading electricity in the day-ahead market based on their power generation capacity and predicted day-ahead market clearing price. Due to the inevitable deviation between the predicted day-ahead market clearing price and the actual value, it is challenging to develop a decomposition scheme for the monthly contracted electricity. Therefore, the uncertainty of the day-ahead market clearing price need to be well considered when the decomposition scheme for the monthly contract electricity of cascade hydropower plants is formulated.
In this paper, it is assumed that the day-ahead market clearing price is given. Moreover, cascade hydropower plants belong to the same HGenCo, and each hydropower plant participates in the market transaction independently. However, in order to give full play to the compensation and regulation function between cascade plants, all hydropower plants are uniformly operated by their owners.
2.2. Uncertainty Treatment of Day-Ahead Market Clearing Price
This section uses the scenario analysis technique to generate a series of scenarios to model and analyze the randomness of day-ahead market clearing price, in order to transform the stochastic optimization problem into an equivalent deterministic one.
- (1)
It is assumed that the forecasted error of the clearing price series obeys the normal distribution at any time period, where and are the mean and standard deviation of the forecasted error, respectively, and they satisfy that .
- (2)
The Latin Hypercube Sampling (LHS) method [
31] is adopted for generating the scenarios for the forecasted error of the day-ahead market price. In this method, the sampling probability distribution is stratified first, and then samples are randomly selected from each layer in turn, which can effectively improve the coverage degree of sampling samples to the distribution space of random variables.
- (3)
To adequately reflect the stochastic characteristics of the day-ahead market clearing price, more price scenarios will be generated through LHS, which mainly aims to avoid a low calculation accuracy due to a small number of scenarios. In this paper, the fast backward/forward method [
33] is adopted to balance the solving accuracy and efficiency, that is, to minimize the number of scenarios while maintaining the main characteristics of price scenarios.
2.3. Objective Function
The goal of optimal monthly contract electricity decomposition is to maximize the expected monthly income, whilst meeting various operational constraints. The cost of cascade hydropower plants is mainly construction cost; thus, power generation cost is not considered in this model. According to the electricity market trading rules, the monthly contract is a physical contract. This implies that although part of the monthly contracted electricity quantity of from hydropower plants can participate in the day-ahead market bidding, it needs to accept a certain penalty. The mathematical expression of the objective function is presented as follows:
where
denotes the target total monthly benefits (in CNY);
denotes the basic income according to the monthly electricity contract (in CNY);
denotes the extra income obtained from the excess settlement of the monthly contracted electricity (in CNY);
denotes the penalty cost for an insufficient amount of monthly contracted electricity (in CNY);
denotes the expected benefits of cascade power plants from participating in the day-ahead market (in CNY);
I and
i are the total number and index of plants, respectively;
T and
t denote the dispatching cycle and dispatching period, respectively;
and
are the monthly contract electricity and electricity price, respectively, of the hydropower plant i (in MWh and CNY/MWh);
denotes monthly contract electricity that actually completed (in MWh);
and
are the electricity prices corresponding to the excess and deficiency of monthly contracted electric quantity, respectively (in CNY/MWh). They satisfy that
, and
is the penalty coefficient of imbalanced contracted electricity;
S and
s are the total number and index of scenarios for day-ahead market clearing price;
denotes the probability of price scenario
s;
denotes the day-ahead market clearing price in scenario
s;
denotes the trading electricity of plant
i in the day-ahead market in time period
t (in MWh).
2.4. Constraints
- (1)
Water balance constraints
where
denote the total inflow of plant
i in period
t (in m
3/s);
denotes the total water discharge of plant
i in period
t (in m
3/s);
is the duration of period
t (in h);
is the water storage at the end of period
t (in m
3).
- (2)
Hydraulic connection constraints
where
denote the local inflow of plant
i in period
t (in m
3/s);
and
denote the generating water flow and water spillage, respectively (in m
3/s). Note that
is set to 0 in this paper because hydropower curtailment is generally not allowed according to China’s clean energy consumption policy.
- (3)
Water level constraints
where
and
denote the upper and lower bounds of the reservoir water level (in m);
is the reservoir water level in period
t (in m);
is the initial water level and
is the target water level at the end of the planning horizon (in m).
- (4)
Water discharge constraints
where
and
denote the lower and upper bounds of the total water discharge of plant
i, respectively (in m
3/s).
- (5)
Power output constraint
where
and
represent the upper and lower bounds of the power output of plant
i, respectively (in MW);
represents the power output of plant
i in period
t (in MW), which satisfies Equation (13).
where
is the output factor of plant
i, and is related to the water head [
34,
35];
is the water head of plant
i in period
t (in m).
- (6)
Water head constraints
where
denotes the tailwater level in period
t (in m).
- (7)
Forebay water level–water storage relationship
represents the forebay water level–water storage relationship function of plant
i.
- (8)
Tailwater level–water discharge relationship
represents the tailwater level–water discharge relationship function of plant
i.
- (9)
Constraints on trading electricity in the day-ahead market
The above formula indicates that the trading electricity of plant i in the day-ahead market in time period t shall not exceed the power generation of the day.
- (10)
Trading electricity constraints
The above formula indicates that the sum of the actually completed monthly contracted electricity and the trading electricity in the day-ahead market of the current month shall be equal to the total monthly power generation of the power plant.
3. Solving Technique
According to the analysis in
Section 1, the optimized model is nonlinear and non-convex, making it difficult to solve by conventional algorithms. To solve such a complex problem, a good idea is to approximate each nonlinear function by a series of linear functions. Hence, in this model, the nonlinear functions are linearized through several linearization techniques, so that the original NLP model is transformed into an MILP formulation. Based on this, a mature optimization solver can be adopted to solve the MILP model.
In the established model, Equations (3) and (4) contain a
function. The water head function (i.e., Equation (15)) and power generation function (i.e., Equation (13)) are also nonlinear functions. Considering that the linear approximation of the water head constraint has been well established by many studies [
29,
30], this work aims to study the linearization of the objective function (Equations (3) and (4)) and the power production function (Equation (13)).
3.1. Linear Approximation of the Objective Function
We introduce a binary variable
, and Equations (3) and (4) can be converted into the following constraints.
where
M is a very large number;
is a binary indicator variable, which is equal to 1 if the amount of monthly contracted electricity that is actually settled is higher than the amount signed off, and otherwise, it is equal to 0.
Equations (20) and (21) are still nonlinear because there is still multiplication of integer variables and continuous variables (i.e.,
). Hence, we introduce two auxiliary variables,
and
, to convert Equations (20) and (21) into the following linear constraints.
When , i.e., the monthly contracted electricity that is actually settled is higher than the amount signed for in the contract, is equal to 0 because of Equations (29) and (30). is then equal to 0 according to Equation (25), which is consistent with the fact that the penalty cost is 0 when then monthly contracted electricity has been settled. Equations (24) and (20) are equivalent at this time due to the constraint of Equation (32). Similarly, when , is equal to 0 and Equations (25) and (21) are equivalent. To sum up, the combination of linear constraints in Equations (22)–(30) is the equivalent transformation of Equations (3) and (4).
3.2. Linear Approximation of the Power Generation Function
The output factor
is closely related to the water head
, while
depends on the generation water flow [
34,
35]. Hence, the power generation function is a very complicated nonlinear function for the generation water flow. If the generation water flow is chosen as a decision variable and the net water head is fixed, the power generation function will become a linear one. Based on the above analysis, the successive approximation (SA) approach is introduced, which is an efficient and practical method to deal with complex nonlinear optimization problems [
36,
37,
38]. The basic idea of this method is to solve a series of fixed water head subproblems using the MILP approach, and the solution for the original complex problem can be obtained after successive calculations. A flow chart for the proposed SA approach is illustrated in
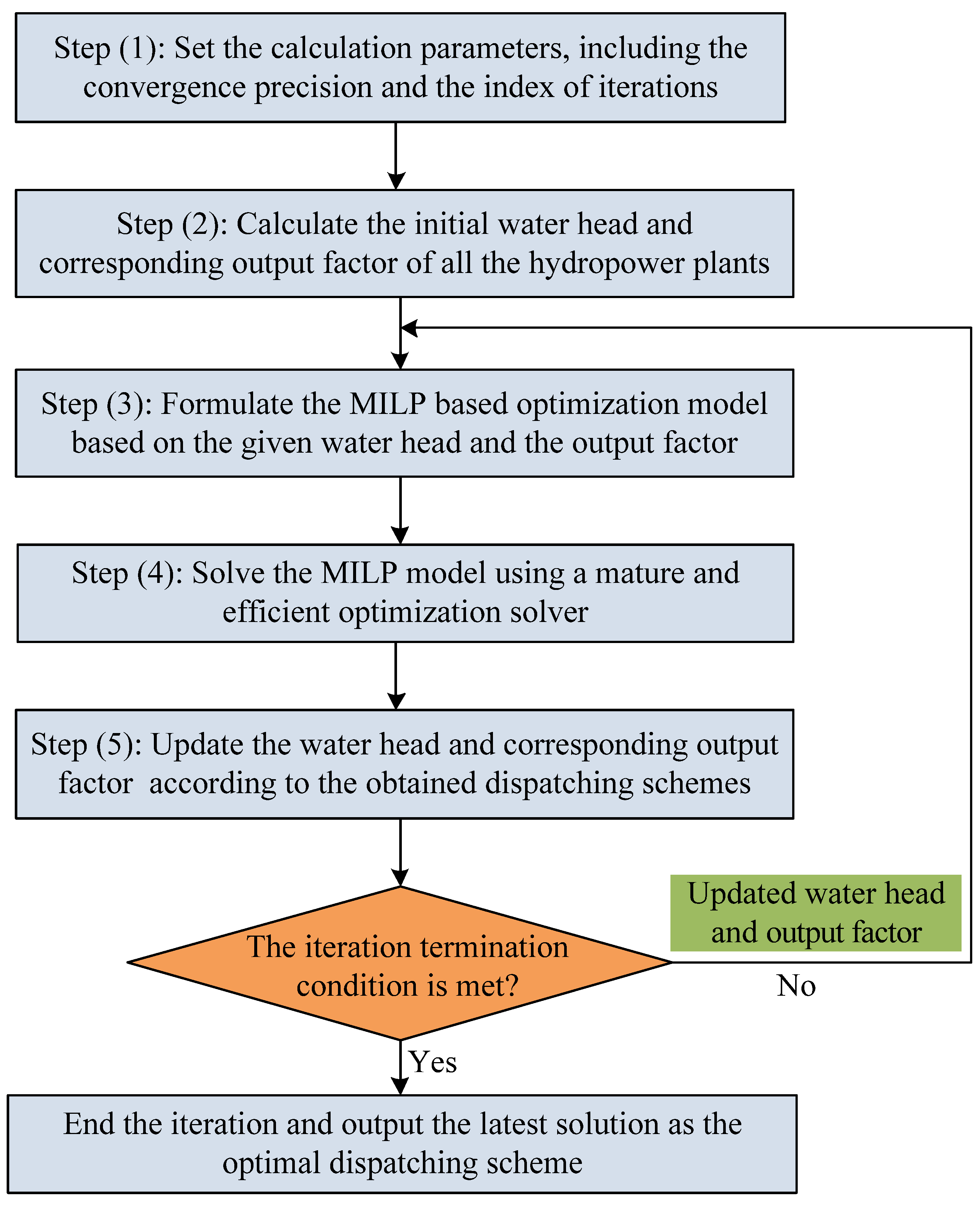
Figure 1, and the specific procedures are as follows.
- (1)
Set the convergence precision of the SA approach and let the index of iterations n = 1.
- (2)
The initial solution has a great influence on the computational efficiency of the SA approach. Thus, to enhance the convergence speed, the initial water head of all the hydropower plants from upstream to downstream
is generated using Equations (31)–(33). The initial output factor of each hydropower plant
is then calculated using Equation (14).
where
and
denotes the total discharge volume and average water discharge, respectively, during the scheduling horizon.
is the average water head of hydropower plant
i during the scheduling horizon.
- (3)
Based on the given water head and the output factor of each hydropower plant, the MILP based model for the optimal decomposition of monthly contracted electricity for cascade hydropower plants is established by using the linearization techniques presented in
Section 3.1 and Ref. [
30].
- (4)
An efficient optimization solver is adopted to solve the MILP model, and the dispatching schemes, including the water discharge, forebay water level, and power output of each hydropower plant, can be obtained.
- (5)
Calculate the new water head and corresponding output factor after the nth iteration using Equations (14)–(17). Judge if . If true, end the iteration and output the latest solution as the optimal dispatching scheme, otherwise let n = n + 1 and repeat steps (3)–(5).
4. Case Studies
In this paper, the monthly contracted electricity decomposition for two cascade hydropower plants was taken as an example to test the proposed model and method. The cascade power plants involved in the calculation include two hydropower plants, upstream plant A and downstream plant B, whose main operating parameters are shown in
Table 1. The actual operational conditions of the cascade hydropower plants during March 2020, including local inflow, monthly contract electricity, contract price, water level at the beginning of month, and control water level at the end of month, were considered as references for the case study. The day-ahead market clearing price is forecast by each hydropower plant at the end of February 2020. The operational control conditions of each hydropower plant are shown in
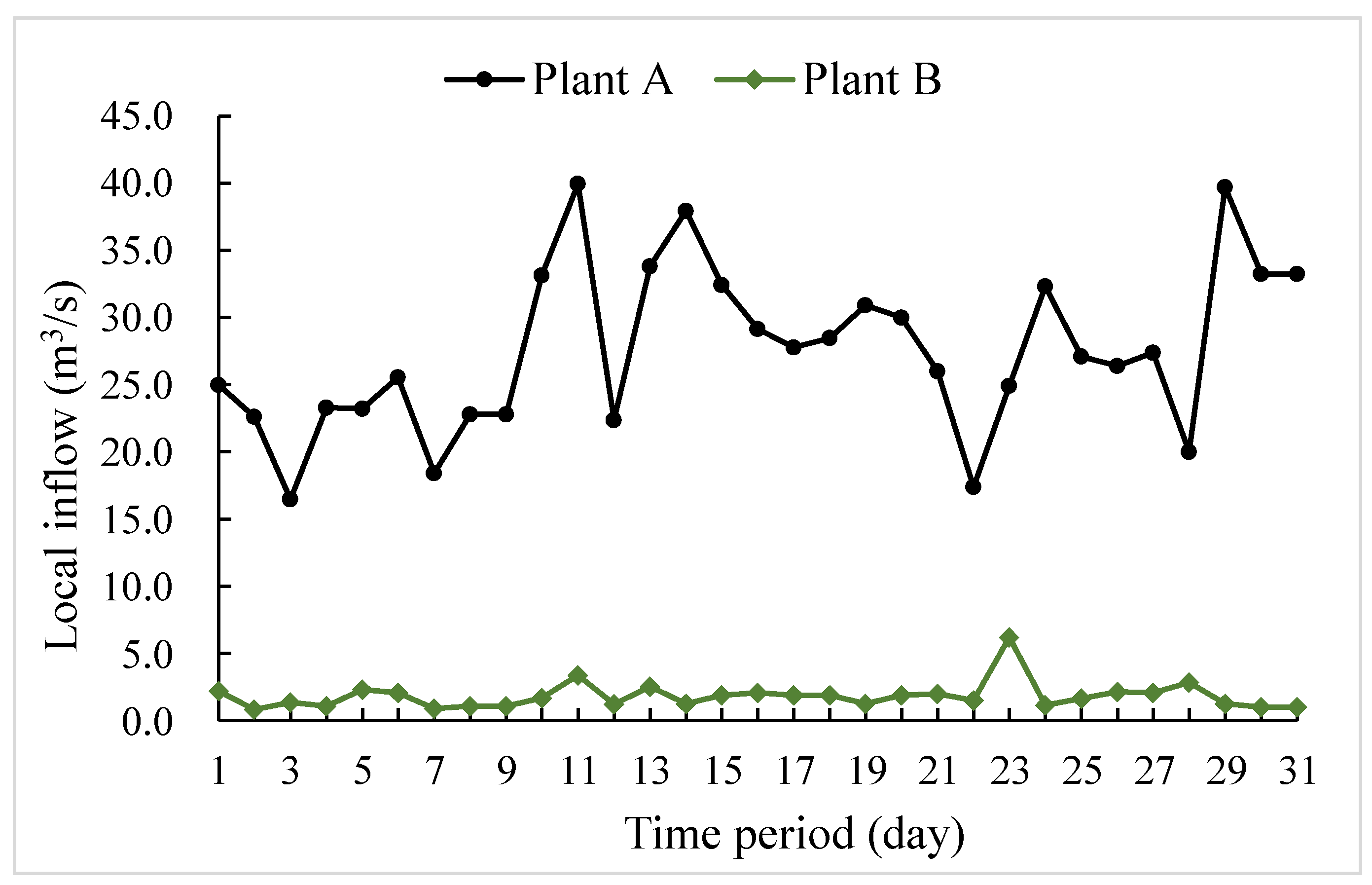
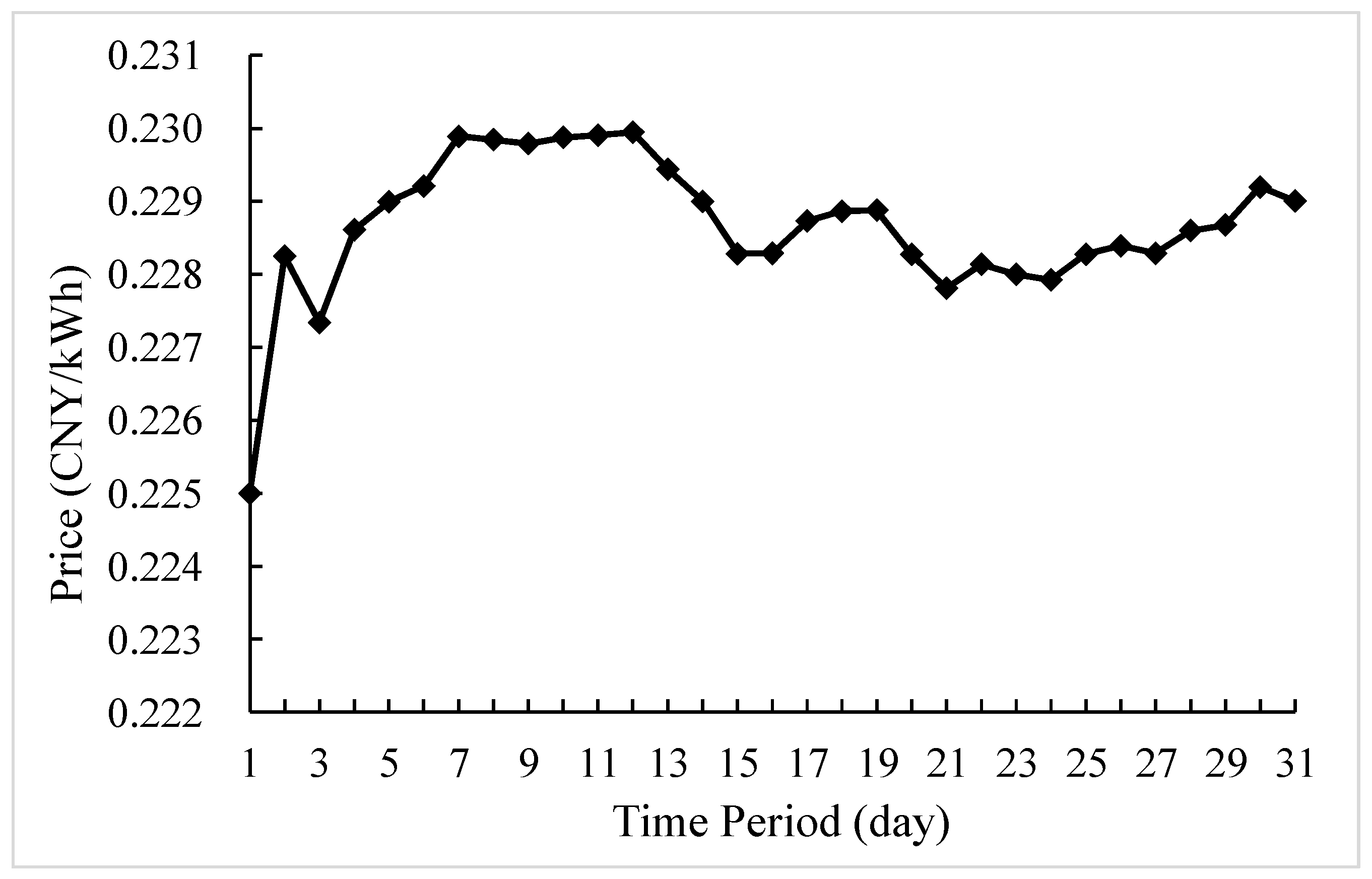
Table 2. The local inflow of each plant and the forecasted day-ahead market clearing price are shown in
Figure 2 and
Figure 3, respectively. The allowable deviation of control water level at the end of the month was set to 0.01 m.
In total, 300 scenarios were generated using the LHS method, and the fast backward/forward method was used to reduce the number of scenarios to 50. In the calculation, the scheduling cycle was 1 month, and the dispatching period was 1 day. The penalty coefficient for imbalanced contracted electricity was set as 0.3. A commercial optimization software package, LINGO solver, was used for solving the proposed model, and the computing environment was a ThinkPad PC with quad-core CPU and 16 GB memory.
The total revenue of the cascade hydropower plants is 578.92 × 104 CNY, including 286.62 × 104 CNY from the monthly contracted electricity revenue and 291.3 × 104 CNY from the day-ahead market trading electricity revenue. The calculation time of the model is 137 s, which fully meets the timeliness requirements of medium- and long-term scheduling of cascade hydropower plants, reflecting the high solving efficiency of the optimization model established in this paper.
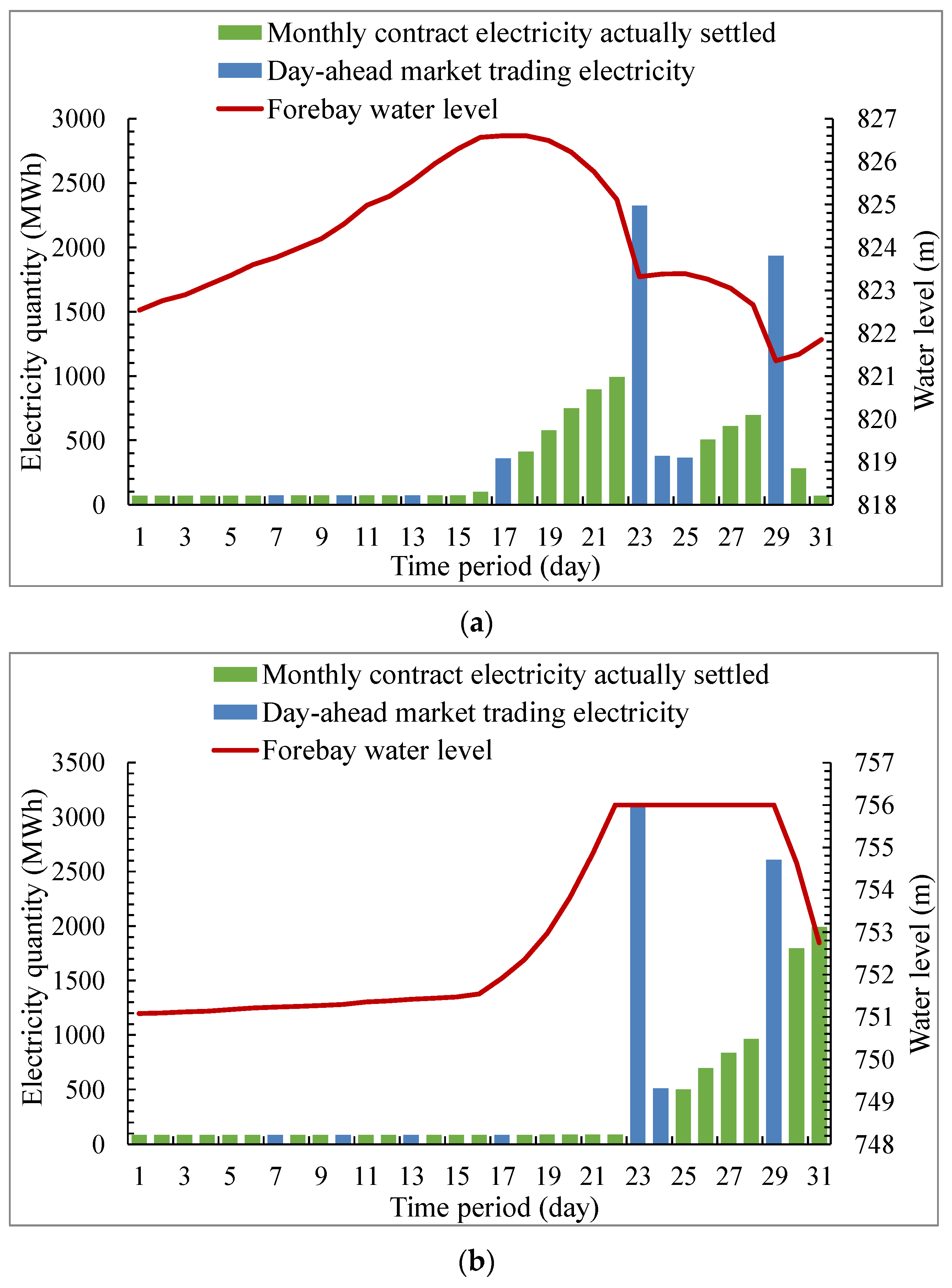
The power generation and water level process of each hydropower plant obtained by the optimized calculation are shown in
Figure 4. As can be seen, the upstream plant A can make full use of its own seasonal regulating storage capacity to realize the temporal and spatial redistribution of runoff, so as to respond to the change of day-ahead market clearing price and improve its own income. During periods with high electricity prices, plant A uses its limited power generation capacity to participate in day-ahead market trading and increase its power output as much as possible to generate more electricity. Conversely, in periods with low electricity prices, plant A only generates electricity with the minimum generating water flow, and almost all the generated electricity goes towards the settlement of the monthly contracted electricity due to the penalty that can be incurred for an imbalance from the contracted electricity. Downstream plant B needs the upstream plant for flow compensation due to its small, regulated storage capacity and almost no local inflow. In periods with low electricity prices, plant B only generates electricity with the minimum flow, continuously raises the water level for water storage, and increases the water head. When electricity prices are high, the highest possible water level is maintained at plant B in order to participate in day-ahead market trading and maximize power generation before the water level gradually falls back to the control water level at the end of the month.
The benefits of the stochastic scheduling model established in this paper (hereinafter referred to as Model (1)), are compared with the traditional deterministic scheduling model based on predicted values (hereinafter referred to as Model (2)). In Model 2, the predicted value of day-ahead market electricity price is taken as the determined input value for scheduling. The two models adopt the same control objectives and constraints, and a comparison of the results is shown in
Table 3. It can be seen that, on the basis of guaranteeing the monthly contracted electricity, the total power generation and the total generation revenue of the cascade hydropower plants optimized by Model 1 is 2720 × 10
4 kWh and 578.92 × 10
4 CNY, respectively, while under Model 2, the values are 2731 × 10
4 kWh and 567.49 × 10
4 CNY, respectively. Compared to the deterministic model, the total revenue of the proposed model increases by 2% when power generation is reduced. This shows that when making a monthly contract electricity decomposition plan, taking into account the uncertainty of the day-ahead market clearing price can significantly increase the expected benefits of the HGenCo.
To verify the impact of penalty coefficient for imbalanced monthly contracted electricity (
τ) on the optimal scheduling results, optimization results with different
τ values are compared and analyzed, which are presented in
Table 4. When
τ is small (
τ = 0.1 or 0.2), the negative deviation penalty price of monthly contracted electricity of plant A and B is generally lower than the day-ahead market clearing price. In this case, cascade hydropower plants will choose to violate the monthly electricity transaction contract and compensate the contract buyer and allow for more generation to participate in the day-ahead market transaction to obtain higher profits. However, when
τ = 0.3 or 0.4, the negative deviation penalty price of the monthly contracted electricity of plant A and B is relatively high. In this case, the cascade hydropower plants will fulfill the monthly contract, and only the remaining generation will participate in the day-ahead market. Therefore, the dispatching agencies should analyze all possible situations when making power trading rules and formulate reasonable penalty coefficients for imbalances of the monthly contracted electricity so as to avoid a large number of defaults and ensure the long-term stable operation of the electricity market.
5. Discussion
As shown in
Figure 3, the periods with the highest forecasted prices are days 7–13. However, there is always an inevitable deviation between the predicted day-ahead market clearing price and the actual value. In this paper, 50 scenarios are generated to represent all possible actual day-ahead market clearing prices. After careful analysis, we found that in most of the scenarios, the high electricity price is mainly concentrated in days 22–30. To obtain higher expected power generation benefits, it is recommended to participate in day-ahead market trading and increase its power output as much as possible to generate more electricity during days 22–30.
To the best of our knowledge, there are very few studies on the decomposition of monthly contracted electricity for cascade hydropower plants connected with the bidding in the day-ahead spot market. Thus, we cannot find other relevant optimization models and compare them. The deterministic scheduling model based on predicted values is usually adopted by the operators of the hydropower plants in practical engineering applications, and the deterministic scheduling model is compared with the proposed optimization model as benchmark model in many literatures [
39,
40,
41]. For deterministic operation, we considered the day-ahead market clearing prices to be a known input of the operation model, assuming that the market clearing prices could be forecast accurately. However, there is always an inevitable deviation between the predicted day-ahead market clearing price and the actual value. To consider the impact of forecast errors on the decision-making process, the stochastic model was adopted to produce operational decisions using multiple day-ahead market clearing price processes to characterize forecast uncertainty. Since the operational decisions were required to satisfy all the scenarios, the total generation profit of the stochastic model is inevitably affected and is only 2% higher than those of deterministic model. However, as the forecast errors of the day-ahead market clearing price are inevitable in actual operation, the proposed model can avoid solutions that imply small profits or major costs, hedging against risk and uncertainty.
As a consequence of the market power of some producers, two types of generation companies can be listed: price-takers [
42] and price-makers [
39]. Price-takers accept market clearing prices without being able to affect them. Instead, price-makers have market power, thus being able to influence market prices to increase profit. In competitive electricity markets, the profit of the generation companies depends not only on their own decisions, but also on the decisions of the other companies. Under perfect competition, the market share of every generation company is small, and no company can affect the market price. In this case, every company takes market prices for granted when devising its offering strategy, acting as a price-taker. However, some generation companies may have a relatively high market share and are capable of exercising their market power, influencing market prices for their own benefit. It means that a perfect competition model cannot be used, since the companies act as price-makers. When devising its offering strategy, a price-maker hydro producer takes into account the fact that it can affect market prices with its offers. Our focus is to obtain the mid-term scheduling strategy of a price-taker hydropower generation company (HGenCo). The case studies in this paper include two hydropower plants with a total installed capacity of 250 MW. The market share of this HGenCo is small and cannot affect the market price.
The penalty coefficient for imbalanced monthly contracted electricity (τ) is very important for the smooth settlement of the monthly contracted electricity. When τ is small (τ = 0.1 or 0.2), cascade hydropower plants will choose to violate the monthly electricity transaction contract and allow for more generation to participate in the day-ahead market transaction to obtain higher profits. While when τ = 0.3 or 0.4, the cascade hydropower plants will fulfill the monthly contract. The value of penalty coefficient depends on the interest tendency of market managers. If the market managers hope to avoid large defaults on medium-and long-term contracts, they can set the penalty coefficient to 0.3 or 0.4. If they want to encourage power plants to participate freely in various markets to reap greater benefits, they can set the penalty coefficient very low, such as 0.1.
The establishment of an optimal scheduling model is based on the operation mechanism of medium- and long-term market and day-ahead spot market. China’s power supply structure and power consumption characteristics have certain uniqueness, and the construction of China’s electricity market is still in the initial stage, so China’s electricity market mechanism has certain differences from other countries. For example, the Nordic electricity market has developed a model of financial contracts plus spot trading. The time span of trading in the financial contract market includes weeks, quarters, and years. Financial contracts do not require physical delivery and are primarily used as a means of price hedging and risk management. This means that, after signing a medium- and long-term contract, the power plants can participate in the spot market without default penalty. Hence this model cannot be generalized to other countries’ markets in our opinion. However, it can provide some reference for other countries that are in the initial stage of electricity market construction, such as India and Brazil.
National and foreign direct investments are needed for economic developments and national projects, including hydropower works, mainly in relation to less-favored economic areas where social risk could appear [
43]. Such hydropower plants are useful to alleviate areas with poverty and solve urban and rural issues of electricity for poor communities [
44,
45]. However, when more cascade hydropower plants are included in the proposed model, the computational efficiency will be reduced to some extent, and the calculation may take several hours due to the consideration of the day-ahead market clearing price uncertainty and multiple iterations of the SA approach. Hence, model decomposition techniques and parallel techniques should be integrated into the solution method in the future research to further improve the solution efficiency and increase the engineering application value of the proposed model.
6. Conclusions
In view of the coexistence of the medium- and long-term contract markets and the day-ahead spot market in China’s electricity market, an optimal decomposition model for the monthly contracted electricity of cascade hydropower plants is established, considering the bidding space of day-ahead market. The validation of the proposal model is applied to the decomposition of the monthly contracted electricity of China’s cascade hydropower plants as an example. The following conclusions are drawn:
- (1)
A scenario analysis technique and several effective linearization strategies are put forward to address the uncertain and nonlinear factors in the optimization model, including the uncertain day-ahead market clearing price, the nonlinear objective function, and the nonlinear power generation function of each hydropower plant. For such a complex research problem, the combination of the SA approach and MILP approach is computationally efficient with a calculation time of 137 s.
- (2)
The total revenue obtained from the proposed stochastic optimization model is 578.92 × 104 CNY. Compared to the deterministic model, the total revenue of the proposed model increases by 2% when power generation is reduced. Furthermore, as the forecast errors of the day-ahead market clearing price are inevitable in actual operation, the proposed model can avoid solutions that imply small profits or major costs, hedging against risk and uncertainty.
- (3)
The penalty coefficient for imbalanced monthly contracted electricity (τ) is very important for the smooth settlement of the monthly contracted electricity. When τ is small (τ = 0.1 or 0.2), cascade hydropower plants will choose to violate the monthly electricity transaction contract and allow for more generation to participate in the day-ahead market transaction to obtain higher profits. While, when τ = 0.3 or 0.4, the cascade hydropower plants will fulfill the monthly contract. Therefore, market managers need to formulate a reasonable penalty coefficient to avoid a large number of defaults and ensure the long-term stable operation of the electricity market.
At present, China’s electricity market construction is still in the preliminary stage, and many factors are still to be studied and tested in practice. Due to the complex operation constraints of cascade hydropower plants and multiple uncertainties, it is challenging to develop a decomposition scheme for the monthly contracted electricity of cascade hydropower plants. This paper can provide guidance for China’s hydropower participation in the electricity market, and also provide reference for other countries that are in the initial stage of electricity market construction, such as India and Brazil. In addition, the uncertainty of runoff and the accelerated solution method of the model will be further considered in the future study.