Flow at an Ogee Crest Axis for a Wide Range of Head Ratios: Theoretical Model
Abstract
:1. Introduction
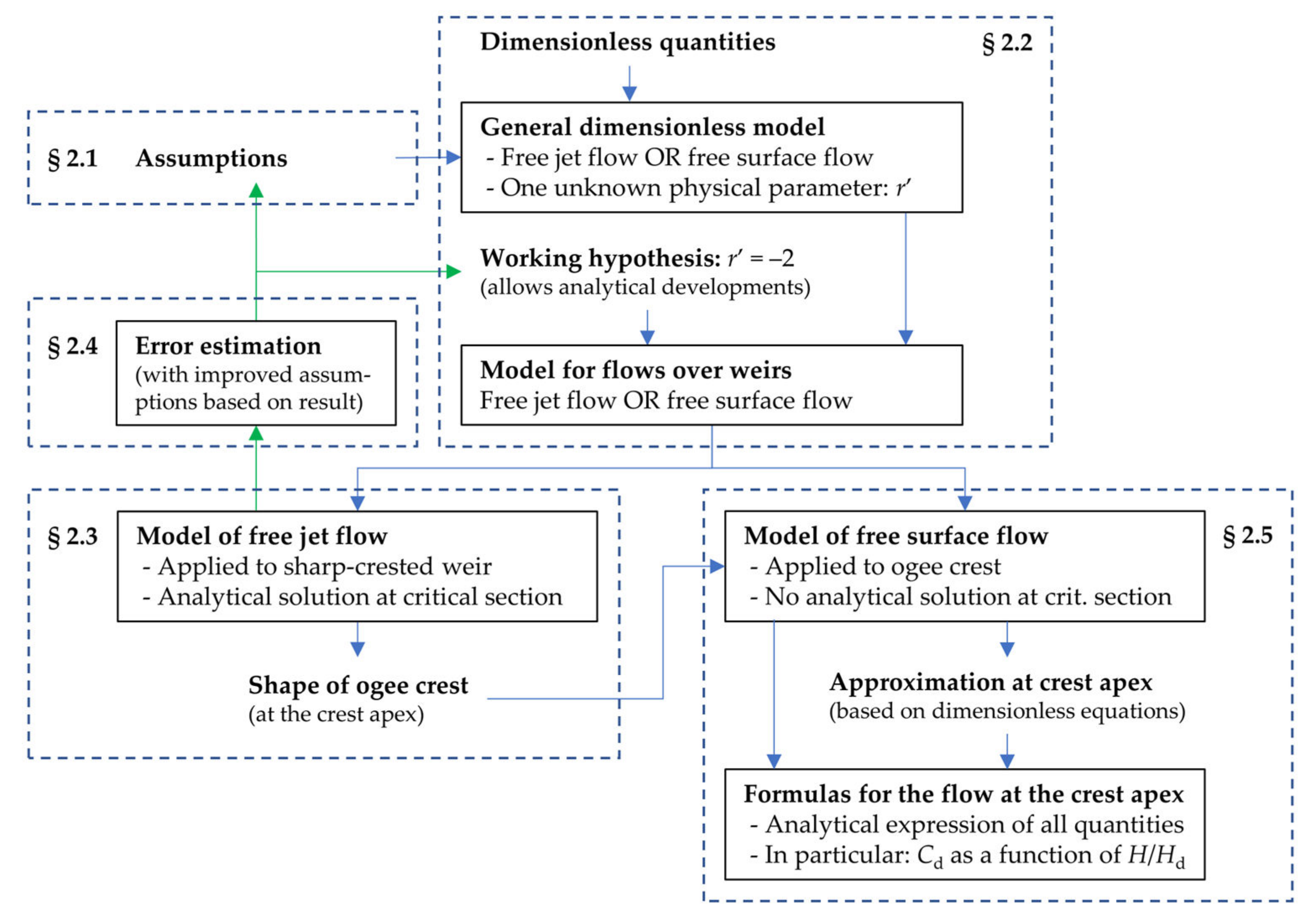
2. Model Development
2.1. Assumptions
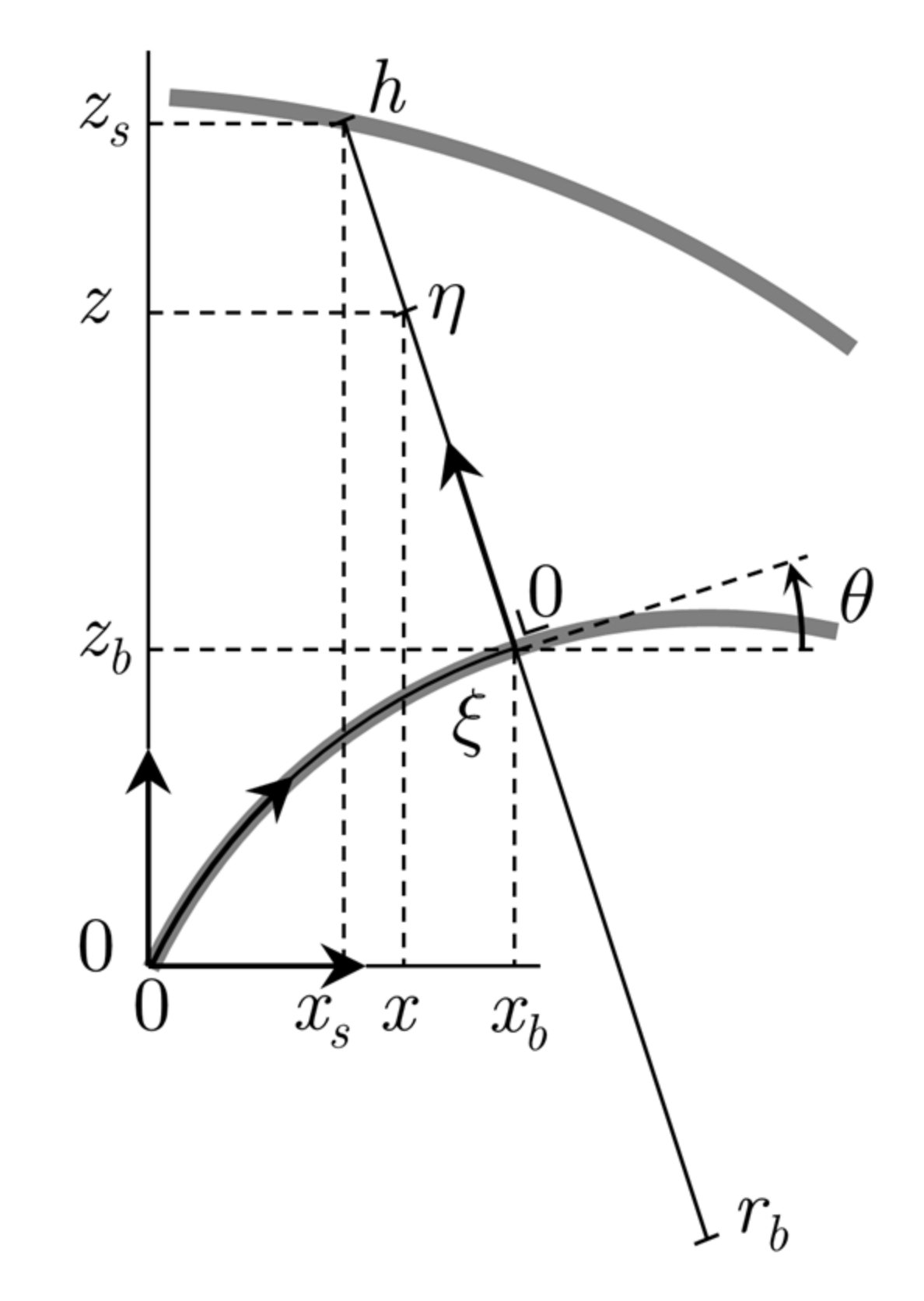
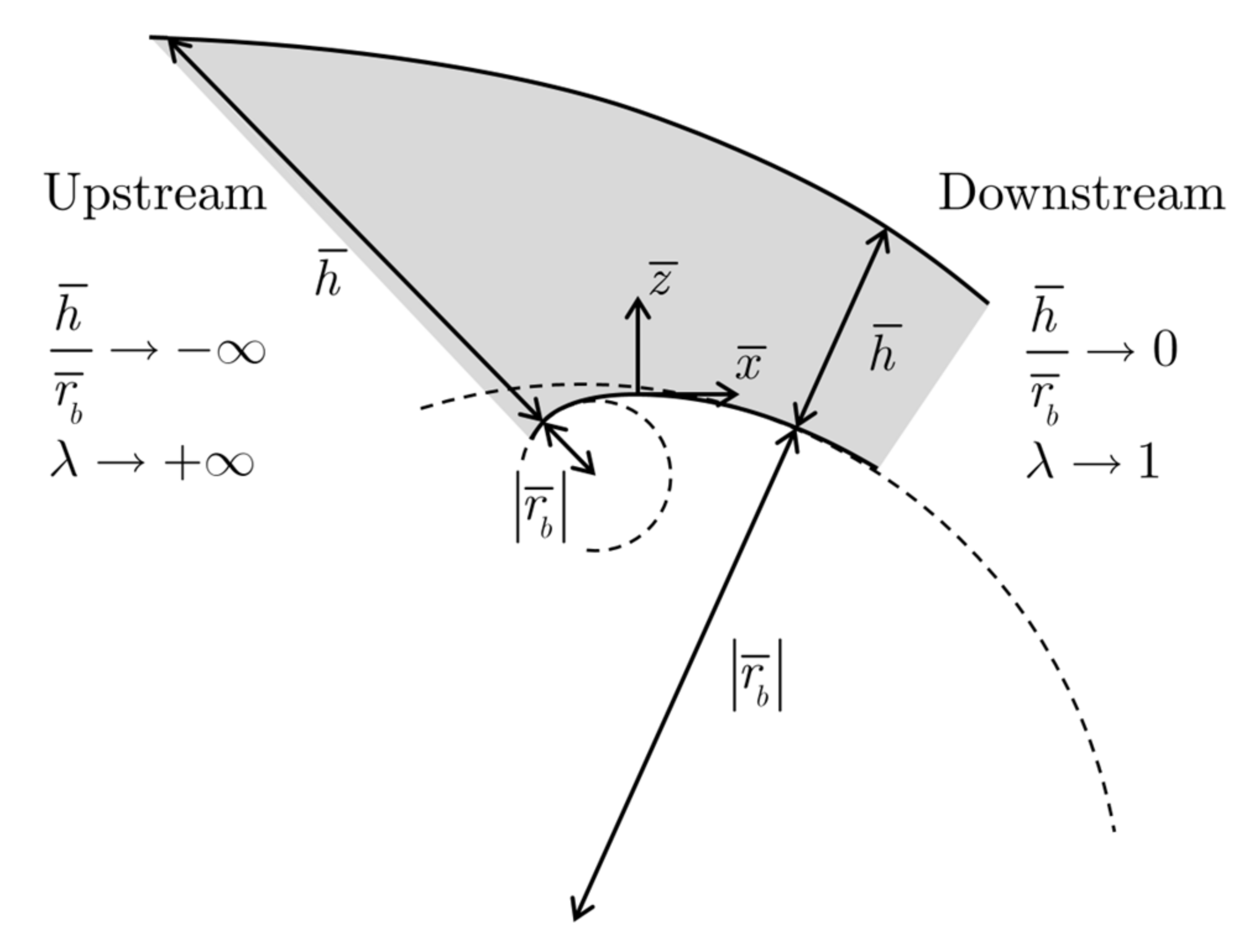
2.1.1. Curvilinear Coordinate System
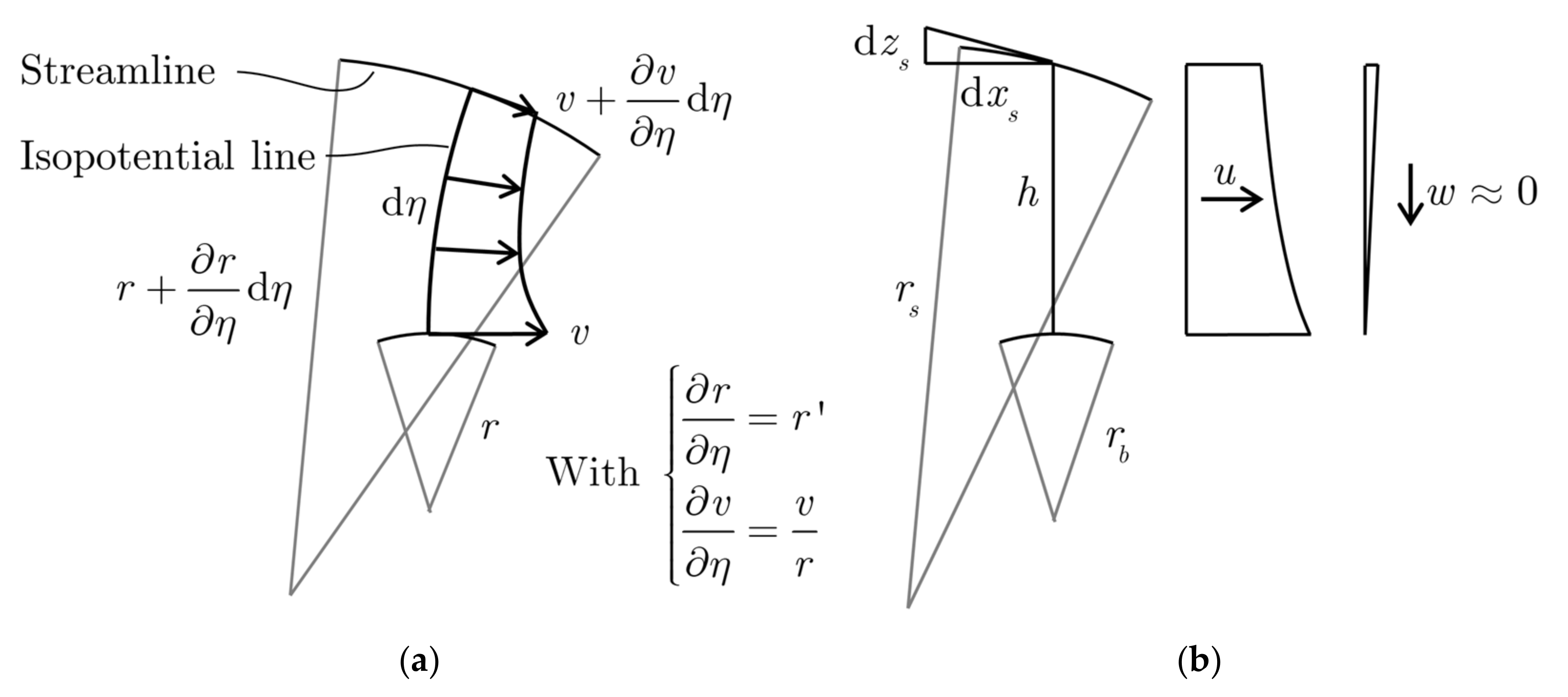
2.1.2. Conservation Principles
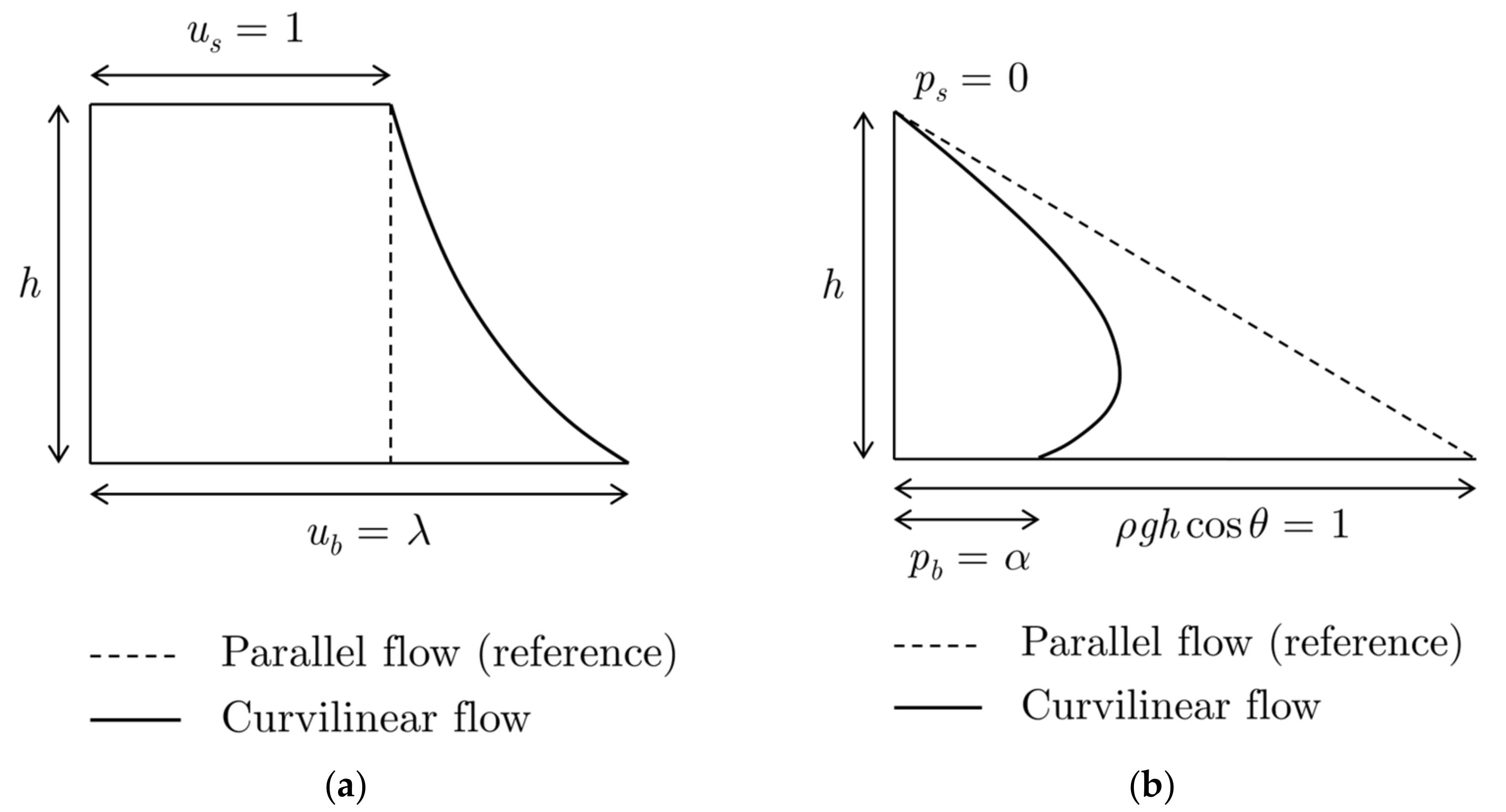
2.1.3. Velocity and Pressure Distributions
2.1.4. Upper and Lower Boundary Conditions
- A lower boundary whose pressure is atmospheric, that is:
- A lower boundary whose shape is imposed by a fixed geometry, which means that the functions xb(ξ) and zb(ξ) in Equation (4) and all their derivatives are known prior to the computation of the flow.
2.2. Dimensionless Quantities and Equations
2.2.1. Velocity and Pressure Distribution Coefficients
2.2.2. Equations with λ and α as Unknowns
2.2.3. Design Head, Hd, as a Reference for all Other Dimensionless Variables
2.2.4. Set of Dimensionless Equations
2.2.5. Working Hypothesis on r′
2.3. Flow over a Sharp-Crested Weir
2.4. Assessment of the Consistency of the Model
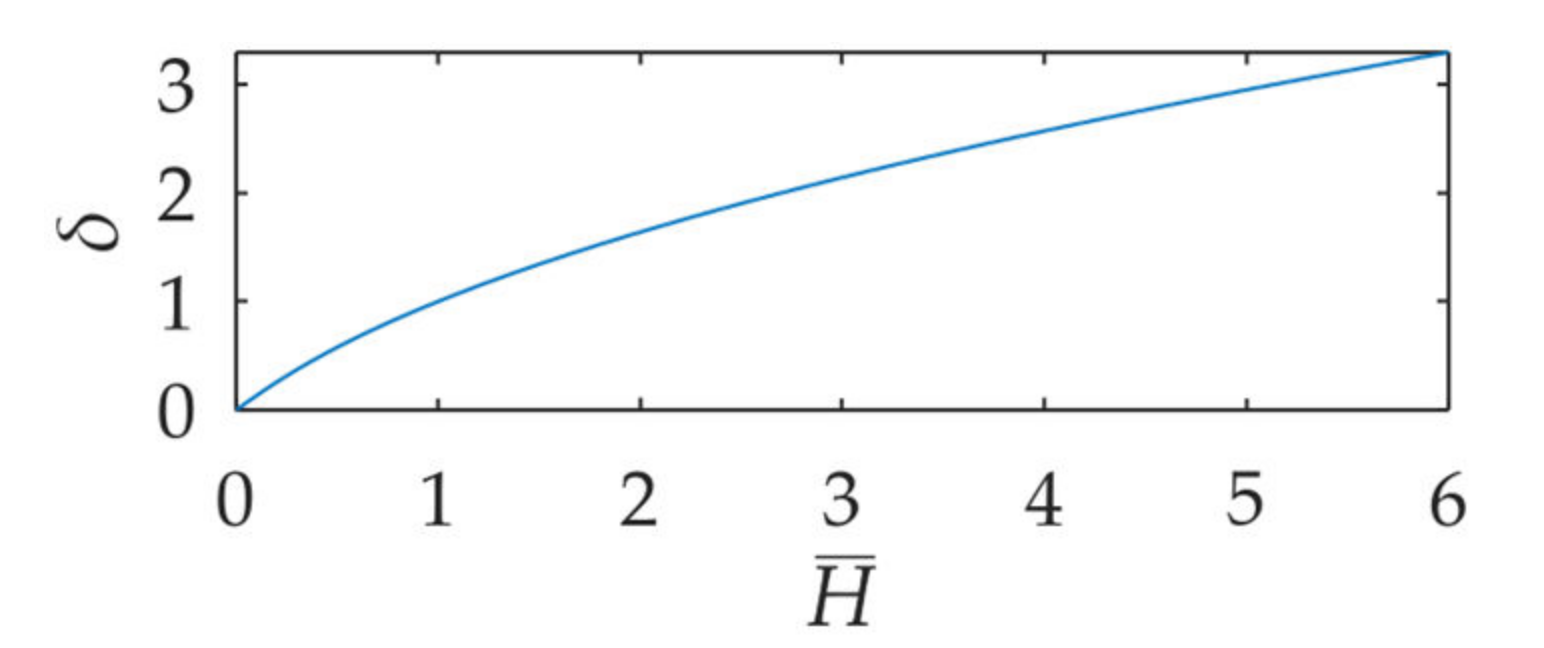
2.4.1. Slope of the Upper Flow Boundary and Assumption w = 0
2.4.2. Curvature of the Upper Flow Boundary and Assumption r′ = −2
2.5. Flow over an Ogee Crest
2.5.1. System of Equations
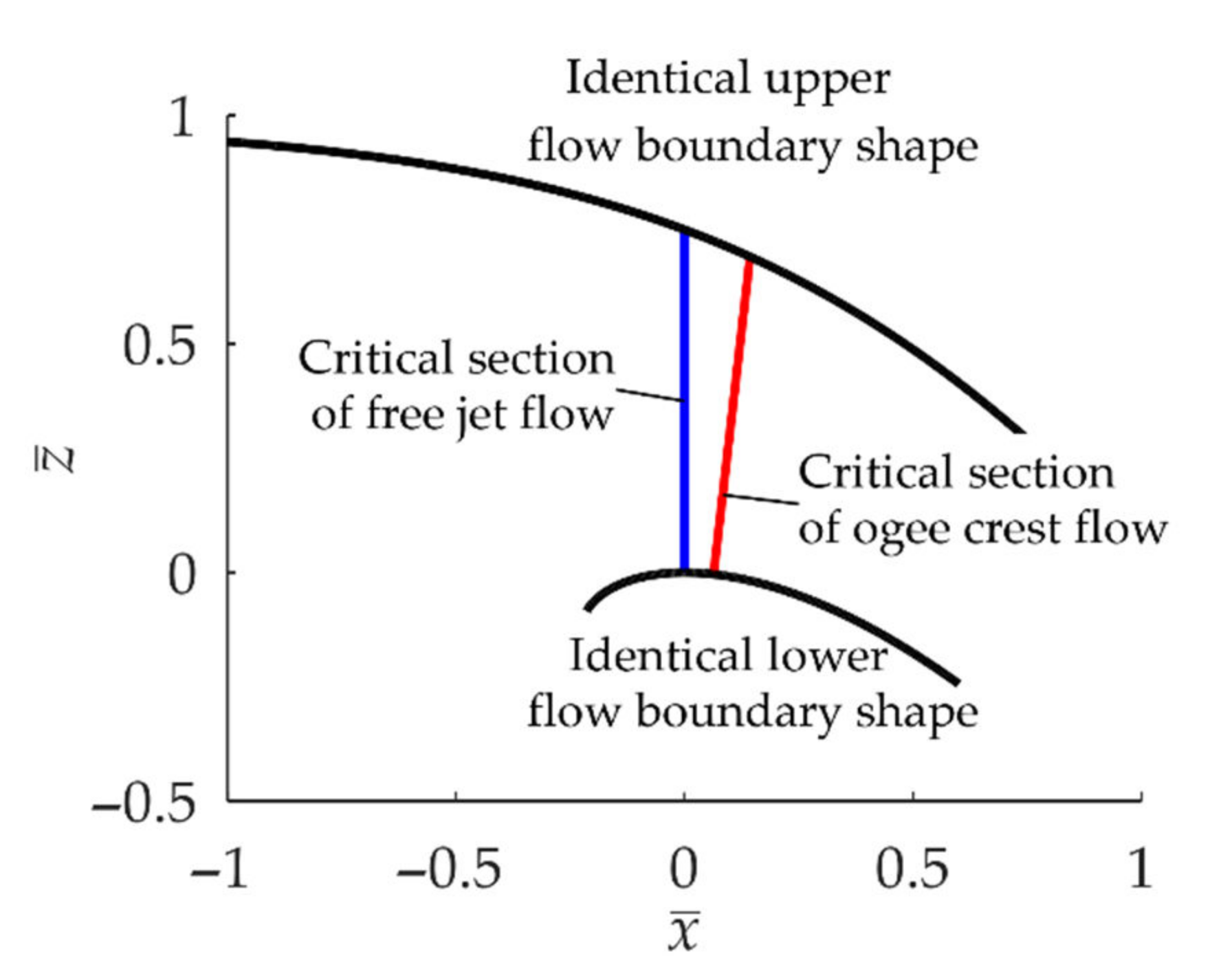
2.5.2. Approximation at the Crest Apex
2.5.3. Formulas for the Flow at the Crest Apex of an Ogee Crest
3. Model Validation
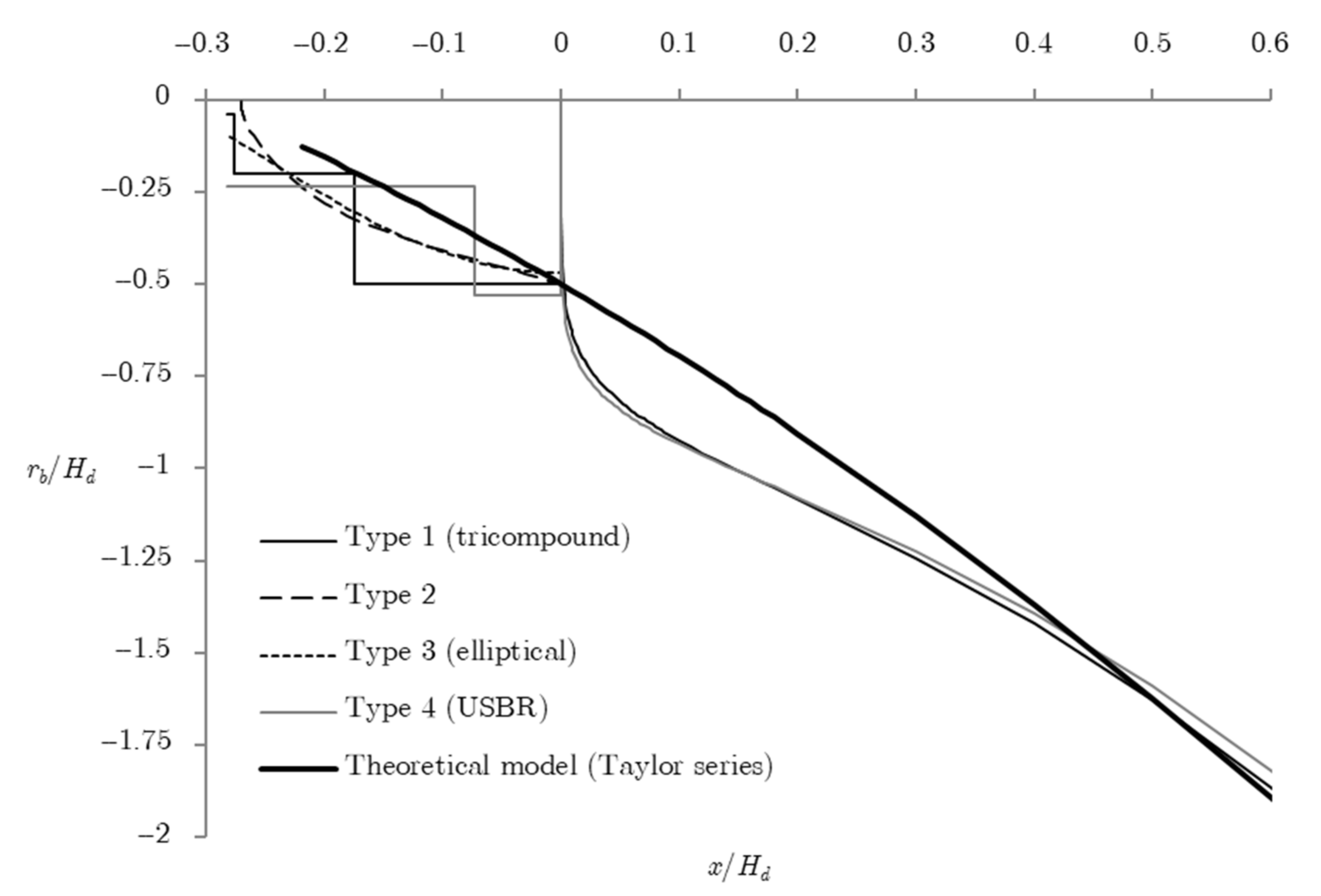
3.1. Ogee Crest
- Type 1: a WES profile with an upstream quadrant composed of three circles of radii 0.04 Hd, 0.2 Hd, and 0.5 Hd and a downstream quadrant given by Equation (105);
- Type 2: an upstream quadrant described by Equation (103) and a downstream quadrant described by Equation (105);
- Type 3: an elliptical upstream quadrant given by Equation (104) and a downstream quadrant given by Equation (105);
- Type 4: a USBR with an upstream quadrant composed of two circles of radii 0.235 Hd and 0.530 Hd and a downstream quadrant given by Equation (106).
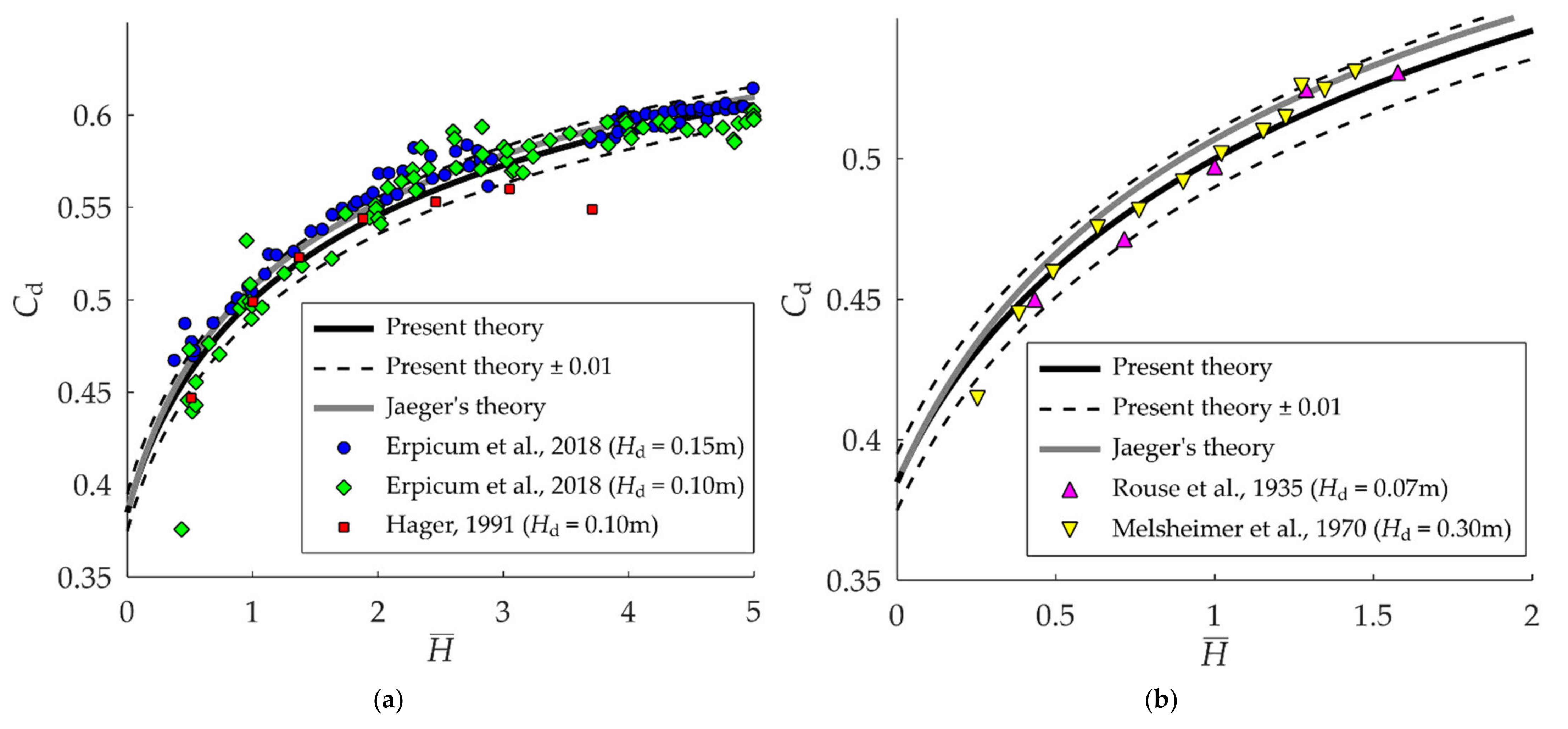
3.2. Discharge Coefficient
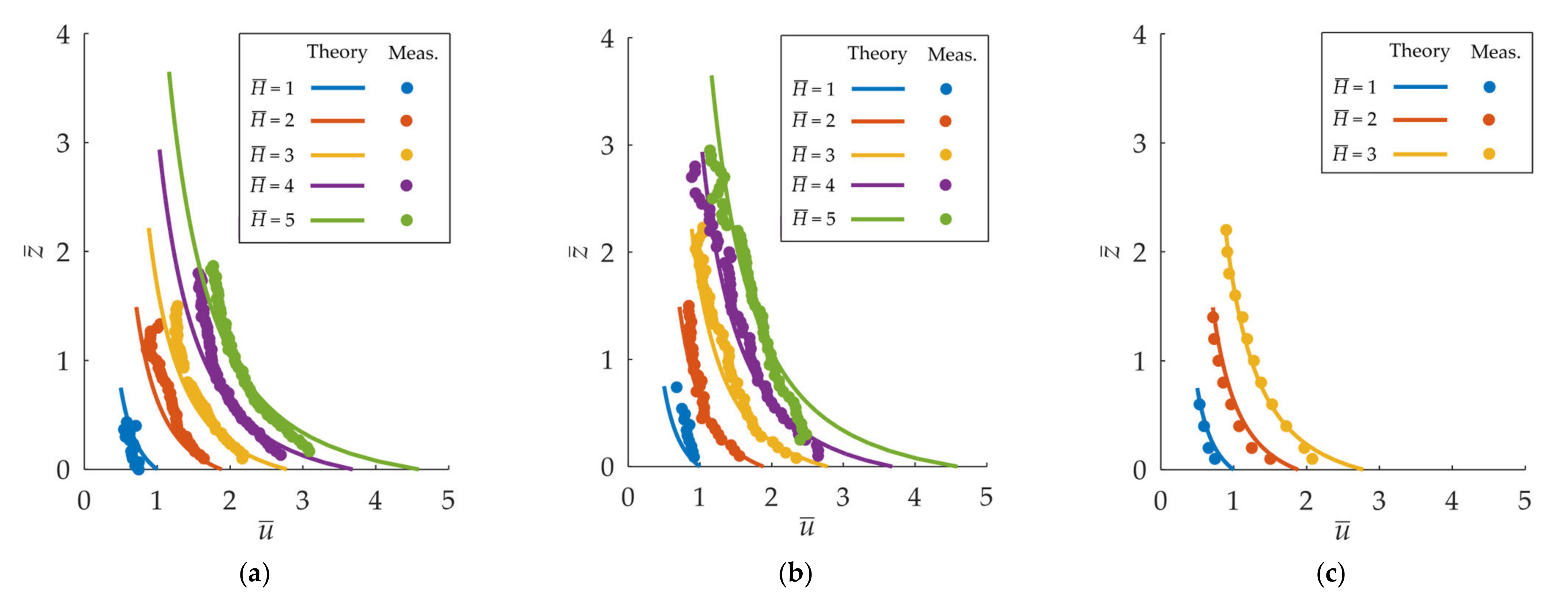
3.3. Velocity Distribution
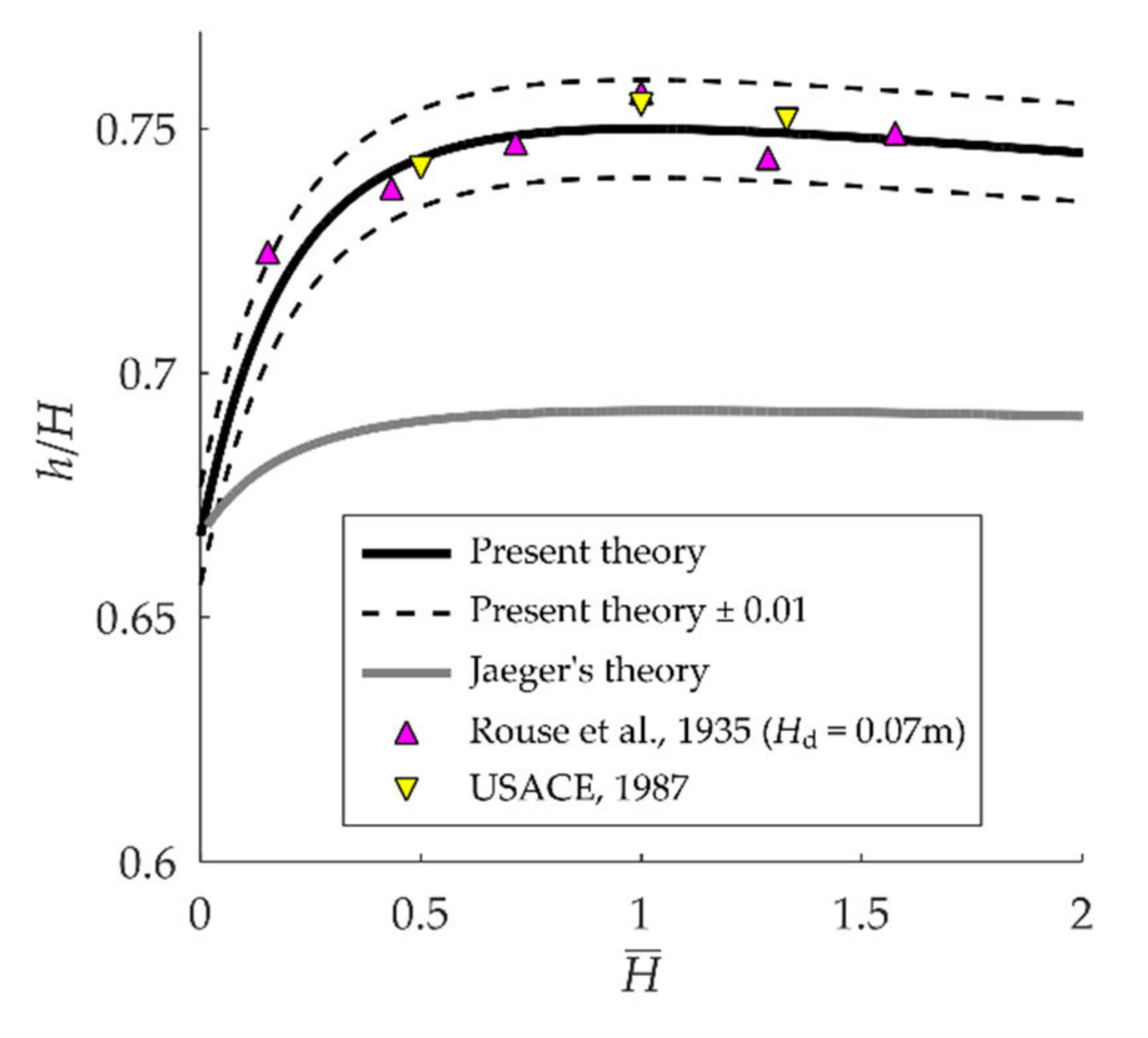
3.4. Water Depth at the Crest Apex
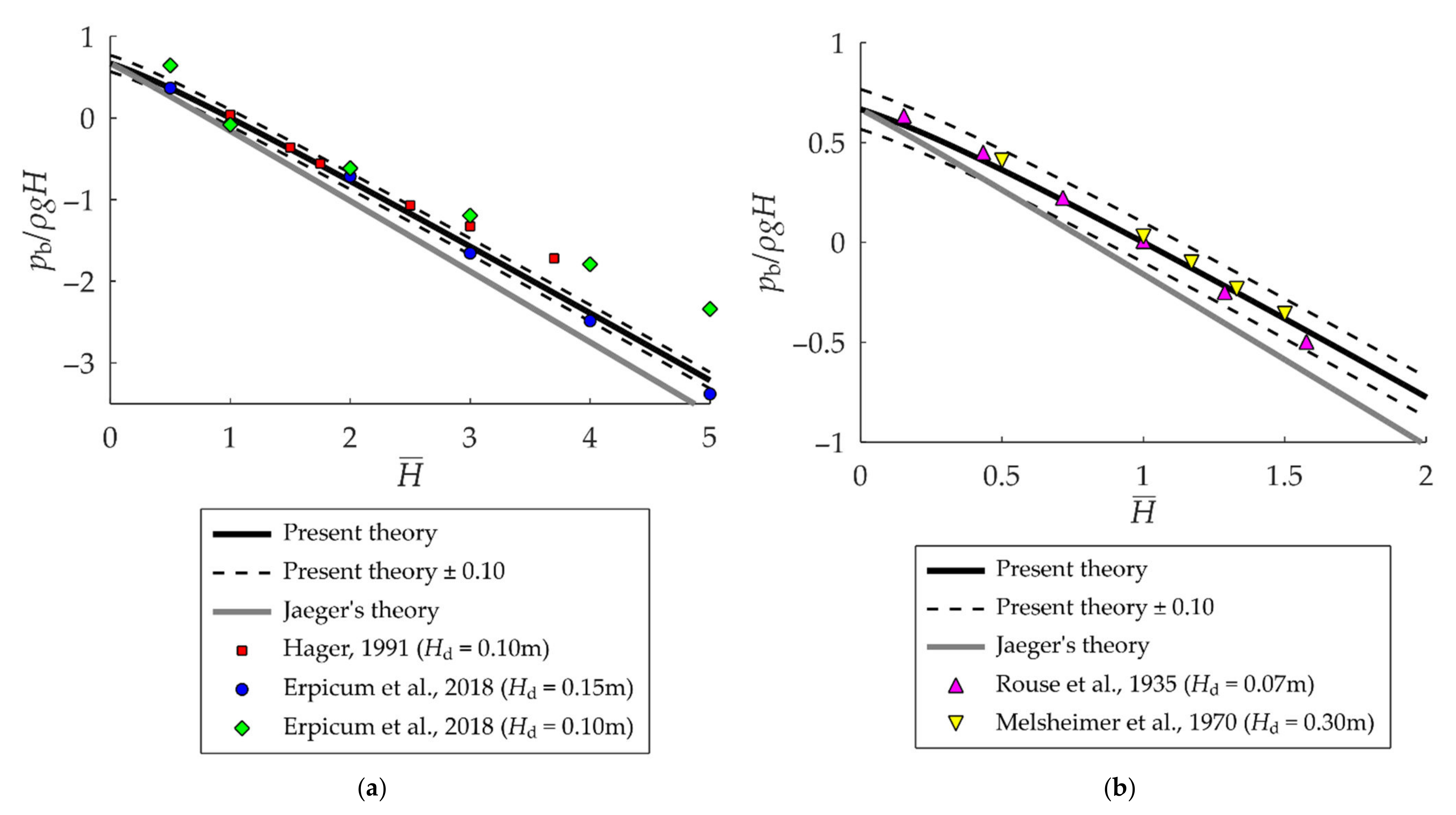
3.5. Crest Pressure at the Crest Apex
3.6. Summary
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hager, W.H.; Schleiss, A.J.; Boes, R.M.; Pfister, M. Hydraulic Engineering of Dams; CRC Press: London, UK, 2020; ISBN 978-0-203-77143-3. [Google Scholar]
- Falvey, H.T. Cavitation. In Chutes and Spillways; United States Department of the Interior, Bureau of Reclamation: Denver, CO, USA, 1990. [Google Scholar]
- USACE. Hydraulic Design of Spillways; U.S. Army Corps of Engineers: Washington, DC, USA, 1990. [Google Scholar]
- Abecasis, F.M. Discussion of “Designing Spillway Crests for High-Head Operation”. J. Hydraul. Div. 1970, 96, 2654–2658. [Google Scholar] [CrossRef]
- Erpicum, S.; Blancher, B.; Vermeulen, J.; Peltier, Y.; Archambeau, P.; Dewals, B.; Pirotton, M. Experimental Study of Ogee Crested Weir Operation Above the Design Head and Influence of the Upstream Quadrant Geometry. In Proceedings of the 7th International Symposium on Hydraulic Structures, Aachen, Germany, 15 May 2018. [Google Scholar]
- Rouse, H.; Reid, L. Model Research on Spillway Crests. Civ. Eng. 1935, 5, 10–14. [Google Scholar]
- Castro-Orgaz, O.; Hager, W.H. Non-Hydrostatic Free Surface Flows. In Advances in Geophysical and Environmental Mechanics and Mathematics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-319-47971-2. [Google Scholar]
- Hager, W.H.; Schleiss, A.J. Constructions Hydrauliques: Écoulements Stationnaires; Presses Polytechniques et Universitaires Romandes: Lausanne, Switzerland, 2009; ISBN 978-2-88074-746-6. [Google Scholar]
- Jaeger, C. Remarques sur quelques écoulements le long de lits à pente variant graduellement. Schweiz. Bauztg. 1939, 114, 231–234. [Google Scholar]
- Cassidy, J.J. Designing Spillway Crests for High-Head Operation. J. Hydraul. Div. 1970, 96, 745–753. [Google Scholar] [CrossRef]
- Hager, W.H. Experiments on Standard Spillway Flow (Including Appendix). Proc. Inst. Civ. Eng. 1991, 91, 399–416. [Google Scholar] [CrossRef]
- Maynord, S.T. General Spillway Investigation: Hydraulic Model Investigation; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1985. [Google Scholar]
- Melsheimer, E.S.; Murphy, T.E. Investigations of Various Shapes of the Upstream Quadrant of the Crest of a High Spillway: Hydraulic Laboratory Investigation; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1970. [Google Scholar]
- Murphy, T.E. Spillway Crest Design; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1973. [Google Scholar]
- Peltier, Y.; Dewals, B.; Archambeau, P.; Pirotton, M.; Erpicum, S. Pressure and Velocity on an Ogee Spillway Crest Operating at High Head Ratio: Experimental Measurements and Validation. J. Hydro-Environ. Res. 2018, 19, 128–136. [Google Scholar] [CrossRef]
- Cassidy, J.J. Irrotational Flow Over Spillways of Finite Height. J. Eng. Mech. Div. 1965, 91, 155–173. [Google Scholar] [CrossRef]
- Ikegawa, M.; Washizu, K. Finite Element Method Applied to Analysis of Flow over a Spillway Crest. Int. J. Numer. Methods Eng. 1973, 6, 179–189. [Google Scholar] [CrossRef]
- Betts, P.L. A Variational Principle in Terms of Stream Function for Free-Surface Flows and Its Application to the Finite Element Method. Comput. Fluids 1979, 7, 145–153. [Google Scholar] [CrossRef]
- Li, W.; Xie, Q.; Chen, C.J. Finite Analytic Solution of Flow over Spillways. J. Eng. Mech. 1989, 115, 2635–2648. [Google Scholar] [CrossRef]
- Yakun, G.; Xianyun, W.; Chigong, W.; Duo, F. Numerical Modelling of Spillway Flow with Free Drop and Initially Unknown Discharge. J. Hydraul. Res. 1998, 36, 785–801. [Google Scholar] [CrossRef]
- Kim, D.G.; Park, J.H. Analysis of Flow Structure over Ogee-Spillway in Consideration of Scale and Roughness Effects by Using CFD Model. KSCE J. Civ. Eng. 2005, 9, 161–169. [Google Scholar] [CrossRef]
- Savage, B.M.; Johnson, M.C. Flow over Ogee Spillway: Physical and Numerical Model Case Study. J. Hydraul. Eng. 2001, 127, 640–649. [Google Scholar] [CrossRef]
- Imanian, H.; Mohammadian, A. Numerical Simulation of Flow over Ogee Crested Spillways under High Hydraulic Head Ratio. Eng. Appl. Comput. Fluid Mech. 2019, 13, 983–1000. [Google Scholar] [CrossRef] [Green Version]
- Dressler, R.F. New Nonlinear Shallow-Flow Equations with Curvature. J. Hydraul. Res. 1978, 16, 205–222. [Google Scholar] [CrossRef]
- Dewals, B.; Erpicum, S.; Archambeau, P.; Detrembleur, S.; Pirotton, M. Depth-Integrated Flow Modelling Taking into Account Bottom Curvature. J. Hydraul. Res. 2006, 44, 785–795. [Google Scholar] [CrossRef]
- Castro-Orgaz, O. Approximate Modelling of 2D Curvilinear Open Channel Flows. J. Hydraul. Res. 2010, 48, 213–224. [Google Scholar] [CrossRef]
- Ramamurthy, A.S.; Vo, N.-D.; Balachandar, R. A Note on Irrotational Curvilinear Flow Past a Weir. J. Fluids Eng. 1994, 116, 378–381. [Google Scholar] [CrossRef]
- Castro-Orgaz, O. Potential Flow Solution for Open-Channel Flows and Weir-Crest Overflow. J. Irrig. Drain. Eng. 2013, 139, 551–559. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Fischer, G. Plane Algebraic Curves; Springer: Berlin/Heidelberg, Germany, 2001; ISBN 978-0-8218-2122-0. [Google Scholar]
- Adams, R.A.; Essex, C. Calculus: A Complete Course; Pearson Canada: Toronto, ON, Canada, 2010; ISBN 978-0-321-54928-0. [Google Scholar]
- Reese, A.J.; Maynord, S.T. Design of Spillway Crests. J. Hydraul. Eng. 1987, 113, 476–490. [Google Scholar] [CrossRef]
- USBR. Design of Small Dams, 3rd ed.; U.S. Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1987; ISBN 978-0-16-003373-5.
- Castro-Orgaz, O. Curvilinear Flow over Round-Crested Weirs. J. Hydraul. Res. 2008, 46, 543–547. [Google Scholar] [CrossRef]
- Hager, W.H. Continuous Crest Profile for Standard Spillway. J. Hydraul. Eng. 1987, 113, 1453–1457. [Google Scholar] [CrossRef]
- Matthew, G.D. On the Influence of Curvature, Surface Tension and Viscosity on Flow over Round-Crested Weirs. Proc. Inst. Civ. Eng. 1963, 25, 511–524. [Google Scholar] [CrossRef]
- Khan, A.A.; Steffler, P.M. Modeling Overfalls Using Vertically Averaged and Moment Equations. J. Hydraul. Eng. 1996, 122, 397–402. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs and Mathematical Tables; Dover: New York, NY, USA, 1972; ISBN 978-0-486-61272-0. [Google Scholar]
- USACE. Hydraulic Design Criteria; U.S. Army Waterways Experiment Station: Vicksburg, MI, USA, 1987. [Google Scholar]


| Lower BC: Atmospheric Pressure | Lower BC: Prescribed Shape | ||||
|---|---|---|---|---|---|
| Known Values | Unknown Values | Equations | Known Values | Unknown Values | Equations |
(39) (34) | (34) | ||||
| 0 | 1 | +∞ | |
|---|---|---|---|
| δ | 0 | 1 | +∞ |
| λ0 | 1 | 2 | +∞ |
| α0 | 1 | 0 | –∞ |
| Cd | 2/33/2 = 0.3849 | 0.5 | 4/33/2 = 0.7698 |
| pb,0/ρgH | 2/3 | 0 | –∞ |
| h0/H | 2/3 | 3/4 | 2/3 |
| Reference | Present Theory | Jaeger’s Theory | ||
|---|---|---|---|---|
| Mean εq | Maximum εq | Mean εq | Maximum εq | |
| Erpicum et al. [5] (Hd = 0.15 m) | 0.8% | 3.1% (H/Hd = 0.459) | 0.5% | 2.6% (H/Hd = 0.459) |
| Erpicum et al. [5] (Hd = 0.10 m) | 0.9% | 7.8% (H/Hd = 0.433) | 1.0% | 8.3% (H/Hd = 0.433) |
| Hager [11] | 0.7% | 1.5% (H/Hd = 0.510) | 1.1% | 2.0% (H/Hd = 0.510) |
| Rouse et al. [6] | 0.4% | 1.7% (H/Hd = 0.253) | 0.6% | 2.0% (H/Hd = 0.253) |
| Melsheimer et al. [13] | 0.5% | 0.9% (H/Hd = 0.715) | 0.8% | 1.5% (H/Hd = 0.715) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stilmant, F.; Erpicum, S.; Peltier, Y.; Archambeau, P.; Dewals, B.; Pirotton, M. Flow at an Ogee Crest Axis for a Wide Range of Head Ratios: Theoretical Model. Water 2022, 14, 2337. https://doi.org/10.3390/w14152337
Stilmant F, Erpicum S, Peltier Y, Archambeau P, Dewals B, Pirotton M. Flow at an Ogee Crest Axis for a Wide Range of Head Ratios: Theoretical Model. Water. 2022; 14(15):2337. https://doi.org/10.3390/w14152337
Chicago/Turabian StyleStilmant, Frédéric, Sebastien Erpicum, Yann Peltier, Pierre Archambeau, Benjamin Dewals, and Michel Pirotton. 2022. "Flow at an Ogee Crest Axis for a Wide Range of Head Ratios: Theoretical Model" Water 14, no. 15: 2337. https://doi.org/10.3390/w14152337
APA StyleStilmant, F., Erpicum, S., Peltier, Y., Archambeau, P., Dewals, B., & Pirotton, M. (2022). Flow at an Ogee Crest Axis for a Wide Range of Head Ratios: Theoretical Model. Water, 14(15), 2337. https://doi.org/10.3390/w14152337







