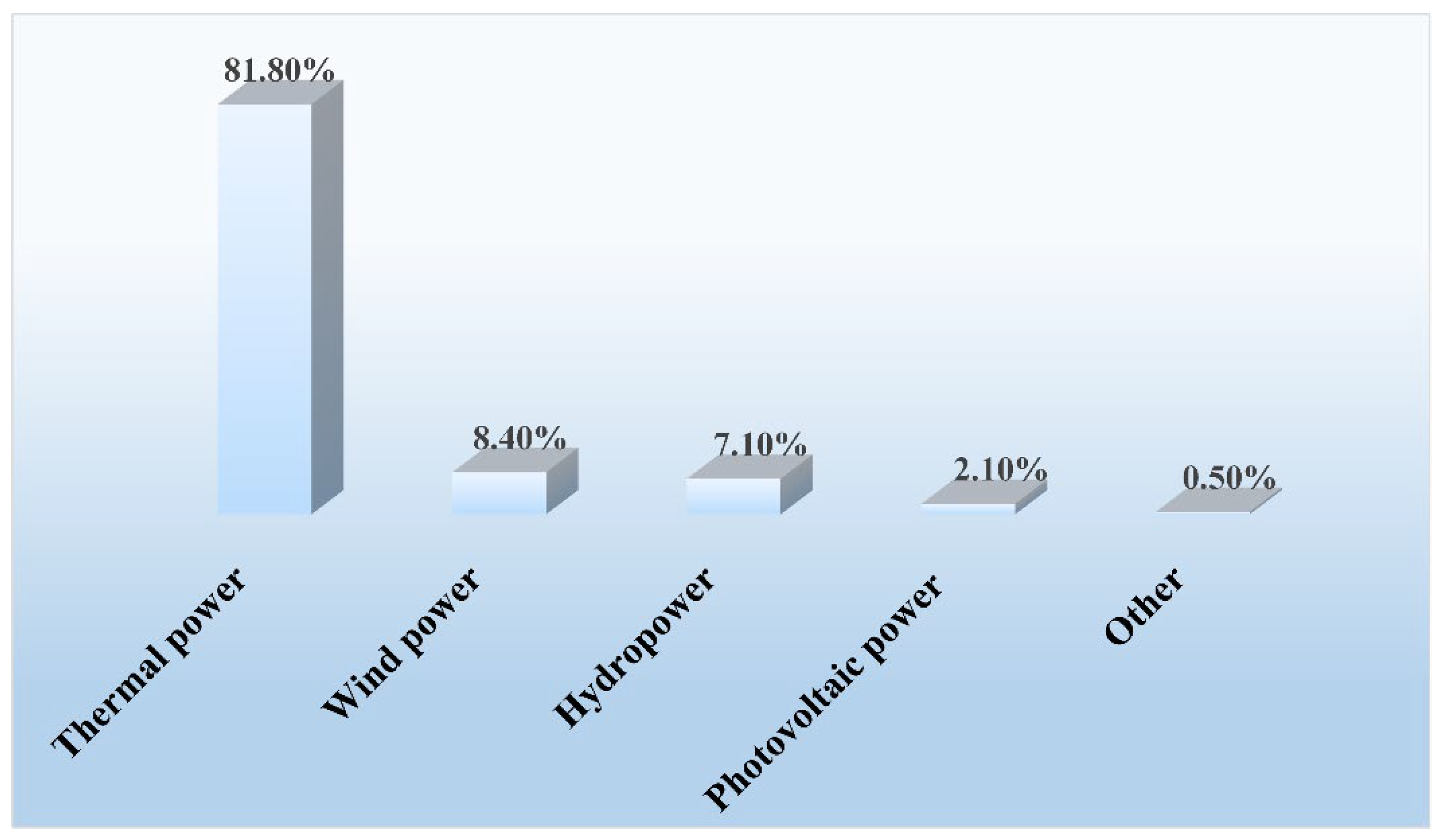
1. Introduction
Hydropower generation is a major part of the power industry and has made great contributions to the progress of world civilization [
1]. Most obviously, hydropower solves many energy supply problems [
2]. It provides pollution-free renewable energy [
3], which is only a reasonable absorption of natural energy by human beings, basically free of pollutants, and realizes the organic combination of industrial progress and environmental protection [
4].
Hydropower generation not only can obtain renewable and clean energy, but can also start and stop quickly, adjust the load, and perform peaking, frequency regulation, and accident backup in the power grid [
5]. The construction of modern hydropower plants is taking on a wider range of tasks, increasingly enhancing the effectiveness of water resources allocation, disaster and drought mitigation, environmental and ecological improvement, and tourism [
6].
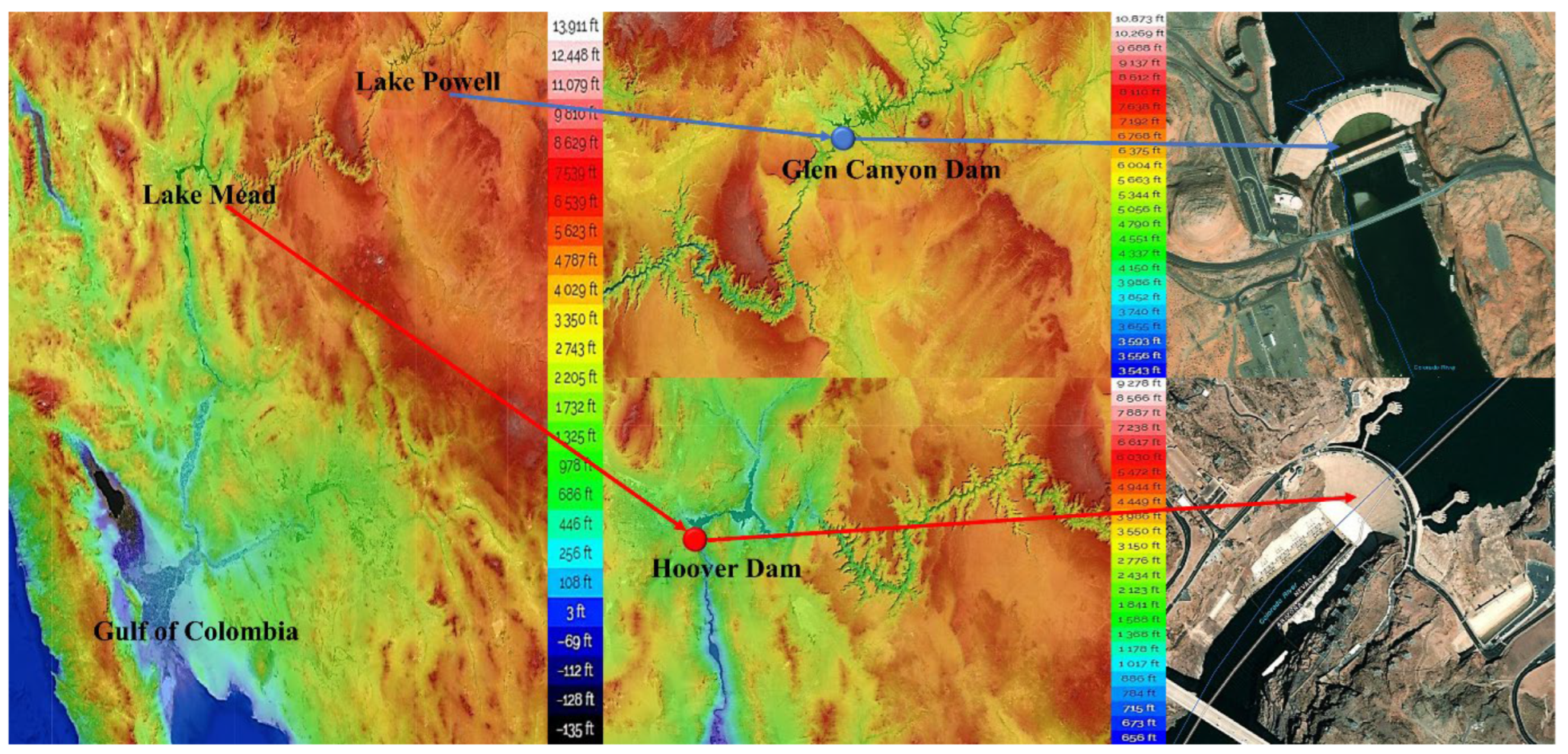
In 1935, the Tennessee Valley Authority built the 2214.4 m high Hoover Dam (HD) on Lake Mead (LM) in the southwest of the United States [
7], with a capacity of 35.2 billion m
3. In 1957, the 216-m-high Glen Canyon Dam (GCD) was built upstream of HD and is managed by the U.S. military [
8]. The GCD impounds water to form Lake Powell (LP), a valuable water resource for the surrounding arid region and a famous tourist area.
GCD and HD have made significant contributions to hydropower generation, flood storage, irrigation, and tourism [
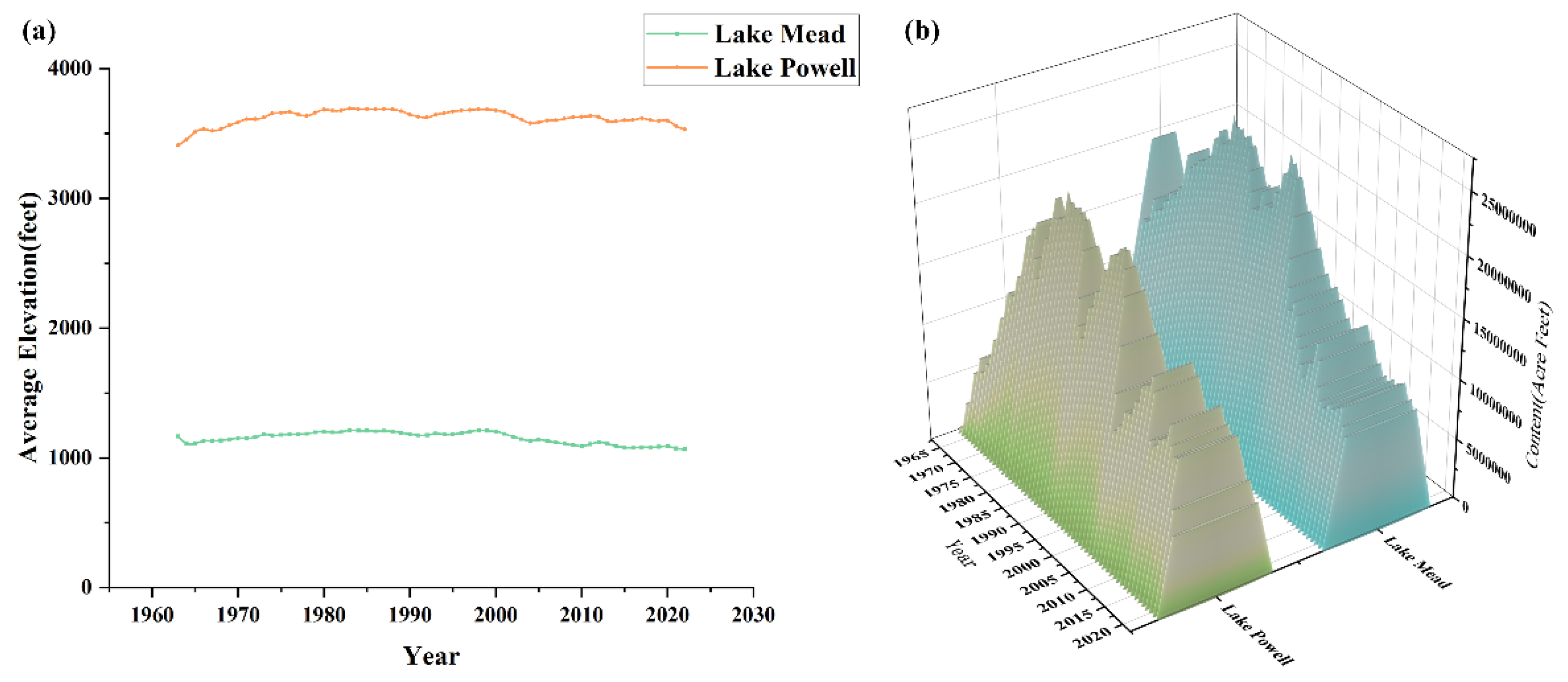
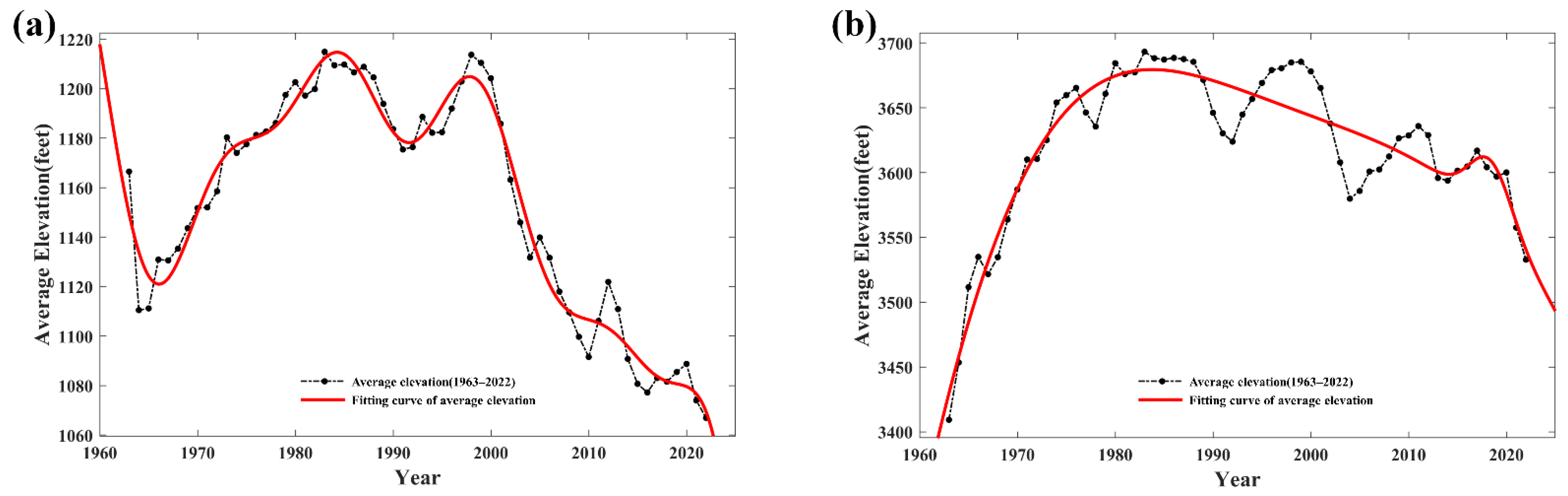
9]. However, according to the U.S. Bureau of Reclamation and the U.S. Geological Survey, by now, LM’s water volume accounted for only 35% of its capacity, while LP’s accounted for 31%, and the storage capacity of each reservoir in the entire basin is only 40% of the reservoir capacity. The water level of LM and its upper reaches of LP has been in a continuous downward trend since 2000 [
10]. The main causes of the imbalance between supply and demand include poor planning of water allocation, rapid population growth, and global warming [
11].
The base of hydropower generation must be a high mountain and deep river area [
2], and it must be the storage place of mineral resources and the habitat of some special organisms or biological species [
12], and most of them are the magnificent and exotic scenery of nature, so it must be a complicated area with intertwined conflicts. It involves not only the problem of electricity, but also the problem of water storage and supply [
13]. This is also a major problem facing the United States at present.
The Colorado River (CR) has more than 25 tributaries, of which the upper Gunnison, Green, and San Juan rivers contribute nearly 11 cubic kilometers of water to the CR each year. All tributaries form the CR Basin, which covers 640,000 square kilometers and spans seven U.S. states and Mexico [
14]. The water supply agreement involving the seven States of the CR Basin states and Mexico was signed nearly 100 years ago [
15,
16], during the historical flood period, and the agreement is based on runoff data that differ significantly from today [
17,
18]. It poses not only the challenge of water scarcity, but even the problem of pollution caused by less water [
19]. It has been pointed out that the current U.S. government’s management of the ecosystem, including water management, lags behind demand, and climate change “constantly reminds people that this system is a poorly designed system, and our management is not well thought out” [
20]. According to the data, the past 20 years have been the most significant period of declining water levels in the two reservoirs, with LM losing more than 2 billion cubic meters of stored water over the past 20 years, equivalent to 800,000 standard 2-m-deep swimming pools. The U.S. Bureau of Reclamation had declared LM to be in the first level water shortage status from 2022. The United States needs to do more to avoid a bigger catastrophe.
The lack of water can also bring about a drop in water levels, which affects the amount of hydroelectricity generated and has an impact on the city’s power supply [
21,
22]. Therefore, it is essential to consider how to optimize a rational, defensible water allocation plan for current and future water supply after taking into account the water demands of states and the conflicts of interest among them [
4,
23].
Mathematical modeling is an important tool for solving water supply and demand problems at dams and for deploying water resources [
24,
25]. First, it is important to fully deploy hydropower resources in the face of limited environmental conditions. Dominique M. Bain et al. quantified the value of hydropower in the operation of the CR power system, examining the value of hydropower and the cost of power under different possible future drought conditions and regional generation scenarios [
26]. Benjamin A. Jones et al. studied the hydropower operating model in the basin in a referendum format [
27]. Mort Webster et al. analyzed the effects of climate on electricity demand and costs, modeling them in terms of hydrology, power system, and economic levels [
28]. For water allocation issues, Niklas S. Christensen et al. analyzed the effects of climate change on hydrology and water resources in the CR Basin [
20]. William Chen et al. addressed dams to regulate human and environmental water demand in rivers by designing water flows [
13]. Projections of hydropower and water resources are also important tools to address this challenge. Syed Azhar Ali et al. predicted the increase of hydropower resources in India in the context of climate change [
29]. Chikamoto et al. predicted the water flow of the CR from the perspective of ocean memory [
23].
In addition, the historical issue of competition between the United States and Mexico for CR water resources cannot be ignored, and how to allocate water resources to adequately meet the needs of both peoples is an important research question [
30,
31].
From the above presentation, it is clear that if a series of mathematical models can be developed that can adequately balance the water and hydropower needs around the watershed, and if these models can effectively contribute to sustainable development, they will have a positive impact on the future of the world’s watersheds, including the CR. This work is based on the five major states with severe water shortages radiating from the middle and lower CR. We have prepared a theoretically sound mathematical solution for water and hydropower resource planning and sustainable development.
This work starts from the basic electricity and water demands of the area under discussion, and fully analyzes the conditions for the healthy operation of the two dams and the lake in which they are located by simplifying the dam generation model, optimizing the water and hydropower distribution model, and considering multiple factors together. The article predicts their service life under extreme conditions and without management action. The paper focuses on the sustainable development of the southwestern United States, including the issue of Mexican rights, at the policy level after a rational analysis. The work also presents a sensitivity analysis of the model developed to explore its generalizability. It concludes with a brief evaluation of the work and suggests ideas for further improvement. We use data and analysis as evidence to explore conservation and development. This work will also demonstrate the broad applicability of our model, to explore water issues more deeply.
Researchers tend to focus on a single perspective on water allocation issues, as illustrated in the previous section. Researchers have chosen their areas of expertise as entry points for in-depth research. A series of studies have provided climate and geographic perspectives on the future development of the CR. Remote sensing images have been borrowed to analyze water evapotranspiration in the CR basin [
32]. A more granular perspective is being used for agricultural water use. Hung et al. examined uncertainties at the system, agent, and parameter levels through uncertainty, clustering, and sensitivity analyses. In their model, CR would face a 13 to 30 year-long water crisis between 2019 and 2060 [
33]. Other studies examine the allocation of CR water resources from market and policy perspectives [
34,
35,
36]. Most of these studies are based on historical facts and market context.
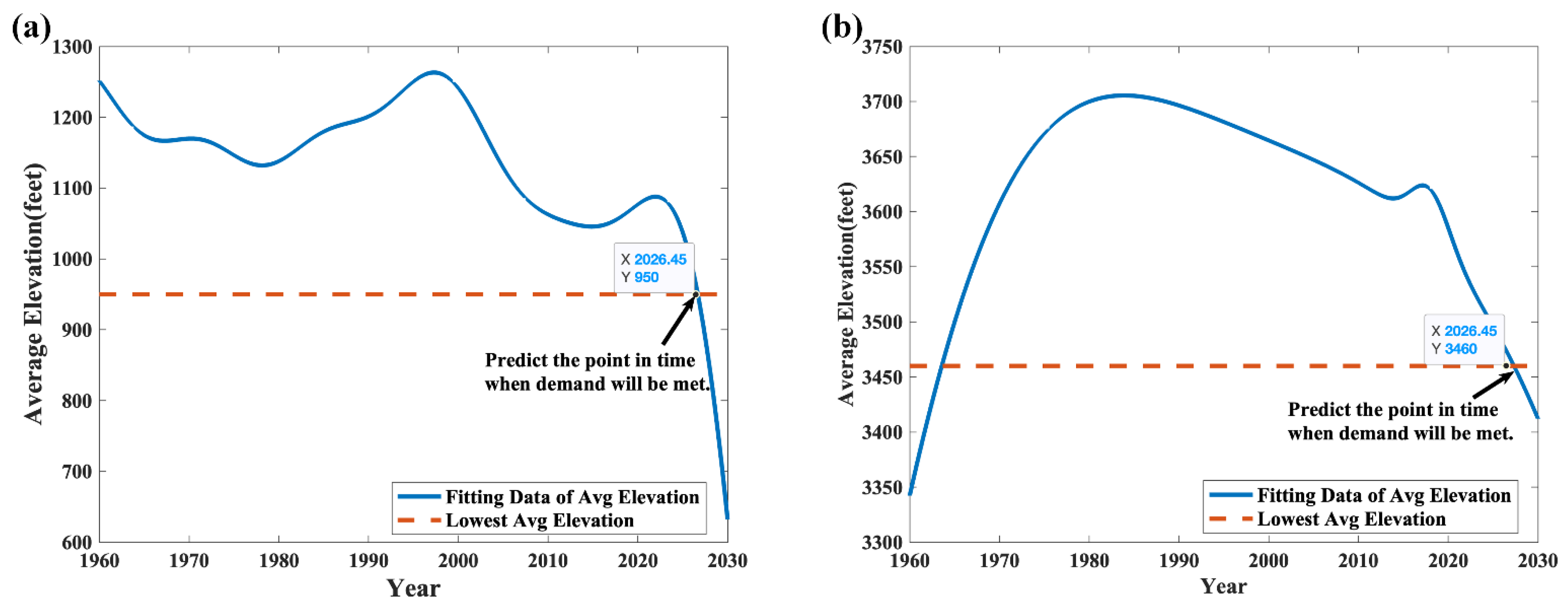
Relatively speaking, the value of our work is in a sense comprehensive and forward-looking. This work adequately addresses water and hydropower needs, taking into account all factors in order to develop a relatively complete and idealized mathematical model. The mathematical model is used to guide policy implementation in a scientifically sound manner. At the same time, the work focuses on the actual water crisis of the people of the five states from both historical and practical perspectives, proposing minimum water requirements of 950 feet and 3460 feet for LM and LP, respectively. The work also warns that if no action is taken, LM and LP will not be able to meet demand in 2026 and 2027, respectively. The need for timely action is also well documented by relevant data type studies [
18]. This work specifies diversions and proportional allocations, including residential, agricultural, and industrial water, with full consideration of the interests of the Mexican downstream of the CR, providing specific followings for historical dilemmas and sustainable development of the CR.
The guiding allocation scheme we propose addresses the real water crisis problem head on, and the scientific validity of the model predictions is fully demonstrated in the paper. The problem of water allocation involving the CR, including the country of Mexico, is historical in nature. Addressing it from a mathematical modeling perspective and complementing it with argumentation is novel and reliable. Our quantitative and qualitative analyses are of great value and provide guidance for subsequent studies involving this area.
We would like to emphasize that the models we have developed are idealized mathematical models whose underlying sources are official data from various governmental organizations, and we believe that our work can have a positive impact on water resources management and sustainable development in the new context.
Figure 1 roughly shows the framework of the work done. Briefly, this work considers the base power demand and water consumption in Step 1, and also accounts for the dam generation model, corresponding to the problem analysis in
Section 2 and the model assumptions in
Section 3.1. In Step 2, the hydropower and water allocation issues are considered mainly in terms of agricultural, demographic, industrial, and geographical factors, corresponding to
Section 3. Step 3 focuses on proposing decision options for the multiple attributes previously proposed, with special attention to the interests of Mexico. Step 4 is based on the newly proposed novel particle swarm optimization (PSO) algorithm for solving the model, giving the minimum water level requirement, and also proposing a water allocation scheme for the CR, taking into account the historical and current situation.
3. Model Assumptions
3.1. Penstock Dam Model
The structure of a hydropower plant is a complex issue, which is influenced by numerous factors, such as water level, water volume and efficiency of the generating unit [
39]. The main purpose of this exercise is to rationalize the deployment of resources. It is imperative to find the answers intuitively and efficiently. Therefore, it is essential that the dam model be fully simplified. The simplified dam model is named the Penstock Dam model.
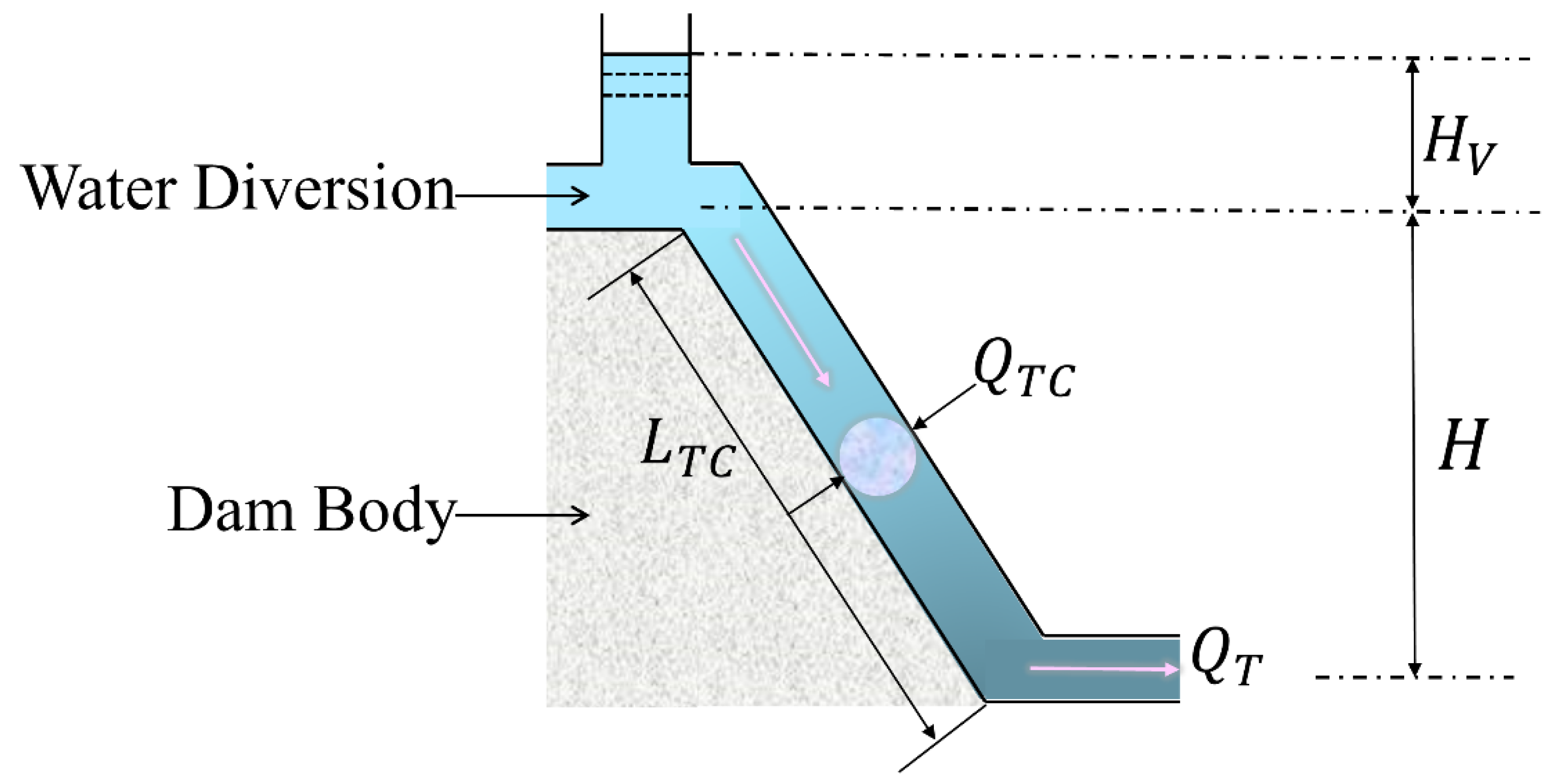
Figure 3 shows a simplified schematic of it.
For the water flow of the pressure pipe, the following formula can be used:
where
is the water flow of the Pressure Pipeline and
H is the static head.
could be used to represent time constant, and it can be calculated by the following formula:
is the amount of water head loss, the calculation formula is as follows:
For
, there is also the formula below:
where the parameter
is calculated as:
At the same time, the formula for calculating the flow rate of water is:
where
, the velocity of sound in water, is 1428 m/s.
The force of the water outflow is calculated as:
where
N is the amount of electricity generated by the dam per unit of time,
g is the acceleration of gravity, and
is the generation factor of the dam.
The force of the water outflow is integrated into the time to obtain the power generation of the dam:
where
represents the amount of electricity generated by the dam over a period of time.
3.2. Hydropower Allocation Model
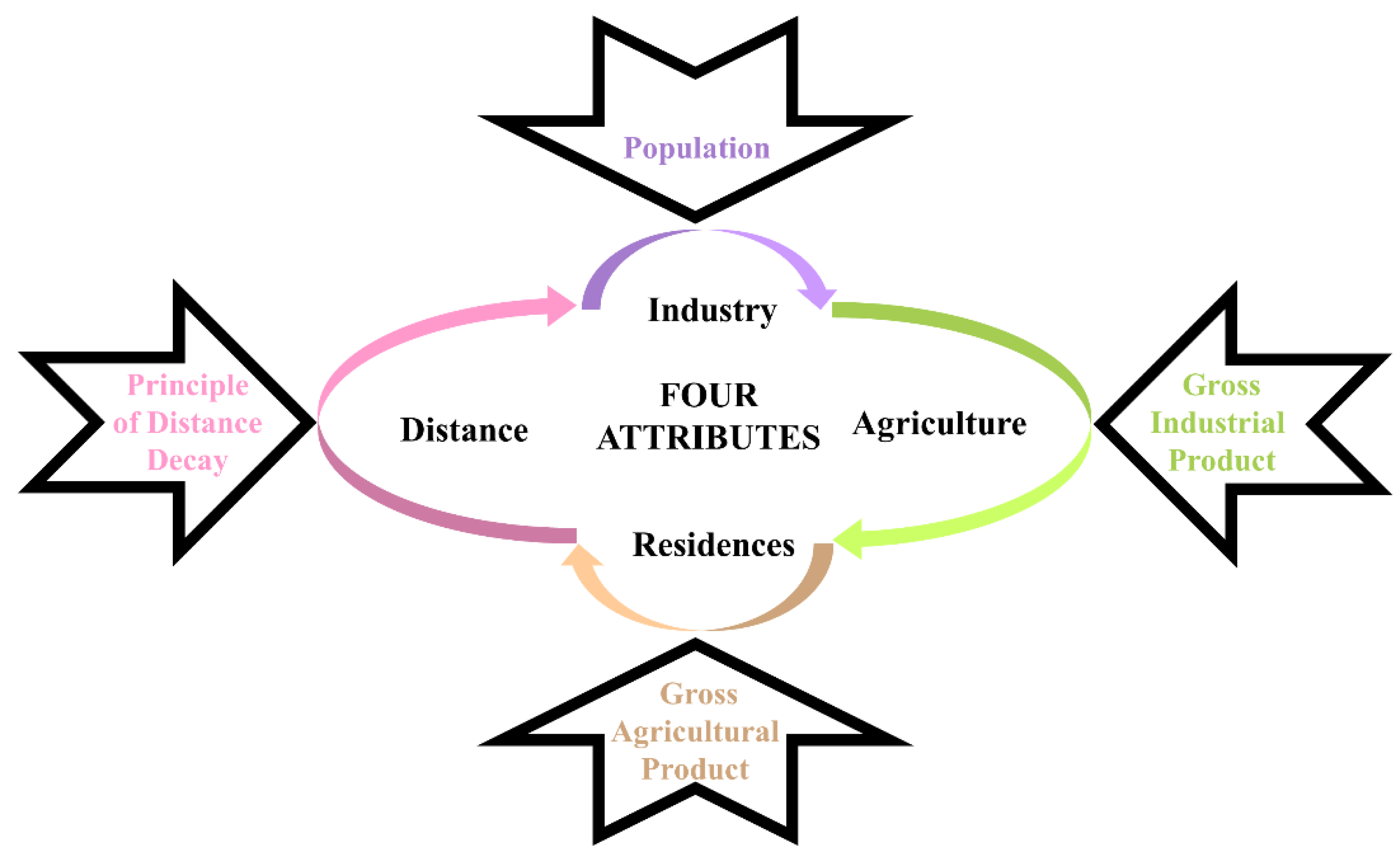
Electricity resources are the lifeblood of the national economy, and it is our unavoidable responsibility to reasonably allocate electricity resources and fully meet the people’s demand for electricity resources. In allocating the power resources of the Hydropower Station, we took the principle of Environment, Equity, Science, and Maximization into account, fully considered the power demand of each industry in each region and the actual geographic situation, selected the multi-attribute decision analysis method in system engineering for the finite scheme, comprehensively analyzed the power demand of 173 counties in five states, and appropriately simplified the model. The specific distribution concept is presented in
Figure 4. We constructed the improved Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) method based on four major attributes using limited data, to provide scientific guidance for power resource allocation.
It is well known that among the five states given in the problem, the Economic Level, Population Size, Geographical Location, and Industrial Structure vary greatly from region to region. Adequately quantifying the attributes and collating the indicators is a difficult task. Politicians believe that the economic foundation determines the super structure. In selecting the indicators, we took the three major types of electricity consumption (agriculture, industry, and residences) as the grasp to organize the 193 counties in 2020 corresponding to agriculture production, industrial production, and population changes from the United States government official online website, which contains the most specific information relating to our model [
40]. They are an important medium to quantify the attributes.
Figure 5 shows the correspondence between attributes and indicators.
When considering the geographic location factor, we introduce the Distance Decay Law (DDL). The essence of the DDL is that the interaction between geographic elements is related to distance, and the interaction between geographic elements is inversely proportional to the square of distance when other conditions are the same [
41]. The theoretical basis of the DDL is the formula of universal gravitation discovered by Newton.
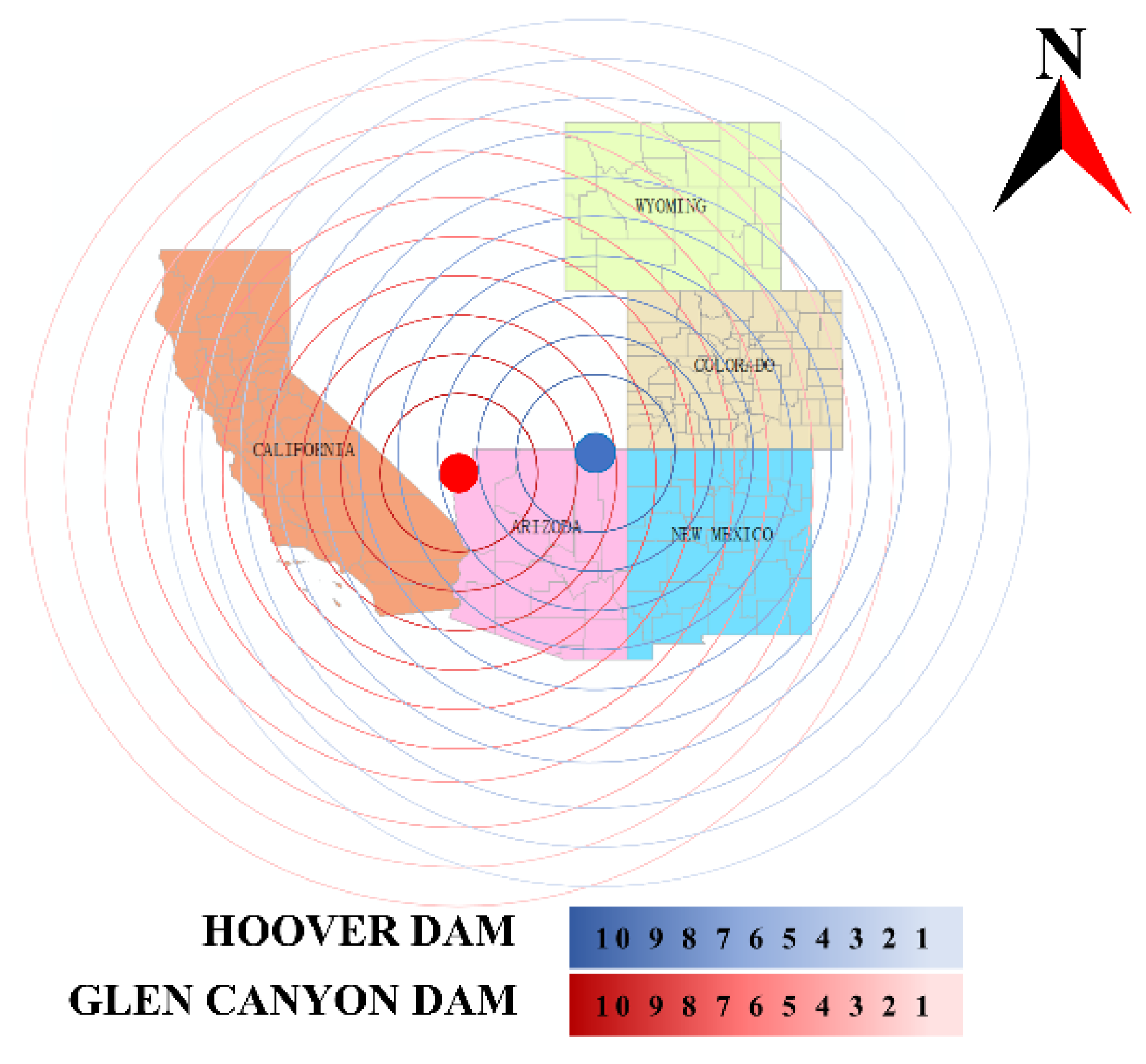
We counted the distance from 193 counties to the two dams, and also combined the power resource allocation principles to quantify the distance index and transformed the distance merit into 10 levels from 1 to 10 points.
Figure 6 graphically illustrates this work.
Population, Gross Agricultural Product, Gross Industrial Product, population, and distance distribution values to GCD and HD were statistically compiled for the 193 counties in the four states in 2020.
Table 2 shows the results for the selected areas.
The TOPSIS method is a common decision-making technique for multi-objective decision analysis of finite solutions in systems engineering [
42]. In recent years, it has also been used in the comprehensive evaluation of multiple indicators. In our problem, we need to consider the power resource allocation of 193 counties in five states, but we cannot accurately consider the importance of the four indicators, and the traditional TOPSIS method needs to determine the attribute weights in advance, which is more subjective [
43]. Based on this background and demand, we propose a model of power resource allocation based on the Novel TOPSIS method.
Firstly,
m evaluation indicators are selected for
n evaluation units for comprehensive evaluation (forwarding of inverse and moderate indicators), and the original data matrix
X is as follows:
Then, the data are normalized as:
Here,
Z is represented as the unit matrix obtained after the normalization of matrix
X.
i and
j represent only the corresponding element positions in the matrix.
k represents the term
k in the summation.
i,
j and
k have no special meaning. Where:
The optimal value and the worst value of each index can constitute the optimal value vector
and the worst value vector
:
The distances of each evaluation unit from the optimal and inferior values can be calculated, respectively:
The relative proximity of each evaluation unit to the optimal value can also be calculated:
The traditional method ranks the relative proximity, and the larger the relative proximity, the closer the evaluation unit i is to the optimal level.
The highlight of this work is the improvement on the traditional method. The first step of the improvement work is to build an extended multi-attribute decision matrix based on the matrix
Z:
where
, corresponding to
m alternatives,
, corresponding to
, and the weights of the attributes
S can be reflected as:
The corresponding weighted normative matrix is calculated as:
From Equation (19), we can see that the smaller the is, the larger the is. To further determine the indicator weights, the objective planning optimization model is constructed as follows.
Let the Lawrencian function be:
Thus, we can obtain:
and it is solved as:
There is and is a minimum value point of the objective function of the optimization model.
In the normalized decision matrix R, satisfies . The value of the objective attribute corresponding to the highest preference is , and the value of the objective attribute corresponding to the lowest preference is , so that . Moreover, the negative ideal solution is (where ).
From this, it is deduced that:
The improved relative proximity is obtained as:
Each of the four attributes is assigned to a weight in this model.
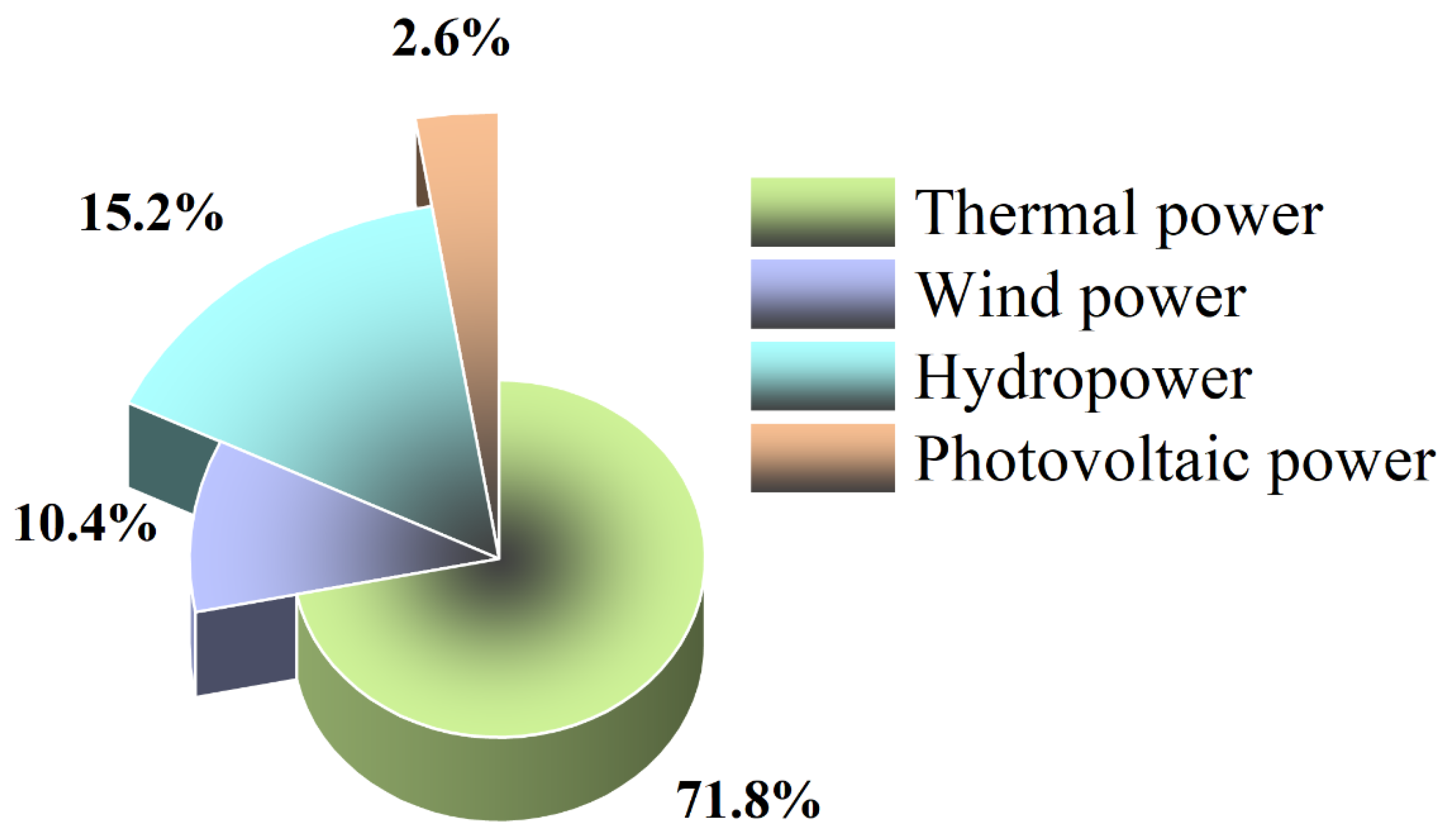
Figure 7 reflects the results obtained from the calculation. From the weight distribution, the power distribution is mainly influenced by the three attributes of agriculture, industry, and residences. Moreover, these three attributes have a similar impact, while the geographical location has a relatively small impact on it. In practical terms, the power resources generated by hydroelectric power plants will be injected into the well-connected power network, and the disadvantages caused by distance (such as loss, time, and other factors) can be almost negligible in front of the three demands of agriculture, industry, and residences. However, when the three demands of agriculture, industry, and residences are almost similar, distance will have a strong impact on our distribution scheme. The weight distribution fully demonstrates the rationality and scientific validity of our improved model.
Figure 7.
The weight distribution of four major attributes. (
a) The HD. (
b) The GCD. The relative proximity of the 193 counties to HD and GCD was calculated using the improved model derivation. The results are presented in
Table 3.
Figure 7.
The weight distribution of four major attributes. (
a) The HD. (
b) The GCD. The relative proximity of the 193 counties to HD and GCD was calculated using the improved model derivation. The results are presented in
Table 3.
3.3. Water Allocation Model
From the water statistics from government’s official website [
44] and visualized images (
Figure 8), some water from GCD will be provided to LP. This fact further illustrates the important relationship between the two waters, which is that LP can be considered a sub-water of LM. From an idealized perspective, the higher elevations would be supplied by LM, not LP. The water supplied from LM, to lower elevations (e.g., CA), can be considered as part of its supply to Powell. When the water level of LM is
M and the water level of LP is
P, to draw water from each lake, the demand models of the five states are referenced to fully consider the water supply requirements of both lakes. At the same time, by the upstream location of LM in dry LP, the two lakes are fully connected and continuously deliver water resources, so the following cases are analyzed to improve our model.
When P > Pmin, M > Mmin, the water levels of the two lakes meet the power generation requirements of the two dams at this time. In reality, the water resources allocation model is related to the water delivery link, i.e., the distance of the two lakes to each state. Thus, it is necessary to consider water allocation in terms of geography to find the optimal solution.
We can visualize through the satellite map that part of the CR connects the two waters. As can be seen in
Figure 9, the water flowing from LP to LM will be in a canyon with an elevation of 4000–5000 ft.
ArcGIS software shows that the average elevation of the area to the left of the yellow line in
Figure 10 would be less than 1000 ft and that the water flowing from LP could theoretically be used in the area to the left of the yellow line. To the northwest of LP, the higher elevation of Death Valley National Park, an important reservoir in north-eastern CA, would allow some of the water from LP to flow there. Again, looking at the entire geomorphic map, in our model, LP would theoretically provide water for the entire CA region. Therefore, we have assigned LP the water supply area within the red boxed line in
Figure 10. For LM, since it is theoretically difficult for water from LP to flow to higher elevations 11/21 within the five states we set, the water supply task for higher elevations is given to LM, i.e., the green boxed part in
Figure 10.
3.4. Other Cases
The water supply of LM should be used preferentially. For the geographic water supply model, it is important to compare the scores that each state gets for distance by assuming that each state applies a single water supply model and improves the criteria for the allocation model to decide on the water supply of a particular lake based on the scores. In other words, if the difference between the distance weighted scores of two lakes to a state exceeds 30, the single lake water is considered to be extracted to provide water for a state, and if it is less than 30, the lake water is extracted to provide water for a state proportionally.
When LP is upstream of LM, it is going to be necessary to compare the five-state water supply geographic scores of the two lakes, while it is important to further consider the water release capacity of GCD. It is assumed that with benefit as the priority decision goal, the upper reaches of the river can flow downstream by gravitational potential energy, which is a process that requires far less cost than the transportation cost of drawing water from the lake. Based on this consideration, the benefit scoring part of the model is used to evaluate the benefit and geographic factors together. This results in the proportion of flow from LP to LM, and thus, the water supply model for both lakes.
5. Evaluation and Improvement of Model
Firstly, the priority of several models innovatively proposed in the work is fully discussed and the important role played by each of them is argued. The PD model is based on the actual power plant situation and the two-sided consideration of model prediction accuracy, cleverly ignoring factors unrelated to the power generation of the hydropower plant and capturing the core elements such as water level height and water flow. Compared with other models of the same type, the PD model has the advantages of easy implementation and high accuracy.
The TOPSIS method is a common decision-making technique for multi-objective decision analysis with finite solution in system engineering. It has a wide application in the comprehensive evaluation of multiple indicators. Considering the importance of the relevant indicators that cannot be accurately obtained for our problem, we have improved the traditional TOPSIS method. The Novel TOPSIS method can determine the weights of relevant indicators more objectively and make the model more accurate compared with the traditional TOPSIS method.
Water resource allocation mainly requires consideration of water transmission distance and transportation cost. Therefore, we consider water resources allocation from a geographical point of view, visualize each area by satellite map to divide it and obtain the water transmission score, and then obtain the water transmission scheme according to the score.
The PD model can obtain the predicted values of dam power generation and total water availability more accurately and easily. The Novel TOPSIS decision model can help us to optimize the allocation of power and water resources according to the relevant requirements. Ultimately, the water allocation model can be used to rationalize the allocation according to distance and transmission costs.
In the previous discussion of the main water and hydropower resources and the balance between them, the essence cannot be separated from the healthy operation of the dam. That is, the adequate deployment of upstream and downstream water resources to meet the water demand of each region and the required water flow for power generation. Therefore, we believe that it is necessary to discuss the previously established PD model to explore its scope of application, so as to further improve this work. From Equation (9), it is easy to see that the power generation of the dam per unit time in the idealized model is proportional to the average water level elevation of the dam.
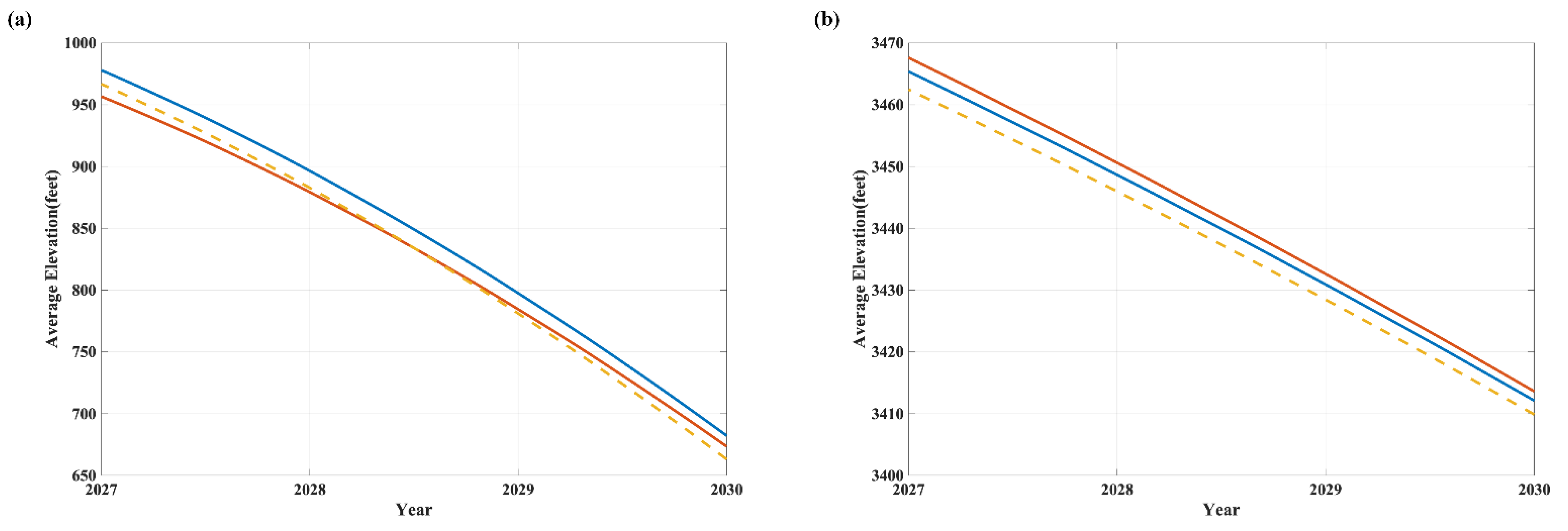
Therefore, to perform a sensitivity analysis of the effect of the mean water elevation on the model results, we have to make a small fluctuation up and down in the mean water elevation, and the effect on the predicting results of the dam water level prediction model is shown in
Figure 17.
It can be seen that when the average water elevation fluctuates slightly up and down by 1%, the predicting values for HD also produce corresponding small changes, i.e., a 0.91% increase and 2.36% decrease. The corresponding increase and decrease for GCD are 1.23% and 1.57%. The results prove that the dam water level prediction model has good sensitivity and can meet our daily needs better. Using a similar approach above, we performed a sensitivity analysis on the dam power generation model as well, where there is a corresponding 5.23% increase in power generation when the input water level height of the dam power generation model changed by 5%. This result is in line with our expectations, while also meeting the needs of our TOPSIS allocation model and PSO algorithm.
In general, models based on idealized assumptions are important for guiding actual water and hydropower resource allocation. However, it has to be admitted that there is a gap between the ideal and the reality. Therefore, this paper also prospectively suggests some points that should be focused on in a realistic analysis, especially assumptions that have a significant impact on the analysis. We believe that this will further enhance the practical value of this work.
First, the dam power generation model presented in this work when studying the allocation is simplified, and the text cleverly considers two dams, in a sense unifying the properties of the two dams, which we consider an interesting means of treatment. However, it must be stated that for different dams and power generation models, a case-by-case analysis should be made to ensure the scientific and accurate nature of the model.
The consideration of geographic factors in the allocation process is also worthy of further research. This work quantifies the complex geographical factors simply in order to simplify the mathematical model. However, in future studies, full consideration of altitude [
49], climate [
50,
51], biology [
52], and other factors is considered necessary.
A direct division of water resources based on a single elevation relationship is not necessarily applicable in all cases. Further studies should specifically consider the relationship between the two reservoirs and the differences in water use by region, and the important role played by groundwater [
52] and geological conditions [
53] should also be considered.
It is important to emphasize that the simplification of assumptions necessary for this paper to consider multiple factors in a holistic manner proves to be valid. Its mathematical modeling perspective presents the complex analysis in a simple and wonderful mathematical language that guides the issues of power generation from the two dams, the allocation of water and hydropower resources in the five states, and the resource entitlements involved in each location.
This work compiles and analyzes the history, present, and future of the CR from a large body of data in which the water and hydropower resources of the southwestern United States and Mexico were fully deployed. Despite the many unique features and developments of the ideas and work, it has to be admitted that they have many limitations. First, the accuracy of the model is still open to question due to the over-reliance on official datasets. Second, some of the work performed is too idealistic, and many of the means of treatment are based on assumptions that do not have a distinct realistic extension value. Third, the mathematical methods used in the targeted research questions selected are not always accurate. Fourth, the model still has limitations. This is mainly due to the fact that the model assumptions we have developed are all built in this particular geographical location and spatio-temporal environment, and their generalizability is not obvious. The future developments are still needed to introduce other important influencing factors, such as climatic conditions and bio-diversity, and modularize the problem with a more scientific model from both the perspective of reference data and practical investigation, and then integrate a complete and scientific planning system to contribute to the sustainable development of the watershed represented by CR.