1. Introduction
MSE walls represent a more economical alternative to traditional gravity-type walls. MSE walls are mainly applied in bridge abutments, wing walls, and areas where excavation and slope construction cannot be conducted. Under poor foundation conditions, MSE walls provide significant technical and cost advantages.
Over the past few decades, due to the contradiction between land restrictions and infrastructure development, an increasing number of MSE walls has been applied in slope construction and research [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12]. Field experiments are an important way to study the failure mechanism of MSE walls, which can be divided into full-scale and proportional experiments [
13,
14,
15,
16]. The relationship among wall deflection, earth pressure behind the wall, wall height, and the secondary geogrid was obtained by measuring the wall pressure and strain in field experiments [
13,
14]. It was confirmed that secondary reinforcement played an important role in decreasing wall-facing deflection and generating a uniform, lateral earth-pressure distribution. Yazdandoust and Ghalandarzadeh [
15] performed shaking table scaled model tests to obtain the failure pattern of reinforced walls, which reflects the influence of a nonuniform acceleration distribution on the value of the seismic coefficient for reinforced soil structures. Safaee et al. [
17] measured values of the most critical dynamic parameters of single-layer and multi-layer walls subjected to different seismic loads. The behavior of wall stability was obtained from the comparison of single-layer and multi-layer walls.
MSE wall stability analysis theory is also an effective way to explore the wall failure mechanism. According to the limit equilibrium method, Bilgin [
1] studied the effect of the reinforcement length on the MSE wall failure mode. In his research, it was concluded that the reinforcement length could be reduced to less than 70% of the wall height under the condition of perfect parameters. In addition, the type of reinforcement exerted an important impact on the wall stability [
18]. However, simple theoretical analysis is limited by the inherent shortcomings of analysis theory.
The most common research topic in numerical parameter analysis is the limit equilibrium theory, which constitutes the theoretical basis of current design manuals [
2,
13,
19,
20]. The influence of the extension and the strengthening of the stability of reinforced soil wall was studied by using the finite element model [
2]. Leshchinsky et al. [
19] proposed a new limit analysis framework verified by parametric analysis. Their research results revealed that the proposed framework was reasonable, including the influence of facing blocks, seismicity, reinforcement length, and secondary reinforcement. Finite element analysis of MSE walls yielded more accurate results, but the calculation process is time-consuming [
20]. By examining the overall stability evaluation of the finite element method, Razeghi et al. [
16] provided suggestions for wall designers to quickly check the overall stability of retaining walls. Jiang et al. [
13] indicated that secondary reinforcement resulted in a uniform, lateral earth-pressure distribution. However, these simulation experiments were based on theoretical analysis of the slope stability, which often produced a high safety factor for circular failure surfaces and a low safety factor for V-shaped failure surfaces. Liu et al. [
21] proposed a novel finite element limit equilibrium method (FELEM) to enhance the applicability of slope stability of FELEM which was validated by five slope problems. The limit equilibrium method must assume a general form of the failure mechanism for calculation, which often leads to inaccurate calculation results [
5]. The influence of geosynthetic reinforcement on the stability of the retaining structure was conducted by using the finite element limit analysis method. Hassen et al. [
22] proposed a new calculation method (multiphase model) to numerically analyze the stability of reinforced soil structures which showed good performance and computing capabilities. Kazimierowicz-Frankowska and Kulczykowski [
23] analyzed that the selected analysis method can accurately predict the deformation of reinforced soil structure under service load. By numerical analysis, Mirmoradi et al. [
24] studied the factors affecting the foundation stability, including foundation stiffness and geometry, wall height, and reinforcement stiffness. The numerical model calculation carried out parameter analysis to investigate the influence of the reinforcement spacing, wall height, and foundation location, and reinforcement design on the stability of back-to-back reinforced soil-retaining walls [
25]. The limit equilibrium method must assume a general form of the failure mechanism for calculation, which often leads to inaccurate calculation results. Finite element analysis of MSE walls yielded more accurate results, but the calculation process is time consuming.
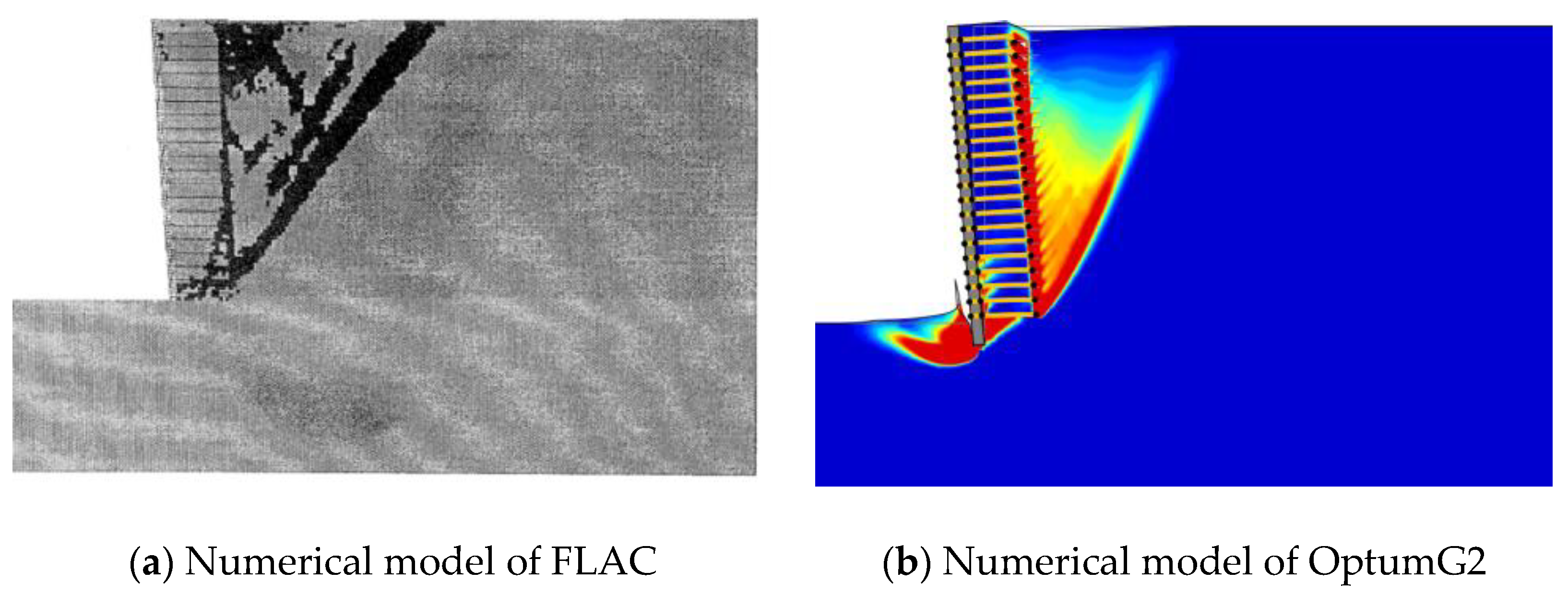
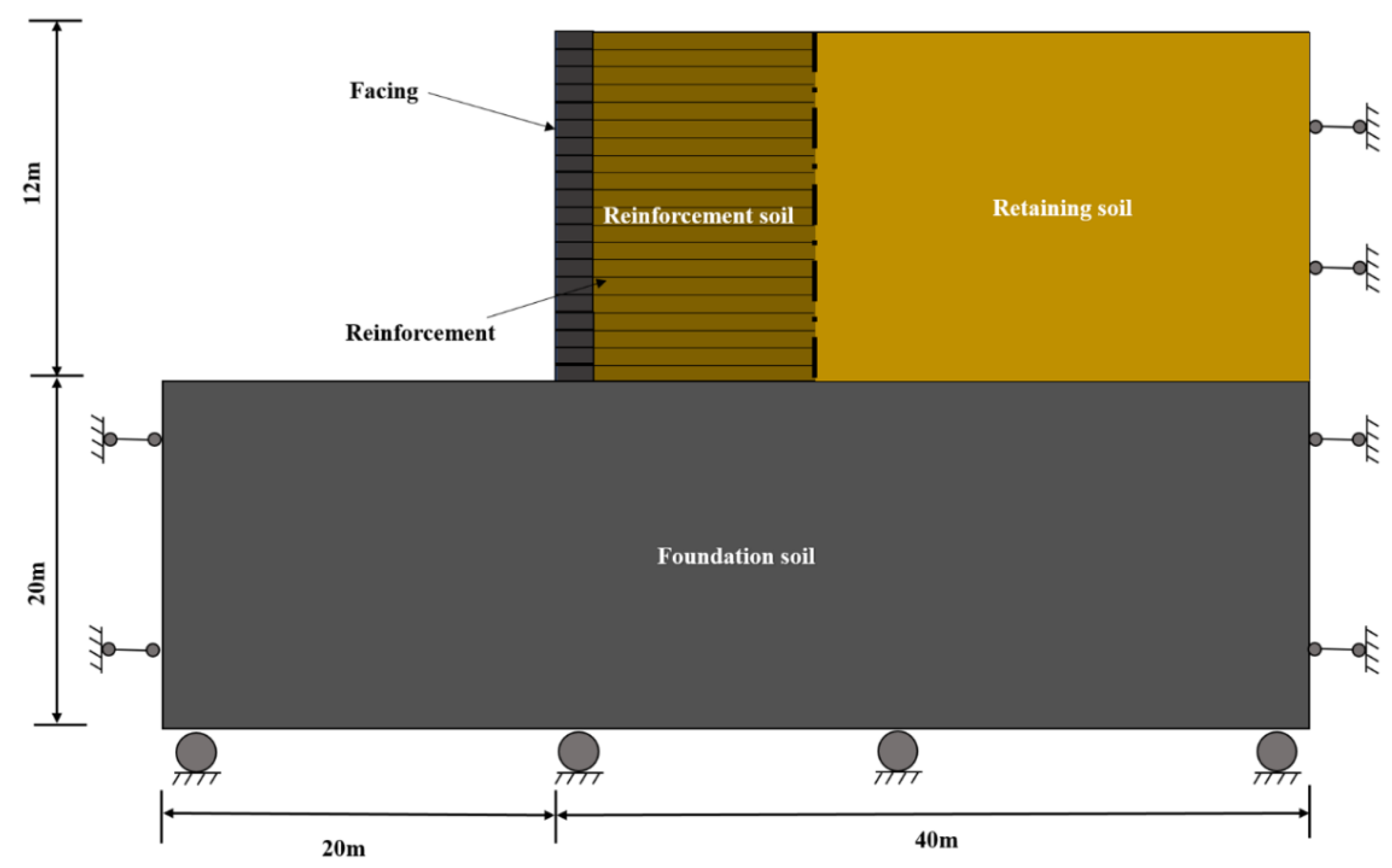
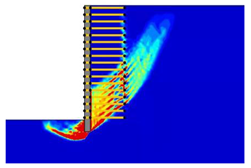
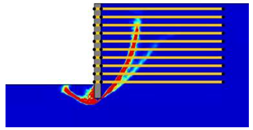
The main objective of this paper is to investigate the stability of reinforced retaining walls using the lower- and upper-bound principles in the classical plasticity theory. The analyses are carried out by the software OptumG2 (Copenhagen, Denmark) [
26], which is based on the methodology in Sloan [
27], giving rigorous lower and upper bounds on the failure load. This is known as numerical limit analysis, which only requires soil strength parameters that are familiar to geotechnical engineers. In this paper, this method is used to examine the effects of wall geometry, reinforcement, and seismic parameters on the failure mechanism and factor of safety of geogrid reinforced retaining walls. As numerical analysis can account for a wider range of influential parameters, it is a useful complement to experimental studies (typically limited). The numerical analysis results can help engineers better understand the mechanism of the problem. The lower and upper bounds are invaluable in practice, which enable accurate failure loads to be obtained by error estimates and the adaptive meshing technique.
5. Recommendations for Design
The existing design method involves internal and external stability analysis based on the limit state method. In this design method, the location of the damaged surface is often assumed, and assessment calculations are then carried out. This method generally incorporates experience-based knowledge, and the assumptions before calculation are often difficult to verify in practical applications. However, this design method does not consider the relationship between the parameters of MSE walls and failure mode. The equilibrium conditions of the analysis method proposed in this paper are applicable to the whole soil area, and the safety factor is defined in a very small range, so that engineers can meet different design requirements in the seismic design of structures according to the range. The research results of this paper provide engineers with rich references. Specific suggestions and contributions are as follows:
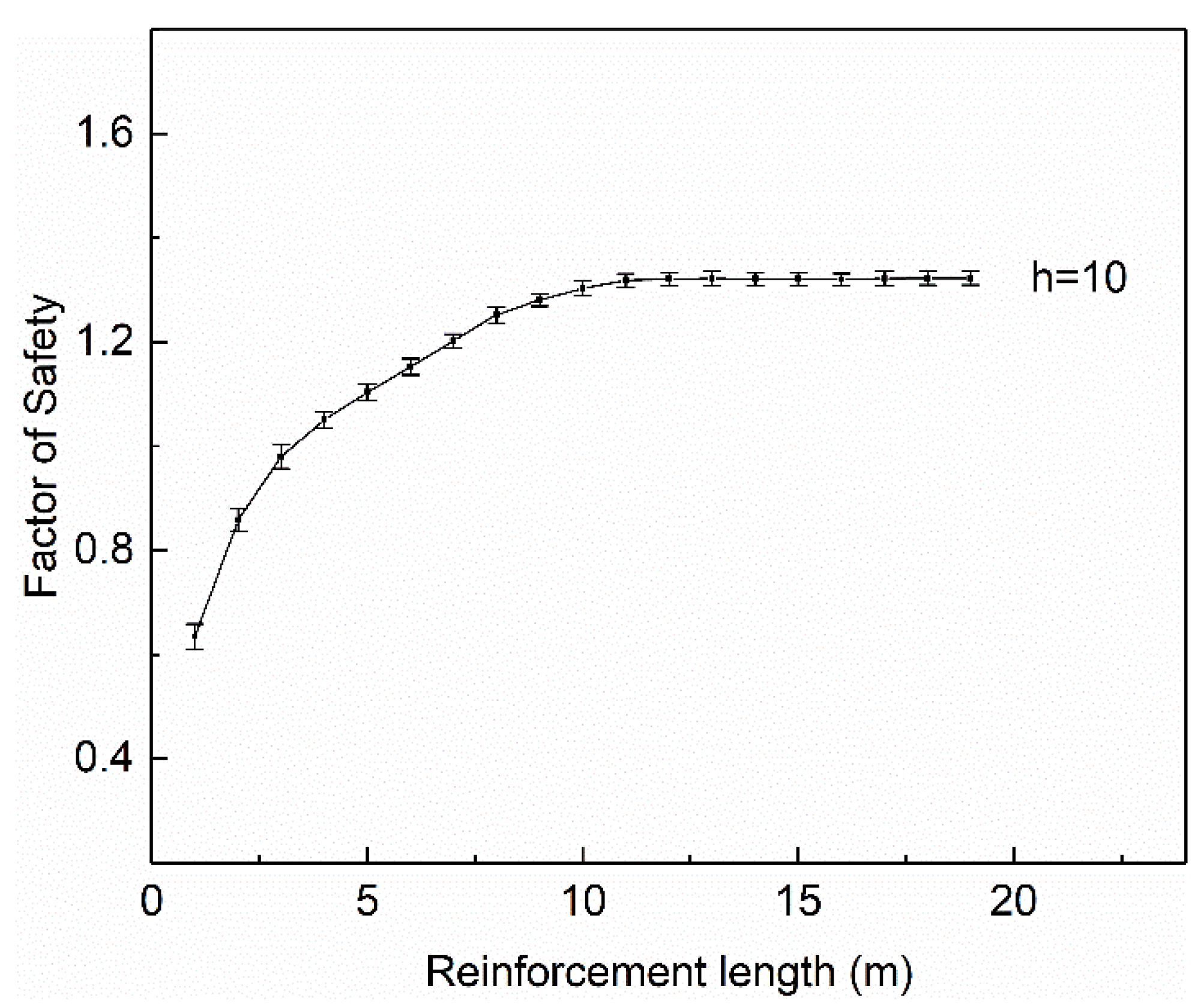
(1) Length of the reinforcement. A minimum reinforcement length of 0.7 H is recommended for MSE walls. In areas with poor foundation conditions and areas of a high seismic grade, larger lengths are required, as listed in
Table 7.
(2) Spacing of the reinforcement. When the spacing of the reinforcement is smaller than 0.6 m, the position of the sliding surface could occur behind the reinforced area. In the simulation analysis experiments in this paper, if the overturning failure mode emerged, the length-to-height ratio of reinforcement varied between 0.23 and 0.4. When the ratio was higher than 0.9, the global failure mode emerged. However, under normal conditions, parametric analysis indicated that the wall stability was not only determined by the length-to-height ratio but also determined by the reinforcement length. When the foundation conditions were limited, the stability of the wall could be improved by increasing the reinforcement length and reducing the spacing, as listed in
Table 8.
(3) Horizontal seismic load. The seismic load could significantly reduce the wall stability. Maintaining the wall in the global failure mode required higher wall design conditions. Under the baseline conditions, the reinforcement length and the length-to-height ratio of reinforcement could be increased to improve the wall stability. When the reinforcement length was limited due to the construction environment, the wall stability could be improved by decreasing the spacing of the reinforcement.
6. Conclusions
The critical reinforcement values resulting in MSE wall failure mechanism transition under the effect of various parameters were studied under different conditions. The influence of the length of the reinforcement in different cases on the stability of MSE walls was studied. The research obtained rich and interesting results, provided design suggestions for engineers, and made contributions to the field of seismic design of retaining walls. According to this research, the following conclusions can be drawn:
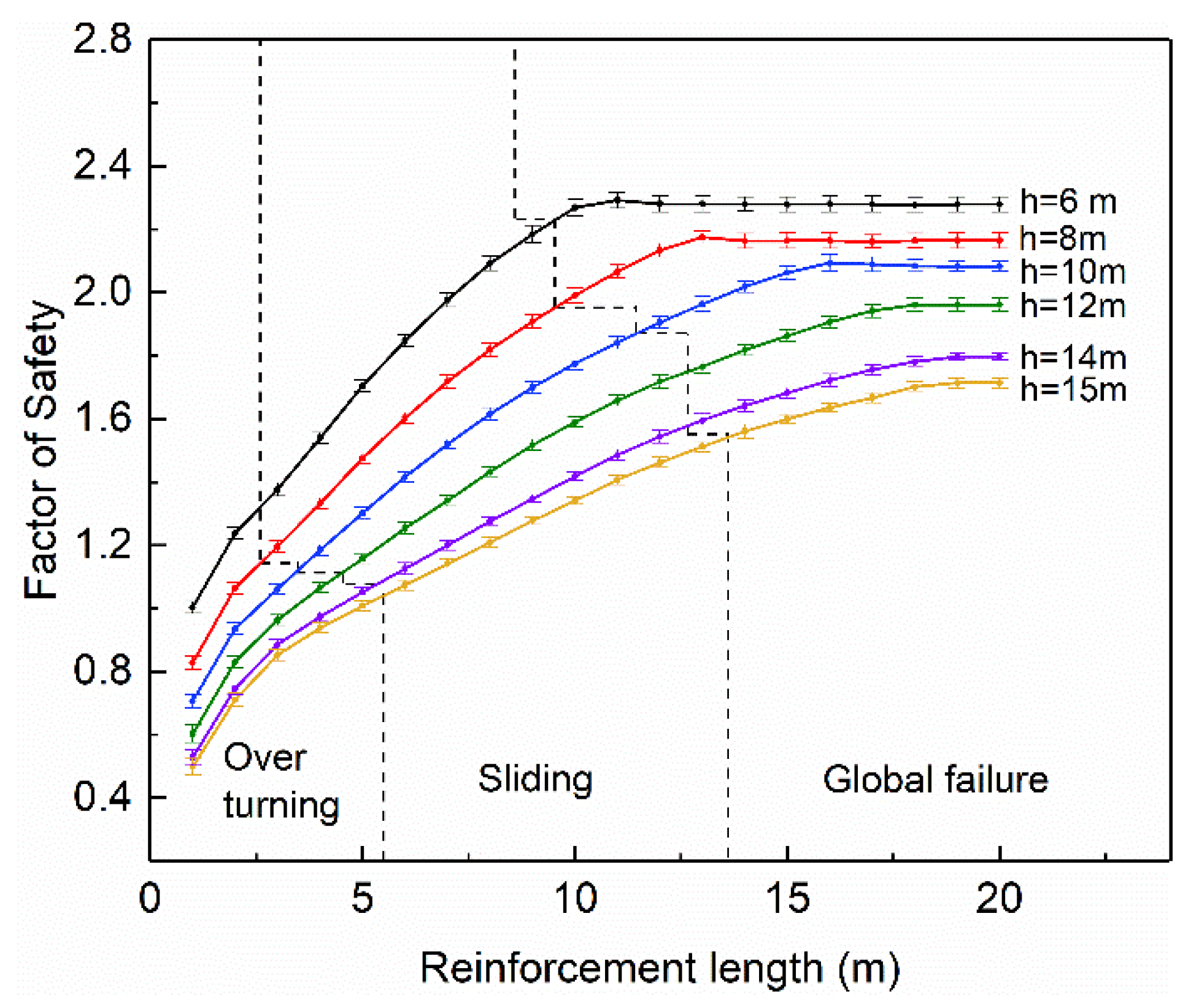
(1) Both the reinforcement length and wall height greatly affected the change in failure mode of MSE walls, based on the parameter study in this paper. When the wall height was greater than 9 m, an increase in height could reduce the strengthening effect of the reinforcement, in which maintaining a favorable failure mode required a longer reinforcement length.
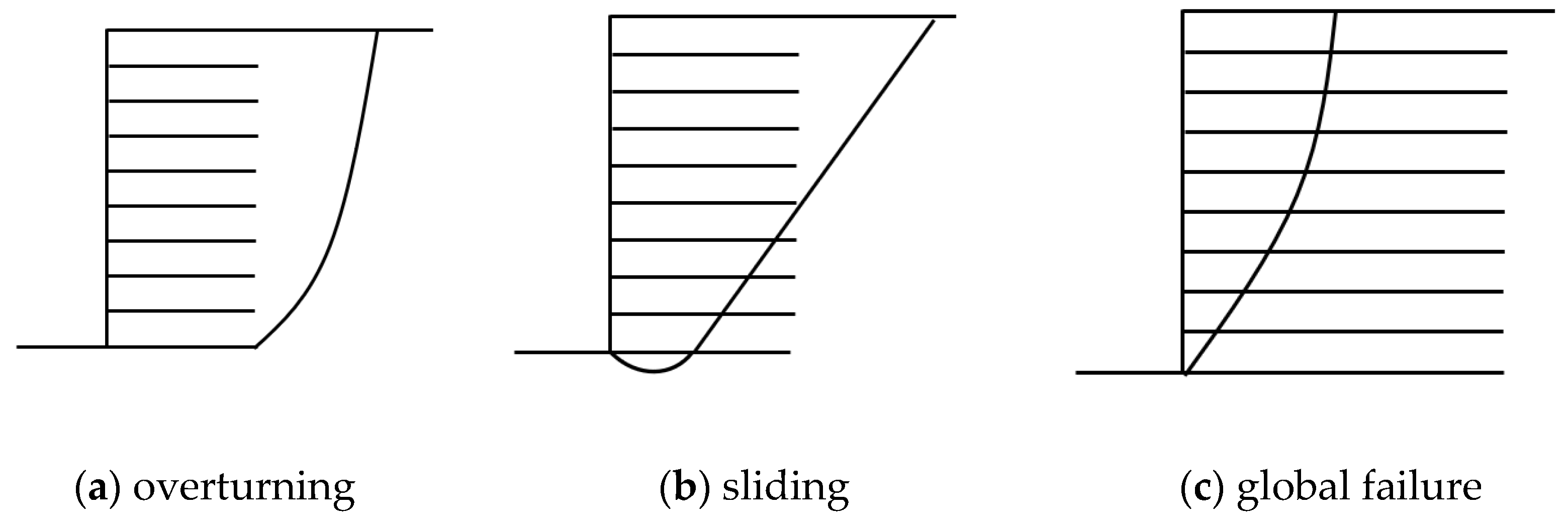
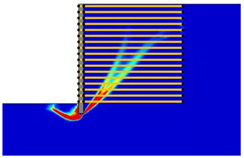
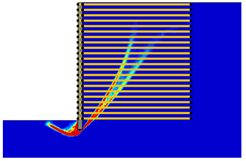
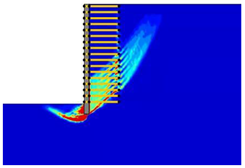
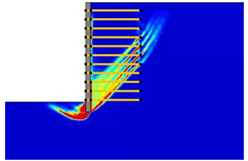
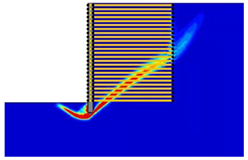
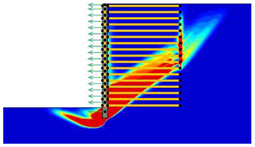
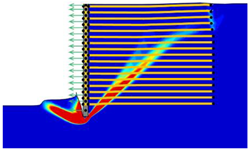
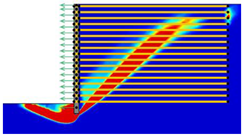
(2) With the properties involved in this paper, the critical length of the reinforcement was determined as approximately 0.4-H and 0.9-H, which divided the various failure modes into overturning failure, sliding failure, and global failure.
(3) The reinforcement spacing was an important factor influencing the failure mode of MSE walls. Increasing the reinforcement spacing from 0.3 to 0.9 m reduced the safety factor and altered the failure mode. In particular, when the reinforcement spacing was above 0.5 m, the critical length of the reinforcement increased from overturning failure to sliding failure, and when the reinforcement spacing was above 0.8 m, the critical length of the reinforcement decreased from sliding failure to global failure.
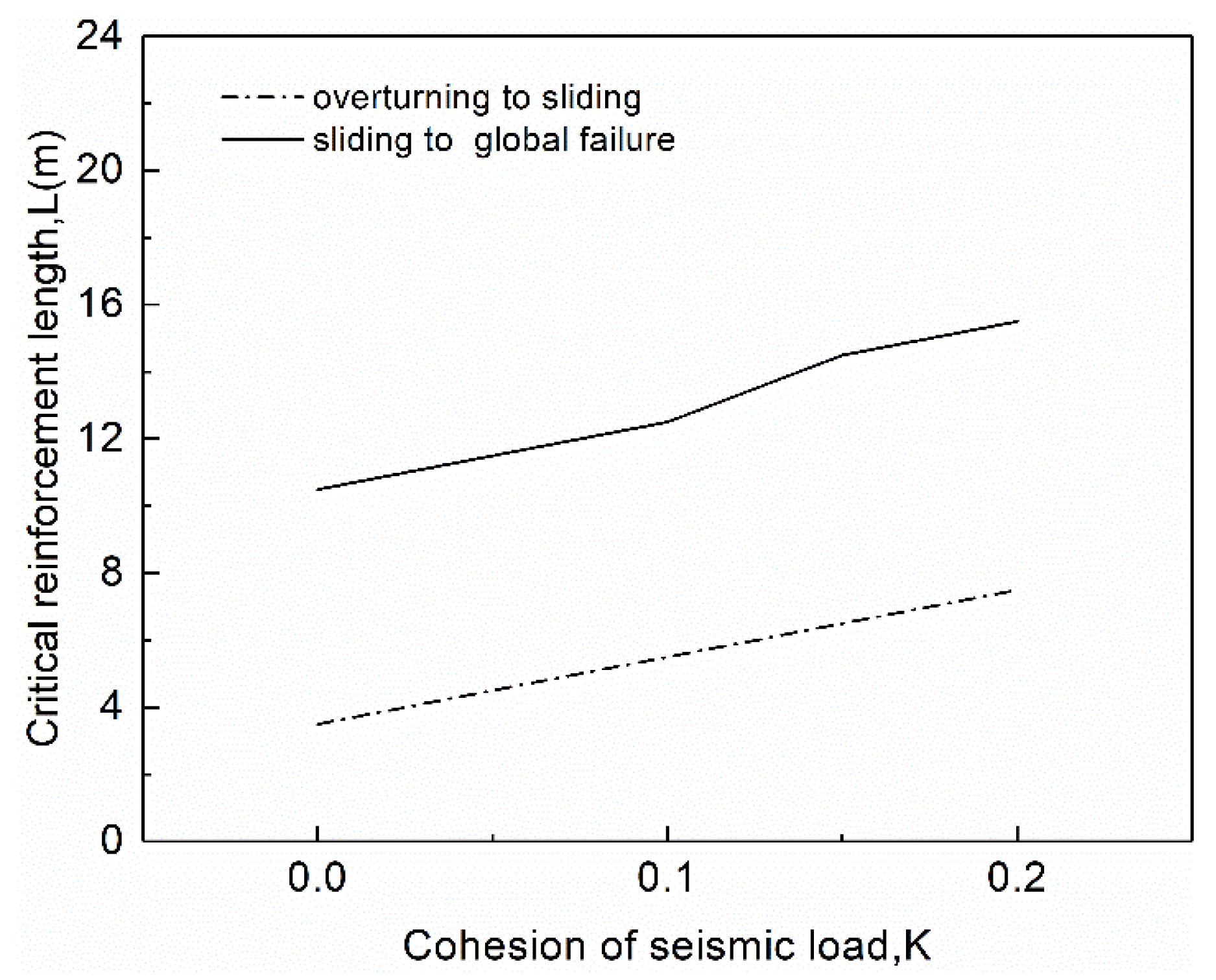
(4) The seismic coefficient obviously affected the stability of MSE walls. The required reinforcement length to maintain the wall stability in the case with a seismic coefficient value of 0.2 was almost 1.5 times larger than that in the case without a seismic load.
The assumption in this study is that elastic–perfectly plastic models cannot consider deformation. In stability analysis, there are numerous parameters in the elastic–plastic constitutive model, and inappropriate parameter selection could cause large errors. The following research direction will be to integrate the advantages of both models for parametric analysis.