Development of an Objective Low Flow Identification Method Using Breakpoint Analysis

Abstract

Low flow events (a.k.a. streamflow drought) are described as episodes where stream flows are lower or equal to a specified minimum threshold level. This threshold is usually predefined at the methodological stage of a study and is generally applied as a chosen flow percentile, determined from a flow duration curve (FDC). Unfortunately, many available methods for choosing both the percentile and FDCs result in a large range of potential thresholds, which reduces the ability to statistically compare the results from the different methods while also losing the natural character of the phenomenon. The aim of this work is to introduce a new approach for low flow threshold calculation through the application of an objective approach using breakpoint analysis. This method allows for the identification of an environmental moment of river transition, from atmospheric feed flows to base flow, which characterizes the moment at the beginning of the hydrological drought. The method allows for not only the capture of the genesis of a low flow event but, above all, unifies the approach toward threshold levels and completely excludes the impact of the subjective researcher’s decisions, which occur at the methodological stage when selecting the threshold criteria or when choosing a respective percentile. In addition, the method can be successfully used in datasets characterized by a high level of discretization, such as numerical model data, where the subsurface runoff component is not described in sufficient detail. Results of this work show that the objective identification method is better able to capture the occurrence of a low flow event, improving the ability to identify hydrologic drought conditions. The proposed method is published together with the Python module objective_thresholds for broad use in other studies.

1. Introduction

Drought, as a long-term hydrologic phenomenon, is difficult to numerically define and parameterize. Especially in the case of surface waters, where it is difficult to define the moment of drought initiation as the conditions are generally a result of numerous surface and atmospheric factors [1]. The lowering of river water levels is usually due to prolonged dry conditions; therefore, river low flows are generally considered an indicator of hydrological drought progression [2]. This indicator is somewhat easier to parameterize than other types of droughts due to a direct relation with river levels; however, one still needs some kind of criterion to define when flows are considered “low”. In response to this, Yevjevich [3] introduced the threshold level method (TLM), which was based on a threshold approach to the phenomenon. The TLM method has been widely accepted by the scientific community, and now, even in the current literature, low flow events (a.k.a., streamflow droughts) are defined as periods when river discharge is not higher than the defined threshold level [4,5]. Such a definition, however, contributed to large discrepancies in later studies [5,6,7,8,9,10,11].

Since the definition of low flows based on a predefined flow threshold was established, the methods for determining it have been extended to include statistical, hydrological, economic, and other criteria [12]. For the hydrological criteria, the value of the threshold has included: (1) lowest average annual flow, (2) highest annual minimum flow, (3) average annual minimum flow, (4) a division using one of the prior conditions using seasonal values or n-day annual minima, and others [4,12,13,14,15]. When applying statistical criteria, the most common approach is to use a specific flow percentile provided by the flow duration curve (FDC); however, the chosen value may differ depending on the study, with exceedance probabilities of p = 70, 80, 90, 95% having been used previously [2,10,12,16,17,18,19,20]. Such a range of criteria for selecting the threshold, which is a critical value in the context of the subsequent analysis of hydrological drought, results in a substantial heterogeneity of the resulting analyses and the inability to compile and compare the results [21]. This issue is compounded by the application of different low flow criteria for varying purposes (e.g., reservoir operations, water resource management, water quality, etc.). Seeing as defining and quantifying hydrologic drought is a common application of low flow analysis, developing an objective method for that purpose provides a useful tool that adds value to many associated scientific and management approaches.

Various levels of probability or graphical and other methods used to identify low flows have further contributed to the development of intermediate criteria. As strictly numerical values do not necessarily carry an environmental context, especially in complex hydrologic environments, additional criteria have begun to emerge that allow for connecting and separating periods of low flow that could have the same origin but were separated as a result of an external event (e.g., storm, reservoir, wastewater drop, etc.). Zelenhasić and Salvai [22] introduced the inter-event time criterion (IT) in which they introduced another parameter to the definition of a low flow: the maximum duration of flows that would not separate events [23]. In terms of IT, it is up to the researcher to determine the critical time (e.g., five days), which indicates the same genesis of successive low flows. Madsen and Rosbjerg [24] modified the criterion to a so-called inter-event time and volume-based criterion (IC) by supplementing the definition with the maximum volume of water supplied during the threshold exceedance time. This affected the method of determining the basic parameters of the low flow event, as accounting for the excess threshold time and associated volume to include within low flow episode parameters became a requirement. Vogel and Stedinger [25] approached this issue differently, considering the low flow in terms of hydrological drought and the related runoff deficiencies. They concluded that the appropriate criterion for the distribution of independent events should be based on the amount of water deficit created in the environment during the low flow and not on the basis of the duration of the threshold exceedance. Vogel and Stedinger [25] adapted the reservoir algorithm concept to the needs of low flow analysis, leading to the sequent peak algorithm (SPA) method.

The existence of various criteria for the division and parameterization of low flows in the literature still contributes to large methodological discrepancies. For the IT and IC criteria, depending on the study, authors use different criteria, e.g., 3-day periods [21], 5- or 6-day periods [9], or even one-month periods [26]. Furthermore, Yahiaoui et al. [27] recommended that the period should be selected each time depending on the needs of the analysis. In addition to the above criteria, the SPA algorithm has also seen wide application in the analysis of low flows [28,29]. Yet another criterion used by researchers with the same frequency is the method based on the value of the “smoothed” n-day moving average [9,30] or the minimum annual mean n-day flow [31].

The evolution of the low flow definition methods described above served to improve the definition of a low flow event to reflect the actual low flow conditions in a river, which is overall useful and encouraged. At the same time, however, the multitude of definition criteria, parameterizations, and assumptions introduces numerous combinations, and it is up to the researcher to choose a specific method appropriate to the research application. These choices have direct consequences on the impact and applicability of the results, as using a common criterion ensures the comparability of results while adjusting the criterion to the problem under study (e.g., temporal, spatial, or environmental dependence) makes the results potentially more locally representative but not directly comparable [32]. Although statistical criteria are currently the most popular, especially the Q₁₀ flow (corresponding to the 10th percentile of the flow), also referred to as Q₉₀ if the cumulative distribution function is used [33] or the 7Q₁₀ criterion (as the 10th percentile of the 7-day average flows) [34], the development of modern methods of numerical modeling introduces another issue: discretization and uniqueness of data.

In the case of observed streamflow, the primary disadvantage is data stationarity [35] or the completeness of the dataset. More often, however, observations suffer from insufficient spatial density, mainly due to the costs of their acquisition and spatial coverage. For this reason, other sources such as statistical or physical model simulations become necessary. In the case of physical models, parameterizations related to complex and/or unknown variables, such as subsurface runoff, lead to differences in accuracy and the representativeness of related processes, which during droughts, are crucial for the correct calculation of the baseline runoff and low flows in the river [6,36,37]. This sometimes leads to a large discretization of the flow values, i.e., the lowest flows can have repeated values in a dataset. If the data uniqueness is greater than 90%, then the use of the Q₁₀ as the threshold will represent statistical information; however, in some cases, for example with the National Water Model (NWM) retrospective data, minimum streamflow values are often repeated for extended periods [38]. In this case, the FDC flattens out on the lower flows, with the 10th percentile being equivalent to higher percentile values (i.e., 15th or 20th percentile). In this case, the use of percentiles as thresholds leads to the separation of values from the respective environmental information or even false statistical results if the threshold is equal to all of the other lowest flows in the data series. Such episodes will have zero volume based on the TLM definition, which further translates into issues in parameterizing low flow episodes.

All the above-mentioned problems lead to the same conclusion: there is a need to develop a criterion for the identification of low flows by means of TLM, which will allow for (1) the minimization (and ideally exclusion) of the subjective assessment of the researcher in the process of selecting threshold criteria, (2) the ability to account for the state of the environment in the process of identifying the onset of hydrological drought, and (3) the application of the methodology in a data series with a significant degree of value discretization. The aim of this work is to develop such a method without also introducing complex or computationally expensive criteria.

The remainder of the article is organized into the following Section 2: overview of the data used, Section 3: description of the method, Section 4: comparison of the newly introduced method to low flows defined using the Q₁₀ method, and Section 5: conclusions. Additionally, Supplementary Materials are available, which include information about how to obtain, install, and use the developed algorithm (a Python module termed objective_thresholds), which will allow researchers to directly apply the method without the need to reconstruct the methodology.

2. Data

The streamflow data used to develop the low flow algorithm came from the National Water Model (NWM) retrospective v.2.1 dataset (NOAA National Water Center, version: Retrospective 2.1, Tuscaloosa, AL, USA), which has a period of record from 1979–2020 [39]. The NWM was developed by the National Oceanic and Atmospheric Administration (NOAA) Office of Water Prediction (OWP) in 2016 to improve the accuracy and spatial coverage of hydrological predictions over the continental United States (CONUS) and is based on the Weather Research and Forecasting–Hydrological Modeling System (WRF-Hydro). While the NWM has undergone numerous upgrades and revisions since its release, the most recent retrospective simulation was used for this project, which utilizes the analysis of record for calibration (AORC) for initialization. Unlike the operational version of the NWM, however, the retrospective data do not incorporate data assimilation.

The study area was limited to the Southeast US, defined by the USGS Region 3 hydrologic unit (South Atlantic-Gulf (SAG)), which constitutes 338,037 NWM retrospective stream nodes (hereafter referred to as nodes) along waterways that ultimately drain into the Atlantic Ocean within and between Virginia and Florida, or the Gulf of Mexico running within and between Florida and Louisiana (Figure 1). After the evaluation of data completeness, a decision was made to include only stations of Strahler order three and higher since 80% of the lower-order nodes showed streamflow values of 0 m³/s, which, from the perspective of drought analysis, introduced the risk of a misrepresentative calculations for both threshold level and drought event statistics. The study dataset, therefore, consisted of 73,891 nodes, from which daily mean flow values were calculated from the hourly model values. Additional criteria of no more than 5% of zero or null data were introduced to avoid computational bias, which resulted in 61,948 nodes.

For the NWM nodes retained for analysis, analysis of FDCs revealed that the average percentage of unique flow values above the 90th percentile was 98%, while below the 10th percentile, it was roughly 50%. Additionally, the nodes below the 10th percentile were characterized by a low variability (

Table 1. Characteristics of the lowest 10% of values from the study data. n—number of data points; n_u—ratio of unique values; Q_m—mean flow [m³/s]; std—standard deviation [m³/s]; var—variance; Cv—coefficient of variation; IQR—inter-quartile range [m³/s].

	n	nu	Qm	std	Cv	IQR
mean	527.7	0.554	0.079	0.014	0.252	0.022
std	333.8	0.353	0.231	0.039	0.196	0.062
var	111438.8	0.125	0.053	0.002	0.038	0.004
Cv	0.633	0.637	2.917	2.825	0.779	2.831
IQR	665	0.703	0.032	0.007	0.133	0.011

, Figure 2). In these nodes, therefore, there is a situation where the lowest 10% (or even 20% in some cases) of the flow values are identical. This is likely because the model is not able to adequately reflect the influence of groundwater inflow on river discharge, especially along smaller river segments, causing predicted annual low flow thresholds to be the same values as annual or monthly minimums and/or overestimating baseflow characteristics [40].

After consideration, a decision was made to exclude 1198 nodes that were characterized by constant minimum flow values (not shown), leading to a final dataset consisting of daily flows for the period from 1 February 1979 to 31 December 2020 for 60,750 nodes (2,551,500 stream years).

3. Methods

3.1. Breakpoint Approach to Low Flow Identification

According to the generally accepted pattern of drought generation and evolution, hydrological drought is the last stage of environmental drought development [5]. The moment when primary river inflow changes from surface or shallow subsurface runoff (which characterizes mean conditions) to groundwater is an indicator of drought initiation; therefore, this transition can be identified as the beginning of low flow conditions. Based on this, then, an underlying assumption for the methodology presented here is that low flow begins at the moment when primary river inflow changes sources and baseflow conditions are reached [5,41,42,43]. To define this transition objectively, one can follow the so-called curve breakpoint method—where the breakpoint is identified as a change in the slope of a trend line within the hydrograph—as the most ecologically relevant moment [44,45]. This approach is often used in flood analysis, where the breakpoint is most often interpreted as water levels reaching bankfull conditions [46,47], but can also be used for drought studies if applied correctly. Considering the range of low flows in a series of sorted values, the breakpoint of the curve will be the moment of change in the river supply from surface runoff to groundwater [43,48]. Tomaszewski [48] proposed this approach by determining the minimum annual (or monthly) flows from a series of data. The moment of supply change is then defined as a point on the curve in which there is a significant change in the slope of the regression line, signifying a change in the series (Figure 3). This point can be used as the estimator of the threshold level for hydrological drought.

When examining various cases of the distribution of annual minima, one may encounter cases in which the change of the trend is inconclusive or absent (Figure 3) [49]. In this case, Tomaszewski [43] suggests adopting the highest annual minimum flow as the threshold. According to observations from an area in eastern Poland, the value of the highest annual minimum flow in catchments where the trend changes were not found coincides with the 30th percentile, while other studies indicated the 20th or 10th percentile [49,50]. This discrepancy may be related to the length of the data series being analyzed when using annual values, as the shorter the data series, the fewer the points from which to derive curves and find the trend change. This approach also fails in the case of data series characterized by a high degree of discretization, like in the case of NWM, as explained in Section 2.

While these issues can be addressed by incorporating the full flow time series in the calculation of the low flow breakpoint, which maximizes the number of data points while minimizing discretization, such an approach introduces the possibility of the breakpoint being defined at the upper end of the FDC in relation to other environmental factors such as over-bank flow conditions. As a result, it is important to truncate the full time series to only include the lower end of the FDC to focus the method on only low flow patterns. To that end, one can assume that low-intensity (a.k.a. shallow) low flows are those related to general environmental water shortage where researchers set limits of low flow around the 30th percentile (or highest of the lowest annual flows). In the case of high-intensity (a.k.a. deep) low flows, which are indicative of severe hydrologic drought, the threshold is usually around the 10th percentile (or the mean of the lowest annual flows or similar methods). This suggests that the expected optimal threshold may be somewhere from the 10th–30th flow percentiles, with any values below the 50th percentile reflective of dry conditions [8,51].

3.2. Breakpoint Algorithm Selection

To determine the breakpoint of the data series corresponding to each node in the study data, several of the most recognized breakpoint algorithms were analyzed, including:

• Fisher-Jenks algorithm (FJ) [52];
• Dynamic programming (DP) [53,54];
• Kernel change detection (KCD) [55,56];
• Binary segmentation (BiS) [57];
• Bottom-up segmentation (BUS) [54,58];
• Window sliding segmentation (WS) [54,59,60];
• K-means algorithm (KM) [61,62];
• Ward method (WA) [63,64].

Apart from the K-means algorithm, all methods were able to replicate the same obtained threshold result over 10 repetitions of the calculations. For KM, only 0.56% of the nodes achieved the same value over the 10 repetitions. This is due to the assumption of the method starting point as each time, the method randomly initiates the cluster centers and then progresses until the stabilization of the distance matrix occurs. Changing the method to start from the same space every time to unify the outputs would add an additional source of researcher intervention into defining the initial conditions, which stands in opposition with developing objective research guidelines.

The highest values of the low flow thresholds were obtained by the KM and KCD algorithms, while the lowest were obtained by the WS algorithm (Figure 4). Among the tested methods, the WS and KM algorithms were characterized by the largest deviations from the mean value, while the FJ and WA algorithms were characterized by the values closest to the mean of all the tested algorithms, with the mean difference not exceeding 0.2% (Figure 4). The execution time (per hundred nodes) of the DP, KCD, BiS, and BUS algorithms exceeded 10 s, whereas WS and KM required around eight seconds, and FJ only four seconds (Figure 4). Considering the above, the FJ algorithm was selected as the preferred breakpoint detection algorithm as it resulted in values closest to the mean of all tested algorithms and had short execution times.

In the absence of a discrete breakpoint in the dataset, represented by the lower range of the FDC, all the methods showed a tendency to select a specific point in the dataset. For example, the KM algorithm tended to choose the highest value as the breakpoint, while WS generally chose the lowest value. Four algorithms (FJ, DP, KCD and BiS) tended to choose a value close to the median of the distribution. To test if the results of the breakpoint algorithms were statistically different from the medians, a T-test was run using series representing the objective threshold based on the FJ algorithm, the median, and the percentile representing the middle probability value of a given range (e.g., for a FDC range of 30% the values of Q₁₅ was considered the middle probability). Since all series were considered part of the same data distribution, a dependent T-test was used. The differences between the objective thresholds, median values, and middle-range flow percentiles were shown to be statistically significant, meaning the series did not result in the same values most of the time (

Table 2. Results of T-tests for the comparison of series representing objective thresholds defined using the FJ algorithm (Q_obj), median value, and middle percentile flow (Q_p) for multiple FDC ranges.

Relation	Qobj–Median	Qobj–Qp	Median–Qp
FDC range	20%
statistics	−54.0508	−59.3941	4.6209
p-value	0.0000	0.0000	0.0000
FDC range	25%
statistics	−51.2043	−58.6077	4.4995
p-value	0.0000	0.0000	0.0000
FDC range	30%
statistics	−39.3186	−44.1184	4.0386
p-value	0.0000	0.0000	0.0001
FDC range	35%
statistics	−22.8904	−25.4409	4.0794
p-value	0.0000	0.0000	0.0000
FDC range	40%
statistics	8.5917	13.9009	3.4002
p-value	0.0000	0.0000	0.0007
FDC range	45%
statistics	38.5965	41.6176	3.2249
p-value	0.0000	0.0000	0.0013
FDC range	50%
statistics	49.8975	50.6962	3.1834
p-value	0.0000	0.0000	0.0015

). This shows that although the FJ method showed a tendency to define the breakpoint of the FDC as a value close to the median, the resulting Q_obj remained statistically significant in its difference from the median.

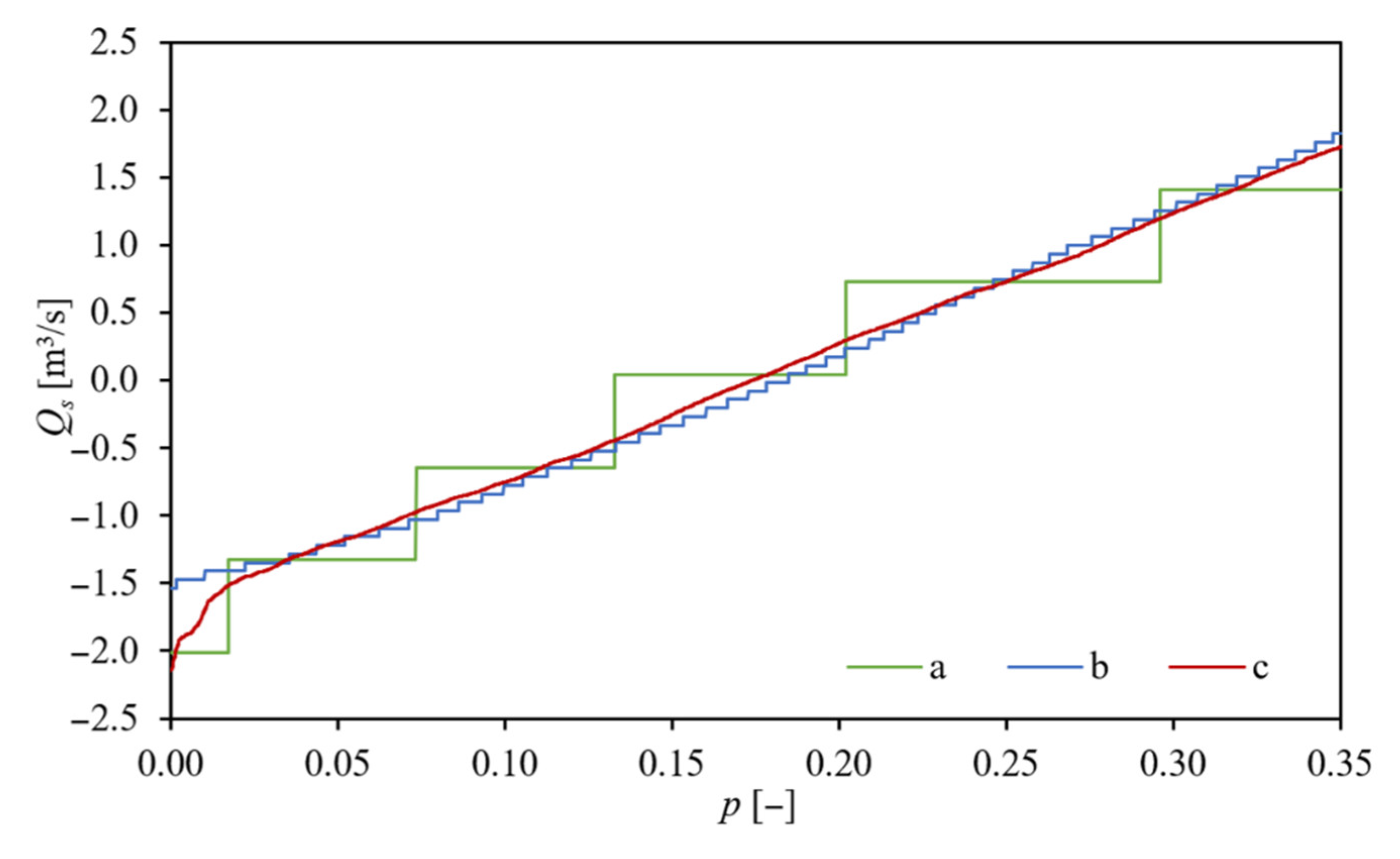
3.3. Objective Threshold Approach Description

Based on the above considerations, a method was derived that takes into account the range of flows from the lower part of the FDC to estimate the breakpoint corresponding to the moment of change when river flow is based on predominantly atmospheric input (in the range of average flows) to groundwater input (or other non-atmospheric supplies, such as reservoir discharge), characteristic of lower flow ranges. The calculation method consists of the following steps:

1.

Determination of the number (n) of points in the daily flow series needed to calculate the breakpoint based on the lower FDC range (by default: below the 35th percentile, as described further in the Results section):

Q: {Q ∈ R + | Q ≤ Q₃₅}

2.

Implementation of the Fisher–Jenks algorithm to define the breakpoint [52] by minimizing deviation of each class from the class mean, while maximizing the deviation of each class from the means of the other classes:

a.

Order flow data series in increasing order and assigning weights (w):

w: i ∈ {1,…,n}

b.

Compute the diameter matrix Di,j to store the distance between all pairs of n observations, such that:

1 ≤ i ≤ j ≤ n

c.

Populate the error matrix with variance of n observations when classified into two classes (one class for atmospheric driven resources, representing mean flow conditions (FDC part above breakpoint), and second for the drought conditions and baseflow (FDC part below breakpoint)):

$$E\left[P_{i,L}\right]=\min \left(D_{1,j-1}+E\left[P_{j-1,L-1}\right]\right)$$

d.

Locate the optimal partition from the error matrix by maximizing inter-class variance and minimizing intra-class variance:

$$E\left[P_{n,2}\right]=E\left[P_{j-1,1}\right]+D_{j,n}$$

3.

Application of the defined breakpoint (Q_t) as the low flow threshold for further analysis of low flow distribution, streamflow droughts, or for water management systems at the alert point, according to the following relation:

$$Q_{lf}=\{\begin{array}{c}0, if Q>Q_t\\ Q, if Q\le Q_t\end{array}$$

where: Q—flow in a specific moment,

• Q_t—threshold flow determined by Fisher-Jenks algorithm,
• Q_lf—flow identified as low flow.

The calculated flow breakpoint value can be directly applied as the threshold in the TLM for low flow or hydrological drought analysis.

The above method can be applied directly in other research by using the lowflow module from the objective_thresholds Python package. More information on the installation and usage of this can be found in Supplementary Materials, available with this article or at the package repository website.

4. Results

Analysis carried out on the study data shows that the 35th percentile of daily flows (indicated in Section 3.3) is sufficient enough to find the curve breakpoint, indicating a change in the river supply, as all of the low flow thresholds identified by the objective breakpoint method did not exceed the 30th percentile of flow, and in most cases (around 83%) the threshold fell within the 15th and 20th percentiles (Figure 5).

The relation between Q₁₀ and Q_obj can be represented by a linear relation (Figure 6), with R² values of around 0.998 for the study area rivers. This relationship reveals that, on average, Q_obj is 1.17 times higher than the Q₁₀ threshold. Higher threshold values relate to an increase in low flow parameters; however, because the values fall in the 10th–30th percentile range, they remain in the range of “shallow” and “deep” streamflow drought as indicated in Section 3. Less than 1% of the cases in the tested data sample had threshold values lower than the associated Q₁₀, although in about 90% of the nodes, the increase did not exceed 100% of the Q₁₀ threshold value (Figure 6). In a few cases, the ratio of Q_obj to Q₁₀ exceeded three; however, these cases corresponded to situations when the threshold value determined by the Q₁₀ was low (~0.01–0.03 m³/s) due to the flattening of the FDC at the lower range (multiple repetitive values), while the threshold determined by the objective breakpoint method was around 0.05–0.10 m³/s.

When comparing the average annual number of days with low flows, determined by the classical Q₁₀ method and the objective breakpoint method, a different distribution of the density function occurred (Figure 7). Concerning the Q₁₀ method, in most cases the duration of low flow events averaged around 30–35 days, with a low variance around this value (Table 2). For low flow duration based on Q_obj, the distribution has a higher mean and variance. In most cases, the average number of low flow days each year is about 60; however, due to a more normal distribution of values in the series, it is possible to better capture the specific environmental conditions occurring in each catchment area individually. Both distributions are left skewed, indicating that there are nodes with a lower number of days with low flow. For Q₁₀, the kurtosis of the distribution was 4.0, while for Q_obj, it was 2.6 (

Table 3. Descriptive statistics for the distribution of the annual number of days with low flow for Q_obj and Q₁₀ methods: μ—mean [m³/s], m—median [m³/s], σ—standard deviation [m³/s], β2—kurtosis, S_kp—skewness, n_σ1,2,3—percent of values within one, two and three σ from μ.

	μ	m	σ	β2	Skp	nσ1	nσ2	nσ3
Qobj	59.64	62.05	16.03	2.635	−1.315	76.76	94.49	97.45
Q10	32.40	36.45	8.816	3.979	−2.012	85.62	92.74	96.49

), implying a much more leptokurtic distribution for Q₁₀ (as shown in Figure 7).

Due to the general increase in the low flow threshold value, using the Q_obj method relative to Q₁₀, the basic parameters of low flow (e.g., number of events, duration, and volume) change accordingly. In the case of the number of low flow events determined using Q₁₀, for each of the analyzed nodes, about 50–100 low flow events were observed during the 42-year study period (upper range was 175). These values increased substantially when using Q_obj, where both the mean and the median increased by about 50 (Figure 8). The maximal number of episodes increased from 200 for Q₁₀ to 300 for Q_obj, which translates to an average of 8.4 days per episode for Q_obj and 6.3 days per episode for Q₁₀ per year. The low flows identified by the objective method are longer, which allows for the inclusion of periods occurring in streamflow, even when additional criteria, of a minimal time of 7 days, are applied [12,38].

The duration of the low flows varied slightly more than the number of events. In the case of Q₁₀, in most cases the low flows did not last more than 2000 days in total over the study period. However, the mean and median values are close to the lower and upper IQR limits, respectively (Figure 8), which indicates that, while outliers shift the median towards the upper limits, the considerable number of low values (around 1000 days) shifts the mean to the lower limit. This introduces inconsistency to the spatial distribution of low flows (Figure 8). When using Q_obj, the range of values is higher, but this corresponds to the percentile range indicated earlier (convergence in relation to the 15–20th percentile) such that as the percentile value is doubled, the duration of low flows is doubled. The mean and median of the distribution are closer to each other and oscillate within the center of the IQR, as in the cases of normally distributed series (Figure 8).

Although the median low flow volume for both methods oscillate around a similar value, it is relatively low. This is due to the large share of low-order rivers in the studied dataset, in which no considerable outflow deficiencies developed. Nodes of Strahler order three and four constitute around 73% of the total nodes, which affects the shifting of the median volume of low flows to a lower range (Figure 8). However, when analyzing the distribution of the values, the wider distribution of the volume observed with Q_obj better captures the diversity of environmental conditions leading to the formation of outflow deficiencies with varying intensity.

Due to the way in which the definition of the TLM method is constructed, where the low flow is a period with a flow equal to or lower than the adopted threshold, the phenomenon of a zero-volume low flow event might occur. This problem is mostly associated with model data, where a small number of unique values in the lower FDC range are present due to high discretization. This leads to the inclusion of days that meet the mathematical criteria for low flow, but due to the occurrence of the same value in the associated outflow hydrograph, the threshold value corresponds to a volume of zero.

In terms of spatial relationships, the analysis was conducted based on Strahler stream order division. Within the study dataset, the highest river order is eight, which included two rivers: the Mobile River and the Apalachicola River. With Q_obj, there is a clear distinction between low flow volumes between these two rivers, while Q₁₀ shows similar volume ranges for both rivers (Figure 9). A similar pattern exists for the distribution of total low flow duration time, where the Mobile River has shorter durations, and the Apalachicola River has longer durations distributed along the reach. For Q₁₀, the duration of low flows is similar among the two rivers, albeit with some outliers showing no distinct spatial pattern along the reach. The distribution of low flow volumes in rivers of order seven is similar for both methods, with four rivers having higher volumes when using Q₁₀ (Figure 9); however, the length of low flows is different with Q₁₀, resulting in no spatial differentiation (with some outliers), while Q_obj varies spatially. In general, most rivers have longer total low flow durations in their upper reaches that decrease downstream, which reflects the natural tendency of smaller tributaries to have a faster response in river levels to environmental events that drive streamflow. This pattern becomes more pronounced at lower Strahler stream orders, where the biggest differences are noted in the spatial distribution of low flow. Along these river reaches, the highest low flow volumes and times occur within the eastern part of the study area in North and South Carolina, as well as central parts of Georgia and Alabama. This relation is, however, not reflected in the Q₁₀ method, where the spatial distribution of low flow volumes and times is relatively equal throughout the study area.

The above observations are highlighted when considering the relation between the duration of low flows and their volumes (Figure 10). In general, Q_obj results in a wider spread of values relative to Q₁₀, representing a greater difference in environmental conditions. This means that either the change in duration times does not affect the volumes, or changes in the volumes are not reflected in the changes in duration. Additionally, Q_obj results in a lower number of nodes with volumes close to 0. It is worth mentioning that for nodes with higher Strahler stream orders (e.g., seven and eight), the relationship changes between the two thresholds. For Q_obj, the volumes are usually close when there are small changes in duration time, while for Q₁₀, the durations are close when volumes are prone to change. This is a direct result of the statistical character of Q₁₀ and the consequences defined earlier. The strength of the relationship between low flow time and volume depends on the stream order; however, when considering the mean correlation values, they are higher for the objective method by approximately 0.22 (Q_obj $\overline{r}=0.57$ and Q₁₀ $\overline{r}=0.35$).

Q₁₀ is unable to accurately represent spatial relations and differences, and due to its statistical nature, results in constant, undifferentiated low flow patterns across the study area (with some randomly occurring outliers). At the same time, Q_obj is able to distinguish spatially varying river characteristics, such that low flows identified by this threshold vary spatially and along the course of individual rivers. Q_obj allows for the accurate capture of the natural character of events like streamflow droughts and introduces the environmental aspects to the analysis, taking into account the specificity of a given river in the studied node. As the objective threshold (Q_obj) fell within the 10th–30th percentile range for all nodes used in this study, it is important to investigate the relationship between not only Q_obj and Q₁₀ but also between Q_obj and Q₃₀ to better understand the pattern of the objective threshold values relative to the static statistical criteria. As shown in Figure 11, while the correlations between Q_obj and both Q₁₀ and Q₃₀ have a strong linear relationship, the slope of the resulting regression lines shows opposite values relative to the 1:1 trend line. In other words, for Q_obj compared to Q₃₀, instead of exceeding the objective threshold value for a given percentile, there is a decrease in value relative to the percentile. This is expected as statistical thresholds inherently maintain a constant frequency of events and always result in the same part of the dataset considered as an event (for Q₁₀ this will be 10% of data and for Q₃₀, 30% of data, regardless of the environmental aspects of the river).

5. Conclusions

Augmenting available hydrological data with numerical model data provides additional information about the state of local-scale environments, and supplements the spatial deficiencies resulting from the limitations of existing river observation networks. However, the inclusion of model data contributes to issues with data quality and interpretation, which are related to the quality of the models themselves, their complexity, and the level of discretization of the resulting data. The computational capabilities of modern computers allow for the use of more advanced and effective computational methods in research; therefore, it is worthwhile to define those methods that can be used in turn to define and describe hydrological conditions, irrespective of the source of the data, especially for the analysis of extreme events such as floods or droughts. For the latter, definitions have historically been based on methods introduced decades ago, and although effective, there are distinct limitations related to the subjective decisions of researchers about the threshold level of low flows or the use of statistical criteria in defining a low flow (e.g., Q₁₀, Q₃₀, 7Q₁₀, etc.). This article presents a new way of defining the low flow threshold based on an objective approach, utilizing a breakpoint method derived from a given streamflow time series, which is more representative of environmental criteria.

The introduced method is based on the use of the Fisher–Jenks algorithm to find the breakpoint of a curve constructed from 35% of the lowest flow values, which corresponds to the lower FDC range. The resulting breakpoint corresponds to the moment of change of the way a river input is derived from primarily atmospheric (representative of normal conditions) to groundwater sources (representative of drought conditions). The use of the objective breakpoint approach allows for the inclusion of these inherent environmental conditions into the TLM method, which then excludes subjective researcher decisions regarding the low flow threshold value or percentile. This allows for a more robust, data-driven approach to defining low flow thresholds that can be applied to both observed and simulated hydrologic time series.

The comparison between Q_obj and the widely used Q₁₀ threshold reveals that Q₁₀ is unable to differentiate spatial patterns, resulting in a similar range of defined low flow events, with skewed, widely spread distributions of low flow parameters. Based on the same data, Q_obj is able to better capture the natural characteristics of rivers, allowing for spatial recognition of the drivers responsible for streamflow drought occurrence. The objective threshold approach outperforms set statistical criteria (e.g., 10th percentile) in terms of spatial pattern recognition by introducing environmental factors into the threshold definition. Additionally, low flow parameters such as duration and volume are closer to a normal distribution when defined using Q_obj, with fewer outliers and volumes close to zero. The correlation between low-flow duration and volume depends on the stream order. On average, stream order to T and V correlation is higher by 0.22 for Q_obj, compared to Q₁₀.

The computational methodology presented in this article can be applied directly to other research by importing a Python module called objective_thresholds. Details on how to install and use the module are available in the Supplementary Materials available with this article and in the module’s documentation in the Python library and its repository.