Inverse Trend in Runoff in the Source Regions of the Yangtze and Yellow Rivers under Changing Environments

Abstract

The source regions of the Yangtze River (SRYZ) and the Yellow River (SRYR) are sensitive areas of global climate change. Hence, determining the variation characteristics of the runoff and the main influencing factors in this region would be of great significance. In this study, different methods were used to quantify the contributions of climate change and other environmental factors to the runoff variation in the two regions, and the similarities and differences in the driving mechanisms of runoff change in the two regions were explored further. First, the change characteristics of precipitation, potential evapotranspiration, and runoff were analyzed through the observational data of the basin. Then, considering the non-linearity and non-stationarity of the runoff series, a heuristic segmentation algorithm method was used to divide the entire study period into natural and impacted periods. Finally, the effects of climate change and other environmental factors on runoff variation in two regions were evaluated comprehensively using three methods, including the improved double mass curve (IDMC), the slope change ratio of cumulative quantity (SCRCQ), and the Budyko-based elasticity (BBE). Results indicated that the annual precipitation and potential evapotranspiration increased during the study period in the two regions. However, the runoff increased in the SRYZ and decreased in the SRYR. The intra-annual distribution of the runoff in the SRYZ was unimodal during the natural period and bimodal in the SRYR. The mutation test indicated that the change points of annual runoff series in the SRYZ and SRYR occurred in 2004 and 1989, respectively. The attribution analysis methods yielded similar results that climate change had the greatest effect on the runoff variation in the SRYZ, with a contribution of 59.6%~104.6%, and precipitation contributed 65.3%~109.6% of the increase in runoff. In contrast, the runoff variation in the SRYR was mainly controlled by other environmental factors such as permafrost degradation, land desertification, and human water consumption, which contributed 83.7%~96.5% of the decrease in the runoff. The results are meaningful for improving the efficiency of water resources utilization in the SRYZ and SRYR.

1. Introduction

As an essential part of the hydrological cycle, river runoff is one of the forms of water resources and the source of water for human production and living. However, with climate change and the growing impact of human activities, the river runoff of some of the world’s rivers has undergone significant changes [1,2,3]. Statistical results indicated that 22% of the 200 largest rivers in the world showed a significant reduction in annual runoff [4]. Climate change has had significant effect on the water cycle in the basin through factors such as precipitation, temperature, sunshine, wind speed, etc. [5,6], with precipitation being the crucial driving factor [7]. In addition, with rapid economic development, human activities are altering the ecological environment of a basin in the form of greenhouse gas emissions, land-use changes, water conservancy construction, and human water consumption, resulting in an increasingly significant effect on river runoff [8,9]. Therefore, evaluating the influence of climate change and human activities on river runoff is meaningful for rational water resources management, protecting ecological balance, and maintaining sustainable socio-economic development [10].

Three common methods are used for exploring and quantitatively describing the runoff variation in a basin, including statistical methods, hydrological model simulation methods, and Budyko-based elasticity method [11,12]. The empirical statistical methods include the double mass curve and the cumulative slope change methods [13]. Although these methods are simple to calculate, they lack a clear physical basis [14]. The hydrological model simulation methods are based on the actual physical processes, and the physical mechanism is relatively complete [15]. In addition, the simulation accuracy of the hydrological methods is also improved with the innovation and popularization of computer technology. However, the hydrological model contains many parameters [6], and the simulation results depend largely on various assumptions in the model, with a significant degree of uncertainty. In contrast, the Budyko-based elasticity method is based on the hydrothermal balance and has a solid physical basis [1,14]. Therefore, this method is intensively used around the world to quantify the impact of various factors on runoff changes [16,17,18,19], and results indicate that the performance of this method is even comparable to the hydrological models [20,21].

The source regions of the Yangtze River (SRYZ) and Yellow River (SRYR) are located in the Qinghai-Tibet Plateau, which is known as the “China Water Tower” [22,23]. Because of its unique geographical location and climatic conditions, the region is an essential ecological protection barrier for China as well as a “sensitive zone” and “initiation zone” for East Asia and even global climate change [24,25]. However, in recent years, the SRYZ and SRYR have experienced a series of problems such as increasing temperature, decreasing permafrost, retreating glaciers, shrinking lakes, and land desertification [24,26,27,28], which caused significant variation in regional water-cycle processes. More importantly, the runoff in the two regions also affected the water resources in the middle and lower reaches [26,28]. Recent studies have reported the runoff variation characteristics and possible impact factors in the SRYZ and SRYR. Shi et al. [29] analyzed the variation characteristics of precipitation in the Three River Headwaters (TRH) region from 1961 to 2014, and the results indicated an increasing trend in precipitation on the annual scale. Bai et al. [30] suggested that the temperature increase in the SRYZ and SRYR was significantly higher than in most parts of China and the world, and further warming and drying will inevitably have a significant effect on the ecosystems in the source regions. Zhang et al. [26] reported that annual runoff and dry-period runoff in the SRYR decreased significantly during 1958–2005, while the runoff in the SRYZ showed an increasing trend, especially during the flood season. Moreover, some scholars have conducted an attribution analysis of runoff variation in the two regions [31,32,33]. However, few studies have compared and analyzed the similarities and differences in runoff variation and the corresponding drivers in the two regions. Furthermore, previous studies usually used a single evaluation method, which leads to the uncertainty in evaluation results. Glaciers and permafrost are widely distributed in this region, and its change has more obvious influence on runoff than other regions. Hence, glaciers, permafrost, and human activities were categorized as other environmental factors in this study. The impacts of climate change and other environmental factors on runoff variation were distinguished by the Budyko-based elasticity method, and the double mass curve and the cumulative slope change methods were also used to verify the results.

The specific objectives of this paper are to (1) analyze the interannual variation trend of precipitation, potential evapotranspiration, and runoff and determine the mutation points of the annual runoff series; (2) analyze the intra-annual distribution characteristics of runoff and investigate the relationships between runoff versus precipitation and potential evapotranspiration; (3) quantify the contribution of various factors to runoff variation; and (4) comprehensively analyze the internal similarities and differences in the driving mechanism of runoff changes in the SRYZ and SRYR. The specific steps of analysis and calculation in this study are shown in Figure 1. The findings can provide key information for improving the ecological environment of the source regions.

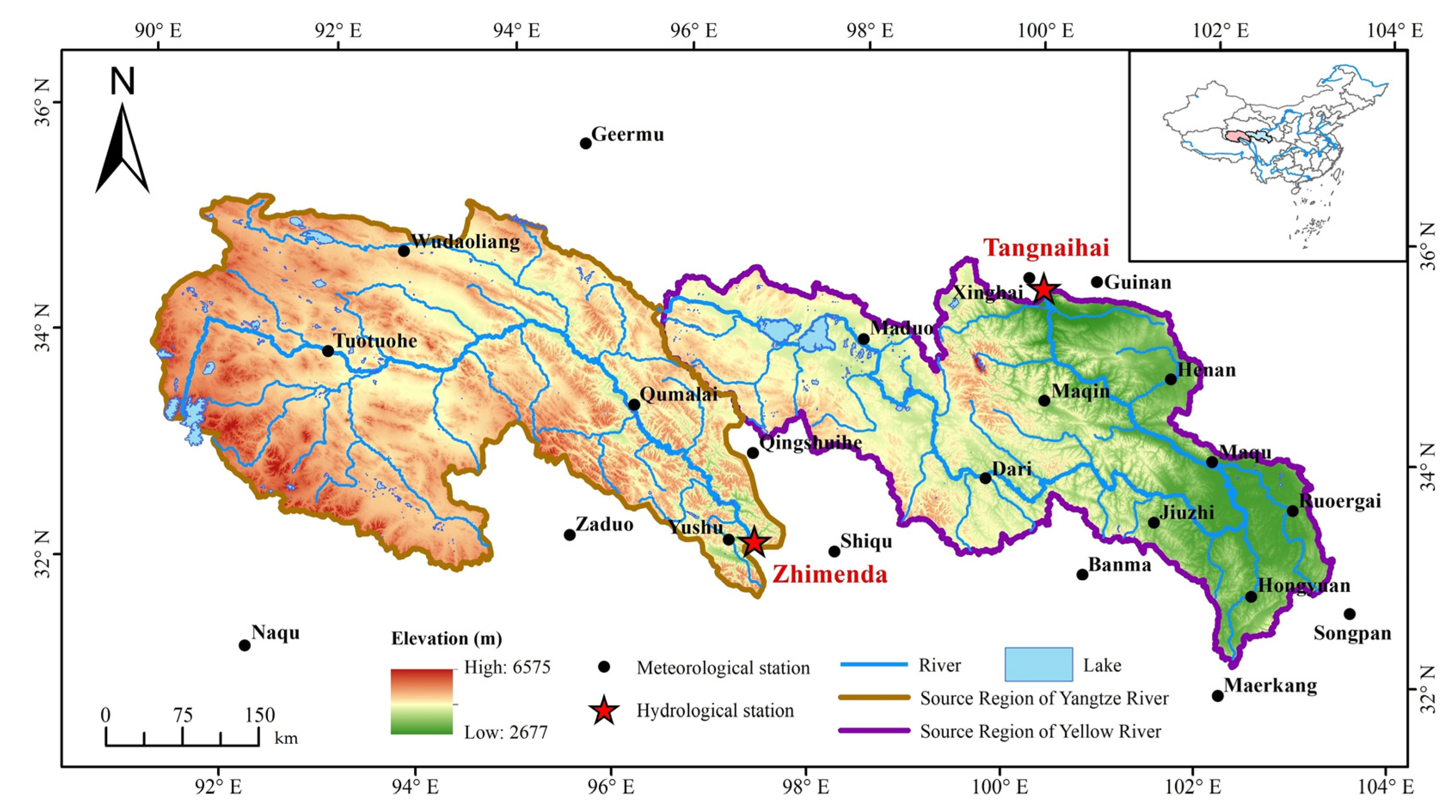
2. Study Area and Datasets

2.1. Study Area

The source regions of the Yangtze River (SRYZ) and the Yellow River (SRYR) are dominated by mountainous landforms with complex topography and an average elevation generally above 4000 m. The climate type of the basin is typical plateau mountain climate, and the vertical climate variation is significant. Glacier resources are abundant, and permafrost is widely distributed in this region.

The area of the SRYZ (32°26′ N~35°45′ N; 90°33′ E~97°15′ E) is about 140,000 km², accounting for 21.9% of Qinghai province and 8.8% of the Yangtze River basin. There are three important tributaries in the basin, including the Dangqu River, Chumaer River, and Tuotuo River, which converge at the Tongtian River and enter the Yangtze River through Zhimenda station (Figure 2). The average annual precipitation over the SRYZ is about 360 mm during 1966–2013, and the annual average temperature ranges from 3 to 5.5 °C [32,34].

The area of SRYR (32°10′~36°59′ N, 90°54′~103°24′ E) is about 120,000 km², accounting for about 15% of the Yellow River Basin, and the Tangnaihai station is the export control station in this region (Figure 2). The average annual precipitation in the SRYR varies between 350 mm and 750 mm during 1961–2013, and the mean annual temperature ranges from −4 to −2 °C [35]. This region is a vital runoff generation in the Yellow River Basin, and the mean annual runoff accounts for about 38% of the total runoff in the Yellow River Basin.

2.2. Data Sources

The observational runoff data of Zhimenda station (1966–2013) and Tangnaihai station (1965–2013) were collected from the Hydrological Year Book published by the Hydrology Bureau of the Ministry of Water Resources of China. There are 8 meteorological stations in the SRYZ and 16 stations in the SRYR. The meteorological stations are evenly distributed in space, which can better reflect the spatial distribution characteristics of the climate. A location map of hydrometeorological stations is shown in Figure 2. The meteorological data of the station were collected from the China Meteorological Data Sharing Service Network, including precipitation, temperature, wind speed, and relative humidity, etc. The potential evapotranspiration of the meteorological station was estimated by the Penman–Monteith method. The average potential evapotranspiration and precipitation of the basin area were obtained by the Thiessen polygon method.

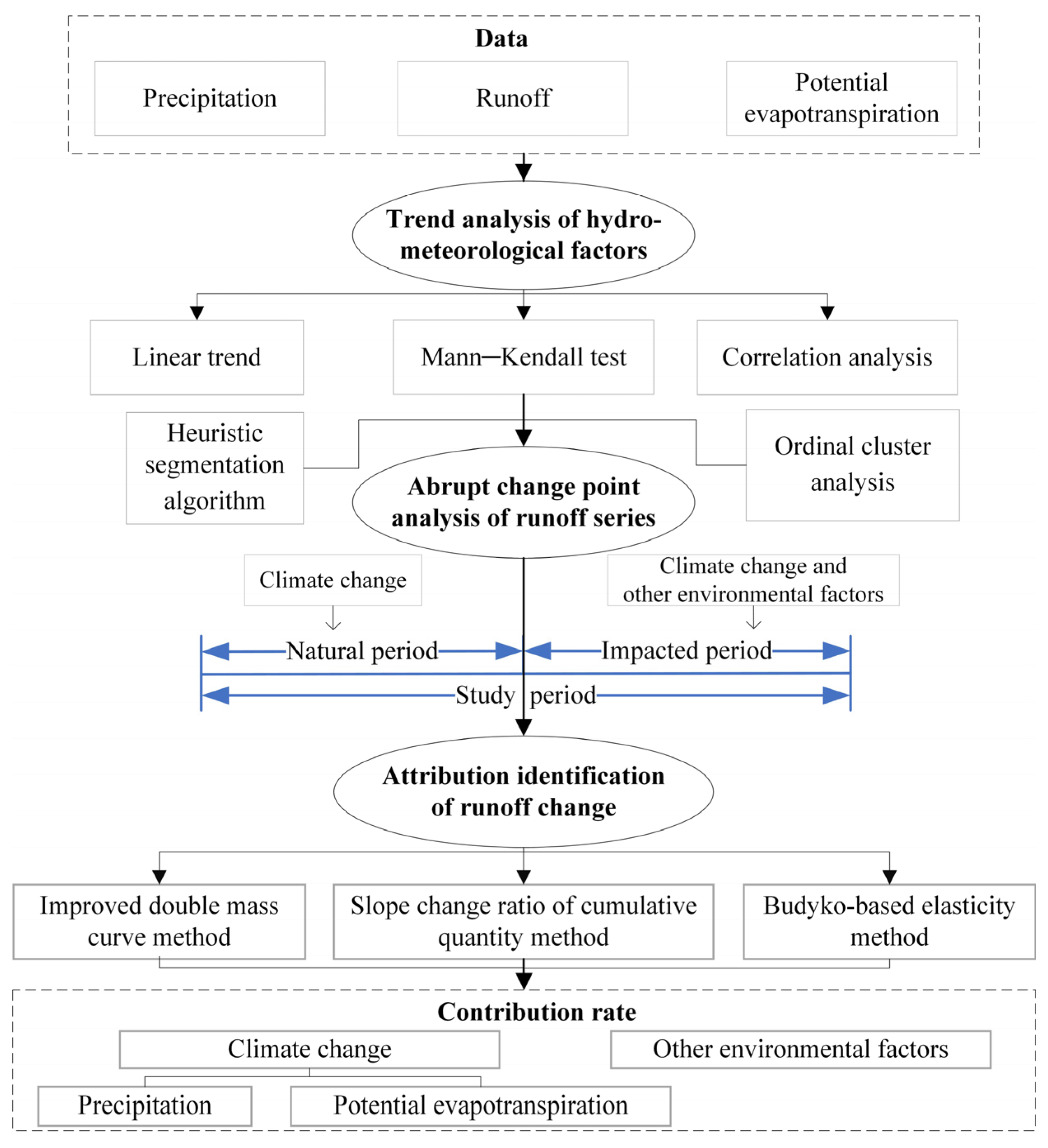
3. Methodology

3.1. Abrupt Change Point Detection

Identifying the abrupt change points of runoff series is a necessary step for the attribution analysis of runoff change [36]. The heuristic segmentation algorithm (HSA) method was proposed by Bernaola-Galvan et al. [37] in 2001, which is based on the idea of moving t-test and improved accordingly. The HSA method can not only effectively detect the mean mutation point existing in the original sequence but also greatly enhance its ability to deal with nonlinear and non-stationary sequences [38]. The main calculation steps are as follows:

Suppose a series x(t) composed of N points; the merging deviation S_Di at point i can be calculated by:

$$S_{Di}={\left(\frac{\left(N_l-1\right)S_l^2+\left(N_r-1\right)S_r^2}{N_l+N_r-2}\right)}^{1/2}·{\left(\frac{1}{N_l}+\frac{1}{N_r}\right)}^{\frac{1}{2}} i=1,2,\dots ,N$$

(1)

where N_l and N_r are the length of left and right subsequences of point i, respectively; S_l and S_r are the standard deviations of the left and right subsequences of point i, respectively.

Construct the statistics T_i for the t-test as follows:

$$T_i=\left|\frac{u_l\left(i\right)-u_r\left(i\right)}{S_{Di}}\right|$$

(2)

where u_l(i) and u_r(i) are the mean value of the left and right subsequences of point i, respectively.

The statistical significance P(T_m) corresponding to the maximum value (T_m) in T_i sequence is calculated as:

$$P\left(T_m\right)\approx {[1-I_{\nu /\left(\nu +T_m^2\right)}\left(\delta \nu , \delta \right)]}^{\gamma }$$

(3)

$$\gamma =4.19In\left(N\right)-11.54$$

(4)

where v = N−2, δ = 0.4, N is the length of the sequence x(t), and I_x(a, b) is an incomplete beta function.

Suppose a critical value of P₀; if P(T_m) ≥ P₀, the point i is the change point. Repeat the calculation according to the above steps for the two new subsequences, and terminate when the length of the subsequence is less than the minimum segmentation scale t₀. The values of P₀ range from 0.5 to 0.95, and the value of t₀ should not be less than 25 [38].

In order to reduce the uncertainty caused by single-mutation detection method, the Mann–Kendall test (MK) method and ordinal cluster analysis (OC) method were also used in this study. As a parameter-free trend-detection technique, the MK method is widely used in climate change-related research due to its powerful functions and advantages, and the detailed calculation steps have been given in previous studies [11,39]. The OC method is another effective method for mutation test. By estimating the optimal segmentation point, this method makes the sum of squared deviations the smallest among the same class and relatively large between the different classes [32]. After determining the change points of the annual runoff sequence through the above three methods, the study period can be divided into the natural and impacted periods.

3.2. Statistical Methods for Attribution Analysis of Runoff Changes

The slope-change ratio of cumulative quantity (SCRCQ) is a method to analyze the effects of different factors to runoff variation. This method first calculates the change rates of the slope of cumulative annual runoff ($S_R$), cumulative annual precipitation ($S_P$), and cumulative annual potential evapotranspiration ($S_{E_P}$); then calculates the contribution of precipitation and potential evapotranspiration to runoff variation according to the slope change rate; and finally separates the contribution rate of other environmental factors. The calculation details are as follows [11]:

$${\eta }_P=\frac{\left(S_{PⅡ}-S_{PⅠ}\right)/S_{PⅠ}}{\left(S_{RⅡ}-S_{RⅠ}\right)/S_{RⅠ}}\times 100\%$$

(5)

$${\eta }_{E_P}=-\frac{\left(S_{E_PⅡ}-S_{E_PⅠ}\right)/S_{E_PⅠ}}{\left(S_{RⅡ}-S_{RⅠ}\right)/S_{RⅠ}}\times 100\%$$

(6)

$${\eta }_c={\eta }_P+{\eta }_{E_P}$$

(7)

$${\eta }_o=100\%-{\eta }_c$$

(8)

where $Ⅰ$ and $Ⅱ$ represent data for the natural and impacted periods, respectively; ${\eta }_P$ and ${\eta }_{E_P}$ are the contribution rates of precipitation and potential evapotranspiration, respectively; ${\eta }_c$ and ${\eta }_o$ are the contribution rates of climate change and other environmental factors, respectively.

The double mass curve method is another popular method besides the SCRCQ method, and the improved double mass curve (IDMC) method used in this study was proposed by Zhang et al. [31]. This method establishes a linear equation of precipitation, potential evapotranspiration, and runoff based on the data of the natural period and then inputs the data of the impacted period into the established relationship to obtain the estimated runoff value, which is compared with the natural runoff to calculate the contribution rate of various factors. The detailed calculation steps can be found in the literature [31].

3.3. Budyko-Based Elasticity Method

The Budyko-based elasticity (BBE) method is based on the principle of water balance. This method calculates the elastic coefficient, which represents the change degree of runoff caused by the change of unit variable, and then quantifies the influence of different factors on runoff. The water balance equation is as follows:

$$R=P-E-\Delta S$$

(9)

where $R$, $P$, and $E$ are the mean annual runoff, precipitation, and actual evapotranspiration during the study period, respectively; $\Delta S$ represents the water storage variation in the catchment, which can be neglected in a long study period [32].

Choudhury [40] and Yang et al. [41] further proposed the water–energy balance equation based on Budyko framework, and the Choudhury–Yang equation is as follows:

$$R=P-\frac{P\times E_p}{{\left(P^n+E_p{}^n\right)}^{1/n}}$$

(10)

where $E_p$ is potential evapotranspiration, and $n$ reflects the underlying surface characteristics including land use, topography, and properties of soil, etc.

Schaake [42] first proposed the concept of runoff elasticity, and the sensitivity of runoff to different influencing factor can be calculated by:

$${\epsilon }_x=\frac{\partial R}{\partial x}\times \frac{x}{R}$$

(11)

where ${\epsilon }_x$ is the runoff elasticity to $P$, $E_p$, and $n$, respectively.

Combined with Equations (10) and (11), the elastic coefficient of ${\epsilon }_x$ can be calculated by:

$${\epsilon }_p=\frac{{\left(1+{\phi }^n\right)}^{1/n+1}-{\phi }^{n+1}}{\left(1+{\phi }^n\right)\left[{\left(1+{\phi }^n\right)}^{1/n}-\phi \right]}$$

(12)

$${\epsilon }_{E_p}=\frac{1}{\left(1+{\phi }^n\right)\left[1-{\left(1+{\phi }^{-n}\right)}^{1/n}\right]}$$

(13)

$${\epsilon }_n=\frac{In\left(1+{\phi }^n\right)+{\phi }^{n}In\left(1+{\phi }^{-n}\right)}{n\left(1+{\phi }^n\right)\left[1-{\left(1+{\phi }^{-n}\right)}^{1/n}\right]}$$

(14)

$$\phi =\frac{E_P}{P}$$

(15)

Runoff variation caused by different driving factors can be calculated by:

$$\Delta R_x={\epsilon }_x\frac{R}{x}\Delta x$$

(16)

where $\Delta R_x$ represents the runoff changes caused by of different factors ($P$, $E_p$, and $n$); $x$ is the mean annual value ($P$, $E_p$, and $n$); $\Delta x$ is the difference in $P$, $E_p$, and $n$ between the natural and impacted periods, respectively.

The contributions of $P$, $E_p$, and $n$ to runoff variation can be calculated by:

$${\eta }_x=\frac{\Delta R_x}{\Delta R}\times 100\%$$

(17)

where ${\eta }_x$ is the contributions of $P$, $E_p$, and $n$, respectively; $\Delta R$ is the change of annual runoff from natural period to impacted period; ${\eta }_c$ and ${\eta }_o$ can be calculated by Equations (7) and (8).

4. Result

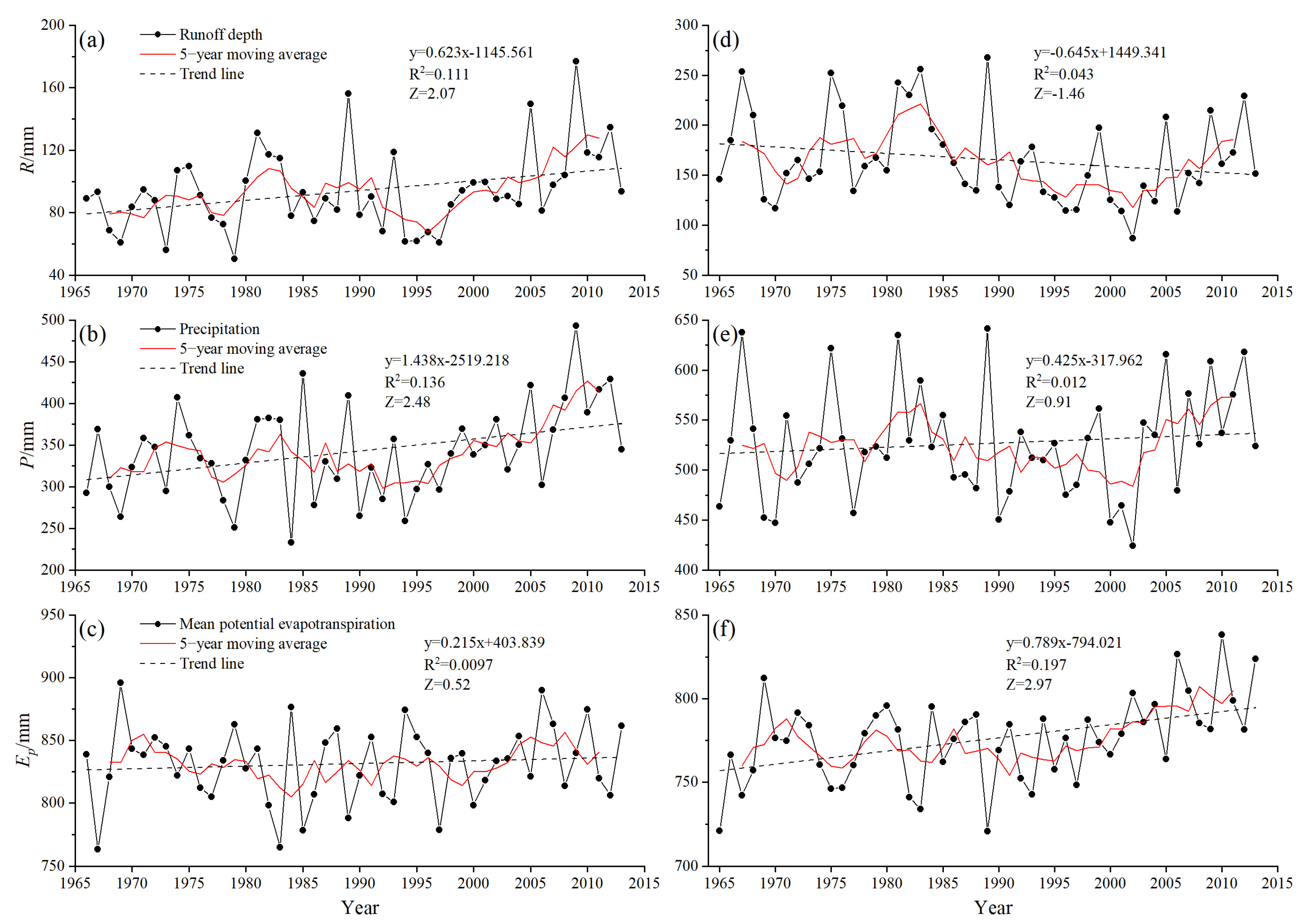
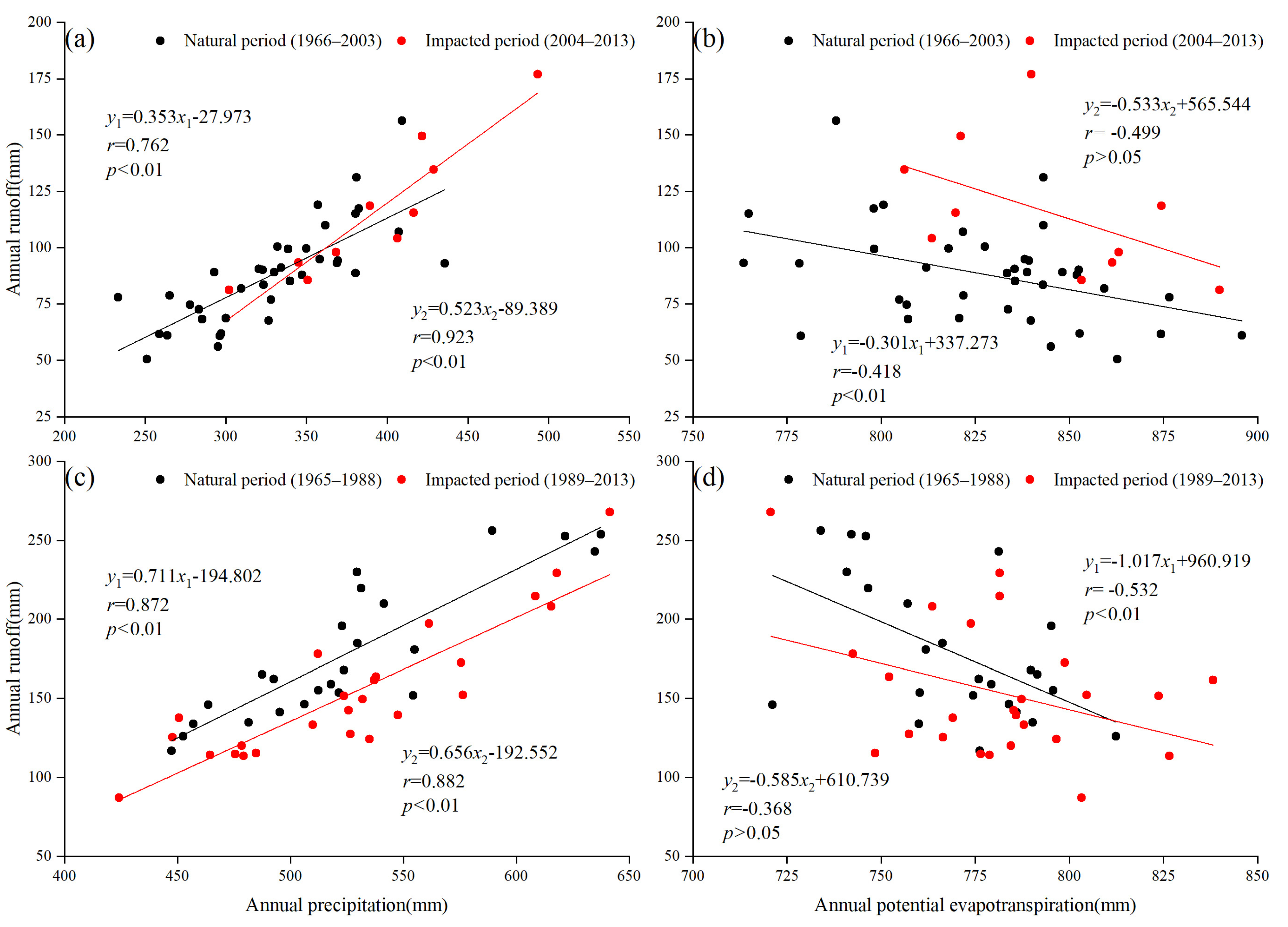
4.1. Variation Characteristics of Hydrometeorological Variables

The temporal variation trends of different variables in the SRYZ and SRYR are shown in Figure 3. From 1965 to 2013, the precipitation, potential evapotranspiration, and runoff in the SRYZ exhibited an upward trend (Figure 3a–c), with linear trend of 14.38 mm/10a, 2.15 mm/10a, and 6.23 mm/10a, respectively. The interannual runoff variation was evident, with a maximum value of 176.94 mm (2009) and a minimum of 50.52 mm (1979). The MK test results indicated a significant increasing trend for annual runoff and precipitation at 0.05 confidence level. For the SRYR, the annual runoff and precipitation during the study period showed an insignificant decreasing and increasing trend (|Z| < 1.96), respectively (Figure 3d,e), while the potential evapotranspiration increased significantly (|Z| > 1.96) (Figure 3f). The highest mean annual runoff was 267.77 mm (1989) and the lowest was 87 mm (2002).

The statistics of the seasonal runoff variation characteristics in the study area are presented in

Table 1. The MK test results of annual and seasonal runoff series in the SRYZ and SRYR.

Region	Result	Spring	Summer	Autumn	Winter
SRYZ	Trend (mm/10a)	0.277	4.377	1.482	0.126
	Z	1.289	2.142 *	1.573	1.484
SRYR	Trend (mm/10a)	−1.226	0.057	−5.100	−0.177
	Z	−1.845	−0.259	−1.974 *	−0.948

Note: Z represents the statistics of MK test; * indicates a significance level of 0.05.

. The runoff in the SRYZ indicated an upward trend in all seasons, and the trend in summer was significant, with a linear change rate of 4.377 mm/10a. In the SRYR, obvious differences in seasonal runoff variation trend could be observed, and the summer runoff increased insignificantly, while the runoff in autumn shown a significant decreasing trend (|Z| > 1.96), with the linear trend of −5.1 mm/10a. The reduction in runoff shown in SRYR might be due to the decrease in water volume in autumn, while the runoff variation in the SRYZ might be attributed to the increase in summer runoff. The runoff in the two regions all exhibited an increasing trend in the summer, but the upward trend was greater in the SRYZ.

The intra-annual runoff distribution of the SRYZ and SRYR is shown in Figure 4. A significant change in intra-annual runoff occurred in the SRYZ, indicating a unimodal distribution in the natural and impacted periods, with the peak values occurring in July and August, respectively (Figure 4a). The average monthly runoff during the impacted period increased when compared with the natural period, with the most significant increase in August and October and the smallest in May. For SRYR, the intra-annual runoff showed a bimodal distribution in the natural period, with two peaks in July and September, while the peak value of runoff occurred in July in the impacted period (Figure 4b). The average monthly runoff in the impacted period presented dramatic reductions compared with the natural period, with the greatest reduction in September and the smallest decrease in June.

The scatter plots of runoff versus precipitation and potential evapotranspiration for the SRYZ and SRYR are shown in Figure 5. The runoff was positively correlated with precipitation in the two regions, and the correlation coefficients were all at the 0.01 significance level. In contrast, the runoff and potential evapotranspiration in the two regions were negatively correlated. Moreover, the correlation between runoff and precipitation of the SRYZ during the impacted period was greater than that in the natural period (Figure 5a), and the increase in slope indicated that the same amount of precipitation produced more runoff during the impacted period. However, the runoff generation level of the SRYR during the impacted period was lower than in the natural period (Figure 5c). In terms of the correlation between potential evapotranspiration and runoff, during the impacted period, the correlation level in the SRYZ was higher than that in the SRYR.

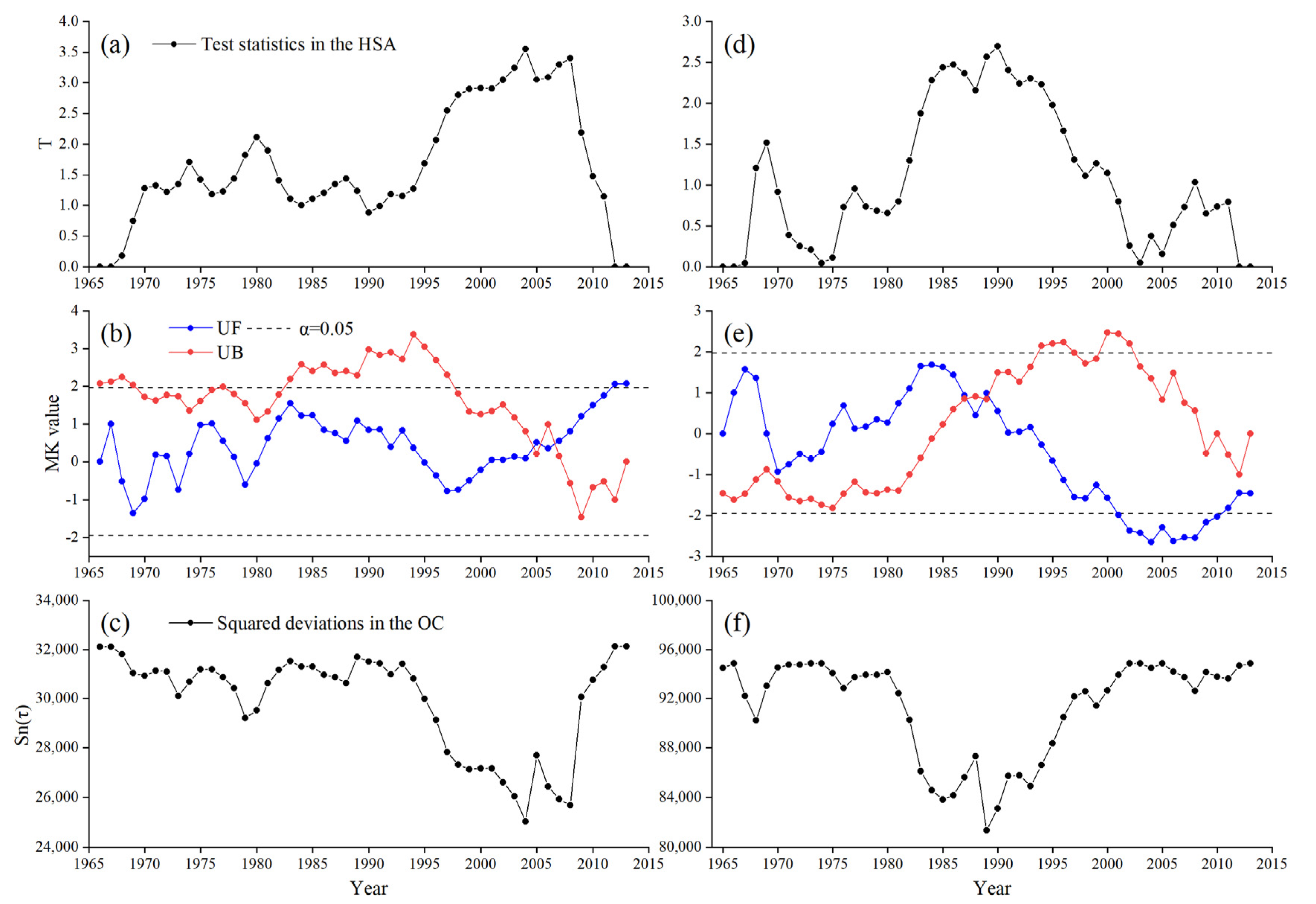
4.2. Change Points Analysis of Runoff Series

There are many approaches to detect time-series mutations in climate change research, and using a single method for detection may lead to biased results. Therefore, the heuristic segmentation algorithm (HSA), ordinal cluster analysis, and MK methods were used to determine the mutation points of the runoff series. Based on the above calculation steps, the diagnosed graphs of the HSA method in the SRYZ and SRYR are shown in Figure 6a,d, respectively. The highest T value in the SRYZ occurred in 2004, and the corresponding value of P was 0.991, which was greater than the critical value (0.9); therefore, 2004 was a possible abrupt change point in the SRYZ. Similarly, 1990 was a possible abrupt change point in the SRYR, with the corresponding P(T_m) value of 0.931, which was also greater than the critical value (0.9).

The MK test result of the runoff series in the SRYZ is shown in Figure 6b. The changing trend of the runoff for the past 48 years had obvious fluctuation characteristics. From 1966 to 1980, the UF curve showed a fluctuating state, and the trend of runoff variation was not obvious. From 1985 to 1995, the UF curve declined obviously, indicating that the runoff decreased during this period. After 2005, the UF curve showed a continuous upward trend, indicating a significant upward trend of runoff. MK method detected three possible change points in 2004, 2005, and 2006. Figure 6e represents the MK test results of runoff series in the SRYR. Results indicated that the UF curve increased obviously from 1975 to 1985, indicating that the runoff increased. Conversely, the UF curve exhibited a downward trend from 1985 to 2004 and passed the significance test at the 0.05 level after 2000. The UF and UB curves crossed in 1987 and 1989, indicating that the runoff series of the SRYR may have changed abruptly in 1987 and 1989.

Based on the results of the ordered clustering method, the abrupt change in the runoff series in the SRYZ and SRYR occurred in 2004 and 1989, respectively (Figure 6c,f). By analyzing the test results of the above three methods comprehensively, it was reliable to identify 2004 and 1989 as the change points of the annual runoff series in the SRYZ and SRYR, respectively. Therefore, the period from 1966 to 2003 was the natural period for the SRYZ, and the period of 2004–2013 was regarded as an impacted period. For the SRYR, the natural period was 1965–1988, and the impacted period was 1989–2013.

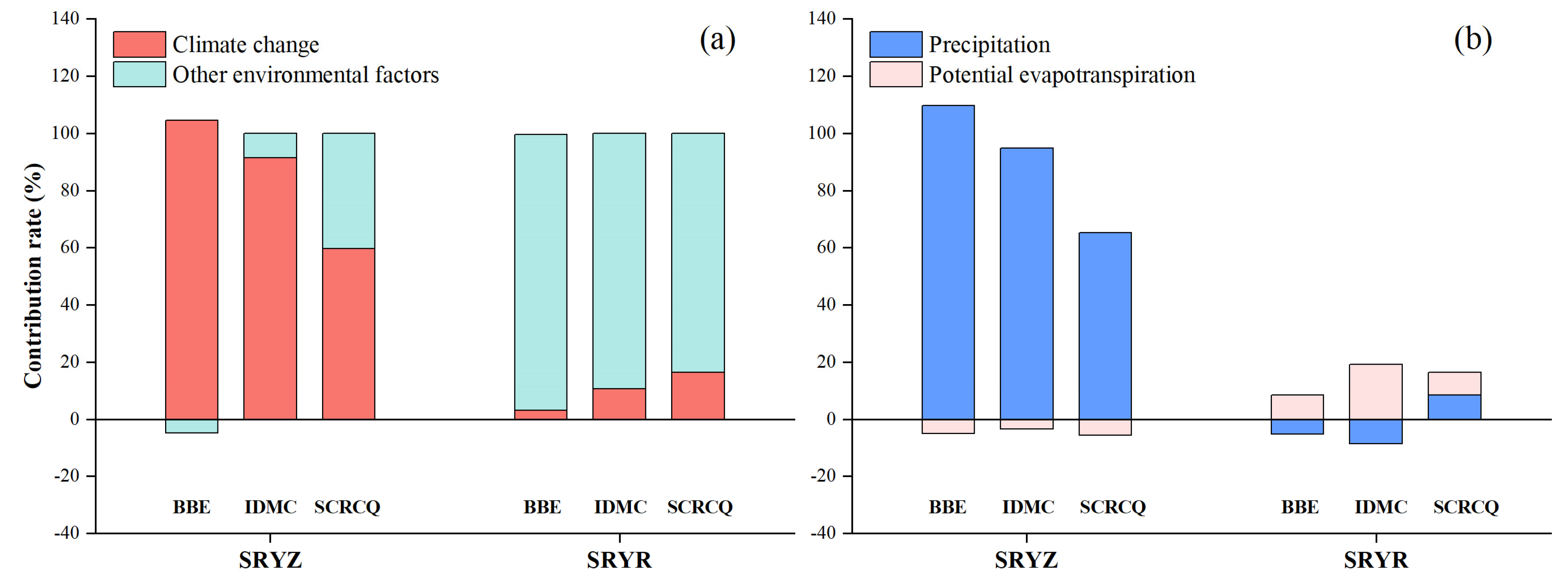
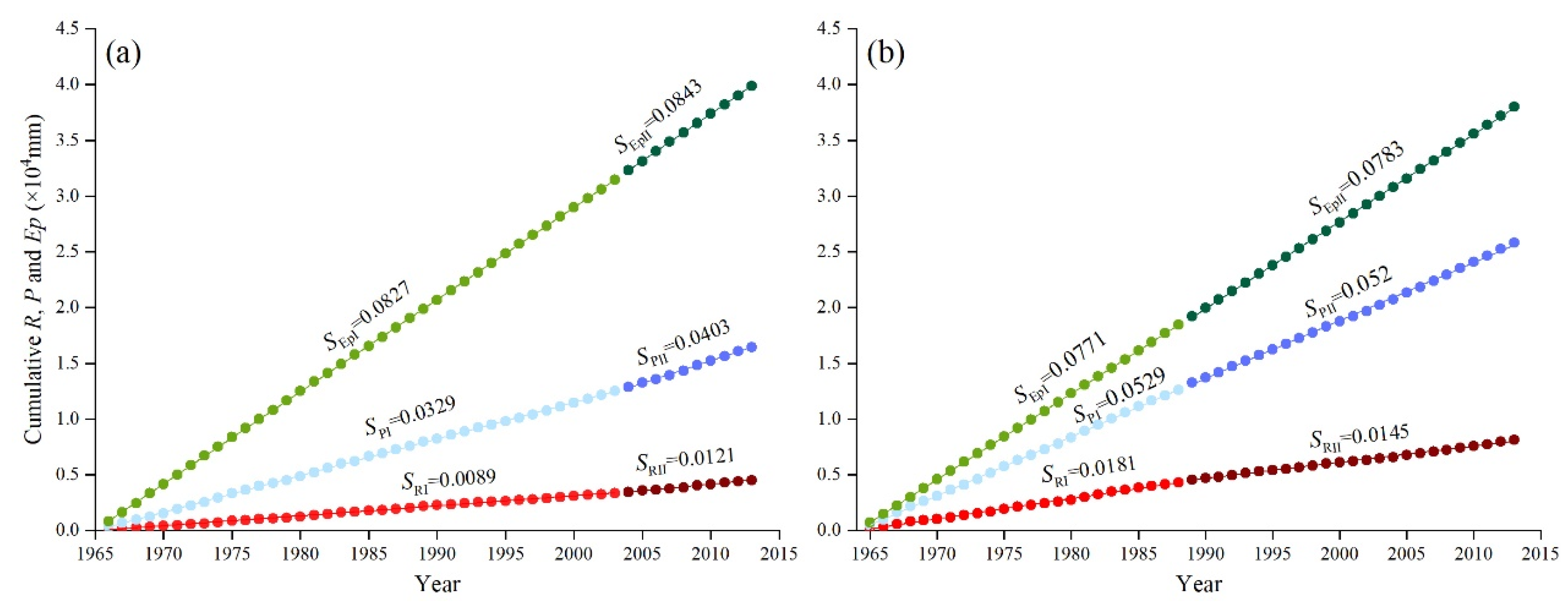
4.3. Contributions of Different Factors to Runoff Variation

The impacts of different factors on the runoff variation in the SRYZ and SRYR were analyzed quantitatively using the IDMC method, and the parameters estimated using the natural period data are presented in

Table 2. Parameters and runoff variation calculated by the improved double mass curve method.

Region	Natural Period	Impacted Period	k1	k2	c	$\Delta {\mathit{R}}_P \left(\mathrm{mm}\right)$	$\Delta {\mathit{R}}_{\mathrm{Ep}} \left(\mathrm{mm}\right)$	$\Delta \mathit{R} \left(\mathrm{mm}\right)$
SRYZ	1966–2003	2004–2013	0.41	−0.06	−27.77	26.29	−0.94	27.73
SRYR	1965–1988	1989–2013	0.93	−0.40	−11.93	2.14	−4.78	−24.89

. The average annual runoff in the SRYZ increased by 27.73 mm during the impacted period, while the mean annual runoff decreased by 24.89 mm in the SRYR. The change in precipitation resulted in an increase of 26.29 mm and 2.14 mm in runoff for the SRYZ and SRYR, respectively. The potential evapotranspiration led to a decrease in runoff of 0.94 mm and 4.78 mm for the SRYZ and SRYR, respectively. The calculated contribution rate of the different factors is shown in Figure 7. The contributions of precipitation and potential evapotranspiration in the SRYZ (SRYR) were 94.8% (−8.6%) and −3.4% (19.2%), respectively. In general, the runoff variation in the SRYZ was attributed to climate change during the impacted period, with a contribution of 91.4%. On the contrary, other environmental factors were responsible for the decrease in the runoff for the SRYR, which accounted for 89.4% of runoff variation.

The cumulative curves of annual precipitation, potential evapotranspiration, and runoff in the SRYZ and SRYR are exhibited in Figure 8, and their linear change slopes in the natural and impacted periods were calculated. All curves had a good-fitting relationship, and the coefficient of determination (R²) was greater than 0.99 (p < 0.01), indicating that more than 99% of the fraction could be reasonably explained. The impacts of climate change and other environmental factors on runoff variation were estimated quantitatively based on the SCRCQ method. The results indicated that precipitation and potential evapotranspiration contributions in the SRYZ were 65.3% and −5.7%, respectively (Figure 7). In the SRYR, the contributions of precipitation and potential evapotranspiration accounted for 8.5% and 7.8%, respectively. Therefore, the contributions of climate change and other environmental factors to runoff variation in the SRYZ (SRYR) were 59.6% (16.3%) and 40.4% (83.7%), respectively.

Based on the BBE method, the calculated elasticity coefficients of runoff to different variables in the SRYZ and SRYR are listed in

Table 3. Multi-year elastic coefficient of runoff on various impact factors in the SRYZ and SRYR.

Region	Period	R/mm	P/mm	Ep/mm	n	Ep/P	εP	εEp	εn
SRYZ	1966–2003	87.99	328.81	827.73	1.04	2.52	1.76	−0.76	−1.55
	2004–2013	115.72	392.20	844.28	1.05	2.15	1.73	−0.73	−1.40
SRYR	1965–1988	178.47	525.28	769.52	1.19	1.46	1.76	−0.76	−1.10
	1989–2013	153.58	527.58	781.39	1.35	1.48	1.91	−0.91	−1.19

. The elasticity coefficients of precipitation, potential evapotranspiration, and surface parameters (n) during the impacted period of the SRYZ were 1.73, −0.73, and −1.4, respectively, indicating that a 1% increase in precipitation, potential evapotranspiration, and n would result in a 1.73% increase, 0.73% decrease, and 1.4% decrease in runoff, respectively. For SRYR, when the potential evapotranspiration and the n increased by 1% during the impacted period, the runoff would decrease by 0.91% and 1.19%, respectively, and the runoff would increase by 1.91% when precipitation increased by 1%. The elastic coefficient of potential evapotranspiration was much lower than that of precipitation, indicating that the sensitivity of runoff to precipitation in the study area was significantly higher than that of potential evapotranspiration.

The BBE method was introduced to further distinguish the impacts of the climatic factors and other environmental factors on runoff variation in the study area, and the results are shown in

Table 4. Contribution of various impact factors to runoff variation in the SRYZ and SRYR based on the BBE method.

Region	Natural Period	Impacted Period	ΔRP	ΔREp	ΔRn	Re (%)	ηP (%)	ηEp (%)	ηo (%)	ηc (%)
SRYZ	1966–2003	2004–2013	30.40	−1.40	−1.36	−0.3	109.6	−5.0	−4.9	0.3
SRYR	1965–1988	1989–2013	1.32	−2.09	−24.02	−0.4	−5.3	8.4	96.5	0.4

Note: Re represents the relative deviation between simulated runoff variation and actual variation; η_c is the contribution of the coupled other factors.

and Figure 7. The relative errors between the estimated runoff changes and the actual runoff changes were within −2%, indicating that this method was reliable and effective for runoff attribution analysis. Precipitation has the most significant effect on runoff variation during the impacted period of the SRYZ, followed by potential evapotranspiration, and n had the least impact, with a contribution of 109.6%, −5.0%, and −4.9%, respectively. In the SRYR, the contributions of precipitation, potential evapotranspiration, and n to runoff variation were −5.3%, 8.4%, and 96.5%, respectively. In general, the contribution rates of climate change and other environmental factors in the SRYZ were 104.6% and −4.9%, respectively. However, in the SRYR, other environmental factors contributed most to the decrease in the runoff, with a contribution of 96.5%.

Although the principles of the IDMC, SCRCQ, and BBE are different, the results of their separation consistently showed that climate change and other environmental factors were the main driving forces for runoff variation in the SRYZ and the SRYR, respectively (Figure 7). The results calculated by the IDMC and BBE were similar, probably because the two methods calculate the contribution based on the relative change in the mean runoff between the impacted and natural periods [31]. However, in the SRYR, the SCRCQ method calculated the contribution value of climate change was lower than the other two methods, probably because the estimated precipitation and potential evapotranspiration data caused errors in the cumulative slope compared with the actual value. Therefore, using multiple methods to separate the effects of different driving forces on runoff variation is more reliable than the results obtained using only one method.

5. Discussion

As the carrier of water resources utilization, runoff variation is crucial to sustainable social and economic development [43], especially in the paramos regions, such as the SRYZ and SRYR [25]. The results of this study showed that climate change had a positive effect on the increase in runoff in the SRYZ, which is consistent with the results of Liu et al. [32] and Zhang et al. [31]. In the SRYR, other environmental factors played a leading role in runoff variation, which is similar to the conclusions obtained by Wang et al. [33].

5.1. Influencing Factors of Runoff in the SRYZ

From 1966 to 2013, the runoff and precipitation in the SRYZ exhibited a significant increasing trend. Precipitation in the SRYZ was mainly concentrated from May to September, which accounted for 88.8% of the annual precipitation, and the runoff accounted for about 72.5% of the total annual runoff [44]. The correlation analysis results showed that the runoff and precipitation were highly correlated during the impacted period, and the summer precipitation showed a significant increase trend based on the MK test. As shown in Figure 3, annual precipitation increased significantly after 2003, but potential evapotranspiration showed a decreasing trend. Precipitation contributed the most (65.3∓112.7%) to the increase in runoff in the SRYZ. The simulation results from the cold region hydrological model (CRHM) also proved that runoff was mainly affected by precipitation in the SRYZ [45], and annual runoff was related to precipitation (62.96%) [46]. In addition, the area of the lake increased by 15.7% in 2010 compared to 1976 due to increased precipitation [47]. Attribution analysis showed that other environmental factors contributed between −5% and 40%, and the contribution of this part comes from glaciers permafrost and human activities. The SRYZ has the highest concentration of glaciers and permafrost in China, accounting for 0.95% and 75% of the whole basin area, respectively [6]. In recent decades, the temperature in the SRYZ increased significantly, with an increase of 0.6 °C/10a, which was about four times of the global mean [48]. Under the background of increasing temperature, the melting of snow and glaciers in the basin increased, and the river runoff also increased [34]. According to the statistics of the Chinese Glacier Inventory (CGI), the glaciers and snow meltwater in the SRYZ accounted for about 9.2% of the total discharge [49]. Han et al. [50] further quantified the effects of snow and glacier meltwater on runoff variation during 2003–2014, which accounted for about 7% and 5% of total runoff, respectively. The degradation of permafrost is another consequence of the rising temperatures. Based on the statistics of the second Tibet Plateau Examination, the area of permafrost decreased by 16% during the past 50 years [34]. From 1981 to 2015, the mean decline rate of the maximum frozen depth of seasonally frozen ground in the SRYZ was 12.3 cm/10a, and the permafrost degradation contributed −11.6 mm to the runoff changes [51]. The decrease in permafrost thickness may increase the soil water storage capacity, resulting in a corresponding reduction in surface runoff. The parameter n in the BBE method exhibited a decreasing trend in the impacted period compared with the natural period, which was related to the vegetation cover of the basin and possibly related to the change of glaciers and permafrost. Despite the absence of the large-scale water-conservancy facilities and a small population in the study area, it has a large area of grassland, and the vegetation degradation caused by overgrazing also affects runoff changes.

5.2. Influencing Factors of Runoff in the SRYR

The SRYR is an important water conservation area in the Yellow River Basin. Under the combined influence of climate change and other environmental factors, the runoff in the SRYR showed an insignificant decreasing trend from 1965 to 2013. On the one hand, the increase in temperature caused significant changes in the glaciers and permafrost in this region. The glacier area in this region only accounts for 0.11% of the basin area, and the contribution of glacier meltwater to the runoff was small (less than 2% of the annual flow) [52]. However, the permafrost area in the SRYR accounts for more than 80%, the permafrost depth of this region exhibited a significant downward trend driven by the increase in temperature, the regional permafrost area ratio decreased by 1.1% per year, and the mean permafrost depth decreased by 0.012 m per year between 1981 and 2015 [53]. Wang et al. [54] further found that, compared with the period from 1990 to 2003, permafrost degradation contributed 38.5% to annual runoff changes during 2004–2015. On the other hand, with the development of the social economy, human activities in this region intensified, which had a greater effect on the runoff change. Ji et al. [55] suggested that the spring, summer, and winter runoff variation were mainly controlled by human activities. The area of arable land increased by about 10% from 1980 to 2010. Irrigation of crops (wheat and rapeseed) in spring requires large amounts of water, but under the influence of global climate change, the water deficit of crops is increasing further, and the demand for irrigation water will further increase [55,56]. Between 1961 and 2004, residential water consumption increased obviously as the population increased nearly twofold, which also contributed to the runoff decrease. The domestic water and livestock drinking water accounted for 1.7% and 9.3% of the natural runoff, respectively [57]. The degradation of grasslands and desertification of land because of overgrazing and cultivation of arable land, and the land desertification in the eastern and southern parts of the SRYR showed an upward trend [58]. However, since the implementation of the Three-River Headwaters Region ecological protection project in 2005, the vegetation degradation and land desertification had improved significantly, and the water storage capacity of the soil improved [58]. In the past decades, the number of lakes in the SRYR decreased significantly, and the two major lakes (Eling Lake and Zhaling Lake) experienced a decline in water levels, which also can be seen as a response to the decrease in the runoff [57]. Additionally, the Huangheyuan hydropower station was completed in 2000, and the total reservoir capacity is 25.01 × 10⁸ m³, accounting for 4.31% of the annual runoff of the entire Yellow River Basin [59]. Considering the need for flood control and power generation, it contributed to the decrease in the runoff. From 1965 to 2013, the contribution rate of climate change to the reduction of runoff in the SRYR ranged from 3.1% to 16.3%. Runoff in this area mainly mainly comes from precipitation, accounting for about 64.1% of all runoff sources [28,60]. As shown in Figure 3, the runoff severely decreased in the 1990s. The high number of light precipitation events and the long duration of precipitation in the 1990s caused runoff decreased significantly during the flood season [61,62]. In addition, with the increase in temperature, the effect of evapotranspiration increased and the soil surface moisture decreased quickly [63], and evapotranspiration played an essential role in affecting runoff variation in the SRYR [35]. Hu et al. [64] also suggested that the decrease in precipitation and the increase in temperature during 1959–2008 were important reasons for the decreased runoff in the SRYR.

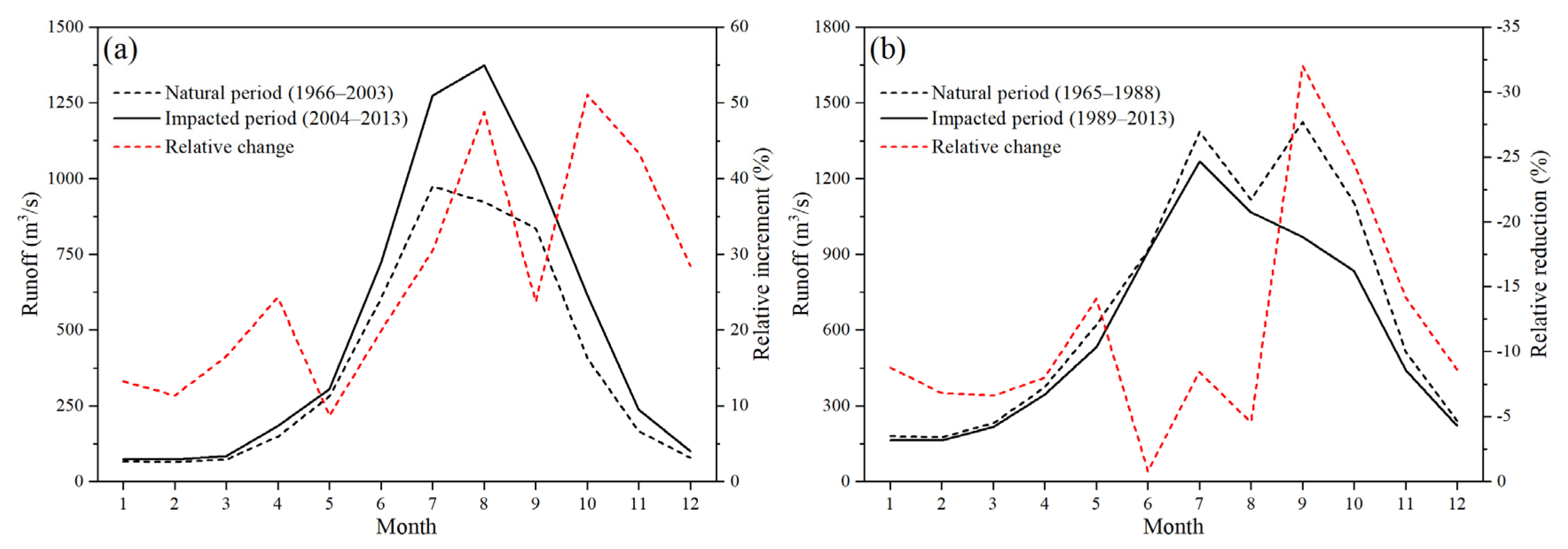
5.3. Comparison of Runoff Variation

The monthly runoff in the SRYR has two peak values during the natural period but only one peak value in the SRYZ. The difference in the intra-annual distribution of precipitation between the two regions was responsible for the different monthly runoff processes [65]. In addition, because the temperature in the SRYZ was generally lower than that in the SRYR, the difference in the formation time of glacier and snowmelt runoff was also one of the reasons for the different intra-annual runoff distribution. In spring and winter, the flow of the SRYR was twice that of the SRYZ, the difference in flow was relatively small in summer, and the difference in flow between the two regions mainly occurred in autumn [66]. The increase in summer runoff in the SRYZ may lead to more severe summer floods in downstream areas, while the decrease in autumn runoff in the SRYR may lead to more severe water shortages in the downstream area in autumn and winter [66]. In summary, the precipitation in the SRYR increased slowly during the study period, but the evaporation increased significantly. Combined with the effects of regional grassland degradation, permafrost ablation, the retreat of glaciers and lakes, and human water consumption, the runoff generation conditions on the underlying surface of the basin deteriorated. Under the same precipitation conditions, the amount of runoff generated will be significantly decreased. This finding was also proven by the results in Figure 5a, where the runoff–precipitation relationship curve for the impacted period was lower than that in the natural period. However, in the SRYZ, runoff is more sensitive to climate change due to its higher elevation, fewer changes in the underlying surface, and fewer human activities. After 2004, annual precipitation increased significantly, and potential evapotranspiration decreased (Figure 3), coupled with the fact that it has more glacial meltwater than the SRYR, thereby leading to a significant increase in runoff. The runoff in the SRYR was more affected by human activities due to its low altitude: the closer to the river source, the greater the impact of climate change, and the closer to the middle river, the greater influence of human activities [33].

5.4. Uncertainties and Limitations

The calculation results in this study are based on the measured data of the gauge station, and the updating errors in observational instruments and measurement rules may lead to non-homogeneity in climate data series, which will affect the accurate description of climate change. However, existing studies have shown that the non-homogeneity of climate data has less effect on large-scale climate change research [67]. This study analyzes the overall climate change characteristics of the study area from a regional perspective, which reduces the possible uncertainty of the climate sequence. Then, the distribution of meteorological stations at high altitudes is sparse, and the errors in measuring instruments and manual operations also lead to uncertainties in the collected hydrometeorological data. It is also difficult to accurately estimate potential evapotranspiration. The relative contribution of the influencing factors was calculated by the BBE method and verified by the IDMC and SCRCQ methods. These methods all assume that climatic and human influences are independent of each other, thereby isolating their contribution to runoff variation. In fact, human activities and climate change are interactive, and ignoring the effects of human activities during the natural period will introduce errors [68]. Additionally, the impact of the spatial and temporal distribution of precipitation on runoff was not considered in the model; it is possibly another error [69]. Finally, only precipitation and potential evapotranspiration were used to represent the impact of climate change on runoff, and the influence of other factors on runoff variation was regarded as the change of parameter n. Thus, it is still a challenge to further distinguish the contribution of various factors on runoff.

6. Conclusions

This study selected the SRYZ and SRYR as the study areas. The annual and seasonal variation characteristics of runoff were analyzed through statistical methods, and the three methods (HSA, MK, and OC) were used to further detect the change points of the runoff series. Then, the IDMC, SCRCQ, and BBE methods were used to quantify the impacts of climate change (precipitation and potential evapotranspiration) and other environmental factors on runoff variation. Finally, the driving mechanism of runoff change in the two regions was analyzed. The main findings are as follows:

(1)

The annual runoff and precipitation in the SRYZ indicated a significant increasing trend during 1966–2013, while the potential evapotranspiration increased insignificantly. From 1966 to 2013, the annual runoff for SRYR exhibited an insignificant decreasing trend, with the rate of −6.45 mm/10a, whereas potential evapotranspiration increased significantly, with the rate of 7.89 mm/10a.

(2)

Runoff in the SRYZ showed an upward trend in all seasons, with the summer runoff increasing significantly. The summer runoff in the SRYR exhibited an insignificant upward trend, and the runoff in the autumn decreased significantly. During the natural period, the intra-annual distribution of runoff in the SRYZ was unimodal and was bimodal in the SRYR.

(3)

By evaluating the three mutation detection results comprehensively, it was determined that the annual runoff series in the SRYZ and SRYR changed abruptly in 2004 and 1989, respectively.

(4)

Climate change was the dominant factor for runoff variation in the SRYZ, with a contribution of 59.6%~104.6%, while the runoff in the SRYR was mainly controlled by other environmental factors, contributing 83.7%~96.5%. Moreover, precipitation changes accounted for 65.3%~109.6% of the increase in annual runoff in the SRYZ, and the potential evapotranspiration contributed 7.8%−19.2% of runoff variation in the SRYR. Generally, the significant increase of runoff in the SRYZ could be attributed to the precipitation and glacial meltwater, while the decrease of runoff in the SRYR was the combined effects of the permafrost degradation, land desertification and human water consumption.