Ozone β-Cyclodextrin Inclusion Complex Characterization and Application in the Remediation of Total Petroleum Hydrocarbons

Abstract

Green remediation is essential in the current practice of water resources management. In this study, a series of ozone β-cyclodextrin (O₃-βCD) inclusion complexes were prepared under a selected range of different ozone concentrations, β-CD concentrations, and solution pHs to test their ozone release rates and efficiencies in the treatment of total petroleum hydrocarbons (TPH) in water. The main objectives of this study are to characterize the O₃-βCD system, mathematically model its ozone release rate, and test its capability in the degradation of pollutants. From the results, it was found that by defining a set of dimensionless parameters, including β-CD to ozone molar ratio and various degrees of ozone saturation, the steady-state conditions in the O₃-βCD system can be represented by a newly developed dimensionless plot. In an optimal condition, the dissolved ozone release rate of 6.8 × 10⁻⁵ mM/min can be achieved in the O₃-βCD system. A mathematical model was successfully developed to estimate the ozone release rate. In the TPH removal experiments, the effects of β-CD to ozone molar ratio and ozone dosage on the removal efficiency were rigorously examined. Overall, an optimal TPH removal of nearly 90% can be achieved in the treatment of 50 mg/L of TPH in water using this inclusion complex reagent.

1. Introduction

Remediation of polluted groundwater using benign reagents plays an important role in sustainable water resources management. Among various remediation options, the advanced oxidation processes (AOPs) are highly effective in the removal of organic pollutants [1,2]. Ozonation is a widely used AOP and has been proven to be successful in soil [3,4,5], wastewater [6,7,8], and groundwater treatment [9] of recalcitrant organic pollutants. Despite being a green reagent with high effectiveness in remediation, ozone still possesses the unfavorable nature of being sparingly soluble and short-lived in water. These disadvantages have severely limited the delivery as well as transport of ozone in the subsurface during in situ chemical oxidation (ISCO) applications. The advent of nanomaterials in wastewater treatment [10,11] sees the potential of using nanotechnology to overcome these disadvantages. For example, the application of micro- and nano-sized bubbles has been employed to enhance the solubility and transport distance of dissolved ozone during remediation [12,13,14]. More recently, cyclodextrin(CD)-based stabilizers [14,15,16] have been used as non-toxic long-term ozone carriers that have the capability to increase the half-life of ozone by as much as 40 times when using HPβ-CD (2-hydroxypropyl-beta-cyclodextrin) [14]. These developments have undoubtedly made the ozonation process a very attractive option for green ISCO.

CDs are edible clathrates of cyclic oligosaccharides with graduated cup-like 3D structures. Their inner cavity is hydrophobic, and the outer surface is hydrophilic due to the presence of the primary hydroxyl group on the narrow side and secondary hydroxyl on the wide side [17]. They are able to form soluble inclusion complexes with organic compounds in solution by host-guest interactions [18]. In wastewater treatment, the β-CD-based adsorbent was able to remove both organic and inorganic pollutants [19]. The hydrophobic cavity of the CD has made it possible to remove residual NAPL (non-aqueous phase liquid) in the subsurface [20] and capture the non-polar organic pollutants and enhance their solubilization and transport in the subsurface [21,22]. From molecular modeling [23], it was found that van der Waals interaction plays a major role in forming the stable organic-CD complex and that β-CD outperforms α-CD and γ-CD in forming the complex, due to superior steric complementarity.

In addition to organic compounds, CD can also form complexes with molecular ozone [14,24]. The O₃-CD complex was found to be very stable and able to gradually release ozone in water [14,16]; however, a significant portion of CD could also be oxidized or mineralized by ozone during the complex formation process [14]. These phenomena imply that there could exist an optimal dosage for maximum ozone release in the O₃-CD complex. A common indicator for dosage quantification is the molar ratio of CD to ozone [14,16]. In Fan’s study [16], the maximum CD to ozone molar ratio investigated is 10 when using nano-sized ozone bubbles in aeration. In another study by Dettmer [14], the CD to ozone molar ratios investigated range from 17.5 to as high as 850, which is a very wide range. Despite having been proven to be a remarkable ozone carrier, mechanisms controlling the release rate of dissolved ozone from the O₃-CD complex and the stoichiometric relationships between ozone and CD during the complex formation process are not yet clear. Currently, an optimal formula for the CD-to-ozone molar ratio that can achieve the most efficient pollutant removal efficiency has not been provided. Overall, mechanisms involved in the interactions between CD and ozone include gas–liquid reactions of gaseous ozone in water, partitioning of O₃ into the CD cavity to form the O₃-CD complex, degradation of CD by O₃, and O₃ release from the O₃-CD complex to the solution. Data of such a multiphase multicomponent dynamic chemical system should be examined using dimensionless parameters [25] and modeled mathematically in order to gain insights into factors controlling the optimal dosage.

Roughly 80% of crude oil is processed to become fuels, and approximately 0.1 to 0.25% of oils eventually dissolve into aquatic and groundwater environments [26]. As a result, total petroleum hydrocarbons (TPH) have become ubiquitous pollutants in the petroleum-polluted subsurface worldwide [27,28,29]. The diesel range organics in TPH (C₁₀-C₂₈) are much less volatile and also less biodegradable than gasoline range organics (C₆-C₁₀) [30] and pose a greater challenge in treatment. Ozonation has been proven to be effective in degrading these petroleum hydrocarbons [6,31,32]. However, the degradation rates of TPH are relatively slow [26] compared to unsaturated hydrocarbons. Consequently, when ozonation is considered, the application of an ozone stabilizer and the implementation of its prolonged ozone release should be essential in the green remediation of groundwater.

In this study, the O₃-CD complex, utilizing β-CD, was prepared first to examine its system dynamics and then reacted with diesel TPH to test for its treatment efficiency. Specific objectives of this study are: (1) to characterize the gas–liquid reactions in the O₃-CD complex system using dimensionless parameters, (2) to develop a mathematical model to predict the ozone release rate, and (3) to examine the capacity of the O₃-CD complex on pollutant removal, exemplified by the treatment of TPH. Describing characteristics of the O₃-CD system in dimensionless form reduces the number of parameters in the system. A mathematical model to predict the ozone release rate in a treatment system provides a tool for analyzing the dynamics of the O₃-CD system. These novelties can greatly assist the characterization of future O₃-CD systems and facilitate their scale-up as well as field operations.

2. Materials and Methods

2.1. Chemicals

β-CD (C₄₂H₇₀O₃₅) was purchased from Sigma-Aldrich Inc. (St. Louis, MO, USA). Potassium dihydrogen phosphate (KH₂PO₄), sodium phosphate (Na₃PO₄), and phosphoric acid (H₃PO₄) from J. T. Baker (Phillipsburg, NJ, USA) were used for preparing buffer solutions. In gaseous and aqueous ozone analyses, potassium iodide (KI) (Sigma-Aldrich Inc., St. Louis, MO, USA) and potassium indigotrisulfonate (C₁₆H₇K₃N₂O₁₁S₃) (Sigma-Aldrich Inc., St. Louis, MO, USA) were used. In TPH analysis, a certified standard (DRH-FTRPH-PAK, AccuStandard, New Haven, CT, USA) of 500 mg/L and hexane (J. T. Baker, Phillipsburg, NJ, USA) were used.

2.2. Preparation and Characterization of O₃-βCD Inclusion Complex

β-CD of 0.44 mM, 0.88 mM, 1.32 mM, and 1.76 mM were first prepared in various buffer solutions of pH 3, pH 5, and pH 7. For their chemical analyses, the HPLC system (LC-6AD, Shimadzu, Kyoto, Japan) with the refractive index detector (RID-10A, Shimadzu, Kyoto, Japan) was employed, and the Inertsil NH₂ column (250 mm × 4.6 mm × 5 μm, GL Science, Tokyo, Japan) was used. In experiments, a 250 mL β-CD solution was first poured into a 1.0 L gas-absorption batch reactor, and the ozone generator (Model OZ2BTUSL-SS-V/PM, Ozotech Inc., Yreka, CA, USA), utilizing pressurized air as gas source, was connected to the reactor. To produce the O₃-βCD inclusion complex, the generator was turned on to purge ozone gas (2.36 L_g/min) through a diffuser into the reactor for 30 min. Three different gaseous ozone concentrations (C_O3(g)) were used in the experiments: 0.274 mmol/L_g, 0.209 mmol/L_g, and 0.155 mmol/L_g. All gaseous concentrations were checked multiple times to ensure they reached constant concentrations prior to experiments. Both gaseous ozone concentrations entering and exiting the reactor were monitored by the iodometric method [33]. Meanwhile, dissolved ozone in the solution was also measured periodically by the indigo method [34]. The wavelengths of the spectrophotometer (Model T-60, PGI Instrument, Sheffield, UK) for the iodometric method and the indigo method were set at 352 nm and 600 nm, respectively. In a separate experiment to measure ozone release rate, the indigo reagent (0.25 L) was added to the freshly prepared O₃-βCD inclusion complex solution under gentle mixing, and the absorbance at 600 nm was monitored continuously. Once ozone is released from the inclusion complex, the absorbance would reduce due to the reaction with ozone. The reduction in absorbance can be used to quantify the mass of ozone released. In monitoring the aqueous ozone concentrations, triplicate samples were taken and analyzed separately in each individual experiment.

2.3. Removal of TPH by O₃-βCD Inclusion Complex

TPH solutions of various concentrations (50 mg/L, 100 mg/L, and 150 mg/L) were prepared by adding diesel fuel (purchased from a local gas station) to DI water buffered at pH 3. Each TPH solution was mixed rigorously using a magnetic stir bar in a sealed amber bottle for 7 days prior to the experiments. In the chemical analysis of TPH, a certified standard of 500 mg/L was used to construct the calibration curve. The analysis was carried out using GC-FID (GC-2014, Shimadzu, Kyoto, Japan), equipped with the 30 m × 0.25 mm × 0.1 μm DB-1 column (Product No. 122-1031, Agilent, Santa Clara, CA, USA). The analytical method for TPH analysis is the EPA-validated test method 8015D [35] for diesel range organics, corresponding to the range of alkanes from C₁₀ to C₂₈. Prior to GC-FID analysis, each 250 mL of TPH-containing water was extracted with 15 mL of hexane, and the hexane phase was analyzed. From GC chromatograms, calibration factors (CFs) from six specific peaks (C₁₀, C₁₂, C₁₄, C₁₆, C₁₈, and C₂₀) were evaluated. Linearity through the origin was assumed when the percent relative standard deviation of the six calibration factors was less than 20%. Under the circumstances, the average calibration factor ($\overline{CF}$) was used for the quantification of TPH. To conduct TPH removal experiments, an O₃-βCD solution of 125 mL at pH 3 was first prepared by purging ozone (0.274 mmol/L_g and 0.155 mmol/L_g) continuously into a β-CD solution (0.44 mM, 0.88 mM, 1.32 mM, 1.76 mM and 2.20 mM) for 30 min. Then, this O₃-βCD solution is mixed with a 125 mL TPH solution (50 mg/L) of pH 3 to start the removal experiment. After a certain reaction time (0.5 h & 24 h), the total 250 mL solution was extracted using hexane and analyzed in triplication by GC-FID for residual TPH. From the analysis results, the overall removal efficiency can be determined.

3. Results

3.1. Dimensionless Characterization of Ozone and β-CD Dynamics

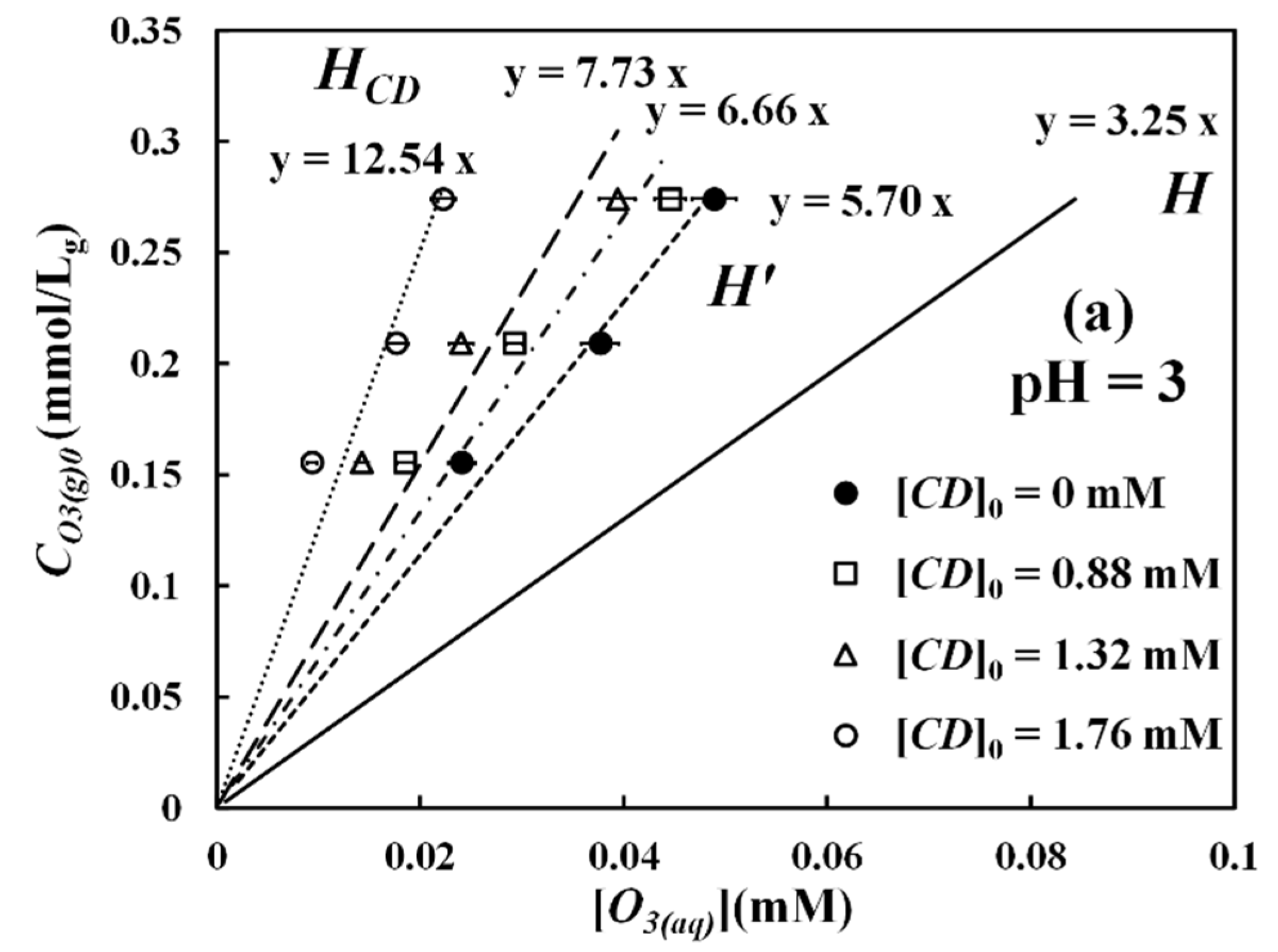
Figure 1 shows the experimental relationships between gaseous ozone ($C_{O3\left(g\right)0}$) (0.155, 0.209, and 0.274 mmol/L_g) and aqueous ozone $\left(\left[O_{3\left(aq\right)}\right]\right)$ concentrations in dynamic equilibrium in the gas-absorption batch reactor under various CD dosages (${\left[CD\right]}_0$) (0.88 mM, 1.36 mM, and 1.76 mM) at pH 3, 5, and 7. The solid lines in the figure represent the theoretical equilibrium relationship, estimated from the dimensionless Henry’s constant (H) [36], defined as

$$H=C_{O3\left(g\right)0}/\left[O_{3\left(aq\right)0}^{*}\right]$$

(1)

where $\left[O_{3\left(aq\right)0}^{*}\right]$ stands for the solubility of the aqueous ozone at a specific pH value. As can be seen in Figure 1, from the data of pure water ([CD]₀ = 0 mM), the equilibrium aqueous concentration ($\left[O_{3\left(aq\right)0}\right]$) is between 57–73% of the aqueous ozone solubility. This degree of ozone saturation in the solution is defined as $\alpha$

$$\alpha =\left[O_{3\left(aq\right)0}\right]/\left[O_{3\left(aq\right)0}^{*}\right]=H\left[O_{3\left(aq\right)0}\right]/C_{O3\left(g\right)0}$$

(2)

With this definition, the slope of the regression line in Figure 1 with respect to pure water can be represented by $H^{\prime }$ as

$$H^{\prime }=C_{O3\left(g\right)0}/\left[O_{3\left(aq\right)0}^{}\right]=H/\alpha$$

(3)

When β-CD is present in the system, from Figure 1, it can be seen that the linear relationship between the gaseous ($C_{O3\left(g\right)0}$) and aqueous ozone ($\left[O_{3\left(aq\right)}\right]$) also exists. Their slopes become steeper as the β-CD concentrations increase. Here, we further define another parameter $\beta$ as

$$\beta =\left[O_{3\left(aq\right)}\right]/\left[O_{3\left(aq\right)0}\right]$$

(4)

Here, β is called the relative degree of saturation and represents the ratio of equilibrium ozone concentration in the O₃-βCD solution to the ozone concentration in pure water. According to Figure 1a, the $\beta$ values in pH 3 roughly range between 0.45 and 0.85 in our reactor system. The slope of the line in Figure 1 when β-CD is present is actually an empirical parameter since chemical reactions are involved. Analogously, this slope can be defined as

$$H_{CD}=C_{O3\left(g\right)0}/\left[O_{3\left(aq\right)}\right]=H/\alpha \beta$$

(5)

Since both α and β values are less than unity, the values of $H_{CD}$ are thus greater than the values of $H^{}$ and $H^{\prime }$ mathematically. A steeper slope or a larger $H_{CD}$ value at a higher β-CD dosage implies that when there is more β-CD in the solution, the equilibrium dissolved ozone concentration ($\left[O_{3\left(aq\right)}\right]$) becomes lower. 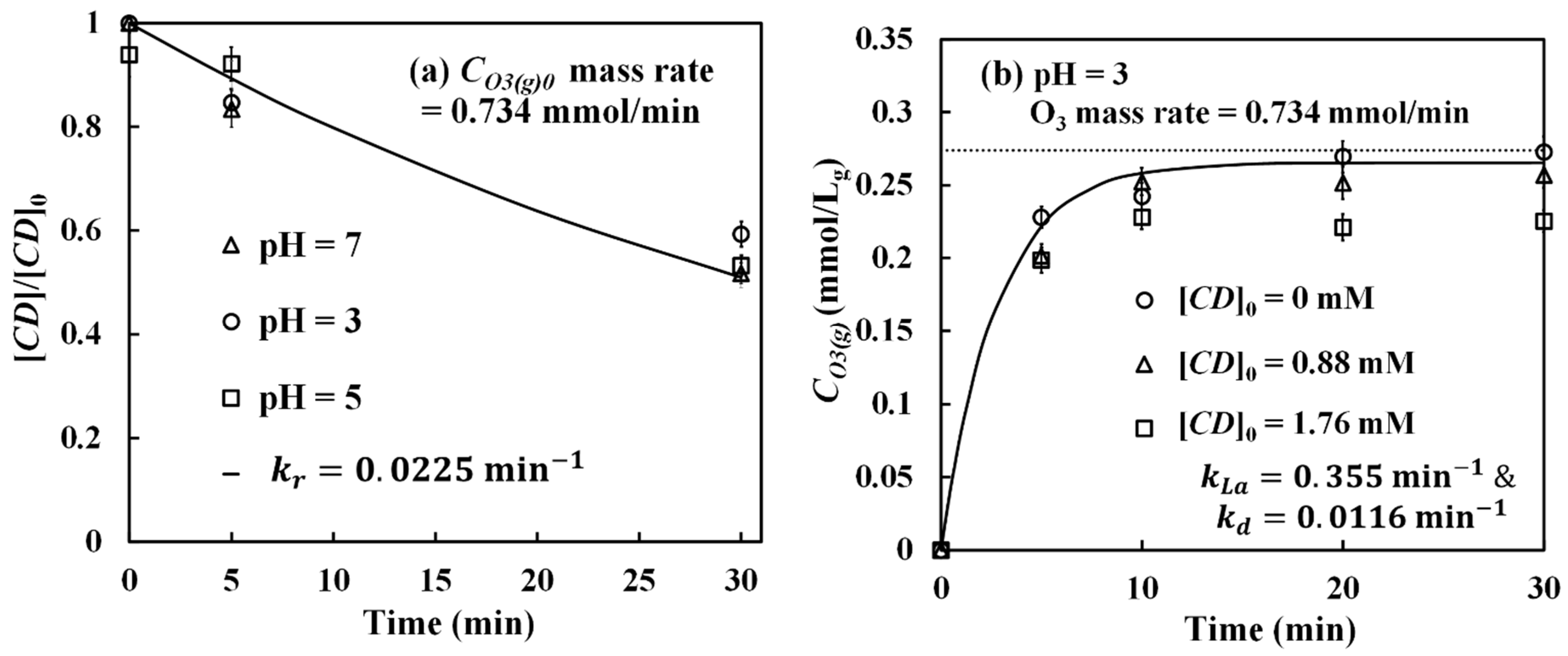In fact, ozone is known to degrade and mineralize CDs to various degrees [14]. The degrees of β-CD degradation in our system during ozonation are demonstrated in Figure 2a, together with the data of gaseous ozone BTCs, as shown in Figure 2b. From Figure 2a, it is seen that about 50% of β-CD was degraded by ozone (0.734 mmol/min) after 30 min, regardless of pH. According to differential equations of gas–liquid mass transfer with chemical reactions, we can solve for these fundamental equations and subsequently optimize pertinent mass transfer and kinetic parameters in the system. These parameters are shown in Figure 2, including the overall gas–liquid mass transfer coefficient ($k_{La}$) of 0.355 min⁻¹, the pseudo-first-order rate constant ($k_r$) for β-CD degradation of 0.0225 min⁻¹, and the ozone self-decomposition rate constant of 0.0116 min⁻¹. These parameters will be employed later in the mathematical modeling of ozone concentration on the CD interface. It should be emphasized that these parameters are system specific and cannot be applied to other systems. In spite of the degradation, the residual β-CD, i.e., the β-CD not degraded, in the solution can form a stable inclusion complex with ozone. Such inclusion is able to shield the complex from further degradation by ozone [14] and, more importantly, to carry dissolved ozone molecules inside the cavity for long-term release. Therefore, in each O₃-βCD interaction in the reactor system, ozone is consumed to degrade β-CD, form the inclusion complex, and finally saturate the aqueous solution. Consequently, steeper slopes or larger $H_{CD}$ values at higher β-CD concentrations mainly result from higher ozone consumption due to reaction with β-CD and formation of O₃-βCD inclusion complex. Notably, the $H_{CD}$ values represent an overall dynamic equilibrium of ozone in the system, involving chemical reactions. 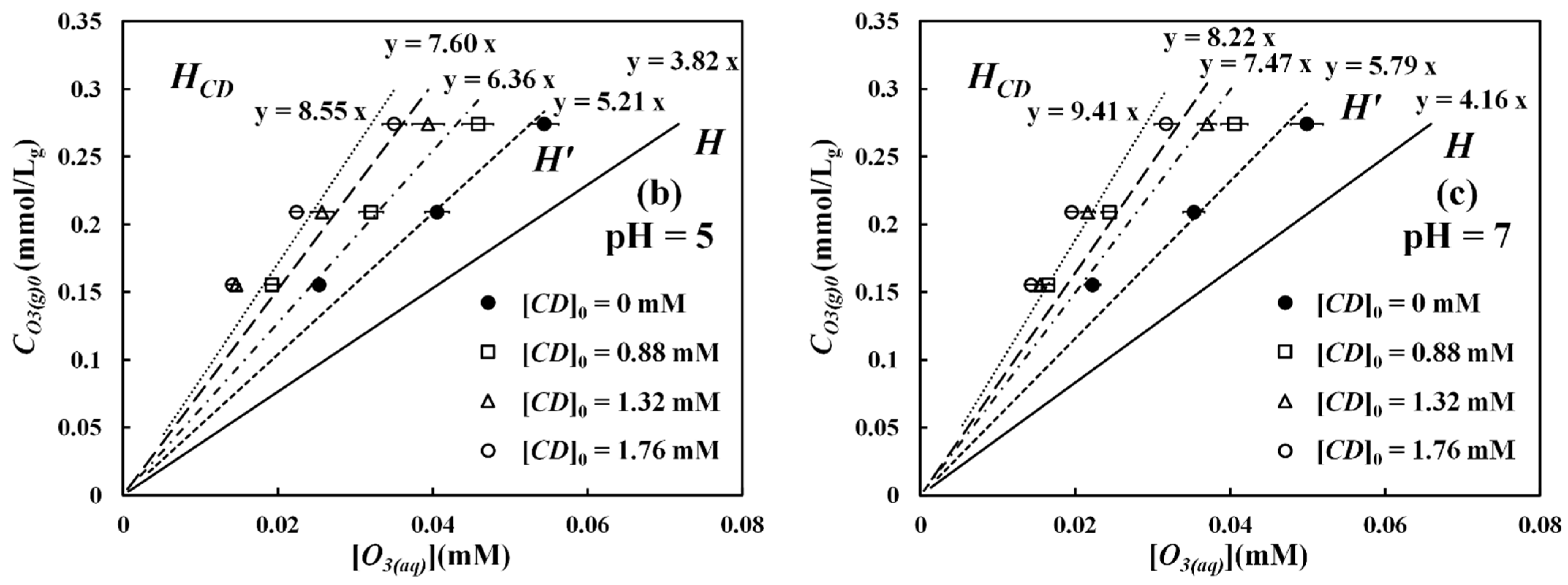It is different from standard Henry’s constant (H) in Equation (6), which describes pure physical equilibrium between gaseous and aqueous ozone. In terms of pH effect, the $H_{CD}$ values are slightly affected by pH, as shown in Figure 1b,c for the data of pH 5 and pH 7. The main reason for these phenomena is that at these pH values, what we have measured using the indigo method is actually the total oxidant concentrations, including both ozone and hydroxyl radical, but not just ozone alone as in pH 3. Although hydroxyl radical is a stronger oxidant than molecular ozone, it is short-lived, unstable, and cannot be included in the cavity of β-CD.

In Figure 1, it is observed that the parameter $H_{CD}$ has a strong dependence on the initial β-CD concentration. It should be noted that $H_{CD}$ is also dependent on mass transfer characteristics of the reactor system, such as gas flow rate, bubble size, gas–water interfacial area, mixing intensity, etc. Ideally, a correlation in dimensionless form is preferred for the description of the O₃-βCD dynamic equilibrium. In practice, the molar ratio of CD to aqueous ozone has been utilized as a principal dimensionless parameter to characterize the O₃-CD systems [14,16]. In order to recast the data of Figure 1 in a dimensionless fashion, we plot the values of β, obtained via Equation (4), as a function of the molar ratio of β-CD to aqueous ozone, defined by

$$\mathrm{CD}/{\mathrm{O}}_3\mathrm{molar}\mathrm{ratio}={\left[CD\right]}_0/[O_{3\left(aq\right)0}]=R$$

(6)

Figure 3 shows the dimensionless relationships of β vs. R under various α values at pH 3, 5, and 7. In Figure 3a, the data ranging between $\alpha =0.504$ and $\alpha =0.586$ demonstrate a good linear relationship, that the β values are inversely proportional to the CD/O₃ molar ratios. This implies that under a constant gaseous ozone concentration (i.e., a constant α value), the steady-state aqueous ozone concentration ([$O_{3\left(aq\right)}$]) (i.e., the β value) would decrease linearly when the β-CD concentration in the solution increases (i.e., at a higher CD/O₃ molar ratio). Essentially, this is what we have found previously in Figure 1. Yet, it is now presented in dimensionless form and thus can be applied universally to conditions of any gaseous ozone input concentrations under various CD dosages. Evidently, the relative degree of aqueous ozone saturation, β, does not only depend on the CD/O₃ molar ratio but also depends on the gaseous ozone feed concentration, the α term. According to the definition of α in Equation (2), its value becomes 1.0 when the gas-absorption reactor is able to attain an aqueous concentration equaling ozone solubility in pure water. In our reactor system, the degree of ozone saturation attained is between 50% to 60%, i.e., between $\alpha =0.504$ and $\alpha =0.586$. In the future, if other reactor systems with different mass transfer efficiencies are used for O₃-CD inclusion complex formation, linear lines with more α values can be added to the plot. Moreover, one of the limitations of the current plot (Figure 3a) is that it is applicable to the O₃-CD system with respect to β-CD only. If other CDs such as α-CD, γ-CD, or HPβ-CD are of interest, their dimensionless plots have to be constructed through independent experiments since their degradation kinetics may differ from that of β-CD. Another limitation is the pH value. Figure 3a is the plot of β vs. CD/O₃ molar ratio specifically for pH 3. Analogous plots for pH 5 and pH 7 are shown in Figure 3b,c, respectively. As the pH value increases, the slopes become flatter in Figure 3b,c, meaning dissolved ozone concentration becomes higher under the same β-CD to ozone molar ratio. This is mainly due to a higher β-CD degradation so that less ozone is taken by β-CD.

3.2. Ozone Release Rate from O₃-βCD Inclusion Complex

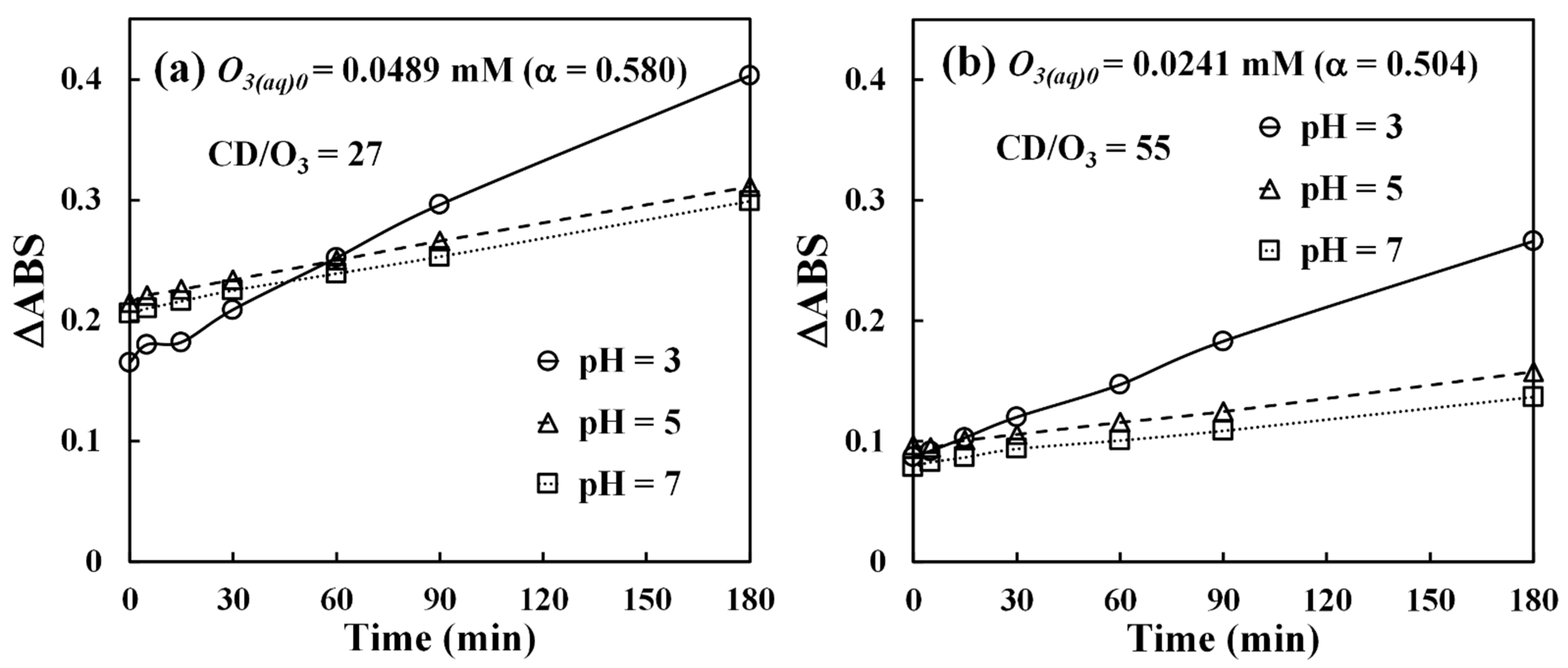
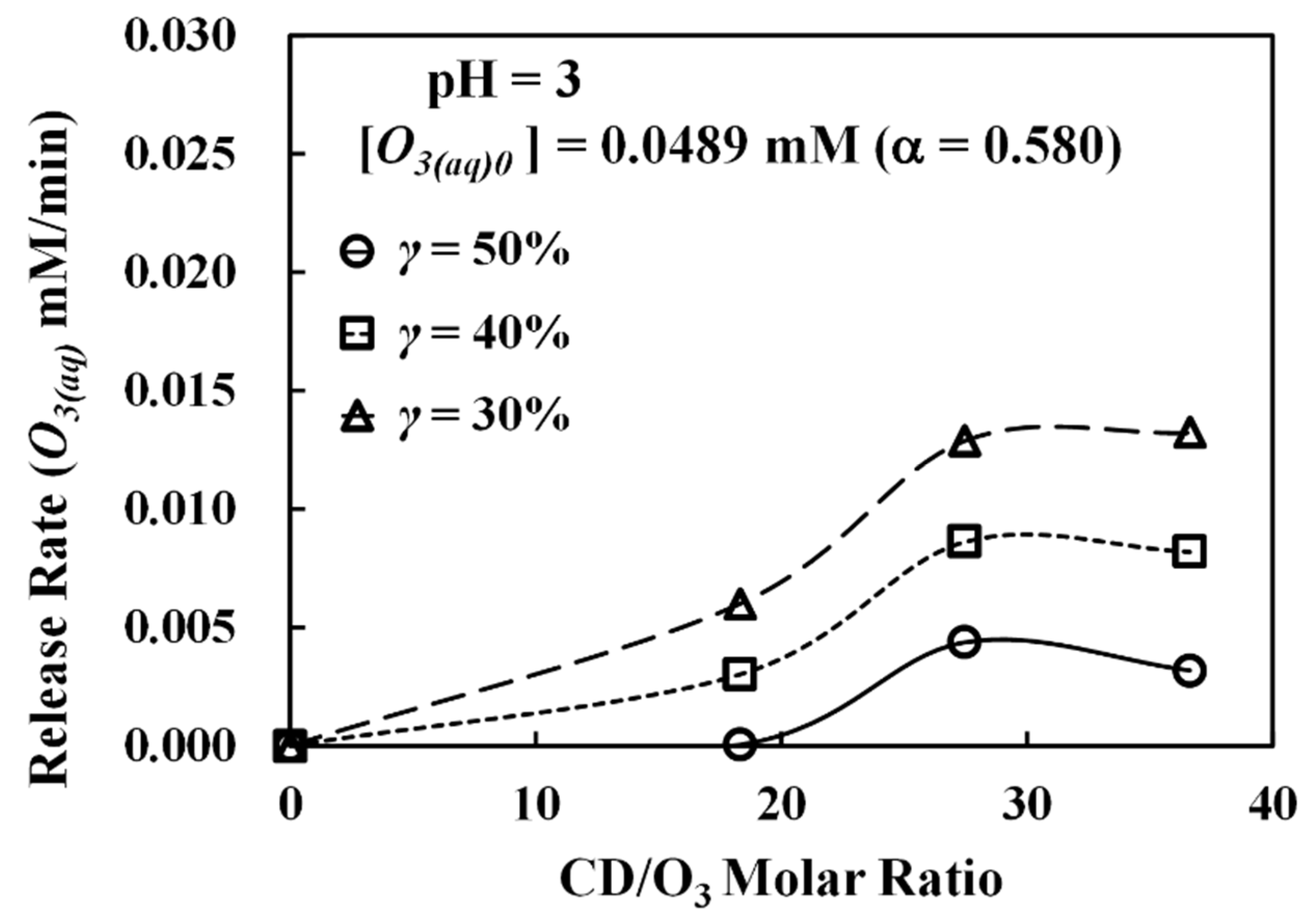
Figure 4 shows the experimental data of dissolved ozone release at pH 3. In Figure 4, the y-axis is expressed in terms of the difference (ΔABS) of indigo absorbance in pure water (ABS_blank) and in the O₃-βCD system (ABS_O3-CD), i.e., ΔABS = ABS_blank − ABS_O3-CD. The ΔABS value is proportional to the dissolved ozone concentration in the solution, which can be calculated by applying Beer’s law with a molar absorptivity of 20,000 M⁻¹ cm⁻¹ for indigo [37] and a path length of 1 cm in our instrument. Figure 4 shows the results conducted under two different initial dissolved ozone (O_3(aq)0) concentrations of 0.0489 mM and 0.0241 mM, corresponding to the α values of 0.580 and 0.504, respectively. To quantify the β-CD dosage in dimensionless form, the CD/O₃ molar ratio (Equation (6)) was used. As seen in Figure 4, a total of five different molar ratios was tested. From data in Figure 4, the ΔABS values for solutions without β-CD (CD/O₃ = 0) level off rapidly, meaning dissolved ozone only appears for a few minutes in these solutions in the presence of indigo. On the other hand, when β-CD is present, their ΔABS values increase gradually, indicating a slow release of dissolved ozone from the O₃-βCD inclusion complex. We can further estimate the ozone release rates from the slopes of these curves. Since the release generally becomes more stable after 30 min as observed in Figure 4, the release rates were calculated by taking the slopes measured from 30 to 180 min, and the results are summarized in Figure 5, presented as a function of the CD/O₃ molar ratio. From Figure 5, it was found that the release rates are in the range of 3.5 × 10⁻⁵ to 6.8 × 10⁻⁵ mM/min. When α = 0.580, the maximum release rate occurs at the CD/O₃ molar ratio of 27.4 but not at the higher ratio of 36. Similar release rate behavior was observed when the α value was 0.504; the maximum rate occurs at the ratio of 55 instead of a larger ratio of 73. Thus, a higher β-CD concentration or a larger molar ratio does not necessarily lead to a higher ozone release rate. Our interpretation is that when there is too much β-CD in the solution, most dissolved ozone is consumed for β-CD degradation, resulting in a low aqueous ozone concentration and causing low efficiency in the formation of the O₃-βCD inclusion complex. On the other hand, when the β-CD concentration is at the lower end, it could be too low to form enough O₃-βCD inclusion complex for efficient ozone release. Consequently, the optimal release rate should exist at an intermediary β-CD dosage, such as at the molar ratio of 27.4, which we found in our system when α = 0.580. Additionally, experiments were repeated under the above two maximum release rate conditions but at pH 5 and pH 7: (1) α = 0.580 and CD/O₃ = 27, and (2) α= 0.504 and CD/O₃ = 55. The results are presented in Figure 6. As seen in Figure 6, the release rates at pH 5 and 7 are very close and are both smaller than the release rates at pH 3. The release rates are around 2.5 × 10⁻⁵ mM/min and 1.6 × 10⁻⁵ mM/min for pH 5 and pH 7, respectively. On average, their release rates are about half of that at pH 3 due to faster decomposition rates of ozone at these pH values.

3.3. Mathematical Modeling of Optimal Ozone Concentration at the Interface

The following differential equation (Equation (7)) describes the mass balance of the aqueous ozone ($O_{3\left(aq\right)}$) in the gas-absorption reactor during the process of O₃-βCD complex formation. In the β-CD solution, aqueous ozone is continuously replenished from gaseous ozone ($C_{O3\left(g\right)0}$) and is also consumed through reactions with β-CD ($\left[CD\right]$), self-decomposition, and mass transfer into the β-CD cavity.

$$\frac{d\left[O_{3\left(aq\right)}\right]}{dt}=k_{La}\left(\frac{C_{O3\left(g\right)0}}{H}-\left[O_{3\left(aq\right)}\right]\right)-k_r\left[CD\right]-k_d\left[O_{3\left(aq\right)}\right]-k_{fa}\left(\left[O_{3\left(aq\right)}\right]-\left[O_{3\left(aq\right)|CD}\right]\right)$$

(7)

In Equation (7), $k_{La}$ is the overall gas–liquid interfacial mass transfer coefficient for ozone (min⁻¹), $C_{O3\left(g\right)0}$ is the input gaseous ozone concentration (mmol/L_g), H is the dimensionless Henry’s constant of ozone (mmol/L_g/mM), $k_r$ is the pseudo-first-order degradation rate constant of β-CD (min⁻¹), $k_d$ is the first-order self-decomposition rate constant of aqueous ozone (min⁻¹), $k_{fa}$ is the overall mass transfer coefficient for ozone from the bulk solution to the O₃-βCD inclusion complex (min⁻¹), and $\left[O_{3\left(aq\right)|CD}\right]$ stands for the dissolved ozone concentration at the water-CD interface (mM).

The concentration of dissolved ozone at the water-CD interface ($O_{3\left(aq\right)|CD}$) in Equation (7) plays a critical role in governing the release of ozone from the O₃-βCD inclusion complex. This term cannot be measured experimentally but can be predicted by solving Equation (7). From the BTCs data in Figure 2b, it should be reasonable to assume that after 30 min of purging, the O₃-βCD system has reached a pseudo-steady-state condition, where the inclusion complex becomes stable, and its concentration variation is unnoticeable. Under such a steady-state condition, Equation (7) can be solved to obtain the interface concentration $\left[O_{3\left(aq\right)|CD}\right]$:

$$\left[O_{3\left(aq\right)|CD}\right]=\frac{\left[O_{3\left(aq\right)}\right]\left(k_{La}+k_d+k_{fa}\right)+k_r\left[CD\right]-(k_{La}/H)C_{O3\left(g\right)0}}{k_{fa}}$$

(8)

In Equation (8), the gaseous ozone ($C_{O3\left(g\right)0}$) concentration is essentially constant at steady state. For the aqueous ozone ($\left[O_{3\left(aq\right)}\right]$) and CD concentration ([CD]), they both can be measured experimentally, as already shown above in Figure 1 and Figure 2. In addition, the mass transfer coefficient $k_{La}$, and the rate constants $k_r$ and $k_d$ for the system can all be optimized with respect to ozone BTC as described above in Figure 2a,b. Given these available terms, the overall mass transfer coefficient $k_{fa}$ becomes the only unknown parameter on the right-hand side of Equation (8). By definition, $k_{fa}$ is the product of $k_f$, the mass transfer coefficient (cm/s), and $a_i$, the specific water–CD interfacial area (cm²/cm³). In fact, the $a_i$ term can further be defined as

$$a_i={10}^{-2}\left(S_{BET}\left[CD\right]M_{CD}\right)$$

(9)

where $S_{BET}$ is the BET surface area (m²/g), and $M_{CD}$ is the molecular weight of β-CD (1135 g/mole). For a typical stirred tank, the liquid–solid mass transfer coefficient can range from 10⁻⁷ to 10⁻² cm/s. Generally, values smaller than 10⁻³ cm/s are considered incomplete mixing [38]. Although macromolecules such as β-CD are not solids, we are assuming that their interfacial mass transfer coefficients are within the same order of magnitude. In our system under moderate mixing, the mass transfer coefficient was assumed to range between 1 × 10⁻⁴ to 1 × 10⁻³ cm/s. Furthermore, from past investigations, the BET surface areas of β-CD and β-CD polymers were found to be in the range of 3 to 6 m²/g [39,40]. To be more conservative, in our calculations, we assume a value of 1.25 m²/g. With these given parameters, the dissolved ozone concentration at the water–CD interface ($\left[O_{3\left(aq\right)|CD}\right]$) can be calculated according to Equation (8).

Table 1. Calculations of steady-state dissolved ozone concentrations at the water-CD interface.

${\mathit{C}}_{\mathit{O}3\left(\mathit{g}\right)0}(\mathbf{mmol}/{\mathbf{L}}_{\mathbf{g}})$	${\left[\mathit{C}\mathit{D}\right]}_0\left(\mathbf{mM}\right)$	${\mathit{H}}_{\mathit{C}\mathit{D}}$	$\left[{\mathit{O}}_{3\left(\mathit{a}\mathit{q}\right)}\right]\left(\mathbf{mM}\right)$	$\left[\mathit{C}\mathit{D}\right]\left(\mathbf{mM}\right)$	$\left[{\mathit{O}}_{3\left(\mathit{a}\mathit{q}\right)|\mathit{C}\mathit{D}}\right]\left(\mathbf{mM}\right)$
	0.88	6.66	0.0457	0.352	0.009387
0.274 (α = 0.580)	1.32	7.73	0.0354	0.528	0.01999
	1.76	12.54	0.0113	0.704	0.007916

H = 3.25; $k_{La}$ = 0.355 min⁻¹; $k_d$ = 0.0116 min⁻¹; $k_r$ = 0.0225 min⁻¹; $k_f$ = 7.0 × 10⁻⁴ cm/s; $S_{BET}$ = 1.25 m²/g; $M_{CD}$ = 1135 g/mol.

lists a set of the calculated results (pH 3) with a $k_f$ value of 7.0 × 10⁻⁴ cm/s. The calculated $\left[O_{3\left(aq\right)|CD}\right]$ concentrations in Table 1 were all slightly less than their corresponding aqueous bulk concentrations ($\left[O_{3\left(aq\right)}\right]$), indicating there is a net diffusive flux of ozone entering from the bulk into the β-CD cavity.

Equation (8) can be further transformed by employing $k_{fa}=k_f{a}_i$, substituting $a_i$ with Equation (9), substituting $C_{O3\left(g\right)0}/H$ with $\left[O_{3\left(aq\right)0}\right]/\alpha$, replacing $\left[O_{3\left(aq\right)}\right]$ with $\beta \left[O_{3\left(aq\right)0}\right]$, and substituting $\left[CD\right]$ with $\left(1-\gamma \right){\left[CD\right]}_0$, where $\gamma$ is the percentage of β-CD degradation at steady state. Then, Equation (8) becomes

$$\left[O_{3\left(aq\right)|CD}\right]=\frac{\beta \left[O_{3\left(aq\right)0}\right]\left(k_{La}+k_d+k_{fa}\right)+k_r\left(1-\gamma \right){\left[CD\right]}_0-(k_{La}/\alpha )\left[O_{3\left(aq\right)0}\right]}{k_f\left[{10}^{-2}\left(S_{BET}\left(1-\gamma \right){\left[CD\right]}_0{M}_{CD}\right)\right]}$$

(10)

Next, by substituting R as ${\left[CD\right]}_0/\left[O_{3\left(aq\right)0}\right]$ as defined in Equation (6), Equation (10) can be rewritten as

$$\left[O_{3\left(aq\right)|CD}\right]=\frac{\beta \left(k_{La}+k_d+k_{fa}\right)+k_r\left(1-\gamma \right)R-k_{La}/\alpha }{{10}^{-2}{k}_f{S}_{BET}\left(1-\gamma \right)R{M}_{CD}}$$

(11)

With fixed kinetic rate constants ($k_d$ & $k_r$) and mass transfer coefficients ($k_{La}$, $k_{fa}$, and $k_f$) plus constant values of α, β, and γ in the system at steady state, Equation (11) becomes dependent on the R value (${\left[CD\right]}_0/\left[O_{3\left(aq\right)0}\right]$) only, i.e., the CD/O₃ molar ratio. In Figure 7, the calculated values of $\left[O_{3\left(aq\right)|CD}\right]$ are plotted as a function of the molar ratio under three different $k_f$ values of 6.0 × 10⁻⁴, 7.0 × 10⁻⁴, and 8.0 × 10⁻⁴ cm/s. From Figure 7, it is evident that the functional relationship between $\left[O_{3\left(aq\right)|CD}\right]$ and the CD/O₃ molar ratio is parabolic, and a maximum value of $\left[O_{3\left(aq\right)|CD}\right]$ exists at an intermediate molar ratio but not at the highest ratio. This is in agreement with what we have observed above regarding ozone release from the O₃-βCD inclusion complex. When there is a very high concentration of β-CD in the solution, ozone is consumed more to react with β-CD and is left with a less dissolved concentration in the solution for the formation of the O₃-βCD complex. Despite a relatively large overall mass transfer coefficient ($k_{fa})$ under a high β-CD concentration, ozone transferred to the β-CD interface is still limited due to low dissolved ozone concentration in the bulk solution. On the other hand, when the β-CD concentration is very low, the available dissolved ozone concentration becomes high in the solution since ozone is not consumed significantly. However, this causes the ozone gas–water mass transfer to become less efficient due to a smaller gradient across the gas–water interface as well as a smaller $k_{fa}$ due to a lower β-CD concentration. This also results in a relatively low mass transfer of dissolved ozone to the β-CD interface. Consequently, a maximum mass transfer condition would exist in-between these two extremes as shown in Figure 7 by Equation (11).

3.4. Ozone Release Rate Calculations and Comparisons

With the calculated ozone concentration at the interface ($\left[O_{3\left(aq\right)|CD}\right]$), we can further estimate the experimental ozone release rate as presented in Figure 5. Here, two assumptions are made. First, given the value of $\left[O_{3\left(aq\right)|CD}\right]$, the resulting ozone release rate ($R_{O3}$) can be calculated by the following equation:

$$R_{O3}\left(mM/min\right)=k_{fa}\left(\left[O_{3\left(aq\right)|CD}\right]-\left[O_{3\left(aq\right)}\right]\right)$$

(12)

The $\left[O_{3\left(aq\right)}\right]$ term in Equation (12) represents the bulk concentration of ozone adjacent to the β-CD interface during the release. In our calculations, we are assuming $\left[O_{3\left(aq\right)}\right]$ equals zero, a condition that ozone is essentially depleted during the release due to reaction. Under this condition, the prediction represents the maximum release rate. Second, it should be noted that in the prediction of $\left[O_{3\left(aq\right)|CD}\right]$ in Figure 7, the same set of parameters were used, i.e., parameters listed in Table 1 are employed for all three different molar ratios. However, in our calculations to estimate the experimental release rate, their $k_f$ and $S_{BET}$ values are individually fitted while other parameters are kept constant as those in Table 1. Since not every single experiment could possess identical mass transfer coefficients, as long as these coefficients are within a reasonable range, they should be considered reasonable. With these assumptions, the model-calculated ozone release rates under a gaseous concentration of 0.274 mmol/L_g (α = 0.580) can be estimated using Equation (12) and their results are shown in

Table 2. Experimental and model-predicted O₃ release rate from the O₃-βCD inclusion complex under different β-CD to O₃ molar ratios at pH 3.

Molar Ratio ${\left[\mathit{C}\mathit{D}\right]}_0/\left[{\mathit{O}}_{3\left(\mathit{a}\mathit{q}\right)0}\right]$	${\mathit{H}}_{\mathit{C}\mathit{D}}$	${\mathit{k}}_{\mathit{f}}(\mathbf{cm}/\mathbf{s})$	${\mathit{S}}_{\mathit{B}\mathit{E}\mathit{T}}({\mathbf{m}}^2/\mathbf{g})$	Exp. O3(aq) mM/min	Model O3(aq) mM/min
18.3	6.66	3.98 × 10−4	1.017	4.36 × 10−5	4.29 × 10−5
27.4	7.73	1.35 × 10−4	1.001	6.88 × 10−5	6.83 × 10−5
36.6	12.54	1.55 × 10−4	1.075	6.36 × 10−5	6.28 × 10−5

H = 3.25; α = 0.580; $C_{O3\left(g\right)0}$ = 0.274 mmol/L_g; $k_{La}$ = 0.355 min⁻¹; $k_d$ = 0.0116 min⁻¹; $k_r$ = 0.0225 min⁻¹; $M_{CD}$ = 1135 g/mol.

below. In the table, specific $k_f$ and $S_{BET}$ values for each molar ratio are also listed. From the results in Table 2, it is evident that the model-calculated values are very close to their experimental ones, with a maximum difference under 3%. The $k_f$ and $S_{BET}$ values are all within a reasonable range as suggested in the literature with respect to mass transfer [38] and β-CD properties [39,40].

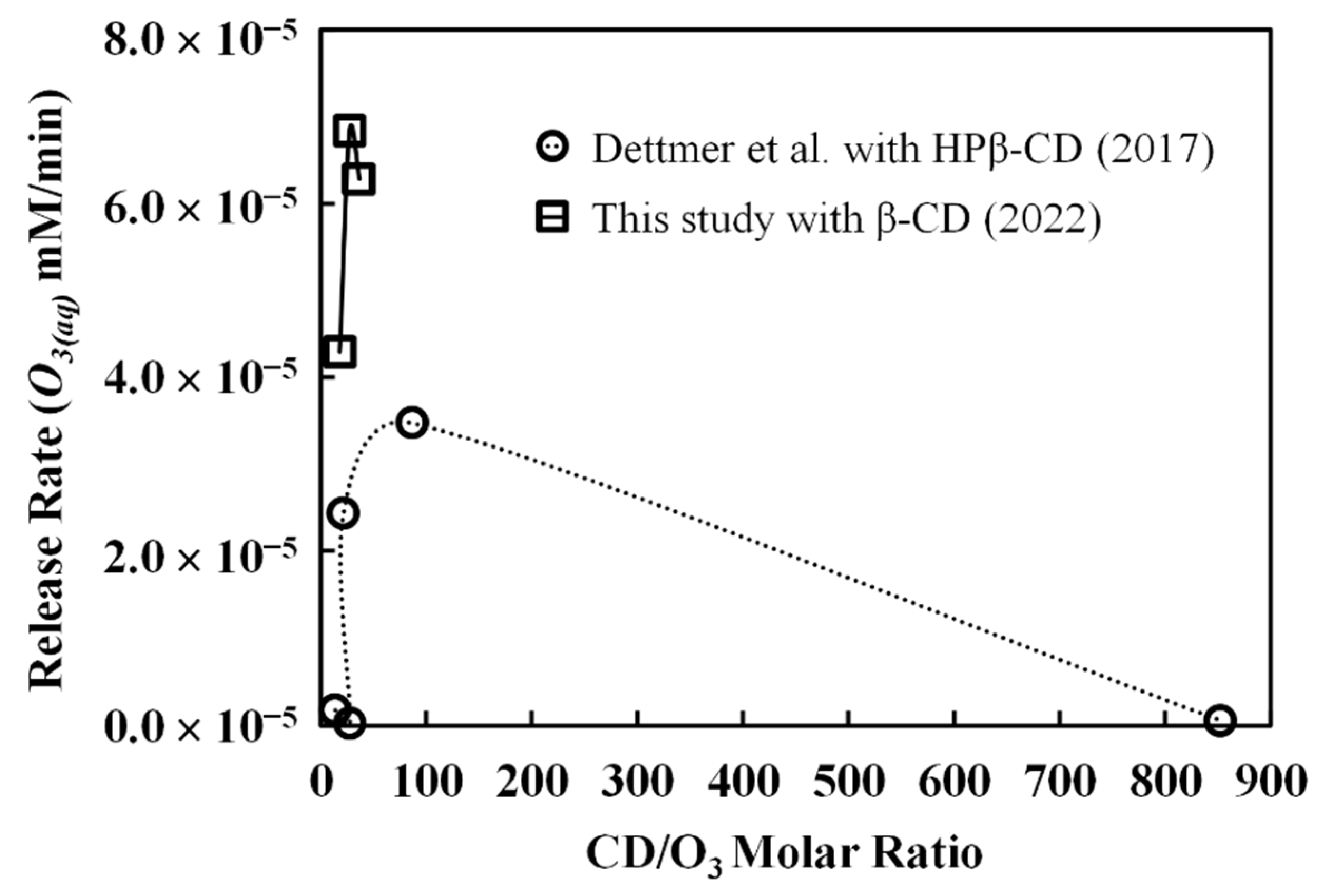
The above-calculated results were further compared with ozone release data from the study by Dettmer et al. [14]. Before the comparisons, experimental material and design differences between Dettmer’s investigation and this study must be addressed. First of all, the CD they used was HPβ-CD but not β-CD. Second, as mentioned earlier, the range of CD to ozone molar ratios they studied is from less than 20 to more than 800, which is very different from our range of molar ratios. Third, in their study, the release rate was not presented directly; instead, the data of cumulative ozone mass release (in mg/L) was plotted as a function of time (hour). From these original data, we calculated the slopes and then converted the units to mM/min in order to compare them with our data. Finally, the time span of their study was from 20 h to as high as 80 h, whereas in this study, the release rate we examined is 3 h. Despite the differences, it is still essential to compare these data to gain insights into the accuracy of our empirical model. In Figure 8, ozone release rates in Table 2 and the release rates from Dettmer’s study are plotted as a function of the CD-to-ozone molar ratio. In Dettmer’s study, the lowest release rate of 1.7 × 10⁻⁷ mM/min occurs at the molar ratio of 28, while the highest release rate of 3.5 × 10⁻⁵ mM/min occurs at the molar ratio of 87. When the molar ratio goes to 850, the release rate is 5.2 × 10⁻⁷ mM/min. These data do show parabolic behaviors, as have been observed in this study, except at a wider range of molar ratios. Our calculated release rates are on the higher ends of their data (>4.0 × 10⁻⁵ mM/min). This is mainly because our prediction represents the initial stage of the ozone release process (<3 h) where the O₃-CD complex’s concentration is high. As the release processes continue to 20 or 40 h, the release rate should decrease due to a lower O₃-CD complex concentration. In addition to the time scale, the differences between HPβ-CD and β-CD could affect the variations in Figure 8. From this comparison, it is seen that the empirical model developed in this study is capable of roughly estimating the early-stage ozone release rate from another independent study. The fact that the model can not only interpret our experimental data of ozone release rate, but can also estimate the release rate of an analogous system does justify its validity.

3.5. TPH Removal by Pure β-CD

Figure 9a demonstrates the removal data of TPH by pure β-CD (0.44, 0.88, 1.32, and 1.76 mM) without any ozone addition at three different initial TPH concentrations (50, 100, and 150 mg/L). The removal experiments were carried out in a batch reactor for 24 h. From Figure 9a, it is seen that the removal percentage essentially increases as the β-CD dosage increases. Meanwhile, a higher removal efficiency was observed at the TPH concentration of 100 mg/L, where the highest removal efficiency was around 80% at a β-CD dosage of 1.76 mM. With the reaction time of 24 h, an equilibrium distribution should have been reached. Figure 9b plots the relationship of the calculated mass of TPH on β-CD vs. the concentration of TPH in water at equilibrium. As seen in Figure 9b, the partitioning behavior is not very linear but seems to have a maximum capacity. The major reason for this trend is likely the nature of TPH. As we know, TPH is not a single-component matter but a multicomponent mixture of C₁₀ to C₂₀ hydrocarbons. For smaller molecules with a multicomponent mixture such as BTEX, linear partitioning behaviors were observed on β-CD [21]. However, for larger molecules such as TPH, some larger constituents might not all fit into the cavity to be removed effectively by β-CD, rendering a maximum capacity in the partitioning of TPH.

3.6. TPH Removal by O₃-βCD Inclusion Complex

In the final phase of the experiments, the O₃-βCD inclusion complex was used to test its potential for the removal of TPH in solution. To exclude the effects of the hydroxyl radical, the experiments were conducted at pH 3 only. Two different reaction schemes were adopted under various conditions. In scheme I, gaseous ozone was first purged in a pH 3 solution containing β-CD for 30 min to form the O₃-βCD complex. Then, the ozone purging was stopped, and the solution was subsequently added to the TPH-containing solution (50 mg/L) to react for 30 min (t_r = 0.5 h). Scheme II had the same ozone purging time as scheme I, but the reaction time was extended to 24 h (t_r = 24 h). Figure 10 shows the comparative results of the overall TPH removal under a wide range of CD/O₃ molar ratios from 9 to 91 and under two different gaseous ozone loading dosages of α = 0.580 and α = 0.504.

From Figure 10, when schemes I and II are compared, it was found that a reaction time of 24 h is important in controlling the TPH removal efficiency. At best, an increase of nearly 30% was observed when the reaction time was increased from t_r = 0.5 h to t_r = 24 h under a CD/O₃ molar ratio of 27.4. It should be emphasized that in scheme I, during the short period of reaction (t_r = 0.5 h), most of the TPH removal is due to direct reactions with residual aqueous ozone in solution, but not reactions with ozone released from the O₃-βCD inclusion complex. The removal due to residual aqueous ozone should be insignificant after 30 min. This implies that the 30% increase in TPH removal is mostly due to degradation by the O₃-βCD inclusion complex. Additionally, it is evident that for the two different gaseous ozone dosages of α = 0.580 and α = 0.504, the best removal efficiencies occur at the CD/O₃ molar ratios of 27.4 and 48.5, respectively. In fact, these removal efficiencies do demonstrate a somewhat parabolic functional dependence on the molar ratio. This behavior is analogous to what we have found regarding the maximum interfacial ozone concentrations, as shown in Figure 7. Recall from the above ozone release data that the maximum release rate equals 6.88 × 10⁻⁵ mM min⁻¹ (α = 0.580) when the CD/O₃ molar ratio is 27.4, as seen in Figure 5 and Table 2. For 24 h, the accumulated mass of dissolved ozone released into the solution should be 0.09907 mM (i.e., 6.88 × 10⁻⁵ mM/min × 24 h/d × 60 min/h). To estimate the average molar concentration of TPH, we use the molecular weight of n-tetradecane (C₁₄H₃₀) as the representative molar mass, and 50 mg/L of TPH would be equivalent to 0.252 mM. Thus, the aforesaid 30% of removal efficiency increase is the removal of 0.0756 mM of TPH (i.e., 0.252 mM × 30% = 0.0756 mM). Thus, the molar ratio between ozone and TPH is 0.09907:0.0756, which is roughly 1.3:1, a reasonable stoichiometry during the chemical degradation of TPH by released ozone. Finally, it should be noted that adding β-CD to the treatment process for a short reaction time (e.g., t_r = 0.5 h) does not necessarily enhance the removal efficiency. For example, as seen in Figure 10, when α = 0.580, the removal efficiency essentially decreases as the molar ratio increases. This is because under the circumstances residual ozone is responsible for the degradation of TPH. More residual ozone is present in the solution when the molar ratio CD/O₃ = 0. Given enough reaction time (e.g., t_r = 24 h), a higher removal efficiency can be achieved through reactions with dissolved ozone released from the O₃-βCD inclusion complex.

4. Discussion

From the above experimental results, it is evident that the molar ratio does play an important role in controlling the O₃ release rate as well as the TPH removal efficiency. From Equation (11), it is possible to mathematically describe the dependence of interfacial ozone concentration ($\left[O_{3\left(aq\right)|CD}\right]$) on the molar ratio, as demonstrated in Figure 7. Furthermore, via Equation (12), the ozone release rate can be well estimated. Since a lot of empirical and theoretical parameters are involved in the model, we summarize the whole procedure in Figure 11 to have a clearer picture of these parameters and to facilitate future applications of the model. In Figure 11, the parameters are categorized into five different groups. Group 1 contains dimensionless parameters we derived in Section 3.1. Their values are dependent on the molar ratio (Group 5). When different types of CD are used, they must first be tested to obtain their corresponding dimensionless saturation diagrams, as shown in Figure 3, to quantify these parameters. Group 2 includes gas–liquid mass transfer coefficient and kinetic rate constants of ozone and CD. This gas–liquid mass transfer coefficient is dependent on mixing intensity and bubble size, while the kinetic rate constants are independent of a reactor system. Group 3 includes the molecular weight and BET surface area of each CD that is used. They are independent of reactor configuration and reaction kinetics. Group 4 contains the interfacial mass transfer parameters on the CD surface, which is the most difficult to obtain. In this study, we were able to estimate their values by fitting the model (Equation (12)) to the experimental data on the ozone release rate.

A significant factor affecting the estimate of ozone release rate is the steady-state concentration of CD in the solution ($\left[CD\right]$), which equals $\left(1-\gamma \right){\left[CD\right]}_0$, with $\gamma$ being the percentage of CD degraded at steady state and ${\left[CD\right]}_0$ the initial CD concentration. In our estimate in Table 2, a 50% CD degradation ($\gamma$ = 50%) is adopted according to the experimental data (i.e., Figure 2a). To understand the effect of $\gamma$ on the ozone release rate, we simulate the ozone release rates under various $\gamma$ values ($\gamma$ = 50%, $\gamma$ = 40%, and $\gamma$ = 30%), and the results are plotted in Figure 12. Note that the specific $k_f$ and $S_{BET}$ values used in the simulation are identical to the first set of parameters in Table 2, which is able to describe the ozone release rate (i.e., 4.29 × 10⁻⁵ mM/min) at the molar ratio of 18.3. In Figure 12, as the percentage of degradation becomes lower, the corresponding ozone release rate increases significantly, as seen in Figure 12. When $\gamma$ = 30% (i.e., $\left[CD\right]=0.7{\left[CD\right]}_0$), the increase in the ozone release rate could be as high as 100-fold from the simulation in comparison to a $\gamma$ value of 50% for the molar ratio of 18.3. In fact, our experimental ozone release data in Figure 5 are all in the range of 3.00 × 10⁻⁵ to 7.00 × 10⁻⁵ mM/min. According to our model, these belong to the condition of a relatively high degree of degradation or large $\gamma$ values when reaching a steady state. From the simulations, a higher ozone release rate could be achieved if the types of CD selected are more resistant to degradation and are able to maintain a higher concentration in the solution at a steady state. Finally, it has to be emphasized that our model (Equation (11)) is derived under the assumption of a steady state. Suppose a system is not at a steady state or when a steady state cannot be reached, then a transient model has to be developed.

5. Conclusions

In this study, the concept of empirical Henry’s constant, $H_{CD}$, was defined and used to describe the steady-state relationship between gaseous and aqueous ozone in the dynamic O₃-βCD system. A new dimensionless plot of the relative degree of aqueous ozone saturation (β) vs. the CD/O₃ molar ratio was also developed. In the dimensionless plot, β is found to be inversely proportional to the molar ratio under a constant ozone loading concentration or equivalently a constant dimensionless α value. This type of dimensionless plot is of practical use in understanding and quantifying the dosage effects of CD and ozone in solution. From data of dissolved ozone release experiments, the O₃-βCD inclusion complex was found to have a maximum ozone release rate of 6.88 × 10⁻⁵ mM/min under an intermediary CD/O₃ molar ratio of 27.4 when the reactor system’s α value equals 0.580. With the mathematical model we developed, the dissolved ozone at the water-CD interface ($\left[O_{3\left(aq\right)|CD}\right]$) can be empirically calculated. Predicted results of $\left[O_{3\left(aq\right)|CD}\right]$ have parabolic dependence on the CD/O₃ molar ratio. Furthermore, experimental ozone release rates at pH 3 can be well estimated to a degree of 3% variations using the model. Additionally, the model’s prediction of the ozone release rate is close to the experimental data of another independent study. Procedures and limitations in using this empirical multiparameter model are highlighted and discussed. With respect to the interactions of TPH with pure β-CD, the partitioning is unconventional and has a tendency to reach a maximum capacity on β-CD, presumably due to the selective partitioning behavior of TPH. Finally, in the removal of TPH by the O₃-βCD inclusion complex, it was found that given enough time, the O₃-βCD complex could slowly release ozone to react and remove the TPH. The maximum removal efficiency occurs at an intermediary CD/O₃ molar ratio. This result is in agreement with the ozone release data as well as the mathematical predictions of $\left[O_{3\left(aq\right)|CD}\right]$. With the correlations and mathematical model we developed in this study, an optimal dosage with respect to a specific O₃-CD system can be estimated. Such optimization can be of importance to field applications.