Effects of Water and Fertilizer Flow Rates on the Mixing Process and Fertilization Uniformity of Cotton under Mulch Drip Irrigation
Abstract
1. Introduction
2. Methods
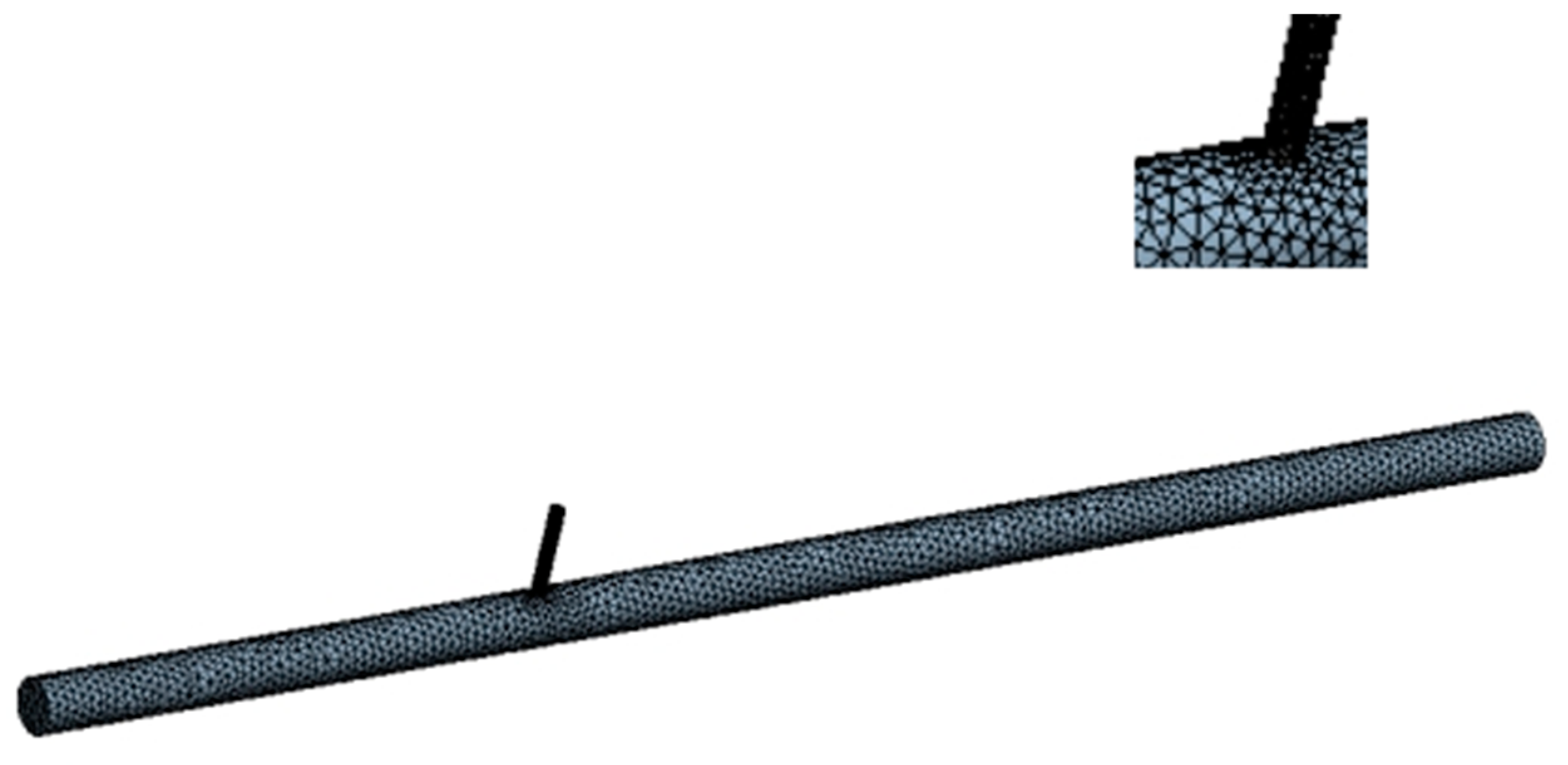
2.1. Numerical Simulation
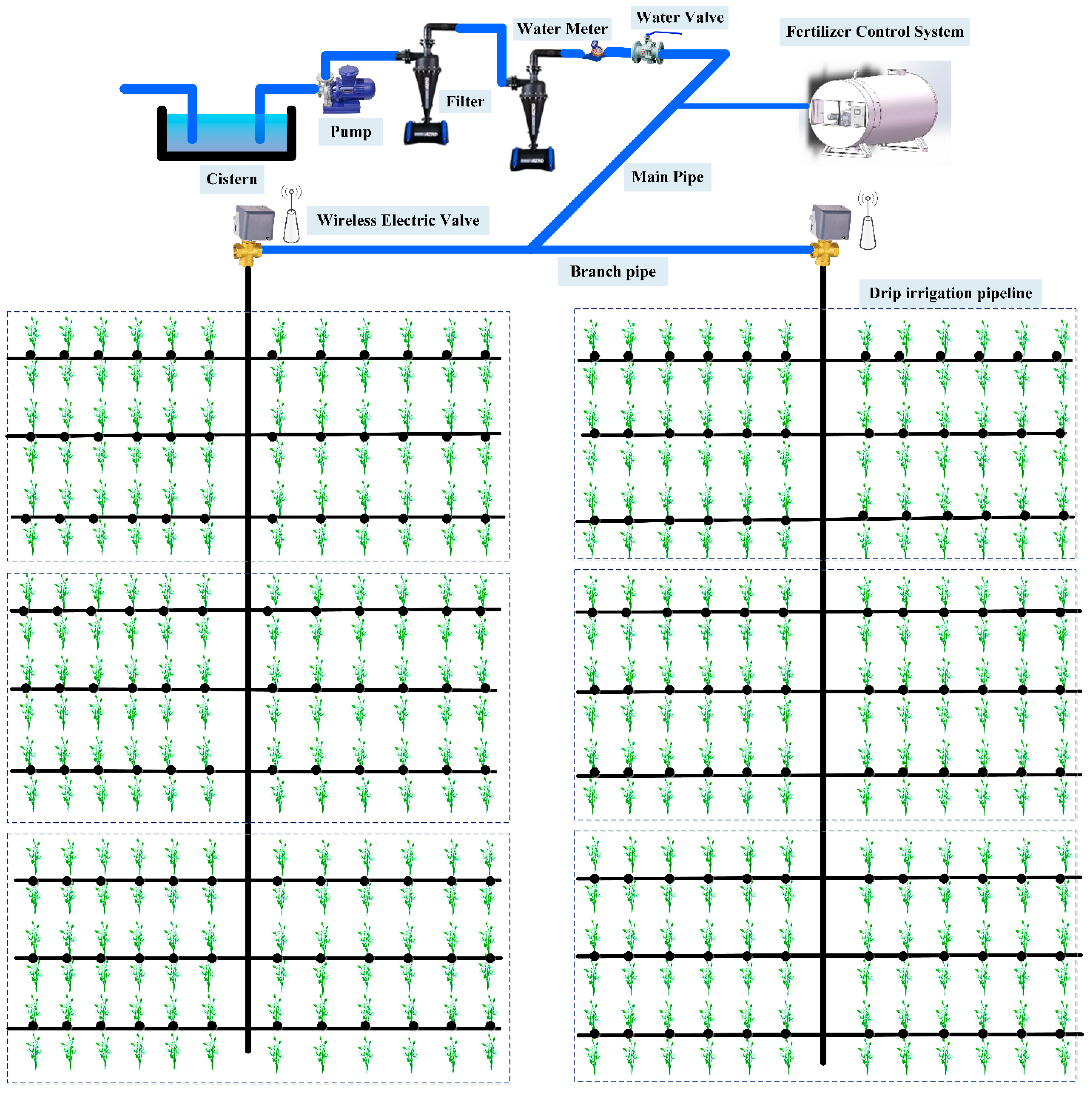
2.2. Field Experiment
- (1)
- The Christensen uniformity coefficient (%)where -the number (water cup flow, fertilizer concentration and fertilizer application) is the observation; -the mean value; and -the number of observation points.
- (2)
- Distribution uniformity factor DUwhere is the mean of the smaller 25 percent of the N observations.
- (3)
- Statistical uniformity (%) iswithwhere -Standard deviation of the observed values.
3. Results and Discussion
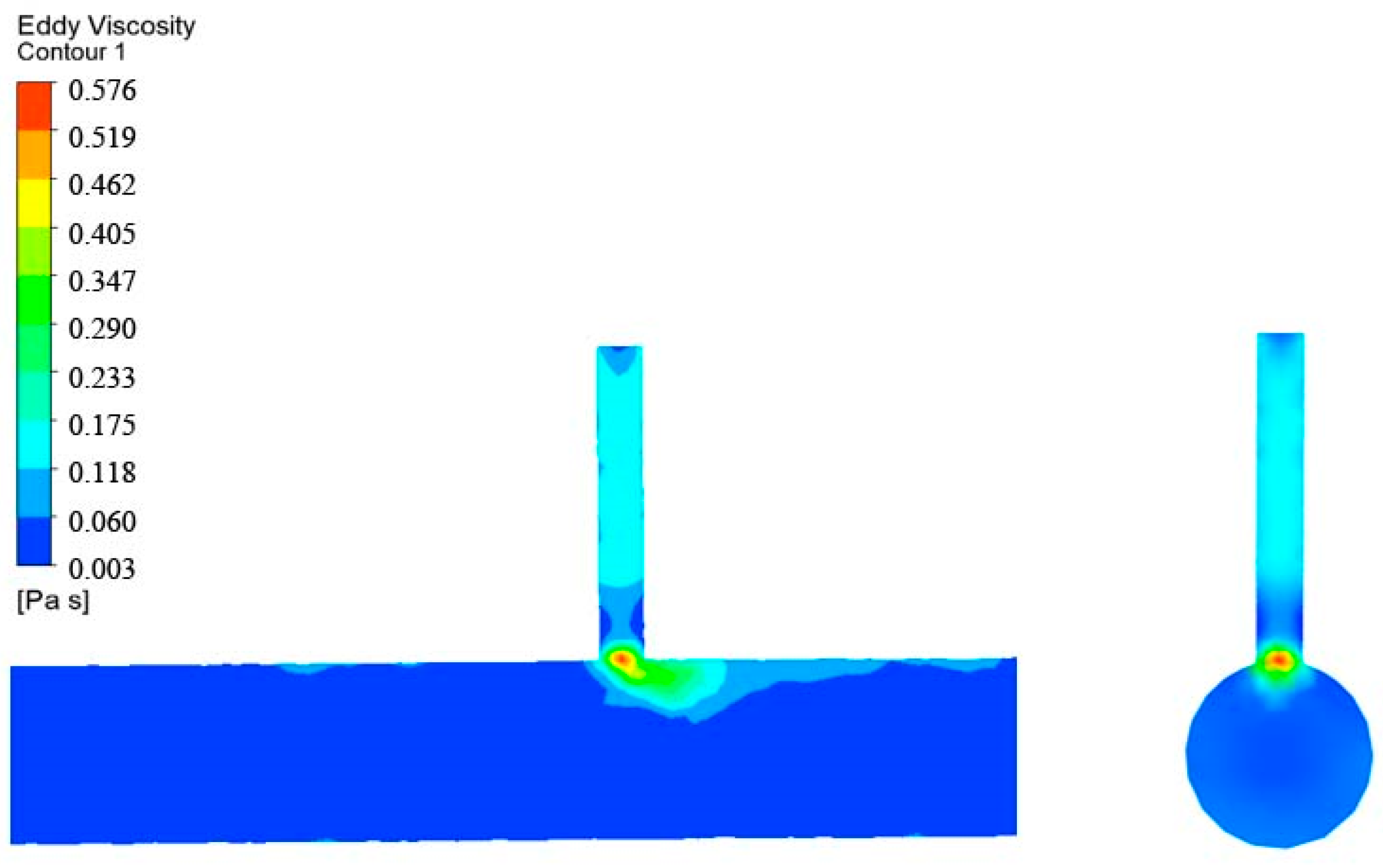
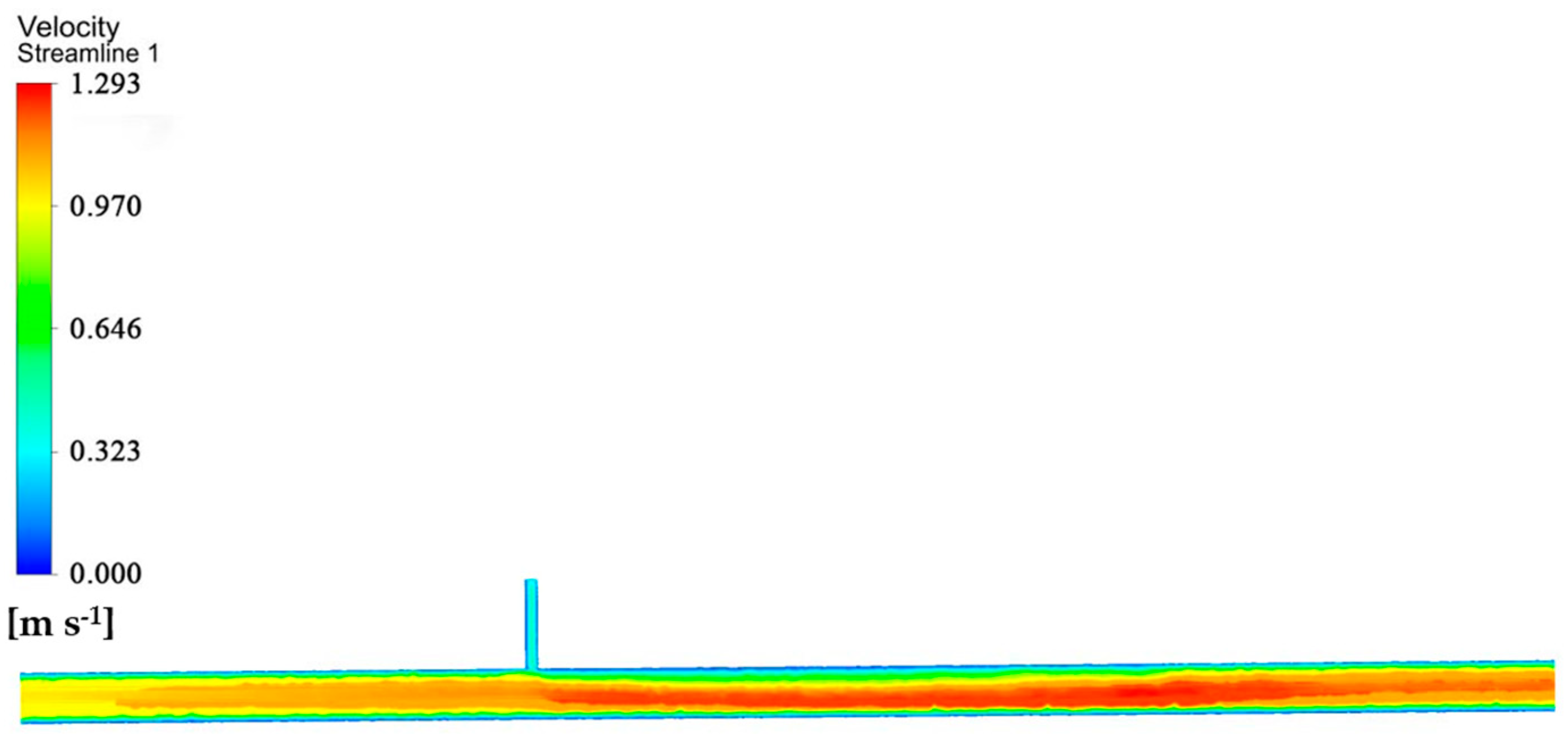
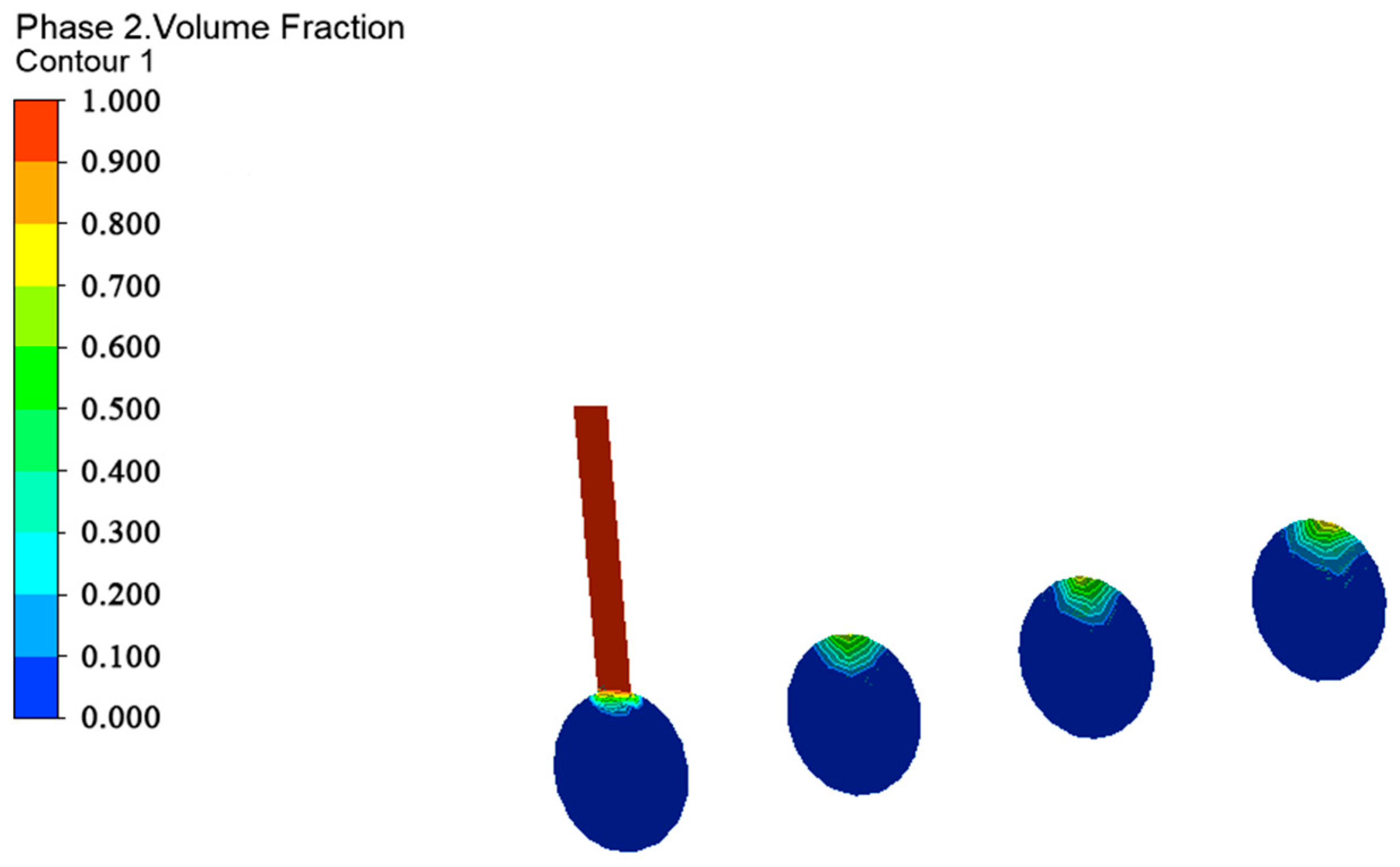
3.1. Analysis of the Mixing Process of Water and Fertilizer in the Pipe
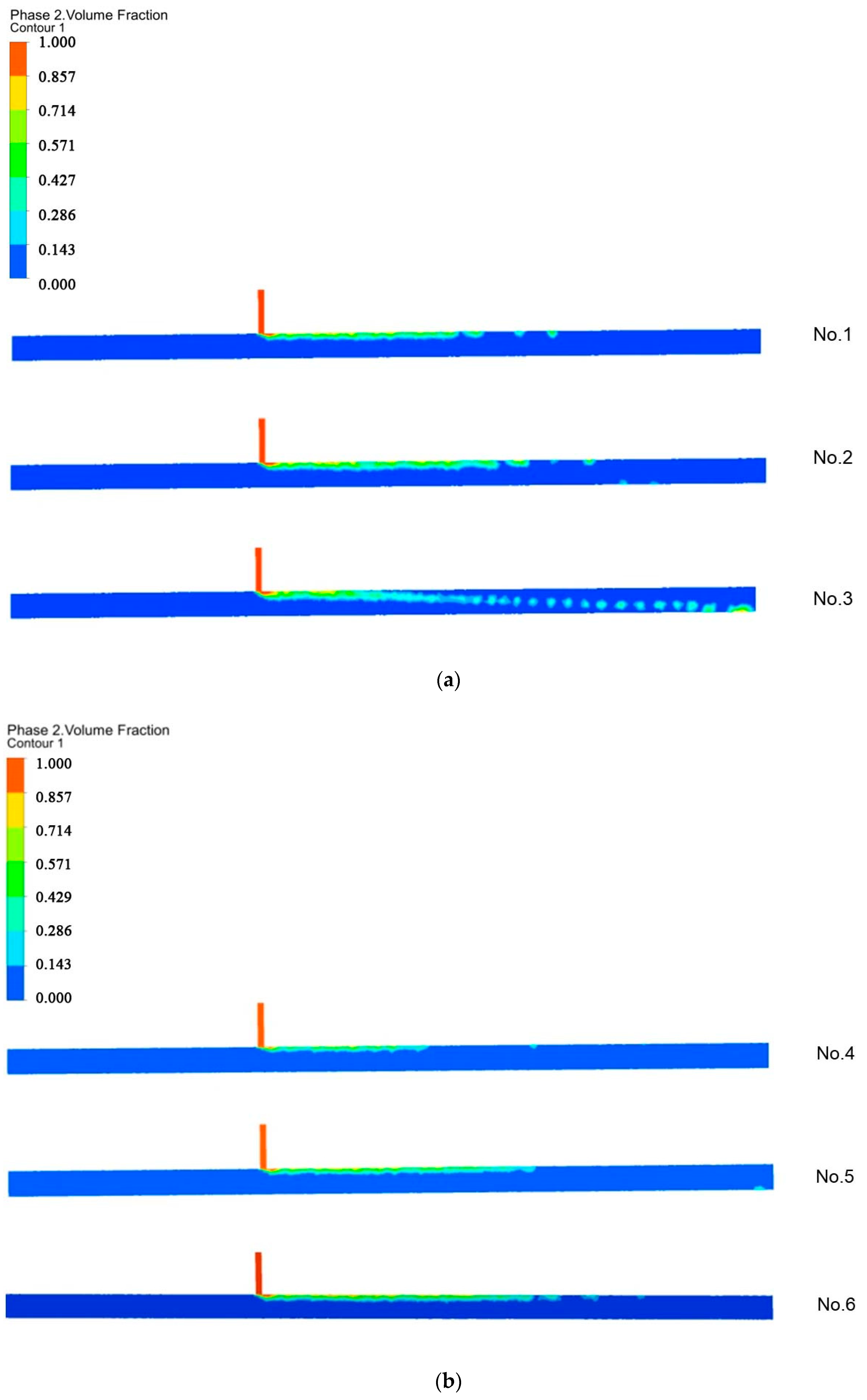
3.2. Effect of Water and Fertilizer Flow Rates on the Mixing Process of Water and Fertilizer
3.3. Effect of Water and Fertilizer Rate on Fertilizer Uniformity
4. Conclusions
- (1)
- The results of the numerical simulation agree with the experimental measurements, which indicate that using a numerical simulation to explore water and fertilizer mixing is feasible. When the fertilizer enters the main pipe and forms a vortex, the vortex is most intense in the center of the water–fertilizer junction, and diffuses in all directions. As time and distance from the fertilizer inlet increases, the flow field in the pipe finally stabilizes, and the fluid flow gradually changes from a turbulent flow to laminar flow.
- (2)
- The mixing effect in the main pipeline is positively correlated with the fertilization uniformity of the irrigation system. In the irrigation system, with a main pipe diameter of 100 mm and fertilizer injection pipe diameter of 20 mm, the water fertilizer flow rate ratio should be between 3–8 to ensure the effect of the mixing process.
- (3)
- The flow rate of water and fertilizer had an effect on the uniformity of the fertilization. In the machine-picked cotton-planting pattern (one film, three tubes and six rows) and the irrigation system with a main pipe diameter of 100 mm and fertilizer injection pipe diameter of 20 mm, using a 0.35 and water flow rate of 2 during fertilizer application in the cotton field planting process in northern Xinjiang is recommended.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lv, X. Management Techniques for Efficient Use of Water and Fertilizer in Cotton under Drip Irrigation; China Agricultural Press: Beijing, China, 2010; pp. 1–70. [Google Scholar]
- Zhengm, H.; Chuan, L.; Zhao, J.; Sun, S.; Zhang, J. Overview of Water and Fertilizer Integration Development. In Proceedings of the 2016 International Conference on Advances in Energy, Environment and Chemical Science, Changsha, China, 23–24 April 2016; Volume 76, pp. 273–277. [Google Scholar]
- Qin, S.; Li, S.; Kang, S.; Du, T.; Tong, L.; Ding, R. Can drip irrigation under film mulch reduce crop evapotranspiration and save water under the sufficient irrigation condition? Agric. Water Manag. 2016, 11, 128–137. [Google Scholar] [CrossRef]
- Wang, J.; Du, G.; Tian, J.; Zhang, Y.; Jiang, C.; Zhang, W. Effect of irrigation methods on root growth, root-shoot ratio and yield components of cotton by regulating the growth redundancy of root and shoot. Agric. Water Manag. 2020, 234, 106120. [Google Scholar] [CrossRef]
- Li, x.; Liu, H.; He, X.; Gong, P.; Lin, E. Water-Nitrogen Coupling and Multi-Objective Optimization of Cotton under Mulched Drip Irrigation in Arid Northwest China. Agronomy 2019, 12, 894. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, Z.; Wang, L.; Tian, C. Comparison of Efficiency-Enhanced Management and Conventional Management of Irrigation and Nitrogen Fertilization in Cotton Fields of Northwestern China. Agriculture 2021, 11, 1134. [Google Scholar] [CrossRef]
- Wang, H.; Wu, L.; Wang, X.; Zhang, S.; Cheng, M.; Feng, H.; Fan, J.; Zhang, F.; Xiang, Y. Optimization of water and fertilizer management improves yield, water, nitrogen, phosphorus and potassium uptake and use efficiency of cotton under drip fertigation. Agric. Water Manag. 2021, 245, 106662. [Google Scholar] [CrossRef]
- Li, J.; Meng, Y.; Li, B. Field evaluation of fertigation uniformity as affected by injector type and manufacturing variability of emitters. Irrig. Sci. 2007, 2, 117–125. [Google Scholar] [CrossRef]
- Tang, P.; Li, H.; Issaka, Z.; Chen, C. Effect of manifold layout and fertilizer solution concentration on fertilization and flushing times and uniformity of drip irrigation systems. Agric. Water Manag. 2018, 200, 71–79. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, C.; Li, H.; Tang, P. Research on Mixing Law of Liquid Fertilizer Injected into Irrigation Pipe. Horticulturae 2022, 8, 200. [Google Scholar] [CrossRef]
- Kartashev, A.; Kartasheva, M.; Terekhin, A. Modeling Operating Regimes in Multiphase Flowmeter Flow Path Using CFD Methods. Int. Conf. Ind. Eng. 2017, 206, 128–133. [Google Scholar] [CrossRef]
- Lahey, R.T., Jr. On the computation of multiphase flows. Nucl. Technol. 2009, 167, 29–45. [Google Scholar] [CrossRef]
- Sun, B.; Lu, Y.; Liu, Q.; Fang, H.; Zhang, C.; Zhang, J. Experimental and Numerical Analyses on Mixing Uniformity of Water and Saline in Pipe Flow. Water 2020, 12, 2281. [Google Scholar] [CrossRef]
- Selvam, P.K.; Kulenovic, R.; Laurien, E. Experimental and numerical analyses on the effect of increasing inflow temperatures on the flow mixing behavior in a T-junction. Int. J. Heat Fluid Flow 2016, 61, 323–342. [Google Scholar] [CrossRef]
- Langhi, M.; Hosoda, T.; Dey, S. Analytical Solution of k-epsilon Model for Nonuniform Flows. J. Hydraul. Eng. 2018, 144, 04018033. [Google Scholar] [CrossRef]
- Skrypnik, I.I.; Voitovych, M.V. On the continuity of solutions of quasilinear parabolic equations with generalized Orlicz growth under non-logarithmic conditions. Ann. Di Mat. Pura Ed Appl. 2021, 201, 1381–1416. [Google Scholar] [CrossRef]
- Arbab, A.I.; Widatallah, H.M. On the Generalized Continuity Equation. Chin. Phys. Lett. 2010, 27, 084703. [Google Scholar] [CrossRef]
- Séro-Guillaume, O.; Calogine, D. The Navier-Stokes equation with memory, and momentum transfer in a porous medium. Comptes Rendus Mec. 2002, 6, 383–389. [Google Scholar] [CrossRef]
- Karlin Iliya, V.; Tomboulides, A.G.; Frouzakis, C.E.; Ansumali, S. Kinetically reduced local Navier-Stokes equations: An alternative approach to hydrodynamics. Phys. Rev. E 2006, 74, 035702. [Google Scholar] [CrossRef]
- Ayhan, H.; Sökmen, C.N. CFD modeling of thermal mixing in a T-junction geometry using LES model. Nucl. Eng. Des. 2012, 253, 183–191. [Google Scholar] [CrossRef]
- Alloush, M.M.; Hanimann, L.; Moukalled, F.; Mangani, L.; Darwish, M. An implicit bounding formulation for the volume fraction equation in multiphase flows. Numer. Heat Transf. Part B Fundam. 2021, 79, 235–254. [Google Scholar] [CrossRef]
- St Joseph, M. (Ed.) Field Evaluation of Micro-Irrigation Systems; ASAE: Washington, DC, USA, 1999. [Google Scholar]
- Lari, K.S.; Van Reeuwijk, M.; Maksimović, Č.; Sharifan, S. Combined bulk and wall reactions in turbulent pipe flow: Decay coefficients and concentration profiles. J. Hydroinformatics 2011, 13, 324–333. [Google Scholar] [CrossRef][Green Version]
- Calomino, F.; Tafarojnoruz, A.; De Marchis, M.; Gaudio, R.; Napoli, E. Experimental and Numerical Study on the Flow Field and Friction Factor in a Pressurized Corrugated Pipe. J. Hydraul. Eng. 2015, 141, 04015027. [Google Scholar] [CrossRef]
- Calomino, F.; Alfonsi, G.; Gaudio, R.; D’Ippolito, A.; Lauria, A.; Tafarojnoruz, A.; Artese, S. Experimental and Numerical Study of Free-Surface Flows in a Corrugated Pipe. Water 2018, 10, 638. [Google Scholar] [CrossRef]
- Widiatmojo, A.; Sasaki, K.; Widodo, N.P.; Sugai, Y. Discrete tracer point method to evaluate turbulent diffusion in circular pipe flow. J. Flow Control. Meas. Vis. 2013, 1, 57–68. [Google Scholar] [CrossRef][Green Version]
- Lari, K.S.; van Reeuwijk, M.; Maksimović, Č. Simplified Numerical and Analytical Approach for Solutes in Turbulent Flow Reacting with Smooth Pipe Walls. J. Hydraul. Eng. 2010, 136, 626–632. [Google Scholar] [CrossRef]
- Rabinovich, E.; Kalman, H. Generalized master curve for threshold superficial velocities in particle- fluid systems. Powder Technol. 2008, 183, 304–313. [Google Scholar] [CrossRef]
- Akbari, S.; Taghavi, S.M. Injection of a heavy fluid into a light fluid in a closed-end pipe. Phys. Fluids 2020, 32, 063302. [Google Scholar] [CrossRef]
- Townsend, J.D. Fertigation-uniformity of fertilizer application through drip irrigation systems. In Proceedings of the 4th International Microirrigation Congress, Albury-Wodonga, NSW, Australia, 23–28 October 1988. [Google Scholar]
- Bracy, R.P.; Parish, R.L.; Rosendale, R.M. Fertigation uniformity affected by injector type. HortTechnology 2003, 13, 103–105. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, F.; Wu, L.; Yan, S.; Xiang, Y. Field evaluation of fertigation uniformity in drip irrigation system with pressure differential tank. Trans. Chin. Soc. Agric. Eng. 2016, 32, 96–101. [Google Scholar]
- Wang, W. Study on the fertilization uniformity of water-fertilizer integrated micro-sprinkler belt. J. Water Resour. Water Eng. 2020, 31, 124–130. [Google Scholar]





| Parameters | Value | Unit |
|---|---|---|
| Density of water | 1.0 × 103 | |
| Density of fertilizer | 1.3 × 103 | |
| Dynamic viscosity of water | 1.01 × 10−3 | |
| Dynamic viscosity of fertilizer | 0.8 | |
| Mixing temperature | 298.15 | |
| Diameter of suspended particles | 5 | |
| Pressure | 1 |
| No. | Flow Velocity of Water v1/(m/s) | Flow Velocity of Fertilizer v2/(m/s) |
|---|---|---|
| 1 | 1 | 0.25 |
| 2 | 1 | 0.35 |
| 3 | 1 | 0.45 |
| 4 | 1.5 | 0.25 |
| 5 | 1.5 | 0.35 |
| 6 | 1.5 | 0.45 |
| 7 | 2 | 0.25 |
| 8 | 2 | 0.35 |
| 9 | 2 | 0.45 |
| No. | Flow Velocity of Fertilizer v1/(m/s) | Flow Velocity of Water v2/(m/s) | Maximum Flow Rate after Mixing vmix−max/(m/s) |
|---|---|---|---|
| 1 | 1 | 0.25 | 1.293 |
| 2 | 1 | 0.35 | 1.352 |
| 3 | 1 | 0.45 | 1.282 |
| 4 | 2 | 0.25 | 1.876 |
| 5 | 2 | 0.35 | 1.912 |
| 6 | 2 | 0.45 | 1.974 |
| 7 | 3 | 0.25 | 2.481 |
| 8 | 3 | 0.35 | 2.505 |
| 9 | 3 | 0.45 | 2.554 |
| No. | Uc (%) | DU (%) | Us (%) |
|---|---|---|---|
| 1 | 90 | 85 | 82 |
| 2 | 91 | 88 | 87 |
| 3 | 89 | 86 | 81 |
| 4 | 88 | 84 | 85 |
| 5 | 92 | 90 | 86 |
| 6 | 90 | 88 | 85 |
| 7 | 95 | 92 | 88 |
| 8 | 93 | 91 | 90 |
| 9 | 94 | 91 | 88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Zhang, L.; Fu, C.; Wang, W.; Yan, Y. Effects of Water and Fertilizer Flow Rates on the Mixing Process and Fertilization Uniformity of Cotton under Mulch Drip Irrigation. Water 2022, 14, 1952. https://doi.org/10.3390/w14121952
Ma X, Zhang L, Fu C, Wang W, Yan Y. Effects of Water and Fertilizer Flow Rates on the Mixing Process and Fertilization Uniformity of Cotton under Mulch Drip Irrigation. Water. 2022; 14(12):1952. https://doi.org/10.3390/w14121952
Chicago/Turabian StyleMa, Xiao, Lixin Zhang, Changxin Fu, Wendong Wang, and Yongchun Yan. 2022. "Effects of Water and Fertilizer Flow Rates on the Mixing Process and Fertilization Uniformity of Cotton under Mulch Drip Irrigation" Water 14, no. 12: 1952. https://doi.org/10.3390/w14121952
APA StyleMa, X., Zhang, L., Fu, C., Wang, W., & Yan, Y. (2022). Effects of Water and Fertilizer Flow Rates on the Mixing Process and Fertilization Uniformity of Cotton under Mulch Drip Irrigation. Water, 14(12), 1952. https://doi.org/10.3390/w14121952




