Diagnosis of Basin Eco-Hydrological Variation Based on Index Sensitivity of Similar Years: A Case Study in the Hanjiang River Basin

Abstract

The variation of hydrological conditions in the basin affects the original stable state of the basin, and the change of eco-hydrological conditions also plays a decisive role in the stability of the basin. In this manuscript, Indicators of Hydrologic Alteration (IHA) was used to diagnose watershed variation from the eco-hydrological perspective, and a new diagnostic method was proposed in the current study, which was the extraction method of the most relevant eco-hydrological indicators based on a similar year sensitive index and the diagnosis method of variation period. This method used the sensitivity of statistical characteristics between similar years to provide the basis for the selection of the most ecologically-relevant hydrogeological indicators (ERHIs), then selected the strong variation indicators from the most relevant eco-hydrological indicators, and finally used the strong variation indicators to diagnose the watershed variation. The runoff data (1960 to 2020) in the Ankang gauging station of the Hanjiang River were analyzed, and the results showed that the indicators of high variation were the average duration index of low discharge in a year and the minimum discharge index of one day in a year. The variation period was from 1973 to 1986. It was concluded that the diagnosis results from the perspective of eco-hydrology were consistent with the actual hydrological situation changes, and this method had certain reliability.

1. Introduction

In recent decades, the rapid development of the social economy, human activities, and climate change has gradually become important factors contributing to environmental change. The large-scale urbanization processes, such as the construction of dams and the implementation of various water conservancy and hydropower projects, have changed the underlying surface conditions and regional water circulation processes [1]. Climate change and human activities have also altered the hydrological cycle at the watershed scale. This hydrological alteration disrupts river continuity, aquatic ecology, and species composition and adaptability of biological communities [2]. At the same time, it will also lead to sudden changes in the hydrological process and hydrological characteristics or even mutate in a certain period of time. All variables change in two basic forms: one is sudden change and the other is variation. Regarding the relationship between mutation and variation, Huang et al. [3] pointed out in 2016 that mutation is a quantitative change from one state to another, whereas variation is a qualitative change; that is, when mutation occurs, variation does not necessarily occur, but when variation occurs, mutation will occur, and the degree of variation is greater than that of mutation. The sudden change or variation of hydrological conditions in the basin will directly affect or change the environment of living organisms, plants, and micro-organisms and may also severely and permanently destroy the original stable state of the basin. Therefore, this warrants the need to study the change of hydrological conditions in the basin for the monitoring and management of watershed systems, i.e., for the implementation of corresponding measures to minimize the influence of human activities and climate change.

Previous research has comprehensively studied the variation diagnosis of hydrological processes. In previous studies, the method of solving the variation points of hydrological regimes in river basins only considered a single hydrological variable, such as annual runoff [4]. Wang et al. [5] used the Mann-Kendall test, the cumulative anomaly method, and a sliding T test to diagnose the runoff sequence variation in the four water basins of Dongting Lake, with average annual flow as an index. It was concluded that the years of variation for each station were 1991, 1987, 1989, and 1973, respectively. Zhang et al. [6] used the linear regression method, the Mann-Kendall test, and the cumulative anomaly method to analyze the variation of annual runoff series at Gangu Station of Sandu River and Suide Station of Dali River; they found that the annual runoff of the two rivers showed a significant decreasing trend (p < 0.01), and the variation occurred around the 1990s. Zhang et al. [7] used the Mann-Kendall test and the moving average method to analyze the influence of Pohe Reservoir on the runoff process of Huanghe River, taking the annual average flow as the index, and they concluded that the inter-annual runoff and annual runoff of Huanghe River in Pohe Reservoir had great influence. Zeng et al. [8] took the completion time of the two hydropower stations as the hydrological mutation point, and they obtained that the hydrological change degree caused by the operation of the upstream hydropower station was 50.1%, which had a great impact on the runoff and ecology of the river. Tang et al. [9] set the year of runoff change and the start time of reservoir regulation as variation points to evaluate the ecological flow in the lower reaches of Hongshui River Basin. Because the flow is influenced by various control factors, a single hydrological variable cannot accurately reflect the change of hydrological regimes in the river basin during the year.

Richter et al. [10] proposed an index system that evaluates the process of hydrological change of water ecology in 1996, that is, Indicators of Hydrologic Alteration (IHA), which quantitatively analyzes the degree of hydrological variation. This index system is widely used to represent the characteristics of hydrological process changes. The IHA system contains 32 indicators, which is a relatively comprehensive and systematic index system recognized at present. It is divided into five groups, namely the average monthly discharge, the annual extreme discharge, the occurrence time of the annual extreme discharge, the frequency and delay of high and low pulses, and the change rate and frequency of discharge change [10,11]. The indicator of hydrologic alteration in the IHA index system can directly reflect the hydrological regime within the river channel. Therefore, in this study, the IHA index was used as a hydrological variable for diagnosis of the hydrological variation in the river basin.

The IHA index system can reflect the hydrological situation in the basin because it covers more than 170 hydrological indicators that have been published. However, since the information redundancy among the 170 hydrological indicators is very prominent [12], there are also the problems of autocorrelation and redundancy among IHA indicators [13]. In order to solve the above problems, many researchers use principal component analysis (PCA) to screen the most ecologically-relevant hydrological indicators for the IHA index system in order to analyze the hydrological regime in the basin. Olden and Poff [12] used the PCA method to test the long-series runoff from multiple locations in the United States of America, discussed the redundancy of more than 170 hydrological indicators, and divided these indicators into nine categories. The analysis showed that the first four principal components could represent 76% of the recorded flow variability [12]. Yang et al., used three methods, including a data mining method based on genetic programming, PCA, and an automatic ecological matrix, to determine six IHA indicators (occurrence time of annual minimum flow, rate of increase, number of flow reversals, annual maximum three-day flow, annual minimum seven-day flow, and May flow) as the most ecologically-relevant hydrogeological indicators (ERHIs) [14]. Gao et al., determined the relationship between IHA parameters by PCA, screened the ERHIs of an artificial simulation dataset, and subsequently measured runoff dataset [15]. Cheng Junxiang et al., used PCA to screen seven IHA indicators, namely the annual maximum 90-day discharge, annual minimum 3-day discharge, annual minimum discharge occurrence time, March discharge, June discharge, flow reversal times, and average annual duration of low discharge as the ERHIs [16]. PCA is a method of dimensionality reduction of variables and subsequent processing [17]. However, the data after dimensionality reduction has a certain fuzziness. The variables obtained after dimensionality reduction are only highly representative but not necessarily highly sensitive, and these selected indicators are not able to accurately reflect the changes of hydrological regimes in river basins.

In previous studies, there was a problem that a single hydrological variable could not fully represent the hydrological situation, and there were some drawbacks in the application of principal component analysis. To solve these problems, a new diagnostic method was proposed in the current study, which is the extraction method of the most relevant eco-hydrological indicators based on similar year-sensitive index and the diagnosis method of variation period. This method replaces the traditional single index with 32 hydrological indexes in the IHA index and uses the similar year-sensitive index extraction method to replace the principal component analysis method to screen the IHA index, which ensures that the selected indicators are highly representative and highly sensitive.

2. Materials and Methods

2.1. Study Area

The Hanjiang River Basin is one of the most resource-intensive areas in the Hubei province (Figure 1). With a total length of 1577 km, the Hanjiang River is the longest tributary of the Yangtze River. Its basin covers an area of 159,000 square kilometers, comprising 20 districts and 78 counties (cities) in Hubei, Shaanxi, Sichuan, Chongqing, and Gansu provinces. The basin is located in the subtropical monsoon region, with a mild and humid climate. The Hanjiang River Basin is mostly mountainous, with a mountainous area of 87,450 square kilometers, accounting for 55% of the whole basin area (159,000 square kilometers), a hilly area of 33,390 square kilometers (21%), a plain area of 36,570 square kilometers (23%), and a lake area of 1590 square kilometers (1%). Mountainous areas are distributed above Laohekou, while the main plains are distributed below Zhongxiang, with hilly areas between them. The average annual precipitation is 873 mm, and water volume is relatively abundant in the area [18]. The multiannual average air temperature is 14.6 °C, and the runoff is unevenly distributed within the year, with 75% of the water concentrated from May to October, and the annual variation is large [19]; that is, since 1960, the average flow rate reached the maximum value of 1350 m³/s in 1983 and the minimum value of 169 m³/s in 1999. Late-June to late-July is the summer flood season, and late-August to mid-October is autumn wet season with abundant precipitation resources [20]. There are many hydropower resources, with the theoretical reserves of water energy of 10.93 million kilowatts and the development capacity of 6.14 million kW [18]. The main tributaries of the Hanjiang River Basin are: Baohe, Danjiang River, Tanghe, Baihe, Duhe, etc. In this paper, the basin variation diagnosis of the Ankang hydrological station in the upper reaches of the Hanjiang River (Figure 1) is determined. The hydrological station is located at a longitude of 109° E and a latitude of 32.67° N. Ankang station is located downstream of the Ankang reservoir. Ankang reservoir was put into use at the end of December 1992, with an area of 77.5 square kilometers and a maximum storage capacity of 2.585 billion cubic meters, affecting the flow of the Ankang hydrological station.

2.2. Data Collection

In this study, the long-series daily discharge data of the Ankang gauging station in the Hanjiang River Basin from 1960 to 2020 were used. The watershed controlled by Ankang gauging station is located in the transitional zone between the north and south of China, with a catchment area of 41,400 km², accounting for 26% of the total area of the Hanjiang River Basin. The multiannual average discharge is 534.81 m³/s, and the coefficient of variation is 0.4. Precipitation is mainly concentrated in June–September every year, and the total amount of precipitation in these four months accounts for nearly 60% of the whole year, with the highest amount in July [21]. The hydrological monitoring data came from the national real-time water and rain data base.

Ankang gauging station is the ecological flow control station of the Hanjiang River Basin, designated by the Ministry of Water Resources in the First Batch of Key Rivers and Lakes Ecological Flow Guarantee Objectives (for Trial Implementation), and it is an important basis for water distribution, ecological flow management, the unified dispatch of water resources, and the total control of water intake.

2.3. Method

2.3.1. Refine IHA Index System

The runoff volume and runoff characteristics of the river basin are affected by seasonal climatic variations. Due to the differences in precipitation and climate in different seasons, the precipitation period can be divided into wet and dry seasons. The wet season refers to the period in which rivers mainly rely on rainfall or snowmelt to replenish water and have a large amount of precipitation, usually in the rainy season or the period when the temperature continues to rise in spring, when the river is rich in water. The dry season refers to the period in which the surface water flow in the basin is exhausted and the precipitation is low and mainly relies on groundwater to replenish water sources. The wet and dry seasons of the basin can be divided according to the hydrological situation of the specific study basin. The precipitation at Ankang Station is mainly concentrated from June to September, so June to September of each year is designated as the wet season, and January to May and October to December of each year are the dry seasons. To ensure that the IHA index system is indicative of the seasonal hydrological regimes, the indicators are divided into the indicators of the wet season and dry season.

In view of the obvious redundancy problem among IHA variables [13], this method further screened the IHA system and generated the ERHIs, so as to reduce the hydrological index and maintain the key information of the original data as much as possible.

2.3.2. ERHIs Selection

Similar years can be understood as a few years with the same hydrological processes in the same basin. Ideally, the hydrological processes in similar years are completely overlapped; therefore, the IHA indicators obtained in similar years must be the same. Due to climate differences in different years and other reasons, hydrological processes in similar years will inevitably be different. The differences in hydrological processes between similar years will be reflected by various hydrological indicators. Among these indicators, there are some indicators that will change strongly due to the slight differences of hydrological processes between similar years. These indicators are referred to as sensitive indicators in this paper.

In order to ensure that the selected ERHIs were reliable, rational, and representative, the ERHIs were selected from sensitive indicators. The sample year and similar year (corresponding to each sample year) were selected at random. The coefficient of variation of each IHA index in the similar year was then calculated, and the IHA index with the top six variation coefficients and the most repeated occurrences was selected as an ERHI. The specific screening process is shown in Figure 2.

• Calculation method of coefficient of variation [22].

The coefficient of variation of the index reflects its discriminating ability among all IHA indicators. The larger the coefficient of variation the greater the distribution variability and information content of the index and the stronger the information resolution ability of the index. On the contrary, if it is weaker, then it should be eliminated. The formula of the coefficient of variation is shown in Equation (1).

$$v_j=\frac{\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(x_{ij}-{\overline{x}}_j\right)}^2}}}{{\overline{x}}_j}$$

(1)

where $v_j$ is the coefficient of variation of the index; $n$ is the number of objects being evaluated; ${\overline{x}}_j$ is the average of the data of each year of the evaluation index; $x_{ij}$ is the value of the $i$ indicator in the $j$ year.

• Euclidean distance [23].

Euclidean distance, also known as Euclidean metric, is a commonly used definition of distance, which refers to the true distance between two points in the m-dimensional space, or the natural length of the vector. The Euclidean formula is divided into two-dimensional space, three-dimensional space, and n-dimensional space. In this paper, the n-dimensional space formula was used to screen similar years. The Euclidean formula is shown in Equation (2).

$$d\left(x,y\right)=\sqrt{{\left(x_1-y_1\right)}^2+{\left(x_2-y_2\right)}^2+{\left(x_n-y_n\right)}^2}=\sqrt{{\displaystyle \sum _{i=1}^n{\left(x_i-y_i\right)}^2}}$$

(2)

where $x_i$ is the abscissa of the element in Euclidean space; $y_i$ is the ordinate of the element in Euclidean space.

2.3.3. Variation Diagnosis

1.

Primary diagnosis.

Although ERHIs will strongly respond to slight changes in the watershed, the variation degree of each indicator is an unknown quantity. In terms of determining the year of variation, if the selection is based on the indicators of weak variation, then it will render low reliability and cannot be used as a standard for selecting the final year of variation. Therefore, this method introduces the Hurst coefficient method to calculate the Hurst coefficient (h) of each ERHI and the correlation function C(t) of the Fractional Brownian Motion increment, and it determines the index variation degree of the selected ERHIs [24,25,26]. The variation degree analysis table of indicators is shown in

Table 1. Variation degree analysis.

C(t)	h	Variation Degree	C(t)	h	Variation Degree
0 ≤ C(t) < rα	0.5 ≤ h < hα	No	0.6 ≤ C(t) < 0.8	0.839 ≤ h < 0.924	Strong
rα ≤ C(t) < rβ	hα ≤ h < hβ	Weak	0.8 ≤ C(t) < 1.0	0.924 ≤ h < 1.0	Extremely strong
rβ ≤ C(t) < 0.6	hβ ≤ h < 0.839	Medium

Note: $\alpha$ and $\beta$ are the significance level, and $\alpha >\beta$; $r_{\alpha }$ and $r_{\beta }$ are the lowest value of the correlation function $C\left(t\right)$, respectively; $h_{\alpha }=\left[1+\ln \left(1+r_{\alpha }\right)/\ln \sqrt{2}\right]/2$,$h_{\beta }=\left[1+\ln \left(1+r_{\beta }\right)/\ln \sqrt{2}\right]/2$.

.

2.

Detailed diagnosis.

According to the primary diagnostic results, the strong variation indicators selected from each section were used for detailed diagnosis. The jump diagnosis method and climate mutation detection method of hydrological variation diagnosis were used to determine the variation year. The diagnostic methods are shown in

Table 2. Diagnostic methods and sources of variation.

Diagnostic Methods	References
Mann-Kendall method	Mann H.B. [27]
Bayesian Analysis	Beck J.L. et al. [28,29]
MTT	Guo et al. [30]
Sequential Clustering method	Wang [31]
Le Page method	Yonetani T. et al. [32]
BG segmentation algorithm	N.G. Leveson [33]

.

Finally, when determining the watershed variation period, there are many possibilities such as staggered periods or overlapping periods. Therefore, the following solutions are summarized:

(a)

If the strong variation index is one index: (I) When the years diagnosed by these methods are concentrated in a certain year, that year is the final variation year of the basin; (II) when the number of variation years is k and these variation years appear more frequently in the diagnostic results, the longest period between the years is taken as the final variation time period of the basin (i.e., k > 1).

(b)

If the strong variation index is two or more indicators: (I) When the variation year corresponding to the same index is concentrated in a certain year: (i) if the corresponding variation year among the indicators is the same, then the year is the final variation year, (ii) if the corresponding variation year among the indicators are different, then the time period between the maximum year and the minimum year is taken as the final variation time period; (II) when the variation year corresponding to the same index is distributed over many years: method II in case (a) was used to find out the variation period of each index. Several possibilities existing between the variation time periods of each index were assessed: (i) if the variation time periods of all indices overlap, the final watershed variation time period is the variation time period obtained by any index, (ii) if the variation time periods of some two or more indicators do not coincide, then the union of all variation time periods is taken as the final variation time period of the basin.

3. Results

3.1. Refine IHA Index System

In this paper, the variation diagnosis of the Hanjiang River Basin was analyzed by using the 61-year daily long-series data of the Ankang gauging station of the Hanjiang River Basin. From Figure 3, it can be seen that there was a high degree of correlation between the IHA index variables of the Ankang section of the Hanjiang River; the absolute value of correlation coefficient is greater than 0.9.

Specifically, there was a high correlation between the annual minimum 1, 3, 7, 30, and 90-day flows with the annual maximum 1, 3, 7, 30, and 90-day flows. There was a high correlation between the annual minimum 1, 3, 7, and 30-day flows with the base flow index, fall rate, and the number of reversals. In addition, there was a high correlation between the flows in December, January, February, and March with the annual minimum 1, 3, 7, 30, and 90-day flows. July, August, September, and October flows also had high correlations with the annual maximum 1, 3, 7, 30, and 90-day flows. There was also a high correlation between the low pulse duration with the fall rate and the number of reversals. Therefore, this paper made a detailed allocation of the IHA index system.

In this study, the Hanjiang River was divided into the wet season from June to September and the dry season from January to May and October to December. The refined IHA index system is shown in

Table 3. Refined IHA index.

Different Season	Group	Redistribution of Hydrological Change Indicators
Dry season	Group 1: Monthly flow	January–May and October–December flows
	Group 2: Magnitude and duration of annual extreme water conditions	Minimum 1, 3, 7, 30, and 90-day flows, Base flow index
	Group 3: Timing of annual extreme water conditions	Date of min
	Group 4: Frequency and duration of low pulses	Low pulse count
		Low pulse duration
	Group 5: Rate and frequency of water condition changes	Rise rate, Fall rate
		Number of reversals
Wet season	Group 1: Monthly flow	June–September flows
	Group 2: Magnitude and duration of annual extreme water conditions	Maximum 1, 3, 7, 30, and 90-day flows
	Group 3: Timing of annual extreme water conditions	Date of max
	Group 4: Frequency and duration of high pulses	High pulse count
		High pulse duration
	Group 5: Rate and frequency of water condition changes	Rise rate, Fall rate
		Number of reversals

.

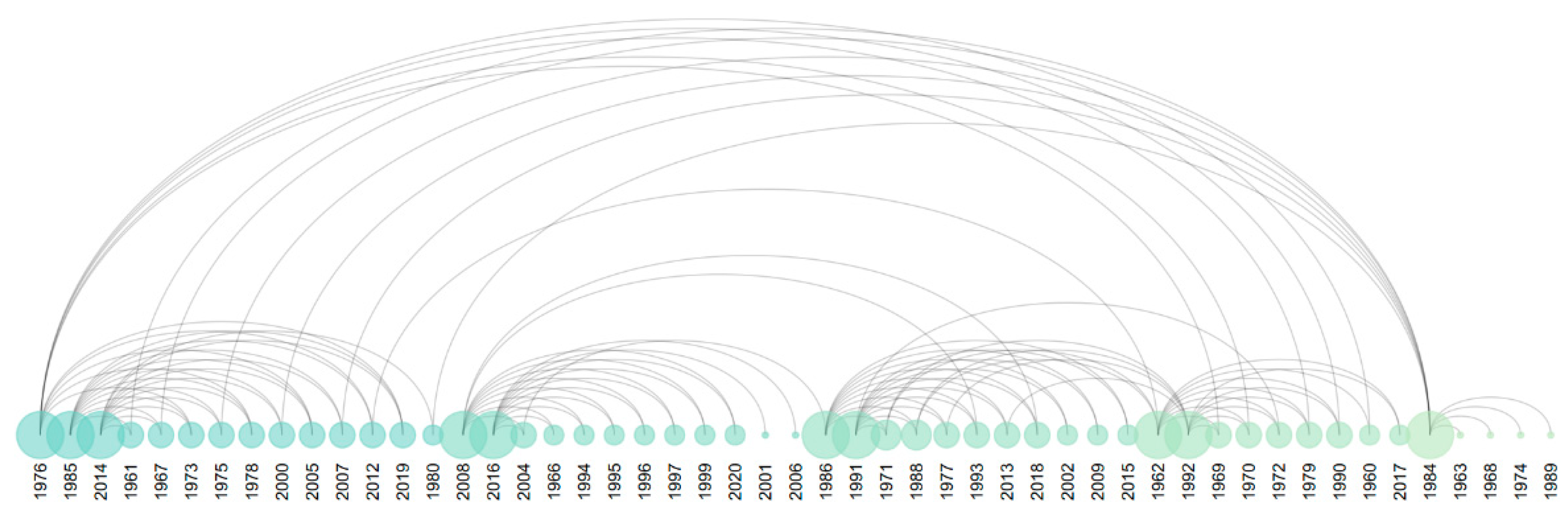
3.2. Determination of Similar Years

Ten years were randomly selected from the 61-year long sequence data as the sample year group. The Euclidean distance screening method was used to select the similar years, corresponding to each sample year based on the statistical value of watershed characteristics, as shown in

Table 4. Sample year and corresponding similar year.

Sample Year	Season	Similar Year
1962	wet	1960	1969	1970	1971	1972	1979	1988	1990	2012	2017
	dry	1965	1971	1972	1980	1990	1994	1996	2009	2015	2019
1976	wet	1960	1969	1970	1973	1978	1979	1990	2005	2012	2019
	dry	1965	1970	1981	1982	1990	1994	1996	2009	2015	2019
1984	wet	1961	1963	1967	1968	1974	1975	1980	1989	2000	2007
	dry	1965	1967	1968	1969	1971	1972	1980	1990	1994	1996
1985	wet	1961	1967	1973	1975	1978	2000	2005	2007	2012	2019
	dry	1967	1968	1969	1971	1972	1975	1980	1990	2000	2003
1986	wet	1971	1977	1988	1993	2002	2004	2009	2013	2015	2018
	dry	1960	1966	1977	1987	1988	1993	1998	2006	2012	2018
1991	wet	1971	1972	1977	1988	1993	2002	2009	2013	2015	2018
	dry	1978	1979	1993	1995	1997	2001	2007	2010	2013	2020
1992	wet	1969	1970	1971	1972	1977	1979	1988	1990	2013	2017
	dry	1969	1970	1971	1972	1977	1979	1988	1990	2013	2017
2008	wet	1966	1993	1994	1995	1996	1997	1999	2004	2018	2020
	dry	1970	1981	1982	1987	1988	1989	2004	2006	2011	2018
2014	wet	1961	1967	1973	1975	1978	1980	2000	2005	2007	2019
	dry	1960	1966	1977	1987	1988	1989	1998	2006	2011	2018
2016	wet	1966	1994	1995	1996	1997	1999	2001	2004	2006	2020
	dry	1960	1966	1977	1987	1988	1993	1998	2006	2012	2018

. Ten similar years corresponding to wet and dry seasons were selected, as shown in Figure 4 and Figure 5.

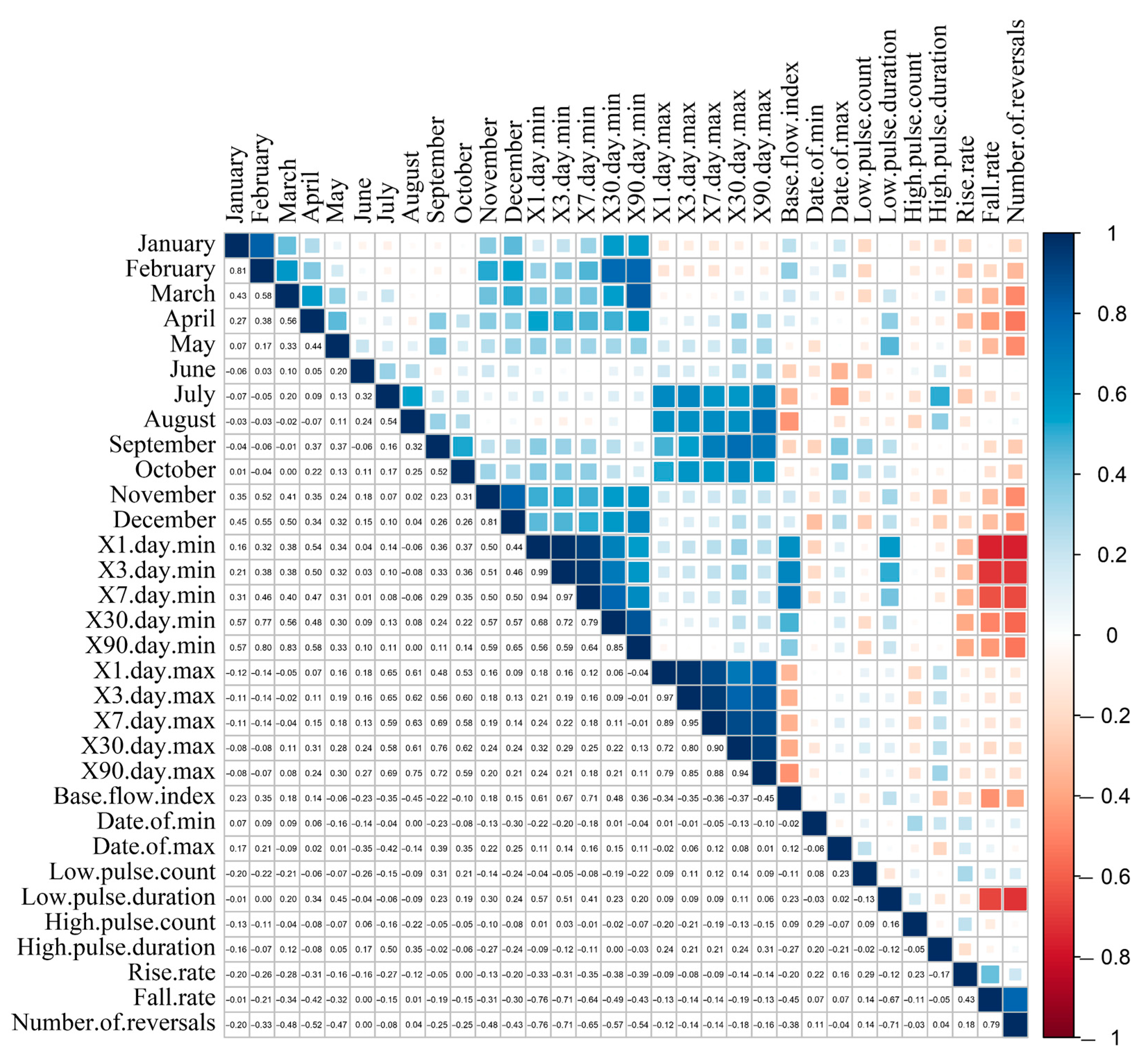
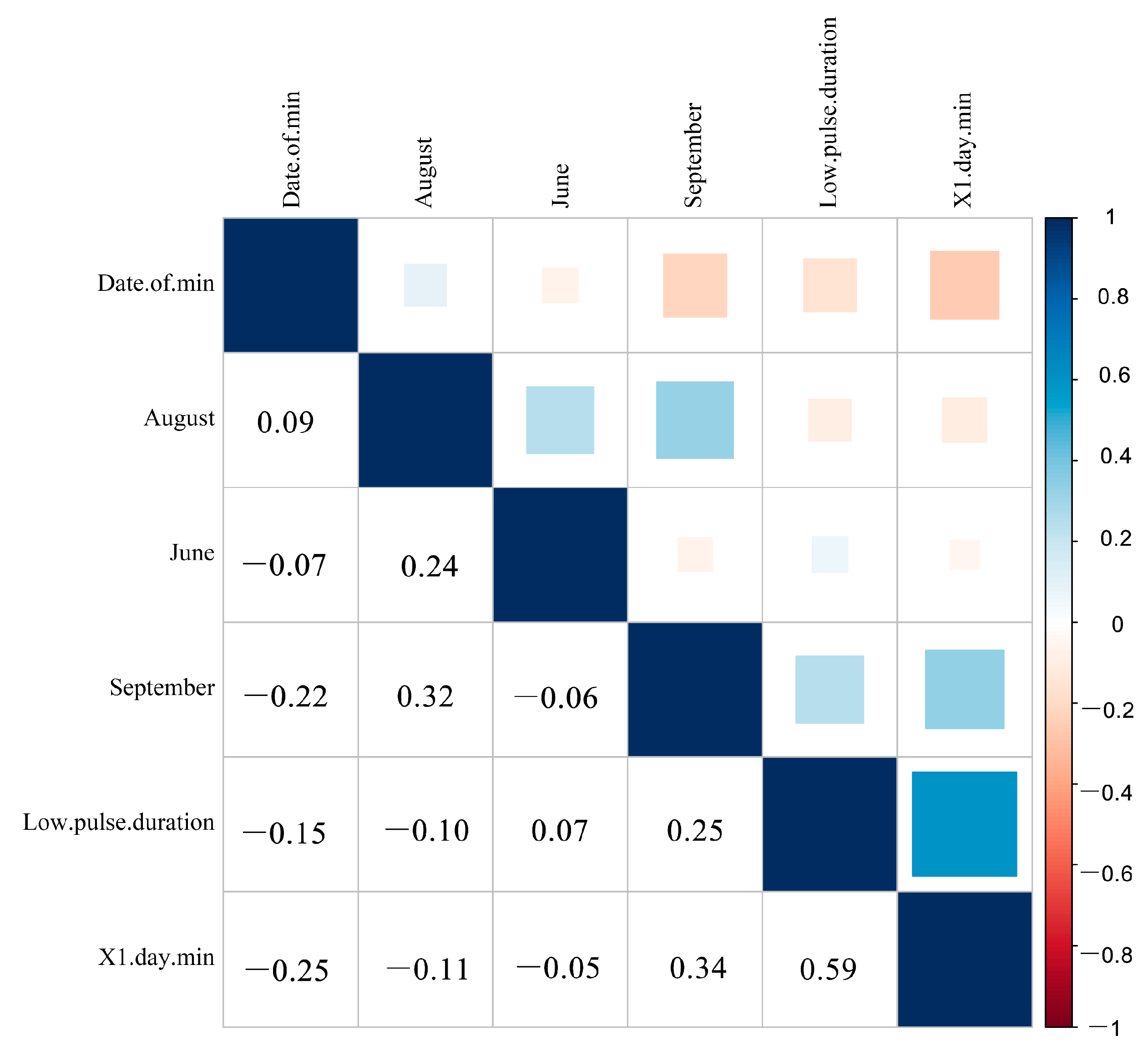
3.3. Determination of ERHIs

The IHA index and the coefficient of variation of each index for the similar year group in the dry season and the similar year group in the wet season corresponding to each sample year were calculated. The first six indices of the variation coefficient in each similar year group were sensitive index, which were used as candidate sets of ERHIs. The frequency of occurrence of each index in the candidate set in the sample year group was recorded, and the study then selected the sensitive indicators of the top six in the frequency of occurrence in the wet season, and the same was repeated for the dry season; a total of twelve were determined. These twelve indicators were sorted according to the frequency of occurrence from highest to lowest, and the top six sensitive indicators were taken as ERHIs. Through the calculation of the PCA method, it was found that the first six indicators with a cumulative contribution rate greater than 80% included June flow, August flow, September flow, low pulse duration, date of min, and 1-day min, so these six indicators were taken as ERHIs. The ranking of twelve indicators in the final selection process is shown in Figure 6.

3.4. Rationality Analysis of ERHIs

3.4.1. Coverage Analysis

The coverage analysis was based on the rationality analysis of the coverage range of ERHIs in different groups and in different seasons.

Table 5. Coverage analysis of indicators.

Group	ERHIs	Seasons
Group 3: Timing of annual extreme water conditions	Date of min	Dry
Group 1: Monthly flow	August flow	Wet
Group 1: Monthly flow	June flow	Wet
Group 1: Monthly flow	September flow	Wet
Group 4: Frequency and duration of high and low pulses	Low pulse duration	Dry
Group 2: Magnitude and duration of annual extreme water conditions	1-day min	Dry

shows the coverage analysis of indicators.

From the table, it can be concluded that the six ERHIs related to the first to fourth groups of indices and reached the full coverage of the wet and dry season.

3.4.2. Redundancy Analysis

The redundancy analysis of ERHIs was carried out to verify the mutual independence and high representativeness of the ERHIs. It can be seen from Figure 7 that there was a small correlation between most of the indicators; that is, there was no redundancy problem in the information, so it can be finally determined as an ERHI.

3.5. Variation Diagnosis

3.5.1. Primary Diagnosis

The ERHIs were preliminarily diagnosed. The Hurst coefficient (h) of each ERHI and the correlation function C(t) of the Fractional Brownian Motion increment were calculated, and the results showed that h and C(t) of the low pulse duration and the annual minimum 1-day flow index were 0.97, 0.91, 0.92, and 0.79, respectively, and these two indexes had a strong variation. The detailed results are shown in Figure 8.

3.5.2. Detailed Diagnosis

The strong variation indicators obtained from the preliminary diagnosis were diagnosed in detail. The diagnostic results showed that there were three methods for diagnosing if the low pulse duration index had a significant variation in 1973 and 1974, respectively, and there were two methods for diagnosing if the low pulse duration index had a significant variation in 1977. There were three methods for diagnosing if the annual minimum 1-day flow index had a significant variation in 1973, and there were four methods for diagnosing if the annual minimum 1-day flow index had a significant variation in 1986. The detailed results are shown in

Table 6. Diagnostic results of the strong variation index and corresponding mutation year.

Diagnostic Methods	Low Pulse Duration	1-Day Min
Mann-Kendall method	1977	——
Bayesian Analysis	1960	1973
MTT	1973,1974,1977	1973,1986
Sequential Clustering method	1973	1986
Le Page method	1973,1974	1973,1986
BG segmentation algorithm	1974	1986

.

4. Discussion

4.1. The Rationality of ERHIs

The coverage rate of ERHIs in the group and the coverage rate of each index in the wet and dry seasons were both high, which means the selected ERHIs had certain rationality. The correlation coefficient (absolute value) between most ERHIs was less than 0.2. It demonstrated that the six ERHIs selected had high reliability and representativeness.

4.2. Rationality of Variation Period

By analyzing the runoff data of the Ankang hydrological station for 61 years with various variation diagnostic methods, it was concluded that the variation time period of the low pulse duration index was between 1973–1977, and the variation time period of the annual minimum 1-day flow index was between 1973–1986.

4.2.1. Runoff Perspective

From Figure 9 and Figure 10, it can be seen that, from 1973, the annual minimum 1-day flow index began to show a downward trend, until after 1986, and the overall level of this index dropped to one-fifth of that before 1973. Meanwhile, the low pulse duration index was divided into two stages: from 1973 to 1977 and after 1977, and the overall level of this index dropped to one-fifth of that before 1973.

4.2.2. Climate Perspective

From 1955 to 2017, there were many abrupt changes in the extreme temperature index and the extreme precipitation index in Ankang City, which were mainly concentrated in the 1960s–1970s and the 1990s–early 21st century [34]. The abrupt changes in the extreme climate and extreme precipitation index were also important reasons for the variation of the annual minimum 1-day flow index. The abrupt change period of the climate and precipitation index also corresponded to the variation time period of the annual minimum 1-day flow index. Except for the 1980s, the temperature in the studied period was higher than that in the benchmark time period (1961–1990), and the precipitation was lower than that in the benchmark time period (1961–1990), which was exactly opposite to the distribution of annual average temperature [34]. In the 1980s, the temperature was lower than that in the benchmark time period, which reduced evaporation in the basin [34]. This was also the reason why the annual minimum 1-day flow had an upward trend in 1974–1976 and 1981–1984. From the 1980s to 1990s, with the increase of temperature and evaporation, the overall flow of the basin decreased, resulting in the annual minimum 1-day flow from 1986 reducing to one-fifth of that before 1973.

4.2.3. Human Factor Perspective

In the 1970s, Ankang City developed a few water conservancy projects, such as the construction of the Ankang Hydropower Station, with changes in the way by which water was allocated to citizens.

Therefore, it was determined that between 1973–1986 was the ecological variation period of Ankang gauging station.

4.3. The limitations of the Methodology

Although the selection of the sample year was random, the determination of the number of sample years was mixed with great human factors. The number of sample years also directly affected its representativeness in long series data. Therefore, the selection of the sample year still needs further improvement.

The longer the sample length, the higher the accuracy of watershed variation diagnosis. Because this study only diagnosed the variation of runoff data from 1960 to 2020, there were some certain differences between the research results and the actual hydrological situation. Therefore, further research is needed on the interpolation extension of runoff series data.

5. Conclusions

(1)

The variation point of total runoff in the watershed cannot be regarded as the variation point of watershed ecology, and the ecological variation points of the watershed are accumulated and formed in a certain period of time. That is, watershed ecological demand is the requirement for the hydrological situation process, and the correct determination of ecological requirements needs a stable runoff series based on the hydrological situation process without variation. Therefore, the project used the analytical relationship and sensitivity analysis of ecology and hydrology. The set of ecological–hydrological sensitive indicators with high sensitivity in the basin was obtained by the similar year method, and the variation diagnosis of sensitive indicators was carried out.

 

In existing studies, most of the indicators were screened by principal component analysis (PCA) for correlation analysis, without considering the sensitivity of ecological indicators to hydrological changes. The stable runoff series was determined by the variation point of the total annual runoff, which does not conform to the characteristics of ecological flow process control. Therefore, it was difficult to reflect the correct ecological requirements of the basin.

(2)

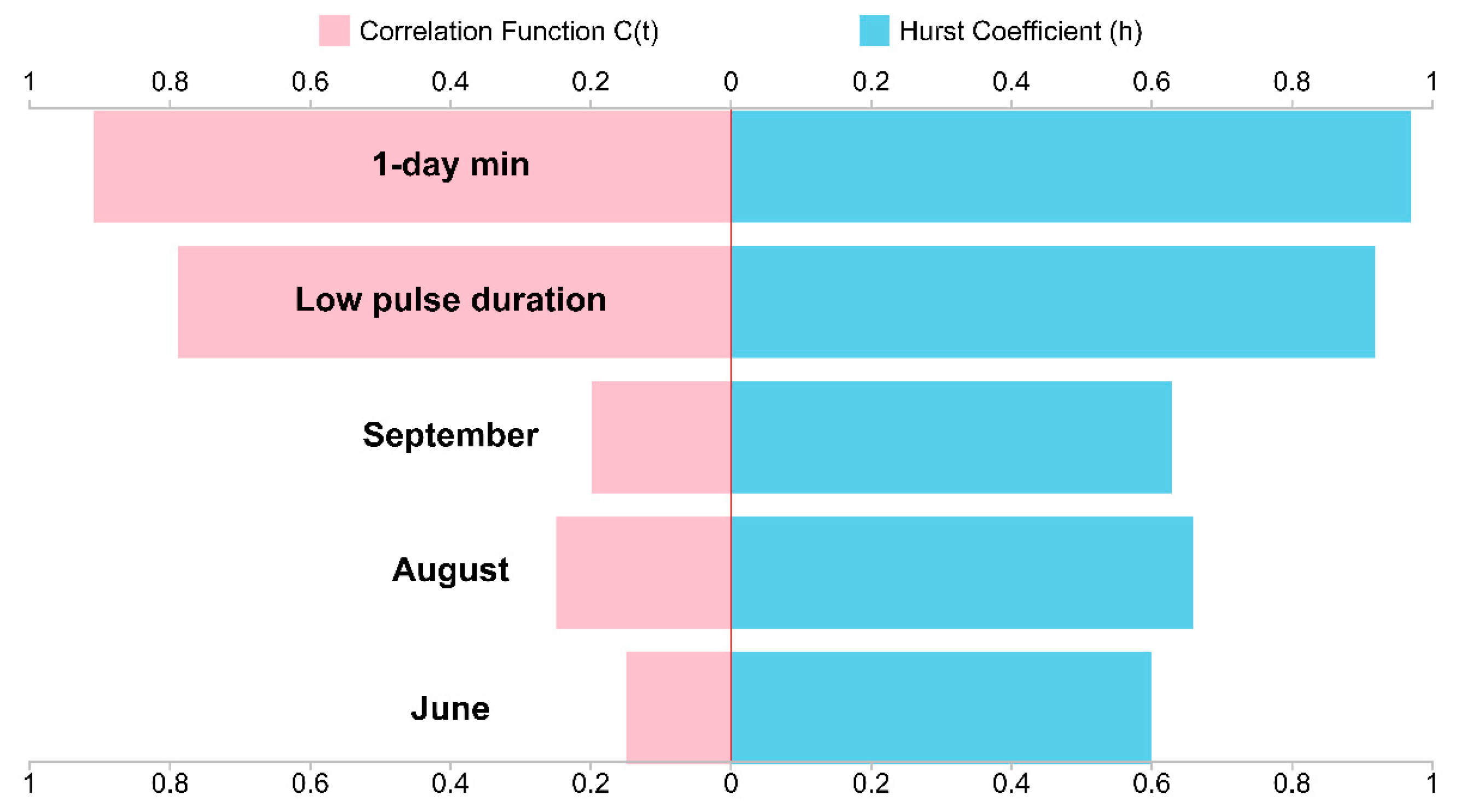
In this study, the IHA index was used to diagnose the hydrological changes in the watershed from the perspective of eco-hydrology. We proposed an extraction method of the most relevant eco-hydrological indicators based on similar year sensitive indices and the diagnostic method of variation period. By using the sensitivity of indicators in different similar years, the problem of outstanding redundancy among IHA indicators was solved. Among the 32 IHA indexes, six indexes were selected as the most relevant hydrological indexes, which were the June flow, August flow, September flow, low pulse duration, date of min, and 1-day min. The period of eco-hydrological variation in the basin was from 1973 to 1986.

(3)

The study found that the periods of extreme climate change and human activities, especially the time of construction of hydraulic structures, were consistent with the variation periods determined by the high variation indicators. It also confirmed that climate change and human activities seriously impacted the hydrological variation within the studied basin. Furthermore, it verified the feasibility of an extraction method for the most relevant eco-hydrological indices based on similar year sensitive indices and the diagnosis method of variation period to diagnose the hydrological variation of river basins.