Filling Gaps in Daily Precipitation Series Using Regression and Machine Learning in Inter-Andean Watersheds
Abstract
1. Introduction
2. Materials and Methods
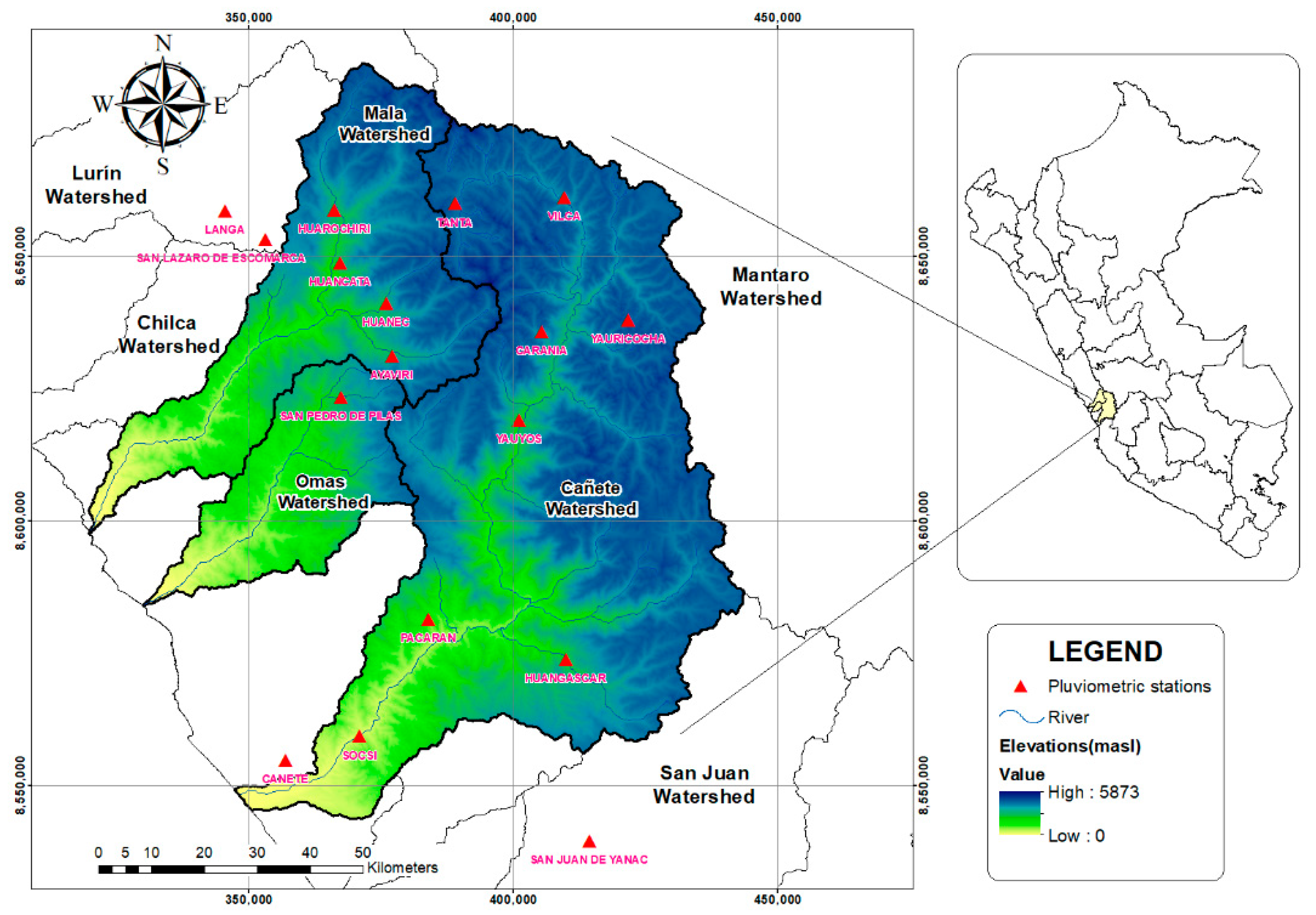
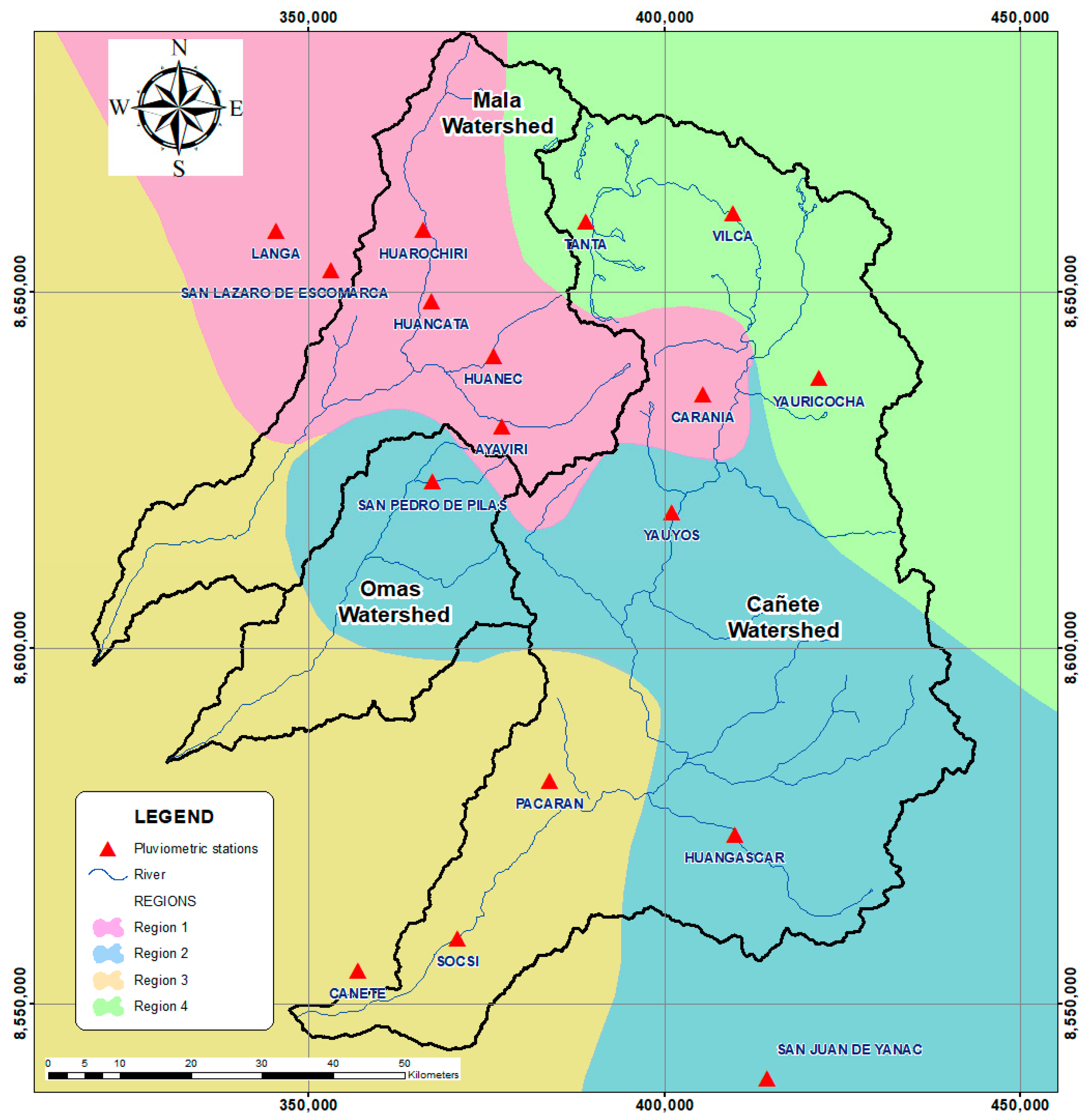
2.1. Study Area
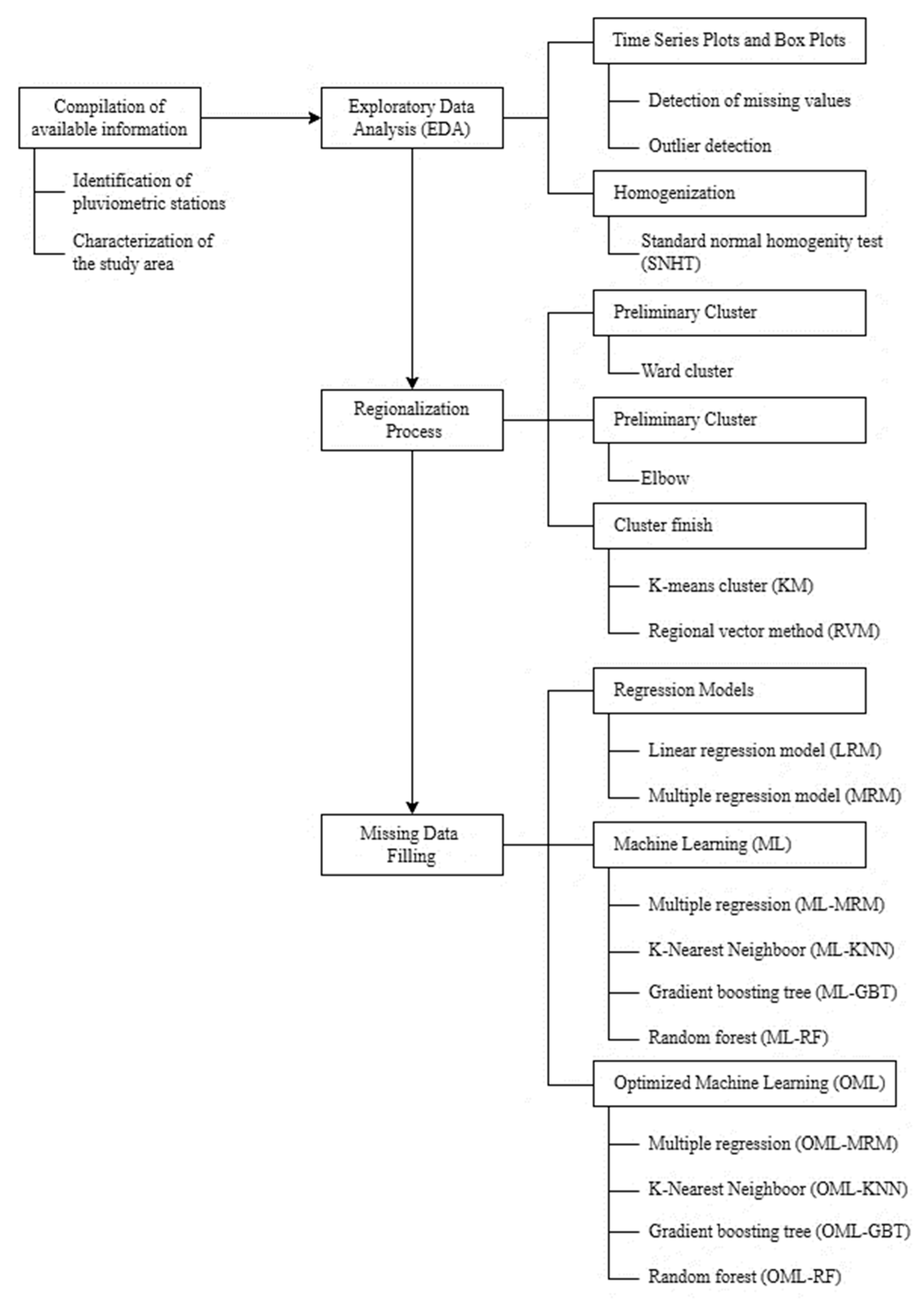
2.2. Methods
2.2.1. Collection of Available Information
2.2.2. Exploratory Data Analysis (EDA)
2.2.3. Regionalization Process
2.2.4. Gap-Filling Model
2.2.5. Bayesian Optimization
2.2.6. Evaluation Metrics
3. Results
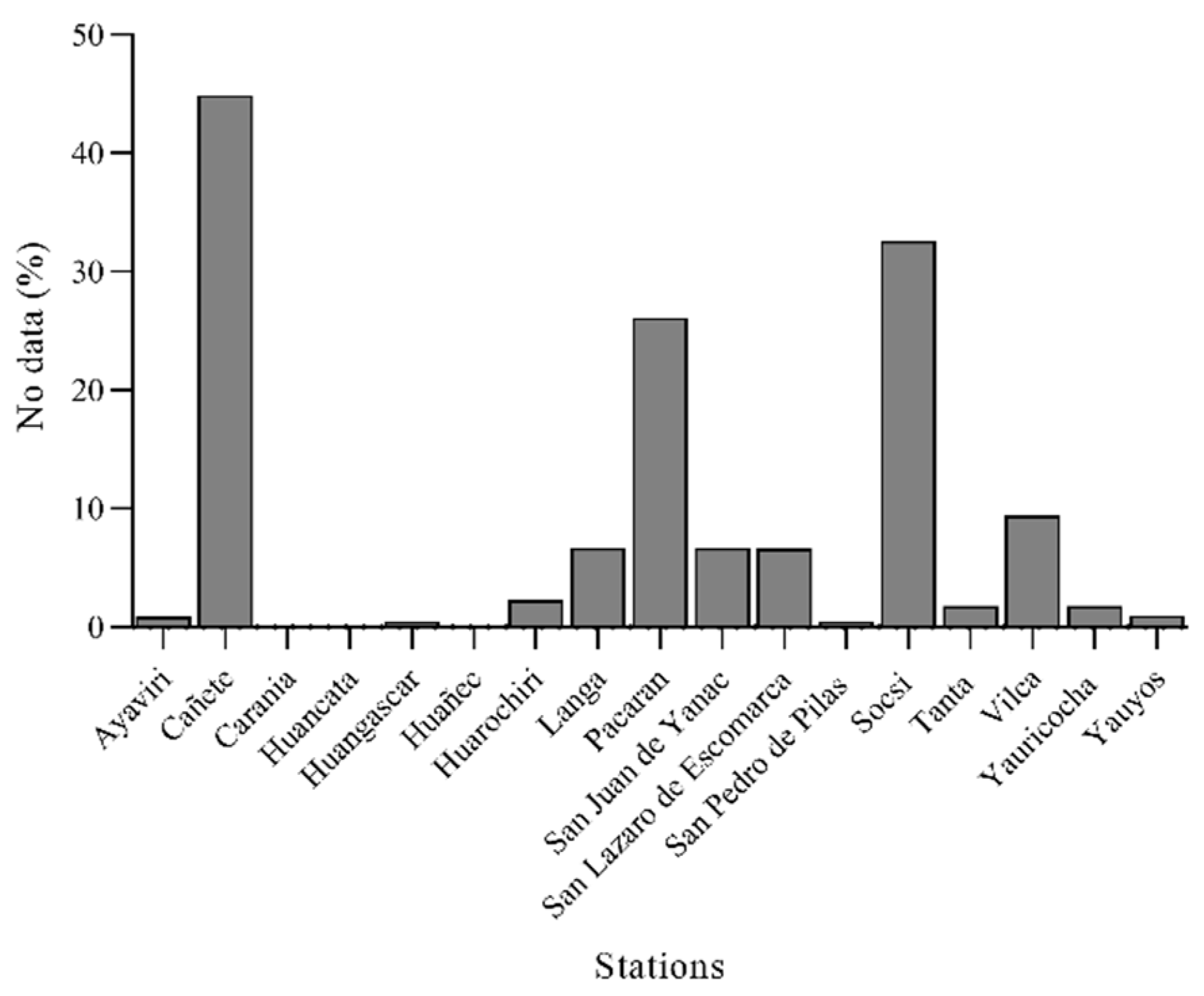
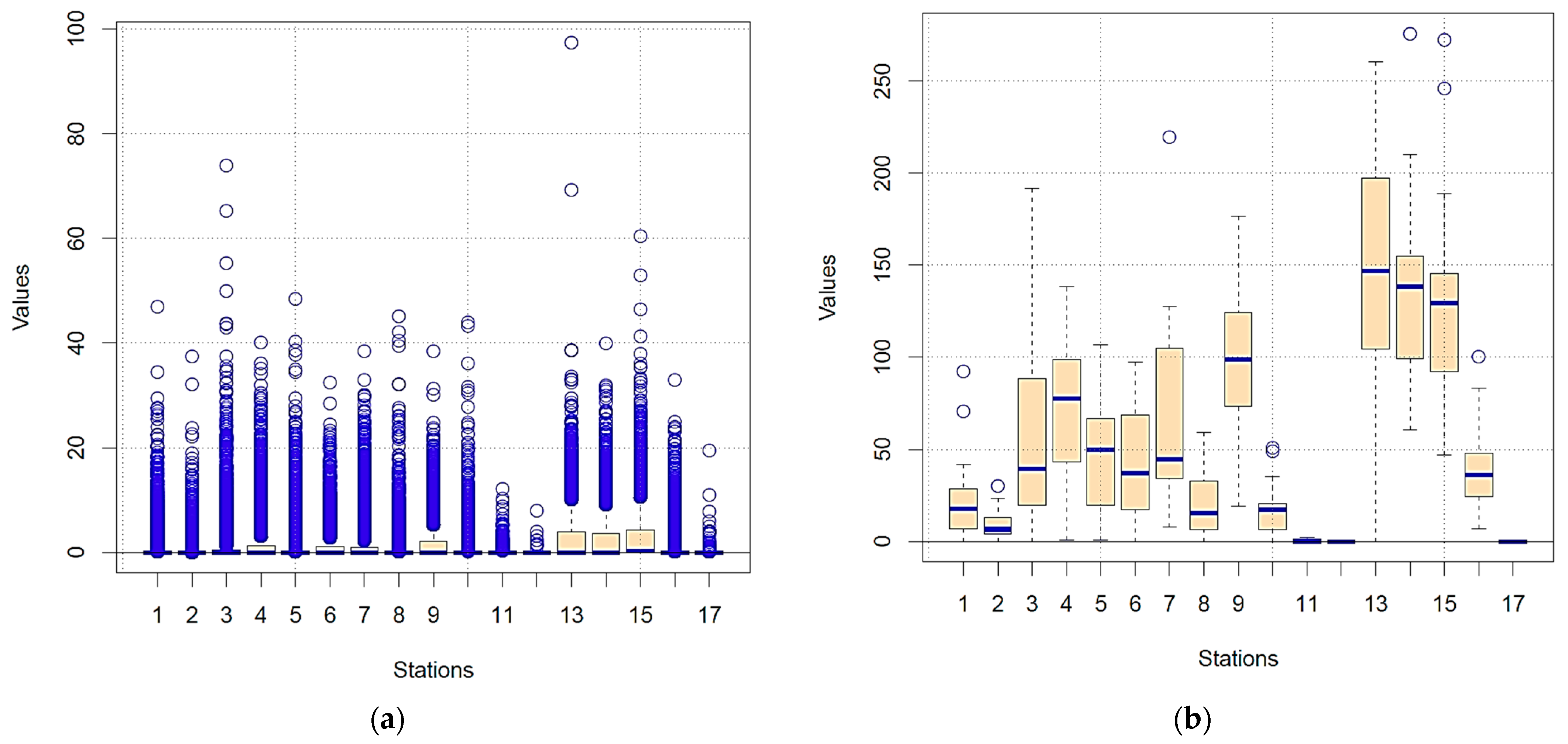
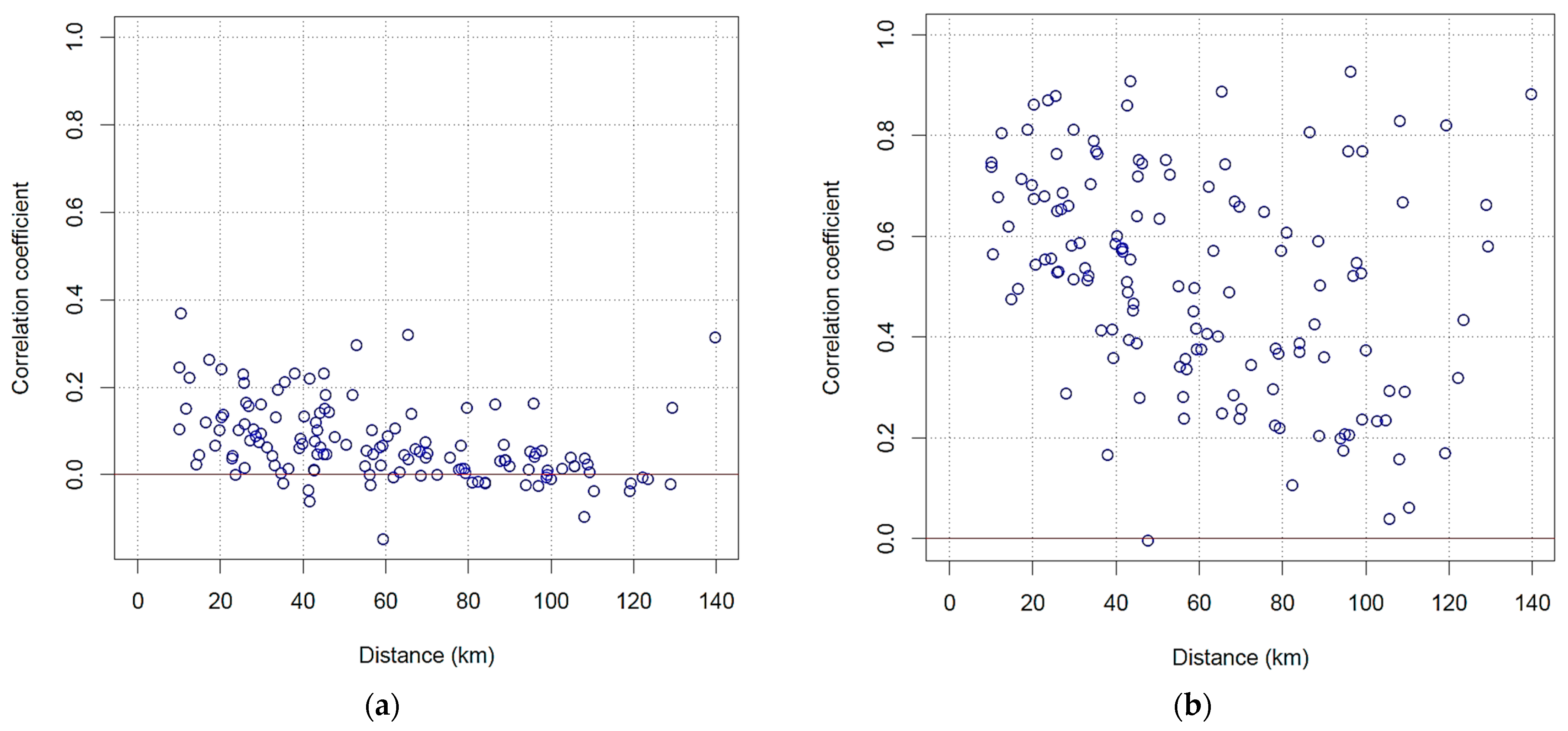
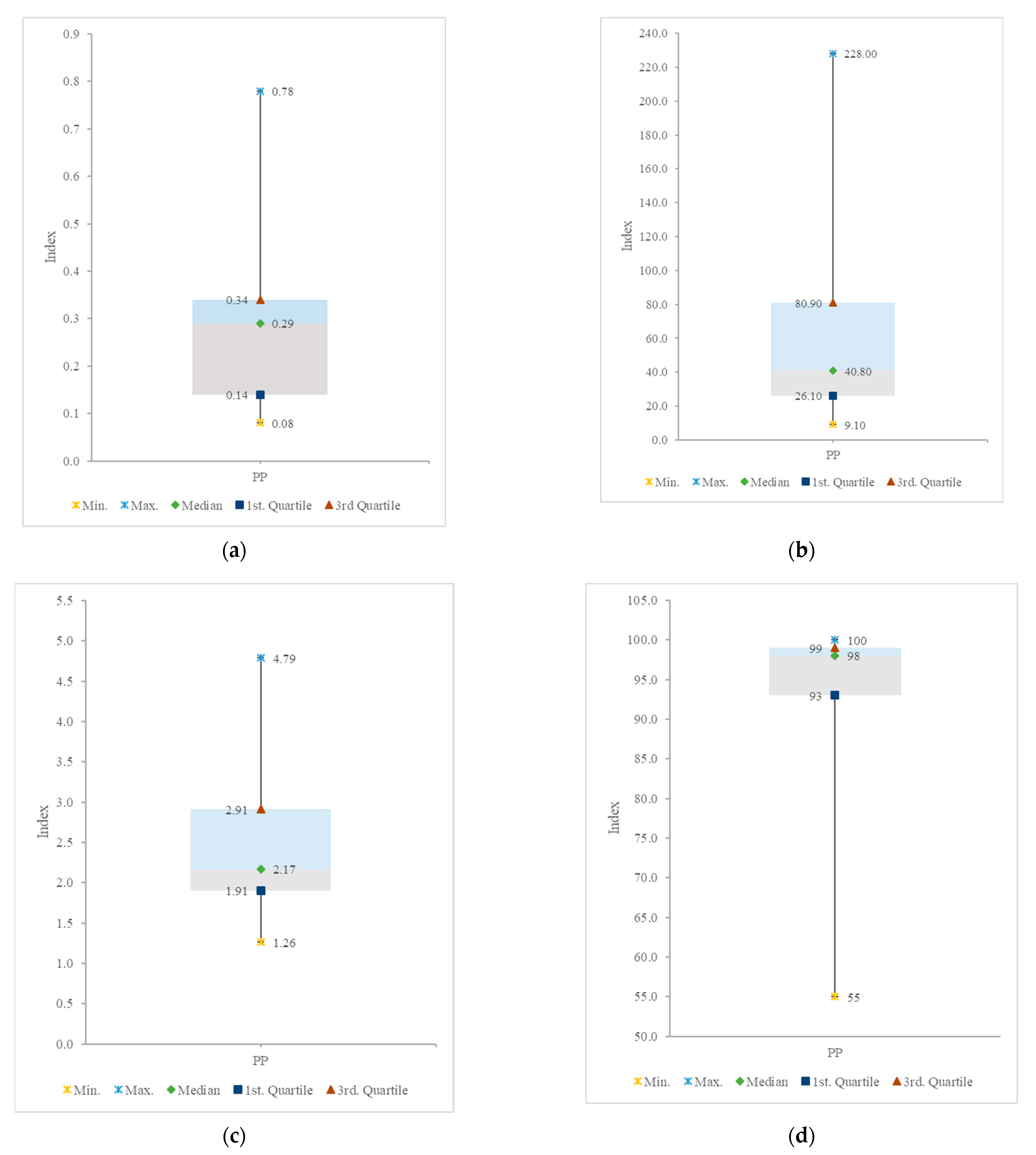
3.1. Analysis of Missing Data, Outliers, and Homogenization
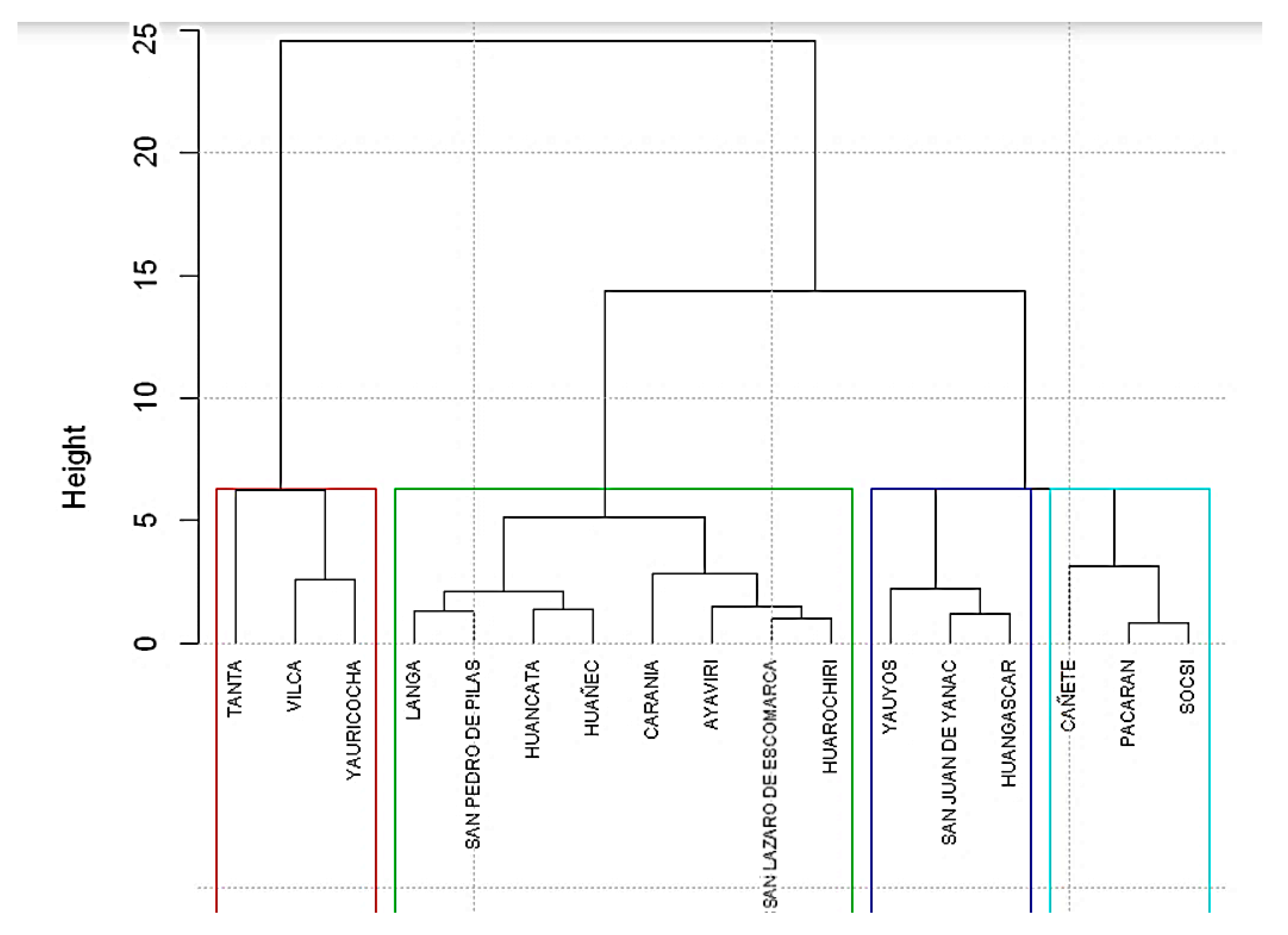
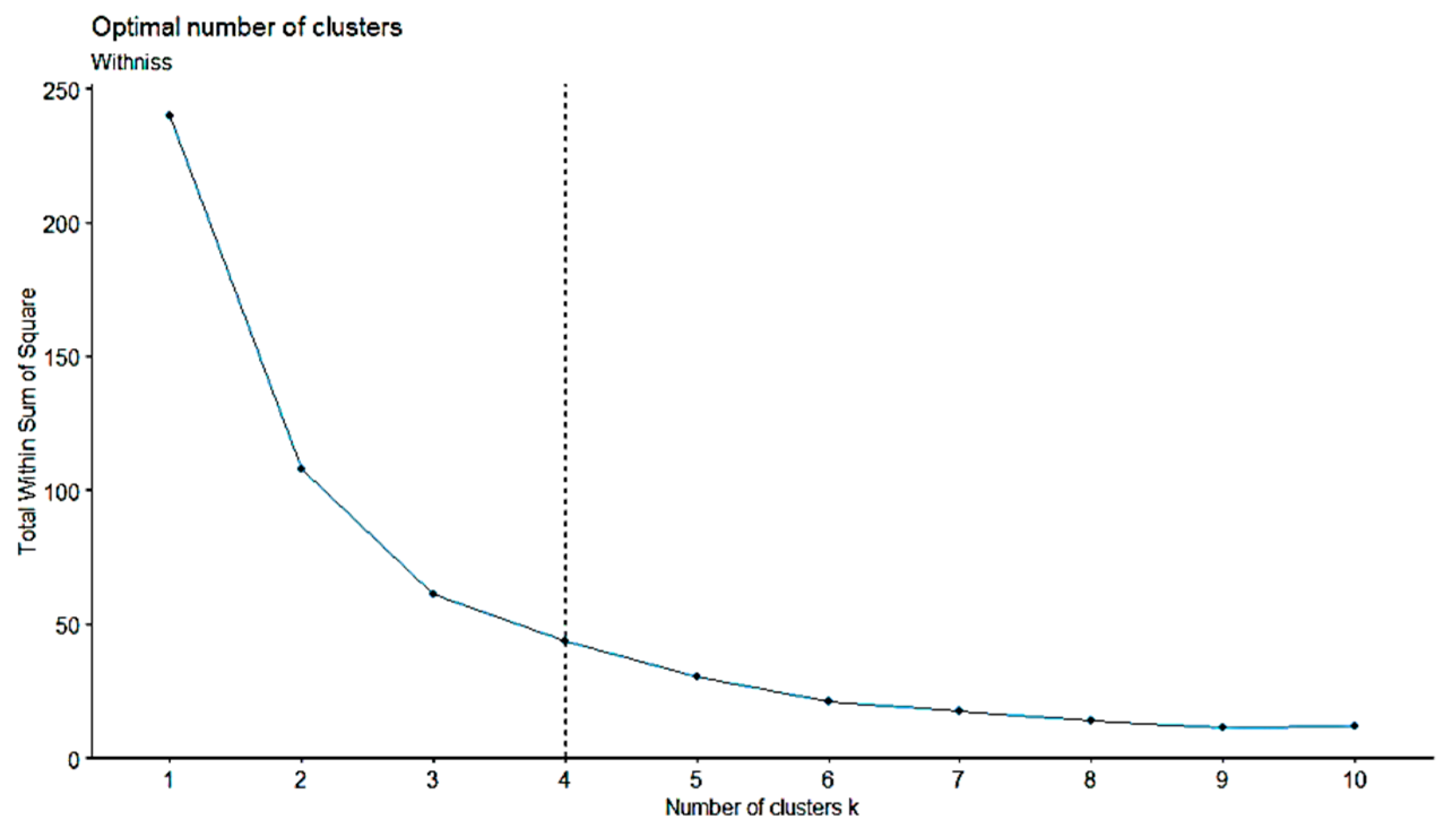
3.2. Regionalization Analysis
3.3. Analysis of the Series Gap-Filling Process
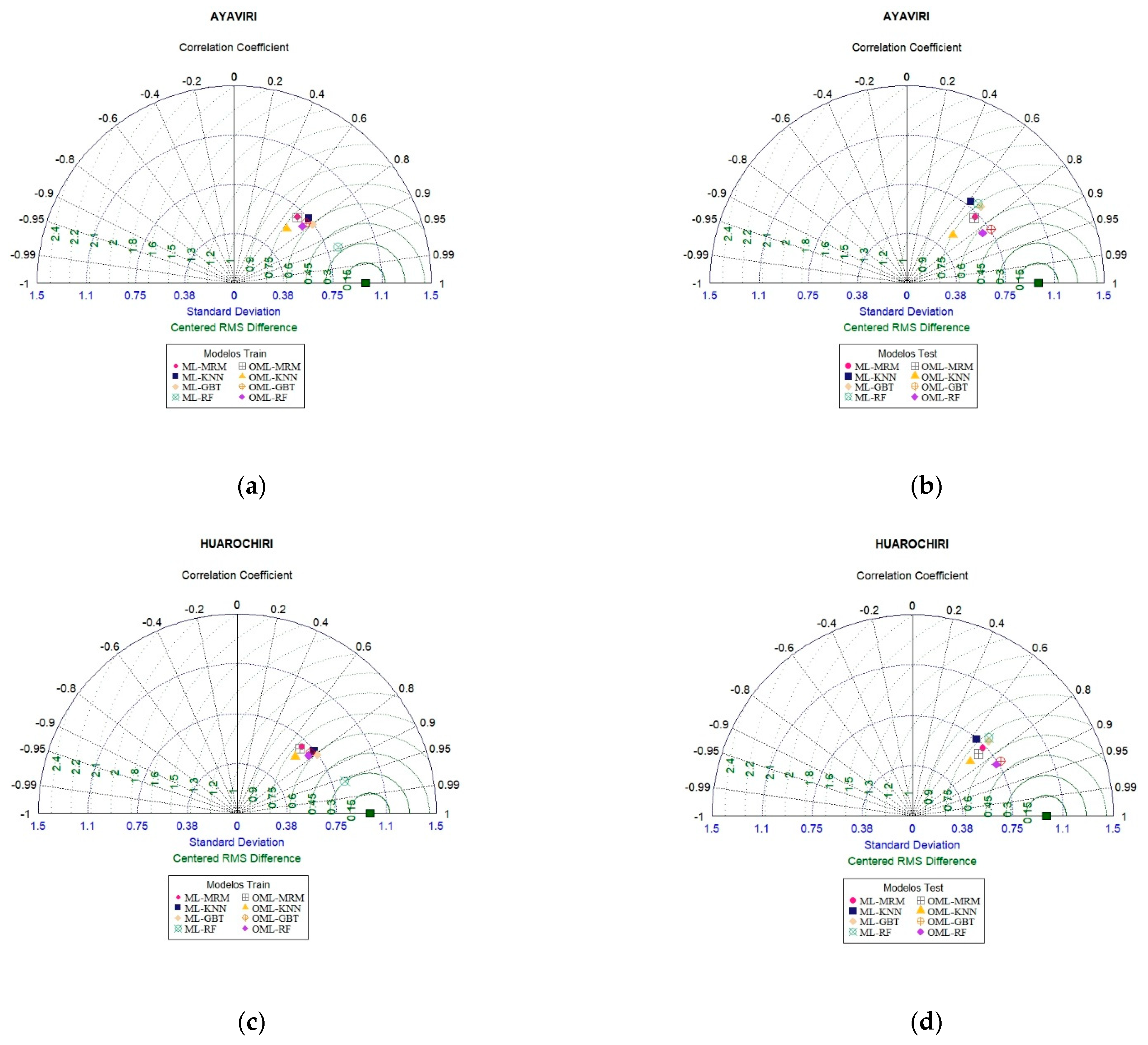
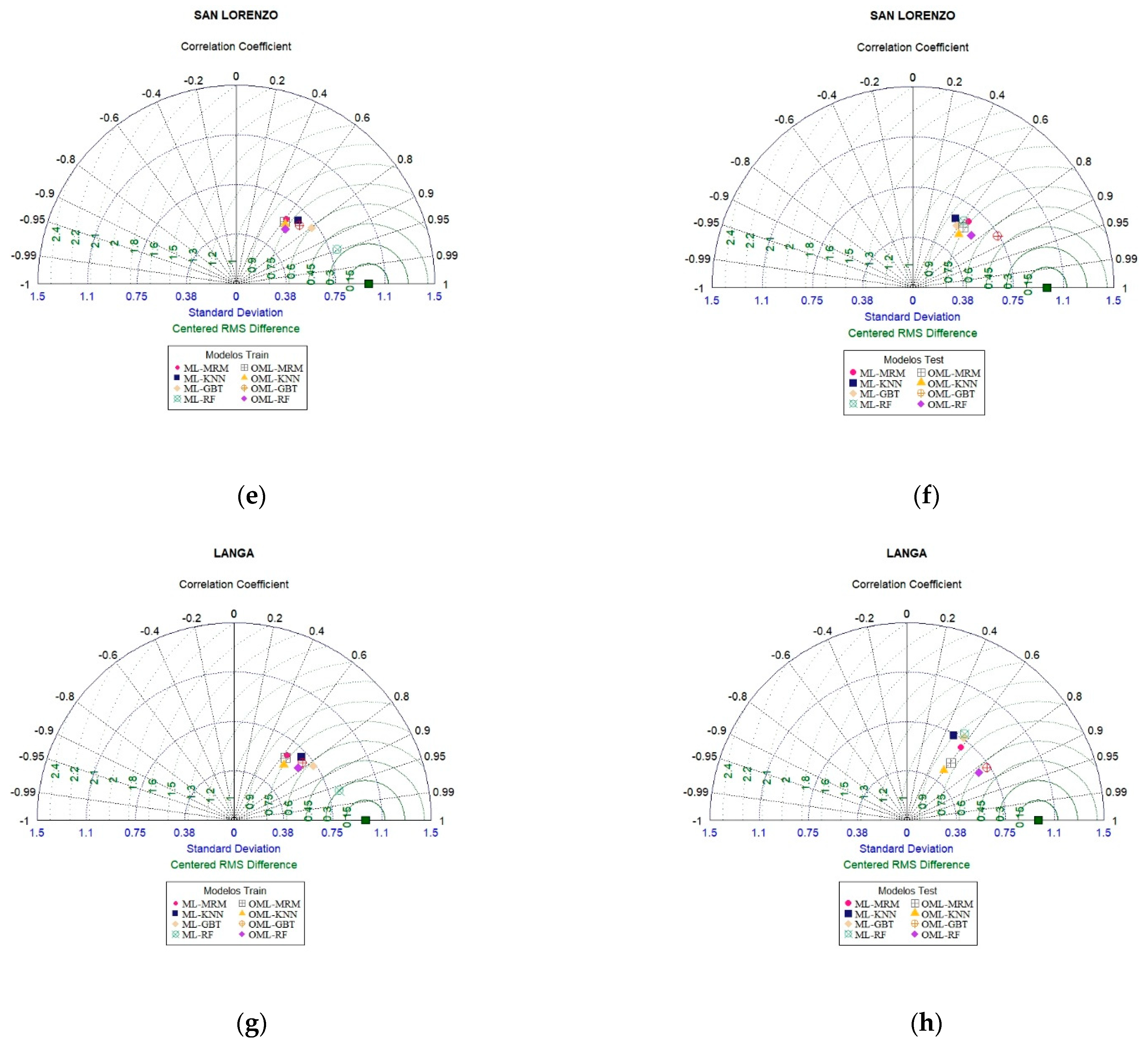
3.4. Assessment of Model Performance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, D.; Christakos, G.; Ding, X.; Wu, J. Adequacy of TRMM satellite rainfall data in driving the SWAT modeling of Tiaoxi catchment (Taihu lake basin, China). J. Hydrol. 2018, 556, 1139–1152. [Google Scholar] [CrossRef]
- Santos, L.O.F.D.; Querino, C.A.S.; Querino, J.K.A.D.S.; Pedreira Junior, A.L.; Moura, A.R.D.M.; Machado, N.G.; Biudes, M.S. Validation of rainfall data estimated by GPM satellite on Southern Amazon region. Rev. Ambiente Água 2019, 14. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, J. Hybrid PSO and GA for Neural Network Evolutionary in Monthly Rainfall Forecasting; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cramer, S.; Kampouridis, M.; Freitas, A.A.; Alexandridis, A.K. An extensive evaluation of seven machine learning methods for rainfall prediction in weather derivatives. Expert Syst. Appl. 2017, 85, 169–181. [Google Scholar] [CrossRef]
- Chen, F.; Gao, Y.; Wang, Y.; Qin, F.; Li, X. Downscaling satellite-derived daily precipitation products with an integrated framework. Int. J. Climatol. 2019, 39, 1287–1304. Available online: https://rmets.onlinelibrary.wiley.com/doi/pdf/10.1002/joc.5879 (accessed on 25 March 2022). [CrossRef]
- Bai, P.; Liu, X. Evaluation of five satellite-based precipitation products in two gauge-scarce basins on the Tibetan Plateau. Remote Sens. 2018, 10, 1316. [Google Scholar] [CrossRef]
- Chivers, B.D.; Wallbank, J.; Cole, S.J.; Sebek, O.; Stanley, S.; Fry, M.; Leontidis, G. Imputation of missing sub-hourly precipitation data in a large sensor network: A machine learning approach. J. Hydrol. 2020, 588, 125126. [Google Scholar] [CrossRef]
- Lavado Casimiro, W.S.; Ronchail, J.; Labat, D.; Espinoza, J.C.; Guyot, J.L. Basin-scale analysis of rainfall and runoff in Perú (1969–2004): Pacific, Titicaca and Amazonas drainages. Hydrol. Sci. J. 2012, 57, 625–642. [Google Scholar] [CrossRef]
- Espinoza Villar, J.C.; Ronchail, J.; Guyot, J.L.; Cochonneau, G.; Naziano, F.; Lavado, W.; De Oliveira, E.; Pombosa, R.; Vauchel, P. Spatio-temporal rainfall variability in the Amazon basin countries (Brazil, Peru, Bolivia, Colombia, and Ecuador). Int. J. Climatol. 2009, 29, 1574–1594. Available online: https://rmets.onlinelibrary.wiley.com/doi/pdf/10.1002/joc.1791 (accessed on 25 March 2022). [CrossRef]
- Rau, P.; Bourrel, L.; Labat, D.; Melo, P.; Dewitte, B.; Frappart, F.; Lavado, W.; Felipe, O. Regionalization of rainfall over the Peruvian Pacific slope and coast. Int. J. Climatol. 2017, 37, 143–158. [Google Scholar] [CrossRef]
- Körner, P.; Kronenberg, R.; Genzel, S.; Bernhofer, C. Introducing Gradient Boosting as a universal gap filling tool for meteorological time series. Meteorol. Z. 2018, 27, 369–376. [Google Scholar] [CrossRef]
- Lavado Casimiro, W.; Espinoza, J.C. Impactos de El Niño y La Niña en las lluvias del Perú (1965–2007). Rev. Bras. De Meteorol. 2014, 29, 171–182. [Google Scholar] [CrossRef]
- Bertsimas, D.; Pawlowski, C.; Zhuo, Y.D. From Predictive Methods to Missing Data Imputation: An Optimization Approach. J. Mach. Learn. Res. 2017, 18, 7133–7171. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V.; Chandramouli, V. Improved weighting methods, deterministic and stochastic data-driven models for estimation of missing precipitation records. J. Hydrol. 2005, 312, 191–206. [Google Scholar] [CrossRef]
- Barrios, A.; Trincado, G.; Garreaud, R. Alternative approaches for estimating missing climate data: Application to monthly precipitation records in South-Central Chile. For. Ecosyst. 2018, 5, 28. [Google Scholar] [CrossRef]
- Xia, Y.; Fabian, P.; Stohl, A. Winterhalter, Forest climatology: Estimation of missing values for Bavaria, Germany. Agric. For. Meteorol. 1999, 96, 131–144. [Google Scholar] [CrossRef]
- Bostan, P.A.; Heuvelink, G.B.M.; Akyurek, S.Z. Comparison of regression and kriging techniques for mapping the average annual precipitation of Turkey. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 115–126. [Google Scholar] [CrossRef]
- Mair, A.; Fares, A. Comparison of Rainfall Interpolation Methods in a Mountainous Region of a Tropical Island. J. Hydrol. Eng. 2011, 16, 371–383. [Google Scholar] [CrossRef]
- Simolo, C.; Brunetti, M.; Maugeri, M.; Nanni, T. Improving estimation of missing values in daily precipitation series by a probability density function-preserving approach. Int. J. Climatol. 2010, 30, 1564–1576. [Google Scholar] [CrossRef]
- Huang, M.; Lin, R.; Huang, S.; Xing, T. A novel approach for precipitation forecast via improved K-nearest neighbor algorithm. Adv. Eng. Inform. 2017, 33, 89–95. [Google Scholar] [CrossRef]
- Gorshenin, A.; Lebedeva, M.; Lukina, S.; Yakovleva, A. Application of Machine Learning Algorithms to Handle Missing Values in Precipitation Data. In Distributed Computer and Communication Networks; Lecture Notes in Computer Science; Vishnevskiy, V., Samouylov, K., Kozyrev, D., Eds.; Springer International Publishing: Cham, Switzerland, 2019; p. 11965. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Gualda, J.E.; García-Marín, A.P. Assessing Machine Learning Models for Gap Filling Daily Rainfall Series in a Semiarid Region of Spain. Atmosphere 2021, 12, 1158. [Google Scholar] [CrossRef]
- Devi, U.; Shekhar, M.S.; Singh, G.P.; Rao, N.N.; Bhatt, U.S. Methodological application of quantile mapping to generate precipitation data over Northwest Himalaya. Int. J. Climatol. 2019, 39, 3160–3170. [Google Scholar] [CrossRef]
- Estévez, J.; Bellido-Jiménez, J.A.; Liu, X.; García-Marín, A.P. Monthly Precipitation Forecasts Using Wavelet Neural Networks Models in a Semiarid Environment. Water 2020, 12, 1909. [Google Scholar] [CrossRef]
- Sattari, M.T.; Rezazadeh-Joudi, A.; Kusiak, A. Assessment of different methods for estimation of missing data in precipitation studies. Hydrol. Res. 2016, 48, 1032–1044. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Newman, A.J.; Wood, A.W.; Papalexiou, S.M.; Vionnet, V.; Whitfield, P.H. SCDNA: A serially complete precipitation and temperature dataset for North America from 1979 to 2018. Earth Syst. Sci. Data 2020, 12, 2381–2409. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M. SC-Earth: A Station-Based Serially Complete Earth Dataset from 1950 to 2019. J. Clim. 2021, 34, 6493–6511. [Google Scholar] [CrossRef]
- Carrera-Villacrés, D.V.; Guevara-García, P.V.; Tamayo-Bacacela, L.C.; Balarezo-Aguilar, A.L.; Narváez-Rivera, C.A.; Morocho-López, D.R. Relleno de series anuales de datos meteorológicos mediante métodos estadísticos en la zona costera e interandina del Ecuador, y cálculo de la precipitación media. Idesia 2016, 34, 81–90. [Google Scholar] [CrossRef]
- Luna Romero, A.E.; Lavado Casimiro, W.S. Evaluación de métodos hidrológicos para la completación de datos faltantes de precipitación en estaciones de la cuenta Jetepeque, Perú. Rev. Tecnológica-ESPOL 2015, 28, 42–52. [Google Scholar]
- Estévez, J.; Gavilán, P.; Giráldez, J.V. Guidelines on validation procedures for meteorological data from automatic weather stations. J. Hydrol. 2011, 402, 144–154. [Google Scholar] [CrossRef]
- Portuguez Maurtua, D.M. Aplicación de la Geoestadística a Modelos Hidrológicos en la cuenca del río Cañete. Master’s Thesis, Universidad Nacional Agraria La Molina, Lima, Peru, 2017. [Google Scholar]
- Guevara Ochoa, C.; Briceño, N.; Zimmermann, E.D.; Vives, L.S.; Blanco, M.; Cazenave, G.; Ares, M.G. Relleno de series de precipitación diaria para largos periodos de tiempo en zonas de llanura: Caso de estudio cuenca superior del arroyo del Azul. Geoacta 2017, 42, 38–60. Available online: http://www.scielo.org.ar/scielo.php?script=sci_arttext&pid=S1852-77442017000100004&lng=es (accessed on 5 March 2020).
- Guijarro, J. Homogenization of climatic series with Climatol. Rep. Técnico State Meteorol. Agency (AEMET) 2018, 3, 1–20. Available online: https://www.climatol.eu/homog_climatol-en.pdf (accessed on 5 March 2020).
- Toreti, A.; Kuglitsch, F.G.; Xoplaki, E.; Della-Marta, P.; Aguilar, E.; Prohom, M.; Luterbacher, J. A note on the use of the standard normal homogeneity test (SNHT) to detect inhomogeneities in climatic time series. Int. J. Climatol. 2011, 31, 630–632. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Alexandersson, H.; Moberg, A. Homogenization of swedish temperature data. Part I: Homogeneity test for linear trends. Int. J. Climatol. 1997, 17, 25–34. [Google Scholar]
- Moberg, A.; Alexandersson, H. Homogenization of swedish temperature data. Part ii: Homogenized gridded air temperature compared with a subset of global gridded air temperature since 1861. Int. J. Climatol. 1997, 17, 35–54. [Google Scholar]
- Pandzic, K.; Kobold, M.; Oskorus, D.; Biondic, B.; Biondic, R.; Bonacci, O.; Likso, T.; Curic, O. Standard normal homogeneity test as a tool to detect change points in climate-related river discharge variation: Case study of the Kupa River Basin. Hydrol. Sci. J. 2020, 65, 227–241. [Google Scholar] [CrossRef]
- Ahmad, N.H.; Deni, S.M. Homogeneity test on daily rainfall series for Malaysia. Mat. Malays. J. Ind. Appl. Math. 2013, 29, 141–150. [Google Scholar]
- Marcolini, G.; Bellin, A.; Chiogna, G. Performance of the Standard Normal Homogeneity Test for the homogenization of mean seasonal snow depth time series. Int. J. Climatol. 2017, 37, 1267–1277. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Yashwant, S.; Sananse, S. Comparisons of Different Methods of Cluster Analysis with Application to Rainfall Data. Int. J. Innov. Res. Sci. 2015, 4, 10861. [Google Scholar] [CrossRef]
- Luna Vera, J.A.; Domínguez Mora, R.T. Un método para el análisis de frecuencia regional de lluvias máximas diarias: Aplicación en los Andes bolivianos. Ingeniare Rev. Chil. De Ing. 2013, 21, 111–124. [Google Scholar] [CrossRef][Green Version]
- Ilbay, M.L.; Barragán, R.Z.; Lavado-Casimiro, W. Regionalization of precipitation, its aggressiveness and concentration in the Guayas river basin, Ecuador. La Granja 2019, 30, 57. [Google Scholar] [CrossRef]
- Hiez, G. L’homogénéité des données pluviométriques. Cah. ORSTOM Série Hydrol. 1977, 14, 29–173. [Google Scholar]
- Brunet-Moret, Y. Homogénéisation des précipitations. Bur. Cent. Hydrol. De L’orstom Á Paris 1979, 16, 147–170. [Google Scholar]
- Vauchel, P. Hydraccess: Progiciel de gestion et d’exploitation de bases de données hydrologiques. In HYDROMED: Séminaire International les Petits Barrages Dans le Monde Méditerranéen: Recueil des Résumés. In Proceedings of the Les Petits Barrages dans le Monde Méditerranéen: Séminaire International, Tunis, North Africa, 28–31 May 2001. [Google Scholar]
- Wang, J.-H.; Hopke, P.K.; Hancewicz, T.M.; Zhang, S.L. Application of modified alternating least squares regression to spectroscopic image analysis. Anal. Chim. Acta 2003, 476, 93–109. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G. Infilling missing precipitation records—A comparison of a new copula-based method with other techniques. J. Hydrol. 2014, 519, 1162–1170. [Google Scholar] [CrossRef]
- Khosravi, G.; Nafarzadegan, A.R.; Nohegar, A.; Fathizadeh, H.; Malekian, A. A modified distance-weighted approach for filling annual precipitation gaps: Application to different climates of Iran. Theor. Appl. Climatol. 2015, 119, 33–42. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, G.; Lu, E. Using the Gradient Boosting Decision Tree to Improve the Delineation of Hourly Rain Areas during the Summer from Advanced Himawari Imager Data. J. Hydrometeorol. 2018, 19, 761–776. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bellido-Jiménez, J.A.; Estévez, J.; García-Marín, A.P. New machine learning approaches to improve reference evapotranspiration estimates using intra-daily temperature-based variables in a semi-arid region of Spain. Agric. Water Manag. 2021, 245, 106558. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Estévez, J.; García-Marín, A.P. Assessing Neural Network Approaches for Solar Radiation Estimates Using Limited Climatic Data in the Mediterranean Sea. Environ. Sci. Proc. 2021, 4, 19. [Google Scholar]
- Gómez Guerrero, J.S.; Aguayo Arias, M.I. Evaluación de desempeño de métodos de relleno de datos pluviométricos en dos zonas morfoestructurales del Centro Sur de Chile. Investig. Geográficas 2019, 99, 1–16. [Google Scholar] [CrossRef]
- Guijarro, J.A.; Guijarro, M.J. Package ‘Climatol’. 2019. Available online: https://doi.org/5.gwdg.de/pub/misc/cran/web/packages/climatol/climatol.pdf (accessed on 5 March 2020).
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]

| ID | Stations | Coordinates | Altitude | Observed Data | Missing Data | |||
|---|---|---|---|---|---|---|---|---|
| Latitude | Longitude | (masl) | No of Data | (%) | No of Data | (%) | ||
| 1 | Ayaviri | −12.38 | −76.13 | 3228 | 6881 | 99.2 | 58 | 0.8 |
| 2 | Cañete | −13.07 | −76.32 | 158 | 3830 | 55.2 | 3109 | 44.8 |
| 3 | Carania | −12.34 | −75.87 | 3875 | 6939 | 100 | 0 | 0 |
| 4 | Huancata | −12.22 | −76.22 | 2700 | 6939 | 100 | 0 | 0 |
| 5 | Huangascar | −12.9 | −75.83 | 2533 | 6908 | 99.6 | 31 | 0.4 |
| 6 | Huañec | −12.29 | −76.14 | 3205 | 6939 | 100 | 0 | 0 |
| 7 | Huarochiri | −12.13 | −76.23 | 3154 | 6787 | 97.8 | 152 | 2.2 |
| 8 | Langa | −12.13 | −76.42 | 2863 | 6484 | 93.4 | 455 | 6.6 |
| 9 | Pacaran | −12.83 | −76.07 | 700 | 5132 | 74 | 1807 | 26 |
| 10 | San Juan de Yanac | −13.21 | −75.79 | 2550 | 6482 | 93.4 | 457 | 6.6 |
| 11 | San Lazaro de Escomarca | −12.18 | −76.35 | 3758 | 6486 | 93.5 | 453 | 6.5 |
| 12 | San Pedro de Pilas | −12.45 | −76.22 | 2600 | 6909 | 99.6 | 30 | 0.4 |
| 13 | Socsi | −13.03 | −76.19 | 500 | 4687 | 67.5 | 2252 | 32.5 |
| 14 | Tanta | −12.12 | −76.02 | 4323 | 6819 | 98.3 | 120 | 1.7 |
| 15 | Vilca | −12.11 | −75.83 | 3864 | 6297 | 90.7 | 642 | 9.3 |
| 16 | Yauricocha | −12.32 | −75.72 | 4675 | 6818 | 98.3 | 121 | 1.7 |
| 17 | Yauyos | −12.49 | −75.91 | 2327 | 6878 | 99.1 | 61 | 0.9 |
| Stations | ACmx | SNHT | RMSE | POD |
|---|---|---|---|---|
| Ayaviri | 0.19 | 47.4 | 2.9 | 99 |
| Cañete | 0.65 | 228.0 | 1.3 | 55 |
| Carania | 0.20 | 26.1 | 2.6 | 100 |
| Huancata | 0.33 | 95.0 | 2.4 | 100 |
| Huangascar | 0.14 | 35.9 | 1.9 | 99 |
| Huañec | 0.29 | 68.7 | 2.2 | 100 |
| Huarochiri | 0.13 | 55.0 | 2.7 | 97 |
| Langa | 0.08 | 80.9 | 2.0 | 93 |
| Pacaran | 0.73 | 166.1 | 1.3 | 73 |
| San Juan de Yanac | 0.10 | 21.5 | 1.5 | 93 |
| San Lazaro de Escomarca | 0.32 | 20.9 | 3.4 | 93 |
| San Pedro de Pilas | 0.15 | 13.4 | 2.0 | 99 |
| Socsi | 0.78 | 40.8 | 1.4 | 67 |
| Tanta | 0.34 | 155.6 | 4.8 | 98 |
| Vilca | 0.34 | 30.5 | 3.9 | 90 |
| Yauricocha | 0.36 | 38.6 | 4.6 | 98 |
| Yauyos | 0.08 | 9.1 | 1.9 | 99 |
| Station | Time | Standard | Station/Vector |
|---|---|---|---|
| (Years) | Deviation | Correlation | |
| Langa | 16 | 0.252 | 0.882 |
| San Lazaro de Escomarca | 16 | 0.263 | 0.664 |
| Ayaviri | 17 | 0.116 | 0.904 |
| Huancata | 19 | 0.341 | 0.863 |
| Huañec | 19 | 0.187 | 0.751 |
| Huarochiri | 14 | 0.159 | 0.851 |
| Carania | 19 | 0.191 | 0.679 |
| Ayaviri | 1 | ||||||
| Carania | 0.48 | 1 | |||||
| Huancata | 0.60 | 0.47 | 1 | ||||
| Huañec | 0.51 | 0.43 | 0.49 | 1 | |||
| Huarochiri | 0.56 | 0.55 | 0.58 | 0.46 | 1 | ||
| San Lazaro de Escomarca | 0.45 | 0.40 | 0.43 | 0.39 | 0.44 | 1 | |
| Langa | 0.45 | 0.38 | 0.46 | 0.38 | 0.46 | 0.55 | 1 |
| Ayaviri | Carania | Huancata | Huañec | Huarochiri | San Lazaro de Escomarca | Langa |
| Regions | Target Station (Y) | Predictor Station (X) | Multiple Predictor Stations (Xm) |
|---|---|---|---|
| Region 1 | Ayaviri | Huancata | Huancata, Langa, San Lazaro de Escomarca, Huañec, Huarochiri, Carania |
| Huarochiri | Huancata | Huancata, Langa, San Lazaro de Escomarca, Ayaviri, Huañec, Carania | |
| San Lazaro de Escomarca | Langa | Langa, Ayaviri, Huancata, Huañec, Huarochiri, Carania | |
| Langa | San Lazaro de Escomarca | San Lazaro de Escomarca, Ayaviri, Huancata, Huañec, Huarochiri, Carania | |
| Region 2 | San Pedro de Pilas | Huangascar | Huangascar, San Juan de Yanac, Yauyos |
| Huangascar | San Pedro de Pilas | San Pedro de Pilas, Yauyos, San Juan de Yanac | |
| Yauyos | San Pedro de Pilas | San Pedro de Pilas, Huangascar, San Juan de Yanac | |
| San Juan de Yanac | San Pedro de Pilas | San Pedro de Pilas, Huangascar, Yauyos | |
| Region 4 | Tanta | Vilca | Vilca and Yauricocha |
| Yauricocha | Vilca | Vilca and Tanta | |
| Vilca | Yauricocha | Yauricocha and Tanta |
| Algorithm | Parameters [Values] | Hyperparameters [Values] |
|---|---|---|
| Multiple Regression | alpha [1] | alpha [logspace(–5, 5, 500)] |
| solver [‘auto’] | solver [‘auto’] | |
| modelo[Ridge] | modelo[Ridge] | |
| K-nearest neighbors | n_neighbors [5] | n_neighbours [linspace(1, 100, 500] |
| leaf_size [30] | leaf_size [1, 3] | |
| algoritm [‘auto’] | algoritm [‘auto’] | |
| modelo[KNeighborsRegressor] | modelo[KNeighborsRegressor] | |
| Gradient boosting tree | n_estimators [100] | n_estimators [50, 100, 1000, 2000] |
| max_feature [‘none’] | max_feature [‘auto’, 3, 5, 7] | |
| max_depth [3] | max_depth [‘None’, 3, 5, 10, 20] | |
| subsample [1] | subsample [0.5, 0.7, 1] | |
| modelo[GradientBoostingRegressor] | modelo[GradientBoostingRegressor] | |
| Random forest | n_estimators [100] | n_estimators [50, 100, 1000, 2000] |
| max_feature [‘auto’] | max_feature [‘auto’, 3, 5, 7] | |
| max_depth [‘None’] | max_depth [‘None’, 3, 5, 10, 20] | |
| modelo[RandomForestRegressor] | modelo[RandomForestRegressor] |
| Stations | Samples | Statistics | LRM | MRM | Machine Learning | Optimized Machine Learning | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MRM | KNN | GBT | RF | MRM | KNN | GBT | RF | |||||
| Ayaviri | Train | R2 | 0.36 | 0.49 | 0.48 | 0.57 | 0.64 | 0.89 | 0.48 | 0.49 | 0.59 | 0.59 |
| Train | RMSE | 3.15 | 2.81 | 2.87 | 2.61 | 2.39 | 1.36 | 2.87 | 2.89 | 2.55 | 2.58 | |
| Train | NSE | 0.36 | 0.49 | 0.48 | 0.57 | 0.64 | 0.88 | 0.48 | 0.47 | 0.59 | 0.58 | |
| Train | PBIAS | 0.00 | 0.00 | 0.00 | 3.92 | 0.00 | −1.73 | 0.00 | 0.45 | 0.00 | 0.38 | |
| Test | R2 | 0.52 | 0.38 | 0.49 | 0.45 | 0.52 | 0.48 | 0.71 | 0.70 | |||
| Test | RMSE | 2.62 | 3.03 | 2.75 | 2.86 | 2.62 | 2.83 | 2.05 | 2.14 | |||
| Test | NSE | 0.52 | 0.36 | 0.47 | 0.43 | 0.52 | 0.44 | 0.71 | 0.68 | |||
| Test | PBIAS | 0.00 | 0.67 | −8.46 | −10.65 | 0.00 | 21.64 | 0.00 | 1.01 | |||
| Huarochiri | Train | R2 | 0.34 | 0.49 | 0.49 | 0.60 | 0.65 | 0.92 | 0.49 | 0.51 | 0.60 | 0.61 |
| Train | RMSE | 3.12 | 2.74 | 2.80 | 2.47 | 2.32 | 1.19 | 2.80 | 2.76 | 2.49 | 2.48 | |
| Train | NSE | 0.34 | 0.49 | 0.49 | 0.60 | 0.65 | 0.91 | 0.49 | 0.50 | 0.60 | 0.60 | |
| Train | PBIAS | 0.00 | 0.00 | 0.00 | 6.48 | 0.00 | −1.39 | 0.00 | 4.38 | 0.00 | 0.47 | |
| Test | R2 | 0.52 | 0.41 | 0.51 | 0.49 | 0.53 | 0.53 | 0.73 | 0.73 | |||
| Test | RMSE | 2.54 | 2.83 | 2.58 | 2.64 | 2.51 | 2.57 | 1.93 | 1.96 | |||
| Test | NSE | 0.52 | 0.40 | 0.50 | 0.48 | 0.53 | 0.51 | 0.72 | 0.71 | |||
| Test | PBIAS | −1.72 | 7.12 | −5.63 | −9.30 | 0.00 | 18.36 | 0.00 | 0.95 | |||
| San Lazaro de Escomarca | Train | R2 | 0.30 | 0.38 | 0.38 | 0.49 | 0.65 | 0.90 | 0.38 | 0.41 | 0.54 | 0.45 |
| Train | RMSE | 3.44 | 3.22 | 3.16 | 2.87 | 2.42 | 1.41 | 3.17 | 3.11 | 2.75 | 3.03 | |
| Train | NSE | 0.30 | 0.38 | 0.38 | 0.49 | 0.64 | 0.88 | 0.38 | 0.40 | 0.53 | 0.43 | |
| Train | PBIAS | 0.00 | 0.00 | 0.00 | 7.01 | 0.00 | −1.96 | 0.00 | 10.88 | 0.00 | 0.14 | |
| Test | R2 | 0.42 | 0.28 | 0.34 | 0.37 | 0.41 | 0.43 | 0.73 | 0.56 | |||
| Test | RMSE | 3.33 | 3.73 | 3.55 | 3.46 | 3.34 | 3.35 | 2.31 | 2.98 | |||
| Test | NSE | 0.42 | 0.27 | 0.33 | 0.37 | 0.41 | 0.41 | 0.72 | 0.53 | |||
| Test | PBIAS | 0.00 | 16.25 | 9.41 | 1.78 | 0.00 | 14.86 | 0.00 | −0.05 | |||
| Langa | Train | R2 | 0.30 | 0.39 | 0.40 | 0.53 | 0.68 | 0.93 | 0.40 | 0.45 | 0.59 | 0.60 |
| Train | RMSE | 1.98 | 1.85 | 1.85 | 1.64 | 1.37 | 0.71 | 1.85 | 1.80 | 1.55 | 1.55 | |
| Train | NSE | 0.30 | 0.39 | 0.40 | 0.53 | 0.67 | 0.91 | 0.40 | 0.43 | 0.58 | 0.58 | |
| Train | PBIAS | 0.00 | 0.00 | 0.00 | 5.79 | 0.00 | −3.09 | 0.00 | 10.61 | 0.00 | 0.60 | |
| Test | R2 | 0.36 | 0.24 | 0.32 | 0.31 | 0.37 | 0.36 | 0.70 | 0.70 | |||
| Test | RMSE | 1.85 | 2.09 | 1.94 | 1.98 | 1.83 | 1.87 | 1.28 | 1.33 | |||
| Test | NSE | 0.35 | 0.17 | 0.28 | 0.26 | 0.37 | 0.34 | 0.69 | 0.67 | |||
| Test | PBIAS | −4.32 | 0.76 | −7.22 | −16.36 | 0.00 | 17.93 | 0.00 | 1.23 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Portuguez-Maurtua, M.; Arumi, J.L.; Lagos, O.; Stehr, A.; Montalvo Arquiñigo, N. Filling Gaps in Daily Precipitation Series Using Regression and Machine Learning in Inter-Andean Watersheds. Water 2022, 14, 1799. https://doi.org/10.3390/w14111799
Portuguez-Maurtua M, Arumi JL, Lagos O, Stehr A, Montalvo Arquiñigo N. Filling Gaps in Daily Precipitation Series Using Regression and Machine Learning in Inter-Andean Watersheds. Water. 2022; 14(11):1799. https://doi.org/10.3390/w14111799
Chicago/Turabian StylePortuguez-Maurtua, Marcelo, José Luis Arumi, Octavio Lagos, Alejandra Stehr, and Nestor Montalvo Arquiñigo. 2022. "Filling Gaps in Daily Precipitation Series Using Regression and Machine Learning in Inter-Andean Watersheds" Water 14, no. 11: 1799. https://doi.org/10.3390/w14111799
APA StylePortuguez-Maurtua, M., Arumi, J. L., Lagos, O., Stehr, A., & Montalvo Arquiñigo, N. (2022). Filling Gaps in Daily Precipitation Series Using Regression and Machine Learning in Inter-Andean Watersheds. Water, 14(11), 1799. https://doi.org/10.3390/w14111799






