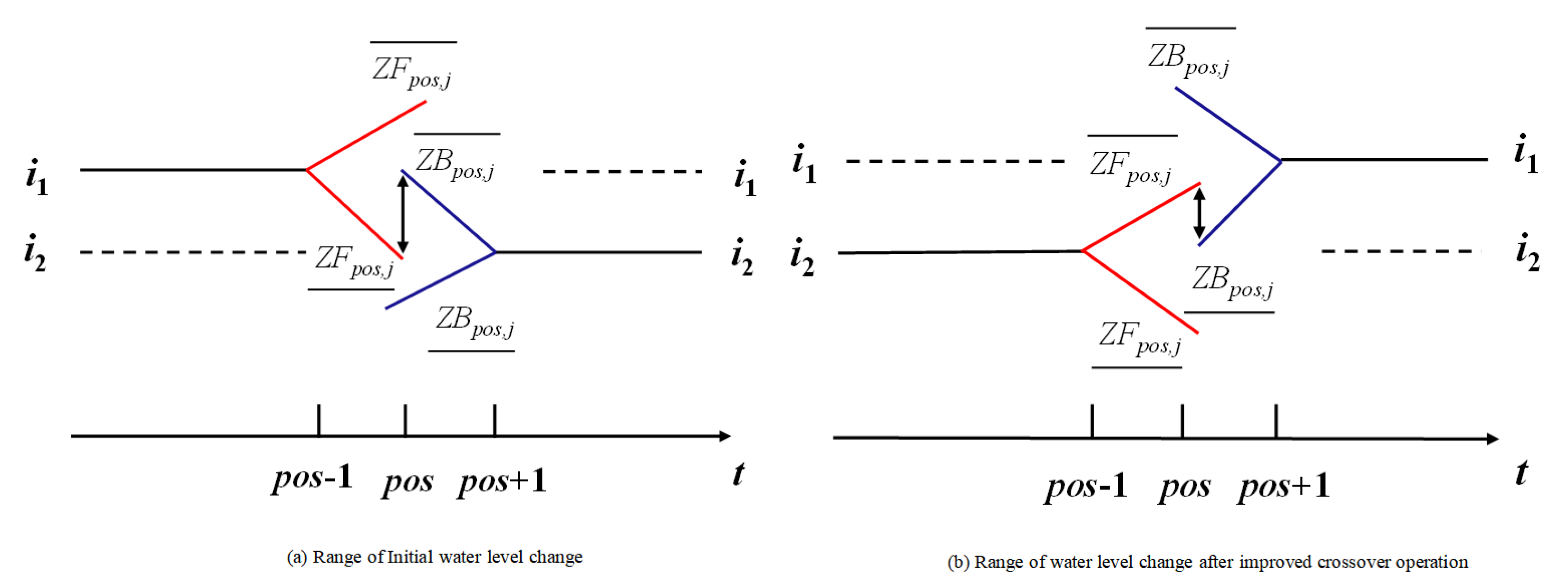
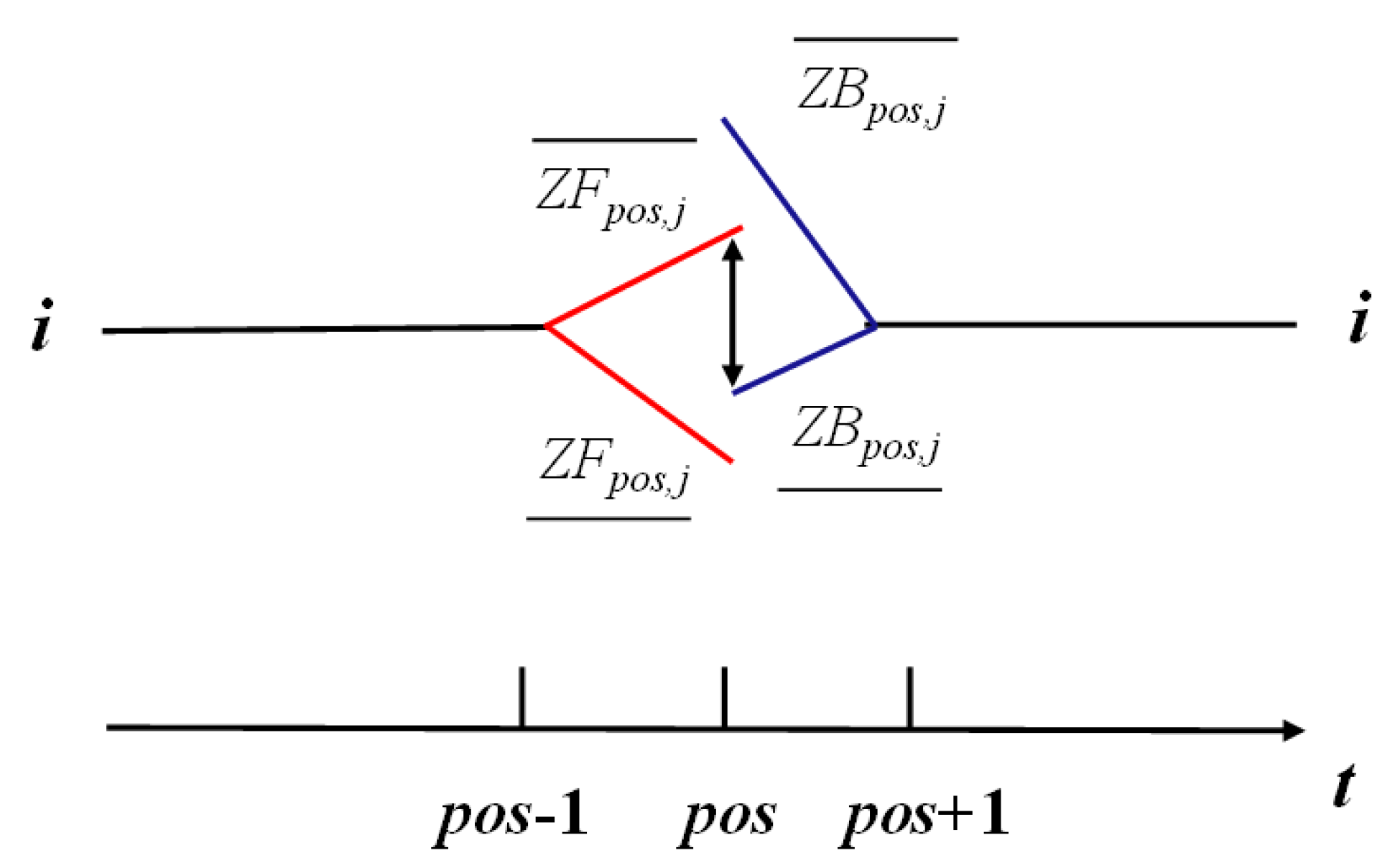
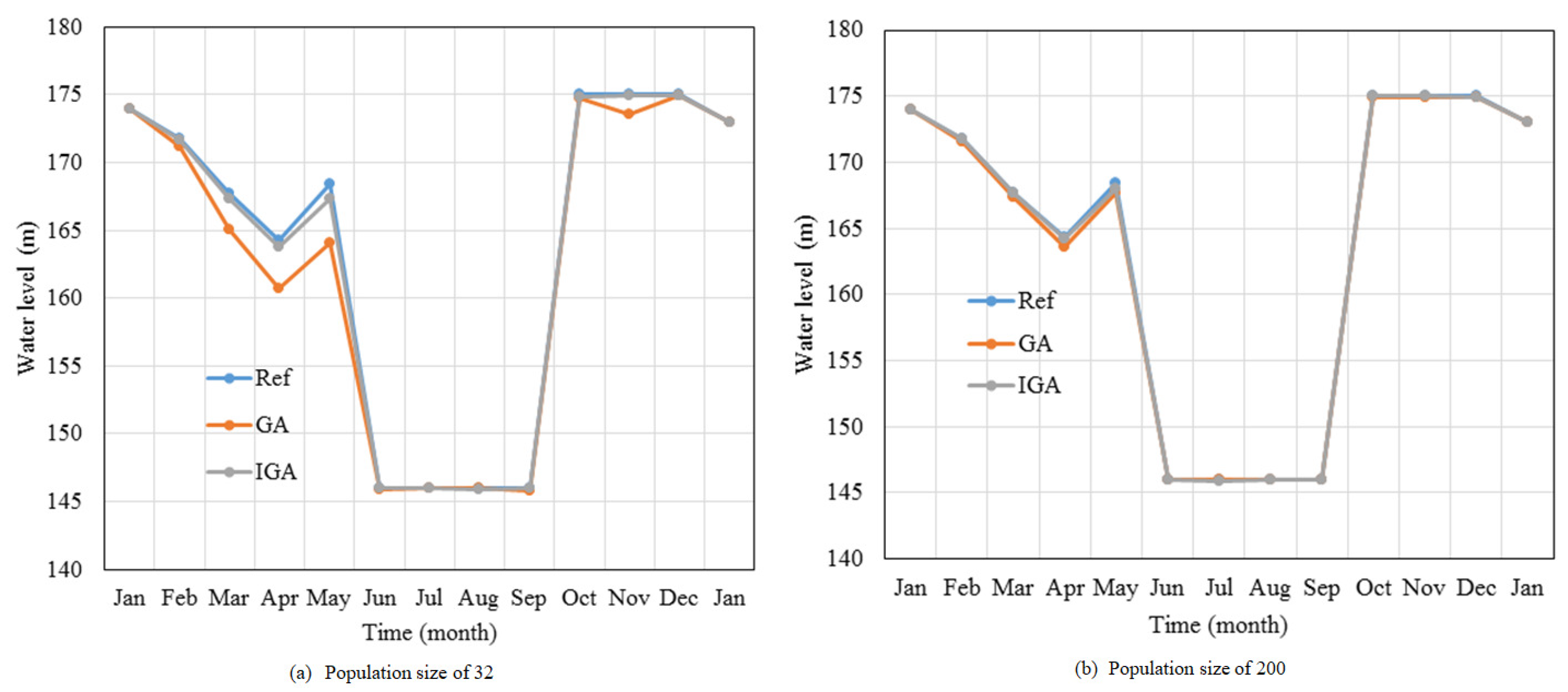
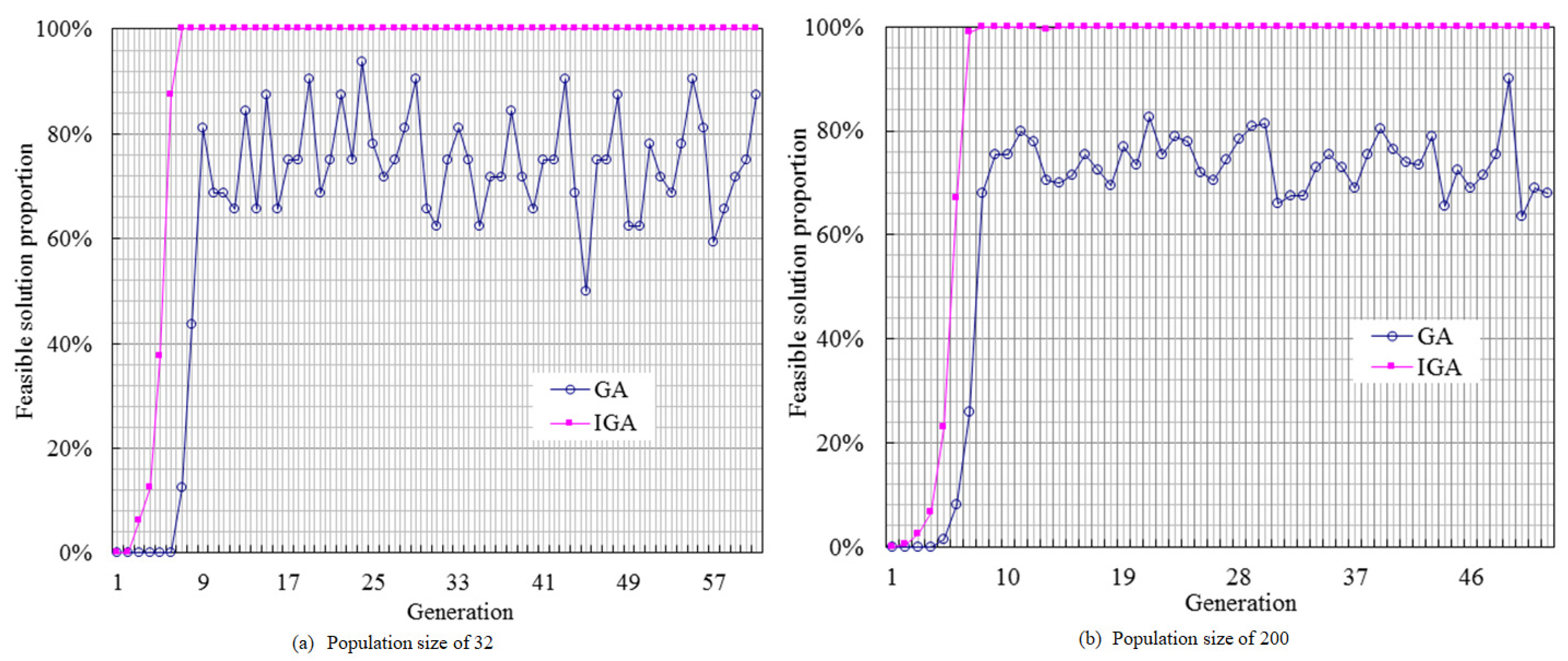
1. Introduction
Accurate forecasts for long forecast periods are fundamental for the formulation of a reservoir operation plan [
1]. However, with the levels of accuracy provided by current meteorological and hydrological forecasting, long-term forecasts for the prediction of inflow to cascade reservoirs may deviate considerably from the actual conditions, resulting in the fact that long-term optimized operation plans thus formulated are not usually feasible [
2]. A long-term scheduling scheme formulated on the basis of runoff forecasts can play a guiding role in the preliminary planning stages of reservoir operation, but with the passage of time, the static scheduling scheme will deviate significantly from the actual situation. Under these conditions, short-term and medium-term reservoir operation plans in the latter part of the scheduling period usually need to be independent of the long-term scheduling scheme and thus are separately formulated [
3,
4]. As a result, there is a lack of effective linkages and correlations between the long-term scheduling scheme and the medium- and short-term operation plans of the reservoir [
5,
6]. This seriously hinders the realization of the goal of maximizing the power generation of cascade reservoirs [
7]. Methods of enhancing the ability of a long-term scheduling scheme to guide the middle-term and short-term operation plans and ways of improving the long-term economic benefits of reservoirs using the current level of forecasting technology are recognized as difficult issues and have been the focus of recent studies [
8,
9]. If these two issues are resolved, it could stimulate the development and application of an automated reservoir operation system [
10].
A complete set of models in an automated reservoir operation system includes a long-term reservoir scheduling model and medium-term and short-term reservoir operation planning models [
11,
12]. Of these, the long-term scheduling model is the main tool for creating annual power generation plans for hydropower plants. It is generally considered the most valuable planning tool since it provides technical support for the hydropower plant to achieve the goal of maximizing hydropower generation [
13,
14]. The long-term reservoir schedule model is intended to maximize the hydropower over an extended period of time and typically has a planning horizon of one year or more [
15]. The problem with a schedule of such long duration lies in its stochastic nature arising from the non deterministic inflow from the river [
16]. The medium-term model serves as a link between the long- and the short-term scheduling models, a means of transforming results from the long-term scheduling process to a form suitable for giving correct input to the short-term scheduling process [
17]. The medium-term model should have a sufficient number of time increments to support the short-term scheduling [
18]. The short-term scheduling is solved as a deterministic problem and is carried out for the purpose of operating the hydropower system economically [
19,
20]. Ideally, the longer-term models could dynamically supply boundary conditions for the models with shorter time horizons in a real-time manner [
21,
22].
The use of accurate forecasts to optimize reservoir operations can increase the power generated by hydropower plants [
23], but this requires the rainfall/runoff forecasts to be of high accuracy and to cover a rather long period [
24]. In recent years, forecasting technology has been continuously improving and has achieved fruitful results in improving the accuracy of runoff forecasts and in extending the forecast period [
25]. The United States’ Global Forecast System (GFS) and the China Meteorological Administration’s T213 model can release precipitation forecast information for the following 10 to 15 days on a rolling basis [
26]; the Global Spectral Model (GSM) of the Japan Meteorological Agency (JMA) is capable of releasing deterministic meteorological forecasts for the following 8 days with a spatial resolution of 125 km [
27]; and the European Centre for Medium-Range Weather Forecasts (ECMWF) is capable of releasing definitive forecasts and ensemble forecasts of future weather conditions for a 15-day period [
28]. At present, the accuracy of medium-term and short-term forecasts has reached levels suitable for industrial utilization, and these are the forecasts that have been used for planning reservoir operations [
29]. Medium-term forecasts are applied in medium-term reservoir operation planning, such as the generation plan covering a week (or 10 days), whereas short-term forecasts are used in short-term decision making, such as determining the daily release levels [
30]. However, the optimization of the long-term reservoir scheduling scheme has greater potential for improving the power generation benefits of a hydropower plant than that of medium-term and short-term reservoir operation plans [
31]. The predicament of current reservoir forecast scheduling is this: short- and medium-term forecasts are reliable but have a limited forecast horizon, ranging from several hours to a few days [
32], whereas long-term forecasts have horizons of several months but suffer from large uncertainties [
33]. Taken together, the forecast uncertainties are the main factor hindering the development of forecast-based reservoir operation.
Various efforts related to forecast-based reservoir operation have been devoted to dealing with uncertainties that lead to loss of profit and additional operational tasks [
34,
35]. However, these studies are still far from actual application. Stojkovic et al. [
36] analyzed the variability of the rainfall/runoff process over both long-term and short-term periods. Maurer and Lettenmaier [
37,
38] evaluated the effects of long-term forecast uncertainties and demonstrated an increase in hydropower profit from an improvement in the long-term forecast. Zhao et al. [
39] investigated the joint and respective effects of long- and short-term forecast uncertainties on reservoir operation and proposed a strategy to reduce potential risks in the decision-making processes. More recently, increasing attention has been paid to adaptive reservoir operation, which enables the operational control system to respond quickly to unexpected risks. Zhang et al. [
40] proposed an approach for deriving adaptive operating rules that consider both historical information and future projections, namely historical and future operating rules (HAFOR). Vonk et al. [
41] used a scenario-based approach to explore the effects of various likely degrees of runoff changes for the future period and further extracted optimal reservoir operating rules through the Water Evaluation and Planning system (WEAP) water allocation model interlinked with Non-dominated Sorting Genetic Algorithm II (NSGA-II). Adaptive management may be a promising approach for effectively guiding reservoir operations, but the operational control models need to be further proved and tested on real-world cases.
Power head utilization planning and the phased control of reservoir water levels during the scheduling period have a significant impact on power generation [
42,
43], especially for hydropower plants with large storage and high regulation capacity [
44]; the controls for the reservoir releases and the power generation water head of a hydropower plant are essentials for maximizing the power generation of the plants. Owing to limitations on forecast accuracy and the length of the forecast period, there is no guarantee that a reservoir operation plan that is developed will be the optimal one [
45]. We need to correct it in a real-time manner according to feedback. To be specific, the reservoir operation plan is meant to be modified using the differences between the expected and the actual conditions. In fact, only in this way can the effective connection of long-term, medium-term, and short-term optimized scheduling schemes be ensured. However, nested long-term/medium-term/short-term reservoir operation planning is a spatial and temporal continuous multistage decision-making process with complex constraints, in which the dimensionality of the decision variables is dependent on the number of reservoirs and on the temporal decision-making interval [
46]. For example, the Three Gorges (TG) reservoir in the Three Gorges–Gezhouba (TG-GZB) cascade has the capacity for quarterly regulation. With a one-year scheduling period and a one-day cyclical time interval, the number of decision variables will reach over a thousand if the GZB reservoir is considered for nested long-/medium-/short-term reservoir operation planning. With a scheduling period of 1h (or 15 min), the number of decision variables will reach tens of thousands. The “curse of dimensionality” is unavoidable for these cases [
47,
48].
Even today, it is still a challenge to avoid the curse of dimensionality resulting from attempting to optimize the reservoir operations. In general, there are two kinds of algorithms for solving the optimization problem for reservoir scheduling, which typically has high dimensionality and nonlinear characteristics. One kind uses classical mathematical programming methods, such as nonlinear programming (NP), dynamic programming (DP), and progressive optimization; these have been widely used with relatively simple models and constraints [
49,
50], with which it is difficult to deal with the curse of dimensionality. The other kind uses artificial and computational intelligence approaches, such as the genetic algorithm (GA) [
51,
52], artificial neural networks [
53], particle swarm optimization [
54], the culture algorithm [
55,
56], and others [
57,
58]. These approaches are based on random probability search mechanisms and do not limit the characteristics of the optimization problem, and thus they have excellent potential for handling high-dimensionality cases [
59]. Nevertheless, the solutions of the artificial and computational intelligence approaches are generally inferior to those of classical mathematical programming methods [
60].
The Chinese TG-GZB cascade is formed by two giant hydropower plants unique in the world, the TG plant, with the largest installed capacity of any hydropower plant in the world, and the GZB plant, having the largest runoff of any hydropower plant in the world [
61]. The two hydropower plants have very close hydraulic and electrical connections [
62]. The TG and GZB reservoirs are all located in the main stream of the Yangtze River with a distance of only 38 km between them, and in addition, the power generated by these two plants is under the administration of the State Grid Corporation of China. There is no question that the operation of the two projects is of considerable significance both for the efficient development and utilization of water resources in the Yangtze River catchment and for the stable operation of the entire power system of China [
63,
64]. In particular, the installed capacity for these two hydropower plants is enormous; a slight change in the power generation head of the reservoirs can have a huge impact on the power generation of the plants [
65]. At the same time, the immense size of the two projects poses significant difficulties for the optimal operation of the reservoirs. To be specific, the giant reservoir has a large reservoir capacity and can hold a relatively high water head for power generation, resulting in an operable space much larger than that of small- or medium-size reservoirs. However, this leads to considerable difficulties in operation because there is such a large range from which to choose an optimal operation curve [
66]. Prior to the completion of the present study, the TG and GZB reservoirs had to be scheduled to operate conservatively [
67], an approach that fails to take advantage of the long-term forecast. In order to cope with a possible drastic decrease in reservoir inflow in later stages, the reservoir tends to hold more water rather than release it for power generation during the early stage of the non-flood season. Under this approach, the hydropower plant is operated to meet the guaranteed minimum output required by the State Grid Corporation of China [
68]. However, when flood season approaches, the reservoir water level needs to be rapidly dropped to below the flood control level in order to defend against possible catchment floods [
69]. This rapid transformation in reservoir operation often results in the abandonment of a large amount of water and thus a huge loss of power generation benefits [
70].
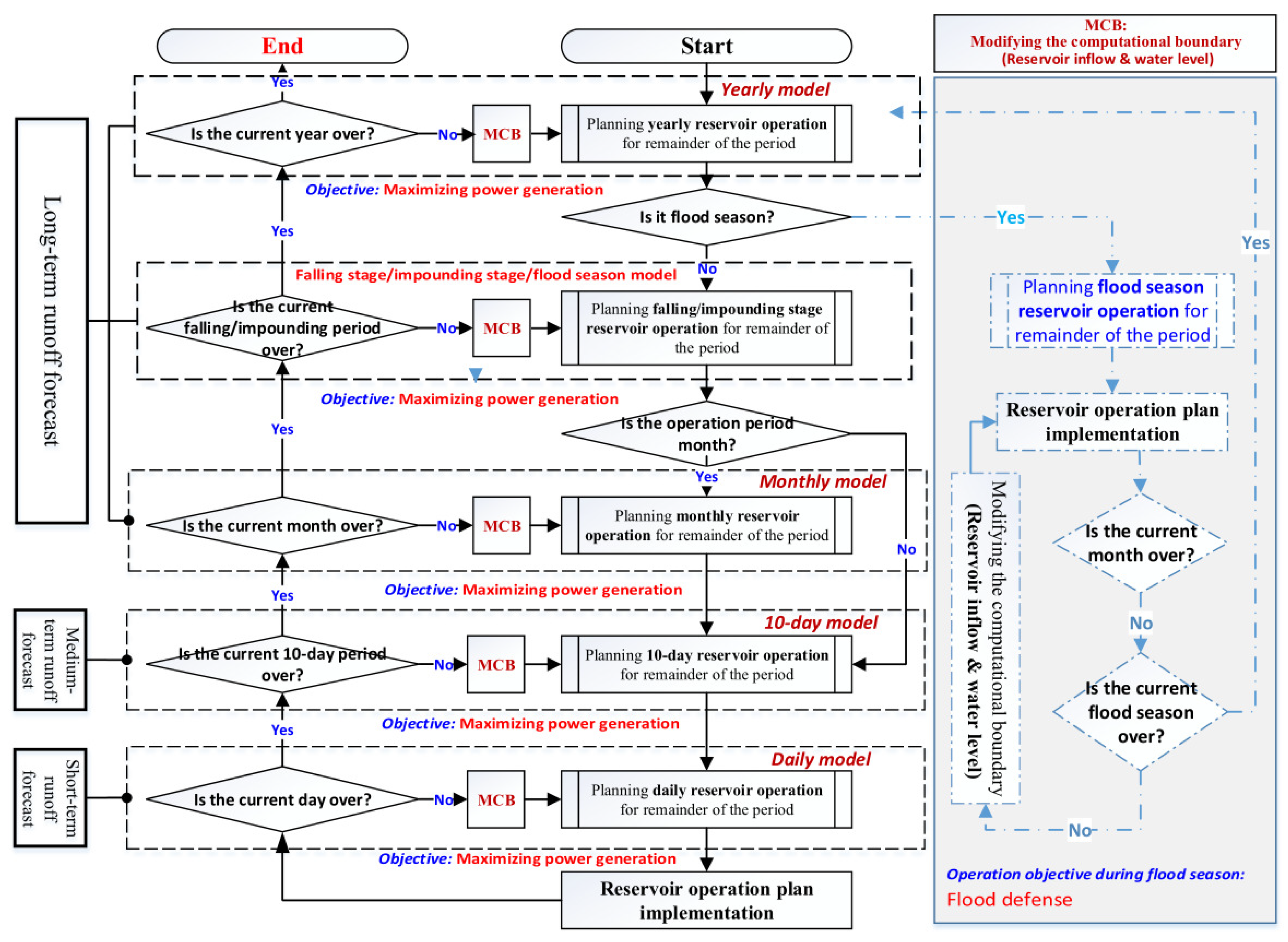
In order to provide technical support for the operation of the TG-GZB cascade, an R & D team led by the authors carried out research on the adaptive scheduling of giant cascade reservoirs. It took the authors more than five years to manage the problem and establish a nested framework for the coupling of optimal reservoir scheduling models with multiple time scales. Furthermore, the authors proposed an effective approach to the nested optimal reservoir scheduling model for overcoming computation failure caused by the curse of dimensionality. On this basis, the authors presided over the development of China’s TG-GZB CSCS, in which the nested long-term/medium-term/short-term reservoir scheduling model is deployed.
The contribution of this paper is to present a credible approach for developing an automated reservoir operation system, in which dynamic correction of the long-term scheduling scheme and the medium-term and short-term reservoir operation plans is achieved. To the best knowledge of the authors, China is the first country to propose nested long-term/medium-term/short-term reservoir schedule modeling and to have deployed the complete set of models in the business system of a cascade reservoir operation.
The rest of this paper is organized as follows:
Section 2 provides an overview of forecast-based reservoir scheduling technologies and their development;
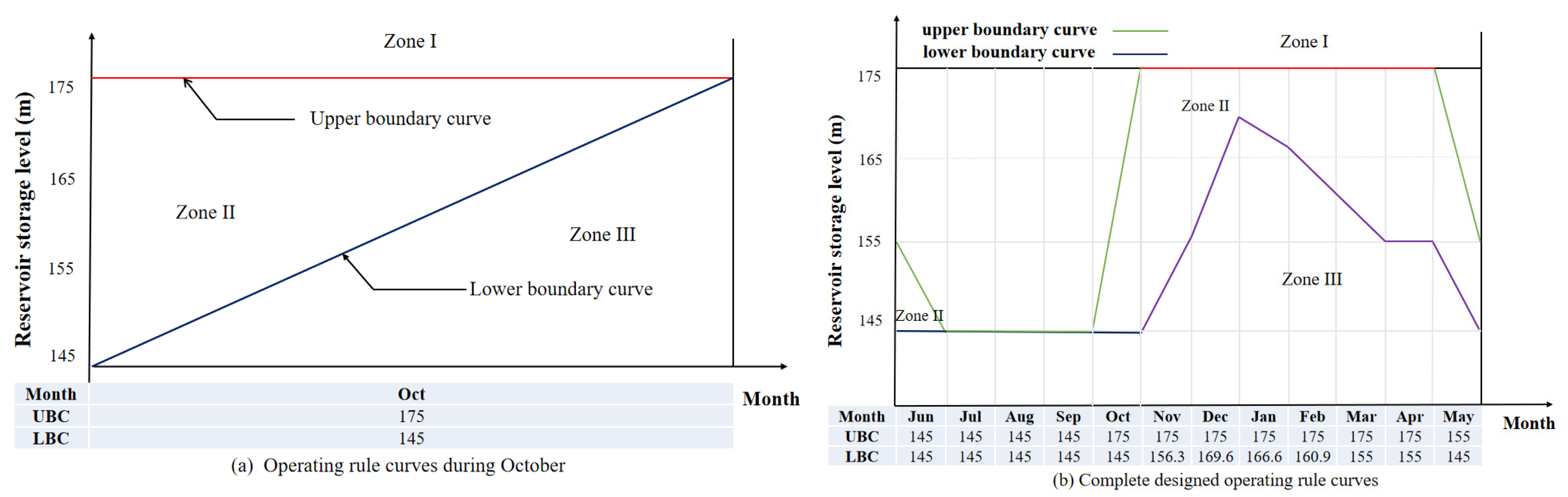
Section 3 outlines the TG-GZB cascade and reservoir operating rule curves.
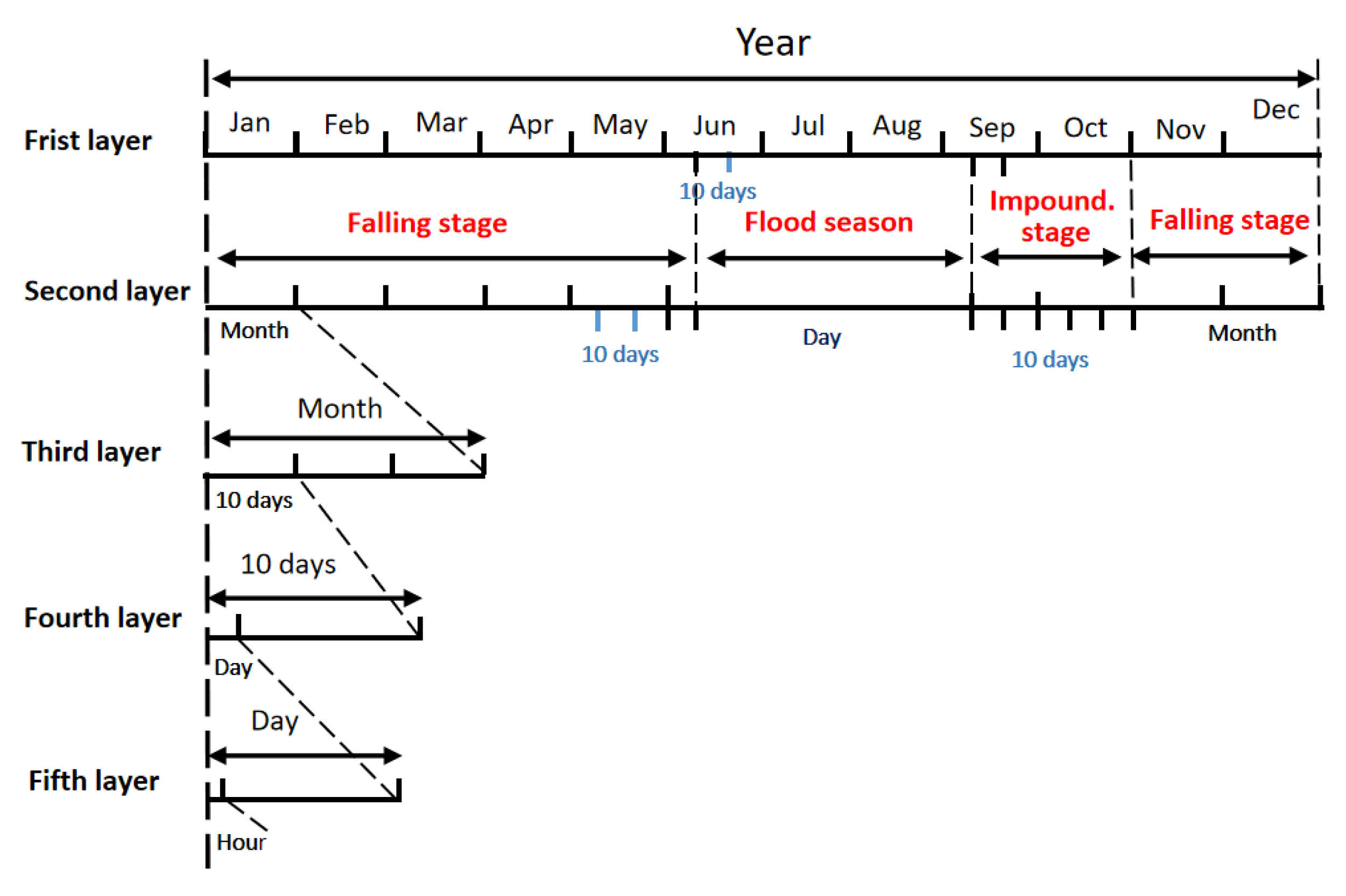
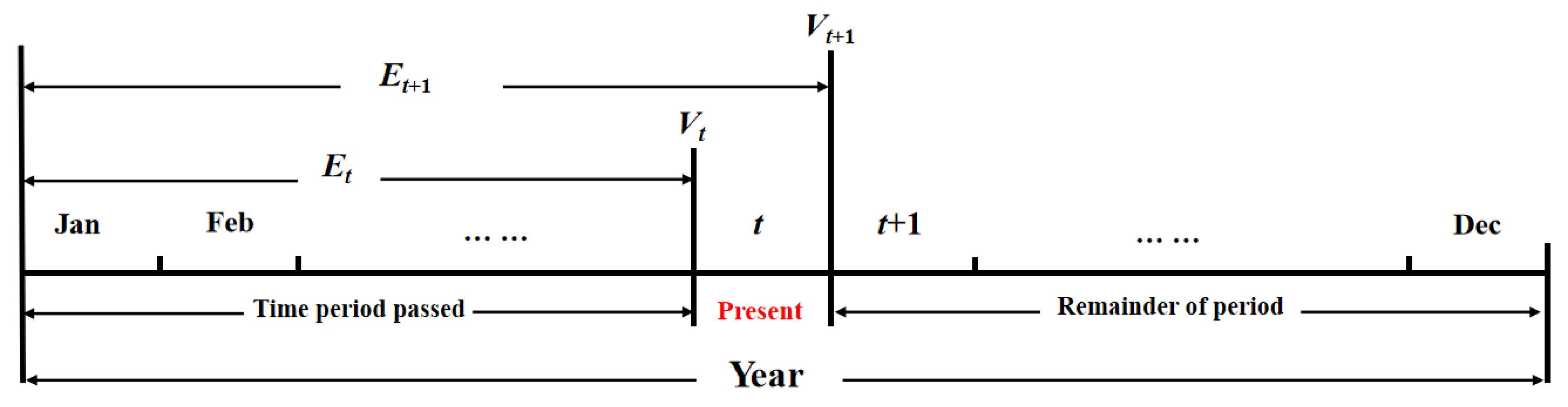
Section 4 is the key part of this paper, introducing the overall technical framework, models, and algorithms used in this study.
Section 5 analyzes the performance of the improved algorithm and gives an example applying the multiple-time-scale nested optimized-scheduling model.
Section 6 summarizes the paper.
2. Forecast-Based Reservoir Operation: A Review
The main work of reservoir operation includes the following tasks: formulating the reservoir scheduling method, preparing the reservoir scheduling plan and determining the various control indicators of the reservoirs, and controlling the reservoir operation in real time. Morozov provided a method to maximize power generation through phased water-level control in reservoirs, and this reservoir operation method and phased water-level control concept gradually developed into the present reservoir operating rule curves [
71,
72]. Almost all large and medium-sized reservoirs around the world have their own reservoir operating rule curves, and some have also developed an annual scheduling scheme and monthly (or biweekly) and daily operation plans based on the operating rule curves [
73]. Shahryar Khalique Ahmad et al. [
74] presents a forecast-informed optimization method for a multiple dam network considering long and short-time scales. With the development of optimized reservoir operation, the guarantee target for reservoir operation has also gradually shifted from single-target scheduling to multi-target comprehensive utilization scheduling and from single-reservoir operation to the cooperative operation of cascade reservoirs.
At present, forecasts for reservoir scheduling include long-term forecasts and medium- and short-term forecasts. Long-term forecasts are the basis for developing non-flood-season scheduling schemes for reservoirs undertaking comprehensive utilization tasks such as water supply, irrigation, and hydroelectric generation.Turner et al. [
75] presented a complex relationship between seasonal streamflow forecast skill and value in reservoir operations. Cassagnole et al. [
76] showed us the impact of the quality of hydrological forecasts on the management and revenue of hydroelectric reservoirs. In China, the reservoir operating rule curves are generally used in combination with long-term forecasts for the preparation of the non-flood-season reservoir scheduling schemes. The long-term forecast-based reservoir operation mainly consists of estimating non-flood-season reservoir benefits (total water supply, total power generation), forecasting the reservoir water levels for key time nodes, preparing scheduling schemes, and arranging the timing for equipment maintenance. By the end of the flood season, these reservoirs will have made quantitative predictions of reservoir runoff, and during the non-flood season, they will allocate processes from the end of the flood season to the following flood season based on the current impoundment of reservoirs and the meteorological and hydrological forecasts, taking into account the statistical laws governing the multi-annual runoff and its influencing factors and calculating the total amount of water available for the period. The results of these calculations are the main reference used in preparing non-flood-season scheduling schemes.
The medium- and short-term forecasts are important references for the preparation of reservoir operation plans during flood season. The main forecast-based medium-/short-term reservoir operations are the following: (1) Increasing reservoir flood control capacity. That is, in the early stages of a flood, a reservoir increases its discharge in order to vacate reservoir capacity. This action can significantly increase the flood control capacity of the reservoir, thus ensuring the safety of the reservoir and the downstream river channel, and reduce the amount of abandoned water as well. (2) Intentionally storing floodwater. Before the end of a flood, the reservoir will close the flood sluice in advance provided that the medium-/short-term forecasts are accurate. This action increases water head for power generation in later periods.
Reservoir scheduling based on meteorological forecasts and hydrological forecasts has high uncertainty due mainly to the nondeterministic nature of future rainfall and runoff. This kind of uncertainty has a more significant negative impact on long-term forecast-based reservoir operation. Nevertheless, long-term forecast-based reservoir operation is more effective in promoting the economic benefits of cascade hydropower plants than that of reservoir operation based on medium- and short-term forecasts. There is a pressing need to incorporate a guiding role for long-term scheduling schemes in short-term and medium-term reservoir operation plans. The authors believe that under the status quo of the science and technology of meteorological and hydrological forecasting, the most feasible approach is to build a nested reservoir operation model system covering long-term, medium-term, and short-term scheduling periods.
6. Conclusions
In this paper, the authors have put forward a nested modeling approach of long-term, medium-term, and short-term reservoir scheduling models. Under this framework, an adaptive strategy for reservoir scheduling can be achieved. In particular, based on the actual needs of the scheduling operation of the TG-GZB cascade reservoirs, this study established a five-tier optimized-scheduling model for nesting the long-term, medium-term, and short-term schedules t. The time interval of the scheduling plan prepared by the model can be as short as 15 min, meeting the real-time scheduling requirements of CSCS. In addition, in this study, some practical and efficient solution algorithms were developed to suit the characteristics of the scheduling model, including the CIMAR-IDP algorithm as well as the IGA.
More importantly, this paper presents a comprehensive introduction to all of the solution algorithms that have ever been used in the CSCS. IDP was the approach used during the trial run period of the CSCS for the TG-GZB cascade; during the trial run, intended to explore the characteristics of the TG-GZB cascade reservoirs, the authors made continual improvements to the algorithm and learned much from the in-depth experience acquired thereby. On that basis, the authors then developed CIMAR-IDP. This solution method resolves most of the problems faced by DP and its improved version. However, during scheduling of the reservoir operation, the authors found some remaining shortcomings with this solution method. For some complex problems, it takes too long to reach a solution, and sometimes it will also cause the curse of dimensionality, with the result that the problem involved cannot be solved. To overcome these problems, the authors proposed the use of GA and improved it (IGA) so that could be applied in practice. At present, IGA and CIMAR-IDP are both used in the scheduling platform. In the preparation of the actual scheduling scheme, the scheduling is first performed according to the IGA results. After the scheduling scheme has been generated from the later CIMAR-IDP algorithm, adjustments are made on the basis of the results of the later calculations. This method ensures that an effective scheduling scheme can be automatically generated by the scheduling model regardless of the working conditions.
In summary, the research content introduced in this paper is the core model and algorithm used in the TG-GZB CSCS. The featured contribution of this study is that the model and solution algorithms we developed have been applied in practice. Our proposed approaches have been implemented for the reservoir operation of the TG-GZB cascade, which proved that the methods and algorithms proposed in this study could be of benefit for use in other cascade reservoir scheduling systems.