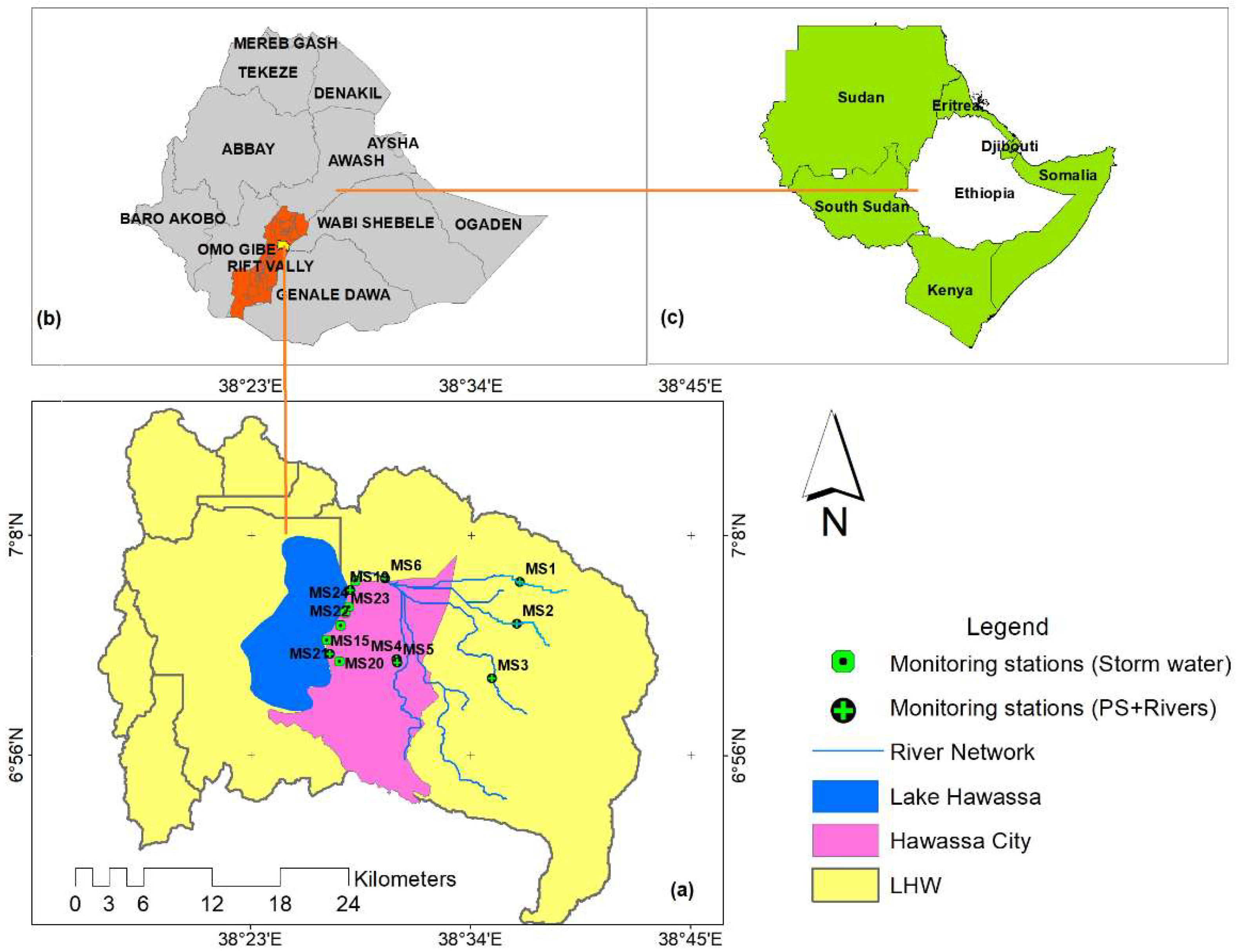
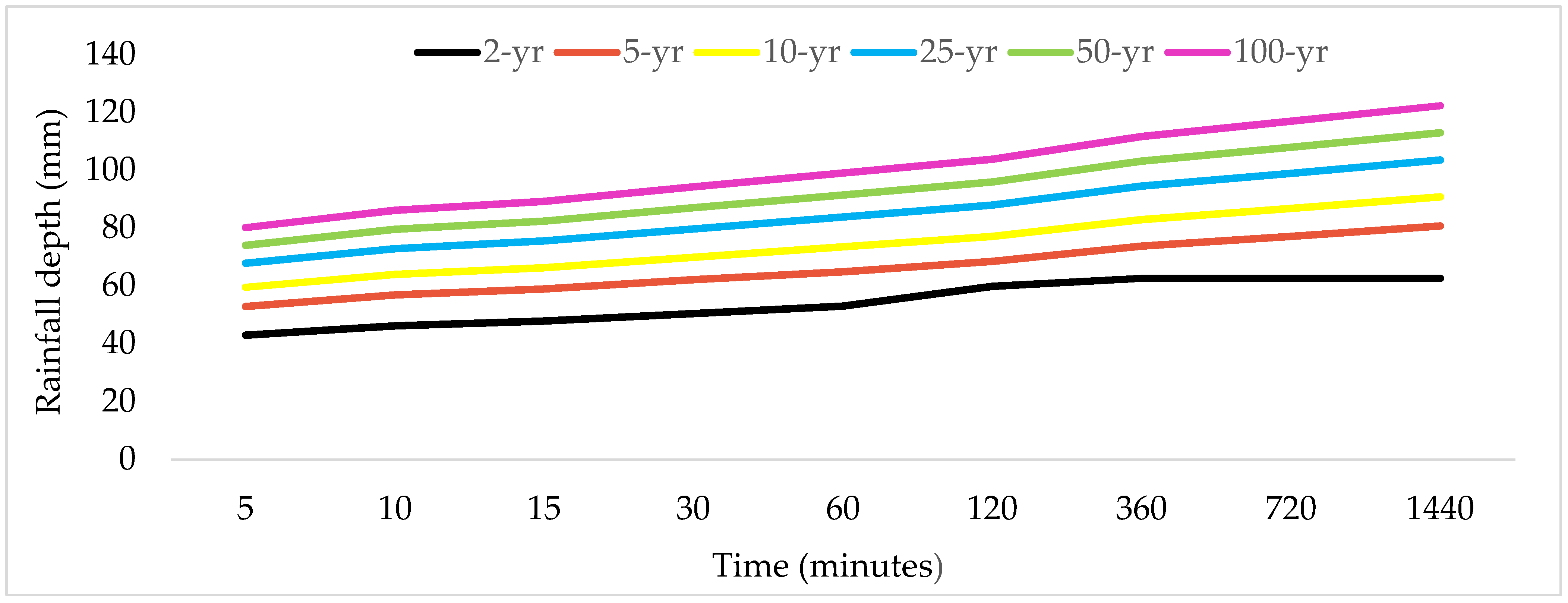1. Introduction
Currently due to the rapid advances in modelling, numerous water quality models were developed with various modelling algorithms for various land use and water bodies for pollutants at different spatio-temporal scales [
1,
2]. The data demand for water quality models increase with the complexity and scope of application [
3].
Generally, most developed countries, namely the US or European countries have established better and advanced surface water quality models [
2]. One of pivotal factors in the primary goals of environmental management would be assessing the water quality despite limited observations [
4]. In the developing world reliable application of water quality models is often challenging owing to lack of sufficient and quality data and access to patented software is limited by finances. Furthermore, nearly for all rivers the gauged data are limited and fragmented. The Rift Valley Lake basin is among the data scarce areas of Ethiopia and the historical measured pollutant flux including sediment data is very limited [
5,
6]. In Hawassa, on the other hand, wastewater management is a big concern because most residents use latrines. Wastewater treatment plants for the partly existing sewer system for buildings with flushing systems is missing [
7] and stormwater is discharged without any treatment. Furthermore, Lake Hawassa is encircled by agricultural land, residential places, industrial and commercial hubs and is located near the city of Hawassa. As a result, it is prone to a range of environmental risks and the water quality deteriorates over time, posing a danger to the biodiversity [
8]. Hence, studying the pollutant load of the basin is necessary to obtain more realistic information [
5].
The estimation of pollutants load from non-point sources is usually accomplished by means of watershed models. However, due to the intensive input data requirements and complexity by most of the models, it is disconcerting to quantify diffuse source loads in developing countries such as Ethiopia owing to limited hydrological, meteorological and water quality data [
9,
10].
In order to fulfil the existing gaps in the developing world such as Ethiopia, setting up frequent monitoring and assessment is a critical task. In this sense, simple models that do not require intensive input datasets are worthwhile common approaches for the prediction of diffuse pollutions from various land uses including urban and industrial land uses [
11,
12,
13].
On such occasion, a common approach such as pollutant export coefficients representing the rate of pollutant loadings by land area, that predict an annual load from land to water, are often a discretionary means to estimate loadings from non-point sources [
6,
14,
15]. Export coefficients modelling is a simple approach that can be adopted for data-poor areas and for preliminary assessments connecting land use to water quality. It is generally based on the postulation that a particular land use will export distinctive magnitudes of pollutants to a downstream water body on a yearly basis [
16]. To justify this postulation, the pollutant export coefficients must be developed for the locally specific conditions [
15]. If this is achieved, reliable and relatively accurate pollutant transport models can be set up to support watershed level point and nonpoint source pollution management [
17].
Therefore, in this study we employed pollutant loading estimator (PLOAD) to determine the pollution loads with the help of export coefficient modelling. The approach was used as a means of preliminary pollutant load estimation at different watersheds in Ethiopia [
6,
9], Tanzania [
18], China [
10,
19], USA [
20], Japan [
15], UK [
12], Lithuania [
21], Egypt [
22], Philippines [
23] and Rwanda [
24].
The watershed of lake Hawassa comprises rural and urban areas. So, for conducting a comprehensive pollutant flux in the watershed, pollutant flux of (i) rivers, (ii) point sources (PS) and (iii) urban stormwater runoff have to be investigated. Namely the impact of stormwater runoff has so far not been addressed and requires a deeper investigation. A prerequisite for this is a reliable runoff information at watershed scale. In recent decades a number of hydrological models have been developed and used to envisage the runoff information in different hydrological units over years. A widely used approach to estimate runoff from spatial data is the Soil Conservation Service curve number (SCS-CN) method [
25,
26]. In this study, we also applied the SCS-CN method to estimate rainfall-runoff depth for the city of Hawassa.
A characteristic problem in the watershed under investigation is the lack of sufficient monitoring water quality data due to budget constraint. This complicates prediction of pollutant loads from point and non-point sources, as land use, emissions and ambient water quality cannot be linked directly. Currently the government focuses on the reduction in the point source pollution. However, estimation of pollutant flux from nonpoint sources in data-limited watersheds in Ethiopia (in general and in the study area in particular) are perplexing, due to lack of baseline data to direct development targets. Thus, the use and identification of simple, cost effective and economical water quality models is greatly imperative to estimate the pollutant flux of rivers and point sources that are in turn helpful for surface water quality management. To support this target, this study is aimed at determining the annual pollutant loads contributions from point, nonpoint sources and stormwater to the Lake Hawassa watershed, identify the probable pollution flux hotspots and calibration of pollutant export coefficient for the study area by integrating PLOAD, SWAT, FLUX32, HEC-GeoHMS and SCS-CN with monitoring data.
3. Result and Discussion
3.1. Flow Simulation and Pollutants Flux in the LHW
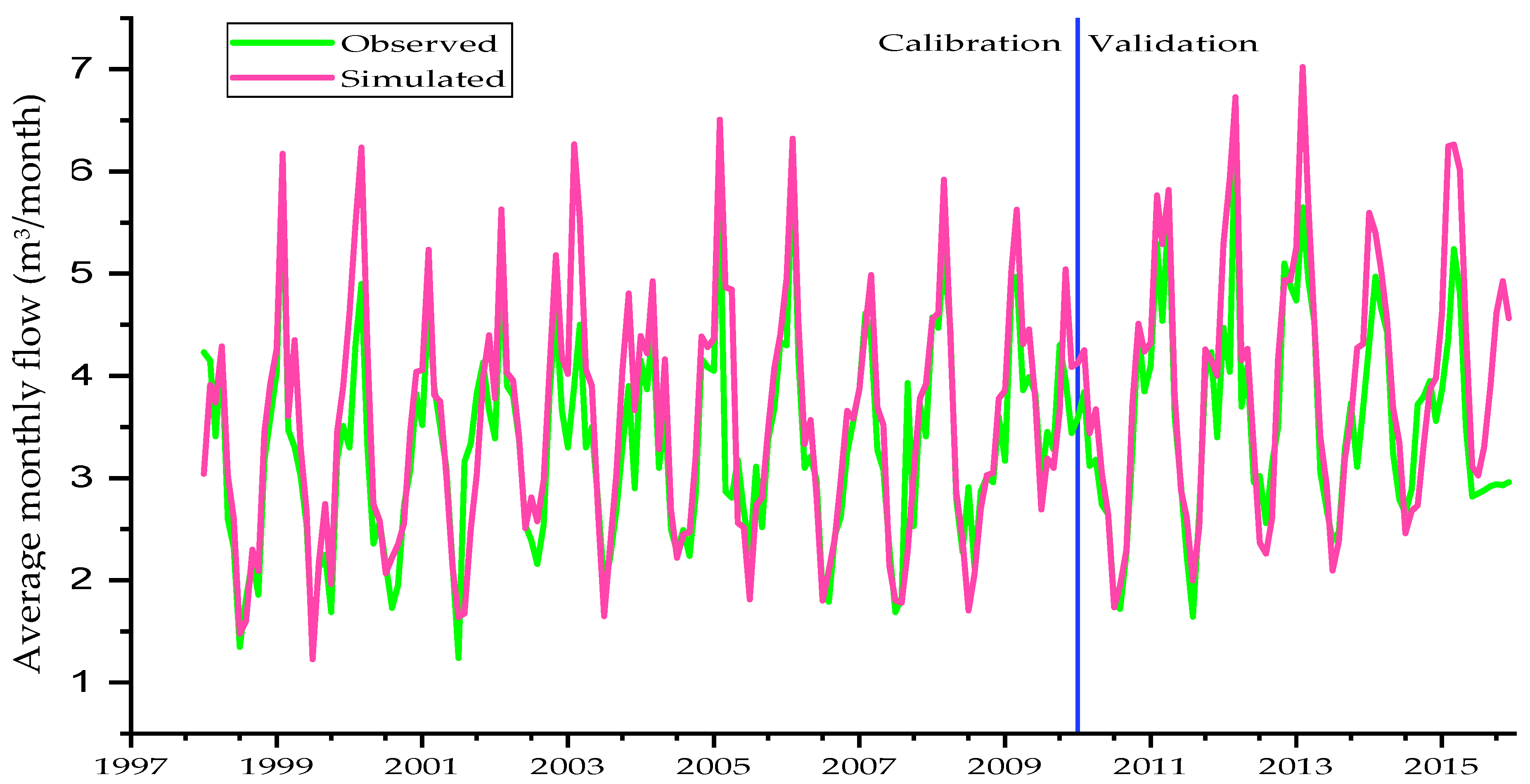
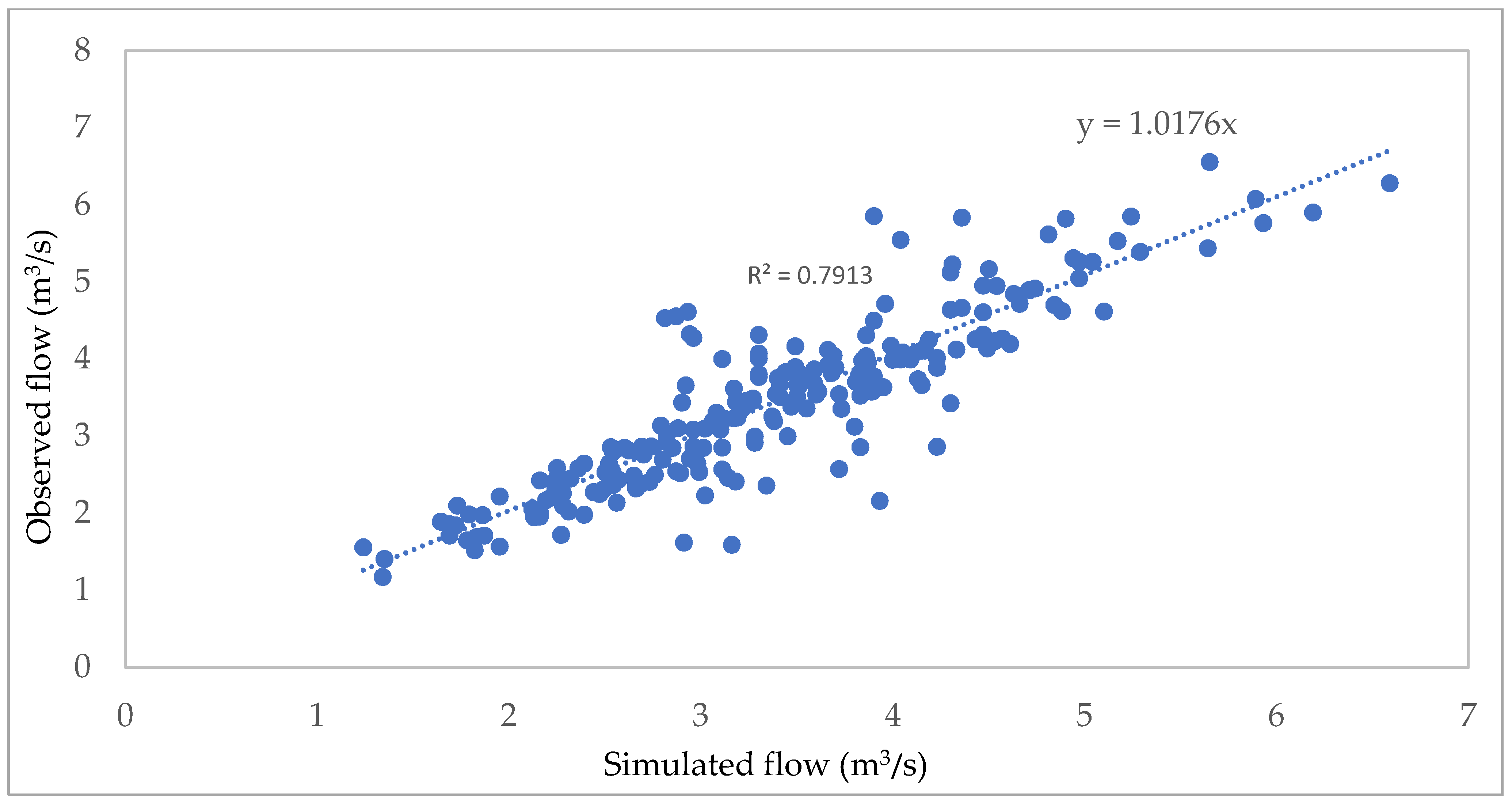
The SWAT model was calibrated in
Figure 3 and
Figure 4 having a coefficient of determination (R
2), Nash–Sutcliffe efficiency (NSE), mean percentage error, mean absolute percentage error and percent bias (PBIAS) values of 0.8, 0.76, 0.69, 10.3 and −11.6 during calibration and 0.8, 0.76, 3.9, 11.6 and −3.9 during validation, respectively. The goodness of fit (R
2, NSE, MPE, MAPE and PBIAS) was found to be very good indicating the performance of the model output for the intended purpose was acceptable. The model performance determined by the Nash-Sutcliff (NSE) was 0.8 during calibration and validation in the study area, which is good for interpreting the model output [
5]. Similar results were reported elsewhere [
88,
89,
90] for the model simulation and observation.
The SWAT generated flow at sub-catchment outlet was used to calculate the load in FLUX32. Accordingly, the flow-weighted concentration calculated by method 6 (Equation (4)) was less than 0.2 of all other methods in FLUX32. The residual plot of bias for flow, date and month at each sub-basin outlet in LHW was in the range of 0–0.05, indicating it is acceptable. Similarly, the plot of slope significance was in the range of 0.8–0.99. The recommended coefficient of variation (CV) is in the range of 0–0.2 during flow-weighted load calculation and it is in the range of 0–0.058, showing surprisingly good performance of FLUX32 in the watershed under investigation (
Table 7).
Similar trends were also reported by Angello et al. [
9] and Belachew et al. [
6] in Ethiopia for FLUX32 program simulation performance indicators.
3.2. Calibration of the PLOAD Model
Pollutant loads estimated via selected export coefficients (
Table 6) by employing the PLOAD model was used as an initial estimate, whilst loads calculated with FLUX32 at selected sub-basin outlets (monitoring stations) in LHW were used for the PLOAD model calibration. During calibration of PLOAD in Excel Solver, the export coefficients were used as independent variables, and their range of values were considered as constraints to set the upper and lower bounds based on the literature during optimization.
Accordingly, at the initial stage of calibration or pre-optimization, the total percentage error between the model predicted and measured load at all monitoring stations for the investigated pollutant parameters are presented in
Table 8. The PLOAD prediction for the COD, BOD
5 and PO
4-P were already relatively accurate before calibration and could be further improved. In contrast, the total relative errors of PLOAD predictions at all monitoring stations for TDS, TN, TP and NOx before optimization were in the order of hundreds or thousands of magnitudes. By optimizing the export coefficients using the solver function, the model error could be reduced considerably.
Still, the PLOAD model underestimated the TDS load at Wedessa (MS3) and Wesha sub-basin (MS1) which are located at the upstream portion of LHW, TN and NOx-N at Tikur-Wuha River catchment outlet (MS6). There is a general trend that the total error increases with the size of the sub-basin. Belachew et al. [
6] in Kombolcha catchment and Angello et al. [
9] in the Akaki River catchment, Ethiopia, have also come up with similar findings.
For COD, BOD
5, TP, and NOx, the export coefficients after optimization showed significant differences for urban, forest land, range land and cultivated land uses. Wetland, bare land and water bodies showed the least variance in pollutant loading, which could be attributable to decreased area coverage and EC contribution in the watershed. Angello et al. [
9] also found similar findings in the Akaki River in Ethiopia.
The pollutant loading estimator was also performed using the mean and median values obtained from the optimized export coefficients. At all monitoring stations, the overall percentage error between the model predicted and measured load was 123.83% for mean and 125.33% for median. Furthermore, the observed PLOAD prediction for both mean and median at monitoring stations demonstrated either an overestimation or underestimation of pollutant loads. As a result, the loads calculated using the mean and median ECs were left out of the equation. Consequently, area-specific ECs has been proven to be a useful technique for estimating pollutant loads in the LHW. For effective pollutant load estimations, Angello et al. [
9], Cheruiyot and Muhandiki [
91] and Shrestha et al. [
15] advised the use of area-specific and local ECs. The optimized EC’s values can be further used for effective management of the nonpoint source pollution in the Watershed. Likewise, the PLOAD was validated for a different data set without change in the optimized export coefficient and showed the model prediction is acceptable with a relatively smaller sum of total errors.
The calibrated pollutant ECs showed that the urban land use showed varying export coefficients as the pollutant loading rate for urban land use for COD, BOD
5, TDS, TP and NOx-N varied with location. The contributions of nonpoint sources among the various urban land uses, as well as the basin’s size, are responsible for the observed spatial differences in ECs (
Table 9).
The agricultural land use for the calibrated pollutant EC’s showed significant variations among monitoring stations. The contribution of pollutant loading rate for agricultural land for COD, BOD5, TDS TN and NOx-N demonstrated, the agricultural land use varies spatially in pollutant loading rate contribution. TP and PO4-P, on the other hand, have revealed a slight variation among the stations.
3.3. Pollutants Flux in LHW by Using PLOAD
The pollutant flux at each of the sub-basin outlets were calculated with the help of FLUX32. A similar approach was also followed by Angello et al. [
9], Belachew et al. [
6], Xin et al. [
92], Liu et al. [
56], Gurung et al. [
20], Lin and Kleiss, [
51], Edwards and Miller [
52] and Shen et al. [
10]. The estimated pollutant flux at each monitoring stations showed that the organic pollution contribution from the point and nonpoint sources prevailing in the study area, where the maximum COD and BOD
5 load was observed at MS6 with 4976.35 and 3543.54 t/y, respectively (
Table 10). This station was located downstream of the two-point sources (the BGI effluent discharge site and the Moha soft drinks factory), as well as receiving flow from the upper streams that make a confluence.
Furthermore, at the same monitoring station, the PO4-P, TN, TP and NOx-N loads were calculated, and the results revealed that the pollutant flux at MS6 (downstream) is greater than the rest of the catchment outlets at upper streams. This is because the land uses at MS6 monitoring stations are dominated by urban lands (large- and small-scale industries), followed by agricultural activities and residential settlements. This river section is highly polluted as most of the untreated household wastes, stormwater runoff from urban and rural areas and industrial effluents are discharged onto it.
The non-point source contribution, on the other hand, was well demonstrated at sub-basins of monitoring stations located in the upper catchment (MS1 to MS3) with the COD and BOD
5 load, as shown in
Table 10, indicating that the pollutant flux from non-point sources is significant even if no identified point sources were present. Moreover, the catchments were dominated by agricultural land uses with small urban areas. Similar findings were also reported by the studies conducted by Belachew et al. [
6] in Ethiopia and Jain et al. [
93] elsewhere. This could be due to relatively small flow and less anthropogenic influence in the upper catchment.
3.4. Pollutant Flux from Point Sources in Hawassa City
Saint George Brewery, BGI (MS4) and Moha soft drinks factory (MS5) have all discharged their effluents into a wetland that feeds the Tikur-Wuha River, which flows into Lake Hawassa. According to the findings of the study, as shown in
Table 11, both point sources contributed significant amounts of pollutant loads to the Tikur-Wuha River (MS6) on top of the non-point pollutant loads from the upper catchment that later joined Lake Hawassa.
On the other hand, Referral hospital and Hawassa Industrial Park were two of the point sources that release their effluents in to Lake Hawassa directly. Referral Hospital is the major known single source for pollutant load contribution to lake Hawassa. Additionally, it may threaten the lake by release of various hazardous substances and pollutants, which are not covered by the investigated parameters. Having known the impact of wastes, Hawassa University constructed a waste stabilization ponds (WSP’s) with the intention that the wastewater released are treated based on the discharge standards of the effluents into the water bodies. Nevertheless, the findings of the study revealed that the existing WSP’s is not efficient enough to treat the effluent with the desired treatment level as it contributes huge amount of pollutant loads into the lake. The hospital contributes 14.9 tons COD, 3.3 tons BOD
5, 2.1 tons TN, 93.9 tons TDS, 0.2 tons TP, 1.7 tons PO
4-P and 0.171 tons NOx-N annually. Additionally, Hawassa industrial park was designed initially to comply the zero-emission standard, with no pollutants discharged directly into the Lake. However, during the study periods, huge amounts of pollutants were discharged directly into the Lake as evidenced by personal observation and informal interview. The result on
Table 11 showed that Hawassa industrial park contributes COD, BOD
5, TN, TDS, TP, PO
4-P and NOx loads with their annual loads of 211.7, 53.7, 4.3, 287.4, 0.7, 3.6 and 0.51 tons, respectively.
3.5. Estimation of Rainfall Depth for the City of Hawassa
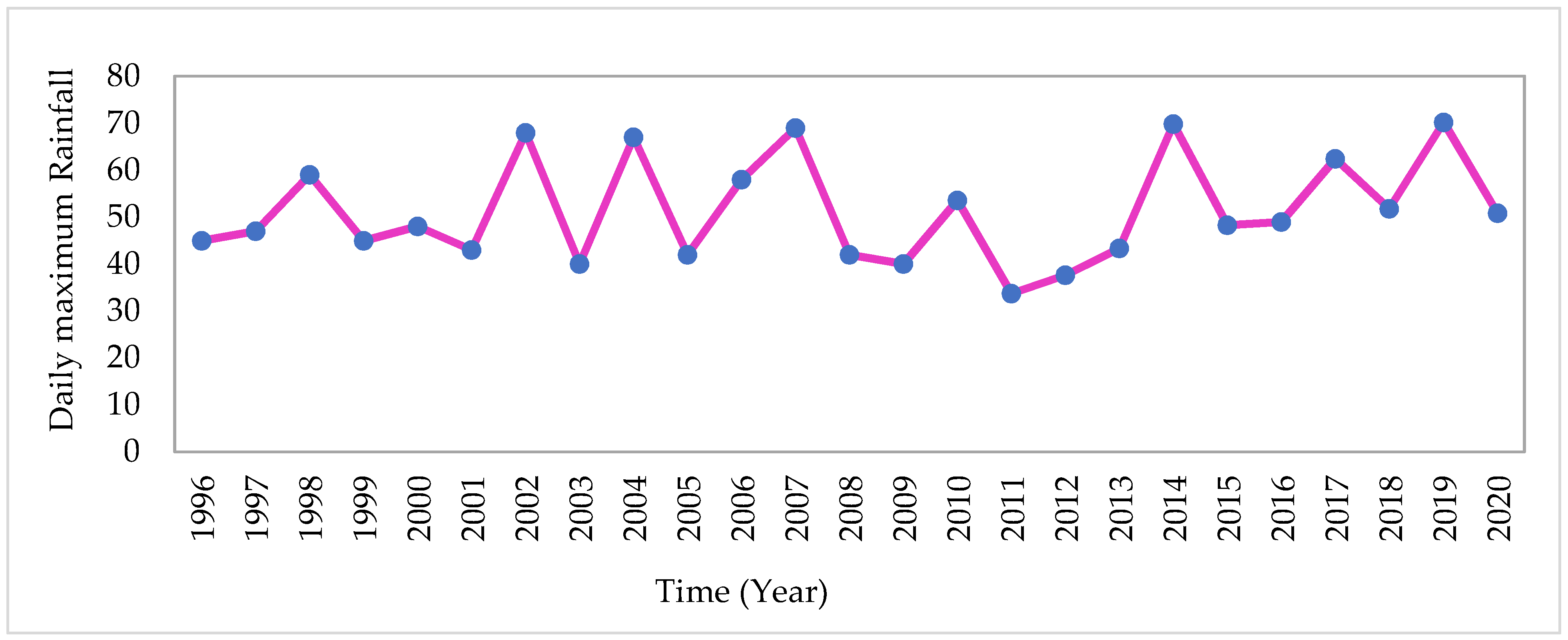
The daily maximum rainfall data for the year 1996 to 2020 (25 years) as shown in
Figure 5 was collected from the Ethiopian meteorology agency for Hawassa City.
The rainfall depth at different durations was plotted in
Figure 6 for short duration rainfall of 5, 10, 15, 30, 60, 120, 360, 720 and 1440 min for a return period of 5, 10, 25, 50 and 100 years by making use of Gumbel’s extreme value distribution and the empirical reduction formula. The rainfall frequency (mm) produced by the 24 h rainfall for 2-year return period (62.7 mm) was then used in the direct runoff determination by SCS-CN method. The obtained result of rainfall frequency of this study in Hawassa City is also in agreement to the intensity duration frequency developed by Ethiopian roads authority for the region containing Hawassa city [
66].
3.5.1. Estimation of Curve Number (CN) for the City of Hawassa
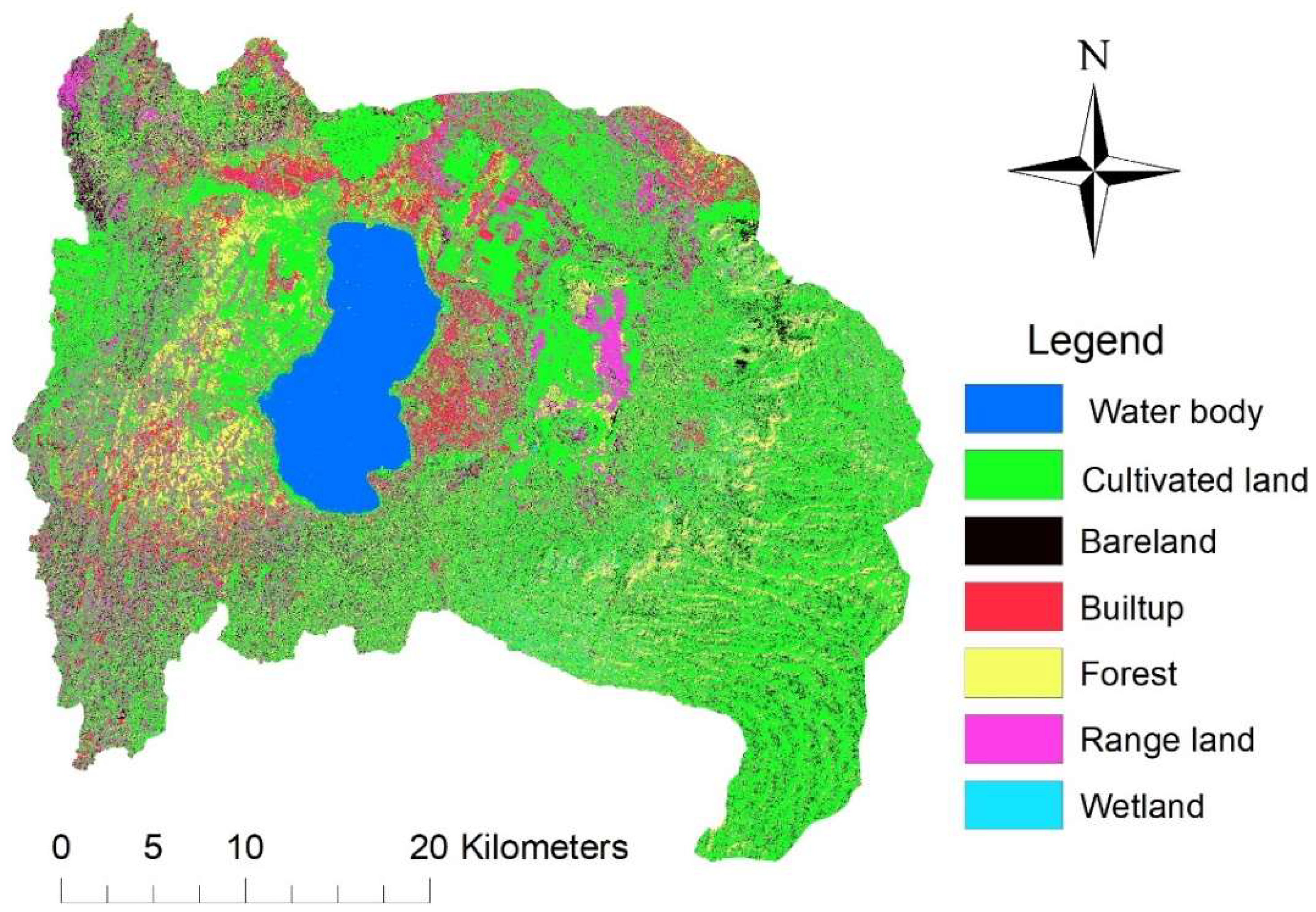
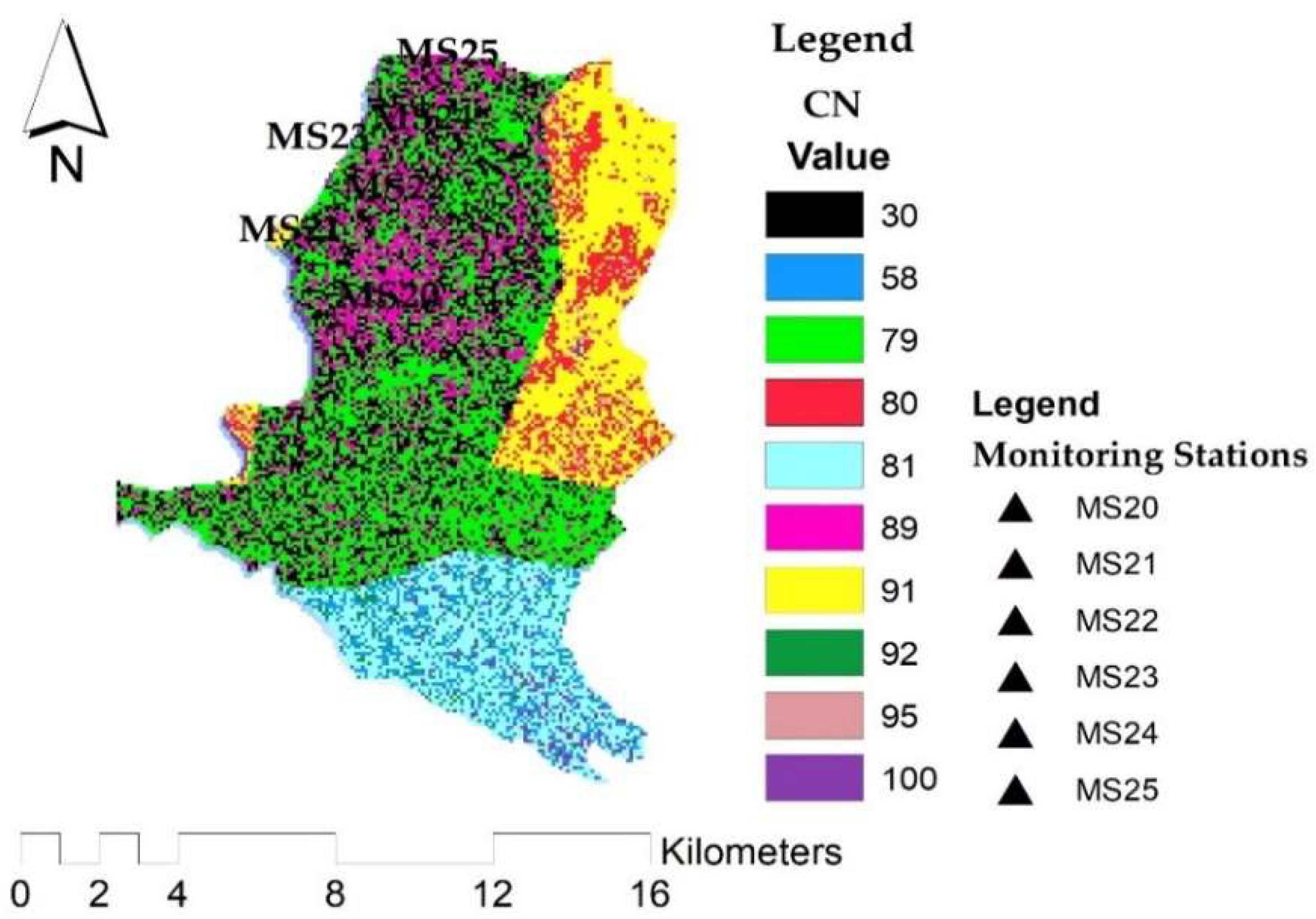
The soil layer, the digital elevation model and land use layers were clipped for Hawassa City. Thereafter, the land use of Hawassa City was reclassified, the hydrologic soil group maps and the land use layer were merged. The CNLookUp table was prepared for land use and sinks in DEM was filled. The land use map, soil hydrologic map and DEM of Hawassa City is shown below in
Figure 7.
Subsequently, the merged land use and hydrologic soil group maps, DEM and the CNLookUp table were combined to create the CN grid using HEC-GeoHMS following the procedures stated by Merwade [
87]. Accordingly, the curve number for monitoring stations in Hawassa City was obtained and used to estimate the runoff depth as shown in
Figure 8.
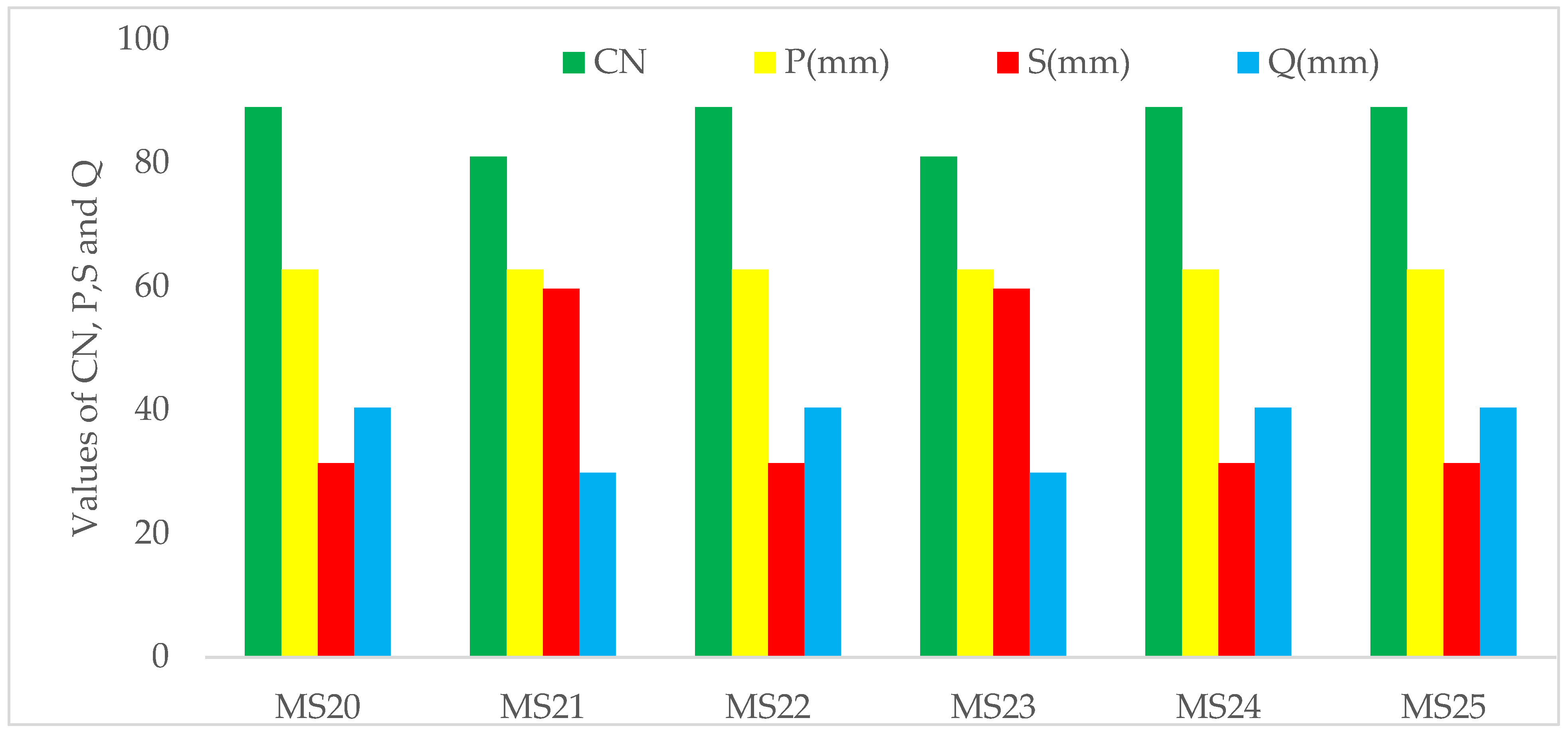
The result showed that the values of CN in Hawassa City ranged from 30–100 indicating high CNs (81–100) corresponding to the urbanized areas of the watershed which has the capability for producing the highest amount of runoff during a storm event. The CN values varies with the subtype of urban land use (i.e., residential, commercial, industrial). Whilst low curve numbers (30–77) corresponding to the forested and cultivated areas that generate little runoff due to high infiltration rate. The result of the study revealed that the CN ranged from 81 for MS21 and MS23 to 89 for MS20, MS22, MS24 and MS25.
3.5.2. Estimation of Runoff Depth for Hawassa City
The runoff depth (Q) can be estimated using Equation (15) based on the rainfall frequency produced by the 24-hr rainfall for a two-year return period (
Figure 6), curve number (
Figure 8) and maximum potential storage Equation (15). As a result, the direct runoff result for the corresponding monitoring stations is depicted in
Figure 9.
3.6. Stormwater Pollutant Flux in Hawassa City
The city of Hawassa has various urban catchments that can convey urban storm runoff with open storm drains and the urban runoff joins the lake at various outfalls. For selected parameters, the stormwater quality characteristics were determined and the results of concentrations of stormwater at monitoring stations were depicted in
Figure 10.
The findings of investigations were higher than that of Wondie [
93,
94], a study conducted in Bahir-dar city, despite the fact that Rădulescu et al. [
95] and Li et al. [
96] reported comparative findings in Romania and China, respectively. The annual pollutant loads (t/y) for selected physicochemical parameters for each monitoring outfall were estimated utilizing the catchment area (ha) and the corresponding direct runoff determined using the 24 h rainfall frequency (mm) for a two-year return period. As a result, the stormwater pollutant loads of selected physicochemical parameters in Hawassa City were tabulated in tons per year (
Table 12).
The most heavily contaminated site, according to this research, was MS20 (near Referral Hospital), which encompasses residential settlements, commercial centers and institutions (hotels, restaurants, cafeteria, hospitals). MS21 (near Amora-Gedel) and MS23 (near Chambalala Hotel) sites include residential settlements, businesses and commercial centers, all of which contribute significantly to pollution load. In the Amora-Gedel site, there are resort, hotels, cafeterias, a fish market, a recreation center and Gudumale, where the people of Sidama celebrate their new year festivities. Consequently, a considerable amount of pollutant load was released into the nearby lake during storm occurrences.
4. Conclusions
In this study, we applied a combination of various models (PLOAD, SWAT, FLUX32, HEC-GeoHMS and SCS-CN) with monitoring data to estimate the pollutant flux in the data-limited LHW. The chosen approach was effective in reckoning the annualized diffused source pollution load and is capable to estimate the impact of the spatially distributed emissions on the pollutant flux of receiving streams. It helps to identify the primary source of scattered pollution and provides an effective way for determining organic pollutants and nutrient loads in data-scarce areas.
Estimates of export coefficients from land use in Ethiopia is hardly common and there have been few previous experiences with estimating pollutant loads from the catchments. Thus, transformation of published export coefficients from other studies to characteristics of study area (land use, soil type, slope, climate) was made. In the catchments with no frequent data, estimation of pollutant flux with ECs involved uncertainties. However, the error can be significantly reduced by calibrating with monitored data. Generally, more detailed studies incorporating frequent monitoring of water quality and quantity for the main rivers are advisable to derive the land use specific pollutant loads that better conform to reality.
The estimated pollutant flux at each monitoring stations showed that the organic and nutrient pollutant contribution from the point and nonpoint sources prevailing in the study area, where the maximum pollutant loads were observed at Tikur-Wuha sub-catchments. This station was located downstream of the two-point sources and received flow from the upper streams where agricultural use is predominant. The integration of HEC-GeoHMS and SCS-CN with the catchment area enabled to determine stormwater pollution load of Hawassa City. Accordingly, Hawassa city has been identified as a key pollutant load driver, owing to increased impacts from clearly identified point sources and stormwater pollutant flux from major outfalls. Agricultural activities, on the other hand, cover a large portion of the catchment and are a considerable contributor to the overall load that reaches the lake. Thus, mitigation measures that are focused on pollutant flux reduction to the lake Hawassa have to target the urban and agricultural activities.