Assessment of Climate and Catchment Control on Drought Propagation in the Tekeze River Basin, Ethiopia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Basin
2.2. Data
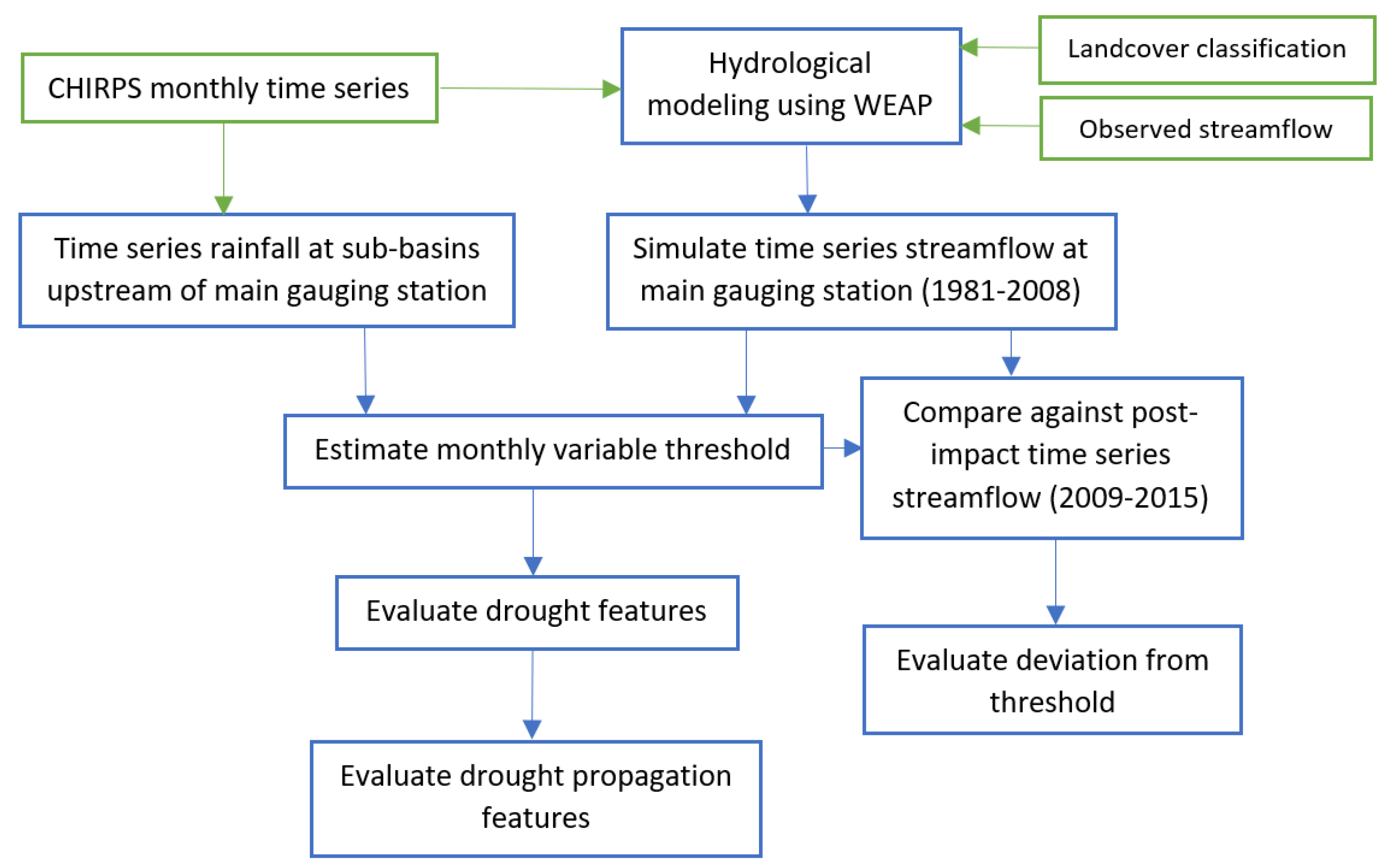
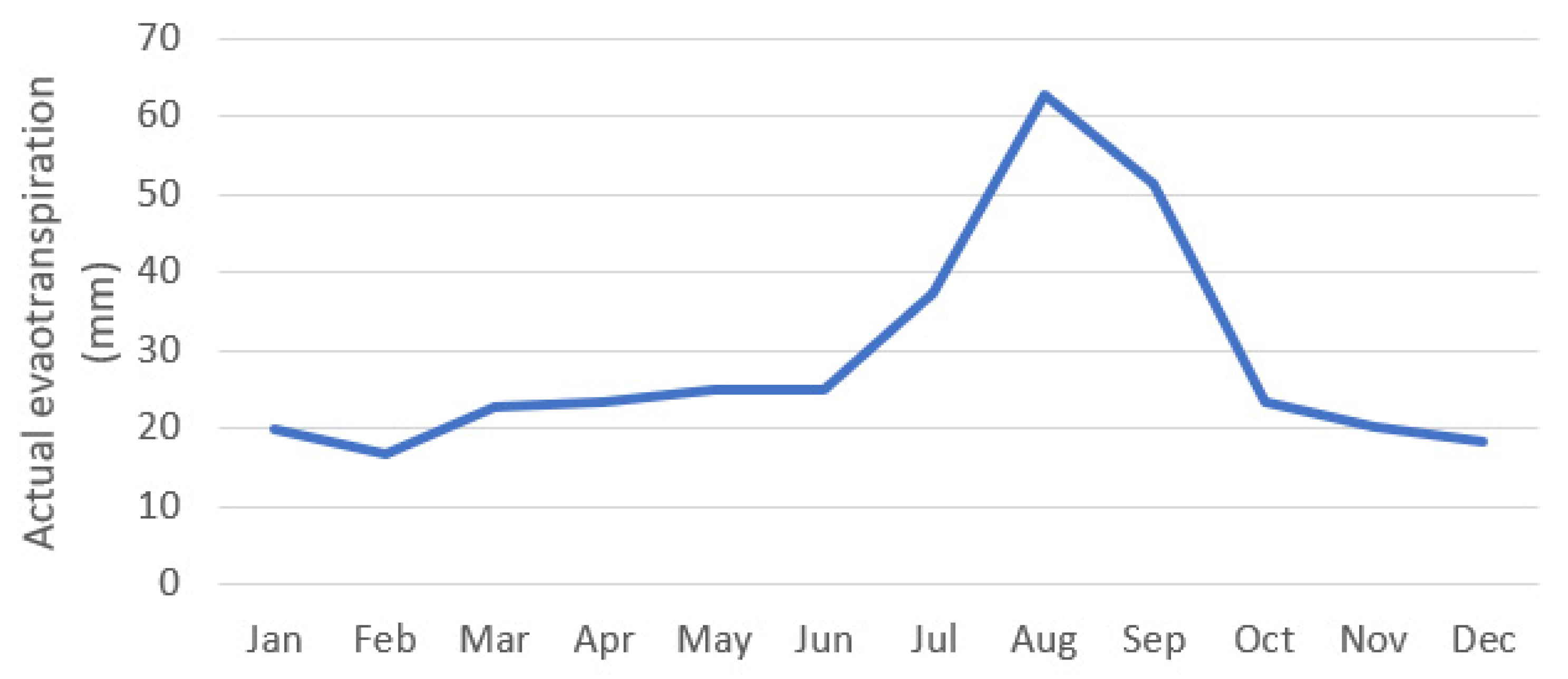
2.3. Hydrological Modeling of Tekeze River Basin (TRB)
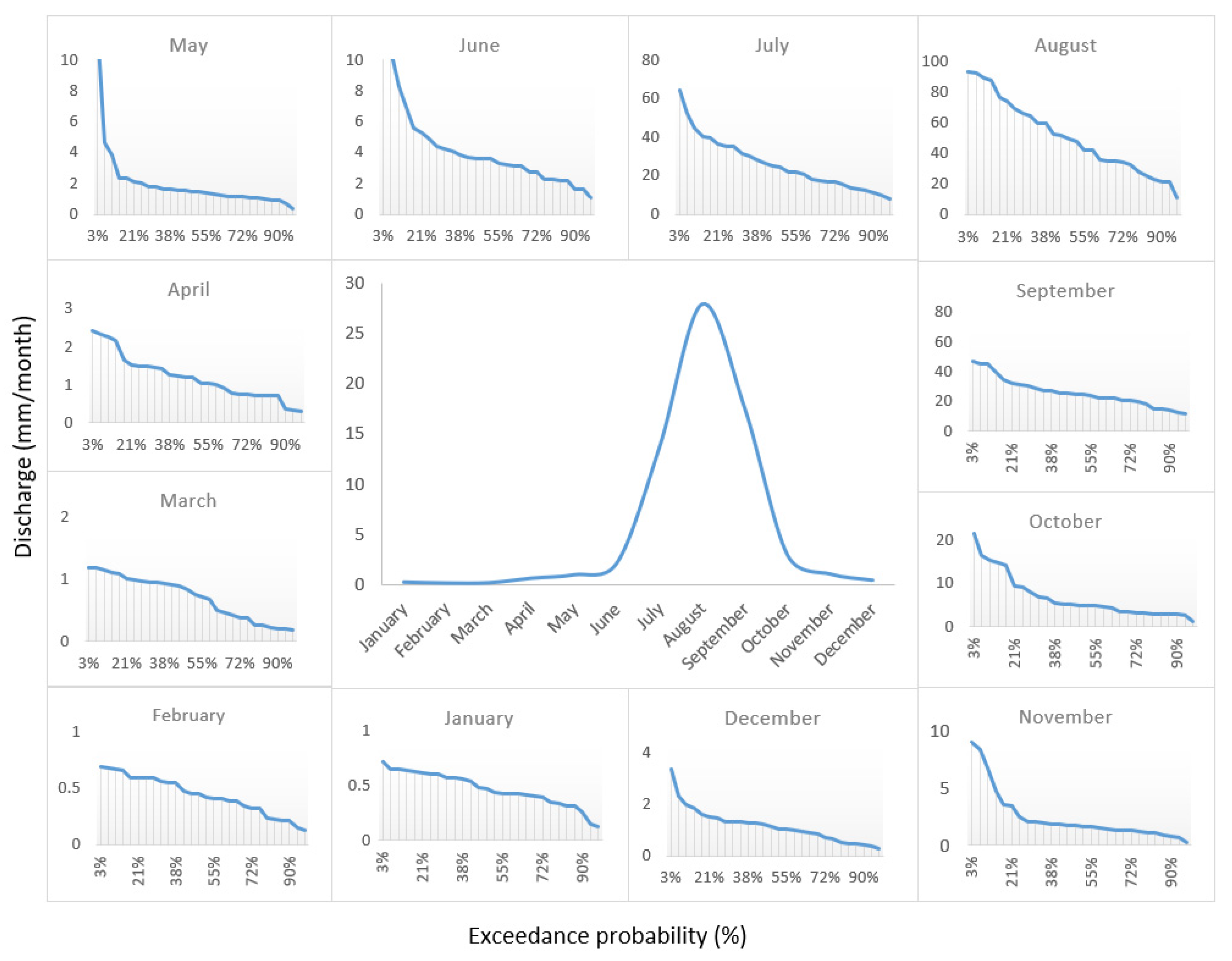
2.4. Selection of a Threshold
2.5. Deriving Monthly Drought Thresholds
3. Results and Discussion
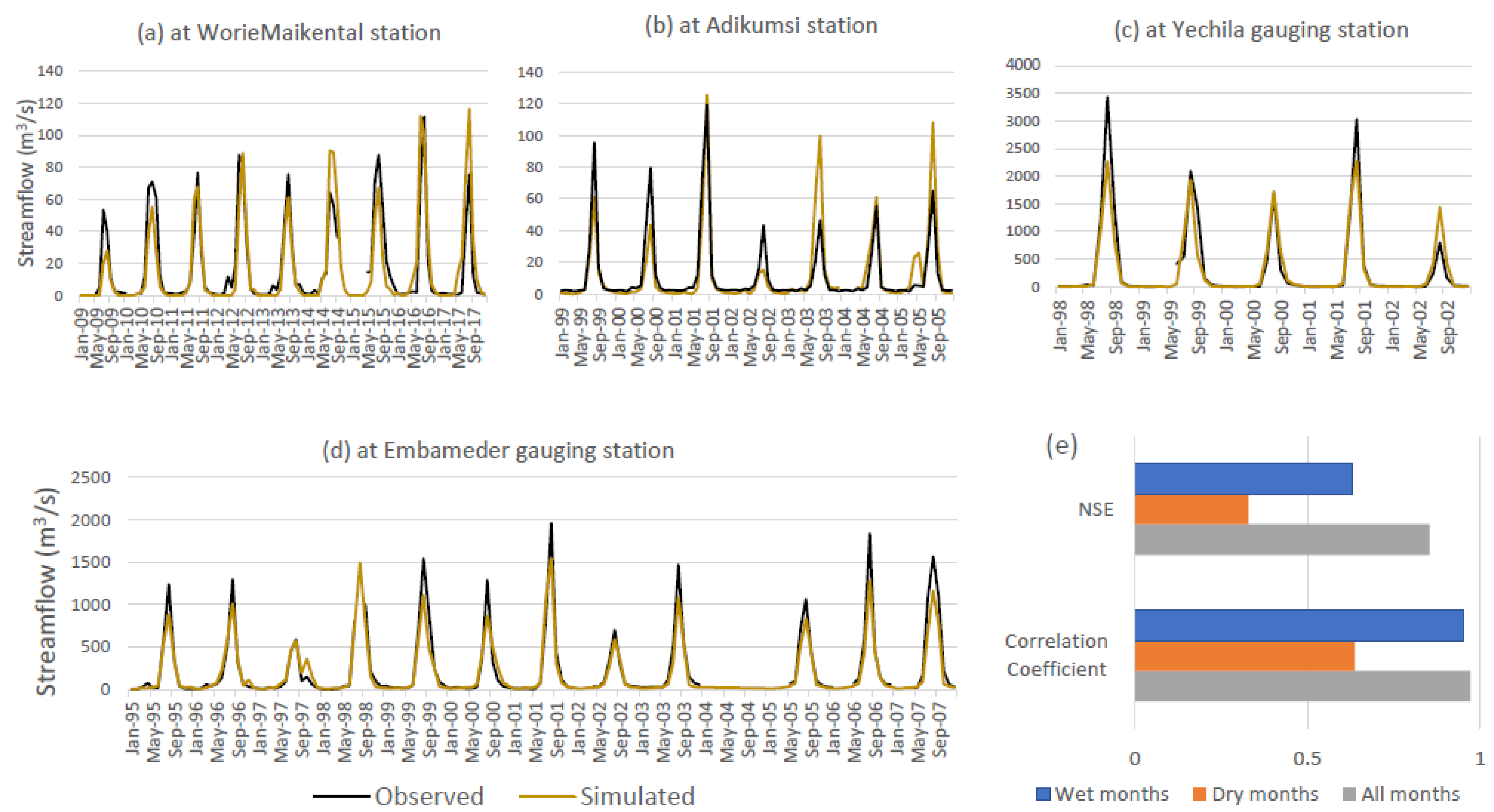
3.1. Calibration and Validation of Streamflow in TRB
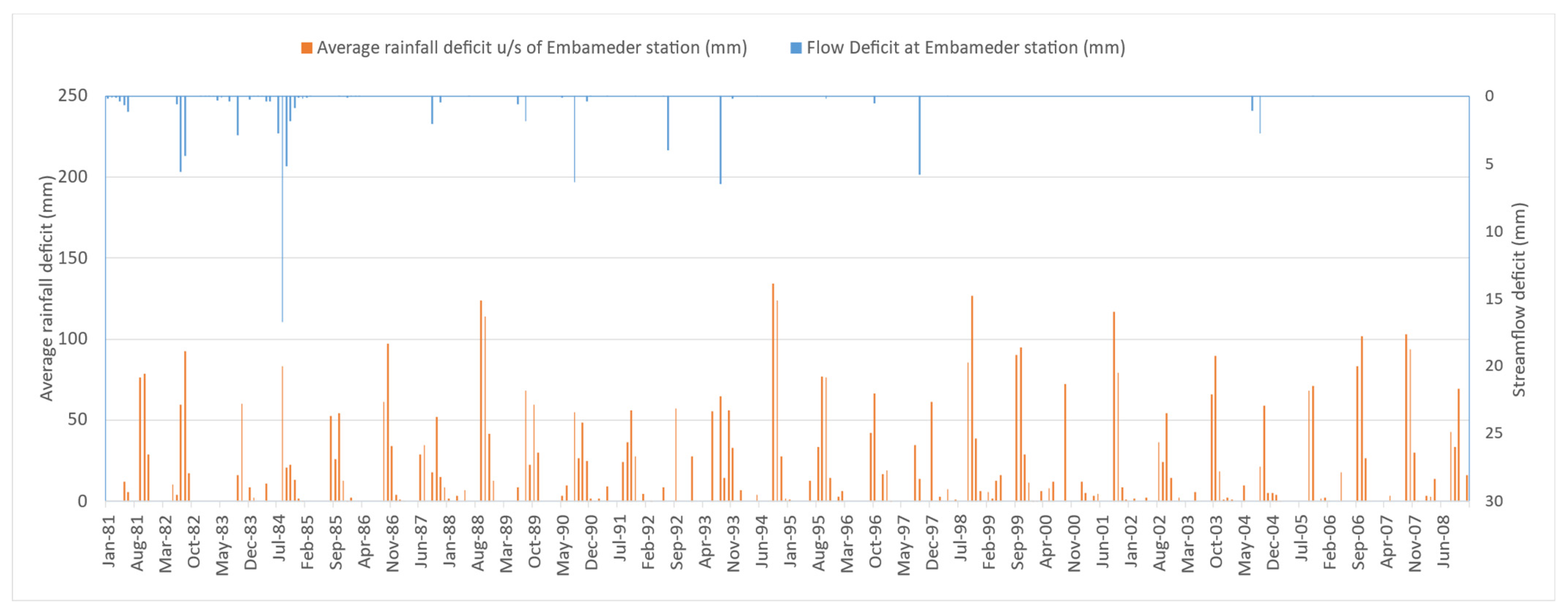
3.2. Duration and Magnitude of Drought
3.3. Drought Typology
3.4. Hydrological Drought in the Post-Impact Period
4. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EM-DAT. CRED/UCLouvain, Brussels, Belgium. Available online: www.emdat.be (accessed on 26 October 2021).
- Zhang, R.; Chen, Z.; Xu, L.-J.; Ou, C.-Q. Meteorological drought forecasting based on a statistical model with machine learning techniques in Shaanxi province, China. Sci. Total Environ. 2019, 665, 338–346. [Google Scholar] [CrossRef] [PubMed]
- Rhee, J.; Im, J. Meteorological drought forecasting for ungauged areas based on machine learning: Using long-range climate forecast and remote sensing data. Agric. For. Meteorol. 2017, 237, 105–122. [Google Scholar] [CrossRef]
- Wang, W.; Ertsen, M.W.; Svoboda, M.D.; Hafeez, M. Propagation of Drought: From Meteorological Drought to Agricultural and Hydrological Drought. Adv. Meteorol. 2016, 2016, 6547209. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Gober, P.; Wheater, H.S. Debates-Perspectives on socio-hydrology: Modeling flood risk as a public policy problem. Water Resour. Res. 2015, 51, 4782–4788. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Stahl, K.; Di Baldassarre, G.; Clark, J.; Rangecroft, S.; Wanders, N.; Gleeson, T.; Van Dijk, A.I.J.M.; Tallaksen, L.M.; Hannaford, J.; et al. Drought in a human-modified world: Reframing drought definitions, understanding, and analysis approaches. Hydrol. Earth Syst. Sci. 2016, 20, 3631–3650. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, V.; Sanderson, M.; Garcia, M.; Konar, M.; Blöschl, G.; Sivapalan, M. Prediction in a so-cio-hydrological world. Hydrol. Sci. J. 2017, 62, 338–345. [Google Scholar]
- Gómez, C.M.G.; Blanco, C.D.P. Do drought management plans reduce drought risk? A risk assessment model for a Mediterranean river basin. Ecol. Econ. 2012, 76, 42–48. [Google Scholar] [CrossRef]
- Apurv, T.; Cai, X. Drought Propagation in Contiguous U.S. Watersheds: A Process-Based Understanding of the Role of Climate and Watershed Properties. Water Resour. Res. 2020, 56, e2020WR027755. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Rangecroft, S.; Coxon, G.; Naranjo, J.A.B.; Van Ogtrop, F.; Van Lanen, H.A.J. Using paired catchments to quantify the human influence on hydrological droughts. Hydrol. Earth Syst. Sci. 2019, 23, 1725–1739. [Google Scholar] [CrossRef] [Green Version]
- Destouni, G.; Jaramillo, F.; Prieto, C. Hydroclimatic shifts driven by human water use for food and energy production. Nat. Clim. Chang. 2013, 3, 213–217. [Google Scholar] [CrossRef]
- Rangecroft, S.; Van Loon, A.F.; Maureira, H.; Verbist, K.; Hannah, D.M. An observation-based method to quantify the human influence on hydrological drought: Upstream–downstream comparison. Hydrol. Sci. J. 2019, 64, 276–287. [Google Scholar] [CrossRef] [Green Version]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.M.; Lopez-Moreno, I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Accurate Computation of a Streamflow Drought Index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef] [Green Version]
- Van Loon, A.F. On the Propagation of Drought: How Climate and Catchment Characteristics Influence Hydrological Drought Development and Recovery; Wageningen University and Research: Wageningen, The Netherlands, 2013. [Google Scholar]
- Sung, J.H.; Chung, E.S. Development of streamflow drought severity–duration–frequency curves us-ing the threshold level method. Hydrol. Earth Syst. Sci. 2014, 18, 3341–3351. [Google Scholar] [CrossRef] [Green Version]
- Yevjevich, V.M. Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts. Doctoral Dissertation, Colorado State University, Fort Collins, CO, USA, 1967. [Google Scholar]
- Belete, K. Sedimentation and Sediment Handling at Dams in Tekeze River Basin, Ethiopia. Doctoral Dissertation, Norwegian University of Science and Technology, Trondheim, Norway, 2007. [Google Scholar]
- Annys, S.; Ghebreyohannes, T.; Nyssen, J. Impact of Hydropower Dam Operation and Management on Downstream Hydrogeomorphology in Semi-Arid Environments (Tekeze, Northern Ethiopia). Water 2020, 12, 2237. [Google Scholar] [CrossRef]
- Smakhtin, V. Low flow hydrology: A review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models’ part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Van Lanen, H.A. (Eds.) Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Van Loon, A.F.; Van Lanen, H.A.J. A process-based typology of hydrological drought. Hydrol. Earth Syst. Sci. 2012, 16, 1915–1946. [Google Scholar] [CrossRef] [Green Version]
- Rees, G.; Marsh, T.J.; Roald, L.; Demuth, S.; Van Lanen, H.A.J.; Kasparek, L. Hydrological data. In Hydrological Drought. Processes and Estimation Methods for Streamflow and Groundwater; Elsevier: Amsterdam, The Netherlands, 2004; pp. 99–138. [Google Scholar]
- Araya, A.; Stroosnijder, L. Assessing drought risk and irrigation need in northern Ethiopia. Agric. For. Meteorol. 2011, 151, 425–436. [Google Scholar] [CrossRef]
- Hengsdijk, H.; Meijerink, G.; Mosugu, M. Modeling the effect of three soil and water conservation practices in Tigray, Ethiopia. Agric. Ecosyst. Environ. 2005, 105, 29–40. [Google Scholar] [CrossRef]




| Name of Sub-Basin | Area (km2) | Forest | Woodland | Shrub/Bush | Cropland | Grassland | Barrenland | Water Body | Afroalpine | Built-Up |
|---|---|---|---|---|---|---|---|---|---|---|
| Tekeze Humera | 11,422.77 | 1.40% | 15.61% | 38.00% | 18.20% | 23.94% | 2.74% | 0.01% | 0.00% | 0.09% |
| Gheba | 5,008.57 | 2.65% | 5.05% | 28.78% | 43.85% | 5.38% | 12.90% | 0.11% | 0.00% | 1.28% |
| Zarema | 2,277.20 | 4.23% | 19.36% | 29.51% | 18.14% | 19.85% | 8.85% | 0.00% | 0.00% | 0.06% |
| Tekeze US TK2 | 10,940.97 | 4.01% | 13.57% | 32.41% | 33.94% | 5.14% | 10.30% | 0.02% | 0.32% | 0.29% |
| Tekeze TK1 | 7,199.85 | 3.49% | 11.49% | 15.46% | 22.40% | 4.98% | 38.18% | 1.40% | 2.58% | 0.03% |
| Angereb Gwany | 21,625.93 | 1.35% | 23.02% | 33.57% | 23.70% | 13.94% | 4.33% | 0.00% | 0.00% | 0.10% |
| Mena | 6,174.08 | 2.39% | 4.76% | 15.05% | 49.07% | 7.46% | 19.76% | 0.00% | 1.13% | 0.38% |
| Tirare | 7,419.70 | 3.97% | 9.32% | 15.67% | 38.10% | 4.66% | 27.52% | 0.39% | 0.25% | 0.13% |
| Kechen Abeba | 11,224.66 | 3.43% | 14.03% | 23.16% | 32.22% | 5.83% | 20.01% | 0.00% | 1.22% | 0.10% |
| Precipitation Deficit at Gauges Upstream of Embameder Station (Depth, mm) | Flow Deficit Embameder (Depth, mm) | |||
|---|---|---|---|---|
| Year | Kechenabeba | Tirare | Tekeze-TK1 | |
| 1983 | 101.21 | 76.01 | 67.70 | 2.89 |
| 1984 | 73.23 | 64.46 | 69.85 | 5.20 |
| 1987 | 99.99 | 74.22 | 84.50 | 2.04 |
| 1997 | 102.47 | 78.17 | 110.89 | 5.79 |
| 2004 | 85.74 | 98.14 | 97.93 | 2.78 |
| Precipitation Deficit at Gauges Upstream of Embameder Station (Depth, mm) | Flow Deficit Embameder (Depth, mm) | |||
|---|---|---|---|---|
| Year | Kechenabeba | Tirare | Tekeze-TK1 | |
| 1982 | 1.53 | 13.65 | 0 | 4.45 |
| 1984 | 139.74 | 32.83 | 73.84 | 16.72 |
| 1989 | 21.10 | 12.59 | 8.31 | 1.87 |
| 1990 | 43.37 | 35.79 | 35.14 | 6.35 |
| 1993 | 79.61 | 5.79 | 20.30 | 6.49 |
| Dry Period | ||
| Month (2009–2015) | Deviation (mm, Human-Influenced) | Deviation (mm, Naturalized) |
| January | 87.76 | 1.86 |
| February | 100.16 | 2.54 |
| March | 115.95 | 6.47 |
| April | 106.31 | 3.64 |
| May | 124.31 | 7.72 |
| June | 111.71 | 12.83 |
| October | 73.54 | 23.10 |
| November | 79.31 | 18.84 |
| December | 76.90 | 5.80 |
| Total | 875.96 | 82.8 |
| Wet Period | ||
| Month (2009–2015) | Deviation (mm, Human-Influenced) | Deviation (mm, Naturalized) |
| July | 107.53 | 89.72 |
| August | 151.28 | 222.26 |
| September | 60.95 | 104.72 |
| Total | 319.75 | 416.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeleke, E.B.; Melesse, A.M.; Kidanewold, B.B. Assessment of Climate and Catchment Control on Drought Propagation in the Tekeze River Basin, Ethiopia. Water 2022, 14, 1564. https://doi.org/10.3390/w14101564
Zeleke EB, Melesse AM, Kidanewold BB. Assessment of Climate and Catchment Control on Drought Propagation in the Tekeze River Basin, Ethiopia. Water. 2022; 14(10):1564. https://doi.org/10.3390/w14101564
Chicago/Turabian StyleZeleke, Ethiopia Bisrat, Assefa M. Melesse, and Belete Berhanu Kidanewold. 2022. "Assessment of Climate and Catchment Control on Drought Propagation in the Tekeze River Basin, Ethiopia" Water 14, no. 10: 1564. https://doi.org/10.3390/w14101564







