Frequency Analysis of the Nonstationary Annual Runoff Series Using the Mechanism-Based Reconstruction Method
Abstract
:1. Introduction
2. Methodology
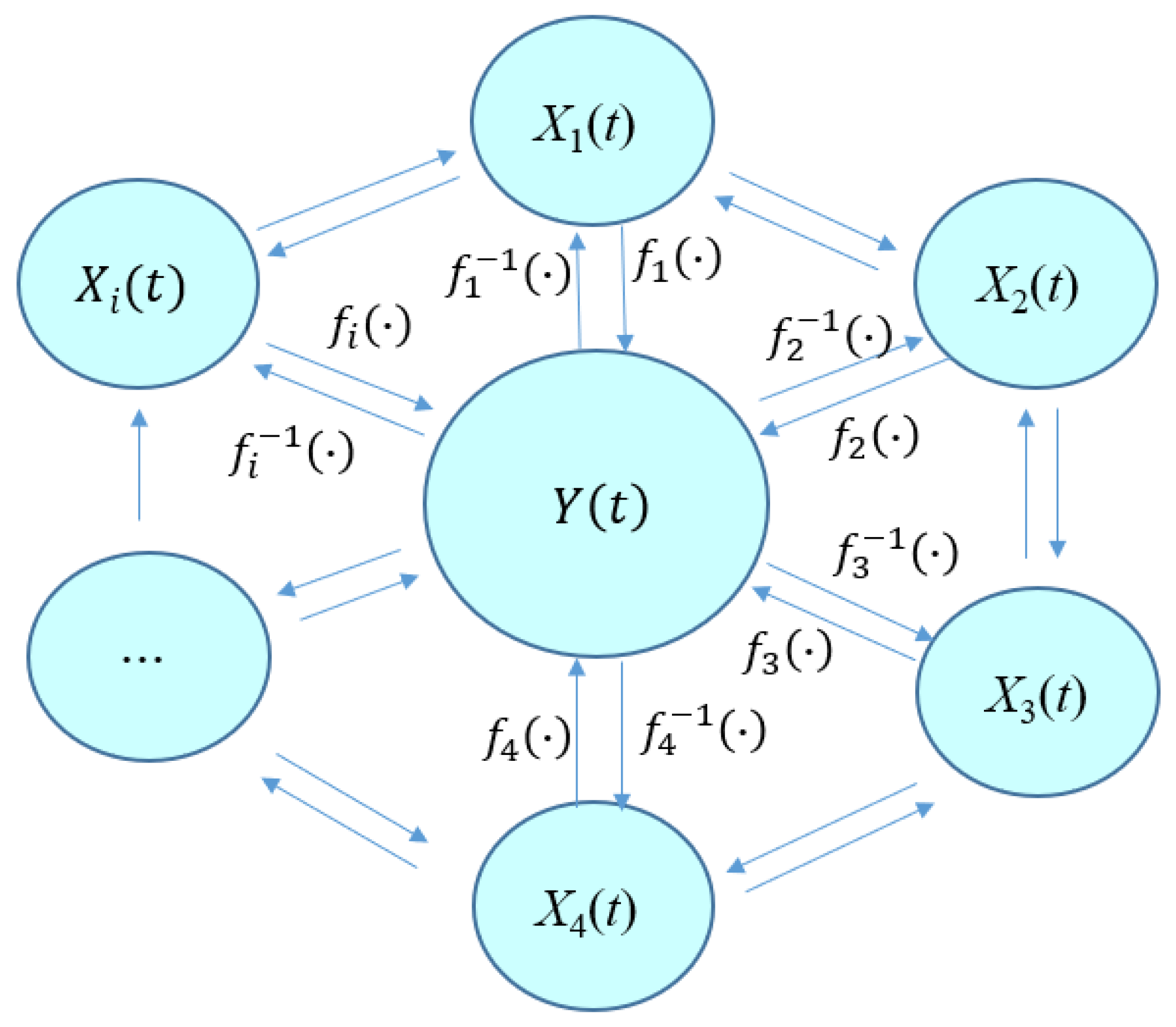
2.1. Me-RS Method
2.2. Frequency Analysis of Nonstationary Annual Runoff Series
2.3. Uncertainty Analysis Using the Bootstrap Method
2.4. Nonstationary Analysis
3. Study Area and Data
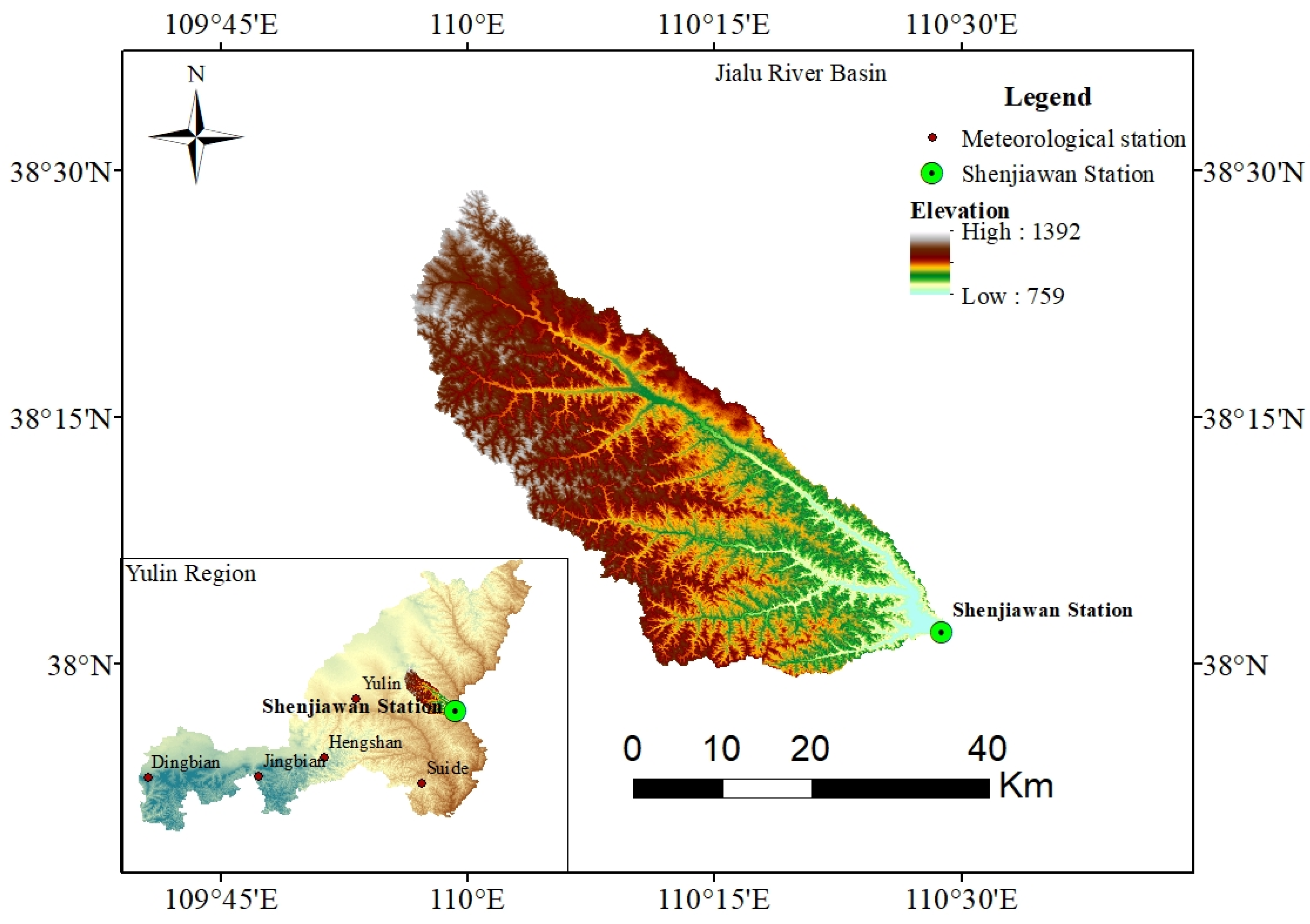
3.1. Study Area
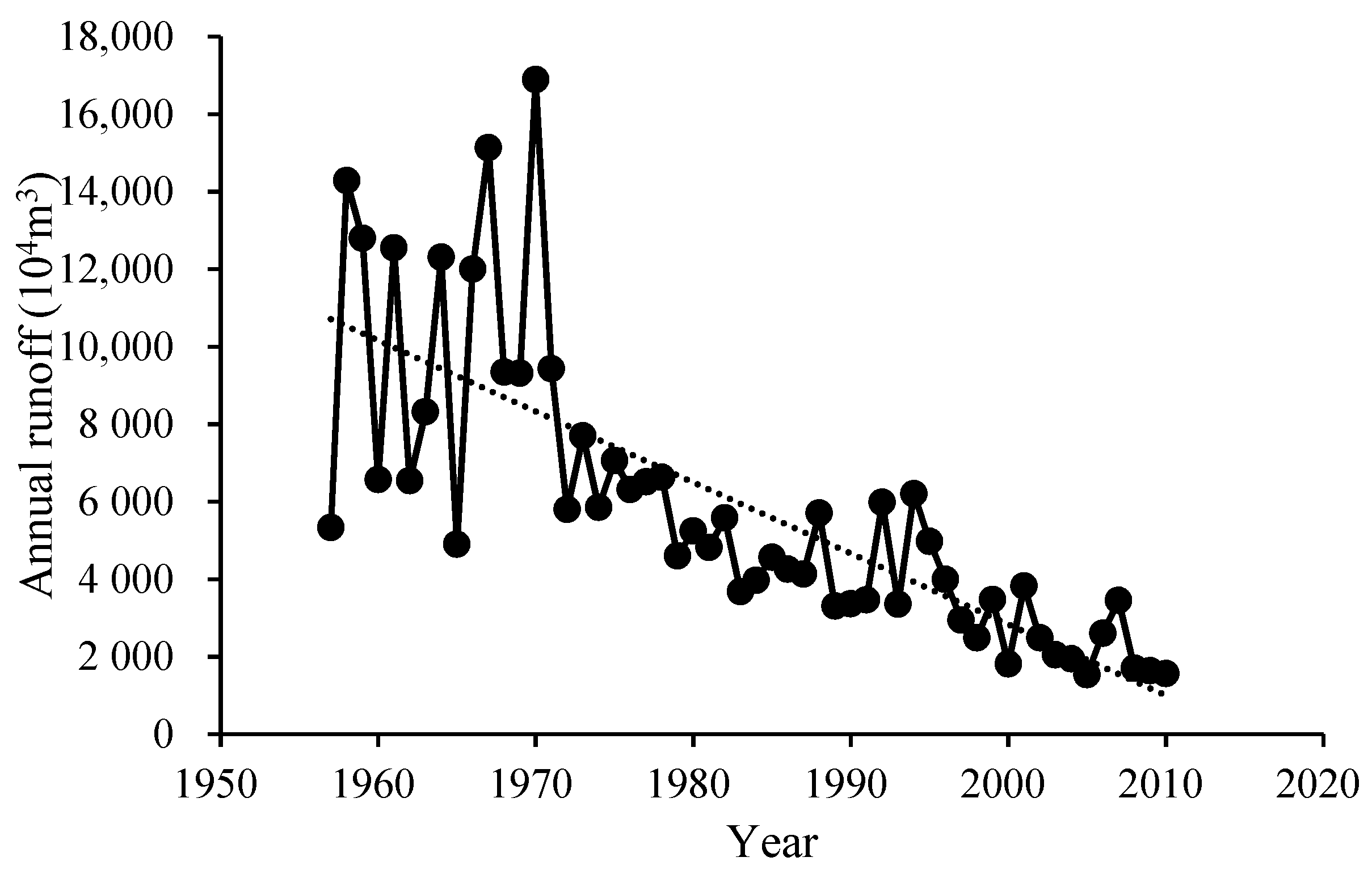
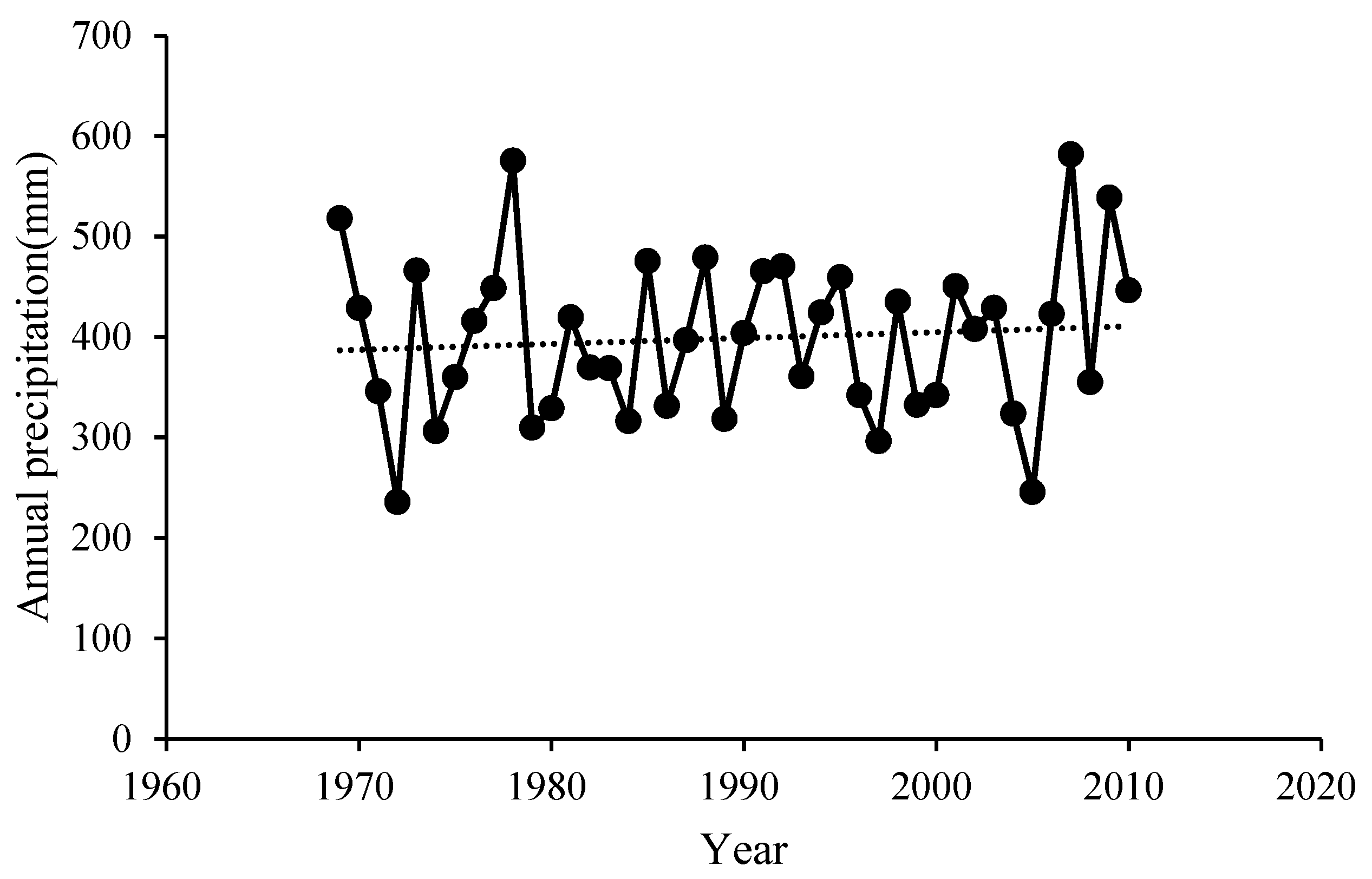
3.2. Data
4. Reconstruction of the Annual Runoff Series
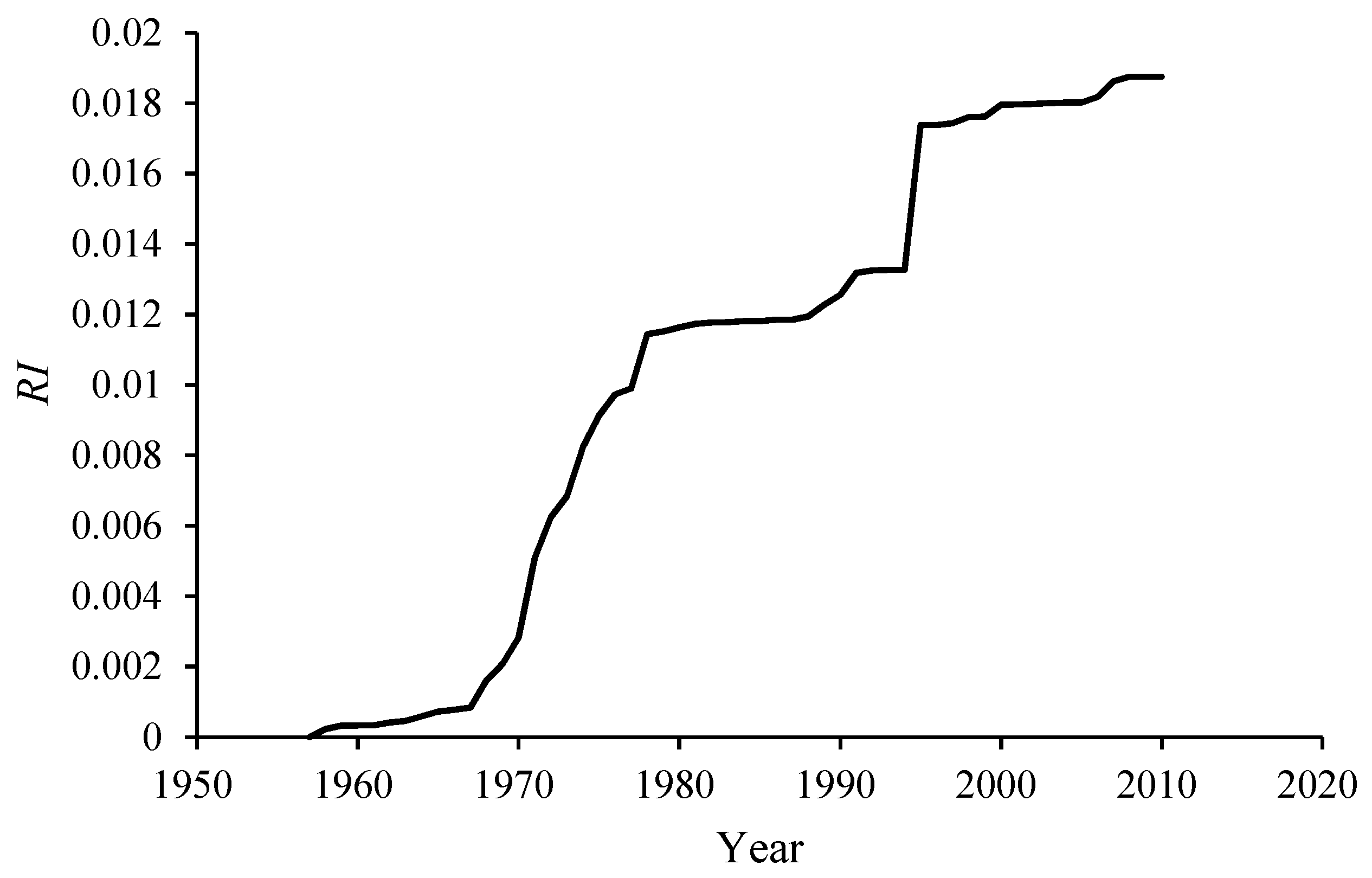
4.1. The Mechanism Function of RI
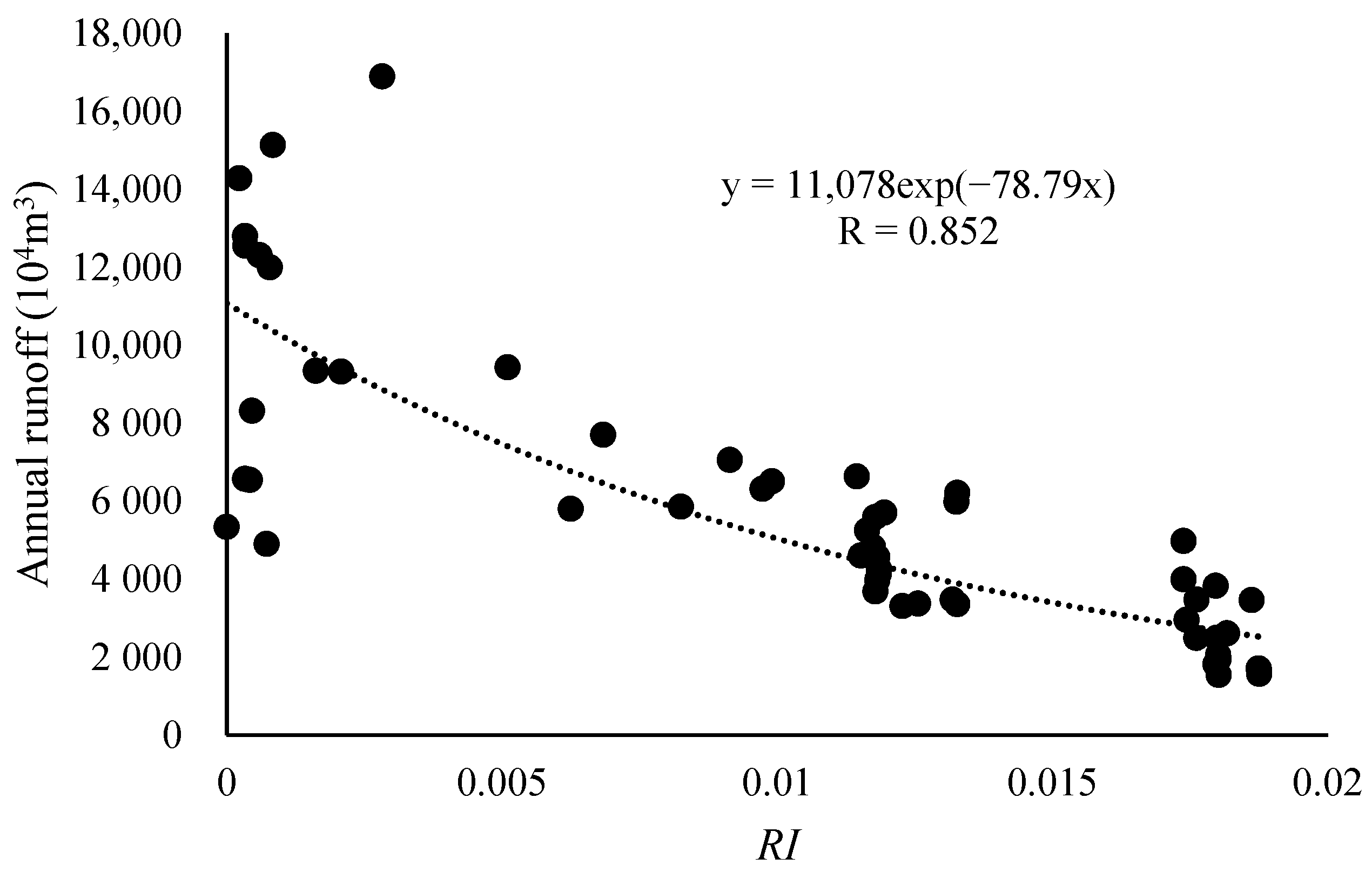
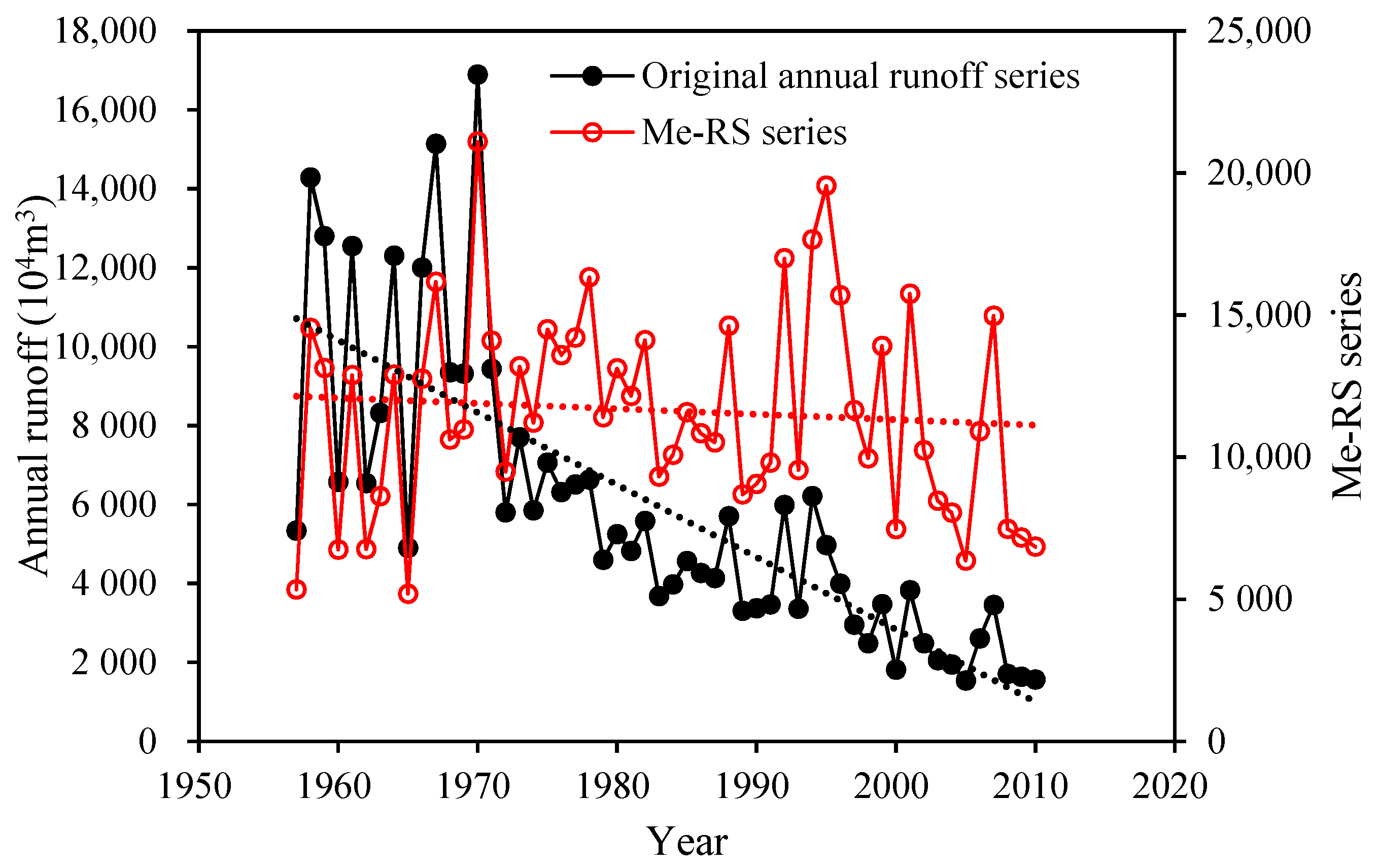
4.2. The Me-RS Function and the Me-RS Series
5. Frequency Analysis of the Annual Runoff Series
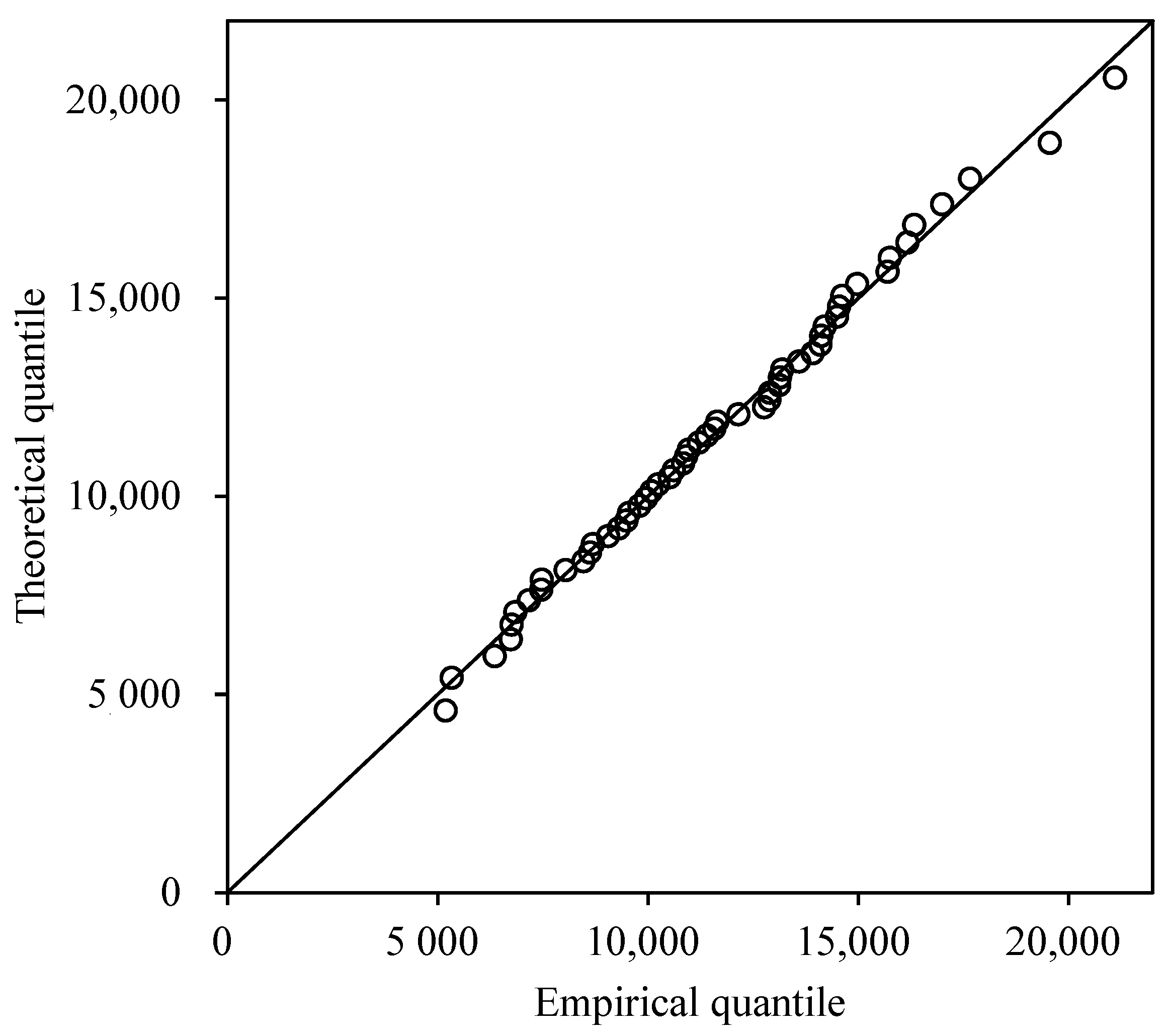
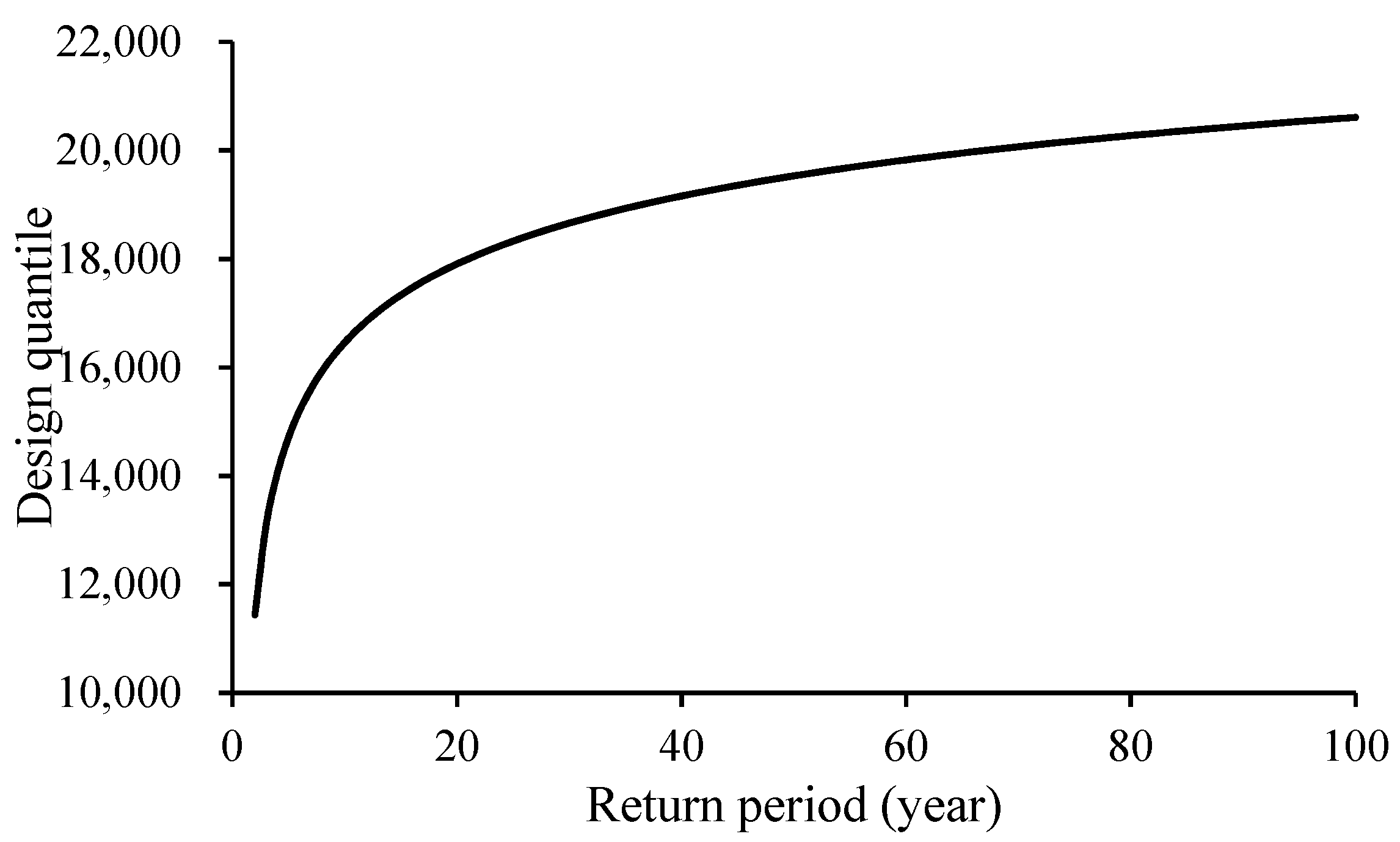
5.1. Calculation of the Design Value of the Me-RS Series
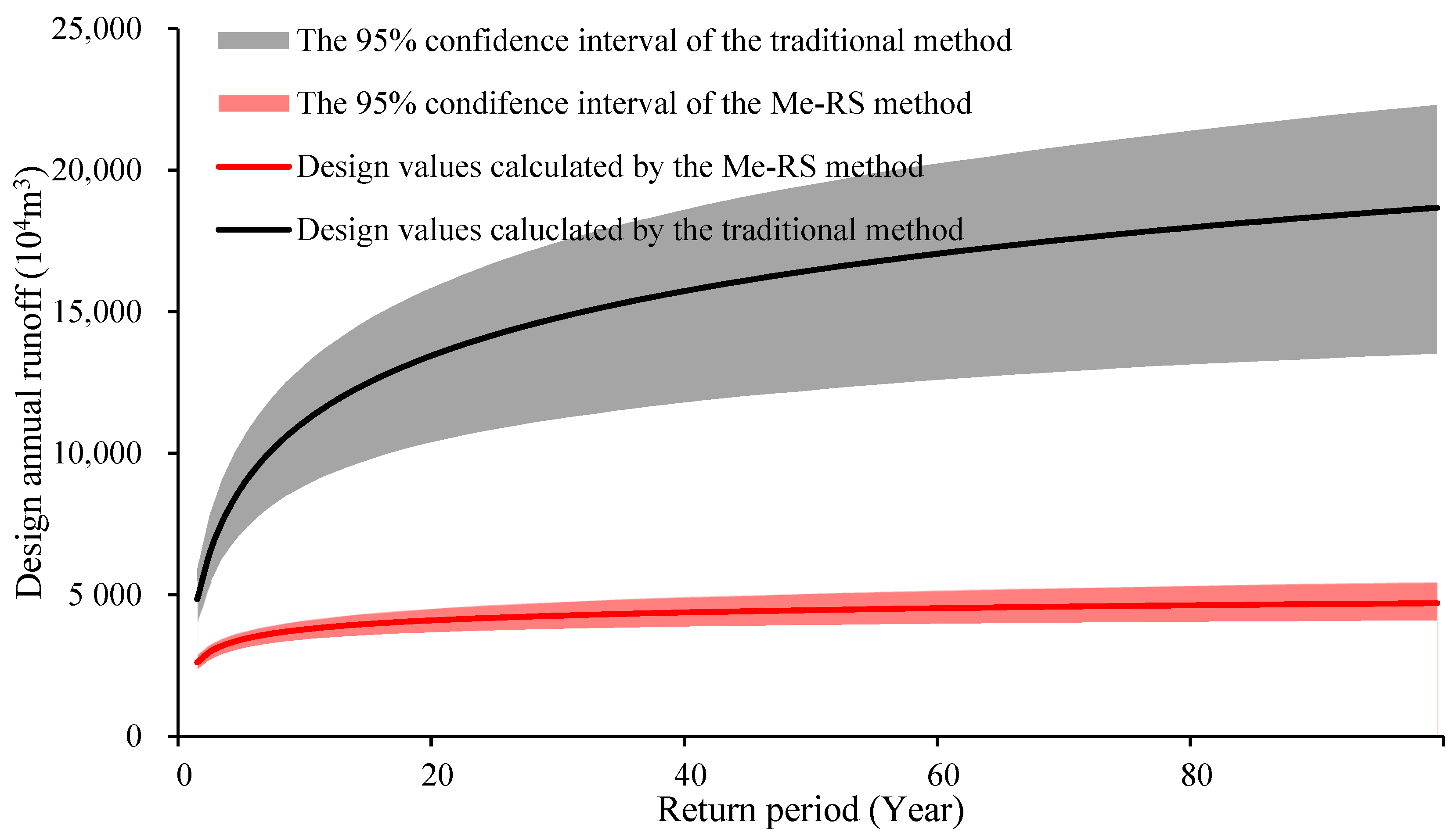
5.2. Calculation of the Design Annual Runoff
6. Discussion
6.1. Rationality Analysis of the Design Annual Runoff
6.2. Comparison with the Traditional Frequency Analysis Method
6.3. Application Problem of the Me-RS Method
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, S.; Qin, Y.; Song, X.; Bai, S.; Liu, Y. Nonstationary frequency analysis of the Weihe River annual runoff series using de-nonstationarity method. J. Hydrol. Eng. 2021, 26, 04021034. [Google Scholar] [CrossRef]
- Zhang, Q.; Singh, V.P.; Sun, P.; Chen, X.; Zhang, Z.; Li, J. Precipitation and streamflow changes in China: Changing patterns causes and implications. J. Hydrol. 2011, 410, 204–216. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Singh, V.P.; Feluch, W. Non-stationary approach to at-site flood frequency modelling I. Maximum likelihood estimation. J. Hydrol. 2001, 248, 123–142. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Kaczmarek, Z.; Feluch, W. Non-stationary approach to at-site flood frequency modelling II. Weighted least squares estimation. J. Hydrol. 2001, 248, 143–151. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Singh, V.P.; Mitosek, H.T. Non-stationary approach to at-site flood frequency modelling III. Flood analysis of Polish rivers. J. Hydrol. 2001, 248, 152–167. [Google Scholar] [CrossRef]
- Vogel, R.M.; Yaindl, C.; Walter, M. Nonstationarity: Flood magnification and recurrence reduction factors in the United States. J. Am. Water Resour. Assoc. 2011, 47, 464–474. [Google Scholar] [CrossRef]
- Zeng, H.; Feng, P.; Li, X. Reservoir flood routing considering the non-stationarity of flood series in north China. Water Resour. Manag. 2014, 28, 4273–4287. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C 2005, 54, 507–544. [Google Scholar] [CrossRef] [Green Version]
- López, J.; Francés, F. Non-stationary flood frequency analysis in continental Spanish rivers, using climate and reservoir indices as external covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef] [Green Version]
- Xiong, L.; Jiang, C.; Du, T. Statistical attribution analysis of the nonstationarity of the annual runoff series of the Weihe River. Water Sci. Technol. 2014, 70, 939–946. [Google Scholar] [CrossRef] [PubMed]
- Salas, J.D.; Obeyskekera, J. Revisiting the concepts of return period and risk for non-stationary hydrologic extreme events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef] [Green Version]
- Yan, L.; Xiong, L.; Guo, S.; Xu, C.Y.; Xia, J.; Du, T. Comparison of four nonstationary hydrologic design methods for changing environment. J. Hydrol. 2017, 551, 132–150. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Bales, J.; Bates, P.D.; Krajewski, W.F. Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Adv. Water Resour. 2009, 32, 1255–1266. [Google Scholar] [CrossRef]
- Olsen, J.R.; Lambert, J.H.; Haimes, Y.Y. Risk of extreme events under nonstationary conditions. Risk Anal. 1998, 18, 497–510. [Google Scholar] [CrossRef]
- Wigley, T.M.L. The effect of changing climate on the frequency of absolute extreme events. Clim. Change 2009, 97, 67–76. [Google Scholar] [CrossRef]
- Parey, S.; Malek, F.; Laurent, C.; Dacunha-Castelle, D. Trends and climate evolution: Statistical approach for very high temperatures in France. Clim. Change 2007, 81, 331–352. [Google Scholar] [CrossRef] [Green Version]
- Parey, S.; Hoang, T.T.H.; Dacunha-Castelle, D. Different ways to compute temperature return levels in the climate change context. Environmetrics 2010, 21, 698–718. [Google Scholar] [CrossRef]
- Hu, Y.; Liang, Z.; Singh, V.P.; Zhang, X.; Wang, J.; Li, B.; Wang, H. Concept of equivalent reliability for estimating the design flood under non-stationary conditions. Water Resour. Manag. 2018, 32, 997–1011. [Google Scholar] [CrossRef]
- Rootzén, H.; Katz, R.W. Design Life Level: Quantifying risk in a changing climate. Water Resour. Res. 2013, 49, 5964–5972. [Google Scholar] [CrossRef] [Green Version]
- Read, L.K.; Vogel, R.M. Reliability, return periods, and risk under nonstationarity. Water Resour. Res. 2015, 51, 6381–6398. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Computer experiments with fractional gaussian noises: Part 1, averages and variances. Water Resour. Res. 1969, 5, 228–241. [Google Scholar] [CrossRef]
- Lins, H.F.; Cohn, T.A. Stationarity: Wanted dead or alive. J. Am. Water Resour. Assoc. 2011, 47, 475–480. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Stationarity is undead: Uncertainty dominates the distribution of extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.; Li, S. Study on mechanism-based reconstruction method to cope with the nonstationary change of hydrological series. J. Hydraul. Eng. 2021, 52, 807–818. (In Chinese) [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Breusch, T.S.; Pagan, A.R. A simple test for heteroscedasticity and random coefficient variation. Econometrica 1979, 47, 1287–1294. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Kolmogorov-Smirnov, A.N.; Kolmogorov, A.; Kolmogorov, M. Sulla determinazione empírica di una legge di distribuzione. G. Institto Ital. Attuari 1933, 4, 83–91. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
| Object | M-K Test for Mean | B-P Test for Variance | Pettitt Test for Change Point | |||
|---|---|---|---|---|---|---|
| Z | Change-Point | p-Value | ||||
| Annual runoff series | −7.49 | 1.96 | 23.27 | 3.84 | 1982 | 6.80 × 10−8 |
| Annual precipitation series | 0.50 | 1.96 | 0.01 | 3.84 | - | - |
| Object | M-K Test for Mean | B-P Test for Variance | Pettitt Test for Change Point | |||
|---|---|---|---|---|---|---|
| Z | Change-Point | p-Value | ||||
| Annual runoff series | −7.49 | 1.96 | 23.27 | 3.84 | 1982 | 6.80 × 10−8 |
| Me-RS series | −0.97 | 1.96 | 0.12 | 3.84 | - | - |
| Distribution | Probability Density Function |
|---|---|
| P-III | |
| WEI | |
| LNO | |
| GU |
| Object | Optimal Distribution | Estimated Parameters |
|---|---|---|
| Me-RS series RSRI,t | WEI |
| Object | Optimal Distribution | Estimated Parameters |
|---|---|---|
| Annual runoff series Rt | WEI |
| Method | Design Value (Width of 95% Confidence Intervals)/104 m3 | ||
|---|---|---|---|
| Frequency of 20% | Frequency of 50% | Frequency of 80% | |
| Me-RS method | 3357.52 (571.35) | 2610.38 (514.76) | 1920.62 (450.62) |
| Traditional method | 8442.30 (3124.45) | 4845.28 (1866.65) | 2734.43 (1133.84) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Qin, Y. Frequency Analysis of the Nonstationary Annual Runoff Series Using the Mechanism-Based Reconstruction Method. Water 2022, 14, 76. https://doi.org/10.3390/w14010076
Li S, Qin Y. Frequency Analysis of the Nonstationary Annual Runoff Series Using the Mechanism-Based Reconstruction Method. Water. 2022; 14(1):76. https://doi.org/10.3390/w14010076
Chicago/Turabian StyleLi, Shi, and Yi Qin. 2022. "Frequency Analysis of the Nonstationary Annual Runoff Series Using the Mechanism-Based Reconstruction Method" Water 14, no. 1: 76. https://doi.org/10.3390/w14010076
APA StyleLi, S., & Qin, Y. (2022). Frequency Analysis of the Nonstationary Annual Runoff Series Using the Mechanism-Based Reconstruction Method. Water, 14(1), 76. https://doi.org/10.3390/w14010076






